Estimation of the Edge Crush Resistance of Corrugated Board Using Artificial Intelligence
Abstract
1. Introduction
2. Materials and Methods
2.1. Paperboard and Cardboard Laboratory Tests

2.2. Artificial Neural Networks–Training Data
2.3. Gaussian Processes
- Be symmetrical. That means that ;
- Be positively defined. That means that the kernel matrix induced by for any set of inputs should be a positive definite matrix.
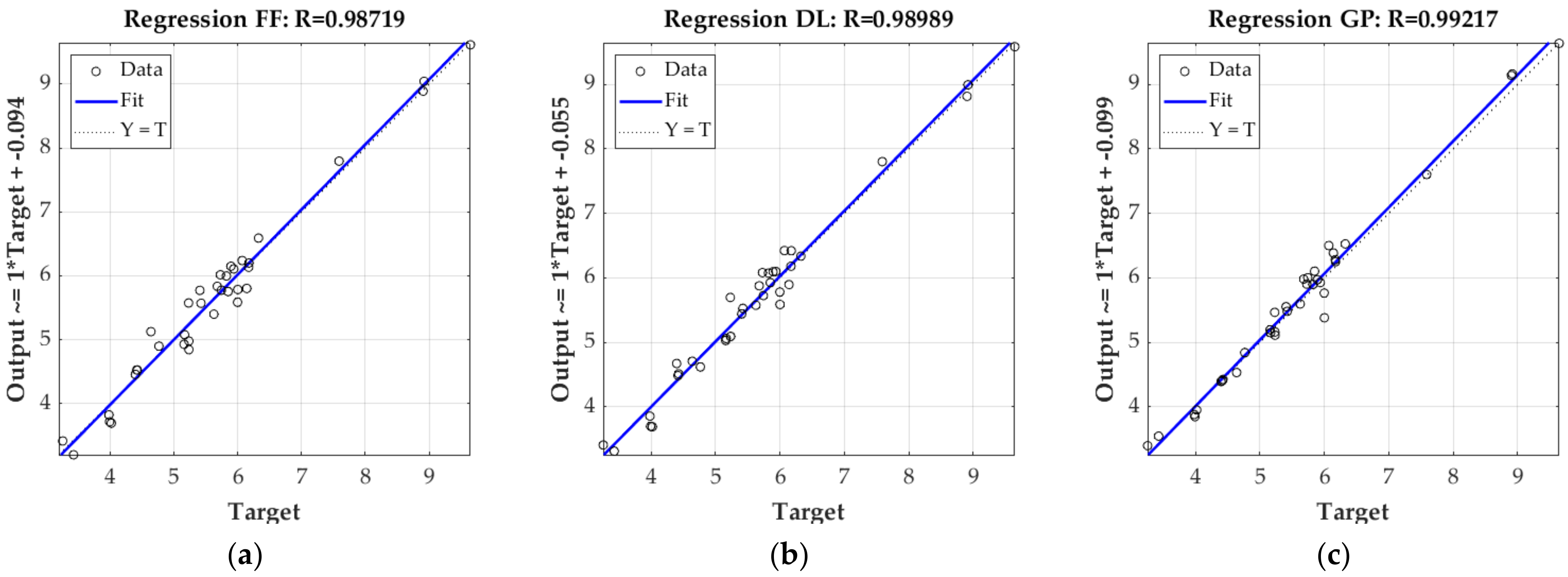
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of the finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
- Kellicutt, K.; Landt, E. Development of design data for corrugated fibreboard shipping containers. Tappi 1952, 35, 398–402. [Google Scholar]
- Gallo, J.; Cortés, F.; Alberdi, E.; Goti, A. Mechanical behavior modeling of containers and octabins made of corrugated cardboard subjected to vertical stacking loads. Materials 2021, 14, 2392. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Park, M.; Choi, D.S.; Jung, H.M.; Hwang, S.W. Finite element-based simulation for edgewise compression behavior of corrugated paperboard for packing of agricultural products. Appl. Sci. 2020, 10, 6716. [Google Scholar]
- Suarez, B.; Muneta, L.M.; Romero, G.; Sanz-Bobi, J.D. Efficient design of thin wall seating made of a single piece of heavy-duty corrugated cardboard. Materials 2021, 14, 6645. [Google Scholar] [CrossRef]
- Pereira, T.; Neves, A.S.L.; Silva, F.J.G.; Godina, R.; Morgado, L.; Pinto, G.F.L. Production Process Analysis and Improvement of Corrugated Cardboard Industry. Procedia Manuf. 2020, 51, 1395–1402. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Piątkowska, A.; Mrówczyński, D. Numerical homogenization of multi-layered corrugated cardboard with creasing or perforation. Materials 2021, 14, 3786. [Google Scholar] [CrossRef]
- Gong, G.; Liu, Y.; Fan, B.; Sun, D. Deformation and compressive strength of corrugated cartons under different indentation shapes: Experimental and simulation study. Packag. Technol. Sci. 2020, 33, 215–226. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.J.; Opara, U.L. Compression strength of ventilated corrugated paperboard packages: Numerical modelling, experimental validation and effects of vent geometric design. Biosyst. Eng. 2016, 151, 231–247. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Garbowski, T.; Knitter-Piątkowska, A. Estimation of the compressive strength of corrugated board boxes with shifted creases on the flaps. Materials 2021, 14, 5181. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Gajewski, T.; Knitter-Piątkowska, A. Influence of Analog and Digital Crease Lines on Mechanical Parameters of Corrugated Board and Packaging. Sensors 2022, 22, 4800. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-L.; Chen, J.; Wu, Y.; Sun, J. Analysis of hazard factors of the use of corrugated carton in packaging low-temperature yogurt during logistics. Procedia Environ. Sci. 2011, 10, 968–973. [Google Scholar] [CrossRef]
- Hung, D.; Nakano, Y.; Tanaka, F.; Hamanaka, D.; Uchino, T. Preserving the strength of corrugated cardboard under high humidity condition using nano-sized mists. Compos. Sci. Technol. 2010, 70, 2123–2127. [Google Scholar] [CrossRef]
- Böröcz, P.; Molnár, B. Measurement and analysis of vibration levels in stacked small package shipments in delivery vans as a function of free movement space. Appl. Sci. 2020, 10, 7821. [Google Scholar] [CrossRef]
- Quesenberry, C.; Horvath, L.; Bouldin, J.; White, M.S. The Effect of pallet top deck stiffness on the compression strength of asymmetrically supported corrugated boxes. Packag. Technol. Sci. 2020, 33, 547–558. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Knitter-Piątkowska, A.; Garbowski, T. Non-Local Sensitivity Analysis and Numerical Homogenization in Optimal Design of Single-Wall Corrugated Board Packaging. Materials 2022, 15, 720. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Knitter-Piątkowska, A.; Garbowski, T. Optimal Design of Double-Walled Corrugated Board Packaging. Materials 2022, 15, 2149. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Piątkowska, A. Analytical determination of the bending stiffness of a five-layer corrugated cardboard with imperfections. Materials 2022, 15, 663. [Google Scholar] [CrossRef]
- Czechowski, L.; Kmita-Fudalej, G.; Szewczyk, W.; Gralewski, J.; Bieńkowska, M. Numerical and experimental study of five-layer non-symmetrical paperboard panel stiffness. Materials 2021, 14, 7453. [Google Scholar] [CrossRef]
- McKee, R.C.; Gander, J.W.; Wachuta, J.R. Edgewise compressive strength of corrugated board. Paperboard Packag. 1961, 46, 70–79. [Google Scholar]
- Maltenfort, G. Compression strength of corrugated containers. Fibre Contain 1956, 41, 106–121. [Google Scholar]
- McKee, R.C.; Gander, J.W.; Wachuta, J.R. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various openings. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Urbanik, T.J.; Frank, B. Box compression analysis of world-wide data spanning 46 years. Wood Fiber Sci. 2006, 38, 399–416. [Google Scholar]
- Allerby, I.M.; Laing, G.N.; Cardwell, R.D. Compressive strength—From components to corrugated containers. Appita Conf. Notes 1985, volume, 1–11. [Google Scholar]
- Fehér, L.; Pidl, R.; Böröcz, P. Compression Strength Estimation of Corrugated Board Boxes for a Reduction in Sidewall Surface Cutouts—Experimental and Numerical Approaches. Materials 2023, 16, 597. [Google Scholar] [CrossRef] [PubMed]
- Cillie, J.; Coetzee, C. Experimental and Numerical Investigation of the In-Plane Compression of Corrugated Paperboard Panels. Math. Comput. Appl. 2022, 27, 108. [Google Scholar] [CrossRef]
- Batelka, J.J.; Smith, C.N. Package Compression Model; Institute of Paper Science and Technology: Atlanta, GA, USA, 1993. [Google Scholar]
- Ristinmaa, M.; Ottosen, N.S.; Korin, C. Analytical Prediction of Package Collapse Loads-Basic considerations. Nord. Pulp Pap. Res. J. 2012, 27, 806–813. [Google Scholar] [CrossRef]
- Schrampfer, K.E.; Whitsitt, W.J.; Baum, G.A. Combined Board Edge Crush (ECT) Technology; Institute of Paper Chemistry: Appleton, WI, USA, 1987. [Google Scholar]
- Słonina, M.; Dziurka, D.; Smardzewski, J. Experimental research and numerical analysis of the elastic properties of paper cell cores before and after impregnation. Materials 2020, 13, 2058. [Google Scholar] [CrossRef]
- Kmita-Fudalej, G.; Szewczyk, W.; Kołakowski, Z. Bending Stiffness of Honeycomb Paperboard. Materials 2023, 16, 156. [Google Scholar] [CrossRef] [PubMed]
- Suarez, B.; Muneta, M.L.M.; Sanz-Bobi, J.D.; Romero, G. Application of homogenization approaches to the numerical analysis of seating made of multi-wall corrugated cardboard. Compos. Struct. 2021, 262, 113642. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Gajewski, T.; Garbowski, T. Sensitivity Analysis of Open-Top Cartons in Terms of Compressive Strength Capacity. Materials 2023, 16, 412. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Chang, S.; Jung, H.M. Numerical prediction of equivalent mechanical properties of corrugated paperboard by 3D finite element analysis. Appl. Sci. 2020, 10, 7973. [Google Scholar] [CrossRef]
- Domaneschi, M.; Perego, U.; Borgqvist, E.; Borsari, R. An industry-oriented strategy for the finite element simulation of paperboard creasing and folding. Packag. Technol. Sci. 2017, 30, 269–294. [Google Scholar] [CrossRef]
- Hallbäck, N.; Korin, C.; Barbier, C.; Nygårds, M. Finite element analysis of hot melt adhesive joints in carton board. Packag. Technol. Sci. 2014, 21, 701–712. [Google Scholar] [CrossRef]
- Allaoui, S.; Benzeggagh, M.L.; Aboura, Z.; Talbi, N. Elastic behaviour of corrugated cardboard: Experiments and modeling. Comp. Struct. 2004, 63, 53–62. [Google Scholar]
- Abbès, B.; Guo, Y.Q. Analytic homogenization for torsion of orthotropic sandwich plates. Appl. Comp. Struct. 2010, 92, 699–706. [Google Scholar] [CrossRef]
- Biancolini, M.E. Evaluation of equivalent stiffness properties of corrugated board. Comp. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T. Determination of transverse shear stiffness of sandwich panels with a corrugated core by numerical homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef]
- Frank, B. Corrugated box compression—A literature survey. Packag. Technol. Sci. 2014, 27, 105–128. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Mrówczyński, D.; Jędrzejczak, R. Crushing of Single-Walled Corrugated Board during Converting: Experimental and Numerical Study. Energies 2021, 14, 3203. [Google Scholar] [CrossRef]
- Garbowski, T.; Grabski, J.K.; Marek, A. Full-field measurements in the edge crush test of a corrugated board—Analytical and numerical predictive models. Materials 2021, 14, 2840. [Google Scholar] [CrossRef] [PubMed]
- Gajewski, T.; Garbowski, T.; Staszak, N.; Kuca, M. Crushing of Double-Walled Corrugated Board and Its Influence on the Load Capacity of Various Boxes. Energies 2021, 14, 4321. [Google Scholar] [CrossRef]
- Jamsari, M.A.; Kueh, C.; Gray-Stuart, E.M.; Dahm, K.; Bronlund, J.E. Modelling the impact of crushing on the strength performance of corrugated fibreboard. Packag. Technol. Sci. 2020, 33, 159–170. [Google Scholar] [CrossRef]
- Bai, J.; Wang, J.; Pan, L.; Lu, L.; Lu, G. Quasi-static axial crushing of single wall corrugated paperboard. Compos. Struct. 2019, 226, 111237. [Google Scholar] [CrossRef]
- TAPPI T 839 om-12; Edge Compression Test for Strength of Corrugated Fiberboard Using the Clamp Method (Short Column Test). TAPPI: Peachtree Corners, GA, USA, 2009.
- TAPPI T 811 om-11; Edgewise Compressive Strength of Corrugated Fibreboard (Short Column Test). TAPPI: Peachtree Corners, GA, USA, 2009.
- ISO 13821:2002; Corrugated Fibreboard—Determination of Edgewise Crush Resistance—Waxed Edge Method. ISO: Geneva, Switzerland, 2002.
- TAPPI T 838 cm-12; Edge Crush Test Using Neckdown. TAPPI: Peachtree Corners, GA, USA, 2009.
- FEFCO NO.8; Edgewise Crush Resistance of Corrugated Fiberboard. FEFCO: Brussels, Belgium, 1997.
- ISO 3037:2013; Corrugated Fibreboard—Determination of Edgewise Crush Resistance (Unwaxed Edge Method). ISO: Geneva, Switzerland, 2013.
- Frank, B. Revisiting clamped ECT. Corrugat. Int. 2007, volume, 7–11. [Google Scholar]
- Popil, R.E. Overview of recent studies at IPST on corrugated board edge compression strength: Testing methods and effects of interflute buckling. BioResources 2012, 7, 2553–2581. [Google Scholar] [CrossRef]
- Pidl, R.; Fehér, L.; Böröcz, P. The Effect of Side Wall Cutout Sizes on Corrugated Box Compression Strength in the Function of Length-to-Width Ratios—An Experimental Study. Appl. Sci. 2022, 12, 6939. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Piątkowska, A.; Marek, A. New edge crush test configuration enhanced with full-field strain measurements. Materials 2021, 14, 5768. [Google Scholar] [CrossRef]
- Gurney, K. An Introduction to Neural Networks, 1st ed.; Routledge: London, UK, 1997. [Google Scholar]
- Toraman, S.; Alakus, T.B.; Turkoglu, I. Convolutional capsnet: A novel artificial neural network approach to detect COVID-19 disease from X-ray images using capsule networks. Chaos Solit. Fractals 2020, 140, 110122. [Google Scholar] [CrossRef]
- Zaborowicz, M.; Zaborowicz, K.; Biedziak, B.; Garbowski, T. Deep Learning Neural Modelling as a Precise Method in the Assessment of the Chronological Ageof Children and Adolescents Using Tooth and Bone Parameters. Sensors 2022, 22, 637. [Google Scholar] [CrossRef] [PubMed]
- Chen, J. Image Recognition Technology Based on Neural Network. IEEE Access 2020, 8, 157161. [Google Scholar] [CrossRef]
- Parret, A. Neural Networks in Economics. Ph.D. Thesis, University of California, Irvine, CA, USA, 2020. [Google Scholar]
- Adamski, M.; Czechlowski, M.; Durczak, K.; Garbowski, T. Determination of the Concentration of Propionic Acid in an Aqueous Solution by POD-GP Model and Spectroscopy. Energies 2021, 14, 8288. [Google Scholar] [CrossRef]
- Spielberg, N.A.; Brown, M.; Kapania, N.R.; Kegelman, J.C.; Gerdes, J.C. Neural network vehicle models for high-performance automated driving. Sci. Robot. 2019, 4, 1975. [Google Scholar] [CrossRef]
- Almonti, D.; Baiocco, G.; Tagliaferri, V.; Ucciardello, N. Artificial Neural Network in Fibres Length Prediction for High Precision Control of Cellulose Refining. Materials 2019, 12, 3730. [Google Scholar] [CrossRef]
- Olejnik, K.; Ciesielski, K. Neural network model of pulp refining process. Chem. Process Eng. 2004, 25, 1411–1416. [Google Scholar]
- Ciesielski, K.; Olejnik, K. Application of Neural Networks for Estimation of Paper Properties Based on Refined Pulp Properties. Fibres Text. East. Eur. 2014, 22, 126–132. [Google Scholar]
- Nieminen, P.; Kärkkäinen, T.; Luostarinen, K.; Muhonen, J. Neural Prediction of Product Quality Based on Pilot Paper Machine Process Measurements. In Proceedings of the ICANNGA’11-10th International Conference on Adaptive and Natural Computing Algorithms, Ljubljana, Slovenia, 14–16 April 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 240–249. [Google Scholar]
- Zhu, J.; Xia, Q.; Rao, M.; Zurcher, J. A Neural Network for Modeling Pulp Process. Pulp Pap. Can. 1997, 98, 35–38. [Google Scholar]
- Dayal, B.S.; MacGregor, J.; Taylor, P.A. Application of Feedforward Neural networks and Partial Least Squares Regression toModeling Kappa Number in a Continuous Kamyr Digester. Pulp Pap. Can. 1994, 95, 26–32. [Google Scholar]
- Garbowski, T.; Knitter-Piątkowska, A.; Winiarski, P. Simplified Modelling of the Edge Crush Resistance of Multi-Layered Corrugated Board: Experimental and Computational Study. Materials 2023, 16, 458. [Google Scholar] [CrossRef] [PubMed]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1999, 5, 989–993. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing: Boston, MA, USA, 1996. [Google Scholar]
- Da, D. Topology Optimization Design of Heterogeneous Materials and Structures; Willey: Hoboken, NJ, USA, 2019. [Google Scholar]
- Da, D. Model reduction on 3D fracture resistance design. J. Comput. Phys. 2022, 463, 111274. [Google Scholar] [CrossRef]
- Da, D. Inverse homogenization design of lattice structures without scale separation. Structures 2021, 29, 796–805. [Google Scholar] [CrossRef]







| Corrugated Board | Component Papers | Corrugated Layers | ||||||
|---|---|---|---|---|---|---|---|---|
| Wave | Grammage | Height | Paper ID | Grammage | Thickness | Height | Period | Take-Up |
| Type | (g/m2) | (mm) | (g/m2) | (mm) | (mm) | (mm) | Factor | |
| B | 410 | 2.912 | TL3125 | 124 ± 6 | 0.27 ± 0.1 | - | - | - |
| WS120 | 118 ± 6 | 0.25 ± 0.1 | 2.55 | 6.34 | 1.337 | |||
| TL3125 | 126 ± 6 | 0.27 ± 0.1 | - | - | - | |||
| C | 590 | 4.110 | KLB170 | 168 ± 8 | 0.36 ± 0.2 | - | - | - |
| S.C.175 | 176 ± 8 | 0.36 ± 0.2 | 3.63 | 7.95 | 1.427 | |||
| KLB170 | 169 ± 8 | 0.36 ± 0.2 | - | - | - | |||
| E | 480 | 1.586 | TLWC160 | 158 ± 8 | 0.17 ± 0.1 | - | - | - |
| WS135 | 133 ± 6 | 0.13 ± 0.1 | 1.16 | 3.50 | 1.236 | |||
| TLW160 | 159 ± 8 | 0.17 ± 0.1 | - | - | - | |||
| BC | 790 | 6.740 | KLB170 | 168 ± 8 | 0.28 ± 0.2 | - | - | - |
| W135 | 136 ± 6 | 0.25 ± 0.1 | 2.55 | 6.34 | 1.337 | |||
| WS80 | 79 ± 4 | 0.22 ± 0.1 | - | - | - | |||
| WS135 | 133 ± 6 | 0.25 ± 0.1 | 3.63 | 7.95 | 1.427 | |||
| KLB170 | 172 ± 8 | 0.28 ± 0.2 | - | - | - | |||
| BE | 600 | 4.150 | TLW140 | 141 ± 7 | 0.28 ± 0.2 | - | - | - |
| WS95 | 94 ± 5 | 0.22 ± 0.1 | 2.55 | 6.34 | 1.337 | |||
| WS80 | 81 ± 4 | 0.22 ± 0.1 | - | - | - | |||
| WS95 | 94 ± 5 | 0.22 ± 0.1 | 1.16 | 3.50 | 1.236 | |||
| TL3125 | 124 ± 6 | 0.28 ± 0.2 | - | - | - | |||
| BE | 590 | 4.120 | TL3125 | 125 ± 6 | 0.32 ± 0.2 | - | - | - |
| WS95 | 94 ± 5 | 0.24 ± 0.1 | 2.55 | 6.34 | 1.337 | |||
| W80 | 79 ± 5 | 0.22 ± 0.1 | - | - | - | |||
| WS95 | 96 ± 5 | 0.24 ± 0.1 | 1.16 | 3.50 | 1.236 | |||
| TL3125 | 124 ± 6 | 0.29 ± 0.2 | - | - | - | |||
| Layer | SCT | Tensile Stiffness | Flute | GRM * | THK * | ANG * | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CD | MD | 45 d | CD | MD | 45 d | Width | Height | TUF * | ||||
| Liner | 1 | 2 | 3 | 4 | 5 | 6 | - | - | - | 7 | 8 | - |
| Flute | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | - |
| Liner | 20 | 21 | 22 | 23 | 24 | 25 | - | - | - | 26 | 27 | - |
| - | - | - | - | - | - | - | - | - | - | - | - | 28 |
| Layer | SCT | Tensile Stiffness | Flute | GRM * | THK * | ANG * | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CD | MD | 45 d | CD | MD | 45 d | Width | Height | TUF * | ||||
| Liner | 1 | 2 | 3 | 4 | 5 | 6 | - | - | - | 7 | 8 | - |
| Flute | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | - |
| Liner | 20 | 21 | 22 | 23 | 24 | 25 | - | - | - | 26 | 27 | - |
| Flute | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | |
| Liner | 39 | 40 | 41 | 42 | 43 | 44 | - | - | - | 45 | 46 | |
| - | - | - | - | - | - | - | - | - | - | - | - | 47 |
| Grade ID | Paper ID | Short-Span Compression Strength | Tensile Stiffness | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CD | MD | 45 Deg | CD | MD | 45 Deg | ||||||||
| (kN/m) | (kN/m) | ||||||||||||
| TL3125 | 2.14 | ±0.12 | 3.97 | ±0.05 | 2.92 | ±0.05 | 373.3 | ±2.1 | 1012.7 | ±6.3 | 572.7 | ±10.8 | |
| B-410 | WS120 | 2.09 | ±0.07 | 4.09 | ±0.15 | 3.14 | ±0.08 | 365.1 | ±8.8 | 1024.6 | ±8.5 | 516.5 | ±9.7 |
| TL3125 | 2.09 | ±0.11 | 4.05 | ±0.11 | 3.11 | ±0.14 | 381.2 | ±11.2 | 1058.3 | ±9.8 | 595.1 | ±10.5 | |
| KLB170 | 3.28 | ±0.18 | 5.96 | ±0.23 | 4.43 | ±0.19 | 527.8 | ±9.1 | 1472.1 | ±20.1 | 929.1 | ±20.3 | |
| C-590 | S.C.175 | 4.18 | ±0.19 | 7.47 | ±0.18 | 5.84 | ±0.07 | 686.1 | ±13.9 | 1476.1 | ±10.9 | 924.7 | ±48.9 |
| KLB170 | 3.19 | ±0.06 | 5.51 | ±0.18 | 4.65 | ±0.13 | 568.1 | ±14.8 | 1445.1 | ±31.7 | 956.2 | ±26.6 | |
| TLWC160 | 2.75 | ±0.20 | 4.20 | ±0.15 | 3.49 | ±0.13 | 412.1 | ±6.8 | 1043.6 | ±11.1 | 635.0 | ±11.2 | |
| E-480 | WS135 | 2.13 | ±0.10 | 4.25 | ±0.15 | 2.95 | ±0.07 | 365.0 | ±9.8 | 1067.5 | ±14.5 | 533.5 | ±8.5 |
| TLW160 | 2.43 | ±0.11 | 4.09 | ±0.13 | 3.21 | ±0.11 | 443.9 | ±1.5 | 1102.1 | ±38.6 | 667.0 | ±5.4 | |
| KLB170 | 3.39 | ±0.12 | 6.14 | ±0.19 | 4.69 | ±0.13 | 618.9 | ±17.6 | 1534.2 | ±6.7 | 990.0 | ±17.5 | |
| W135 | 2.19 | ±0.09 | 4.27 | ±0.10 | 3.09 | ±0.13 | 369.1 | ±11.2 | 1113.5 | ±9.8 | 572.4 | ±22.6 | |
| BC-790 | WS80 | 1.50 | ±0.08 | 2.30 | ±0.09 | 1.91 | ±0.04 | 317.1 | ±4.2 | 699.1 | ±3.3 | 445.0 | ±5.8 |
| WS135 | 2.23 | ±0.04 | 4.37 | ±0.15 | 3.18 | ±0.06 | 385.9 | ±12.0 | 1147.4 | ±7.6 | 623.5 | ±8.0 | |
| KLB170 | 3.30 | ±0.18 | 5.98 | ±0.32 | 4.66 | ±0.20 | 592.7 | ±8.3 | 1418.9 | ±23.6 | 838.2 | ±12.7 | |
| TLW140 | 2.61 | ±0.13 | 3.92 | ±0.09 | 3.08 | ±0.11 | 506.0 | ±7.1 | 1000.0 | ±12.6 | 622.6 | ±11.7 | |
| WS95 | 1.69 | ±0.09 | 2.99 | ±0.16 | 2.26 | ±0.09 | 331.9 | ±5.5 | 872.7 | ±6.0 | 498.6 | ±10.3 | |
| BE-600 | WS80 | 1.42 | ±0.03 | 2.56 | ±0.17 | 1.88 | ±0.08 | 273.2 | ±3.8 | 812.8 | ±12.3 | 424.8 | ±7.2 |
| WS95 | 1.52 | ±0.08 | 3.16 | ±0.13 | 2.46 | ±0.06 | 290.7 | ±6.7 | 885.5 | ±18.9 | 508.4 | ±14.7 | |
| TL3125 | 2.13 | ±0.09 | 3.83 | ±0.13 | 2.93 | ±0.10 | 440.6 | ±3.4 | 1082.2 | ±13.3 | 623.3 | ±35.4 | |
| TL3125 | 2.26 | ±0.13 | 3.64 | ±0.08 | 3.06 | ±0.11 | 412.9 | ±11.6 | 961.3 | ±10.0 | 587.0 | ±3.4 | |
| WS95 | 1.50 | ±0.06 | 2.69 | ±0.13 | 2.01 | ±0.09 | 294.3 | ±8.6 | 756.4 | ±13.8 | 427.4 | ±8.8 | |
| BE-590 | W80 | 1.47 | ±0.08 | 2.34 | ±0.06 | 1.94 | ±0.08 | 343.5 | ±5.8 | 696.5 | ±14.5 | 459.8 | ±5.0 |
| WS95 | 1.75 | ±0.10 | 2.96 | ±0.18 | 2.15 | ±0.06 | 332.0 | ±4.0 | 854.7 | ±4.2 | 474.4 | ±11.0 | |
| TL3125 | 2.32 | ±0.07 | 3.75 | ±0.06 | 2.87 | ±0.17 | 413.8 | ±4.7 | 883.1 | ±20.9 | 588.3 | ±14.5 | |
| Board ID | Edge Crush Resistance | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CD (0 Deg) | 15 Deg | 30 Deg | 45 Deg | 60 Deg | 75 Deg | |||||||
| (kN/m) | ||||||||||||
| B-410 | 5.48 | ±0.09 | 5.17 | ±0.12 | 4.40 | ±0.03 | 3.88 | ±0.10 | 3.05 | ±0.10 | 2.29 | ±0.13 |
| C-590 | 9.68 | ±0.10 | 9.07 | ±0.14 | 7.60 | ±0.02 | 6.24 | ±0.12 | 4.83 | ±0.10 | 3.49 | ±0.23 |
| E-480 | 6.37 | ±0.17 | 5.92 | ±0.08 | 5.99 | ±0.26 | 5.47 | ±0.27 | 5.16 | ±0.17 | 4.56 | ±0.18 |
| BC-790 | 10.41 | ±0.13 | 9.56 | ±0.37 | 8.38 | ±0.29 | 6.96 | ±0.10 | 6.00 | ±0.17 | 4.31 | ±0.16 |
| BE-600 | 8.95 | ±0.14 | 8.39 | ±0.06 | 7.76 | ±0.14 | 6.46 | ±0.18 | 5.66 | ±0.32 | 4.30 | ±0.35 |
| BE-590 | 9.68 | ±0.10 | 9.07 | ±0.14 | 7.60 | ±0.02 | 6.24 | ±0.12 | 4.83 | ±0.10 | 3.49 | ±0.22 |
| Model | Mean Absolute Error (%) | ||
| Method | 3-Layer Cardboard | 5-Layer Cardboard | |
| FF (full) | 3.163 | 1.575 | |
| FF (small) | 2.273 | 1.921 | |
| DL (full) | 2.985 | 3.093 | |
| DL (small) | 3.948 | 2.916 | |
| GP (full) | 2.484 | 1.317 | |
| GP (small) | 2.260 | 2.150 | |
| Analytical [78] | 1.760 | 2.987 | |
| FEM-1 [78] | 1.640 | 2.260 | |
| FEM-2 [78] | 4.010 | 4.227 | |
| Empirical-1 [78] | 3.547 | 10.60 | |
| Empirical-2 [78] | 1.997 | 9.800 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garbowski, T.; Knitter-Piątkowska, A.; Grabski, J.K. Estimation of the Edge Crush Resistance of Corrugated Board Using Artificial Intelligence. Materials 2023, 16, 1631. https://doi.org/10.3390/ma16041631
Garbowski T, Knitter-Piątkowska A, Grabski JK. Estimation of the Edge Crush Resistance of Corrugated Board Using Artificial Intelligence. Materials. 2023; 16(4):1631. https://doi.org/10.3390/ma16041631
Chicago/Turabian StyleGarbowski, Tomasz, Anna Knitter-Piątkowska, and Jakub Krzysztof Grabski. 2023. "Estimation of the Edge Crush Resistance of Corrugated Board Using Artificial Intelligence" Materials 16, no. 4: 1631. https://doi.org/10.3390/ma16041631
APA StyleGarbowski, T., Knitter-Piątkowska, A., & Grabski, J. K. (2023). Estimation of the Edge Crush Resistance of Corrugated Board Using Artificial Intelligence. Materials, 16(4), 1631. https://doi.org/10.3390/ma16041631








