Deep-Learning-Based Acoustic Metamaterial Design for Attenuating Structure-Borne Noise in Auditory Frequency Bands
Abstract
1. Introduction
1.1. Motivation and Relevant Works
1.2. Contribution and Scope
- To the best of the authors’ knowledge, this is the first study using deep learning in the design of phononic plates for synthesizing the flexural wave band gap.
- To the best understanding of the authors, this is the first study to employ the Mindlin plate formulation in modeling the phononic elastic plate for AI-assisted metamaterial design.
- Although this study aimed at a specific engineering scheme, the proposed design framework can be easily adapted to different circumstances. By demonstrating the explicit procedures from the initial performance requirements to the final results, this study fills the gap between existing studies and the application end, expediting the real applications in practice.
2. Problem Statement
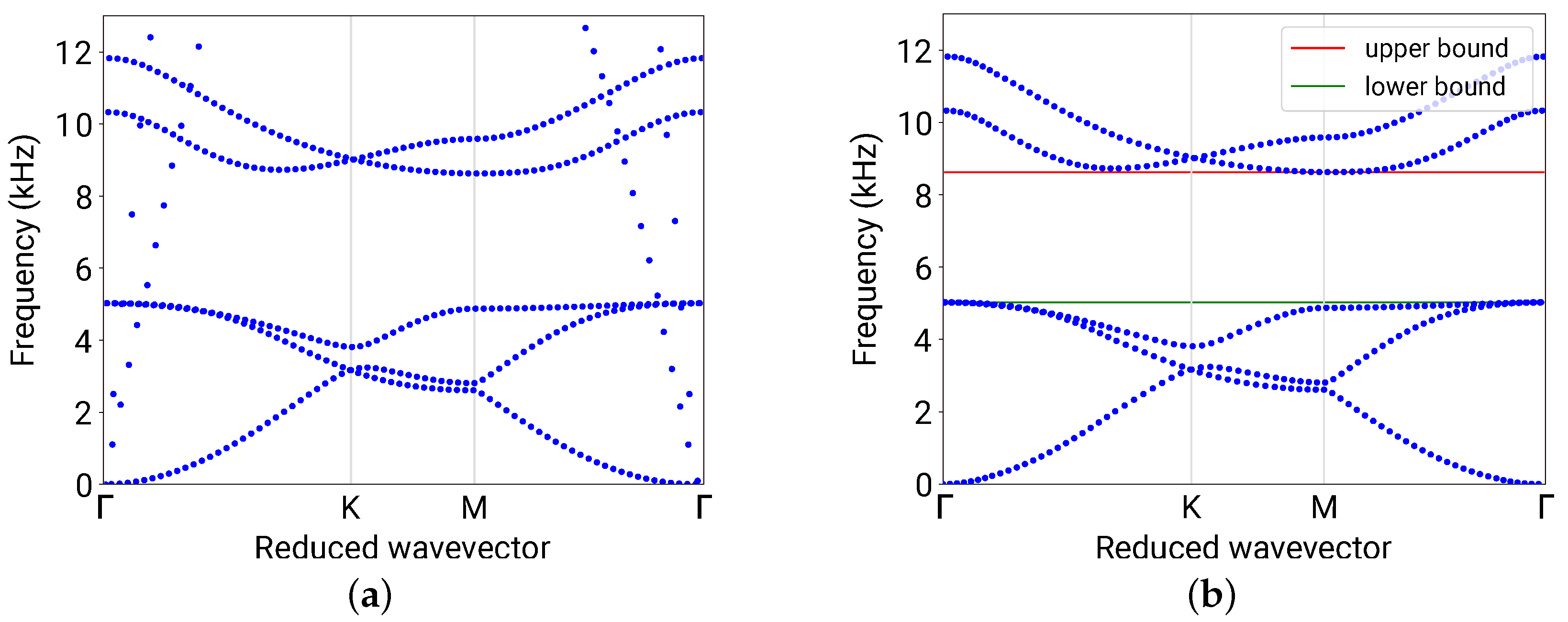
2.1. Theoretical Background
2.2. Finite-Element Analysis and Data Generation
3. Methodology
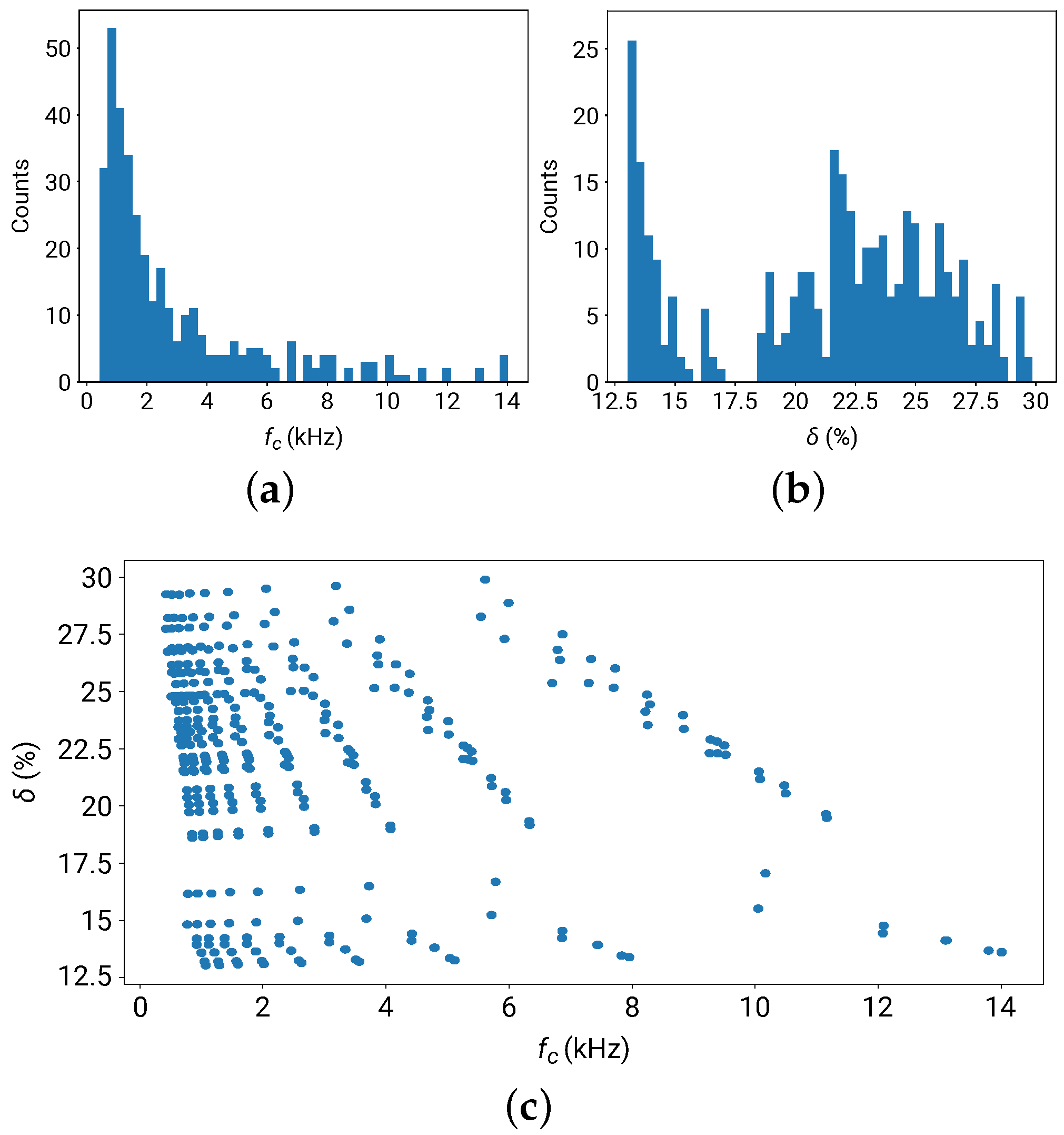
3.1. Data Preparation
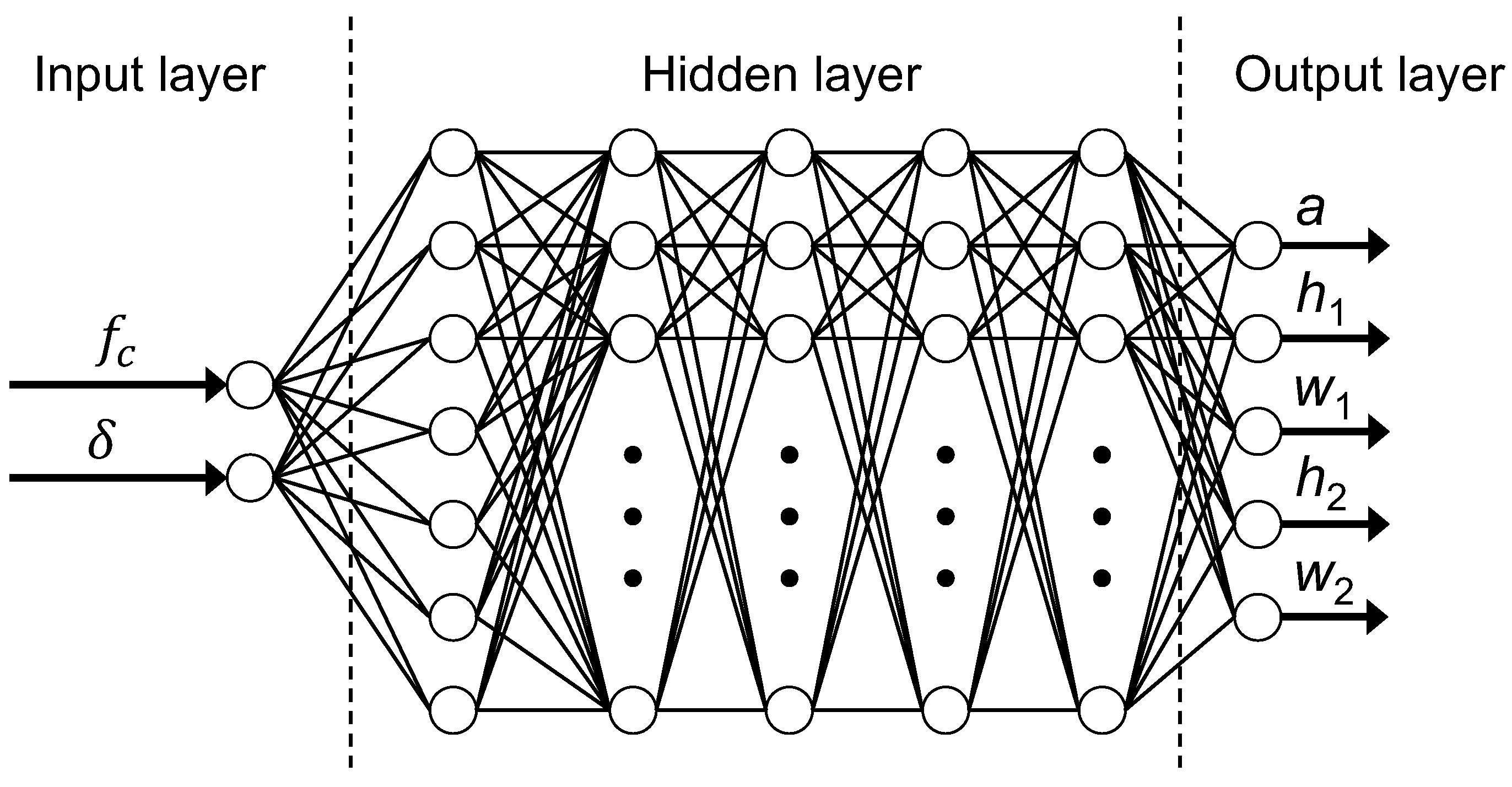
3.2. Network Architecture
3.3. Network Training
4. Neural Network Testing Results and Discussion
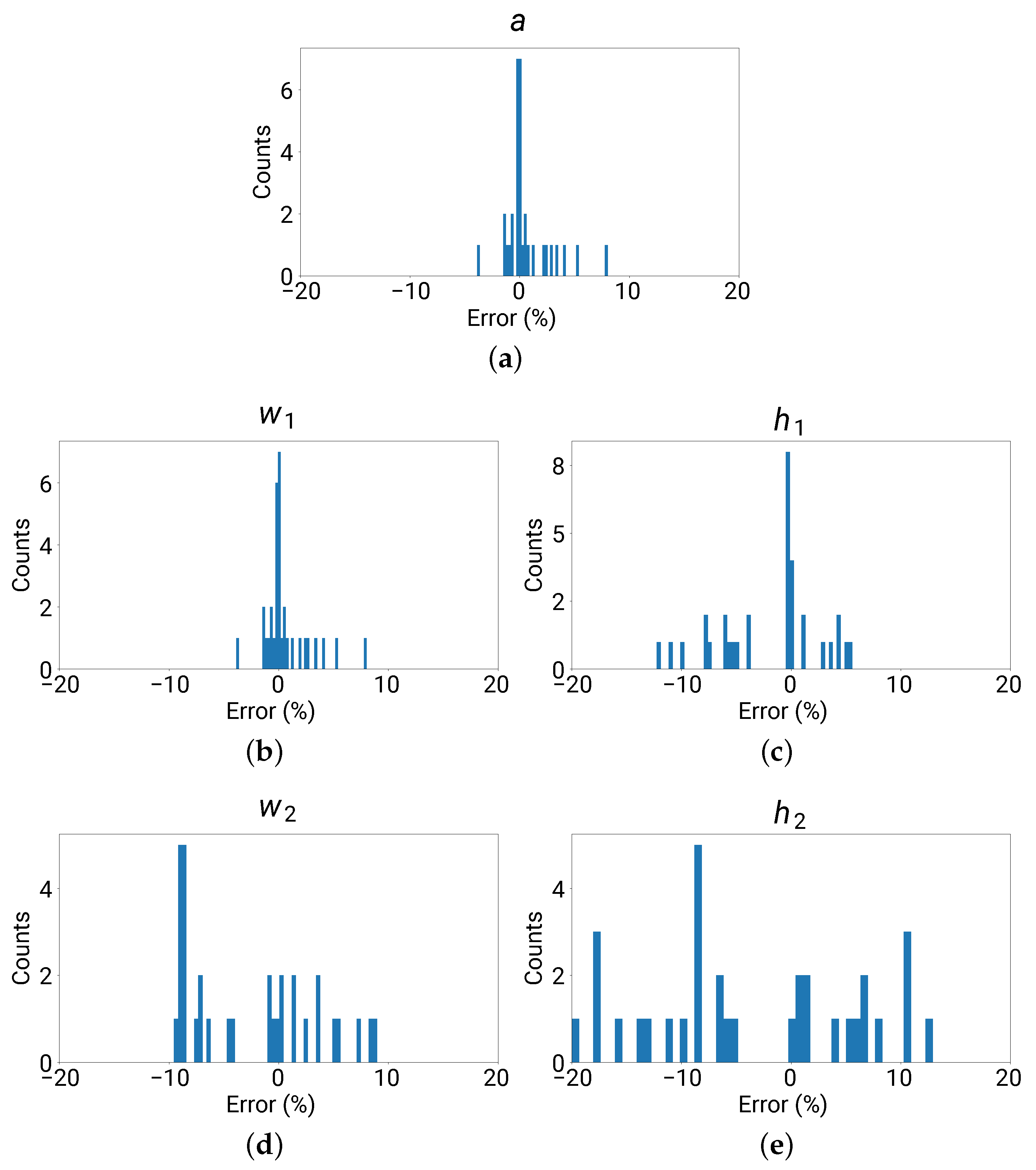
4.1. Error Metrics for Parameters
4.2. Network Prediction Results
4.3. Baseline Reference
5. Validation of the Metamaterial Performance
5.1. Model Description
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Houser, D.S.; Yost, W.; Burkard, R.; Finneran, J.J.; Reichmuth, C.; Mulsow, J. A review of the history, development and application of auditory weighting functions in humans and marine mammals. J. Acoust. Soc. Am. 2017, 141, 1371–1413. [Google Scholar] [CrossRef] [PubMed]
- Sjöberg, M.M.; Kari, L. Non-linear behavior of a rubber isolator system using fractional derivatives. Veh. Syst. Dyn. 2002, 37, 217–236. [Google Scholar] [CrossRef]
- Richards, C.; Singh, R. Characterization of rubber isolator nonlinearities in the context of single-and multi-degree-of-freedom experimental systems. J. Sound Vib. 2001, 247, 807–834. [Google Scholar] [CrossRef]
- Göransson, P. Acoustic and vibrational damping in porous solids. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 89–108. [Google Scholar] [CrossRef]
- Jaouen, L.; Renault, A.; Deverge, M. Elastic and damping characterizations of acoustical porous materials: Available experimental methods and applications to a melamine foam. Appl. Acoust. 2008, 69, 1129–1140. [Google Scholar] [CrossRef]
- Sujon, M.A.S.; Islam, A.; Nadimpalli, V.K. Damping and sound absorption properties of polymer matrix composites: A review. Polym. Test. 2021, 104, 107388. [Google Scholar] [CrossRef]
- Brûlé, S.; Javelaud, E.; Enoch, S.; Guenneau, S. Experiments on seismic metamaterials: Molding surface waves. Phys. Rev. Lett. 2014, 112, 133901. [Google Scholar] [CrossRef] [PubMed]
- Aravantinos-Zafiris, N.; Sigalas, M. Large scale phononic metamaterials for seismic isolation. J. Appl. Phys. 2015, 118, 064901. [Google Scholar] [CrossRef]
- Colombi, A.; Colquitt, D.; Roux, P.; Guenneau, S.; Craster, R.V. A seismic metamaterial: The resonant metawedge. Sci. Rep. 2016, 6, 27717. [Google Scholar] [CrossRef] [PubMed]
- Qahtan, A.S.; Huang, J.; Amran, M.; Qader, D.N.; Fediuk, R.; Wael, A.D. Seismic Composite Metamaterial: A Review. J. Compos. Sci. 2022, 6, 348. [Google Scholar] [CrossRef]
- Gao, N.; Zhang, Z.; Deng, J.; Guo, X.; Cheng, B.; Hou, H. Acoustic metamaterials for noise reduction: A review. Adv. Mater. Technol. 2022, 7, 2100698. [Google Scholar] [CrossRef]
- Oudich, M.; Gerard, N.J.; Deng, Y.; Jing, Y. Tailoring Structure-Borne Sound through Bandgap Engineering in Phononic Crystals and Metamaterials: A Comprehensive Review. Adv. Funct. Mater. 2022, 33, 2206309. [Google Scholar] [CrossRef]
- Lin, S.C.S.; Huang, T.J.; Sun, J.H.; Wu, T.T. Gradient-index phononic crystals. Phys. Rev. B 2009, 79, 094302. [Google Scholar] [CrossRef]
- Wu, T.T.; Hsu, J.C.; Sun, J.H. Phononic plate waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2146–2161. [Google Scholar] [PubMed]
- Liu, T.W.; Semperlotti, F. Tunable acoustic valley–hall edge states in reconfigurable phononic elastic waveguides. Phys. Rev. Appl. 2018, 9, 014001. [Google Scholar] [CrossRef]
- Liu, T.W.; Semperlotti, F. Experimental evidence of robust acoustic valley Hall edge states in a nonresonant topological elastic waveguide. Phys. Rev. Appl. 2019, 11, 014040. [Google Scholar] [CrossRef]
- Liu, T.W.; Semperlotti, F. Synthetic Kramers pair in phononic elastic plates and helical edge states on a dislocation interface. Adv. Mater. 2021, 33, 2005160. [Google Scholar] [CrossRef]
- Ma, J. Phonon Engineering of Micro-and Nanophononic Crystals and Acoustic Metamaterials: A Review. Small Sci. 2022, 3, 2200052. [Google Scholar] [CrossRef]
- Wu, T.T.; Wu, L.C.; Huang, Z.G. Frequency band-gap measurement of two-dimensional air/silicon phononic crystals using layered slanted finger interdigital transducers. J. Appl. Phys. 2005, 97, 094916. [Google Scholar] [CrossRef]
- Wu, T.T.; Hsu, Z.C.; Huang, Z.G. Band gaps and the electromechanical coupling coefficient of a surface acoustic wave in a two-dimensional piezoelectric phononic crystal. Phys. Rev. B 2005, 71, 064303. [Google Scholar] [CrossRef]
- Su, M.; Olsson, R., III; Leseman, Z.; El-Kady, I. Realization of a phononic crystal operating at gigahertz frequencies. Appl. Phys. Lett. 2010, 96, 053111. [Google Scholar] [CrossRef]
- Liu, T.W.; Lin, Y.C.; Tsai, Y.C.; Ono, T.; Tanaka, S.; Wu, T.T. Evidence of a Love wave bandgap in a quartz substrate coated with a phononic thin layer. Appl. Phys. Lett. 2014, 104, 181905. [Google Scholar] [CrossRef]
- Liu, T.W.; Tsai, Y.C.; Lin, Y.C.; Ono, T.; Tanaka, S.; Wu, T.T. Design and fabrication of a phononic-crystal-based Love wave resonator in GHz range. AIP Adv. 2014, 4, 124201. [Google Scholar] [CrossRef]
- Huang, K.X.; Shui, G.S.; Wang, Y.Z.; Wang, Y.S. Meta-arrest of a fast propagating crack in elastic wave metamaterials with local resonators. Mech. Mater. 2020, 148, 103497. [Google Scholar] [CrossRef]
- Huang, K.X.; Shui, G.S.; Wang, Y.Z.; Wang, Y.S. Discrete scattering and meta-arrest of locally resonant elastic wave metamaterials with a semi-infinite crack. Proc. R. Soc. A 2021, 477, 20210356. [Google Scholar] [CrossRef]
- Alam, Z.; Sharma, A.K. Functionally Graded Soft Dielectric Elastomer Phononic Crystals: Finite Deformation, electro-elastic longitudinal waves, and band gaps tunability via electro-mechanical loading. Int. J. Appl. Mech. 2022, 14, 2250050. [Google Scholar] [CrossRef]
- Sharma, A.K.; Kosta, M.; Shmuel, G.; Amir, O. Gradient-based topology optimization of soft dielectrics as tunable phononic crystals. Compos. Struct. 2022, 280, 114846. [Google Scholar] [CrossRef]
- Sharma, A.K.; Joglekar, M.; Joglekar, D.; Alam, Z. Topology optimization of soft compressible phononic laminates for widening the mechanically tunable band gaps. Compos. Struct. 2022, 289, 115389. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, M.; Zuo, S.; Huang, H.; Wu, H. An investigation on interior noise reduction using 2D locally resonant phononic crystal with point defect on car ceiling. J. Vib. Control 2019, 25, 386–396. [Google Scholar] [CrossRef]
- Wu, X.; Kong, Y.; Zuo, S.; Liu, P. Research on multi-band structural noise reduction of vehicle body based on two-degree-of-freedom locally resonant phononic crystal. Appl. Acoust. 2021, 179, 108073. [Google Scholar] [CrossRef]
- Zuo, S.; Liu, P.; Wu, X.; Zhang, Q.; Kong, Y.; Zhou, D. Study on broad flexural wave bandgaps of piezoelectric phononic crystal plates for the vibration and noise attenuation. Thin-Walled Struct. 2022, 178, 109481. [Google Scholar] [CrossRef]
- Tan, K.T.; Huang, H.; Sun, C. Optimizing the band gap of effective mass negativity in acoustic metamaterials. Appl. Phys. Lett. 2012, 101, 241902. [Google Scholar] [CrossRef]
- Wu, T.T.; Chen, Y.T.; Sun, J.H.; Lin, S.C.S.; Huang, T.J. Focusing of the lowest antisymmetric Lamb wave in a gradient-index phononic crystal plate. Appl. Phys. Lett. 2011, 98, 171911. [Google Scholar] [CrossRef]
- Feurtado, P.A.; Conlon, S.C.; Semperlotti, F. A normalized wave number variation parameter for acoustic black hole design. J. Acoust. Soc. Am. 2014, 136, EL148–EL152. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.M.; Hsu, J.C.; Senesky, D.G.; Pisano, A.P. Anchor loss reduction in AlN Lamb wave resonators using phononic crystal strip tethers. In Proceedings of the 2014 IEEE International Frequency Control Symposium (FCS), Taipei, Taiwan, 19–22 May 2014; pp. 1–5. [Google Scholar]
- Allaire, G.; Jouve, F.; Toader, A.M. Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Zhang, N.; Kang, Z. Topological shape optimization of microstructural metamaterials using a level set method. Comput. Mater. Sci. 2014, 87, 178–186. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. Optimal design of periodic structures using evolutionary topology optimization. Struct. Multidiscip. Optim. 2008, 36, 597–606. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials. Comput. Mech. 2009, 43, 393. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Liu, L.; Yan, J.; Cheng, G. Optimum structure with homogeneous optimum truss-like material. Comput. Struct. 2008, 86, 1417–1425. [Google Scholar] [CrossRef]
- Liu, Z.F.; Wu, B.; He, C.F. Band-gap optimization of two-dimensional phononic crystals based on genetic algorithm and FPWE. Waves Random Complex Media 2014, 24, 286–305. [Google Scholar] [CrossRef]
- Bilal, O.R.; Hussein, M.I. Ultrawide phononic band gap for combined in-plane and out-of-plane waves. Phys. Rev. E 2011, 84, 065701. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Zigoneanu, L.; Popa, B.I.; Cummer, S.A. Design of an acoustic metamaterial lens using genetic algorithms. J. Acoust. Soc. Am. 2012, 132, 2823–2833. [Google Scholar] [CrossRef] [PubMed]
- Hussein, M.I.; Hamza, K.; Hulbert, G.M.; Saitou, K. Optimal synthesis of 2D phononic crystals for broadband frequency isolation. Waves Random Complex Media 2007, 17, 491–510. [Google Scholar] [CrossRef]
- Oh, J.H.; Ahn, Y.K.; Kim, Y.Y. Maximization of operating frequency ranges of hyperbolic elastic metamaterials by topology optimization. Struct. Multidiscip. Optim. 2015, 52, 1023–1040. [Google Scholar] [CrossRef]
- Jensen, J.S.; Sigmund, O. Phononic band gap structures as optimal designs. In Proceedings of the IUTAM Symposium on Asymptotics, Singularities and Homogenisation in Problems of Mechanics, Liverpool, UK, 8–11 July 2002; Springer: Dordrecht, The Netherlands, 2003; pp. 73–83. [Google Scholar]
- Yi, G.; Youn, B.D. A comprehensive survey on topology optimization of phononic crystals. Struct. Multidiscip. Optim. 2016, 54, 1315–1344. [Google Scholar] [CrossRef]
- Wormser, M.; Wein, F.; Stingl, M.; Körner, C. Design and additive manufacturing of 3D phononic band gap structures based on gradient based optimization. Materials 2017, 10, 1125. [Google Scholar] [CrossRef]
- Park, J.H.; Ma, P.S.; Kim, Y.Y. Design of phononic crystals for self-collimation of elastic waves using topology optimization method. Struct. Multidiscip. Optim. 2015, 51, 1199–1209. [Google Scholar] [CrossRef]
- Du, Z.; Chen, H.; Huang, G. Optimal quantum valley Hall insulators by rationally engineering Berry curvature and band structure. J. Mech. Phys. Solids 2020, 135, 103784. [Google Scholar] [CrossRef]
- Wu, R.T.; Liu, T.W.; Jahanshahi, M.R.; Semperlotti, F. Design of one-dimensional acoustic metamaterials using machine learning and cell concatenation. Struct. Multidiscip. Optim. 2021, 63, 2399–2423. [Google Scholar] [CrossRef]
- Miao, X.B.; Dong, H.W.; Wang, Y.S. Deep learning of dispersion engineering in two-dimensional phononic crystals. Eng. Optim. 2021, 55, 125–139. [Google Scholar] [CrossRef]
- Ma, W.; Liu, Z.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.; Liu, Y. Deep learning for the design of photonic structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Jin, Y.; He, L.; Wen, Z.; Mortazavi, B.; Guo, H.; Torrent, D.; Djafari-Rouhani, B.; Rabczuk, T.; Zhuang, X.; Li, Y. Intelligent on-demand design of phononic metamaterials. Nanophotonics 2022, 11, 439–460. [Google Scholar] [CrossRef]
- Jiang, W.; Zhu, Y.; Yin, G.; Lu, H.; Xie, L.; Yin, M. Dispersion relation prediction and structure inverse design of elastic metamaterials via deep learning. Mater. Today Phys. 2022, 22, 100616. [Google Scholar] [CrossRef]
- Du, Z.; Ding, X.; Chen, H.; Liu, C.; Zhang, W.; Luo, J.; Guo, X. Optimal design of topological waveguides by machine learning. Front. Mater. 2022, 9, 1075073. [Google Scholar] [CrossRef]
- He, L.; Wen, Z.; Jin, Y.; Torrent, D.; Zhuang, X.; Rabczuk, T. Inverse design of topological metaplates for flexural waves with machine learning. Mater. Des. 2021, 199, 109390. [Google Scholar] [CrossRef]
- Mindlin, R. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Hsu, J.C.; Wu, T.T. Efficient formulation for band-structure calculations of two-dimensional phononic-crystal plates. Phys. Rev. B 2006, 74, 144303. [Google Scholar] [CrossRef]
- Bloch, F. Über die quantenmechanik der elektronen in kristallgittern. Z. Phys. 1929, 52, 555–600. [Google Scholar] [CrossRef]
- Bragg, W.H.; Bragg, W.L. The reflection of X-rays by crystals. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1913, 88, 428–438. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Goffaux, C.; Sánchez-Dehesa, J. Two-dimensional phononic crystals studied using a variational method: Application to lattices of locally resonant materials. Phys. Rev. B 2003, 67, 144301. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.T.; Sheng, P. Analytic model of phononic crystals with local resonances. Phys. Rev. B 2005, 71, 014103. [Google Scholar] [CrossRef]
- Sigalas, M.; Economou, E.N. Band structure of elastic waves in two dimensional systems. Solid State Commun. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Wu, T.T.; Huang, Z.G.; Lin, S. Surface and bulk acoustic waves in two-dimensional phononic crystal consisting of materials with general anisotropy. Phys. Rev. B 2004, 69, 094301. [Google Scholar] [CrossRef]
- Tanaka, Y.; Tomoyasu, Y.; Tamura, S.I. Band structure of acoustic waves in phononic lattices: Two-dimensional composites with large acoustic mismatch. Phys. Rev. B 2000, 62, 7387. [Google Scholar] [CrossRef]
- Hsieh, P.F.; Wu, T.T.; Sun, J.H. Three-dimensional phononic band gap calculations using the FDTD method and a PC cluster system. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 148–158. [Google Scholar] [CrossRef]
- Sun, J.H.; Wu, T.T. Propagation of surface acoustic waves through sharply bent two-dimensional phononic crystal waveguides using a finite-difference time-domain method. Phys. Rev. B 2006, 74, 174305. [Google Scholar] [CrossRef]
- Sun, J.H.; Wu, T.T. Propagation of acoustic waves in phononic-crystal plates and waveguides using a finite-difference time-domain method. Phys. Rev. B 2007, 76, 104304. [Google Scholar] [CrossRef]
- Kafesaki, M.; Economou, E.N. Multiple-scattering theory for three-dimensional periodic acoustic composites. Phys. Rev. B 1999, 60, 11993. [Google Scholar] [CrossRef]
- Psarobas, I.; Stefanou, N.; Modinos, A. Scattering of elastic waves by periodic arrays of spherical bodies. Phys. Rev. B 2000, 62, 278. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.T.; Sheng, P.; Goertzen, A.L.; Page, J.H. Elastic wave scattering by periodic structures of spherical objects: Theory and experiment. Phys. Rev. B 2000, 62, 2446. [Google Scholar] [CrossRef]
- Zaki, S.E.; Basyooni, M.A.; Belaid, W.; Tihtih, M.; Ibrahim, J.E.F.; Attia, G. Terahertz resonance frequency through ethylene glycol phononic multichannel sensing via 2D MoS2/PtSe2 structure. Mater. Chem. Phys. 2022, 292, 126863. [Google Scholar] [CrossRef]
- Khelif, A.; Aoubiza, B.; Mohammadi, S.; Adibi, A.; Laude, V. Complete band gaps in two-dimensional phononic crystal slabs. Phys. Rev. E 2006, 74, 046610. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Larabi, H.; Vasseur, J.; Hladky-Hennion, A. Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B 2008, 78, 104105. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y.; Assouar, B.M.; Hou, Z. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 083049. [Google Scholar] [CrossRef]
- Comsol, A.B. Structural Mechanics Module User’s Guide; COMSOL AB: Stockholm, Sweden, 2021. [Google Scholar]
- Liu, T.W. Theoretical and Experimental Analysis of Topological Elastic Waveguides. Ph.D. Thesis, Purdue University Graduate School, West Lafayette, IN, USA, 2022. [Google Scholar]
- Lehoucq, R.B.; Sorensen, D.C.; Yang, C. ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Achenbach, J. Wave Propagation in Elastic Solids; North-Holland/American Elsevier: New York, NY, USA, 1973. [Google Scholar]
- Wu, R.T.; Jahanshahi, M.R. Deep Convolutional Neural Network for Structural Dynamic Response Estimation and System Identification. J. Eng. Mech. 2019, 145, 04018125. [Google Scholar] [CrossRef]

| Case # | Mean Error in Design Parameters | Error in | Error in |
|---|---|---|---|
| 1 | 1.25% | 0.13% | 0.98% |
| 2 | 7.44% | 0.18% | 0.69% |
| 3 | 6.47% | 4.71% | 0.37% |
| Algorithm | Error in | Error in |
|---|---|---|
| DNN | 2.26% | 1.75% |
| SVR | 12.5% | 6.91% |
| RFR | 4.04% | 1.60% |
| XGB | 4.08% | 1.76% |
| KNN | 2.47% | 2.04% |
| Algorithm | Hyperparameter | Description | Value/Function |
|---|---|---|---|
| kernel type | Kernel function | RBF | |
| SVR | C | Penalty parameter | 80 |
| gamma | Kernel coefficient | 5 | |
| RFR | criterion | Function to measure the quality of a split | absolute_error |
| max_depth | Max. depth of the tree | 40 | |
| max_features | # of features to consider when looking for the best split | sqrt | |
| min_samples_leaf | Min. # of samples required to be at a leaf node | 1 | |
| min_samples_split | Min. # of samples required to split an internal node | 3 | |
| n_estimators | Number of trees in the forest | 130 | |
| objective | Learning objective | reg:squarederror | |
| max_depth | Max. depth of the tree | 17 | |
| min_child_weight | Min. sum of instance weight | 3 | |
| XGB | colsample_bytree | Subsample ratio of columns | 1 |
| eta | Learning rate | 0.15 | |
| subsample | Subsample ratio of training instances | 0.5 | |
| n_estimators | Number of trees in XGBoost | 170 | |
| weights | Weight function used in prediction | distance | |
| KNN | p | Power parameter for the Minkowski metric | 1 |
| n_neighbors | Number of neighbors | 3 |
| Algorithm | Training Time (s) | Peak Memory during Training (MB) | Prediction Time (s) | Peak Memory during Prediction (MB) | Number of Parameters |
|---|---|---|---|---|---|
| DNN | 298.9139 | 0.9641 | 0.0019 | 0.0130 | 5097 |
| SVR | 0.0589 | 0.0434 | 0.0049 | 0.0181 | 3 |
| RFR | 1.1470 | 0.1987 | 0.0288 | 0.0438 | 6 |
| XGB | 0.4008 | 0.0904 | 0.0043 | 0.0226 | 7 |
| KNN | 0.0027 | 0.0215 | 0.0041 | 0.0181 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.-W.; Chan, C.-T.; Wu, R.-T. Deep-Learning-Based Acoustic Metamaterial Design for Attenuating Structure-Borne Noise in Auditory Frequency Bands. Materials 2023, 16, 1879. https://doi.org/10.3390/ma16051879
Liu T-W, Chan C-T, Wu R-T. Deep-Learning-Based Acoustic Metamaterial Design for Attenuating Structure-Borne Noise in Auditory Frequency Bands. Materials. 2023; 16(5):1879. https://doi.org/10.3390/ma16051879
Chicago/Turabian StyleLiu, Ting-Wei, Chun-Tat Chan, and Rih-Teng Wu. 2023. "Deep-Learning-Based Acoustic Metamaterial Design for Attenuating Structure-Borne Noise in Auditory Frequency Bands" Materials 16, no. 5: 1879. https://doi.org/10.3390/ma16051879
APA StyleLiu, T.-W., Chan, C.-T., & Wu, R.-T. (2023). Deep-Learning-Based Acoustic Metamaterial Design for Attenuating Structure-Borne Noise in Auditory Frequency Bands. Materials, 16(5), 1879. https://doi.org/10.3390/ma16051879







