Mechanistic Model with Empirical Pitting Onset Approach for Detailed and Efficient Virtual Analysis of Atmospheric Bimetallic Corrosion
Abstract
1. Introduction
2. Theory and Model Development
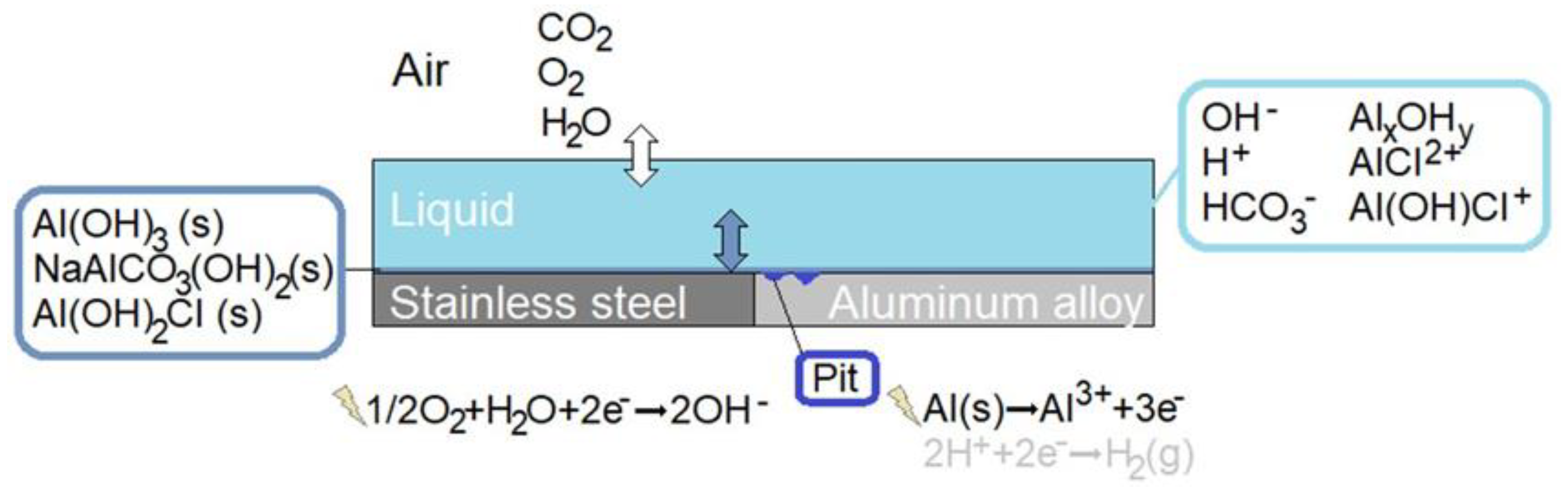
2.1. Electrochemical Reactions
2.2. Mass Transport and Chemical Reactions
2.3. The Liquid Film—Solid Corrosion Products Interaction
2.3.1. Precipitation and Dissolution of Solid Species
2.3.2. Metal Dissolution Sites
2.4. The Liquid Film—Atmosphere Interface
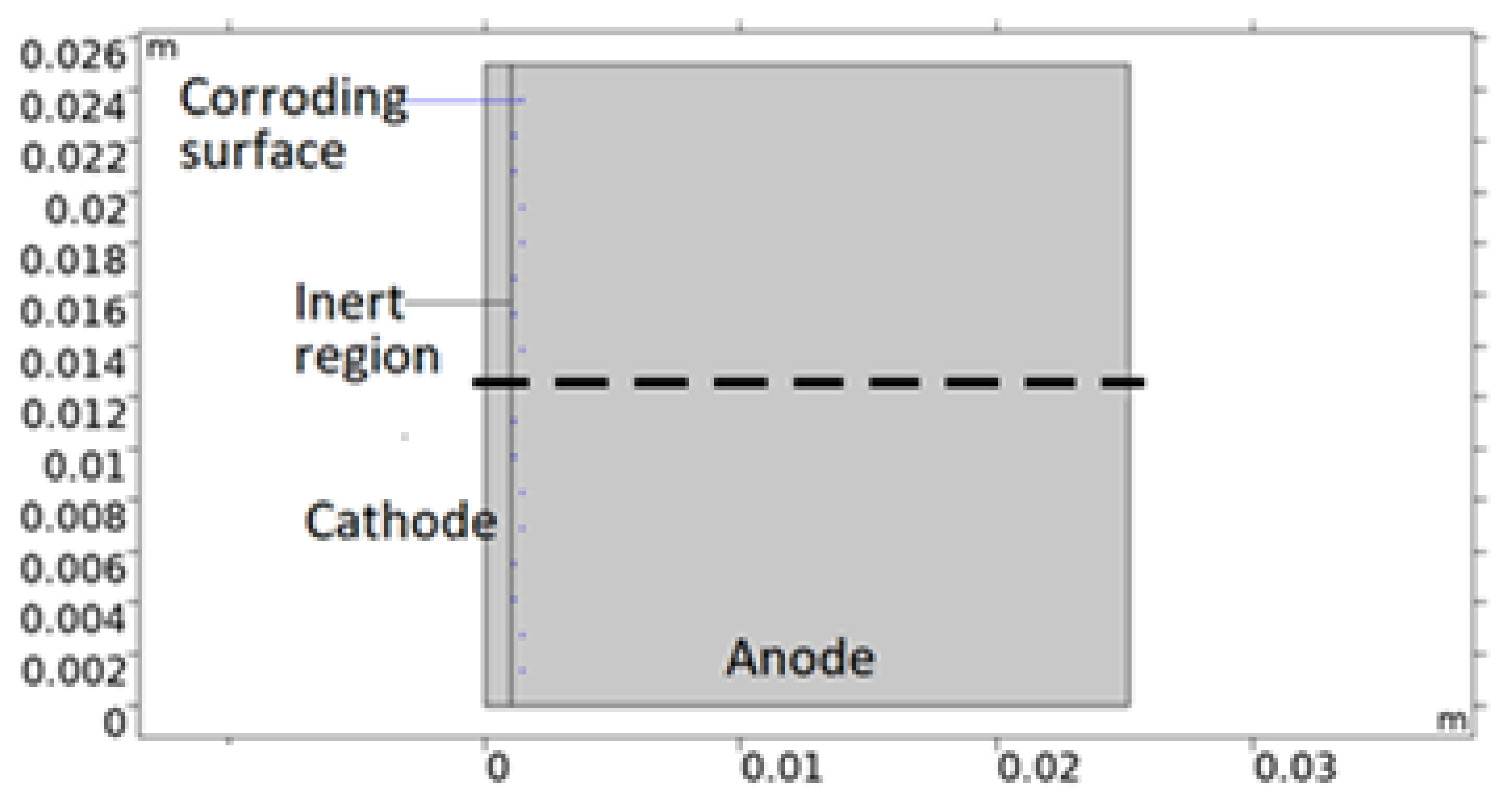
2.5. Model Geometry
3. Model Calibration Strategy
4. Calibration Cell Work
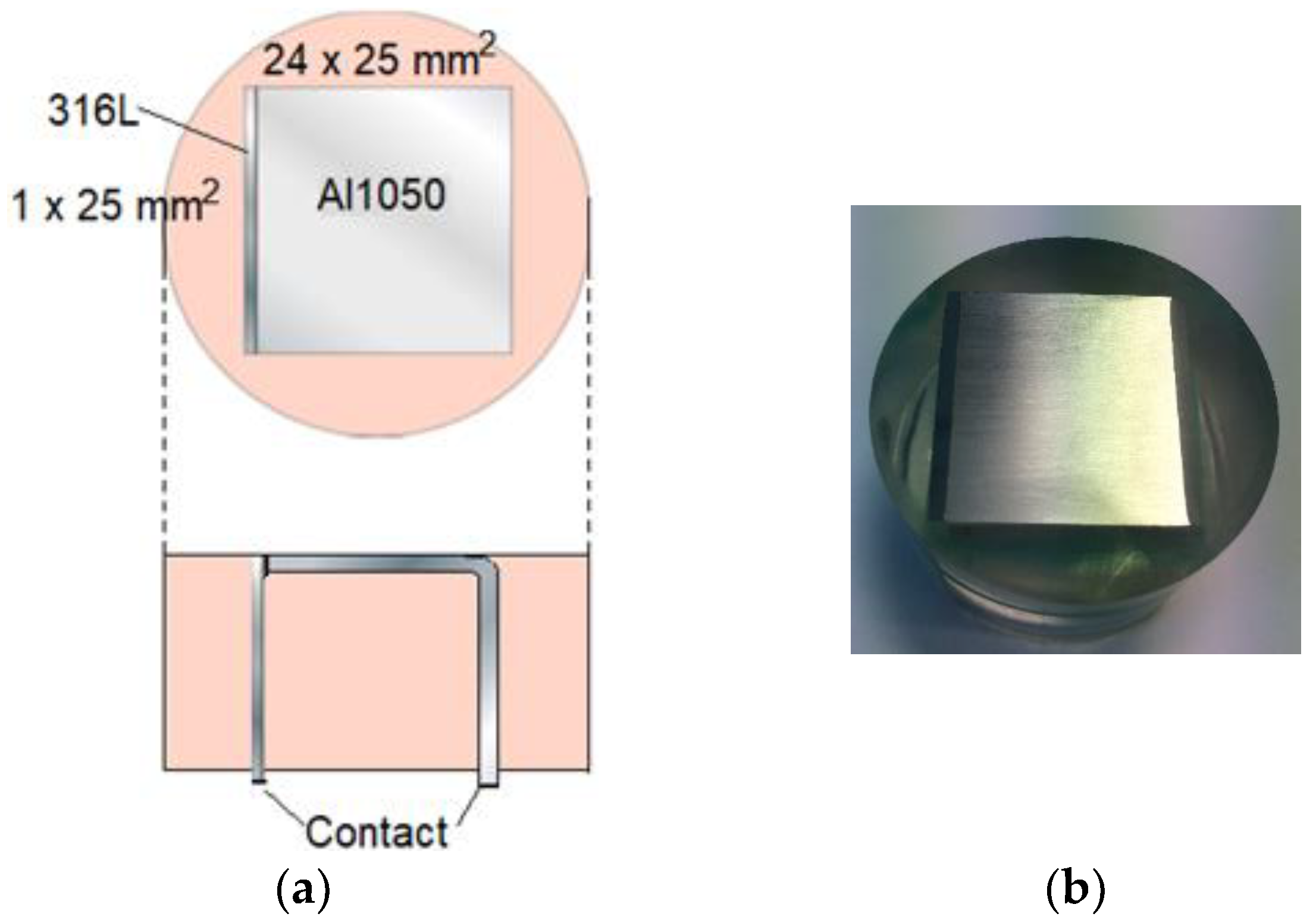
4.1. Specifications
4.2. Exposure Procedure
4.3. Post-Exposure Measurements
4.3.1. Geometrical Surface Characterization—Mapping of Localized Corrosion
4.3.2. FT-IR Microscopy
5. Results and Discussion
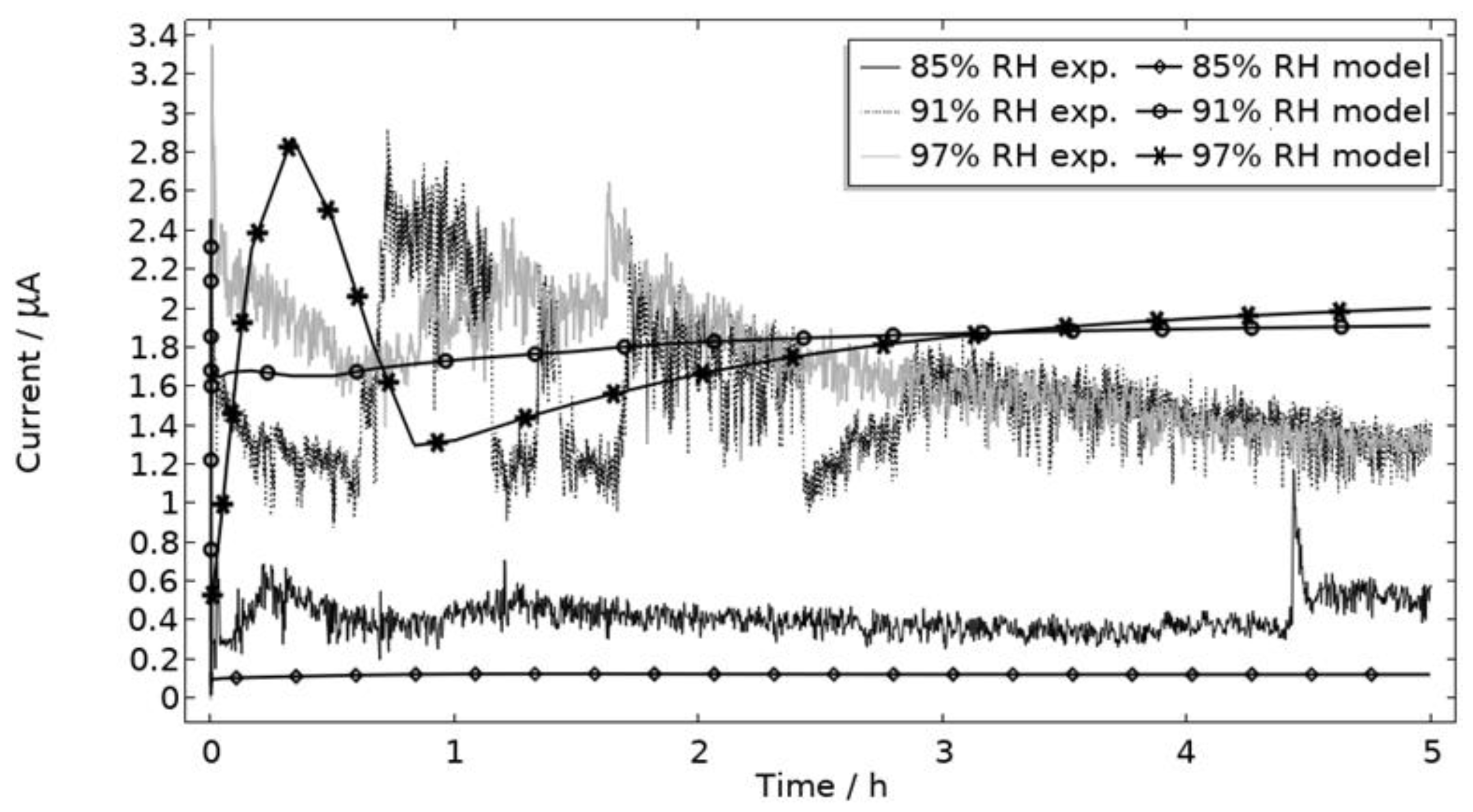
5.1. Calibration Cell Work
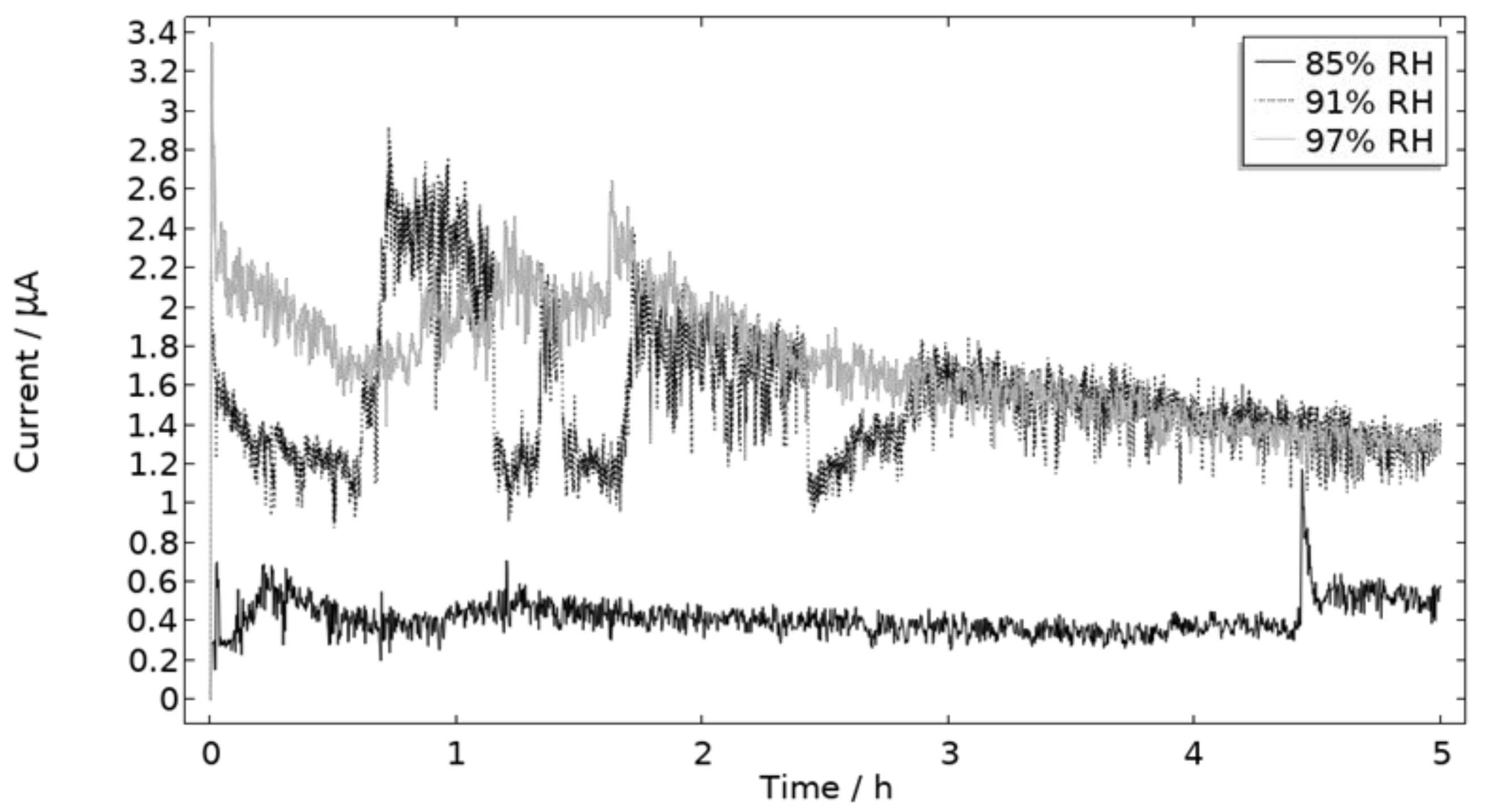
5.1.1. Exposure
5.1.2. Geometrical Characteristics of Localized Corrosion
5.1.3. FT-IR Microscopy
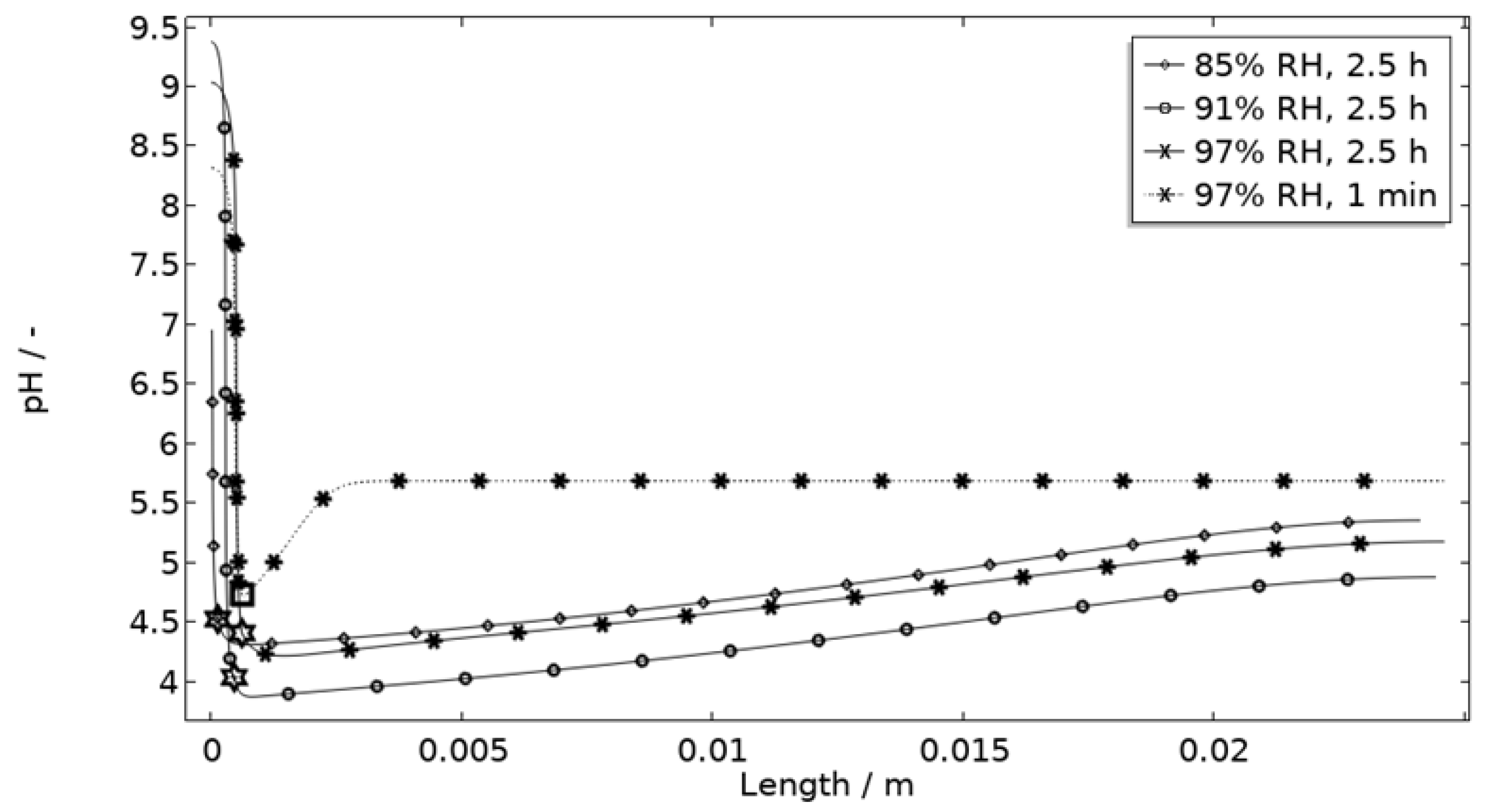
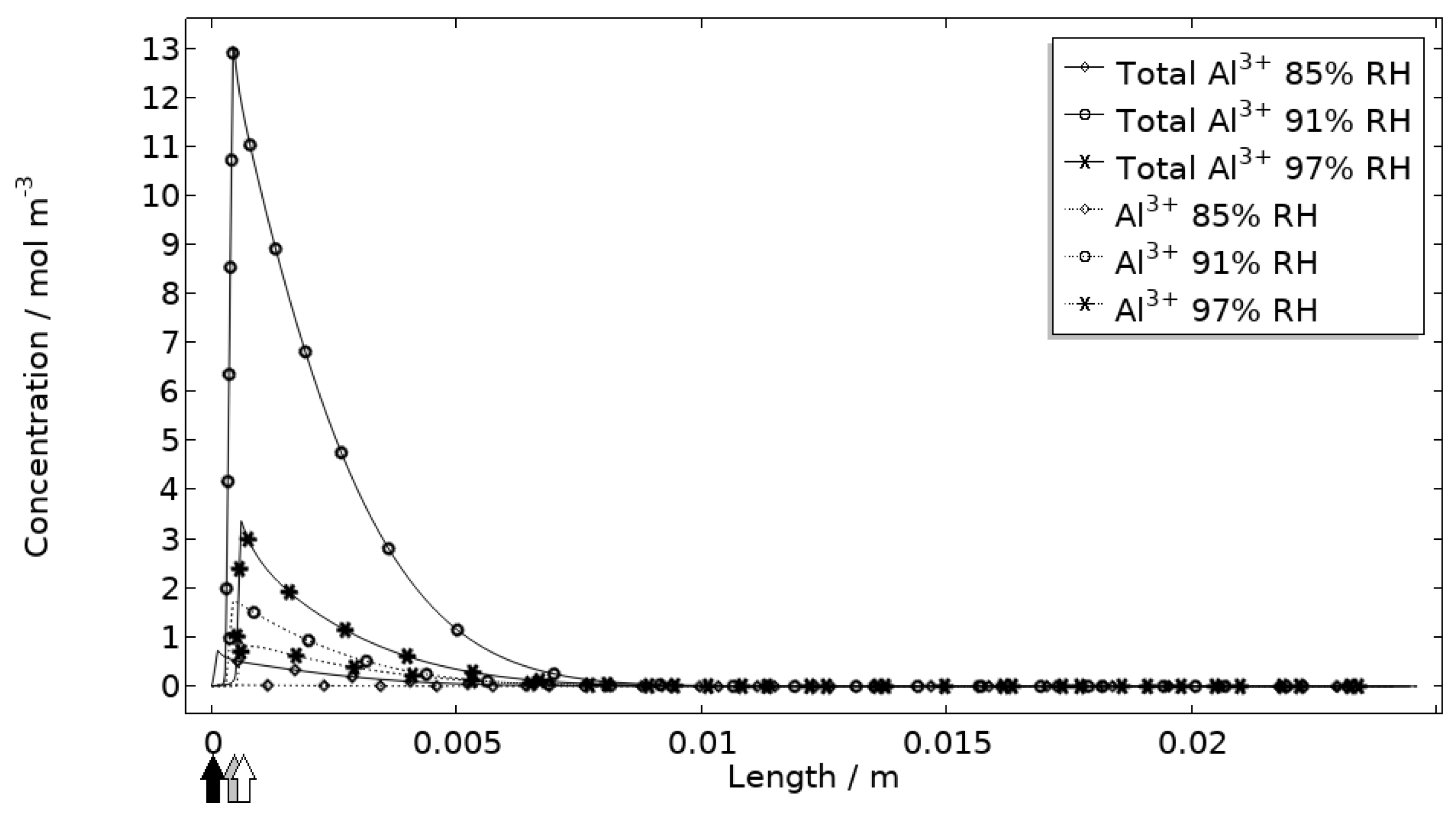
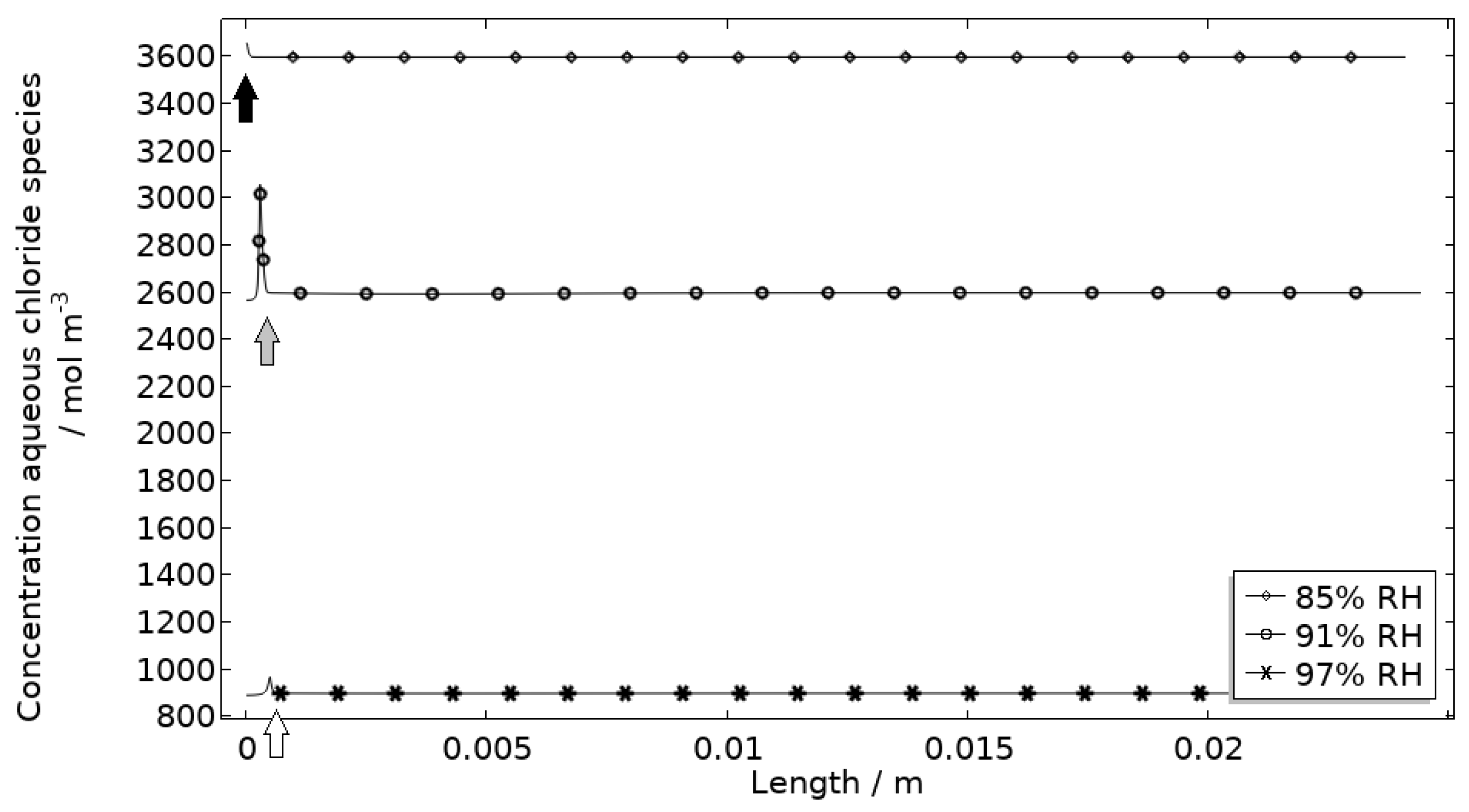
5.2. Model
5.2.1. Calibrated Model Characteristics
5.2.2. Evaluation of Model Restrictions
Geometry Description
Corrosion Products
6. Conclusions
- The description was set up in a manner that reduced the computation time, enabled analysis of local chemical behavior, and highlighted material damage as a single pit depth.
- Analysis of many underlying phenomena associated with atmospheric corrosion was possible for a certain NaCl load at three different RHs. The behavior of aqueous species, corrosion products, and the largest pit depth could be simulated for a 5 h long exposure.
- A well-structured calibration strategy was shown to be of utmost importance. A combination of post-exposure (geometrical mapping of pits and FT-IR) and in operando (galvanic current) measurements were necessary. These were all performed on an experimental calibration cell.
- The empirical pitting onset approach, although dictated by several simplifications, showed to be promising to simulate the galvanic system in a realistic way. The limitations were mainly observed when simulating the beginning of the exposure and were linked to the spread in pitting onset over time. The model matched the experimental measurements better for the two higher RHs (91% and 97%). An explanation for this can be linked to the simplified pit shape approximation.
- The simulated corrosion products could be correlated to experiments. However, quantitative means of measuring the products should be aimed to fully elucidate the behavior.
- It was seen that the calibration cell requires the exposures to be repeated, due to some reproducibility issues, especially when RH was decreased. Uneven wetting was the most likely cause for the inconsistency.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| a | Activity | [mol/m3] |
| c | Concentration | [mol/m3] |
| D | Diffusion coefficient | [m2/s] |
| dpit | Pit depth | [m] |
| F | Faraday’s constant, 96487 | [As/mol] |
| H | Henry’s constant | [M/atm] |
| I | Ionic strength | [mol dm−3] |
| i | Current density | [A m−2] |
| K | Equilibrium constant | [Mn] |
| Ks | Solubility product constant | [Mn] |
| L | Distance | [m] |
| kprec | Precipitation of solid corrosion products | [mol m−2 · s−1] |
| m0 | Total amount of solid corrosion product per monolayer area | [mol m−2] |
| mAl | Amount of aluminum dissolved per area | [mol m−2] |
| m′Al | Amount of chloride- corrected aluminum dissolution per area | [mol m−2] |
| ms | Amount of solid corrosion product per area | [mol m−2] |
| M | Molar mass | [kg mol−1] |
| N | Flux in electrolyte/liquid | [mol m−2 · s−1] |
| n | Number of electrons in electrochemical reaction | [-] |
| Nb | Flux boundary | [mol m−2 · s−1] |
| Nm | Number of monolayers | [-] |
| Npit | Number of conically shaped pits | [-] |
| R | Universal gas constant, 8.3143 | [J mol−1 K−1] |
| Ri | Volumetric reaction term for i | [mol m−3 t−1] |
| rpit | Radius conically shaped pits | [m] |
| Sb | Source term chemical reactions | [mol m−3 t−1] |
| S′b | Source term electrochemical reactions | [mol m−3 t−1] |
| T | Temperature | [K] |
| t | Time | [s] |
| x | Length dimension | [m] |
| z | Ion charge number | [-] |
| V | Potential in electrolyte | [V] |
| α | Transfer coefficient | [-] |
| γ | Activity coefficient | [-] |
| δ | Thickness of | |
| θ | Degree of coverage | [-] |
| θall | Degree of coverage of pit/corroding surface | [-] |
| κ | Liquid conductivity | [S m−1] |
| ν | Stoichiometric coefficient | [-] |
| ρ | Density | [kg m−3] |
| τ | Total molar amount of alumina per area consumed | [-] |
| χ | Open pit fraction | [-] |
| Subscripts | ||
| aq | Aqueous | |
| cell | Galvanic corrosion cell | |
| cs | Corroding surface | |
| i | Index for species | |
| R | Reaction indication | |
| ref | Reference | |
| s | Solid corrosion product | |
| sat | Saturated | |
| tot | Total |
References
- Leygraf, C.; Wallinder, I.O.; Tidblad, J.; Graedel, T. Atmospheric Corrosion, 2nd ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 272–281. [Google Scholar]
- Ström, M. A century with salt spray testing. Time for a final phasing out by a replacement based on newly developed more capable test regimes. In Proceedings of the EUROCORR, European Corrosion Congress, Pisa, Italy, 8–12 September 2014. [Google Scholar]
- Simillion, H.; Dolgikh, O.; Terryn, H.; Deconinck, J. Atmospheric corrosion modelling. Corros. Rev. 2014, 32, 73–100. [Google Scholar] [CrossRef]
- Sharland, S.M. A review of the theoretical modelling of crevice and pitting corrosion. Corros. Sci. 1987, 27, 289–323. [Google Scholar] [CrossRef]
- Zamani, G.; Porter, J.F.; Mufti, A.A. A survey of computational efforts in the field of corrosion engineering. Int. J. Numer. Methods Eng. 1986, 23, 1295–1311. [Google Scholar] [CrossRef]
- Liu, C.; Kelly, R.G. A Review of the application of finite element method (FEM) to localized corrosion modeling. Corrosion 2019, 75, 1285–1299. [Google Scholar] [CrossRef]
- Hebert, K.; Alkire, R. Dissolved metal species mechanism for initiation of crevice corrosion of aluminum: II. Mathematical model. J. Electrochem. Soc. 1983, 130, 1007–1014. [Google Scholar] [CrossRef]
- Sharland, S.M.; Tasker, P.W. A mathematical model of crevice pitting corrosion—I. The physical model. Corros. Sci. 1988, 28, 603–620. [Google Scholar] [CrossRef]
- Watson, M.K.; Postlethwaite, J. Numerical simulation of crevice corrosion of stainless steels and nickel alloys in chloride solutions. Corrosion 1990, 46, 522–530. [Google Scholar] [CrossRef]
- Vuillemin, B.; Oltra, R.; Cottis, R.; Crusset, D. Consideration of the formation of solids and gases in steady state modelling of crevice corrosion propagation. Electrochim. Acta 2007, 52, 7570–7576. [Google Scholar] [CrossRef]
- Kennell, G.F.; Evitts, R.W.; Heppner, K.L. A critical crevice solution and IR drop crevice corrosion model. Corros. Sci. 2008, 50, 1716–1725. [Google Scholar] [CrossRef]
- White, S.P.; Weir, G.J.; Laycock, N.J. Calculating chemical concentrations during the initiation of crevice corrosion. Corros. Sci. 2005, 42, 605–629. [Google Scholar] [CrossRef]
- Laycock, N.J.; White, S.P. Computer simulation of single pit propagation in stainless steel under potentiostatic control. J. Electrochem. Soc. 2001, 148, B264–B275. [Google Scholar] [CrossRef]
- Organ, L.; Scully, J.R.; Mikhailov, A.S.; Hudson, J.L. A spatiotemporal model of interactions among metastable pits and the transition to pitting corrosion. Electrochim. Acta 2005, 51, 225–241. [Google Scholar] [CrossRef]
- Organ, L.; Tiwary, Y.; Scully, J.R.; Mikhailov, A.S.; Hudson, J.L. Interactions among metastable pits on heterogeneous electrodes. Electrochim. Acta 2007, 52, 6784–6792. [Google Scholar] [CrossRef]
- Scheiner, S.; Hellmich, C. Stable pitting corrosion of stainless steel as diffusion-controlled dissolution process with a sharp moving electrode boundary. Corros. Sci. 2007, 49, 319–346. [Google Scholar] [CrossRef]
- McCafferty, E. The electrode kinetics of pit initiation on aluminum. Corros. Sci. 1995, 37, 481–492. [Google Scholar] [CrossRef]
- Guseva, O.; Schmutz, P.; Suter, T.; von Trzebiatowski, O. Modelling of anodic dissolution of pure aluminium in sodium chloride. Electrochim. Acta 2009, 54, 4514–4524. [Google Scholar] [CrossRef]
- Topa, V.; Demeter, A.S.; Hotoiub, L.; Deconinck, D.; Deconinck, J. A transient multi-ion transport model for galvanized steel corrosion protection. Electrochim. Acta 2012, 77, 339–347. [Google Scholar] [CrossRef]
- Cross, S.R.; Gollapudi, S.; Schuh, C.A. Validated numerical modeling of galvanic corrosion of zinc and aluminum coatings. Corros. Sci. 2014, 88, 226–233. [Google Scholar] [CrossRef]
- Deshpande, K.B. Validated numerical modelling of galvanic corrosion for couples: Magnesiumalloy (AE44)–mild steel and AE44–aluminium alloy (AA6063) in brine solution. Corros. Sci. 2010, 52, 3514–3522. [Google Scholar] [CrossRef]
- Munn, R.S.; Devereux, O.F. Numerical modeling and solution of galvanic corrosion systems: Part I. Governing differential equation and electrodic boundary conditions. Corrosion 1991, 47, 612–618. [Google Scholar] [CrossRef]
- Munn, R.S.; Devereux, O.F. Numerical modeling and solution of galvanic corrosion systems: Part II. Finite-element formulation and descriptive examples. Corrosion 1991, 47, 618–634. [Google Scholar] [CrossRef]
- Deshpande, K.B. Effect of aluminium spacer on galvanic corrosion between magnesium and mild steel using numerical model and SVET experiments. Corros. Sci. 2012, 62, 184–191. [Google Scholar] [CrossRef]
- Thébault, F.; Vuillemina, B.; Oltraa, R.; Allely, C.; Oglec, K. Reliability of numerical models for simulating galvanic corrosion processes. Electrochim. Acta 2012, 82, 349–355. [Google Scholar] [CrossRef]
- Palani, S.; Hack, T.; Deconinck, J.; Lohner, H. Validation of predictive model for galvanic corrosion under thin electrolyte layers: An application to aluminium 2024-CFRP material combination. Corros. Sci. 2014, 78, 89–100. [Google Scholar] [CrossRef]
- King, A.D.; Lee, J.S.; Scully, J.R. Finite element analysis of the galvanic couple current and potential distribution between Mg and 2024-T351 in a Mg rich primer configuration. J. Electrochem. Soc. 2016, 163, C342–C356. [Google Scholar] [CrossRef]
- Xiao, J.; Chaudhuri, S. Predictive modeling of localized corrosion: An application to aluminum alloys. Electrochim. Acta 2011, 56, 5630–5641. [Google Scholar] [CrossRef]
- Abodi, L.C.; DeRose, J.A.; Van Damme, S.; Demeter, A.; Suter, T.; Deconinck, J. Modeling localized aluminum alloy corrosion in chloride solutions under non- equilibrium conditions: Steps toward understanding pitting initiation. Electrochim. Acta 2012, 63, 169–178. [Google Scholar] [CrossRef]
- Mizuno, D.; Kelly, R.G. Galvanically induced intergranular corrosion of AA5083-H131 under atmospheric exposure conditions: Part 2—Modeling of the damage distribution. Corrosion 2012, 69, 681–692. [Google Scholar] [CrossRef]
- Guseva, O.; DeRose, J.A.; Schmutz, P. Modelling the early stage time dependence of localized corrosion in aluminium alloys. Electrochim. Acta 2013, 88, 821–831. [Google Scholar] [CrossRef]
- Yin, L.; Jin, Y.; Leygraf, C.; Pan, J. A FEM model for investigation of micro-galvanic corrosion of Al alloys and effects of deposition of corrosion products. Electrochm. Acta 2016, 192, 310–318. [Google Scholar] [CrossRef]
- Yin, L.; Jin, Y.; Leygraf, C.; Birbilis, N.; Pan, J. Numerical simulation of micro-galvanic corrosion in Al alloys: Effect of geometric factors. J. Electrochem. Soc. 2017, 164, C75–C84. [Google Scholar] [CrossRef]
- Yin, L.; Jin, Y.; Leygraf, N.; Pan, J. Numerical Simulation of Micro-Galvanic Corrosion of Al Alloys: Effect of Chemical Factors. J. Electrochem. Soc. 2017, 164, C768–C778. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, L.; Jin, Y.; Pan, J.; Leygraf, C. Numerical Simulation of Micro-Galvanic Corrosion in Al Alloys: Steric Hindrance Effect of Corrosion Product. J. Electrochem. Soc. 2017, 164, C1035–C1043. [Google Scholar] [CrossRef]
- Murer, N.; Oltra, R.; Vuilemin, B.; Neel, O. Numerical modelling of the galvanic coupling in aluminium alloys: A discussion on the application of local probe techniques. Corros. Sci. 2010, 52, 130–139. [Google Scholar] [CrossRef]
- Deshpande, K.B. Numerical modeling of micro-galvanic corrosion. Electrochim. Acta 2001, 56, 1737–1745. [Google Scholar] [CrossRef]
- Thébault, F.; Vuillemin, B.; Oltra, R.; Allely, C.; Ogle, K. Modeling bimetallic corrosion under thin electrolyte films. Corros. Sci. 2011, 53, 201–207. [Google Scholar] [CrossRef]
- Simillion, H.; Van den Steen, N.; Montoya, R.; Terryn, H. Dimension reduction for computational enhancements in thin film electrochemical modelling. J. Electrochem. Soc. 2016, 163, C873–C882. [Google Scholar] [CrossRef]
- Ruiz-Garcia, A.; Jimenez-Gonzalez, E.; Cano, E.; Mayen-Mondragon, R.; Genesca, J.; Montoya, R. The corrosion products in a carbon steel/aluminum alloy galvanic couple under thin electrolyte films: An efficient model. Electrochem. Commun. 2019, 104, 106485. [Google Scholar] [CrossRef]
- Cui, F.; Presuel-Moreno, F.J.; Kelly, R.G. Experimental and computational evaluation of the protection provided by an aluminum cladding to AA2024-T3 exposed at a seacoast environment. Corrosion 2006, 62, 251–263. [Google Scholar] [CrossRef]
- Venkatraman, M.S.; Cole, I.S.; Emmanuel, B. Model for corrosion of metals covered with thin electrolyte layers: Pseudo-steady state diffusion of oxygen. Electrochim. Acta 2011, 56, 7171–7179. [Google Scholar] [CrossRef]
- Okada, N.; Matsumoto, M.; Nishihara, K.; Kimoto, M.; Kudo, T.; Fujimoto, S. Numerical analysis model of galvanic corrosion with ion movement and reaction. ISIJ Int. 2010, 50, 743–751. [Google Scholar] [CrossRef]
- Lee, J.M. Numerical analysis of galvanic corrosion of Zn/Fe interface beneath a thin electrolyte. Electrochim. Acta 2006, 51, 3256–3260. [Google Scholar] [CrossRef]
- Van den Steen, N.; Simillion, H.; Dolgikh, O.; Terryn, H.; Deconinck, J. An integrated modeling approach for atmospheric corrosion in presence of a varying electrolyte film. Electrochim. Acta 2016, 187, 714–723. [Google Scholar] [CrossRef]
- Van den Steen, N.; Simillion, H.; Thierry, D.; Terryn, H.; Deconinck, J. Comparing modeled and experimental accelerated corrosion tests on steel. J. Electrochem. Soc. 2017, 164, C554–C562. [Google Scholar] [CrossRef]
- Hoerlé, S.; Mazaudier, F.; Dillman, P.; Santarini, G. Advances in understanding atmospheric corrosion of iron. II. Mechanistic modelling of wet-dry cycles. Corros. Sci. 2004, 46, 1431–1465. [Google Scholar] [CrossRef]
- Ahmad, Z. Principles of Corrosion Engineering and Corrosion Control, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2006; pp. 550–575. [Google Scholar]
- Lim, M.L.C.; Kelly, R.G.; Scully, J.R. Overview of intergranular corrosion mechanisms, phenomenological observations, and modeling of AA5083. Corrosion 2016, 72, 198–220. [Google Scholar] [CrossRef] [PubMed]
- Adjel, S.; Merakeb, N.; Benchouia, S.; Ehlers, S.; Baccouche, M. Effect of corrosion pit density on the fatigue life of aluminum 1050A. Int. J. Adv. Manuf. Technol. 2018, 97, 3163–3177. [Google Scholar] [CrossRef]
- Ezuber, H.; El-Houd, A.; El-Shawesh, F. A study on the corrosion behavior of aluminum alloys in seawater. Mater. Des. 2008, 29, 801–805. [Google Scholar] [CrossRef]
- Pride, S.T.; Scully, J.R.; Hudson, J.L. Metastable pitting of aluminum and criteria for the transition to stable pit growth. J. Electrochem. Soc. 1994, 141, 3028–3040. [Google Scholar] [CrossRef]
- Frankel, G.S.; Hunkeler, F. Metastable pitting of stainless steel. Corrosion 1987, 43, 429–436. [Google Scholar] [CrossRef]
- Williams, D.E.; Stewart, J.; Balkwill, P.H. The nucleation, growth and stability of micropits in stainless steel. Corros. Sci. 1994, 36, 1213–1235. [Google Scholar] [CrossRef]
- Hamann, C.H.; Hamnett, A.; Vielstich, W. Electrochemistry, 2nd ed.; Wiley: Weinheim, Germany, 2007; p. 96. [Google Scholar]
- Drazic, D.M.; Popic, J. Corrosion rates and negative difference effects for Al and some Al alloys. J. Appl. Electrochem. 1999, 29, 43–50. [Google Scholar] [CrossRef]
- Drazic, D.M.; Popic, J. Hydrogen evolution on aluminium in chloride solutions. J. Electroanal. Chem. 1993, 357, 105–116. [Google Scholar] [CrossRef]
- Curioni, M.; Scenini, F. The mechanism of hydrogen evolution during anodic polarization of aluminium. Electrochim. Acta 2015, 180, 712–721. [Google Scholar] [CrossRef]
- Newman, J.; Balsara, N.P. Electrochemical Systems, 4th ed.; Wiley: Hoboken, NJ, USA, 1991; pp. 81–104, 229–247. [Google Scholar]
- Battino, R.; Rettich, T.R.; Tominaga, T. The solubility of nitrogen and air in liquids. J. Phys. Chem. Ref. Data 1984, 13, 563–600. [Google Scholar] [CrossRef]
- Petrucci, R.H.; Herring, F.G.; Bissonnette, C.; Madura, J.D. General Chemistry: Principles and Modern Applications, 10th ed.; Pearson: North York, ON, Canada, 2007. [Google Scholar]
- Diamond, L.W.; Akinfiev, N.N. Solubility of CO2 in water from −1.5 to 100 °C and from 0.1 to 100 MPa: Evaluation of literature data and thermodynamic modelling. Fluid Phase Equilib. 2003, 208, 265–290. [Google Scholar] [CrossRef]
- Steel, L.; Liu, Q.; Mackay, E.; Maroto-Valer, M.M. CO2 solubility measurements in brine under reservoir conditions: A comparison of experimental and geochemical modeling methods. Greenhouse Gases Sci. Technol. 2016, 6, 197–217. [Google Scholar] [CrossRef]
- MINEQL+, Version 4.6. Software Program. Informer Technologies, Inc.: Los Angeles, CA, USA, 2007.
- Baes, C.F.; Mesmer, R.E. The Hydrolysis of Cations; Reprint Edition; Wiley: Hoboken, NJ, USA, 1986. [Google Scholar]
- Foley, R.T.; Nguyen, T.H. The chemical nature of aluminum corrosion: V. Energy transfer in aluminum dissolution. J. Electrochem. Soc. 1982, 129, 464–467. [Google Scholar] [CrossRef]
- May, H.M.; Helmke, P.A.; Jackson, M.L. Gibbsite solubility and thermodynamic properties of hydroxy-aluminum ions in aqueous solution at 25 °C. Geochim. Cosmochim. Acta 1979, 43, 861–868. [Google Scholar] [CrossRef]
- Bénézeth, P.; Palmer, D.A.; Anovitz, L.M.; Horita, J. Dawsonite synthesis and reevaluation of its thermodynamic properties from solubility measurements: Implications for mineral trapping of CO2. Geochim. Cosmochim. Acta 2007, 71, 4438–4455. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J.; Smith, D. Elements of Physical Chemistry, 6th ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Nordsveen, M.; Nesic, S.; Nyborg, R.; Stangeland, A. A mechanistic model for carbon dioxide corrosion of mild steel in the presence of protective iron carbonate films—Part 1: Theory and verification. Corrosion 2003, 59, 443–455. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd ed.; Dover Publications: Mineola, NY, USA, 2002; pp. 392–431. [Google Scholar]
- Wang, X.; Conway, W.; Burns, R.; McCann, N.; Maeder, M. Comprehensive study of the hydration and dehydration reactions of carbon dioxide in aqueous solution. J. Phys. Chem. A 2010, 114, 1734–1740. [Google Scholar] [CrossRef] [PubMed]
- Cavanaugh, M.K.; Buchheit, R.G.; Birbilis, N. Modeling the environmental dependence of pit growth using neural network approaches. Corros. Sci. 2010, 52, 3070–3077. [Google Scholar] [CrossRef]
- Zaid, B.; Saidi, D.; Benzaid, A.; Hadji, S. Effects of pH and chloride concentration on pitting corrosion of AA6061 aluminum alloy. Corros. Sci. 2008, 50, 1841–1847. [Google Scholar] [CrossRef]
- Birbilis, N.; Buchheit, R.G. Investigation and discussion of characteristics for intermetallic phases common to aluminum alloys as a function of solution pH. J. Electrochem. Soc. 2008, 155, C117–C126. [Google Scholar] [CrossRef]
- Mizuno, D.; Kelly, R.G. Galvanically induced intergranular corrosion of AA5083-H131 under atmospheric exposure conditions: Part 1—Experimental characterization. Corrosion 2013, 69, 580–592. [Google Scholar] [CrossRef]
- Robinson, R.A. The vapour pressures of solutions of potassium chloride and sodium chloride. Transact. R. Soc. N. Z. 1945, 75, 203–217. [Google Scholar]
- Greenspan, L. Humidity fixed points of binary saturated aqueous solutions. J. Res. Natl. Bur. Stand.—A. Phys. Chem. 1977, 81, 89–96. [Google Scholar] [CrossRef]
- Turner, R.C.; Ross, G.J. Conditions in solution during the formation of gibbsite in dilute A1 salt solutions. 4. Effect of C1 concentration and temperature and a proposed mechanism for gibbsite formation. Can. J. Chem. 1970, 48, 723–729. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Qvarfort, R. New electrochemical cell for pitting corrosion testing. Corros. Sci. 1988, 28, 135–140. [Google Scholar] [CrossRef]
- Alexander, C.L.; Liu, C.; Alshanoon, A.; Katona, R.M.; Kelly, R.G.; Carpenter, J.; Bryan, C.; Schindelholz, E. Oxygen Reduction on Stainless Steel in Concentrated Chloride Media. J. Electrochem. Soc. 2018, 165, C869–C877. [Google Scholar] [CrossRef]
- Riesgraf, D.A.; May, M.L. Infrared Spectra of Aluminum Hydroxide Chlorides. Appl. Spectrosc. 1978, 32, 362–366. [Google Scholar] [CrossRef]
- Teagarden, D.L.; Kozlowski, J.F.; White, J.L.; Hem, S.L. Aluminum chlorohydrate I: Structure studies. J. Pharm. Sci. 1981, 70, 758–761. [Google Scholar] [CrossRef] [PubMed]
- Le Bozec, N.; Persson, D.; Nazarov, A.; Thierry, D. Investigation of Filiform Corrosion on Coated Aluminum Alloys by FTIR Microspectroscopy and Scanning Kelvin Probe. J. Electrochem. Soc. 2002, 149, B403–B408. [Google Scholar] [CrossRef]
- Serna, C.J.; Lyons, J.C.; White, J.L.; Hem, S.L. Stabilization of aluminum hydroxide gel by specifically adsorbed carbonate. J. Pharm. Sci. 1983, 72, 769–771. [Google Scholar] [CrossRef] [PubMed]







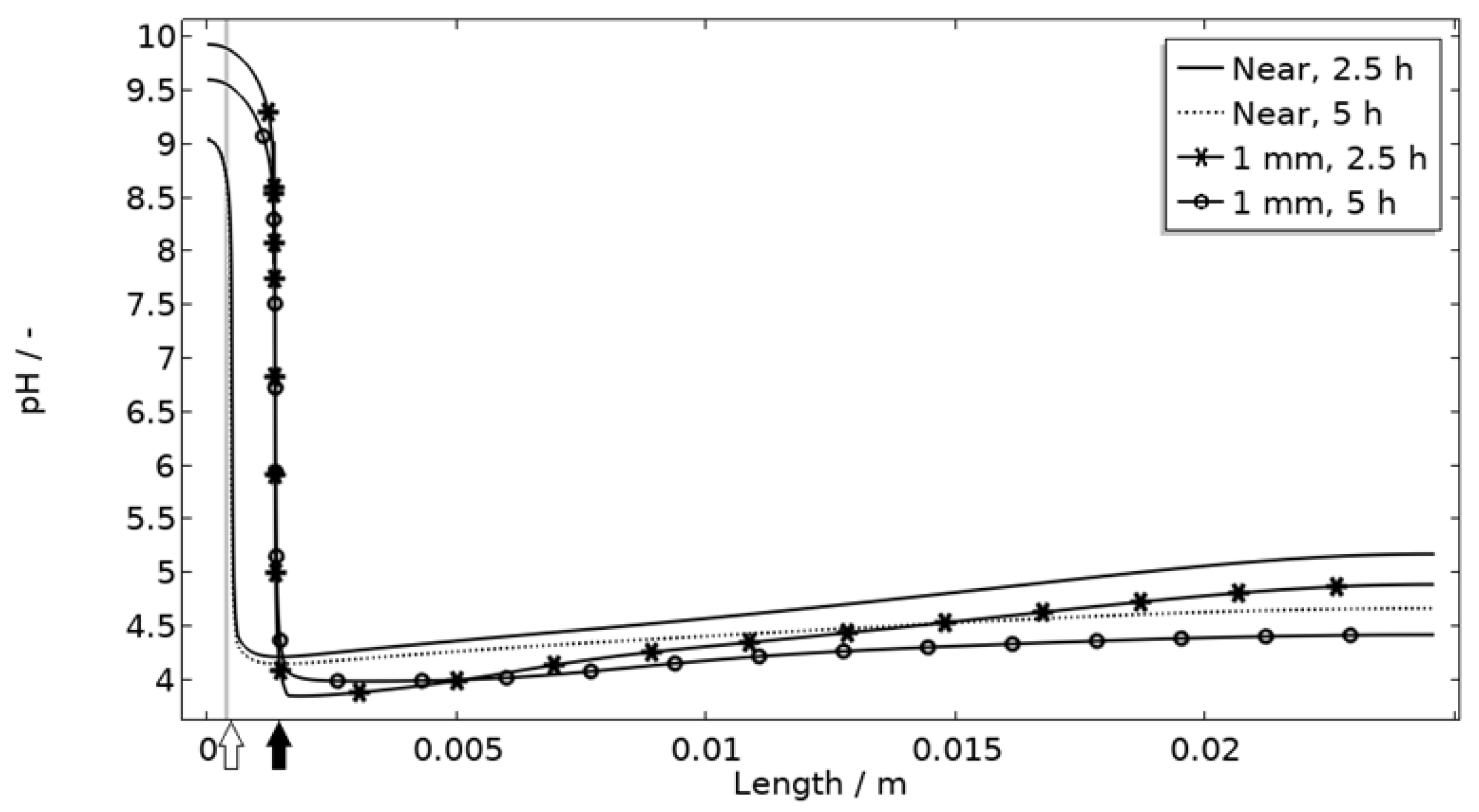
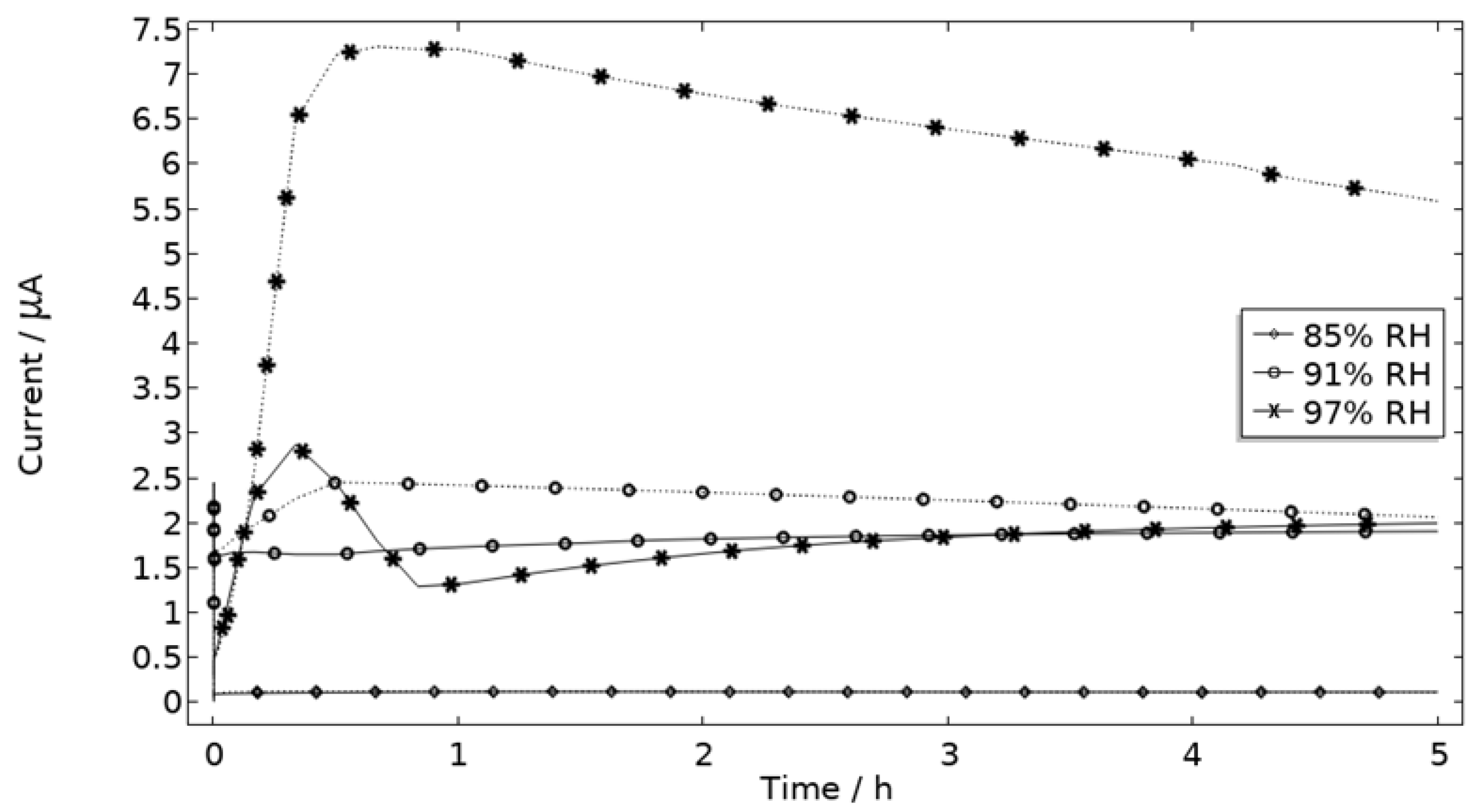

| Reaction | Property and Value | Comment |
|---|---|---|
| O2(g) ↔ O2(aq) | = 0.26875 mol/m3 | For 0.21 bar, temperature and NaCl dependent [60,61] 1 |
| CO2(g) ↔ CO2(aq) | H= 3.39 · 10−2 M/atm | For 324 ppm (1 bar atmosphere), temperature [62] and NaCl [63] dependent 1 |
| H2O ↔ H+ + OH− | logK = −14 | [64] |
| H2CO3 ↔ HCO3- + H+ | logK = −6.34 | [64] |
| HCO3- ↔ CO32- + H+ | logK = −6.34 | [64] |
| Al3+ + H2O ↔ AlOH2+ + H+ | logK = −4.97 | [64] |
| Al3+ + 2H2O ↔ Al(OH)2+ + 2H+ | logK = −9.3 | [65] |
| Al3+ + 3H2O ↔ Al(OH)3(aq) +3H+ | logK = −16.791 | [65] |
| Al3+ + 4H2O ↔ Al(OH)4- +4H+ | logK = −23 | [64] |
| 2Al3+ + 2H2O ↔ Al2(OH)24+ + 2H+ | logK = −7.7 | [65] |
| AlOH2+ + Cl− ↔ Al(OH)Cl+ | logK = 0.516 | [66] |
| Al3+ + Cl− ↔ AlCl2+ | logK = 0.477 | [66] |
| Al(OH)3(aq) ↔ Al(OH)3(s) | logKs = 8.41 | Derived from [64,65,67] |
| NaAlCO3(OH)2(s) + 2H2O ↔ Al(OH)4- + HCO3- + Na+ + H+ | logKs= −17.86 | [68] |
| Al(OH)Cl+ + H2O ↔ Al(OH)2Cl(s) + H+ | logKs = −21.03 | Estimation from Foley and Nguyen [66] |
| AlCl2+ + 2H2O → Al(OH)2Cl(s) + 2H+ Al(OH)Cl+ + H2O → Al(OH)2Cl(s) + H+ | k = 4 · 10−6 s−1 | Two irreversible reactions, same rate constant [32]. Full precipitation of formed Al(OH)2Cl assumed. |
| Property | Value | Comment |
|---|---|---|
| 1.33 · 10−9 m2/s | [69] | |
| 2.03 · 10−9 m2/s | [69] | |
| 5.41 · 10−10 m2/s | [31] | |
| 9.30 · 10−9 m2/s | [69] | |
| 5.30 · 10−9 m2/s | [69] | |
| 9.22 · 10−10 m2/s | [69] | |
| 1.18 · 10−9 m2/s | [69] | |
| 1.92 · 10−9 m2/s | [70] | |
| 2.42 · 10−9 m2/s | NaCl concentration dependent [30]. Value for infinitely diluted solution. |
| Property | Value | Comment |
|---|---|---|
| pH | 7 | Initial pH. |
| MAl | 2.698 · 10−2 kg/mol | Density aluminum at 25 °C. |
| ρAl | 2710 kg/m3 | Molar mass aluminum at 25 °C. |
| Nm · m0 | 1.5 · 10−4 mol/m2 | From model calibration. Total molar site availability per area for precipitation. |
| kprec | 1 · 10−8 mol/(m2s) | From model calibration. Rate constant for precipitation (and dissolution) of solid corrosion products/precipitates. is the total concentration of aluminum ions. |
| τ | 9.22 · 10−10 m2/s | From model calibration. Total molar amount of aluminum metal per area consumed at the pit for it to be fully open. |
| θall | 1.18 · 10−9 m2/s | From model calibration. Allowed span for coverage of pit opening. |
| Property | Value | ||
|---|---|---|---|
| 85% RH | 91% RH | 97% RH | |
| 3600 mol/m3 | 2600 mol/m3 | 900 mol/m3 | |
| δ | 4.21 · 10−6 m | 5.83 · 10−6 m | 1.68 · 10−5 m |
| Property | Pit Depth/μm | Projected Area/mm2 | ||||
|---|---|---|---|---|---|---|
| 85% RH | 91% RH | 97% RH | 85% RH | 91% RH | 97% RH | |
| Total projected area pits | - | - | - | 2.886.10–2 | 4.226.10–1 | 1.620.10–1 |
| Five deepest pit average (FDPA) | 6.11 | 9.70 | 29.18 | 5.254.10–3 | 6.694.10–2 | 5.912.10–3 |
| Name | Chemical Formula | Location |
|---|---|---|
| Dawsonite | NaAlCO3(OH)2 | Outer parts and outside of localized corrosion attack. |
| Amorphous aluminum hydroxide cont. carbonate | Al(OH)3−2x(CO3)x | At the localized corrosion attack. |
| Aluminum hydroxy chlorides | Al2(OH)5Cl·2H2O Al(OH)Cl2, Al(OH)2Cl | At the localized corrosion attack. |
| Sodium carbonate | Na2CO3 · xH2O | On the stainless-steel surface. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavalis, T.G.; Ström, M.; Persson, D.; Wendel, E.; Ahlström, J.; Törne, K.B.; Taxén, C.; Rendahl, B.; Voltaire, J.; Eriksson, K.; et al. Mechanistic Model with Empirical Pitting Onset Approach for Detailed and Efficient Virtual Analysis of Atmospheric Bimetallic Corrosion. Materials 2023, 16, 923. https://doi.org/10.3390/ma16030923
Zavalis TG, Ström M, Persson D, Wendel E, Ahlström J, Törne KB, Taxén C, Rendahl B, Voltaire J, Eriksson K, et al. Mechanistic Model with Empirical Pitting Onset Approach for Detailed and Efficient Virtual Analysis of Atmospheric Bimetallic Corrosion. Materials. 2023; 16(3):923. https://doi.org/10.3390/ma16030923
Chicago/Turabian StyleZavalis, Tommy G., Mats Ström, Dan Persson, Erik Wendel, Johan Ahlström, Karin Beaussant Törne, Claes Taxén, Bo Rendahl, Joakim Voltaire, Katarina Eriksson, and et al. 2023. "Mechanistic Model with Empirical Pitting Onset Approach for Detailed and Efficient Virtual Analysis of Atmospheric Bimetallic Corrosion" Materials 16, no. 3: 923. https://doi.org/10.3390/ma16030923
APA StyleZavalis, T. G., Ström, M., Persson, D., Wendel, E., Ahlström, J., Törne, K. B., Taxén, C., Rendahl, B., Voltaire, J., Eriksson, K., Thierry, D., & Tidblad, J. (2023). Mechanistic Model with Empirical Pitting Onset Approach for Detailed and Efficient Virtual Analysis of Atmospheric Bimetallic Corrosion. Materials, 16(3), 923. https://doi.org/10.3390/ma16030923






