Optimizing the Compressive Properties of Porous Aluminum Composites by Varying Diamond Content, Space Holder Size and Content
Abstract
1. Introduction
2. Methodology
2.1. Experimental Procedure
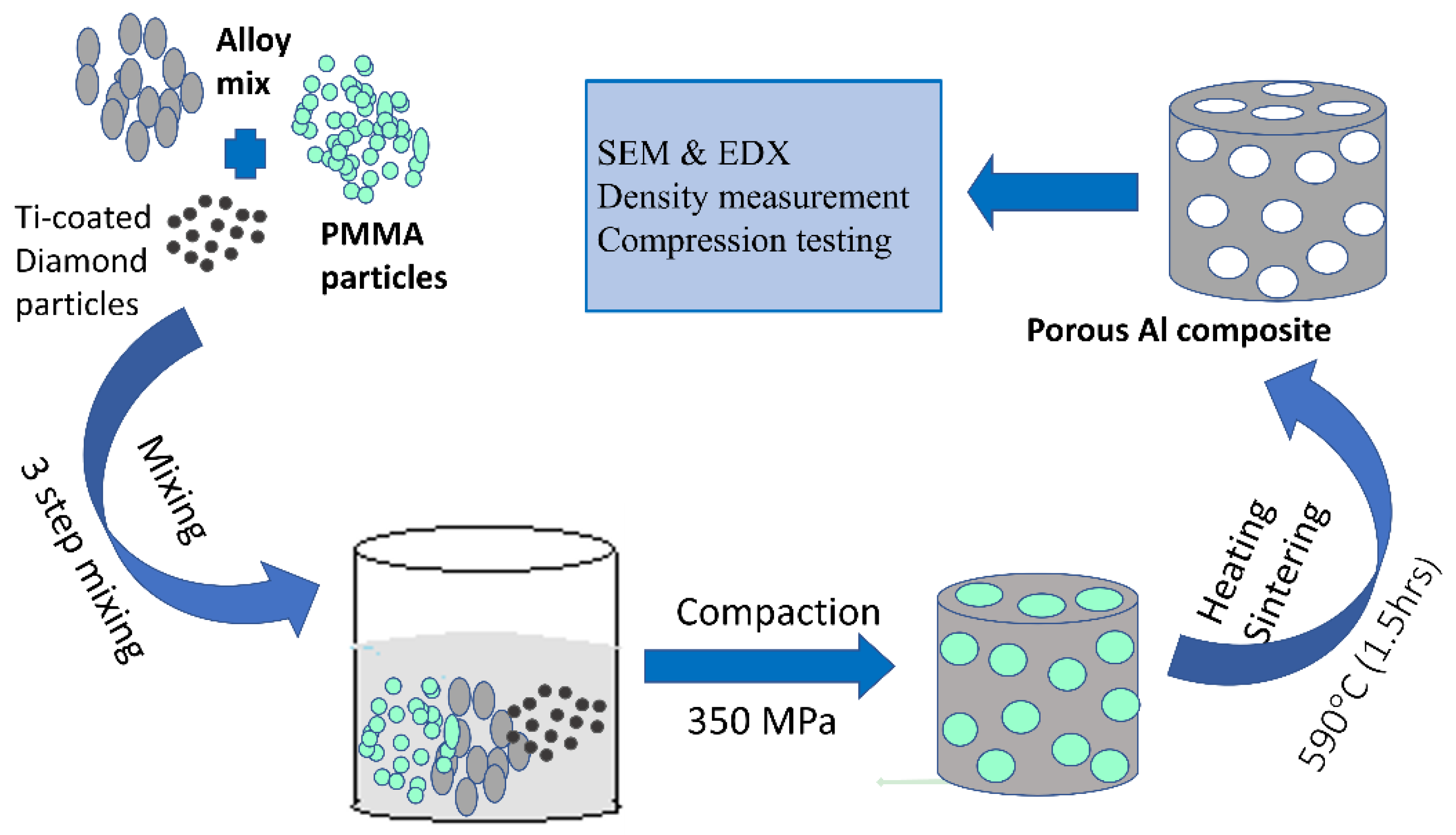
2.1.1. Fabrication of Porous Al Composites
2.1.2. Characterization
2.2. Taguchi’s Design of Experiments (DOE)
3. Results and Discussion
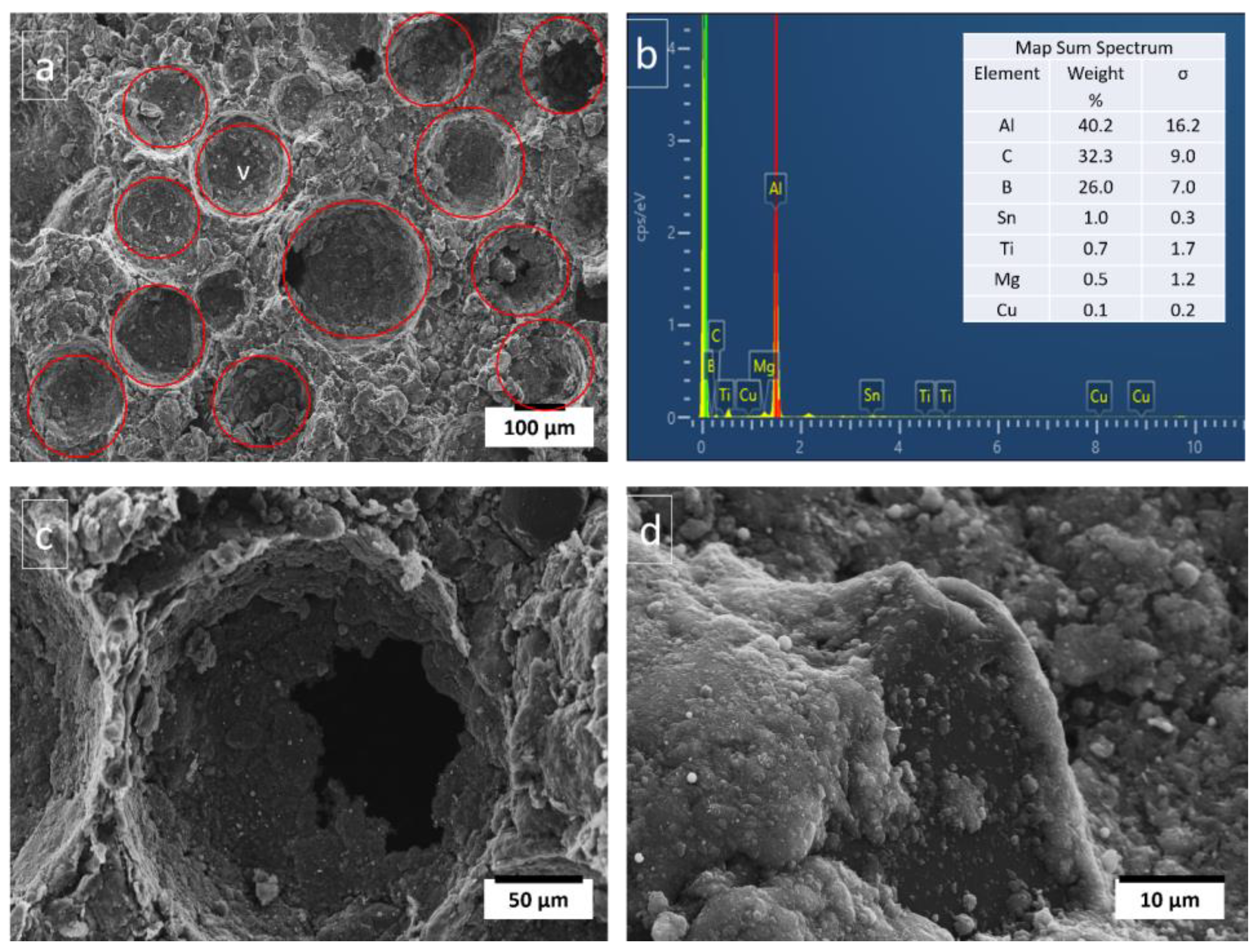
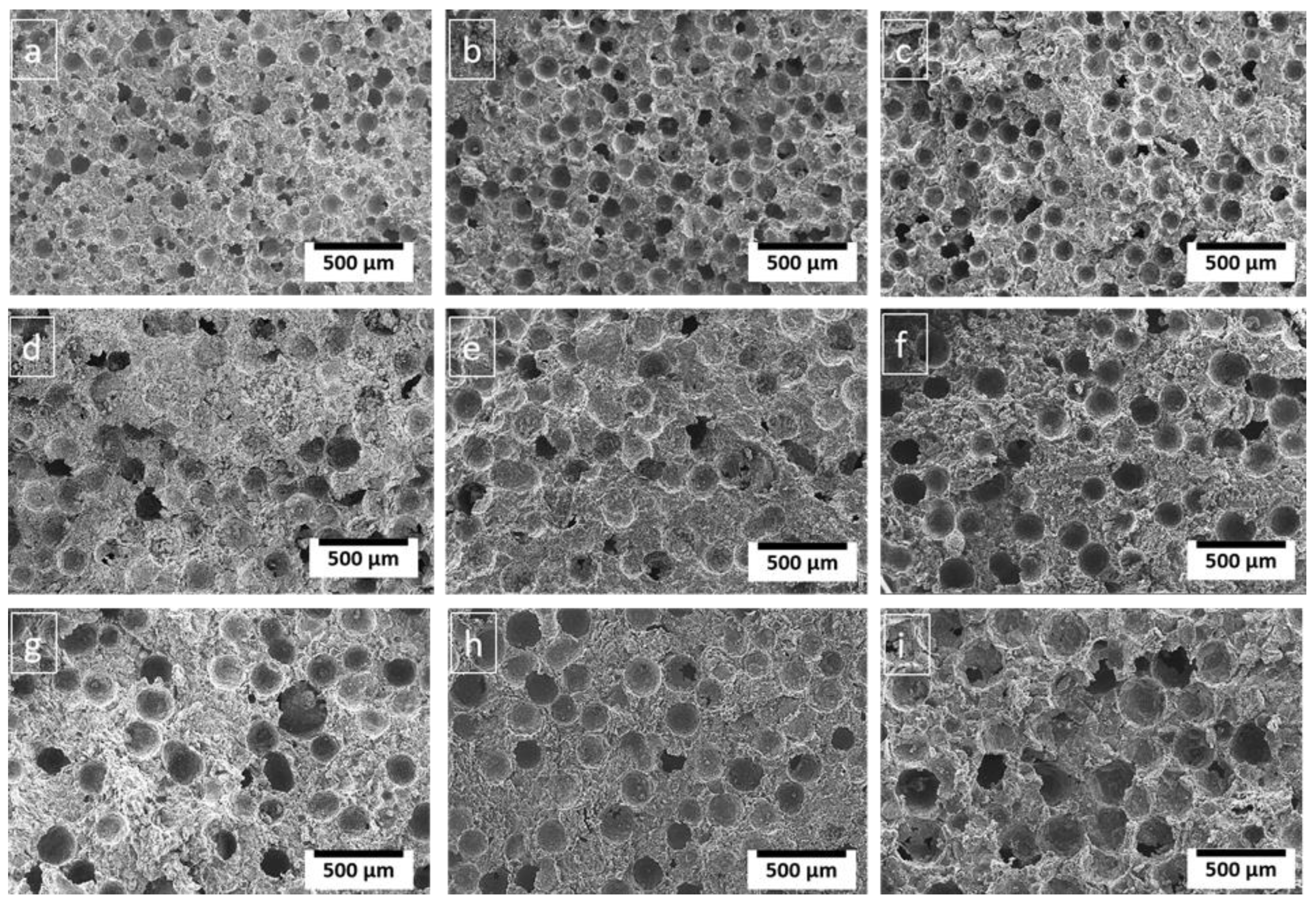
3.1. Morphology
3.2. Effect of Diamond Particle Content
3.3. Effect of PMMA Particle Size
3.4. Effect of PMMA Content
3.5. Optimization Results
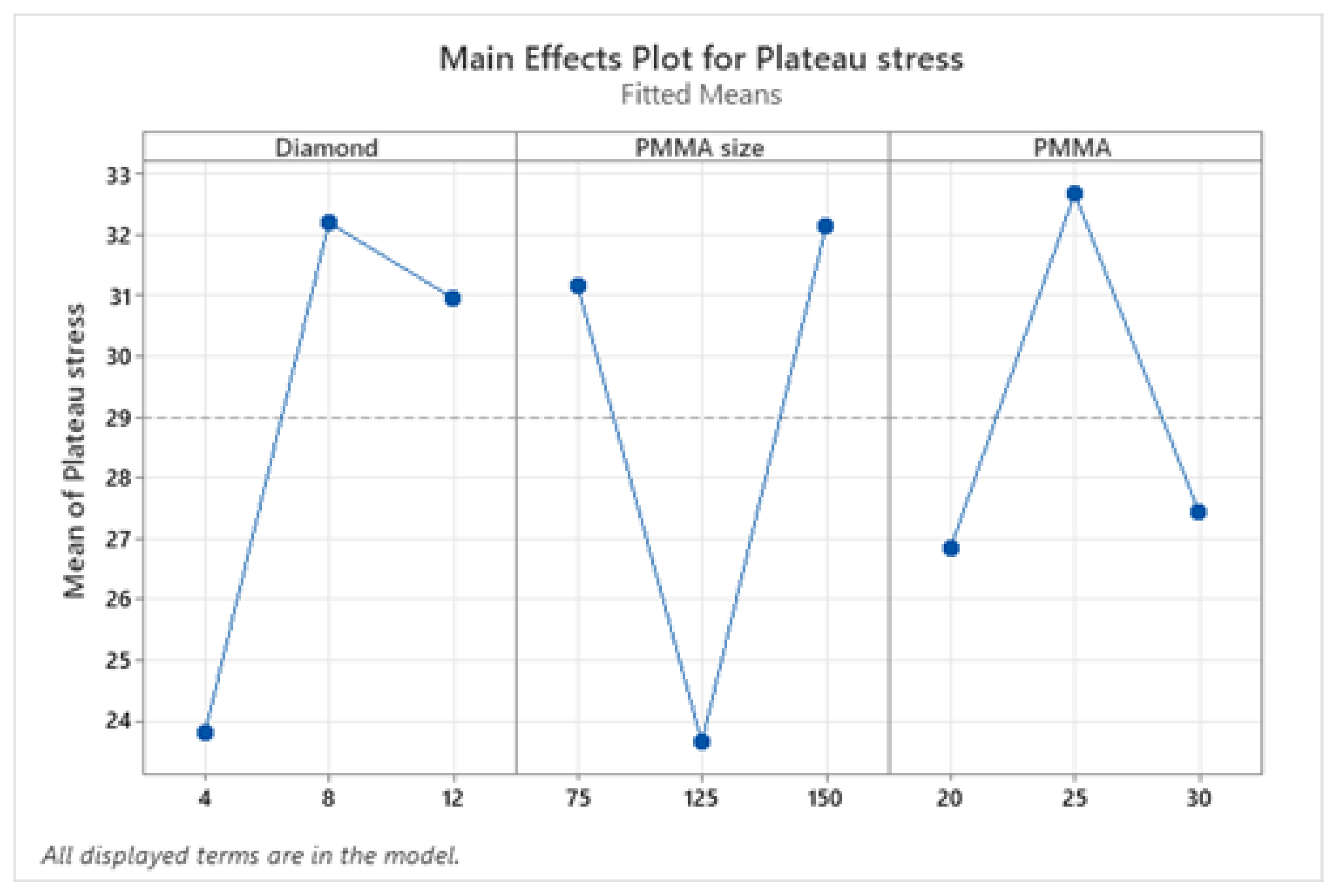
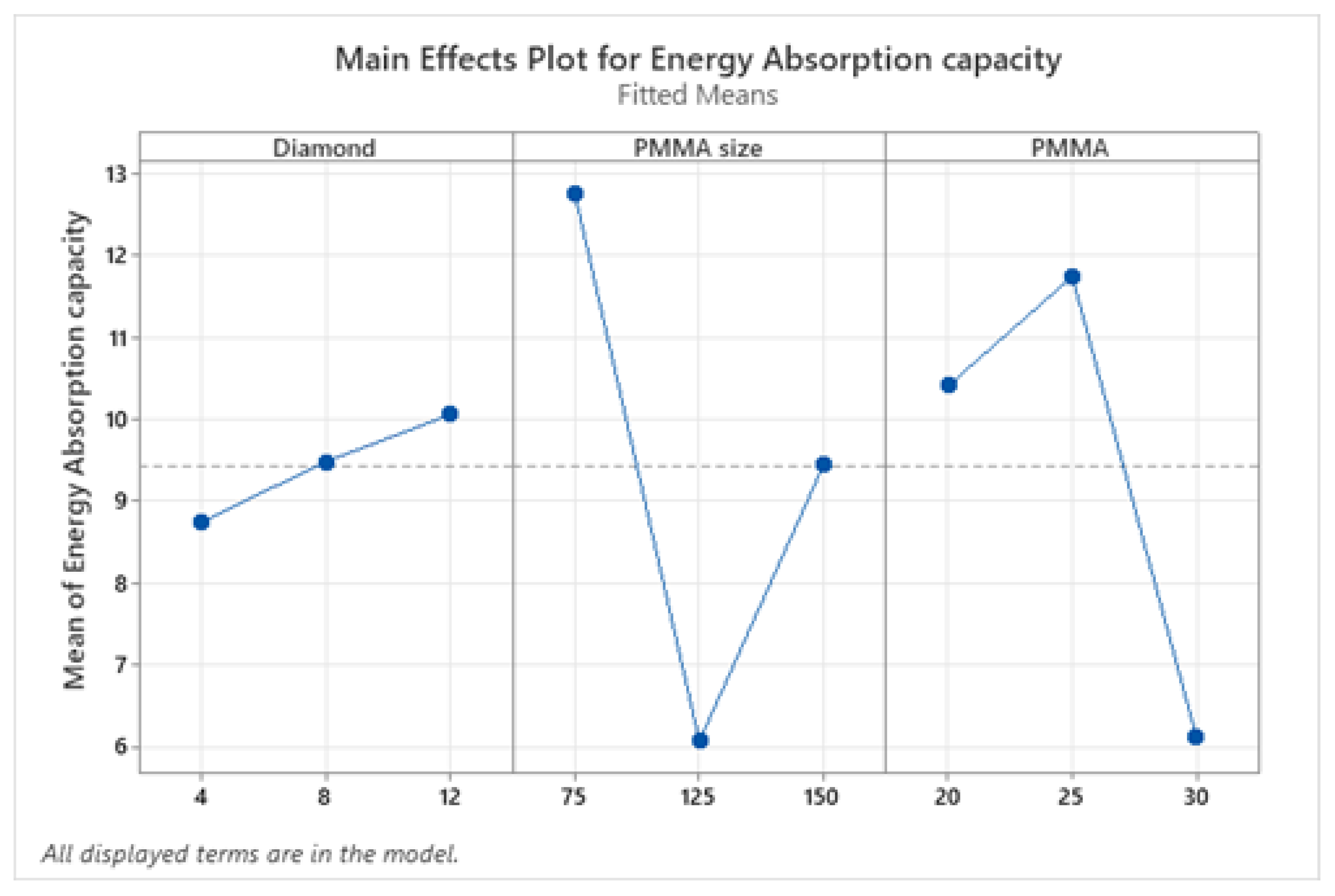
3.5.1. Analysis of Means
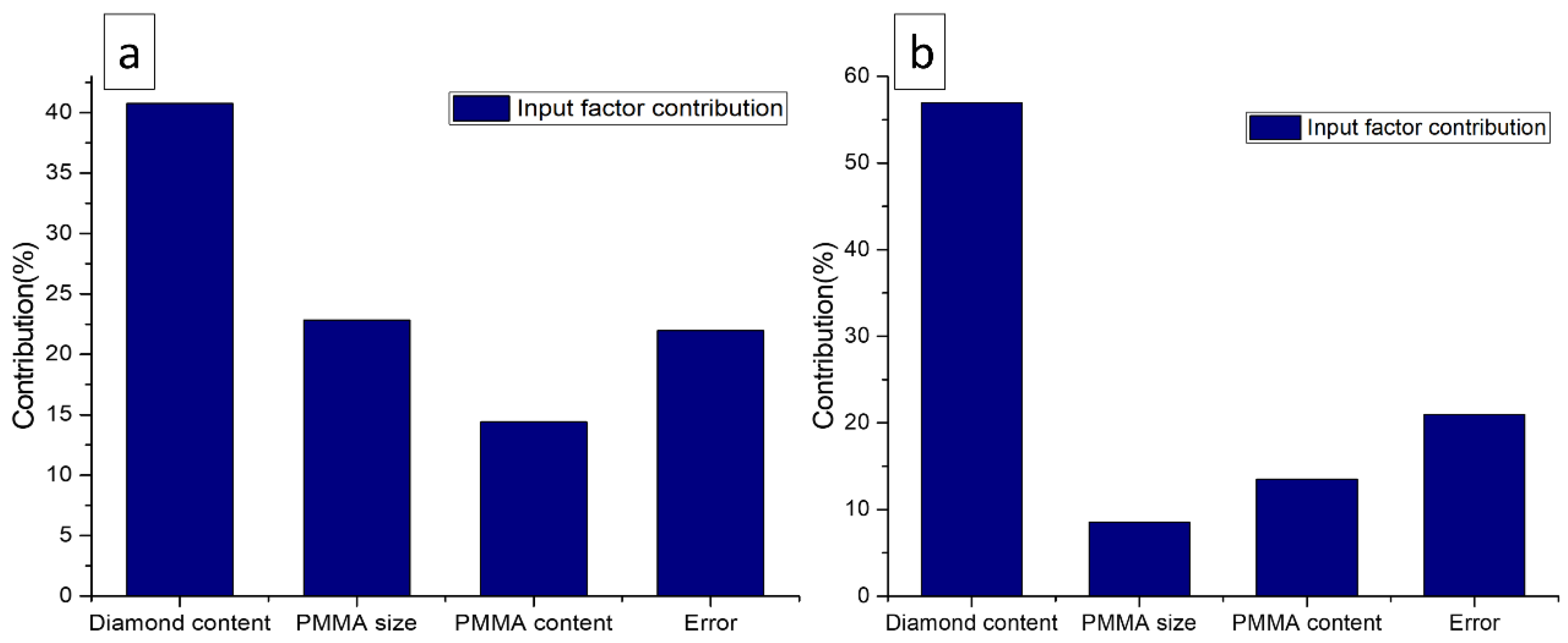
3.5.2. Analysis of Variance (ANOVA)
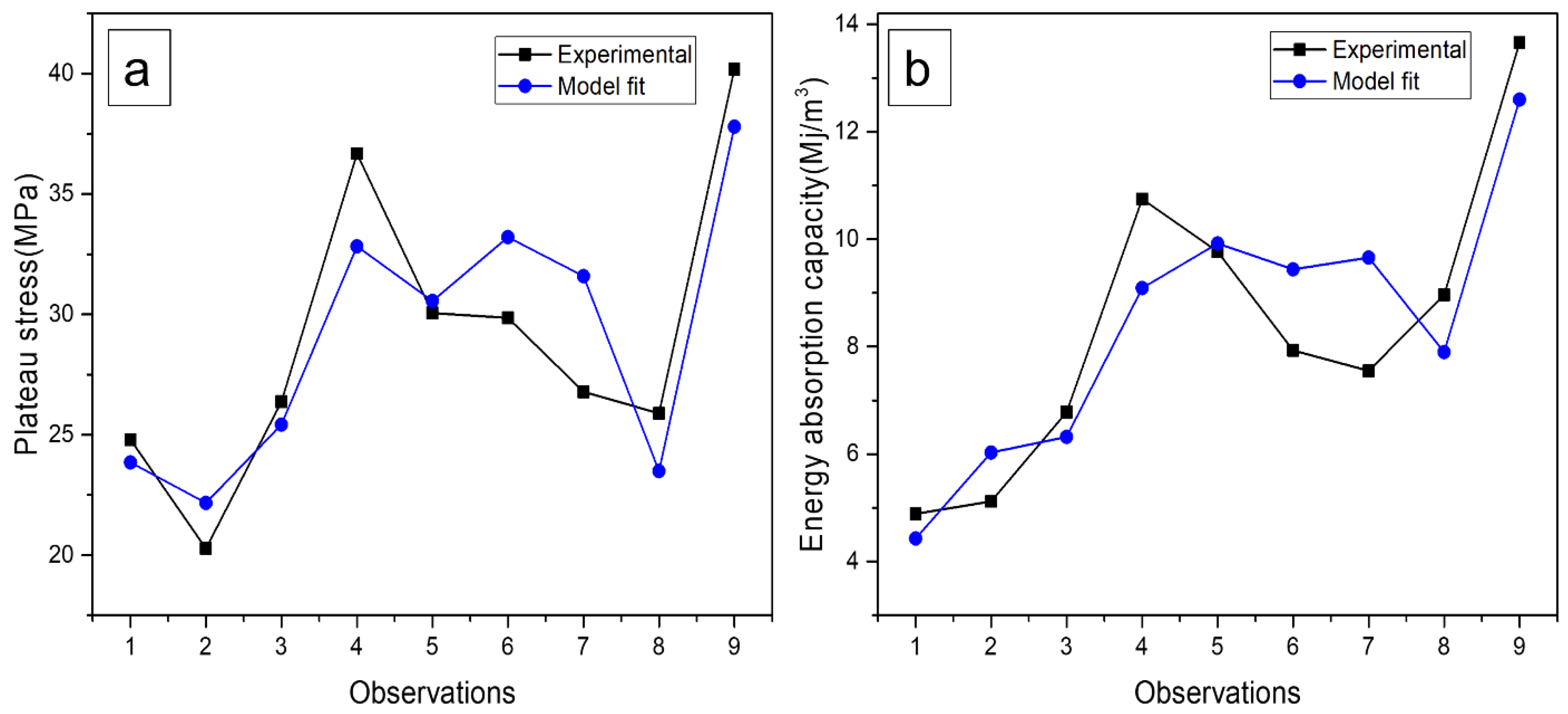
3.6. Regression Analysis
3.7. Response Optimization
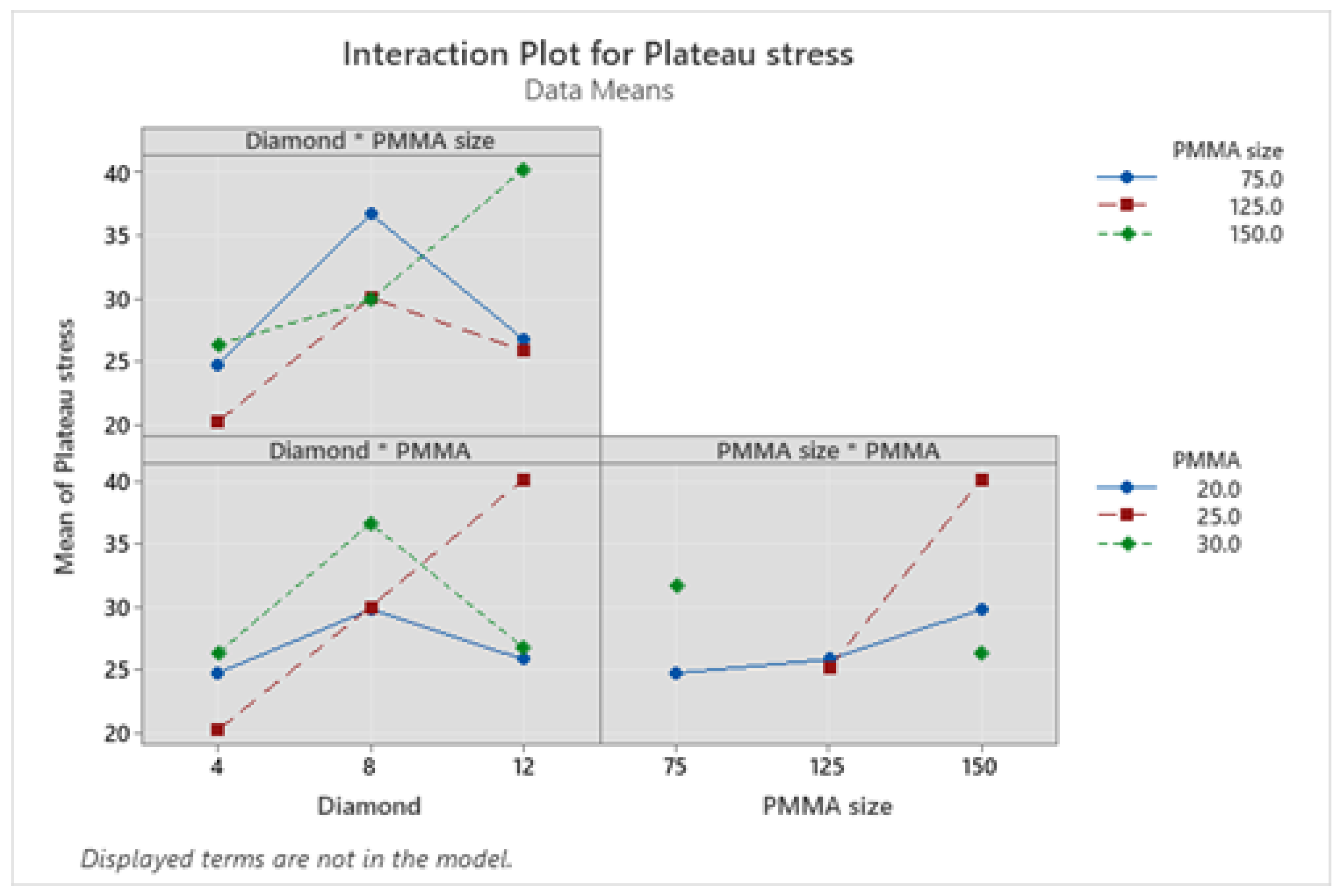
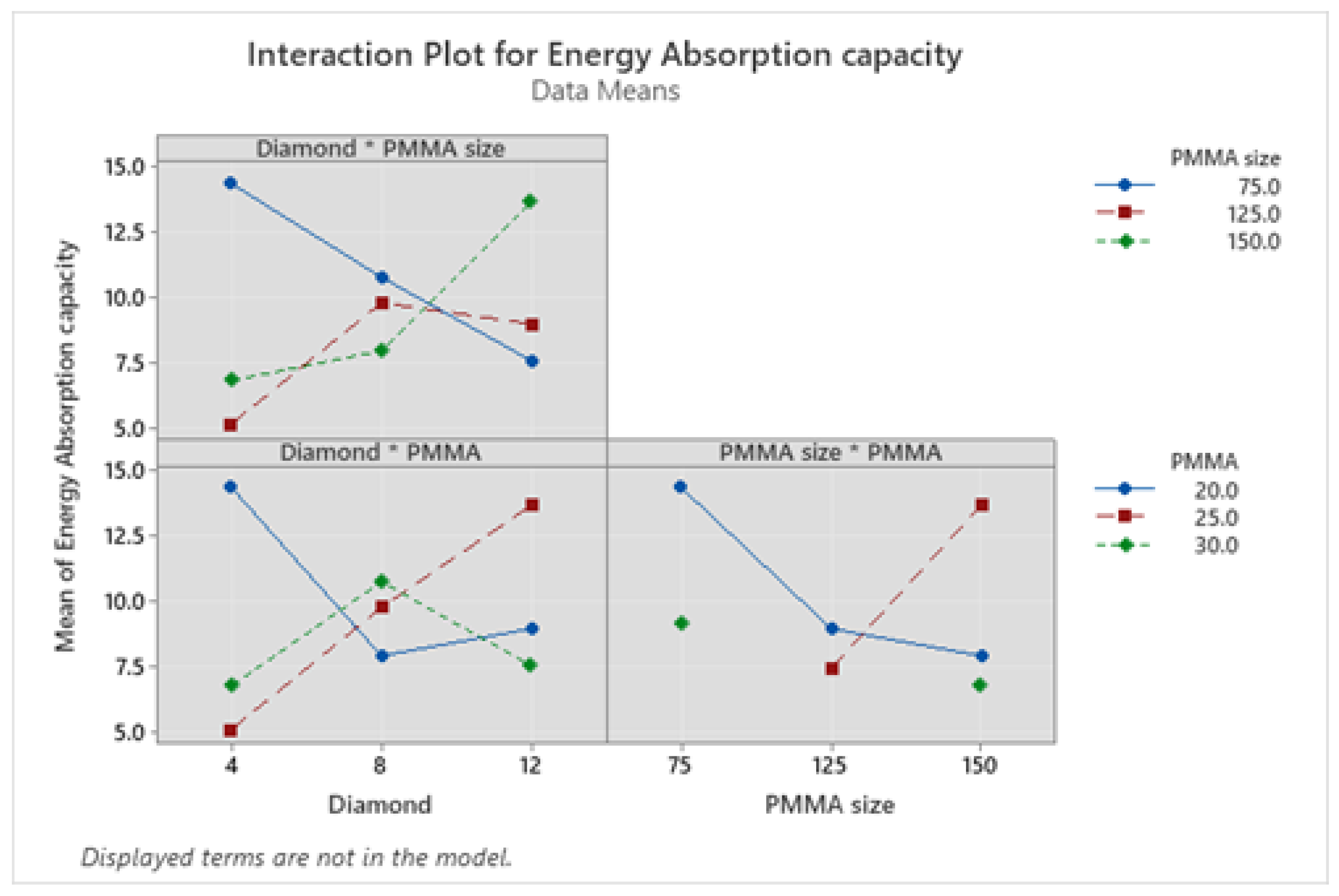
3.8. Interaction Plots
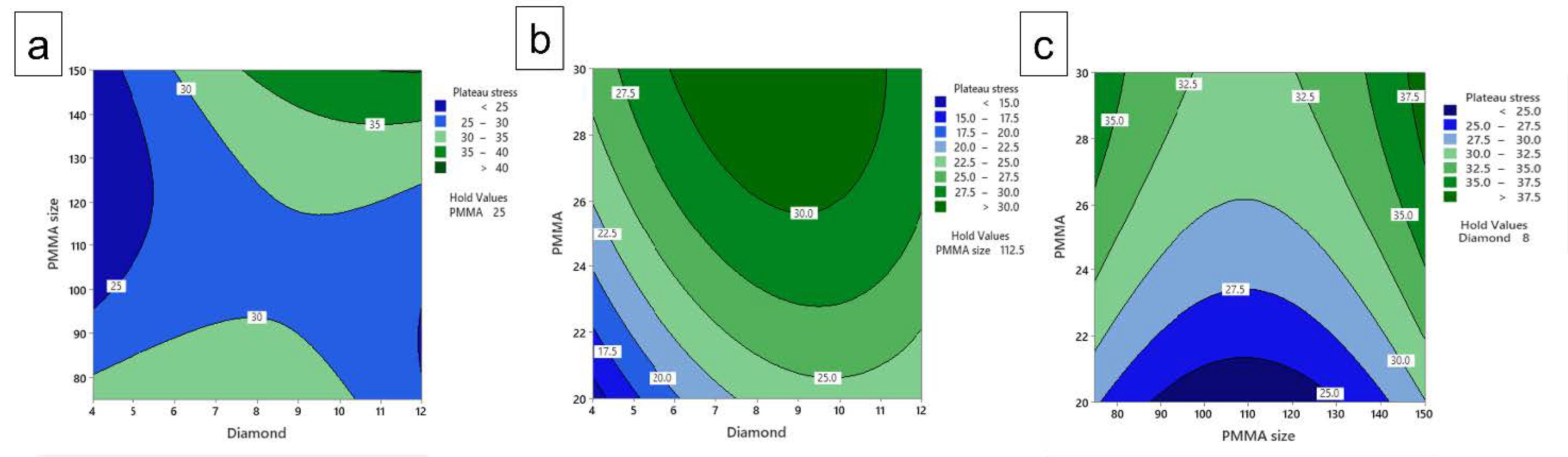
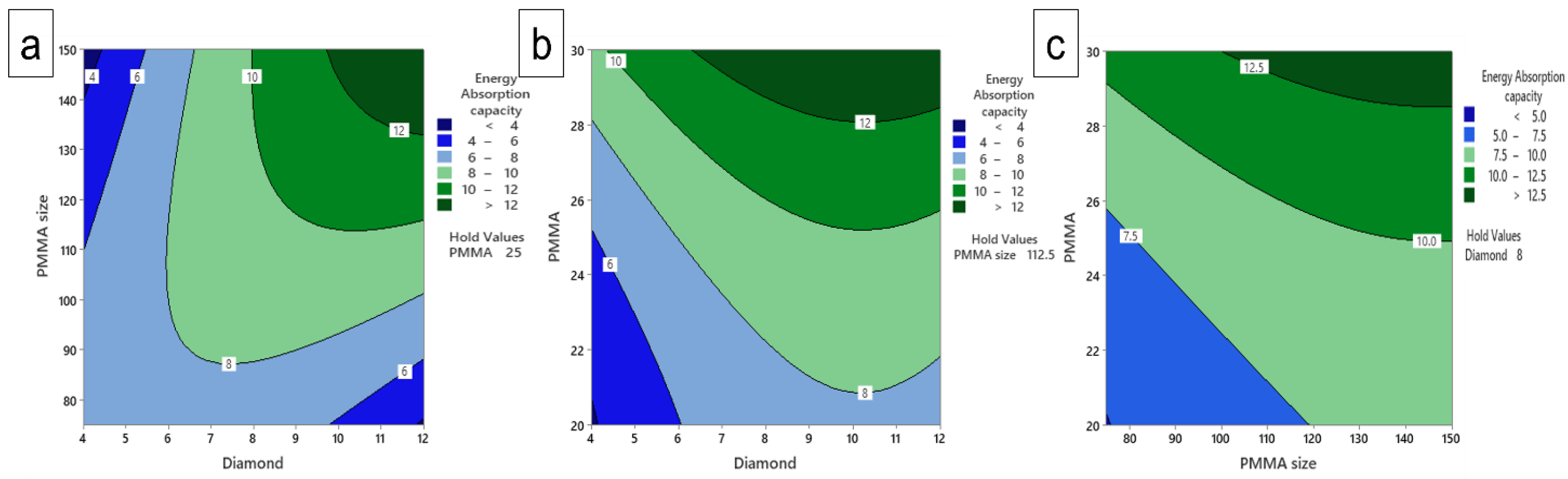
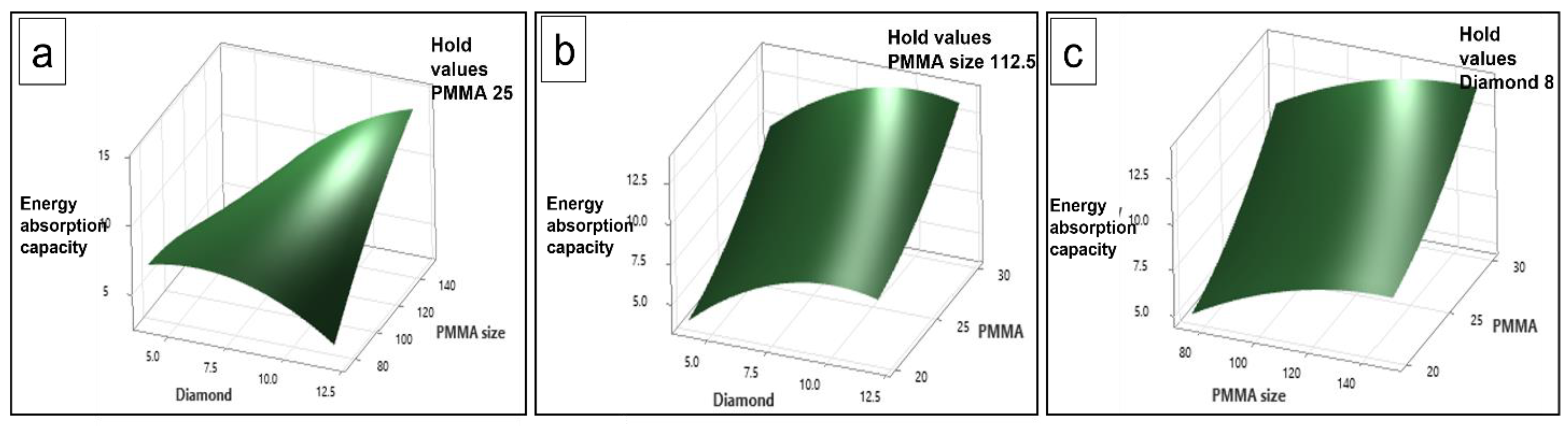
3.9. Contours Plot
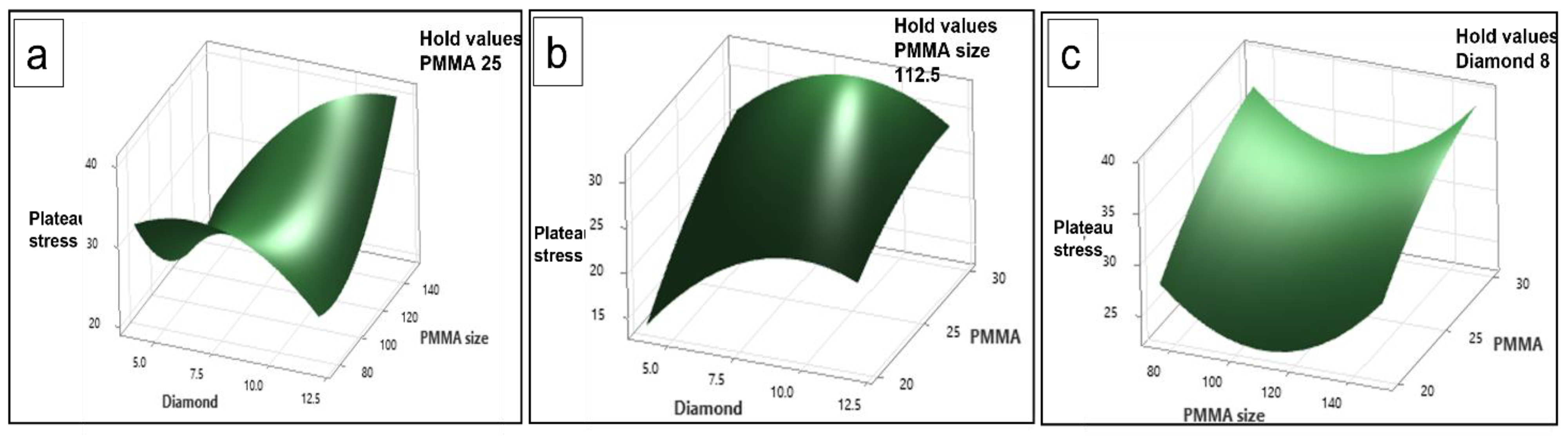
3.10. Surface Plots
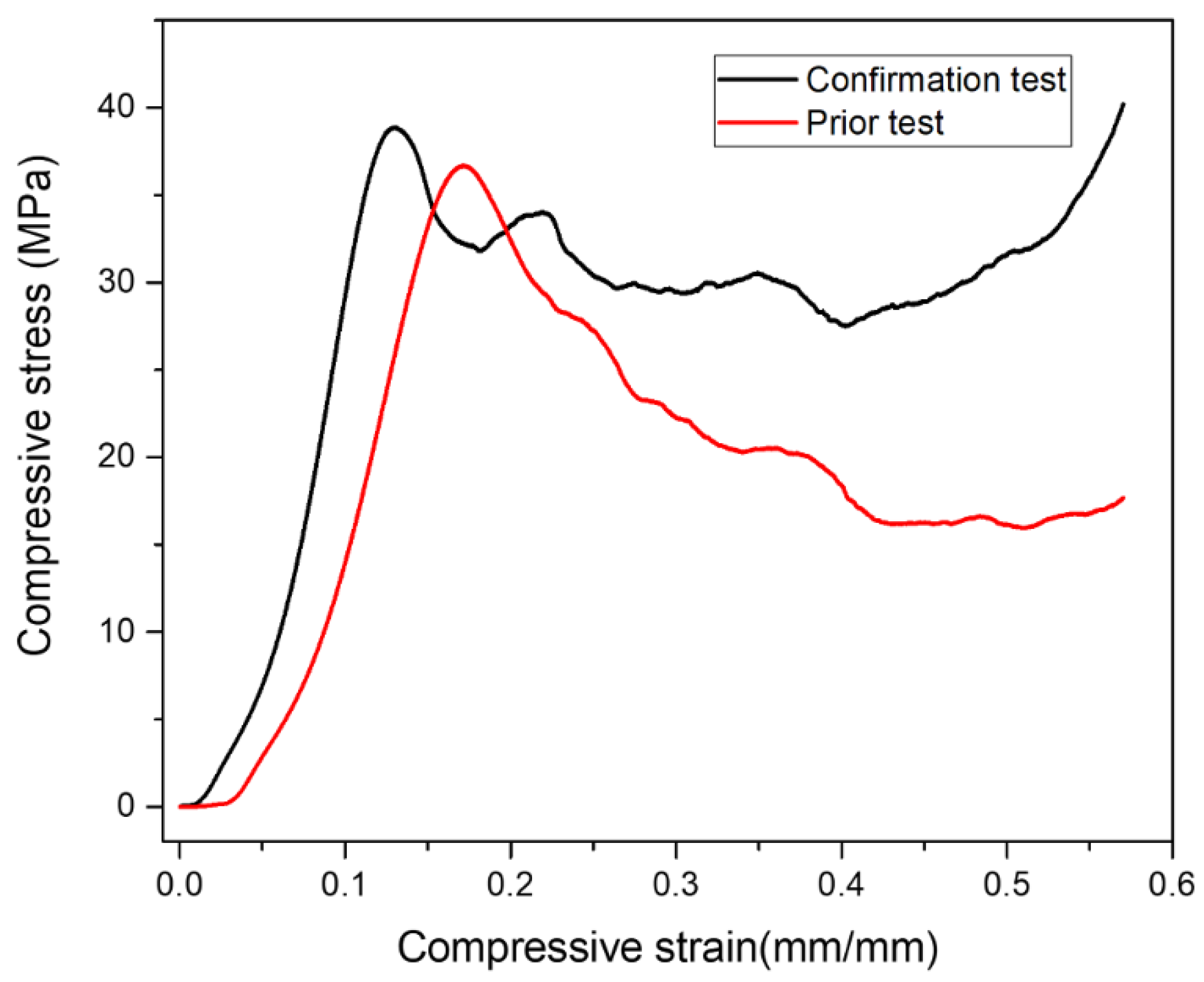
3.11. Confirmation Test
4. Conclusions
- In this study, the effect of reinforcement content, space holder size, and space holder particle content on the compressive properties of porous Al composites using experimental, numerical, and optimization methods was investigated.
- The developed composites exhibited a spherical porous structure with Ti-coated diamond particles distributed uniformly within the Al matrix alloy.
- The densities and porosities also improved due to the presence of Ti-coated diamond particles that were well bonded with the Al matrix alloy, revealing improved wettability and also by the inclusion of additives like Mg, Sn, Cu, and B, which aided in liquid sintering.
- The higher values of plateau stress and energy absorption were obtained at the diamond content of 12 wt.%, PMMA particle size of 150 μm, and PMMA particle content of 25 wt.%.
- The effect of input factors on compressive properties was investigated by applying statistical and regression analyses, model prediction, contour, and surface plots. The linear regression equation values were compared to the results of the experimental tests. The response optimized results included Ti-coated diamond content of 12 wt.%, a PMMA particle size of 150 m, and a PMMA particle content of 25 wt.%.
- Finally, the findings were validated by running the confirmation test under optimal conditions. With the lowest percentage deviation in plateau stress and energy absorption capacity, the model was found to be reliable and significant.
- The findings of the present study agree well with the −6.4% and 11.1% marginal discrepancy in plateau stress and energy absorption capacity values, respectively. This difference can be attributed to the other factors, such as processing parameters and varying compositions, that also affect the compressive properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tatt, T.K.; Muhamad, N.; Sulong, A.B.; Paramasivam, S.; Huey, H.S.; Anuar, S.A. Review on Manufacturing of Metal Foams. ASM Sci. J. 2021, 16, 1–8. [Google Scholar] [CrossRef]
- Parveez, B.; Jamal, N.A.; Maleque, A.; Yusof, F.; Jamadon, N.H.; Adzila, S. Review on advances in porous Al composites and the possible way forward. J. Mater. Res. Technol. 2021, 14, 2017–2038. [Google Scholar] [CrossRef]
- Parveez, B.; Jamal, N.A.; Anuar, H.; Ahmad, Y.; Aabid, A.; Baig, M. Microstructure and Mechanical Properties of Metal Foams Fabricated via Melt Foaming and Powder Metallurgy Technique: A Review. Materials 2022, 15, 5302. [Google Scholar] [CrossRef]
- Salehi, A.; Babakhani, A.; Zebarjad, S.M. Microstructural and mechanical properties of Al-SiO2 nanocomposite foams produced by an ultrasonic technique. Mater. Sci. Eng. A 2015, 638, 54–59. [Google Scholar] [CrossRef]
- Daoud, A. Compressive response and energy absorption of foamed A359–Al2O3 particle composites. J. Alloys Compd. 2009, 486, 597–605. [Google Scholar] [CrossRef]
- Moradi, M.R.; Moloodi, A.; Habibolahzadeh, A. Fabrication of Nano-composite Al-B4C Foam via Powder Metallurgy-space Holder Technique. Procedia Mater. Sci. 2015, 11, 553–559. [Google Scholar] [CrossRef]
- Yang, K.; Yang, X.; He, C.; Liu, E.; Shi, C.; Ma, L.; Li, Q.; Li, J.; Zhao, N. Damping characteristics of Al matrix composite foams reinforced by in-situ grown carbon nanotubes. Mater. Lett. 2017, 209, 68–70. [Google Scholar] [CrossRef]
- Yang, X.; Hu, Q.; Li, W.; Song, H.; Zou, T.; Zong, R.; Sha, J.; He, C.; Zhao, N. Compression-compression fatigue performance of aluminium matrix composite foams reinforced by carbon nanotubes. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 744–756. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.; Zhang, M.; Li, J.; Shi, C.; Zhao, N.; Zou, T. A novel approach to obtain in-situ growth carbon nanotube reinforced aluminum foams with enhanced properties. Mater. Lett. 2015, 161, 763–766. [Google Scholar] [CrossRef]
- Aliyi, I.M. Metal Matrix Composites Reinforced with Diamond Particles. Ph.D. Dissertation, Universidade de Coimbra, Coimbra, Portugal, 2019. [Google Scholar]
- Yin, S.; Xie, Y.; Cizek, J.; Ekoi, E.J.; Hussain, T.; Dowling, D.P.; Lupoi, R. Advanced diamond-reinforced metal matrix composites via cold spray: Properties and deposition mechanism. Compos. Part B Eng. 2017, 113, 44–54. [Google Scholar] [CrossRef]
- Yoshida, K.; Morigami, H. Thermal properties of diamond/copper composite material. Microelectron. Reliab. 2004, 44, 303–308. [Google Scholar] [CrossRef]
- Chung, C.Y.; Chu, C.H.; Lee, M.T.; Lin, C.M.; Lin, S.J. Effect of titanium addition on the thermal properties of diamond/Cu-Ti composites fabricated by pressureless liquid-phase sintering technique. Sci. World J. 2014, 2014, 713537. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhang, H.; Zhang, Y.; Li, J.; Wang, X. Effect of copper content on the thermal conductivity and thermal expansion of Al-Cu/diamond composites. Mater. Des. 2012, 39, 87–92. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, Z.; Zhao, N. Effect of pore size and relative density on the mechanical properties of open cell aluminum foams. Scr. Mater. 2007, 56, 169–172. [Google Scholar] [CrossRef]
- Mohd Razali, R.N.; Abdullah, B.; Ismail, M.H.; Ahmad, U.K.; Idham, M.F.; Rasmli, A. Mechanical properties of aluminium foam by conventional casting combined with NaCL space holder. Appl. Mech. Mater. 2013, 393, 156–160. [Google Scholar] [CrossRef]
- Yang, X.; Hu, Q.; Du, J.; Song, H.; Zou, T.; Sha, J.; He, C.; Zhao, N. Compression fatigue properties of open-cell aluminum foams fabricated by space-holder method. Int. J. Fatigue 2019, 121, 272–280. [Google Scholar] [CrossRef]
- Prajapati, J. Metal Foam by Space Holder Technique. In Proceedings of the 3rd International Conference on Recent Development in Engineering Science Humanities and Management, Chandigarh, India, 26 March 2017; pp. 134–139. [Google Scholar]
- Surace, R.; De Filippis, L.A.C.; Ludovico, A.D.; Boghetich, G. Influence of processing parameters on aluminium foam produced by space holder technique. Mater. Des. 2009, 30, 1878–1885. [Google Scholar] [CrossRef]
- French, A.D. Idealized powder diffraction patterns for cellulose polymorphs. Cellulose 2014, 21, 885–896. [Google Scholar] [CrossRef]
- Jamal, N.A.; Tan, A.W.; Yusof, F.; Katsuyoshi, K.; Hisashi, I.; Singh, S.; Anuar, H. Fabrication and compressive properties of low to medium porosity closed-cell porous Aluminum using PMMA space holder technique. Materials 2016, 9, 254. [Google Scholar] [CrossRef]
- Tan, P.P.; Mohamad, H.; Anasyida, A.S. Properties of Porous Magnesium Using Polymethyl Methacrylate (PMMA) as a Space Holder. J. Phys. Conf. Ser. 2018, 1082, 012063. [Google Scholar] [CrossRef]
- ASTM C373-88; Standard Test Method for Water Absorption, Bulk Density, Apparent Porosity, and Apparent Specific Gravity of Fired Whiteware Products. ASTM: West Conshohocken, PA, USA, 2006. [CrossRef]
- Luecke, W.E.; Ma, L.; Graham, S.M.; Adler, M.A. Repeatability and Reproducibility of Compression Strength Measurements Conducted According to ASTM E9; NIST: Gaithersburg, MD, USA, 2010; p. 39.
- Baumeister, J.; Banhart, J.; Weber, M. Aluminium foams for transport industry. Mater. Des. 1997, 18, 217–220. [Google Scholar] [CrossRef]
- Bekoz, N.; Oktay, E. Effects of carbamide shape and content on processing and properties of steel foams. J. Mater. Process. Technol. 2012, 212, 2109–2116. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Cole, D.R. Characterization and analysis of porosity and pore structures. Pore Scale Geochemical Process. 2015, 80, 61–164. [Google Scholar] [CrossRef]
- Chu, K.; Jia, C.C.; Liang, X.B.; Chen, H. Effect of sintering temperature on the microstructure and thermal conductivity of Al/diamond composites prepared by spark plasma sintering. Int. J. Miner. Metall. Mater. 2010, 17, 234–240. [Google Scholar] [CrossRef]
- Yu, J.; Sun, X.; Li, Q.; Li, X. Preparation of Al2O3 and Al2O3-ZrO2 ceramic foams with adjustable cell structure by centrifugal slip casting. Mater. Sci. Eng. A 2008, 476, 274–280. [Google Scholar] [CrossRef]
- Mondal, D.P.; Goel, M.D.; Bagde, N.; Jha, N.; Sahu, S.; Barnwal, A.K. Closed cell ZA27-SiC foam made through stir-casting technique. Mater. Des. 2014, 57, 315–324. [Google Scholar] [CrossRef]
- Alizadeh, A.; Taheri-Nassaj, E.; Baharvandi, H.R. Preparation and investigation of Al-4 wt% B4C nanocomposite powders using mechanical milling. Bull. Mater. Sci. 2011, 34, 1039–1048. [Google Scholar] [CrossRef]
- Bazzaz Bonabi, S.; Kahani Khabushan, J.; Kahani, R.; Honarbakhsh Raouf, A. Fabrication of metallic composite foam using ceramic porous spheres “Light Expanded Clay Aggregate” via casting process. Mater. Des. 2014, 64, 310–315. [Google Scholar] [CrossRef]
- Yu, S.; Luo, Y.; Liu, J. Effects of strain rate and SiC particle on the compressive property of SiC p/AlSi 9 Mg composite foams. Mater. Sci. Eng. A 2008, 487, 394–399. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, Y.; Zhao, H.; Liu, K.; Liu, Y.; Wu, M.; Lu, P. Preparation of Bio-Based Foams with a Uniform Pore Structure by Nanocellulose/Nisin/Waterborne-Polyurethane-Stabilized Pickering Emulsion. Polymers 2022, 14, 5159. [Google Scholar] [CrossRef]
- Kahani Khabushan, J.; Bazzaz Bonabi, S.; Moghaddasi Aghbagh, F.; Kahani Khabushan, A. A study of fabricating and compressive properties of cellular Al-Si (355.0) foam using TiH2. Mater. Des. 2014, 55, 792–797. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Y.; Wang, L.; Wang, F.; Xu, H.; Huang, W.; You, X. Preparation and properties of controllable aluminum foam. Mater. Res. Express 2021, 8, 026526. [Google Scholar] [CrossRef]
- Xia, X.C.; Chen, X.W.; Zhang, Z.; Chen, X.; Zhao, W.M.; Liao, B.; Hur, B. Effects of porosity and pore size on the compressive properties of closed-cell Mg alloy foam. J. Magnes. Alloy. 2013, 1, 330–335. [Google Scholar] [CrossRef]
- Bekoz, N.; Oktay, E. Mechanical properties of low alloy steel foams: Dependency on porosity and pore size. Mater. Sci. Eng. A 2013, 576, 82–90. [Google Scholar] [CrossRef]
- Liu, B.; Huang, W.; Wang, H.; Wang, M.; Li, X. Study on the load partition behaviors of high particle content B 4C/Al composites in compression. J. Compos. Mater. 2014, 48, 355–364. [Google Scholar] [CrossRef]



| Alloy Matrix | Al | Mg | Sn | Cu | B | Reinforcement | Ti-Diamond | Space Holder | PMMA |
| Wt.% | 94 | 1 | 2 | 2 | 1 | 4, 8, 12 | 20, 25, 30 |
| Factors | Symbol | Unit | Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|---|
| Diamond content | A | wt.% | 4 | 8 | 12 |
| PMMA size | B | µm | 75 | 125 | 150 |
| PMMA content | C | wt.% | 20 | 25 | 30 |
| S.no | Diamond (wt.%) | PMMA Size (µm) | PMMA (wt%) | Plateau Stress (MPa) | Energy Absorption Capacity (Mj/m3) |
|---|---|---|---|---|---|
| 1 | 4 | 75 | 20 | 24.8 | 4.89 |
| 2 | 4 | 125 | 25 | 20.27 | 5.12 |
| 3 | 4 | 150 | 30 | 26.37 | 6.78 |
| 4 | 8 | 75 | 30 | 36.68 | 10.75 |
| 5 | 8 | 125 | 25 | 30.06 | 9.77 |
| 6 | 8 | 150 | 20 | 29.86 | 7.93 |
| 7 | 12 | 75 | 30 | 26.79 | 7.55 |
| 8 | 12 | 125 | 20 | 25.89 | 8.96 |
| 9 | 12 | 150 | 25 | 40.2 | 13.66 |
| S.no | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Porosity (%) | 21 | 24 | 30 | 29 | 26 | 18 | 31 | 20 | 25 |
| Bulk density | 1.94 | 2.06 | 1.76 | 2.08 | 2 | 1.92 | 2 | 1.867 | 1.774 |
| Relative density | 0.72 | 0.76 | 0.65 | 0.77 | 0.74 | 0.71 | 0.74 | 0.69 | 0.66 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Diamond | 2 | 122.95 | 40.76% | 122.95 | 61.47 | 1.85 | 0.350 |
| PMMA size | 2 | 68.91 | 22.85% | 91.66 | 45.83 | 1.38 | 0.420 |
| PMMA | 2 | 43.46 | 14.41% | 43.46 | 21.73 | 0.66 | 0.604 |
| Error | 2 | 66.29 | 21.98% | 66.29 | 33.14 | ||
| Total | 8 | 301.61 | 100.00% |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Diamond | 2 | 35.326 | 56.96% | 35.326 | 17.663 | 2.72 | 0.269 |
| PMMA size | 2 | 5.300 | 8.54% | 6.047 | 3.024 | 0.46 | 0.683 |
| PMMA | 2 | 8.388 | 13.52% | 8.388 | 4.194 | 0.64 | 0.608 |
| Error | 2 | 13.009 | 20.97% | 13.009 | 6.504 | ||
| Total | 8 | 62.023 | 100.00% |
| Obs | Plateau Stress | Fit | SE Fit | Resid | Std Resid | Del Resid |
|---|---|---|---|---|---|---|
| 1 | 24.80 | 23.85 | 5.50 | 0.95 | 0.55 | 0.43 |
| 2 | 20.27 | 22.17 | 4.62 | −1.90 | −0.55 | −0.43 |
| 3 | 26.37 | 25.42 | 5.50 | 0.95 | 0.55 | 0.43 |
| 4 | 36.68 | 32.83 | 4.62 | 3.85 | 1.12 | 1.30 |
| 5 | 30.06 | 30.56 | 4.62 | −0.50 | −0.15 | −0.10 |
| 6 | 29.86 | 33.21 | 5.08 | −3.35 | −1.23 | −1.79 |
| 7 | 26.79 | 31.59 | 4.62 | −4.80 | −1.40 | −6.62 |
| 8 | 25.89 | 23.49 | 5.50 | 2.40 | 1.40 | 6.62 |
| Obs | Energy Absorption Capacity | Fit | SE Fit | Resid | Std Resid | DFITS |
|---|---|---|---|---|---|---|
| 1 | 4.89 | 4.43 | 2.43 | 0.46 | 0.60 | 1.4955 |
| 2 | 5.12 | 6.03 | 2.05 | −0.91 | −0.60 | −0.6289 |
| 3 | 6.78 | 6.32 | 2.43 | 0.46 | 0.60 | 1.4955 |
| 4 | 10.75 | 9.09 | 2.05 | 1.66 | 1.09 | 1.6322 |
| 5 | 9.77 | 9.92 | 2.05 | −0.15 | −0.10 | −0.0922 |
| 6 | 7.93 | 9.44 | 2.25 | −1.51 | −1.26 | −3.6402 |
| 7 | 7.55 | 9.66 | 2.05 | −2.11 | −1.39 | −7.2209 |
| 8 | 8.96 | 7.90 | 2.43 | 1.06 | 1.39 | 17.1717 |
| 9 | 13.66 | 12.60 | 2.43 | 1.06 | 1.39 | 17.1717 |
| Response | Goal | Lower | Target | Upper | Weight | Importance | ||
|---|---|---|---|---|---|---|---|---|
| Energy Absorption capacity | Maximum | 4.89 | 13.66 | 1 | 1 | |||
| Plateau stress | Maximum | 20.27 | 40.20 | 1 | 1 | |||
| Solution | ||||||||
| Solution | Diamond | PMMA size | PMMA | Energy Absorption capacity Fit | Plateau Stress Fit | Composite Desirability | ||
| 1 | 12 | 150 | 25 | 12.6029 | 37.7998 | 0.879515 | ||
| Variable Settings | ||||||||
| Diamond | 12 | |||||||
| PMMA size | 150 | |||||||
| PMMA | 25 | |||||||
| Response | Fit | SE Fit | 95% CI | 95% PI | Fit | |||
| Energy Absorption capacity | 12.60 | 2.43 | (2.13, 23.08) | (−2.57, 27.77) | ||||
| Plateau stress | 37.80 | 5.50 | (14.16, 61.44) | (3.56, 72.04) | ||||
| Responses | Prediction | Experimentation | Error (%) |
|---|---|---|---|
| Plateau stress (MPa) | 37.79 | 40.21 | −6.4 |
| Energy absorption capacity (Mj/m3) | 12.60 | 11.20 | 11.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parveez, B.; Jamal, N.A.; Maleque, M.A.; Rozhan, A.N.; Aabid, A.; Baig, M. Optimizing the Compressive Properties of Porous Aluminum Composites by Varying Diamond Content, Space Holder Size and Content. Materials 2023, 16, 921. https://doi.org/10.3390/ma16030921
Parveez B, Jamal NA, Maleque MA, Rozhan AN, Aabid A, Baig M. Optimizing the Compressive Properties of Porous Aluminum Composites by Varying Diamond Content, Space Holder Size and Content. Materials. 2023; 16(3):921. https://doi.org/10.3390/ma16030921
Chicago/Turabian StyleParveez, Bisma, Nur Ayuni Jamal, Md Abdul Maleque, Alya Naili Rozhan, Abdul Aabid, and Muneer Baig. 2023. "Optimizing the Compressive Properties of Porous Aluminum Composites by Varying Diamond Content, Space Holder Size and Content" Materials 16, no. 3: 921. https://doi.org/10.3390/ma16030921
APA StyleParveez, B., Jamal, N. A., Maleque, M. A., Rozhan, A. N., Aabid, A., & Baig, M. (2023). Optimizing the Compressive Properties of Porous Aluminum Composites by Varying Diamond Content, Space Holder Size and Content. Materials, 16(3), 921. https://doi.org/10.3390/ma16030921








