A Trilinear Model for the Load–Slip Behavior of Headed Stud Shear Connectors
Abstract
1. Introduction
2. Analytical Trilinear Model
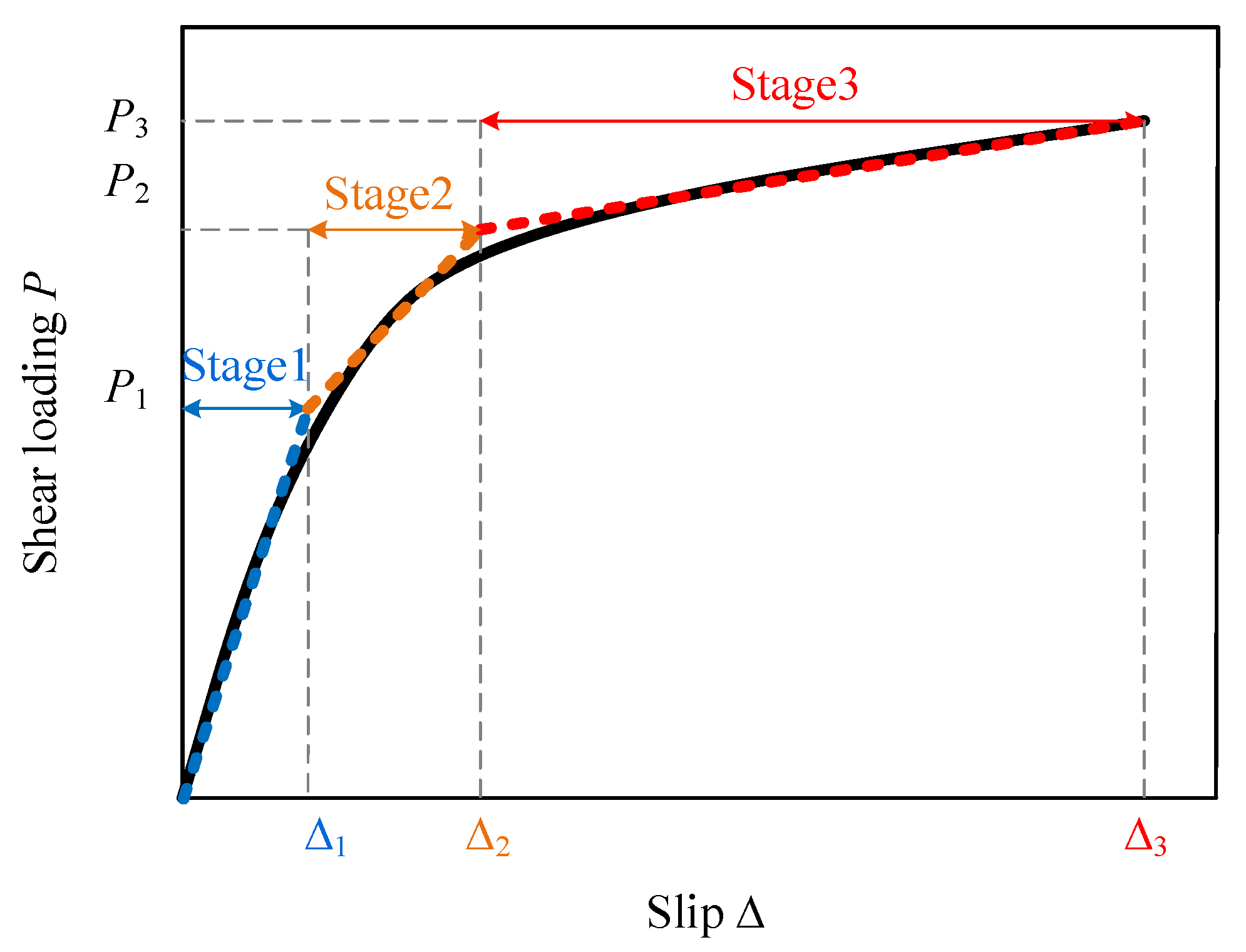
2.1. Three Stages and a Trilinear Model of the Load–Slip Behaviors
2.2. The Quantitative Properties of the First Two Stages
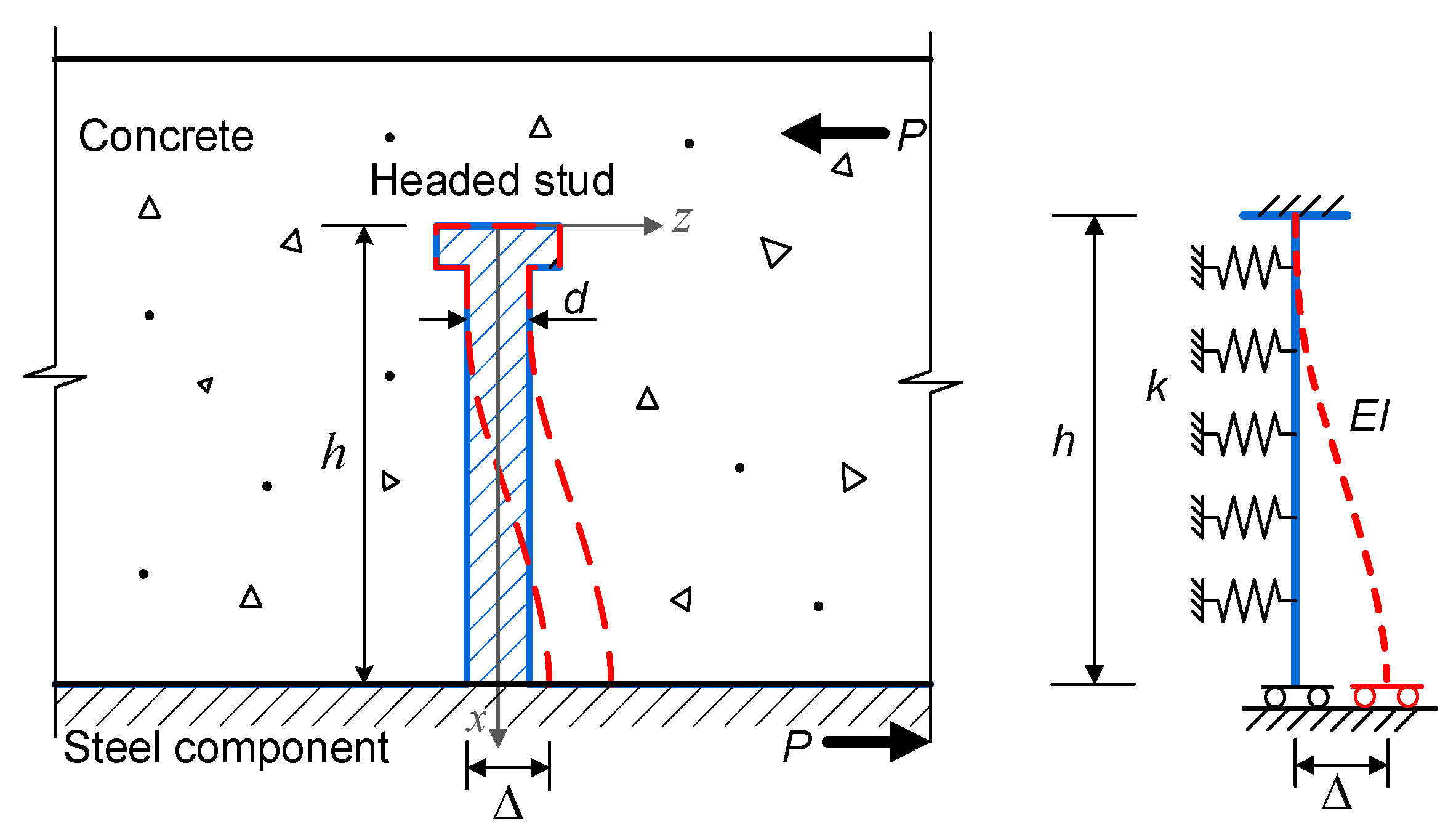
2.3. The Equivalent Stiffness of the Foundation Idealized from the Surrounding Concrete
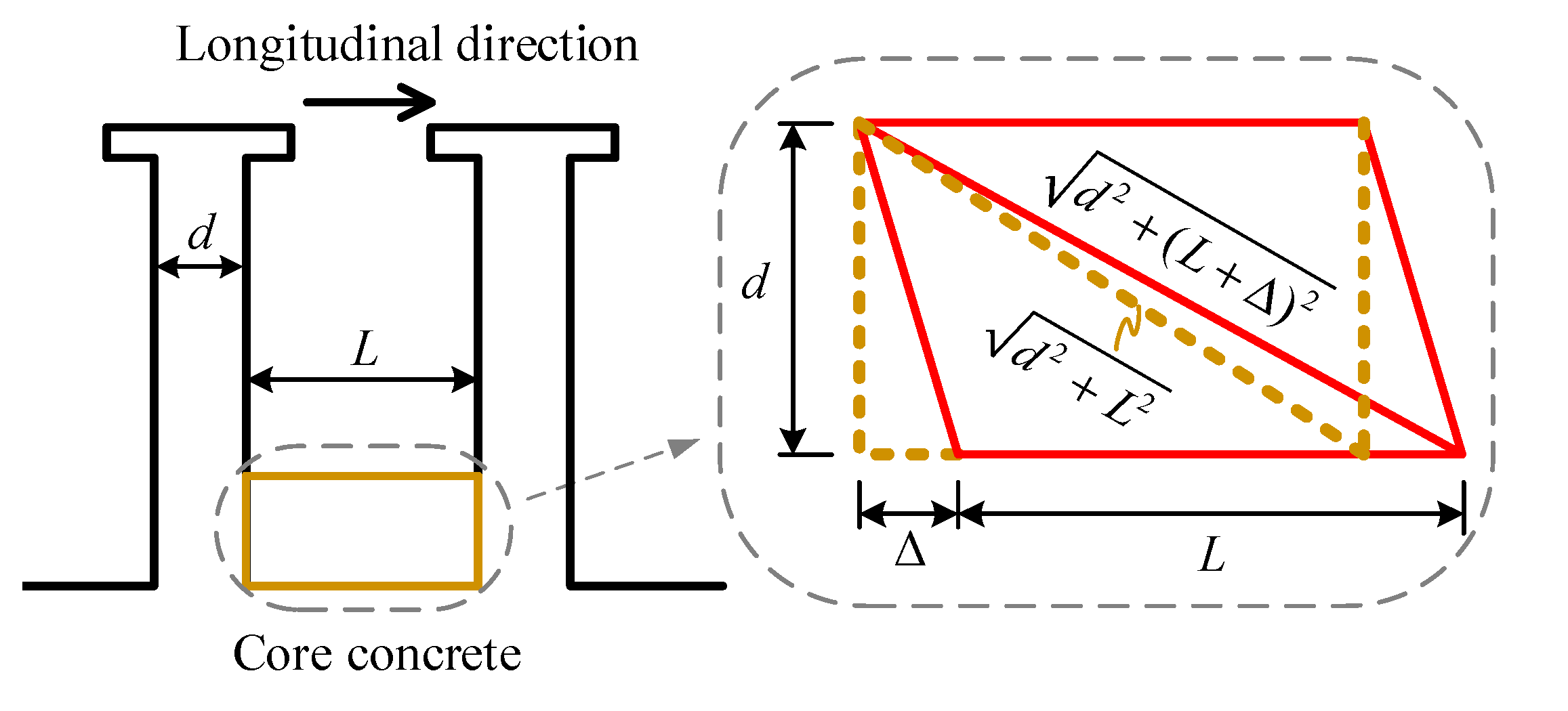
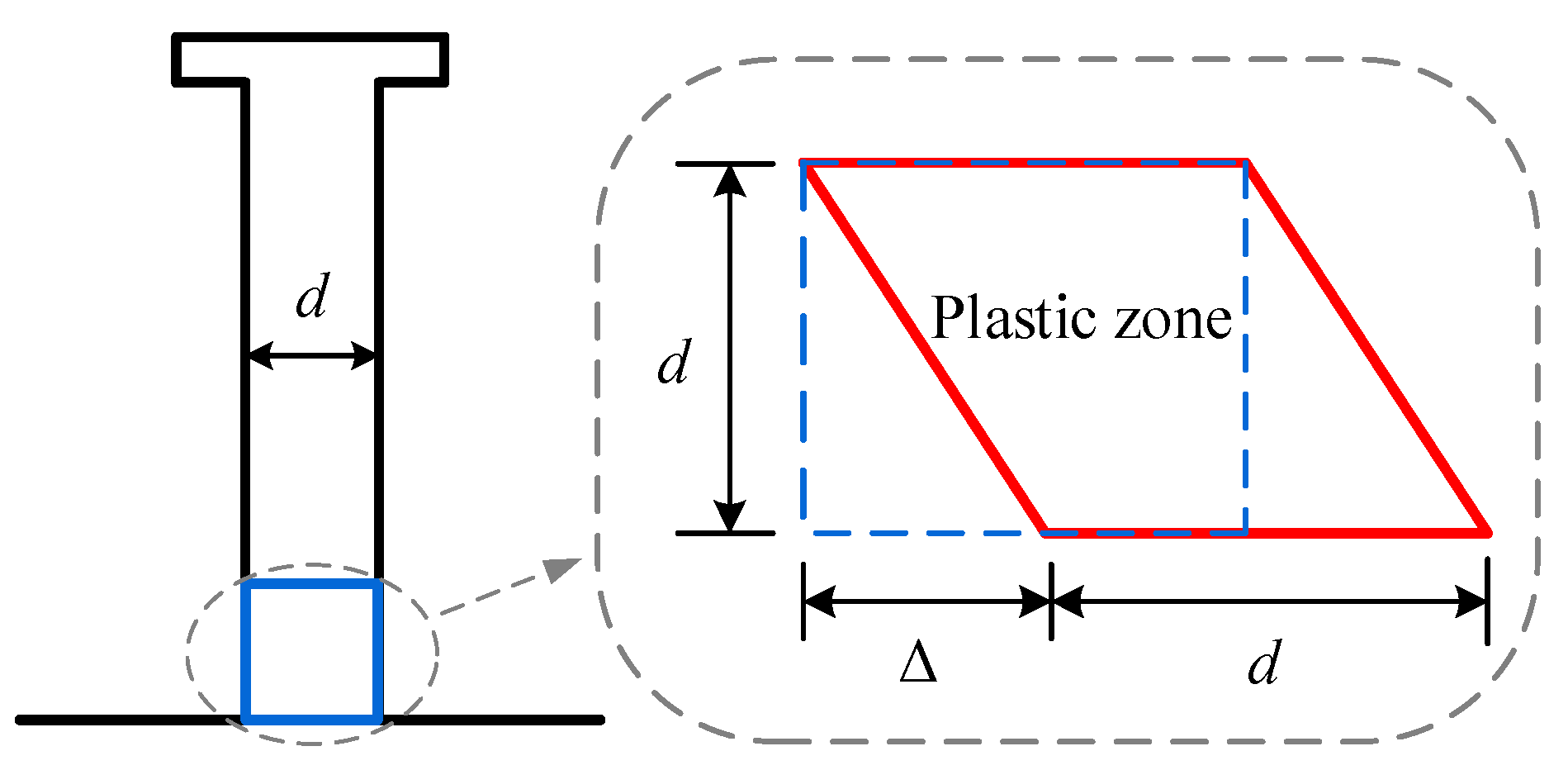
2.4. The Degradation of the Surrounding Concrete
2.5. Stage 3 of the Load–Slip Curve
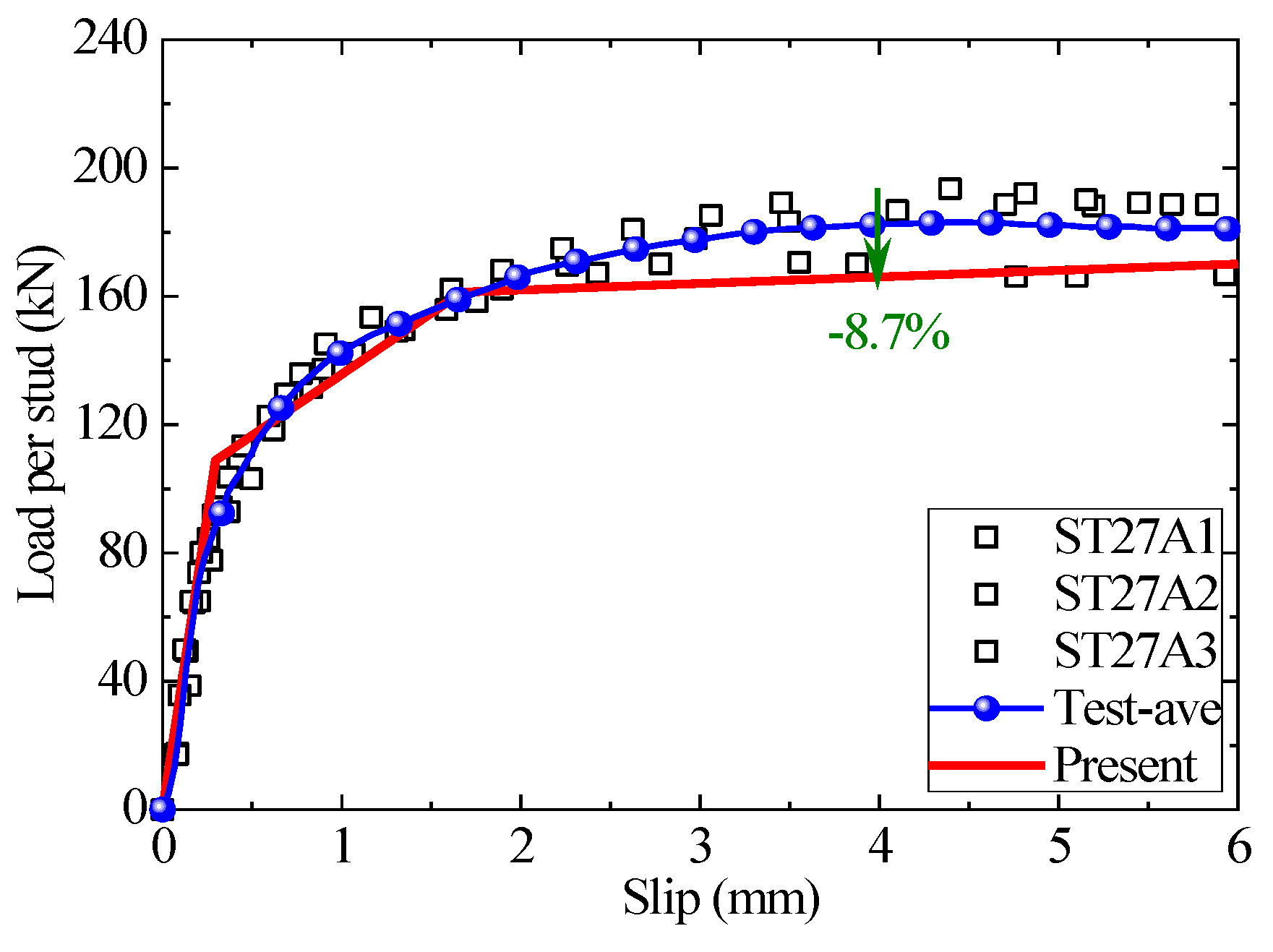
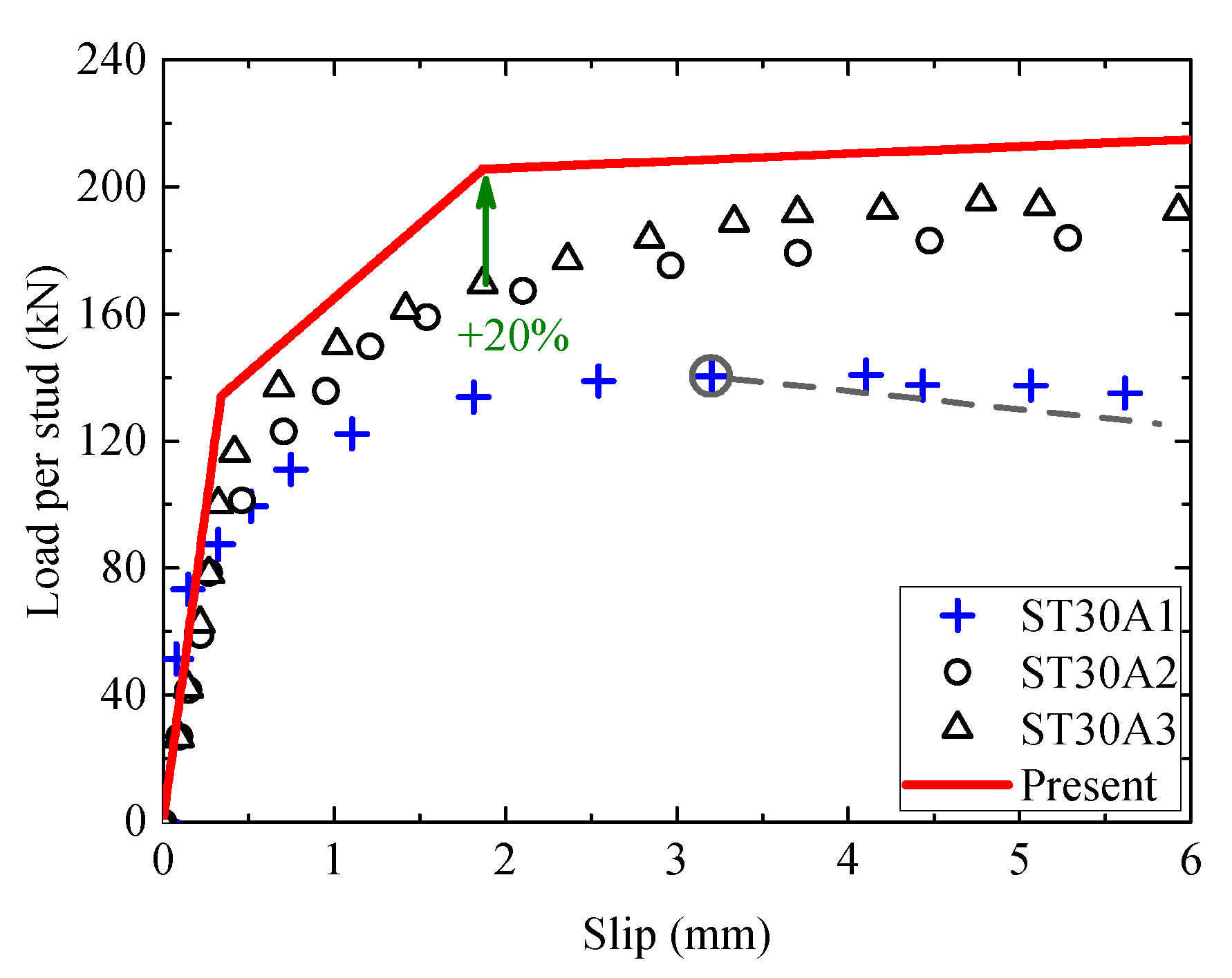
3. Validation of the Trilinear Model and Discussions
3.1. Load–Slip Curves
3.2. Initial Shear Stiffness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Viest, I.M. Investigation of Stud Shear Connectors for Composite Concrete and Steel T-Beams. ACI J. Proc. 1956, 52, 875–892. [Google Scholar] [CrossRef]
- Ollgaard, J.G.; Slutter, R.G.; Fisher, J.W. Shear Strength of Stud Connectors in Lightweight and Normalweight Concrete. Eng. J. Am. Inst. Steel Constr. 1971, 8, 55–64. [Google Scholar]
- Oehlers, D.J.; Johnson, R.P. The Strength of Stud Shear Connections in Composite Beams. Struct. Eng. 1987, 65, 44–48. [Google Scholar] [CrossRef]
- Hiragi, H.; Matsui, S.; Fukumoto, Y. Derivation Strength Equations of Headed Stud Shear Connectors-Static Strengths. Struct. Eng. 1989, 35, 1221–1232. [Google Scholar]
- Okada, J.; Yoda, T.; Lebet, J.-P. A Study of the Grouped Arrangements of Stud Connectors on Shear Strength Behavior. Struct. Eng./Earthq. Eng. 2006, 23, 75s–89s. [Google Scholar] [CrossRef]
- Smith, A.L.; Couchman, G.H. Strength and Ductility of Headed Stud Shear Connectors in Profiled Steel Sheeting. J. Constr. Steel Res. 2010, 66, 748–754. [Google Scholar] [CrossRef]
- Badie, S.S.; Tadros, M.K.; Kakish, H.F.; Splittgerber, D.L.; Baishya, M.C. Large Shear Studs for Composite Action in Steel Bridge Girders. J. Bridg. Eng. 2002, 7, 195–203. [Google Scholar] [CrossRef]
- Badie, S.S.; Morgan Girgis, A.F.; Tadros, M.K.; Nguyen, N.T. Relaxing the Stud Spacing Limit for Full-Depth Precast Concrete Deck Panels Supported on Steel Girders (Phase I). J. Bridg. Eng. 2010, 15, 482–492. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Luo, J.; Lebet, J.-P. Experimental Study on Stud Shear Connectors with Large Diameter and High Strength. In Proceedings of the 2011 International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 22–24 April 2011; pp. 340–343. [Google Scholar]
- Lee, P.-G.; Shim, C.-S.; Chang, S.-P. Static and Fatigue Behavior of Large Stud Shear Connectors for Steel–Concrete Composite Bridges. J. Constr. Steel Res. 2005, 61, 1270–1285. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Kim, S.E. Finite Element Modeling of Push-out Tests for Large Stud Shear Connectors. J. Constr. Steel Res. 2009, 65, 1909–1920. [Google Scholar] [CrossRef]
- Chuah, C.; Shima, H.; Noritake, K. Strength and Deformational Behaviors of Studs Embedded in High Strength Prestressed Concrete. Proc. Jpn. Concr. Inst. 1991, 13, 1033–1038. (In Japanese) [Google Scholar]
- An, L.; Cederwall, K. Push-out Tests on Studs in High Strength and Normal Strength Concrete. J. Constr. Steel Res. 1996, 36, 15–29. [Google Scholar] [CrossRef]
- Nie, J.; Tan, Y.; Wang, H. Design computation of Headed Stud Shear Connectors for Steel-High Strength Concrete Composite Beam. J. Tsinghua Univ. (Sci. Tech.) 1999, 39, 94–97. (In Chinese) [Google Scholar] [CrossRef]
- Hegger, J.; Döinghaus, P. High Performance Steel and High Performance Concrete in Composite Structures. In Proceedings of the Composite Construction in Steel and Concrete IV, Banff, AB, Canada, 28 May–2 June 2002; American Society of Civil Engineers: Reston, VA, USA, 2002; pp. 891–902. [Google Scholar]
- Hegger, J.; Sedlacek, G.; Döinghaus, P.; Trumpf, H. Untersuchungen Zur Duktilität Der Verbundmittel Bei Anwendung von Hochfestem Stahl Und Hochfestem Beton. Stahlbau 2001, 70, 436–446. [Google Scholar] [CrossRef]
- Döinghaus, P.; Goralski, C.; Will, N. Design Rules for Composite Structures with High Performance Steel and High Performance Concrete. In Proceedings of the High Performance Materials in Bridges, Kona, HI, USA, 29 July–3 August 2001; American Society of Civil Engineers: Reston, VA, USA, 2003; pp. 139–149. [Google Scholar]
- Wang, S.; Fang, Z.; Chen, G.; Jiang, H.; Teng, S. Numerical Analysis on Shear Behavior of Grouped Head Stud Shear Connectors between Steel Girders and Precast Concrete Slabs with High-Strength Concrete-Filled Shear Pockets. J. Bridg. Eng. 2021, 26, 04021030. [Google Scholar] [CrossRef]
- Kim, J.-S.S.; Kwark, J.; Joh, C.; Yoo, S.-W.W.; Lee, K.-C.C. Headed Stud Shear Connector for Thin Ultrahigh-Performance Concrete Bridge Deck. J. Constr. Steel Res. 2015, 108, 23–30. [Google Scholar] [CrossRef]
- Cao, J.; Shao, X. Finite Element Analysis of Headed Studs Embedded in Thin UHPC. J. Constr. Steel Res. 2019, 161, 355–368. [Google Scholar] [CrossRef]
- Kruszewski, D.; Zaghi, A.E.; Wille, K. Finite Element Study of Headed Shear Studs Embedded in Ultra-High Performance Concrete. Eng. Struct. 2019, 188, 538–552. [Google Scholar] [CrossRef]
- Hu, Y.; Yin, H.; Ding, X.; Li, S.; Wang, J. Shear Behavior of Large Stud Shear Connectors Embedded in Ultra-High-Performance Concrete. Adv. Struct. Eng. 2020, 23, 3401–3414. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, S.; He, W.; Hou, Z.; He, D.; Yang, T. Numerical Study on the Tensile Performance of Headed Stud Shear Connectors with Head-Sectional Damage. Materials 2022, 15, 2802. [Google Scholar] [CrossRef]
- Chen, Z. Non-Concrete Breakout Failure Modes of Concrete Mechanical Anchors in Tension-a Literature Review. Constr. Build. Mater. 2023, 366, 130222. [Google Scholar] [CrossRef]
- Mirza, O.; Uy, B. Effects of the Combination of Axial and Shear Loading on the Behaviour of Headed Stud Steel Anchors. Eng. Struct. 2010, 32, 93–105. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, Y.; He, J. Behavior of Stud Connectors under Combined Shear and Tension Loads. Eng. Struct. 2014, 81, 362–376. [Google Scholar] [CrossRef]
- Tan, E.L.; Varsani, H.; Liao, F. Experimental Study on Demountable Steel-Concrete Connectors Subjected to Combined Shear and Tension. Eng. Struct. 2019, 183, 110–123. [Google Scholar] [CrossRef]
- Xu, C.; Sugiura, K.; Masuya, H.; Hashimoto, K.; Fukada, S. Experimental Study on the Biaxial Loading Effect on Group Stud Shear Connectors of Steel-Concrete Composite Bridges. J. Bridg. Eng. 2015, 20, 04014110. [Google Scholar] [CrossRef]
- EN1994-1-1; Eurocode 4—Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004; ISBN 978-0-7277-3151-7.
- ACI318-14; Building Code Requirements for Structural Concrete. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2014; ISBN 9780870319303.
- GB50917-2013; Code for Design of Steel and Concrete Bridges. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2013.
- Tong, L.; Chen, L.; Wen, M.; Xu, C. Static Behavior of Stud Shear Connectors in High-Strength-Steel–UHPC Composite Beams. Eng. Struct. 2020, 218, 110827. [Google Scholar] [CrossRef]
- Hu, Y.; Qiu, M.; Chen, L.; Zhong, R.; Wang, J. Experimental and Analytical Study of the Shear Strength and Stiffness of Studs Embedded in High Strength Concrete. Eng. Struct. 2021, 236, 111792. [Google Scholar] [CrossRef]
- Hu, Y.; Zhong, R.; Meloni, M.; Wang, J. A Novel Shear Strength Prediction Approach for Headed Shear Studs Embedded in Ultrahigh-Performance Concrete. J. Struct. Eng. 2021, 147, 04021181. [Google Scholar] [CrossRef]
- Meng, H.; Wang, W.; Xu, R. Analytical Model for the Load-Slip Behavior of Headed Stud Shear Connectors. Eng. Struct. 2022, 252, 113631. [Google Scholar] [CrossRef]
- Soroushian, P.; Obaseki, K.; Rojas, M.C. Bearing Strength and Stiffness of Concrete under Reinforcing Bars. Mater. J. 1987, 84, 179–184. [Google Scholar]
- Moradi, A.R.; Soltani, M.; Tasnimi, A.A. A Simplified Constitutive Model for Dowel Action across RC Cracks. J. Adv. Concr. Technol. 2012, 10, 264–277. [Google Scholar] [CrossRef]
- Xu, C.; Sugiura, K. FEM Analysis on Failure Development of Group Studs Shear Connector under Effects of Concrete Strength and Stud Dimension. Eng. Fail. Anal. 2013, 35, 343–354. [Google Scholar] [CrossRef]
- Xu, C.; Sugiura, K.; Wu, C.; Su, Q. Parametrical Static Analysis on Group Studs with Typical Push-out Tests. J. Constr. Steel Res. 2012, 72, 84–96. [Google Scholar] [CrossRef]
- Gattesco, N.; Giuriani, E. Experimental Study on Stud Shear Connectors Subjected to Cyclic Loading. J. Constr. Steel Res. 1996, 38, 1–21. [Google Scholar] [CrossRef]
- Shim, C.S.; Lee, P.-G.G.; Yoon, T.Y. Static Behavior of Large Stud Shear Connectors. Eng. Struct. 2004, 26, 1853–1860. [Google Scholar] [CrossRef]
- Buttry, K. Behaviorof Stud Shear Connectors in Lightweight and Normal-Weight Concrete. Master’s Thesis, University of Missouri, Columbia, MO, USA, August 1965. [Google Scholar]
- Xue, L. Constitutive Modeling of Void Shearing Effect in Ductile Fracture of Porous Materials. Eng. Fract. Mech. 2008, 75, 3343–3366. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Q.; Yao, Y.; Qi, J.; Xiu, H. Static Behavior of Grouped Large Headed Stud-UHPC Shear Connectors in Composite Structures. Compos. Struct. 2018, 206, 202–214. [Google Scholar] [CrossRef]
- Johnson, R.P.; Molenstran, N. Partial Shear Connection in Composite Beams for Buildings. Proc. Inst. Civ. Eng. 1991, 91, 679–704. [Google Scholar] [CrossRef]
- Lorenc, W.; Kubica, E. Behavior of Composite Beams Prestressed with External Tendons: Experimental Study. J. Constr. Steel Res. 2006, 62, 1353–1366. [Google Scholar] [CrossRef]
- Su, Q.; Yang, G.; Bradford, M.A. Static Behaviour of Multi-Row Stud Shear Connectors in High- Strength Concrete. Steel Compos. Struct. 2014, 17, 967–980. [Google Scholar] [CrossRef]
- Xue, D.; Liu, Y.; Yu, Z.; He, J. Static Behavior of Multi-Stud Shear Connectors for Steel-Concrete Composite Bridge. J. Constr. Steel Res. 2012, 74, 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, A.; Chen, B.; Zhang, J.; Pi, Y.L.; Bradford, M.A. Experimental and Numerical Study of Shear Connection in Composite Beams of Steel and Steel-Fibre Reinforced Concrete. Eng. Struct. 2020, 215, 110707. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2015.
- GB50017-2017; Standard for Design of Steel Structures. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2017.
- JSSC: Standard on Push-out Test for Headed Stud (Draft); Japanese Society of Steel Construction: Tokyo, Japan, 1996.
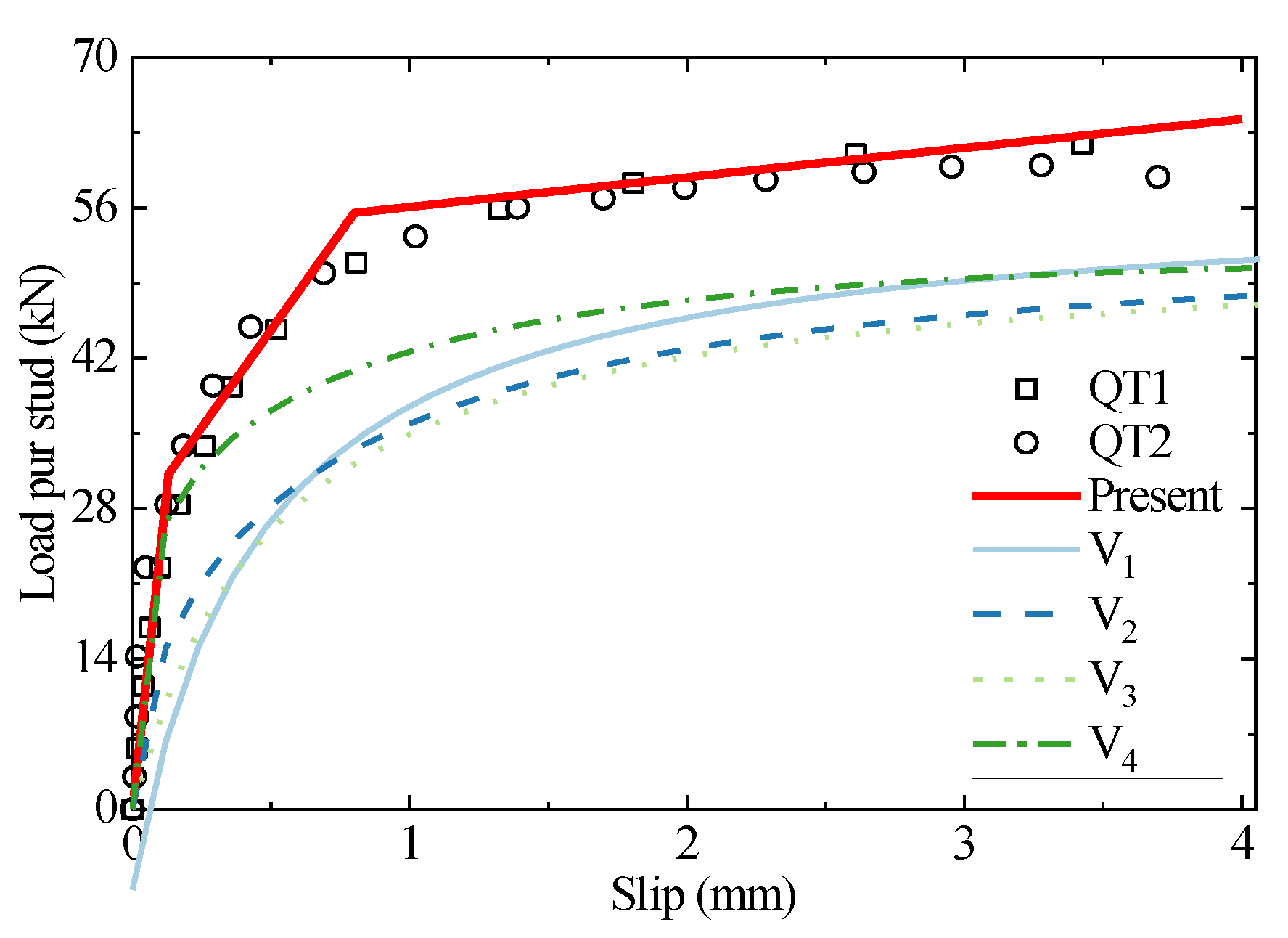
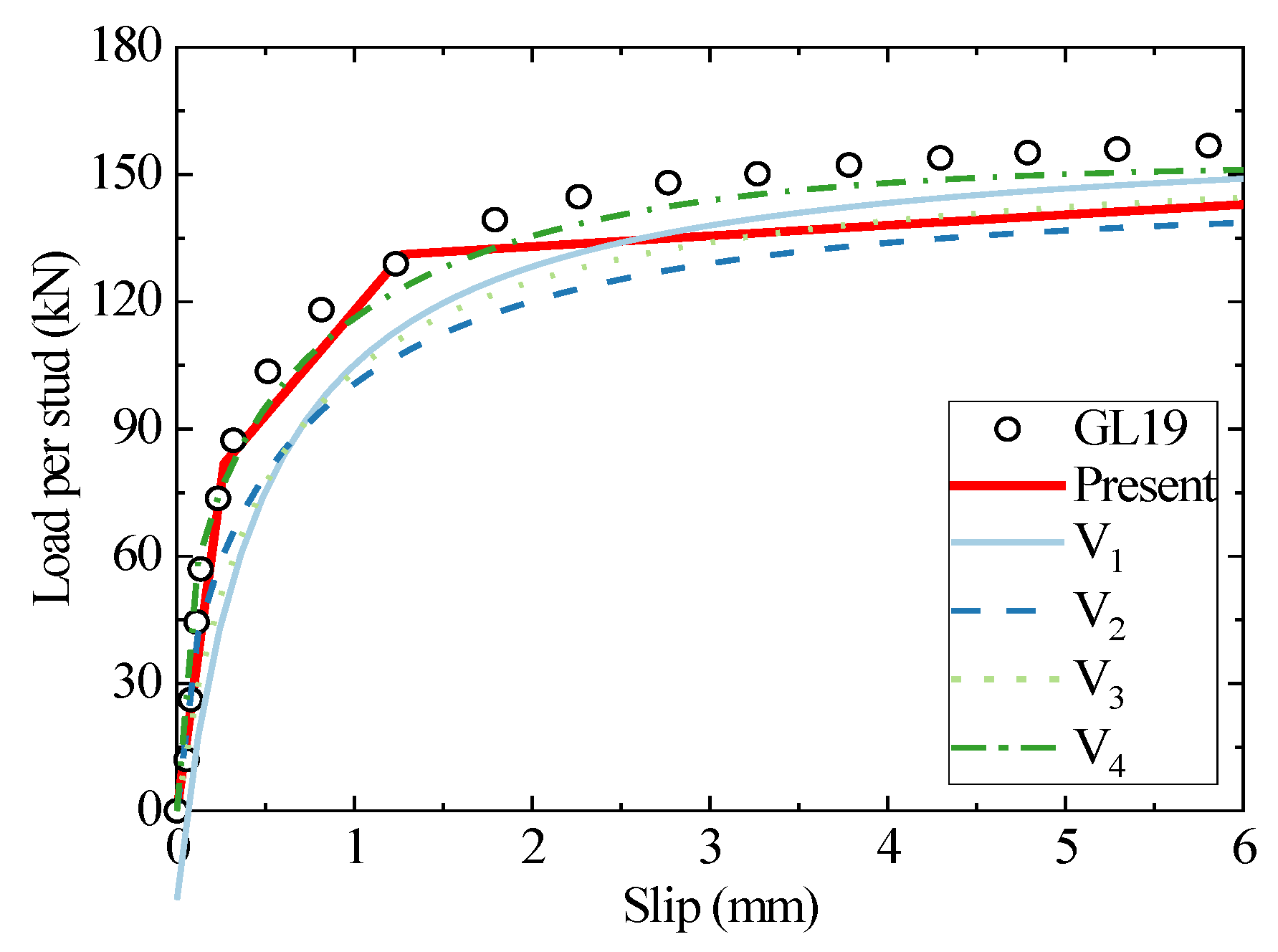

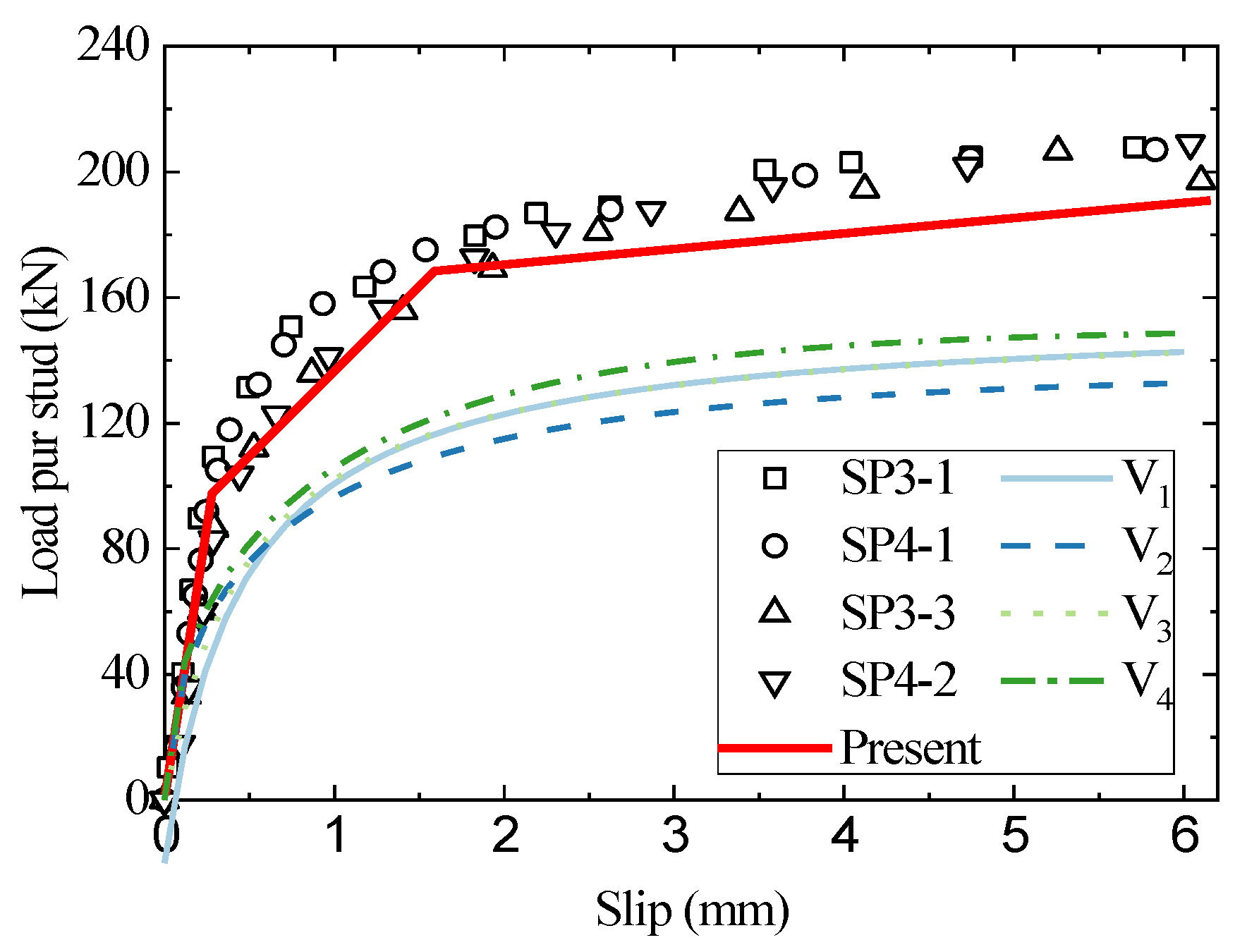
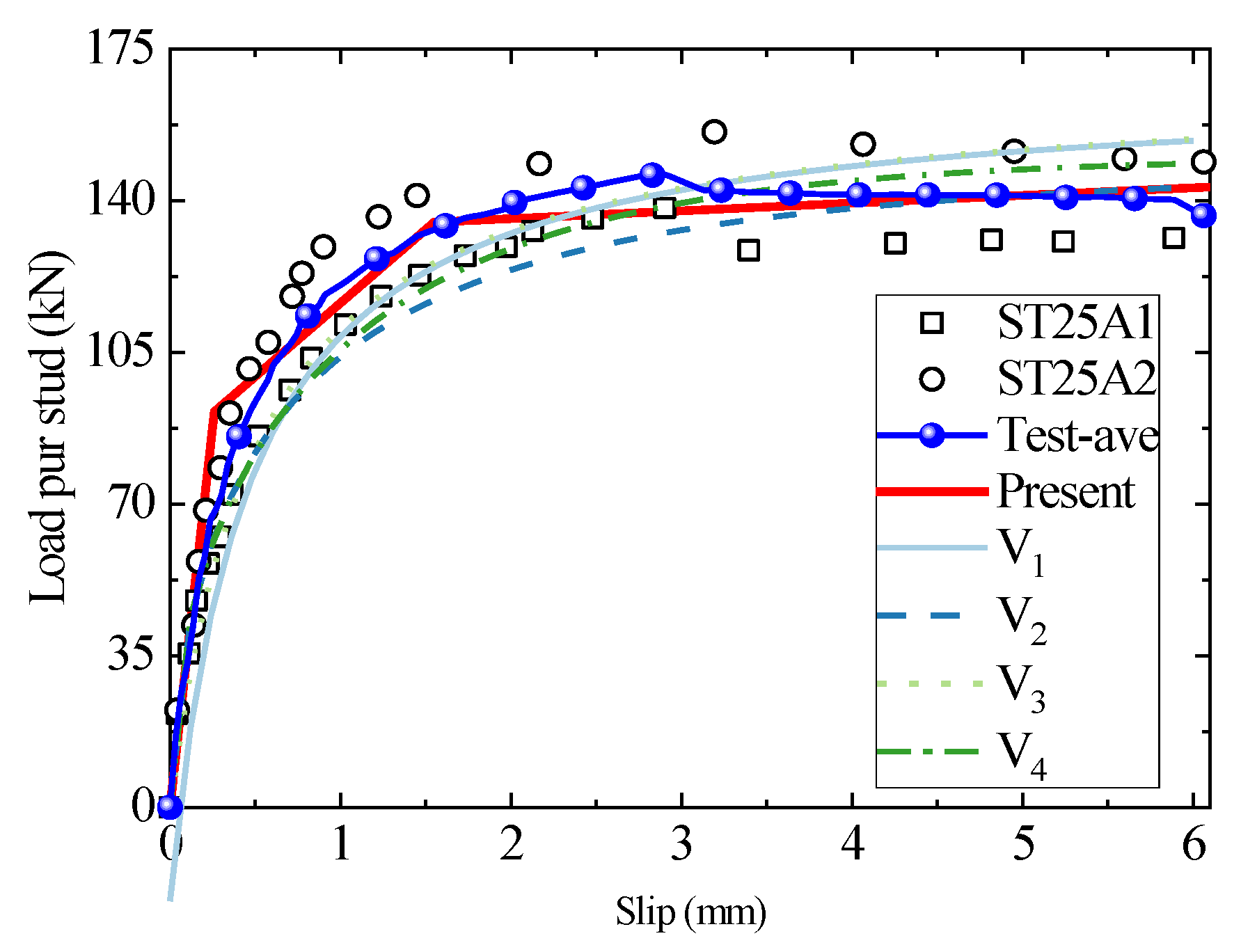

| No. | Specimen | D (mm) | fcly (MPa) | Ec (GPa) | Rc (mm) | Xm (mm) | Rc/d | Xm/d |
|---|---|---|---|---|---|---|---|---|
| 1 | D13-C40 | 13 | 40 | 34.56 | 12.50 | 13.13 | 0.96 | 1.01 |
| 2 | D13-C32 | 13 | 32 | 32.64 | 13.60 | 13.31 | 1.05 | 1.02 |
| 3 | D13-C24 | 13 | 24 | 29.87 | 14.20 | 13.61 | 1.09 | 1.05 |
| 4 | D16-C40 | 16 | 40 | 34.56 | 15.50 | 16.58 | 0.97 | 1.04 |
| 5 | D16-C32 | 16 | 32 | 32.64 | 16.80 | 16.82 | 1.05 | 1.05 |
| 6 | D16-C24 | 16 | 24 | 29.87 | 18.10 | 17.19 | 1.13 | 1.07 |
| 7 | D19-C40 | 19 | 40 | 34.56 | 19.00 | 20.12 | 1.00 | 1.06 |
| 8 | D19-C32 | 19 | 32 | 32.64 | 20.00 | 20.40 | 1.05 | 1.07 |
| 9 | D19-C24 | 19 | 24 | 29.87 | 21.80 | 20.86 | 1.15 | 1.10 |
| 10 | D22-C40 | 22 | 40 | 34.56 | 22.60 | 23.72 | 1.03 | 1.08 |
| 11 | D22-C32 | 22 | 32 | 32.64 | 25.00 | 24.06 | 1.14 | 1.09 |
| 12 | D22-C24 | 22 | 24 | 29.87 | 26.00 | 24.60 | 1.18 | 1.12 |
| Parameters | QT1 QT2 QT3 | GL19 | SP3-1 SP3-3 SP4-1 SP4-3 | SP3-2 SP4-2 | ST25A1 ST25A2 ST25A3 | ST25B1 ST25B2 ST25B3 | ST27A1 ST27A2 ST25A3 | ST30A1 ST30A2 ST30A3 |
|---|---|---|---|---|---|---|---|---|
| d (mm) | 13 | 19 | 22 | 22 | 25 | 25 | 27 | 30 |
| h (mm) | 80 | 100 | 150 | 150 | 155 | 155 | 155 | 155 |
| fy (MPa) | 400 | 500 | 445 | 445 | 328 | 328 | 328 | 328 |
| fu (MPa) | 480 | 530 | 530 | 530 | 426 | 426 | 426 | 426 |
| fcu (MPa) | 50 | 50 | 60 | 50 | 40 | 50 | 40 | 40 |
| εy | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| εu | 0.1 | 0.1 | 0.1 | 0.1 | 0.34 | 0.34 | 0.34 | 0.34 |
| Es (Gpa) | 200 | 210 | 210 | 210 | 213 | 213 | 213 | 213 |
| L (mm) | 60 | 100 | 110 | 110 | 250 | 250 | 250 | 250 |
| Specimen | Tests | Equation (1) | Equation (2) | Equation (3) | Equation (4) | Present | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ktest kN/mm | Kp1 kN/mm | Error % | Kp2 kN/mm | Error % | Kp3 kN/mm | Error % | Kp4 kN/mm | Error % | Kp kN/mm | Error % | |
| QT1 | 63.4 | 42.9 | −32.33 | 41.4 | −34.7 | 40.0 | −36.9 | 50.9 | −19.7 | 68.0 | 7.3 |
| QT2 | 64.3 | 42.9 | −33.28 | 41.4 | −35.6 | 40.0 | −37.8 | 50.9 | −20.8 | 68.0 | 5.8 |
| GL19 | 145.8 | 121.9 | −16.39 | 119.5 | −18.0 | 117.1 | −19.7 | 135.9 | −6.8 | 137.6 | −5.6 |
| SP3-2 | 162.5 | 112.3 | −30.89 | 116.5 | −28.3 | 115.1 | −29.2 | 115.8 | −28.7 | 156.9 | −3.4 |
| SP4-2 | 172.8 | 112.3 | −35.01 | 116.5 | −32.6 | 115.1 | −33.4 | 115.8 | −33.0 | 156.9 | −9.2 |
| SP3-1 | 184.0 | 116.0 | −36.96 | 112.7 | −38.8 | 120.4 | −34.6 | 123.8 | −32.7 | 159.8 | −13.2 |
| SP4-1 | 181.5 | 116.0 | −36.09 | 112.7 | −37.9 | 120.4 | −33.7 | 123.8 | −31.8 | 159.8 | −12.0 |
| SP3-3 | 170.9 | 116.0 | −32.12 | 112.7 | −34.1 | 120.4 | −29.5 | 123.8 | −27.6 | 159.8 | −6.5 |
| SP4-3 | 166.4 | 116.0 | −30.29 | 112.7 | −32.3 | 120.4 | −27.6 | 123.8 | −25.6 | 159.8 | −4.0 |
| ST25A1 | 132.4 | 124.4 | −6.04 | 124.6 | −5.9 | 127.6 | −3.6 | 121.6 | −8.2 | 138.8 | 4.8 |
| ST25A2 | 148.4 | 124.4 | −16.17 | 124.6 | −16.0 | 127.6 | −14.0 | 121.6 | −18.1 | 138.8 | −6.5 |
| ST25B1 | 163.4 | 143.5 | −12.18 | 139.0 | −14.9 | 136.1 | −16.7 | 124.4 | −23.9 | 159.0 | −2.7 |
| ST25B2 | 171.6 | 143.5 | −16.38 | 139.0 | −19.0 | 136.1 | −20.7 | 124.4 | −27.5 | 159.0 | −7.3 |
| ST25B3 | 176.4 | 143.5 | −18.65 | 139.0 | −21.2 | 136.1 | −22.8 | 124.4 | −29.5 | 159.0 | −9.9 |
| ST27A1 | 134.2 | / | / | / | / | / | / | / | / | 128.1 | −4.5 |
| ST27A2 | 136.5 | / | / | / | / | / | / | / | / | 128.1 | −6.2 |
| ST27A3 | 133.8 | / | / | / | / | / | / | / | / | 128.1 | −4.3 |
| ST30A1 * | 86.5 | / | / | / | / | / | / | / | / | 87.5 | 1.2 |
| ST30A2 * | 82.3 | / | / | / | / | / | / | / | / | 87.5 | 6.3 |
| ST30A2 * | 91.4 | / | / | / | / | / | / | / | / | 87.5 | −4.3 |
| Averaged absolute error | 25.20 | 26.38 | 25.73 | 23.84 | 6.24 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, H.; Wang, W.; Xu, R. A Trilinear Model for the Load–Slip Behavior of Headed Stud Shear Connectors. Materials 2023, 16, 1173. https://doi.org/10.3390/ma16031173
Meng H, Wang W, Xu R. A Trilinear Model for the Load–Slip Behavior of Headed Stud Shear Connectors. Materials. 2023; 16(3):1173. https://doi.org/10.3390/ma16031173
Chicago/Turabian StyleMeng, Hao, Wei Wang, and Rongqiao Xu. 2023. "A Trilinear Model for the Load–Slip Behavior of Headed Stud Shear Connectors" Materials 16, no. 3: 1173. https://doi.org/10.3390/ma16031173
APA StyleMeng, H., Wang, W., & Xu, R. (2023). A Trilinear Model for the Load–Slip Behavior of Headed Stud Shear Connectors. Materials, 16(3), 1173. https://doi.org/10.3390/ma16031173






