Microhardness, Indentation Size Effect and Real Hardness of Plastically Deformed Austenitic Hadfield Steel
(This article belongs to the Section Manufacturing Processes and Systems)
Abstract
1. Introduction
2. Experimental Method and Data Analysis
2.1. The Sample Materials
2.2. Methods of Microhardness Testing and Characterisation
2.3. Methods of Data Analyses
2.3.1. Calculations of the Meyer Index n, Real Hardness H0, and ISE Significance Coefficient η
2.3.2. Prediction of Hardness Using the Theoretical Models
3. Results
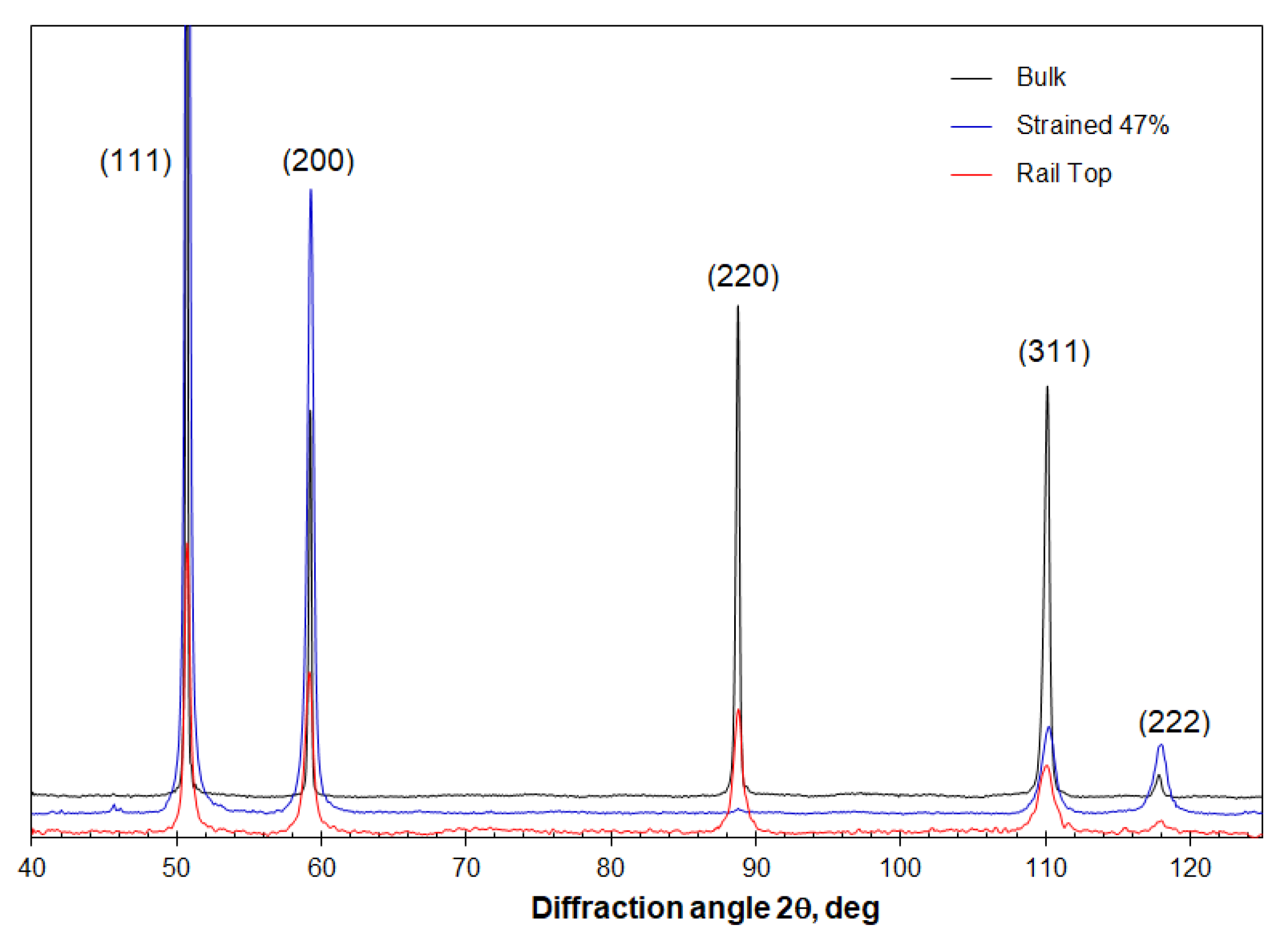
3.1. Effect of Straining on The Microstructure of the Austenitic Hadfield Steel
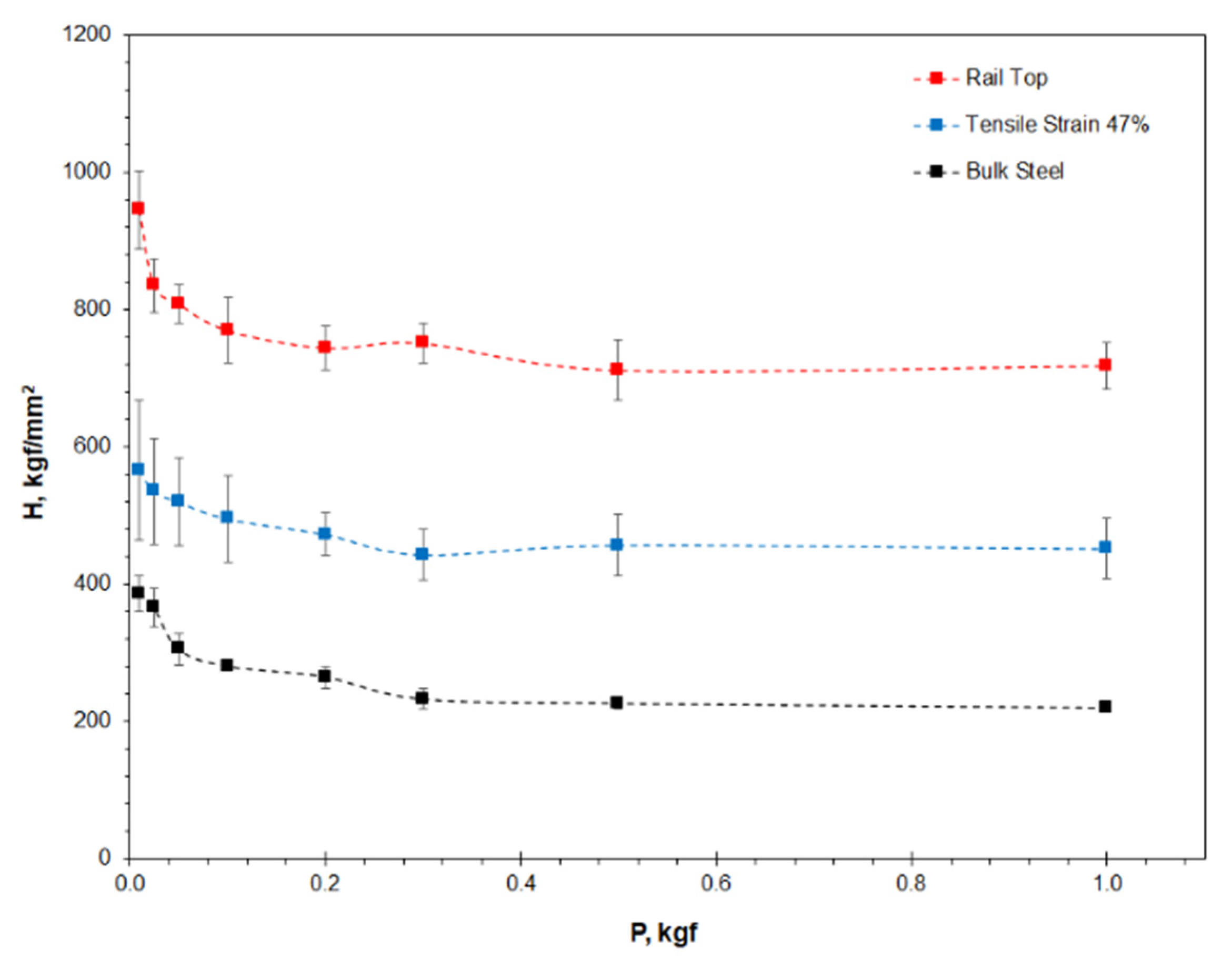
3.2. The Vickers Microhardness Property Determined by Indentation
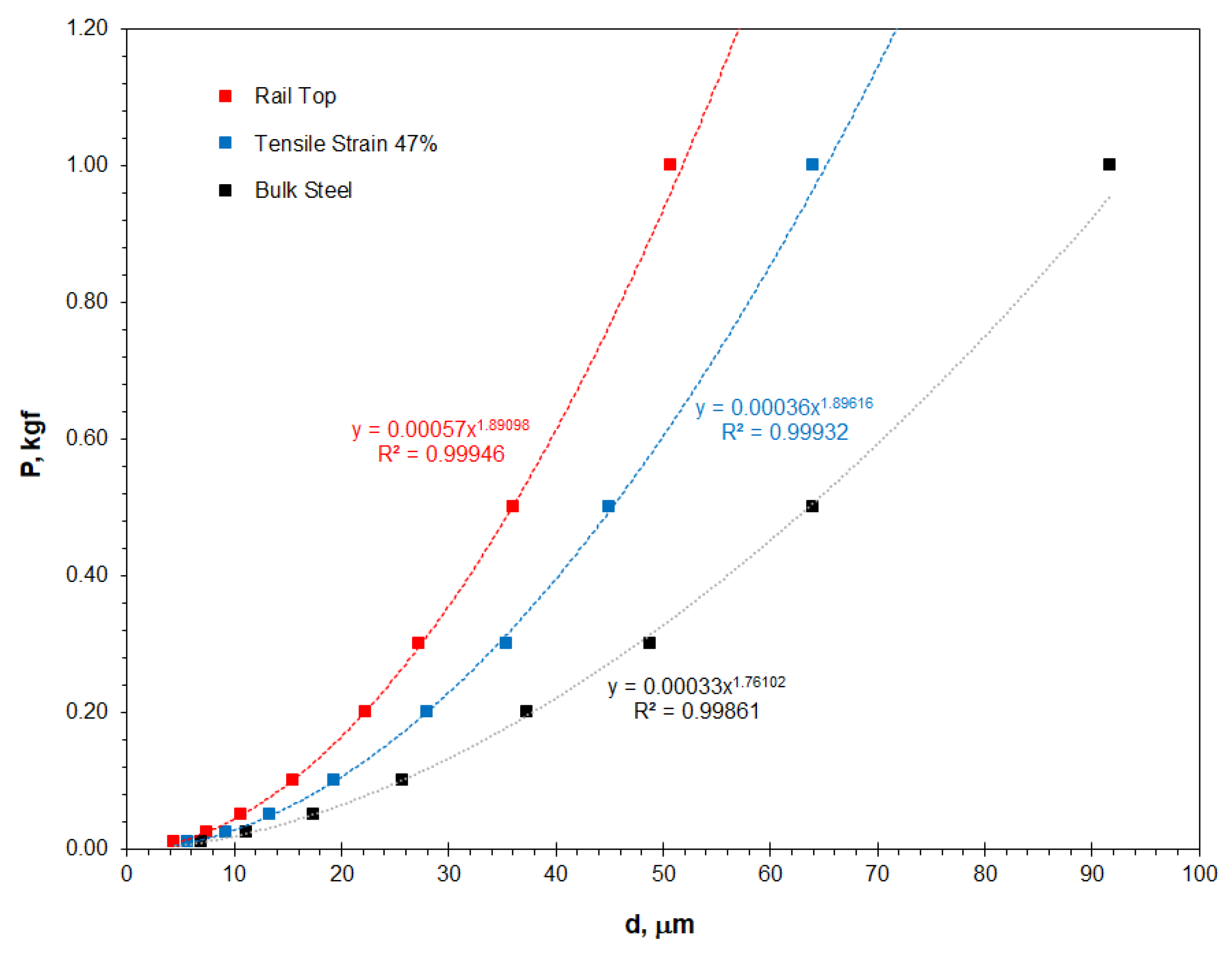
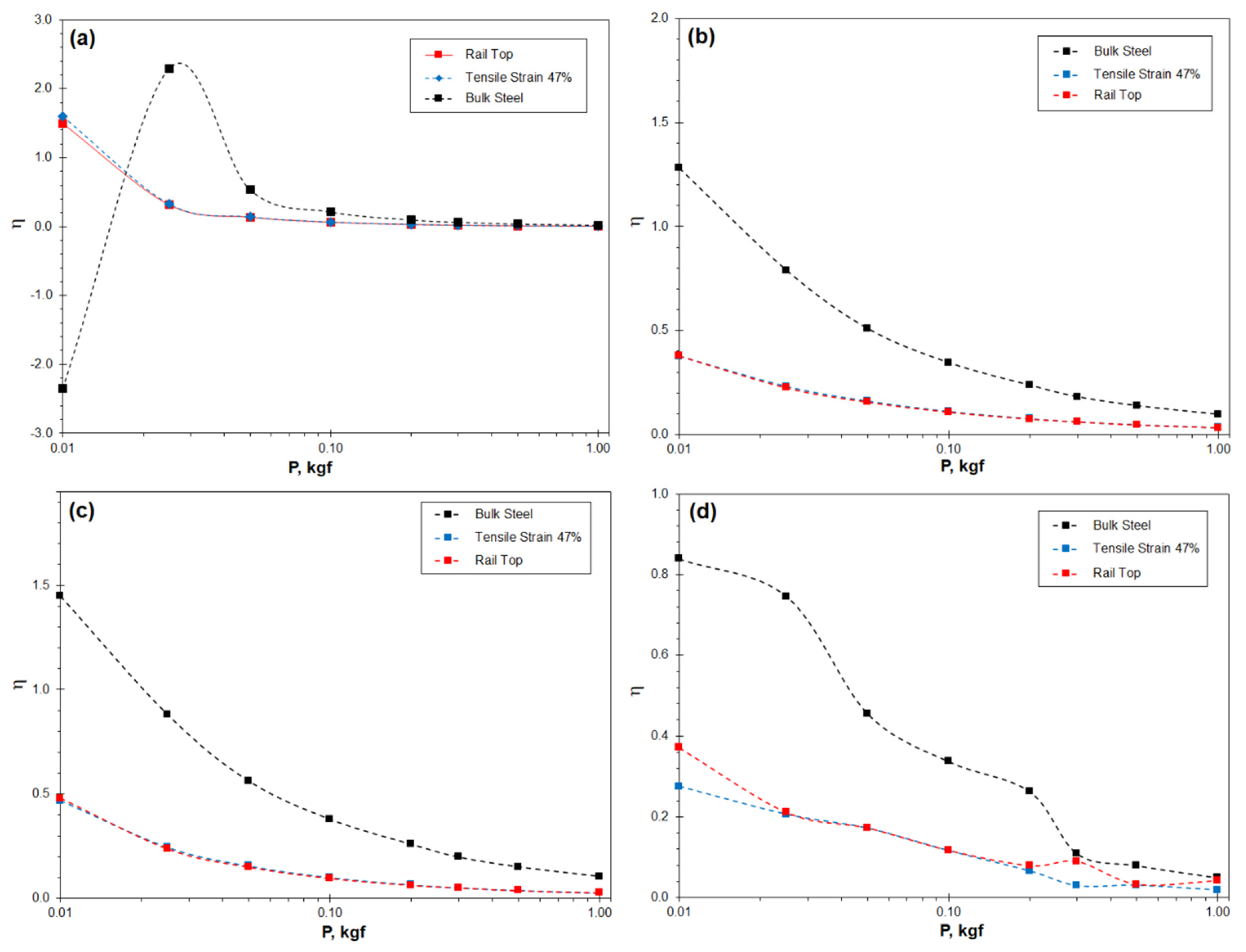
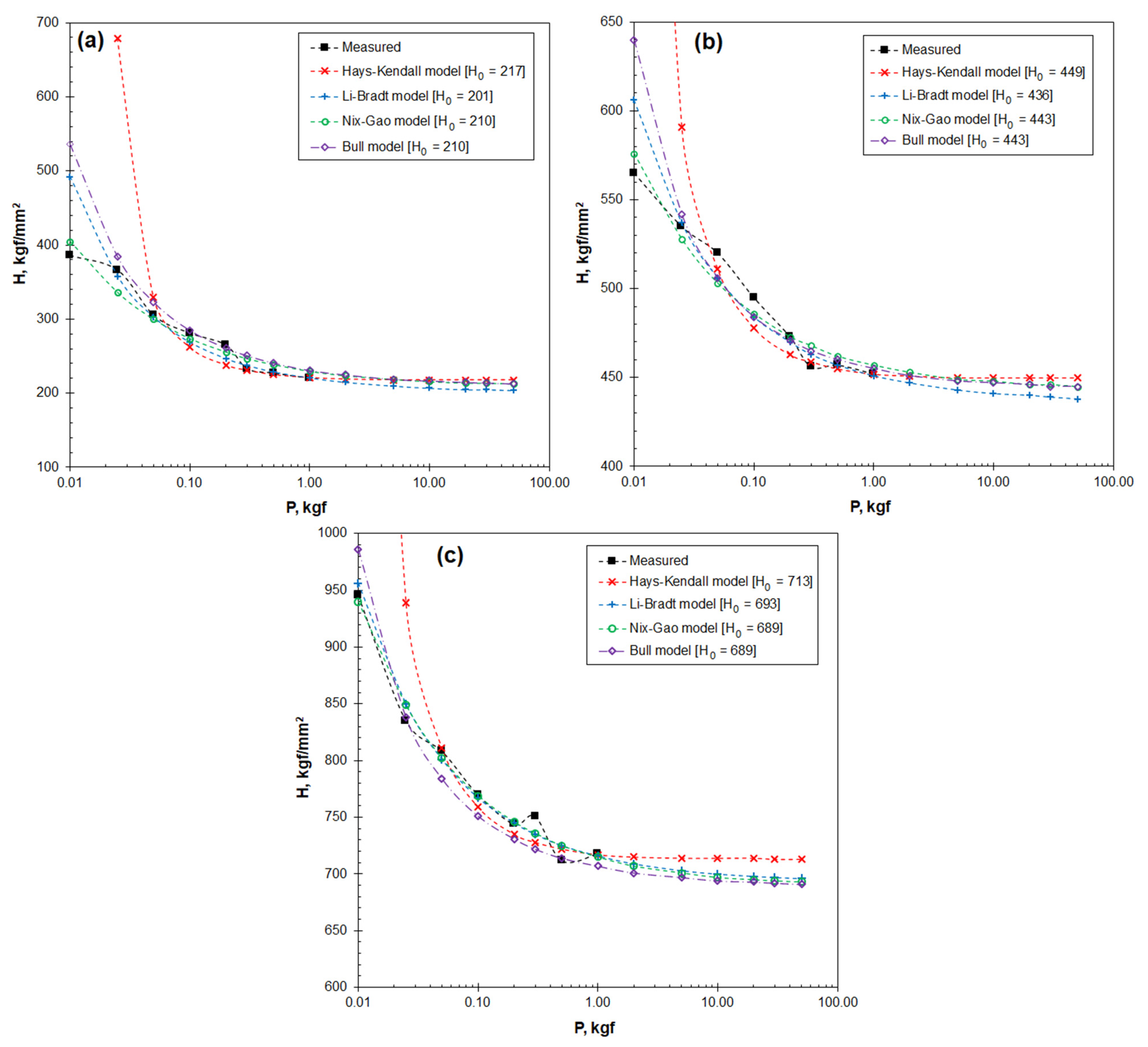
3.3. The Real Hardness and ISE Significance Determined Using the Theoretical Models
3.4. Compatibility of the Theoretically Projected Hardness to the Measured Hardness
3.5. Case Studies: Initial Applications of the Established Method
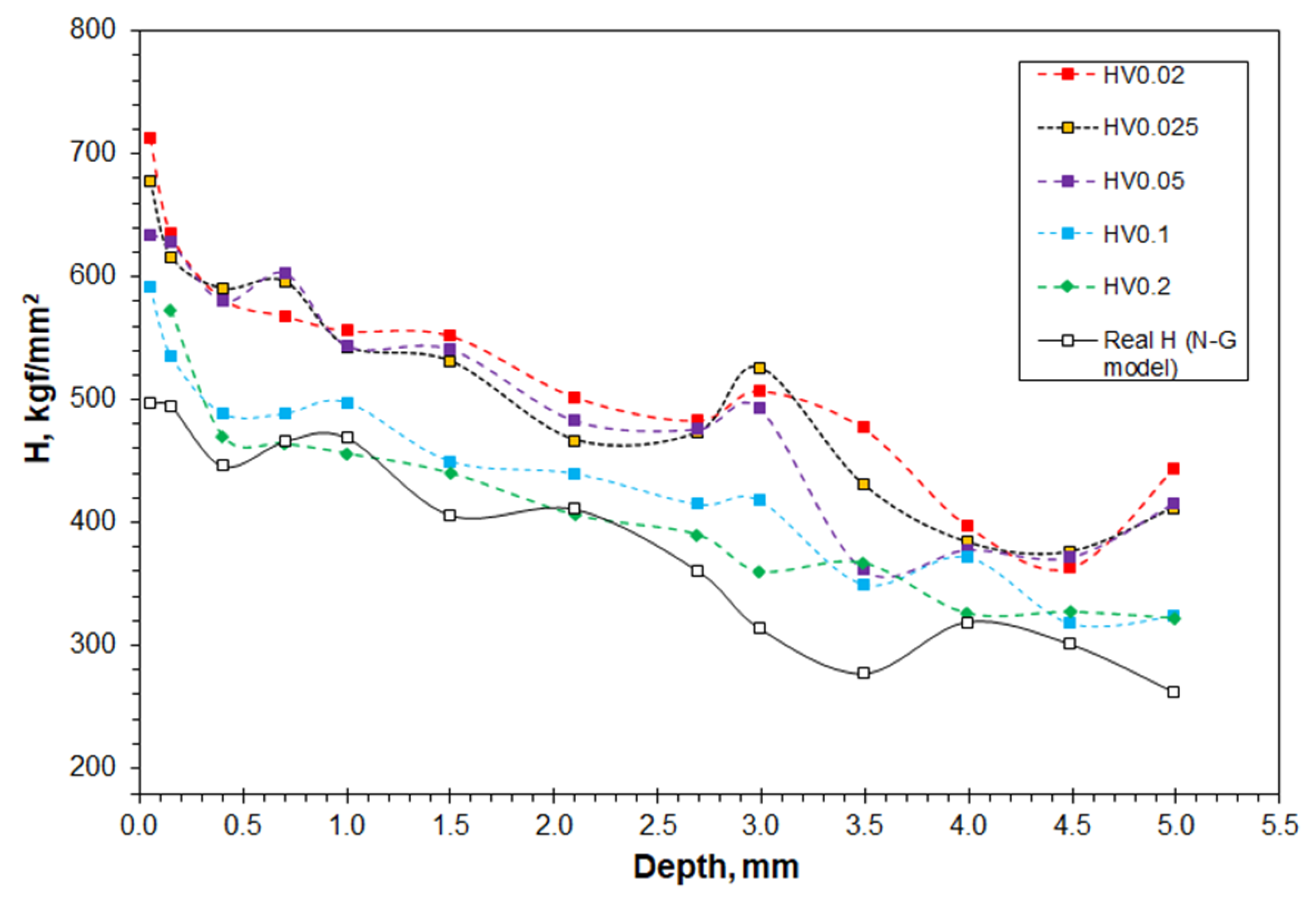
3.5.1. The Microhardness Properties of the Worn Surfaces of Steels Having Different Microstructure
3.5.2. The Subsurface Hardness Profile of the Worn Hadfield Steel Turnout
4. Discussion
4.1. Selection of Theoretical Models to Determine the ISE-Independent Real Hardness
4.2. The Origin of ISE
4.3. Effect of Mechanical Straining on the ISE and Real Hardness of Hadfield Steels
4.4. Effect of Microstructure on the ISE Properties
5. Conclusions
- The real hardness of small-scale materials can be determined by Vickers microhardness indentation and subsequent analysis using the Nix-Gao model. The origin of ISE derives from the mismatch between the experimentally determined P ~ d relationship and Kick’s law (P = A · d2). Within the limitation of the present experimental activity, the results suggest that Kick’s law should be replaced by Meyer’s power law (P = A · dn) with n < 2.
- Because of the ISE, indentation hardness measured under small loads does not present the real hardness property and the real strain-hardening ratio. The plastically strained samples exhibited not only strong work hardening, but also different ISE significance, as compared to the non-deformed bulk steel. The bulk steel retained the lowest A and n values, obtaining the lowest hardness and the strongest ISE significance. The strained samples showed increased an A value, with the n approaching 2, indicating higher hardness and lower ISE significance, respectively. The sample experienced the extreme plastic straining showed the highest A value, reaching a real hardness of 689 kgf/mm2.
- When the indentation loads were in macro scale, the four theoretical models show good precision in calculating the real hardness and in predicting the Vickers hardness values at various loads. When the indentation loads were in micro scale, the Nix-Gao model outperformed the other theoretical models in these calculations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Broitman, E. Indentation hardness measurements at macro, micro, and nanoscale: A critical overview. Tribol. Lett 2017, 65, 23. [Google Scholar] [CrossRef]
- Chicot, D.; Roudet, F.; Soom, A.; Lesage, J. Interpretation of instrumental hardness measurements on stainless steel with different surface preparation. Surf. Eng. 2007, 23, 32–39. [Google Scholar] [CrossRef]
- Liu, S. Size effect analysis and experimental study of microhardness indentation of metal materials. Fail. Anal. Prev. 2019, 14, 225–231. [Google Scholar]
- Bull, S.J.; Page, T.F.; Yoffe, E.H. An explanation of the indentation size effect in ceramics. Philos. Mag. Lett. 1989, 59, 281–288. [Google Scholar] [CrossRef]
- Sargent, P.M. Indentation size effect and strain-hardening. J. Mater. Sci. Lett. 1989, 8, 1139–1140. [Google Scholar] [CrossRef]
- Farges, G.; Degout, D. Interpretation of the indentation size effect in Vickers microhardness measurements—Absolute hardness of materials. Thin Solid Films 1989, 181, 365–374. [Google Scholar] [CrossRef]
- Li, H.; Bradt, R.C. The microhardness indentation load/size effect in rutile and cassiterite single crystals. J. Mater. Sci. 1993, 28, 917–926. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Atkinson, M. Calculation of characteristic macro-hardness from low-load indentation tests. Mater. Sci. Eng. 1995, A197, 165–169. [Google Scholar] [CrossRef]
- Attaf, M.T. Connection between the loading curve models in elastoplastic indentation. Mater. Lett. 2004, 58, 3491–3498. [Google Scholar] [CrossRef]
- Karan, S.; Sen Gupta, S.P. Vickers microhardness studies on solution-grown single crystals of magnesium sulphate hepta-hydrate. Mater. Sci. Eng. 2005, A398, 198–203. [Google Scholar] [CrossRef]
- Sarangi, S.S.; Lavakumar, A.; Singh, P.K.; Katiyar, P.K.; Ray, R.K. Indentation size effect in steels with different carbon contents and microstructures. Mater. Sci. Technol. 2022. [Google Scholar] [CrossRef]
- Hays, C.; Kendall, E.C. An analysis of Knoop microhardness. Metallography 1973, 6, 275–282. [Google Scholar] [CrossRef]
- Song, P.; Yabuuchi, K.; Spaetig, P. Insights into hardening, plastically deformed zone and geometrically necessary dislocations of two ion-irradiated FeCrAl(Zr)-ODS ferritic steels: A combined experimental and simulation study. Acta Mater. 2022, 234, 117991. [Google Scholar] [CrossRef]
- Yan, W.; Fang, L.; Sun, K.; Xu, Y. Effect of surface hardening on wear behaviour of Hadfield steel. Mater. Sci. Eng. 2007, 460–461, 542–549. [Google Scholar] [CrossRef]
- Liu, Y.G.; Li, M.Q.; Liu, H.J. Surface nanocrystallization and gradient structure developed in the bulk TC4 alloy processed by shot peening. J. Alloy. Compd. 2016, 685, 186–193. [Google Scholar] [CrossRef]
- Nagarajan, B.; Kumar, D.; Fan, Z.; Castagne, S. Effect of deep cold rolling on mechanical properties and microstructure of nickel-based superalloys. Mater. Sci. Eng. 2018, A728, 196–207. [Google Scholar] [CrossRef]
- Harzallah, R.; Mouftiez, A.; Felder, E.; Harriri, S.; Maujean, J.P. Rolling contact fatigue of Hadfield steel X120Mn12. Wear 2010, 269, 647–654. [Google Scholar] [CrossRef]
- Chen, C.; Lv, B.; Ma, H.; Sun, D.; Zhang, F. Wear behaviour and the corresponding work hardening characteristics of Hadfield steel. Tribol. Int. 2018, 121, 389–399. [Google Scholar] [CrossRef]
- Zambrano, O.A.; Tressia, G.; Souza, R.M. Failure analysis of a crossing rail made of Hadfield steel after severe plastic deformation induced by wheel-rail interaction. Eng. Fail. Analys. 2020, 115, 104621. [Google Scholar] [CrossRef]
- Shariff, S.M.; Pal, T.K.; Padmanabham, G.; Joshi, S.V. Comparative study on dry sliding wear behaviour of various railroad steels. Trans. ASME J. Tribol. 2011, 133, 021602. [Google Scholar] [CrossRef]
- Yin, C.H.; Liang, Y.L.; Jiang, Y.; Yang, M.; Long, S.L. Formation of nano-laminated structures in a dry sliding wear induced layer under different wear mechanisms of 20CrNi2Mo steel. Appl. Surf. Sci. 2017, 423, 305–313. [Google Scholar] [CrossRef]
- Machado, P.C.; Pereira, J.I.; Sinatora, A. Subsurface microstructural dynamic recrystallization in multiscale abrasive wear. Wear 2021, 486–487, 204111. [Google Scholar] [CrossRef]
- Akhter, R.; Zhou, Z.; Xie, Z.; Munroe, P. Influence of substrate bias on the scratch, wear and indentation responses of TiSiN nanocomposite coatings. Surf. Coat. Technol. 2021, 425, 127687. [Google Scholar] [CrossRef]
- Ghorbal, G.B.; Tricoteaux, A.; Thuault, A.; Ageorges, H.; Rouder, F.; Chicot, D. Mechanical properties of thermally sprayed porous alumina coating by Vickers and Knoop indentation. Ceram. Int. 2020, 46, 19843–19851. [Google Scholar] [CrossRef]
- Xue, H.; Li, K.; Wang, S.; Zhao, K. Hardness indentation size effect analysis of 316L austenitic stainless steels during cold working. China Mech. Eng. 2019, 30, 105–112. [Google Scholar]
- Niu, M.; Yang, Y.; Zhang, C.; Han, X.; Li, Z. The effect of cold rolling and annealing on the microstructure and irradiation hardening resistance of V-5Cr-5Ti alloys. Nucl. Phys. Rev. 2021, 38, 319–325. [Google Scholar]
- Peng, Z.; Gong, J.; Miao, H. On the description of indentation size effect in hardness testing for ceramics: Analysis of the indentation data. J. Europ. Ceram. Soc. 2004, 24, 2193–2201. [Google Scholar] [CrossRef]
- Balos, S.; Rajnovic, D.; Sidjanin, L.; Cekic, O.E.; Moraca, S.; Trivkovic, M.; Dedic, M. Vickers hardness indentation size effect in selective laser melted MSI maraging steel. J. Mech. Eng. Sci. 2021, 235, 1724–1730. [Google Scholar] [CrossRef]
- Zhu, P.; Zhao, Y.; Agarwal, S.; Henry, J.; Zinkle, S.J. Toward accurate evaluation of bulk hardness from nanoindentation testing at low indent depths. Mater. Design 2022, 213, 110317. [Google Scholar] [CrossRef]
- Das, A.; Altstadt, E.; Kaden, C.; Kapoor, G.; Akhmadaliev, S.; Bergner, F. Nanoindentation Response of Ion-Irradiated Fe, Fe-Cr Alloys and Ferritic-Martensitic Steel Eurofer 97: The Effect of Ion Energy. Front. Mater. 2022, 8, 811851. [Google Scholar] [CrossRef]
- Lu, S.; Roudet, F.; Montagne, A.; Coorevits, T.; Guilbert, G.; Mouftiez, A.; Betrancourt, D.; Chicot, D. Vickers hardness of NiW coatings as a potential replacement for Cr-VI: A methodology to consider size effect and tip defect in classical microindentation. Surf. Coat. Technol. 2022, 447, 128812. [Google Scholar] [CrossRef]
- Luo, Q.; Zhu, J. Wear property and wear mechanisms of high-manganese austenitic Hadfield steel in dry reciprocal sliding. Lubricants 2022, 10, 37. [Google Scholar] [CrossRef]
- Luo, Q.; Li, J.; Yan, Q.; Li, W.; Gao, Y.; Kitchen, M.; Bowen, L.; Farmilo, N.; Ding, Y. Sliding wear of medium-carbon bainitic/martensitic/austenitic steel treated by short-term low-temperature austempering. Wear 2021, 476, 203732. [Google Scholar] [CrossRef]
- Guo, S.L.; Sun, D.Y.; Zhang, F.C.; Feng, X.Y.; Qian, L.H. Damage of a hadfield steel crossing due to wheel rolling impact passages. Wear 2013, 305, 267–273. [Google Scholar] [CrossRef]
- Abbasi, M.; Kheirandish, S.; Kharrazi, Y.; Hejazi, J. On the comparison of the abrasive wear behaviour of aluminium alloyed and standard Hadfield steel. Wear 2010, 268, 202–207. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, S.; Zang, M. Microstructure and impact wear properties of high-manganese steel. Tribology 2018, 38, 291–298. [Google Scholar]
- Cai, C.; Song, R.; Liu, S.; Feng, Y.; Pei, Z. Wear behaviour and subsurface layer work hardening mechanism of Fe-24.1Mn-1.21C-0.48Si steel. Proc. Eng. 2017, 207, 2251–2256. [Google Scholar] [CrossRef]






| Models and Equations | H0 | ISE Parameter | η | |||
|---|---|---|---|---|---|---|
| Y | X | |||||
| Hays-Kendall | P = W + · d2 | P | d2 | 1.8544 · | W = | |
| Li-Bradt | P = a · d + · d2 = a + | d | 1.8544 · a1 | a = | ||
| Bull | P = W + a · d + · d2 (Y = a0 + a1 · X + a2 · X2) | P | d | 1.8544 · a2 | W = a = | · (a1 + ) |
| Nix-Gao | H = H0 · +· | = | − 1 | |||
| Sample | Indentation Load, kgf | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.025 | 0.05 | 0.1 | 0.2 | 0.3 | 0.5 | 1.0 | |
| Rail Top | 945 ± 57 | 835 ± 39 | 808 ± 28 | 770 ± 48 | 744 ± 32 | 751 ± 29 | 712 ± 43 | 718 ± 34 |
| Tensile Strain 47% | 565 ± 102 | 535 ± 76 | 520 ± 64 | 495 ± 62 | 473 ± 31 | 443 ± 37 | 457 ± 44 | 452 ± 44 |
| Bulk Steel | 386 ± 26 | 366 ± 28 | 305 ± 23 | 281 ± 5 | 265 ± 16 | 233 ± 15 | 227 ± 9 | 220 ± 6 |
| Theoretical Models | Bulk Steel | Tensile Bar | Rail Top |
|---|---|---|---|
| Hays-Kendall | 217 ± 3 | 449 ± 2 | 713 ± 4 |
| Li-Bradt | 201 ± 5 | 436 ± 3 | 693 ± 7 |
| Bull | 210 ± 13 | 443 ± 7 | 689 ± 7 |
| Nix-Gao | 210 ± 13 | 443 ± 7 | 689 ± 7 |
| Average | 210 | 443 | 697 |
| deviation | 3.1% | 1.2% | 1.9% |
| Theoretical Models | Bulk Steel | Tensile Bar | Rail Top |
|---|---|---|---|
| Hays-Kendall | 258 ± 4 | 467 ± 6 | 734 ± 6 |
| Li-Bradt | 232 ± 8 | 448 ± 8 | 696 ± 5 |
| Bull | 226 ± 9 | 414 ± 6 | 680 ± 9 |
| Nix-Gao | 234 ± 21 | 459 ± 10 | 682 ± 9 |
| Average | 238 | 447 | 698 |
| deviation | 5.6% | 5.2% | 3.6% |
| Models | Bulk Steel | Rail Top | Tensile Bar | |
|---|---|---|---|---|
| Hays-Kendall | Range | 19–313 | 3–104 | 9–56 |
| mean ± dev | 96 ± 145 | 32 ± 48 | 23 ± 22 | |
| Li-Bradt | Range | 2–106 | 1–15 | 2–41 |
| mean ± dev | 29 ± 43 | 7 ± 6 | 14 ± 16 | |
| Nix-Gao | Range | 5–30 | 1–14 | 0–17 |
| mean ± dev | 14 ± 10 | 6 ± 5 | 9 ± 6 | |
| Bull | Range | 4–150 | 3–41 | 2–75 |
| mean ± dev | 39 ± 63 | 20 ± 14 | 22 ± 30 | |
| Properties | Rail Top | Tensile Bar | Bulk Steel | |
|---|---|---|---|---|
| Meyer’s constant A and index n | A | 0.00057 | 0.00036 | 0.00033 |
| n | 1.891 | 1.896 | 1.761 | |
| ISE significance coefficient η | Mean value | 0.14 | 0.11 | 0.36 |
| Range | 0.04–0.37 | 0.02–0.27 | 0.05–0.84 | |
| Hardness H | H0 | 689 | 443 | 210 |
| HV0.01 | 945 | 565 | 386 | |
| HV1 | 718 | 452 | 220 | |
| Strain-hardening ratio ( · 100%) | By HN-G | 3.3 | 2.1 | 1.0 |
| By HV0.01 | 2.4 | 1.5 | 1.0 | |
| By HV0.01–0.2 | 2.6 | 1.6 | 1.0 | |
| By HV1 | 3.3 | 2.1 | 1.0 | |
| Steels | Meyer’s Index n | ISE Significance Coefficient η | ||
|---|---|---|---|---|
| Bulk | Worn | Bulk | Worn | |
| Austenitic Mn18 | 1.69 | 1.81 | 0.63 | 0.29 |
| Pearlitic rail | 1.92 | 1.78 | 0.10 | 0.31 |
| Martensitic 300M | 1.89 | 1.77 | 0.13 | 0.42 |
| Mean | 1.83 | 1.79 | 0.29 | 0.34 |
| Deviation | 0.13 | 0.02 | 0.30 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Kitchen, M. Microhardness, Indentation Size Effect and Real Hardness of Plastically Deformed Austenitic Hadfield Steel. Materials 2023, 16, 1117. https://doi.org/10.3390/ma16031117
Luo Q, Kitchen M. Microhardness, Indentation Size Effect and Real Hardness of Plastically Deformed Austenitic Hadfield Steel. Materials. 2023; 16(3):1117. https://doi.org/10.3390/ma16031117
Chicago/Turabian StyleLuo, Quanshun, and Matthew Kitchen. 2023. "Microhardness, Indentation Size Effect and Real Hardness of Plastically Deformed Austenitic Hadfield Steel" Materials 16, no. 3: 1117. https://doi.org/10.3390/ma16031117
APA StyleLuo, Q., & Kitchen, M. (2023). Microhardness, Indentation Size Effect and Real Hardness of Plastically Deformed Austenitic Hadfield Steel. Materials, 16(3), 1117. https://doi.org/10.3390/ma16031117







