Author Contributions
Conceptualization, A.L., G.W.-V. and R.F.; methodology, A.L, G.W.-V. and R.F.; software, A.G. and R.F.; validation, K.S.-W., A.G., A.L., G.W.-V. and R.F.; formal analysis, K.S.-W. and A.G.; investigation, K.S.-W., A.G. and R.F.; resources, K.S.-W., A.G., A.L., J.T., G.W.-V. and R.F.; writing—original draft preparation, K.S.-W., A.G., A.L., G.W.-V. and R.F.; writing—review and editing, K.S.-W., A.L., G.W.-V. and R.F.; visualization, K.S.-W. and A.G.; supervision, A.L., G.W.-V. and R.F.; project administration, R.F.; funding acquisition, R.F. All authors have read and agreed to the published version of the manuscript.
Figure 1.
A photograph of the concrete sample for which simulations were performed (a). Computed tomography reconstruction of: (b) aggregates in the sample—yellow color, and (c) mortar—green color. The steel rod is shown in gray.
Figure 1.
A photograph of the concrete sample for which simulations were performed (a). Computed tomography reconstruction of: (b) aggregates in the sample—yellow color, and (c) mortar—green color. The steel rod is shown in gray.
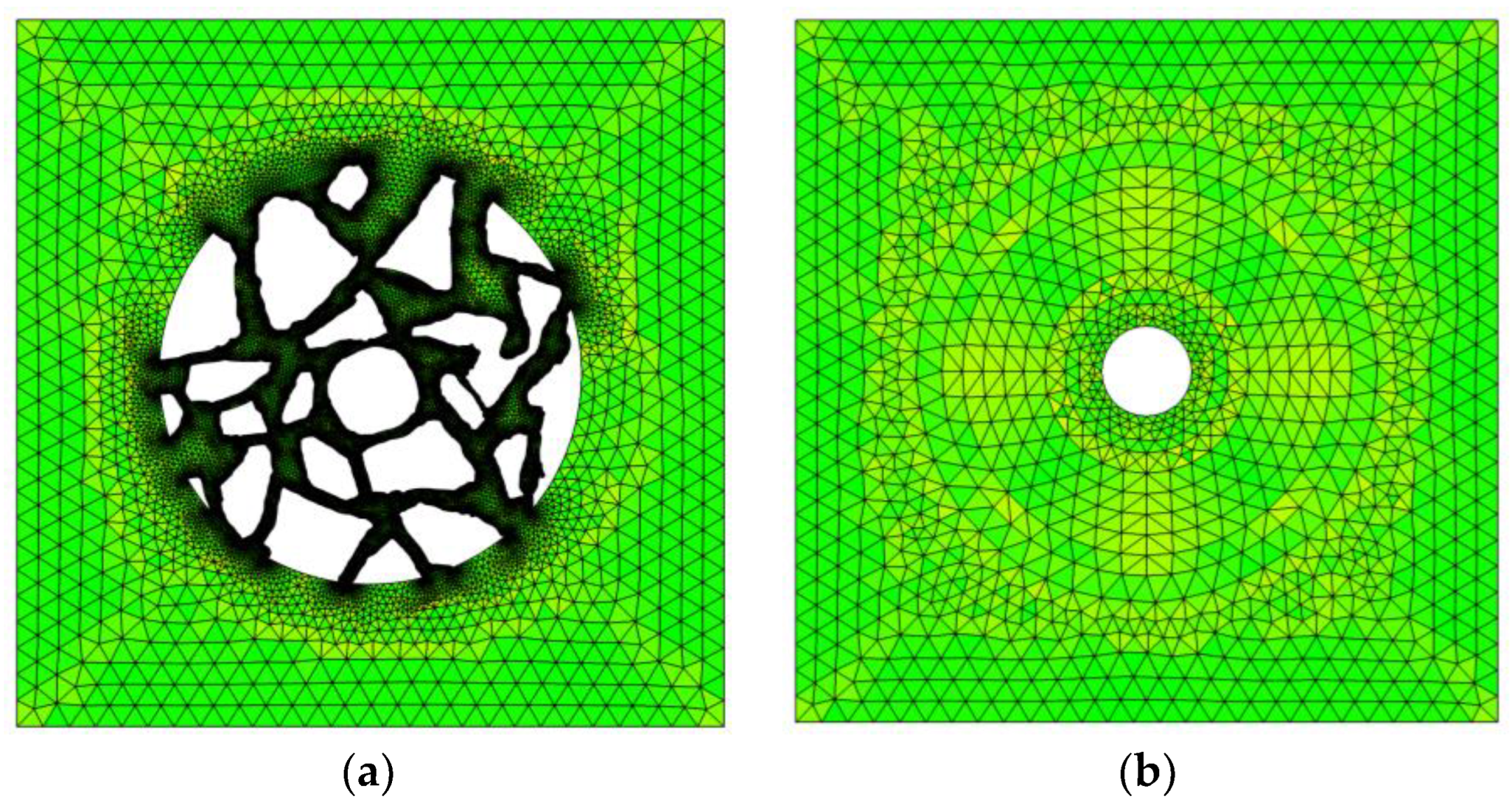
Figure 2.
2D mesh used in numerical calculations of (a) cement and (b) mortar cylinder-shaped samples immersed in an aqueous solution.
Figure 2.
2D mesh used in numerical calculations of (a) cement and (b) mortar cylinder-shaped samples immersed in an aqueous solution.
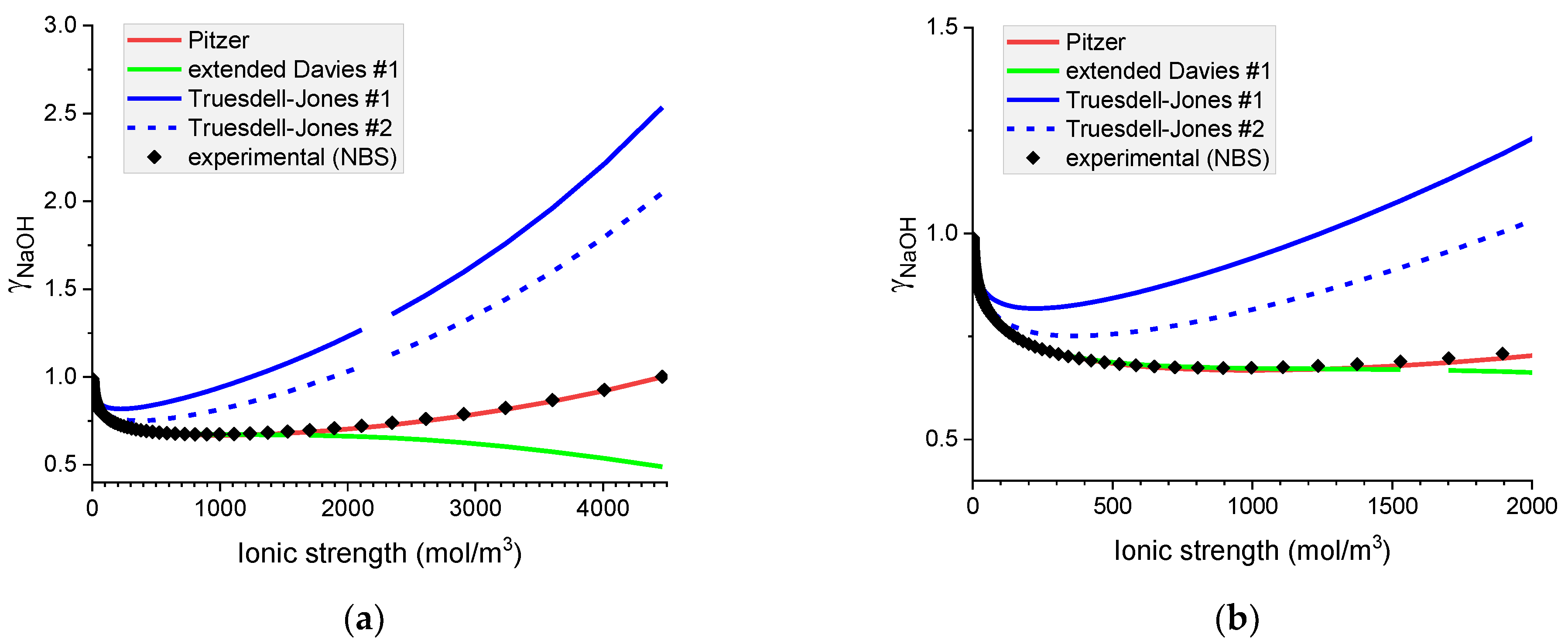
Figure 3.
Molar mean ionic activity coefficients in aqueous NaOH for concentrated (a) and diluted (b) solutions. Comparison of calculated activity coefficients with experimental results (NBS) based on the Pitzer, extended Davies, and Truesdell–Jones models at 25 °C.
Figure 3.
Molar mean ionic activity coefficients in aqueous NaOH for concentrated (a) and diluted (b) solutions. Comparison of calculated activity coefficients with experimental results (NBS) based on the Pitzer, extended Davies, and Truesdell–Jones models at 25 °C.
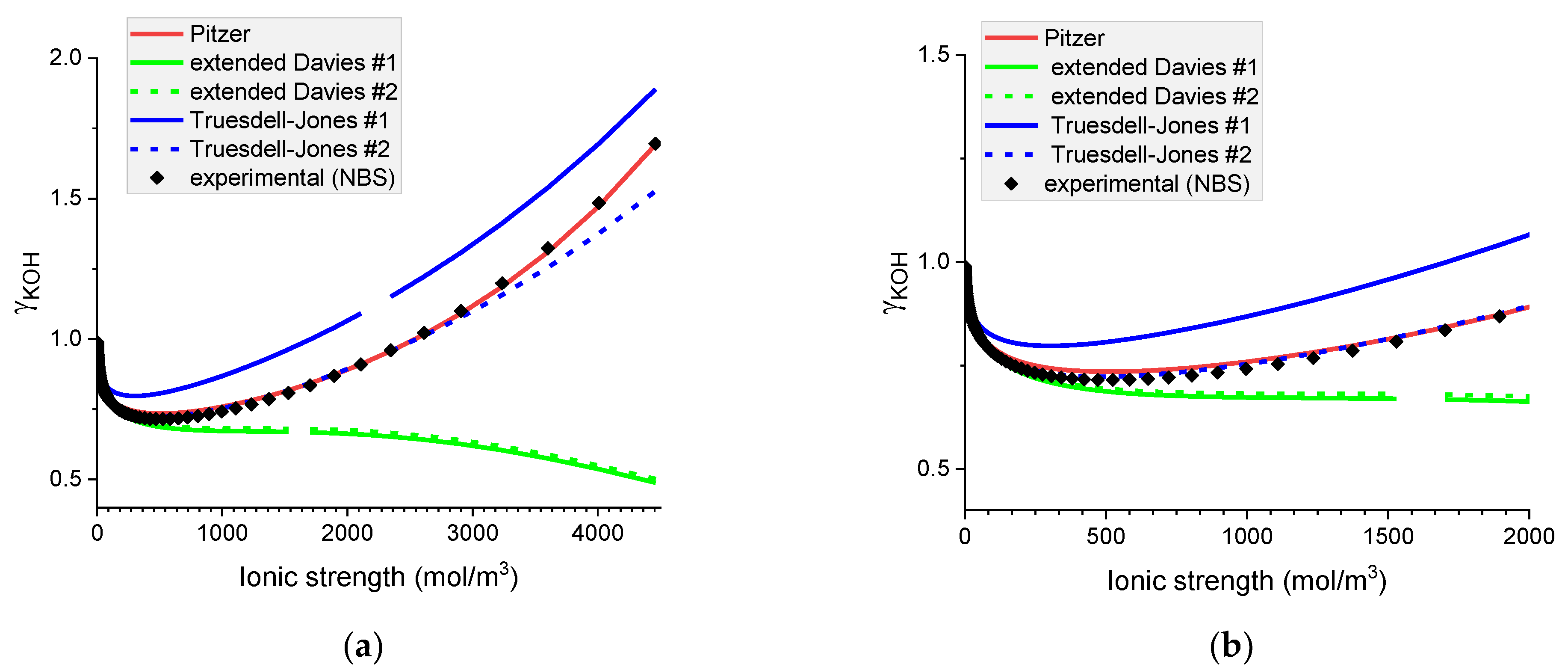
Figure 4.
Molar mean ionic activity coefficients in aqueous KOH for (a) concentrated and (b) dilute solutions. Comparison of calculated activity coefficients based on the Pitzer, extended Davies, and Truesdell–Jones models with experimental results (NBS) at 25 °C.
Figure 4.
Molar mean ionic activity coefficients in aqueous KOH for (a) concentrated and (b) dilute solutions. Comparison of calculated activity coefficients based on the Pitzer, extended Davies, and Truesdell–Jones models with experimental results (NBS) at 25 °C.
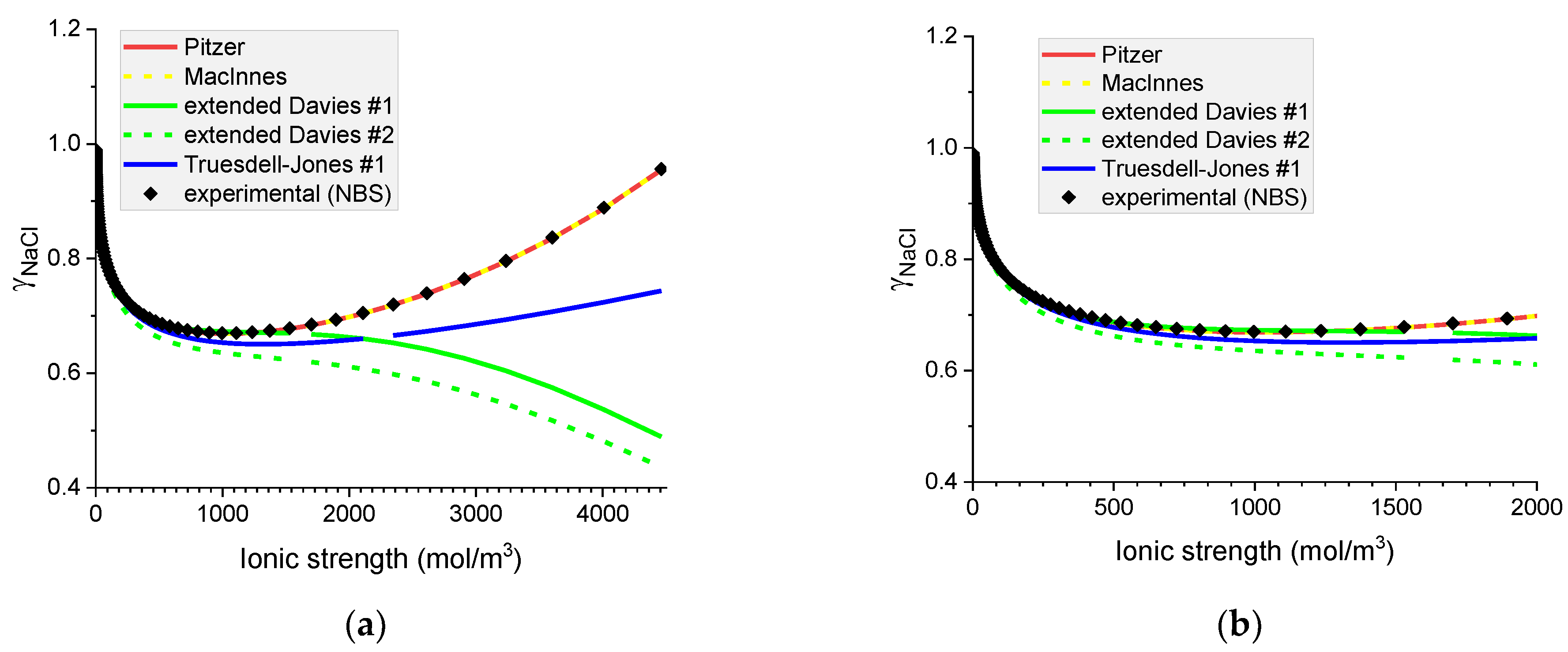
Figure 5.
Molar mean ionic activity coefficients in aqueous NaCl for (a) concentrated, (b) dilute solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models with experimental results (NBS) at 25 °C.
Figure 5.
Molar mean ionic activity coefficients in aqueous NaCl for (a) concentrated, (b) dilute solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models with experimental results (NBS) at 25 °C.
Figure 6.
Molar mean ionic activity coefficients in aqueous KCl for (a) concentrated and (b) dilute solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models with experimental results (NBS) at 25 °C.
Figure 6.
Molar mean ionic activity coefficients in aqueous KCl for (a) concentrated and (b) dilute solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models with experimental results (NBS) at 25 °C.
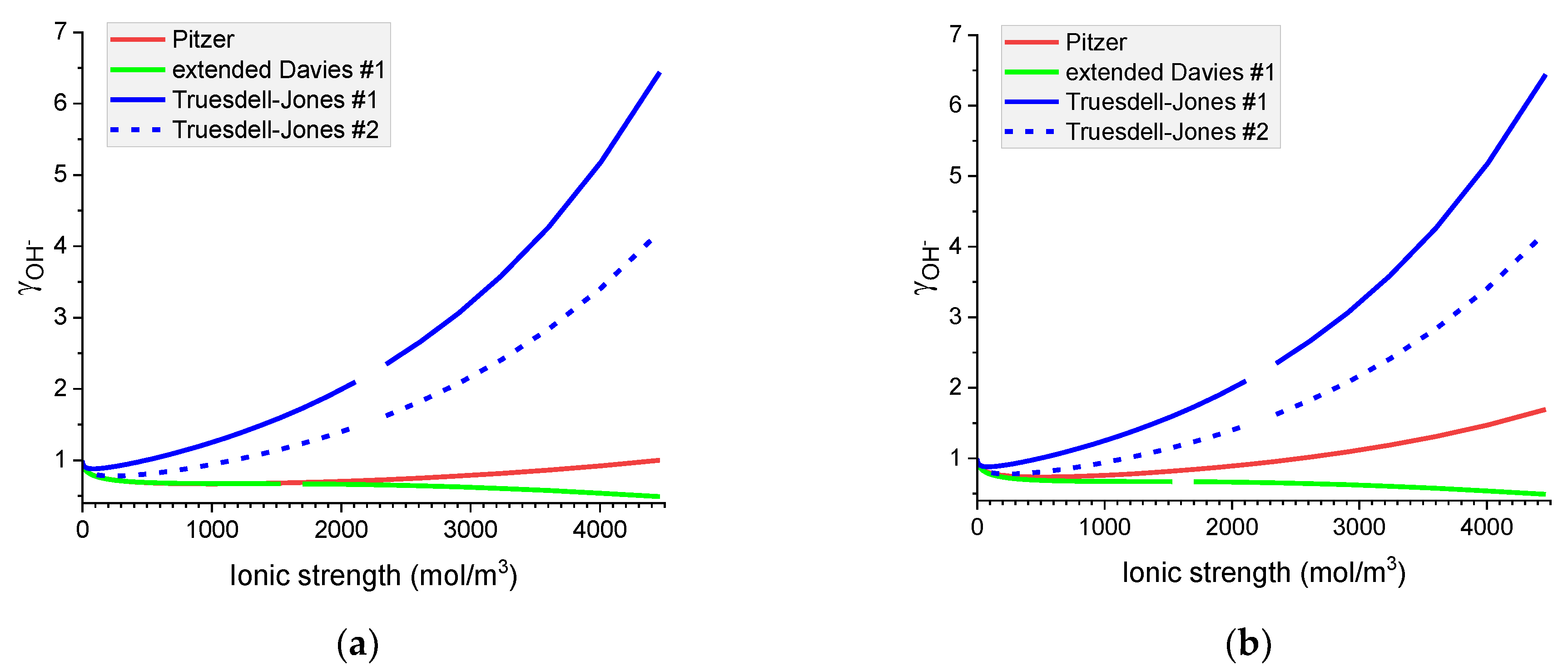
Figure 7.
Molar OH− individual activity coefficients in aqueous (a) NaOH and (b) KOH solutions. Comparison of calculated activity coefficients based on the Pitzer, extended Davies, and Truesdell–Jones models at 25 °C.
Figure 7.
Molar OH− individual activity coefficients in aqueous (a) NaOH and (b) KOH solutions. Comparison of calculated activity coefficients based on the Pitzer, extended Davies, and Truesdell–Jones models at 25 °C.
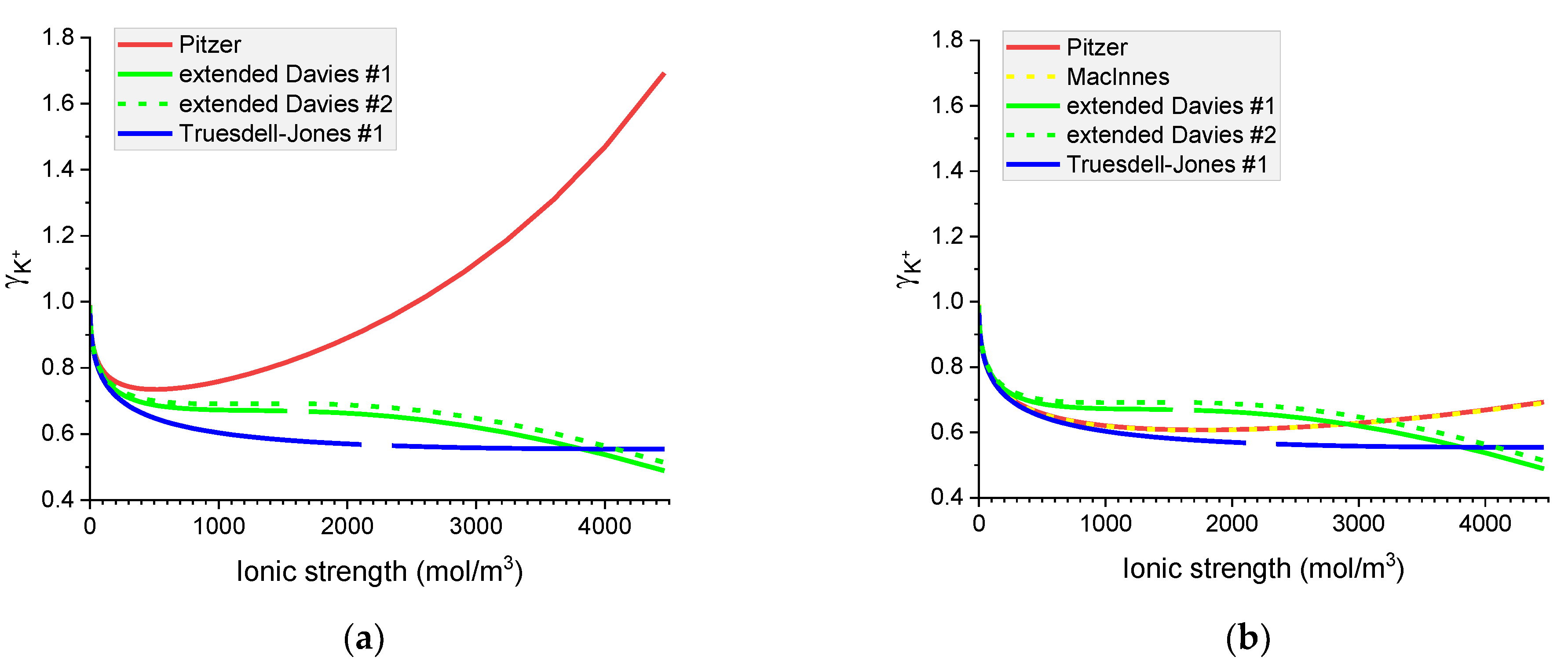
Figure 8.
Molar K+ individual activity coefficients in aqueous (a) KOH and (b) KCl solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models at 25 °C.
Figure 8.
Molar K+ individual activity coefficients in aqueous (a) KOH and (b) KCl solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models at 25 °C.
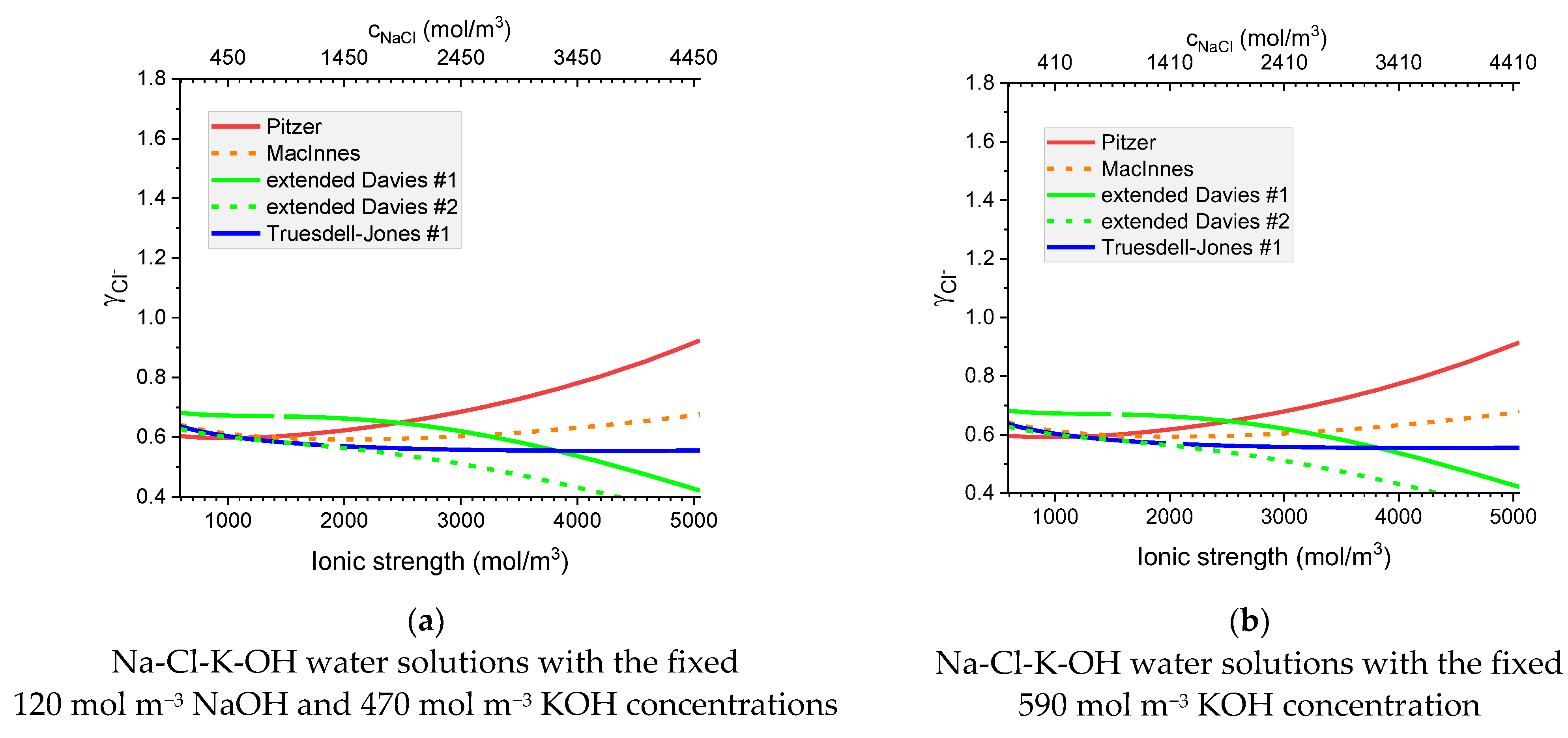
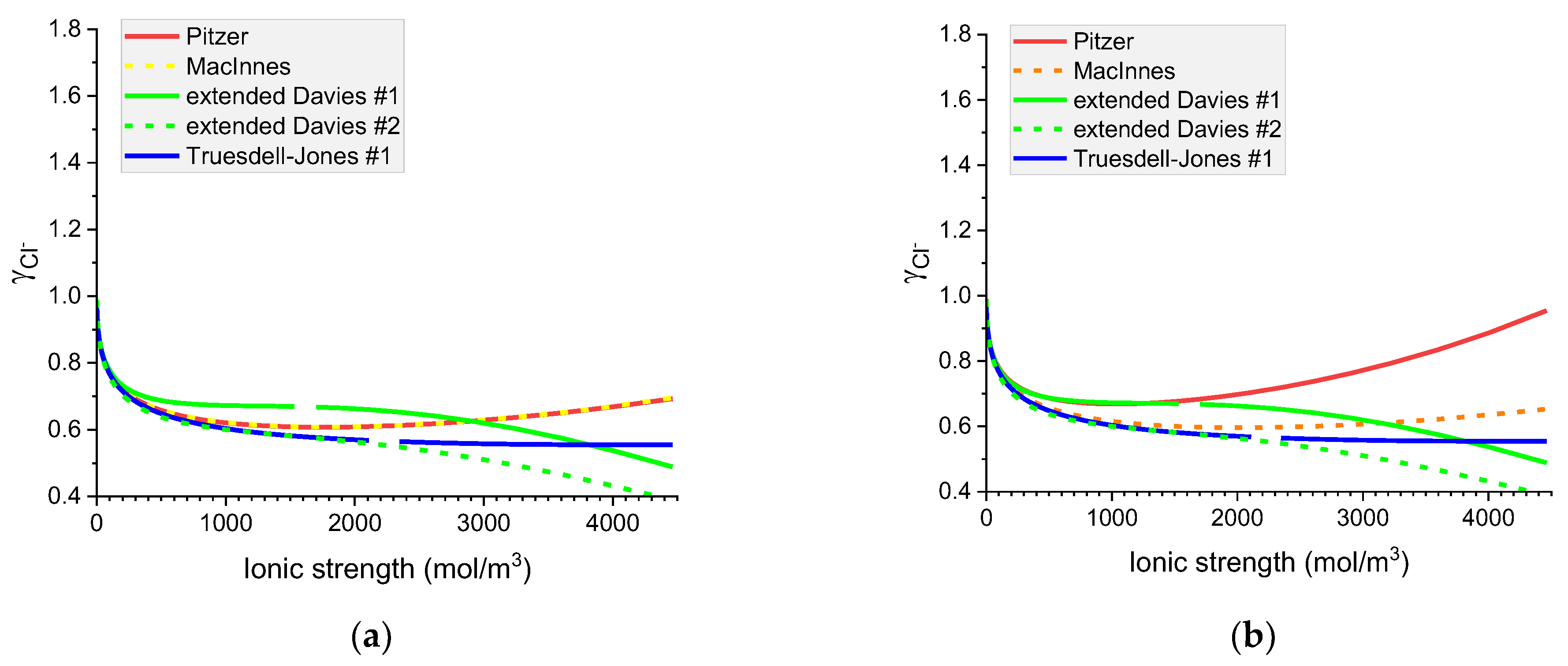
Figure 9.
Molar Cl− individual activity coefficients in aqueous (a) KCl and (b) NaCl solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models at 25 °C.
Figure 9.
Molar Cl− individual activity coefficients in aqueous (a) KCl and (b) NaCl solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models at 25 °C.
Figure 10.
Molar Na+ individual activity coefficients in aqueous (a) NaOH and (b) NaCl solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models at 25 °C.
Figure 10.
Molar Na+ individual activity coefficients in aqueous (a) NaOH and (b) NaCl solutions. Comparison of calculated activity coefficients based on the Pitzer, MacInnes, extended Davies, and Truesdell–Jones models at 25 °C.
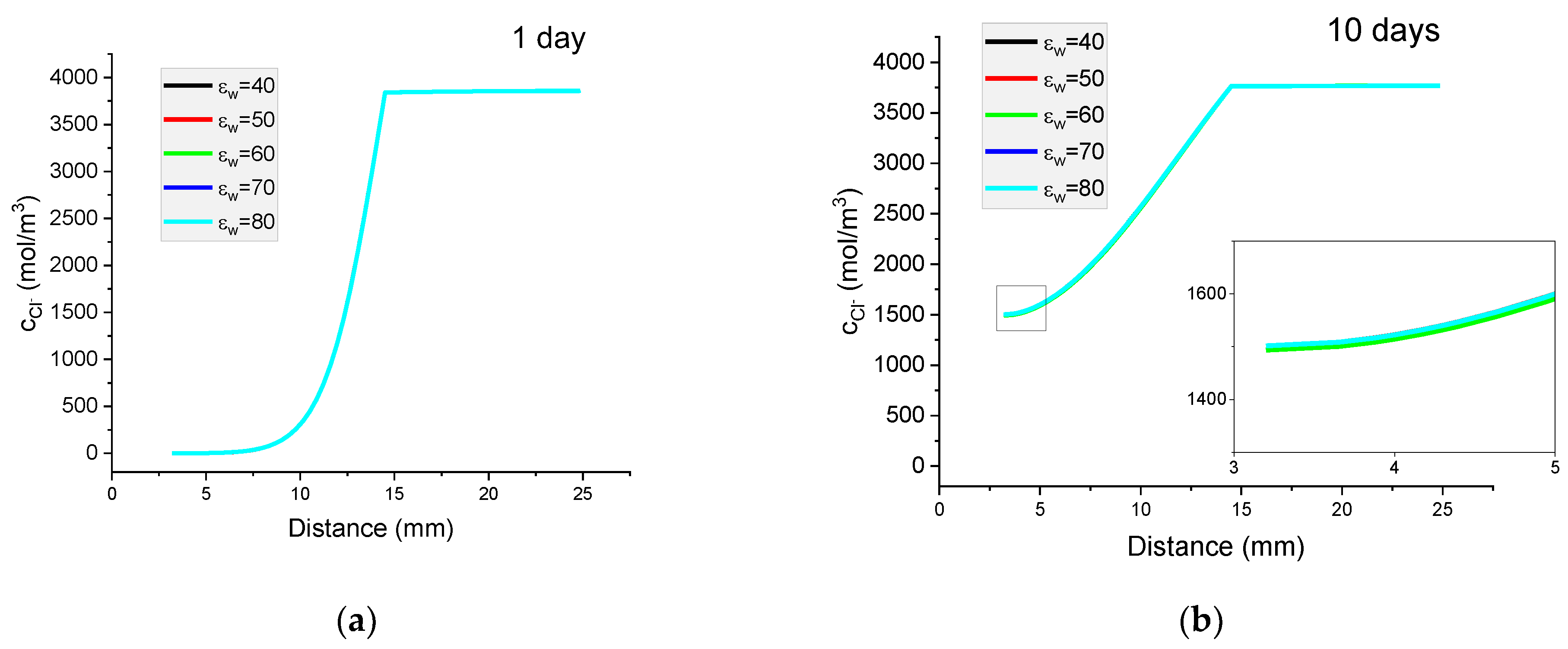
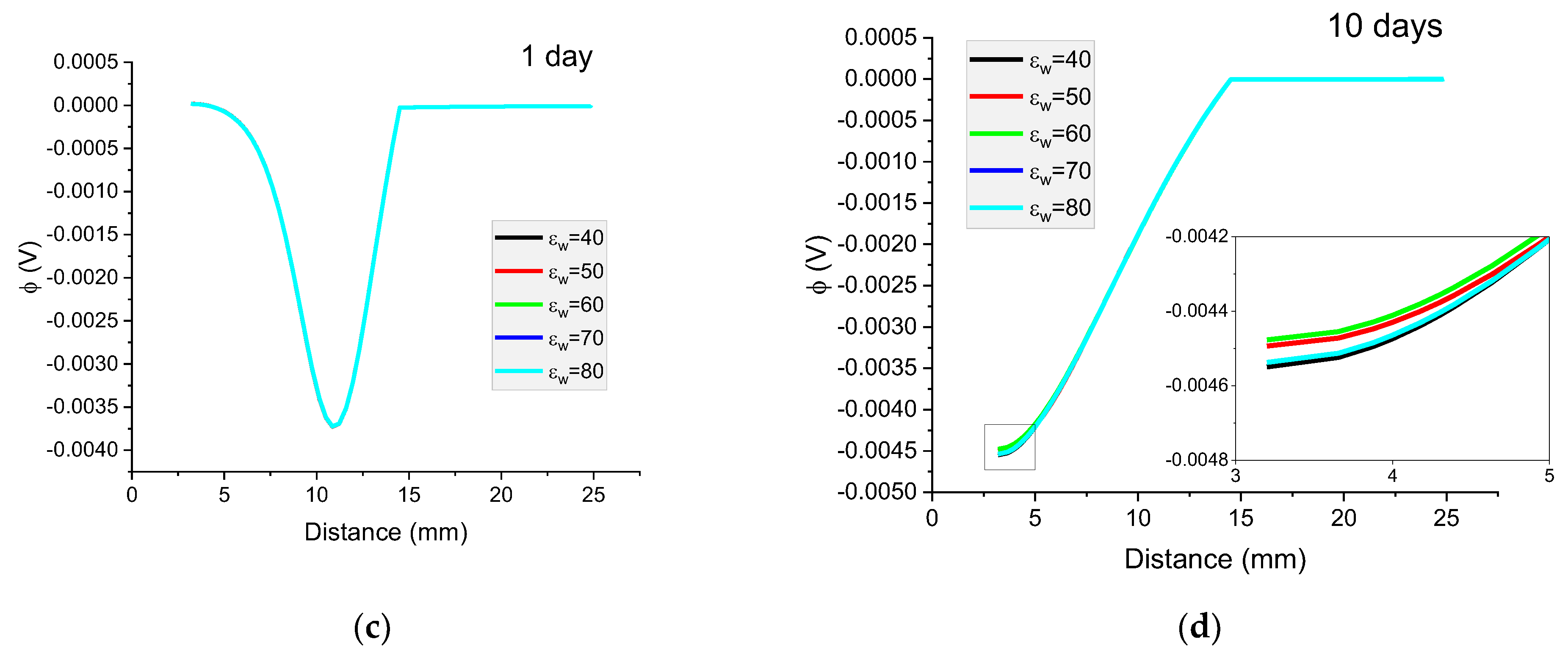
Figure 13.
The influence of relative permeability on calculated concentration profiles of chloride ions in the mortar immersed in 20 wt% NaCl water solution after (a) 1 day; (b) 10 days; and potential distribution after (c) 1 day and (d) 10 days.
Figure 13.
The influence of relative permeability on calculated concentration profiles of chloride ions in the mortar immersed in 20 wt% NaCl water solution after (a) 1 day; (b) 10 days; and potential distribution after (c) 1 day and (d) 10 days.
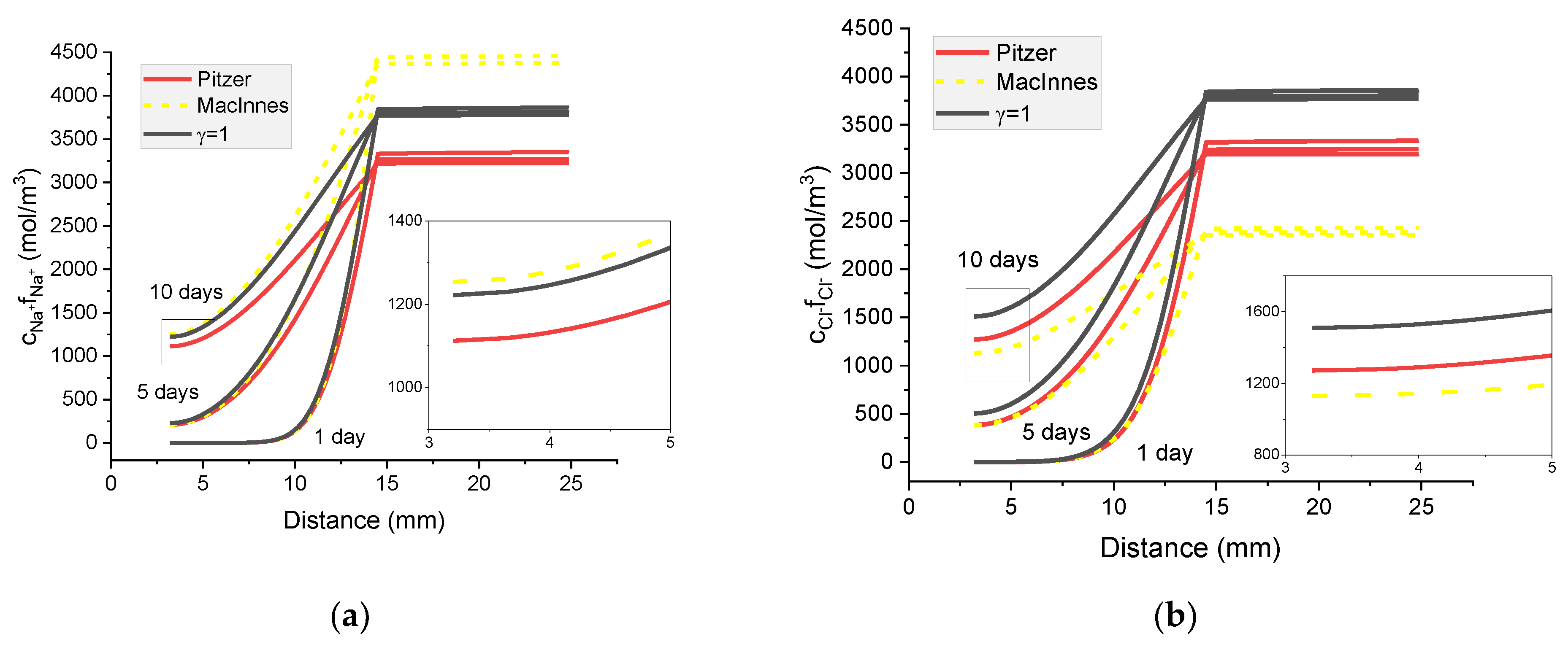
Figure 14.
Calculated activity profiles of ions in the mortar immersed in 20 wt% NaCl water solution. (a) Na+; (b) Cl−; (c) K+; (d) OH− for the Pitzer model and MacInnes scaling—comparison with ions concentrations (γ = 1).
Figure 14.
Calculated activity profiles of ions in the mortar immersed in 20 wt% NaCl water solution. (a) Na+; (b) Cl−; (c) K+; (d) OH− for the Pitzer model and MacInnes scaling—comparison with ions concentrations (γ = 1).
Figure 15.
Calculated activities profiles of ions in the mortar immersed in 5 wt% NaCl water solution. (a) Na+; (b) Cl−; (c) K; (d) OH− For the Pitzer model, MacInnes scaling, extended Davies and Truesdell–Jones models—comparison with ions concentrations (γ = 1).
Figure 15.
Calculated activities profiles of ions in the mortar immersed in 5 wt% NaCl water solution. (a) Na+; (b) Cl−; (c) K; (d) OH− For the Pitzer model, MacInnes scaling, extended Davies and Truesdell–Jones models—comparison with ions concentrations (γ = 1).
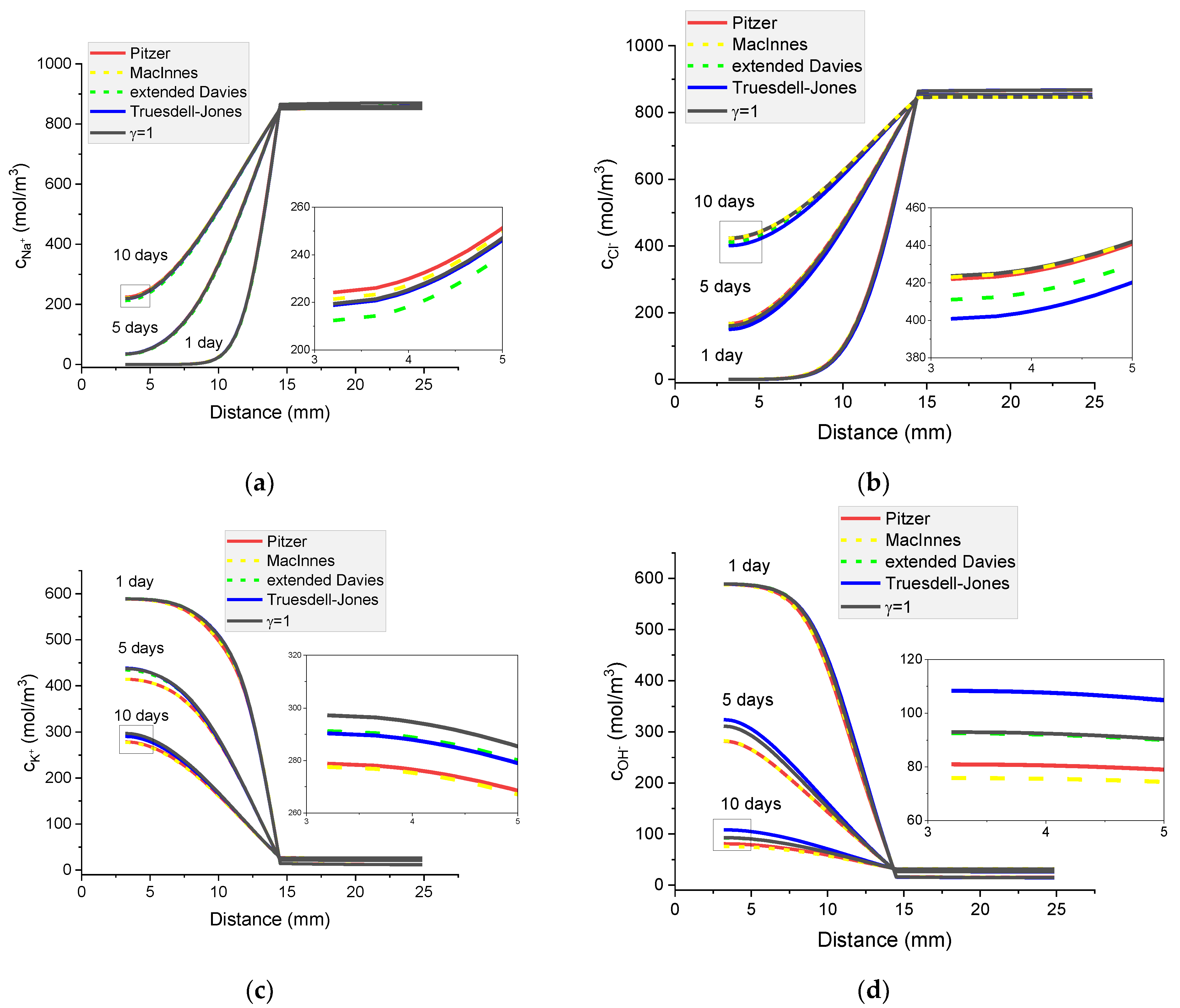
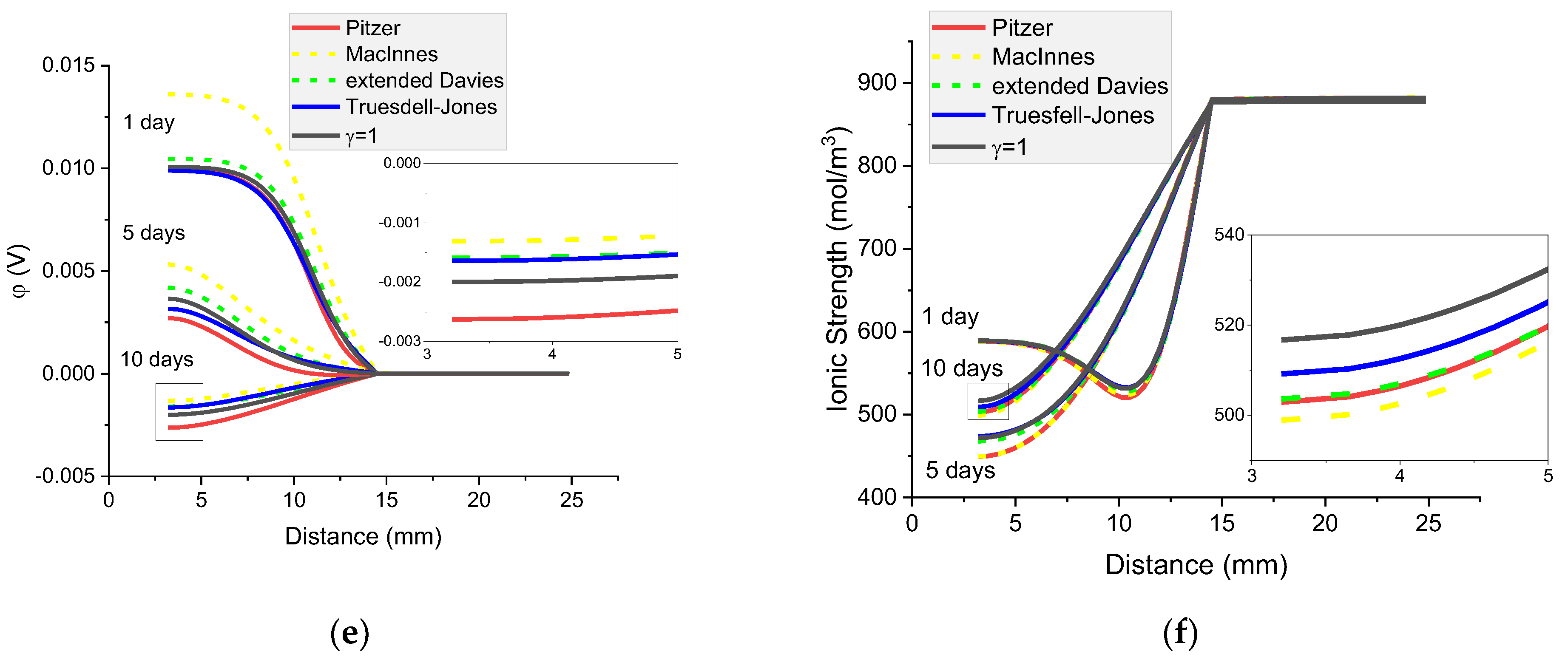
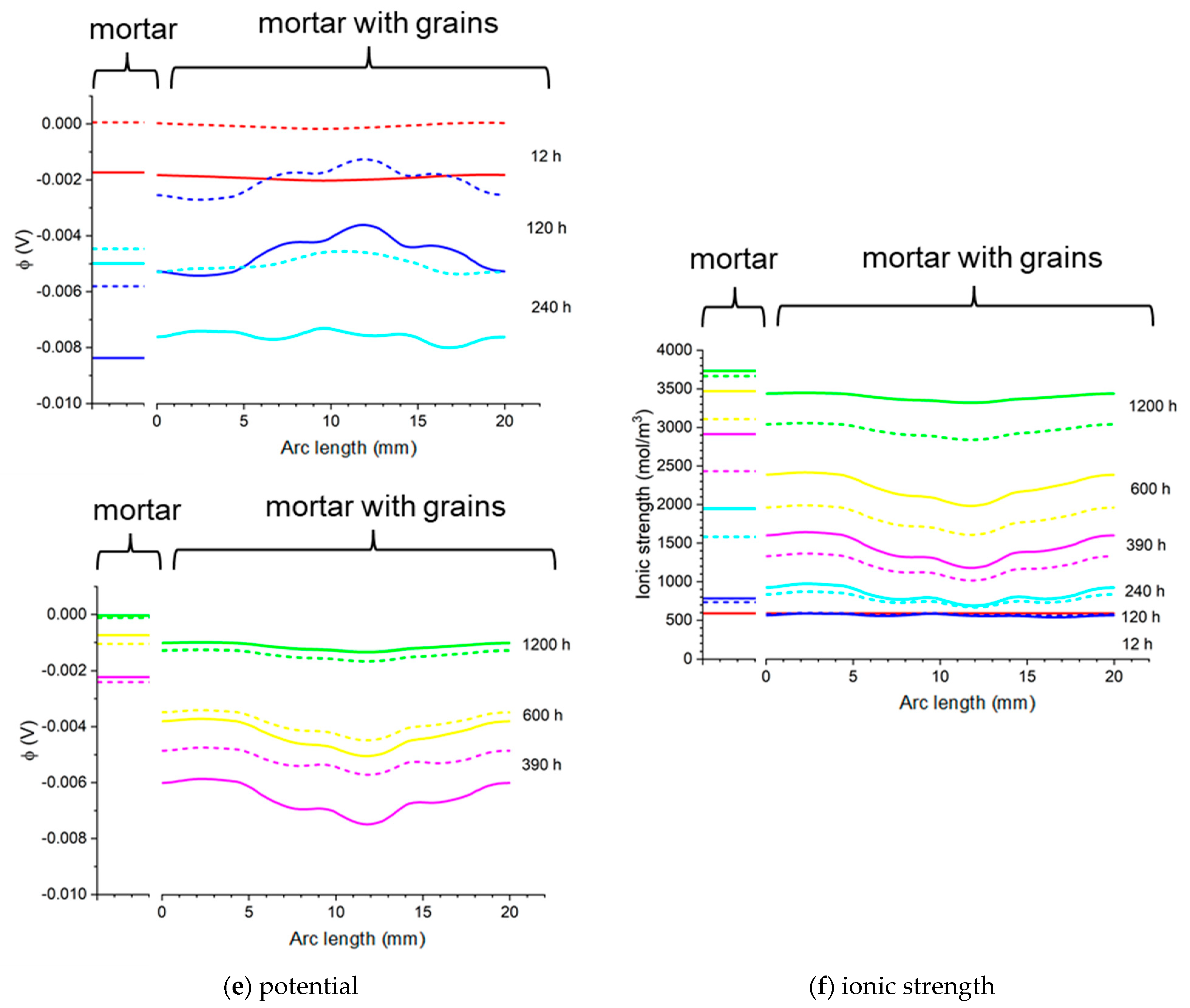
Figure 16.
Calculated concentration profiles of ions in the mortar immersed in 5 wt% NaCl water solution. (a) Na+; (b) Cl−; (c) K+; (d) OH−; electrical potential (e) and ionic strength (f) after 1, 5, and 10 days.
Figure 16.
Calculated concentration profiles of ions in the mortar immersed in 5 wt% NaCl water solution. (a) Na+; (b) Cl−; (c) K+; (d) OH−; electrical potential (e) and ionic strength (f) after 1, 5, and 10 days.
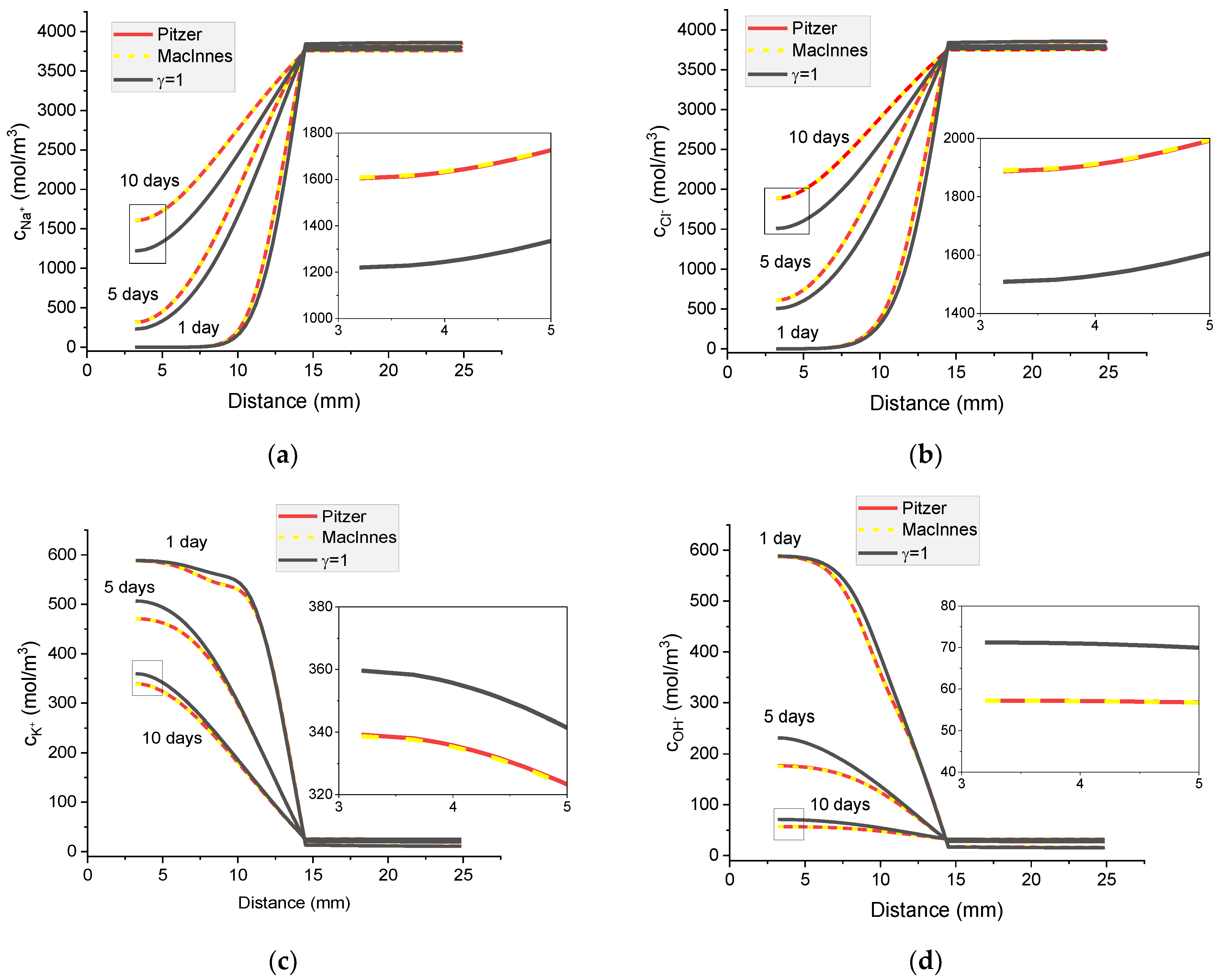
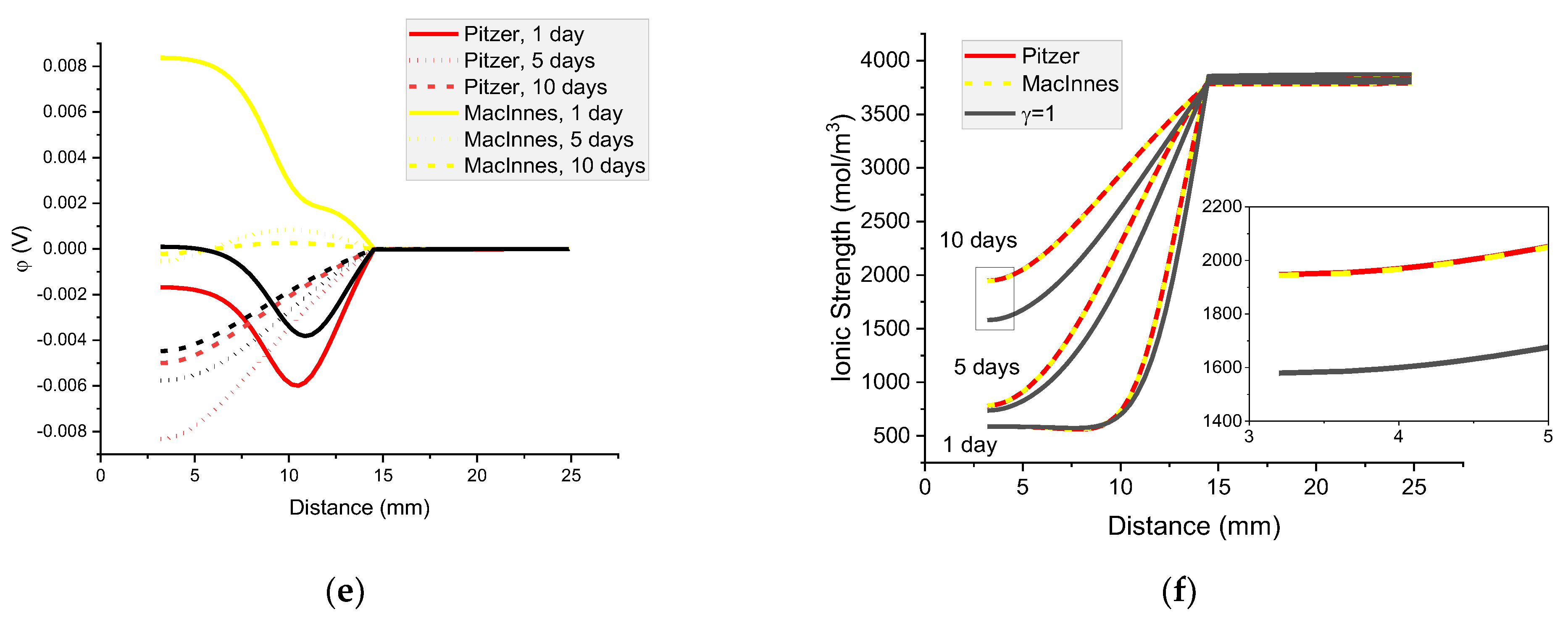
Figure 17.
Calculated concentration profiles of ions in the mortar immersed in 20 wt% NaCl water solution. (a) Na+; (b) Cl− Cl−; (c) K+; (d) OH−; electrical potential (e) and ionic strength (f). Pitzer model (red), MacInnes (yellow), ideal solution (γ = 1) (black) after 1, 5, and 10 days.
Figure 17.
Calculated concentration profiles of ions in the mortar immersed in 20 wt% NaCl water solution. (a) Na+; (b) Cl− Cl−; (c) K+; (d) OH−; electrical potential (e) and ionic strength (f). Pitzer model (red), MacInnes (yellow), ideal solution (γ = 1) (black) after 1, 5, and 10 days.
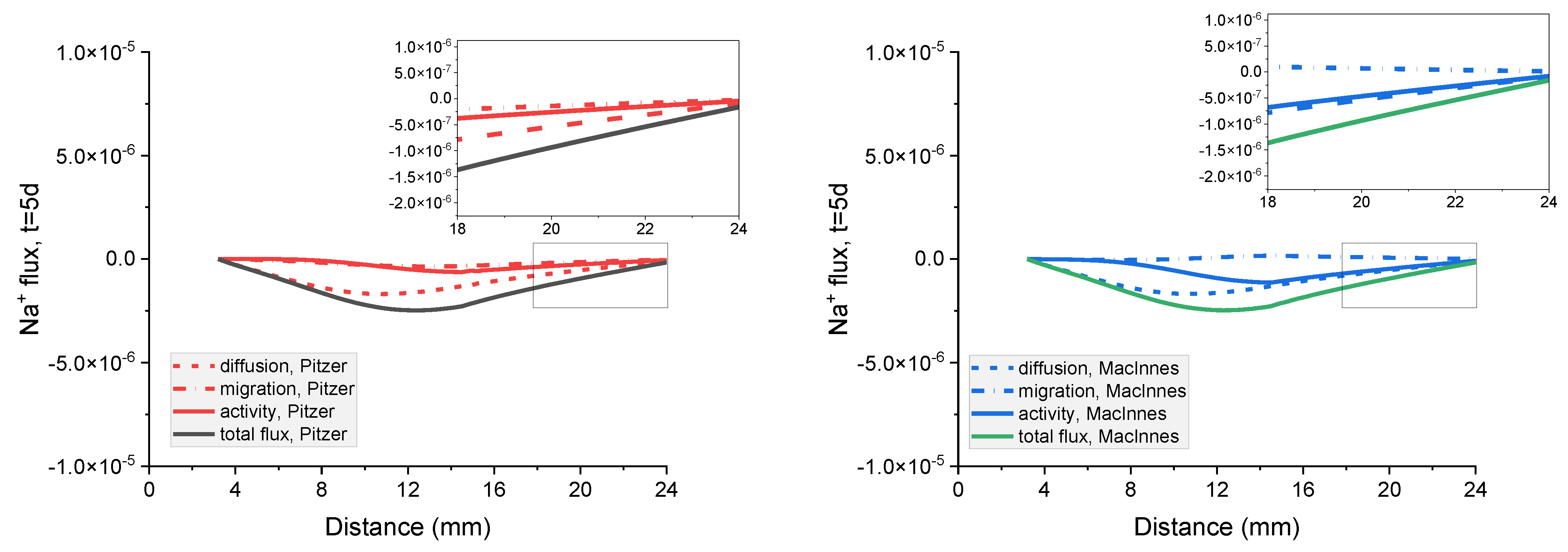
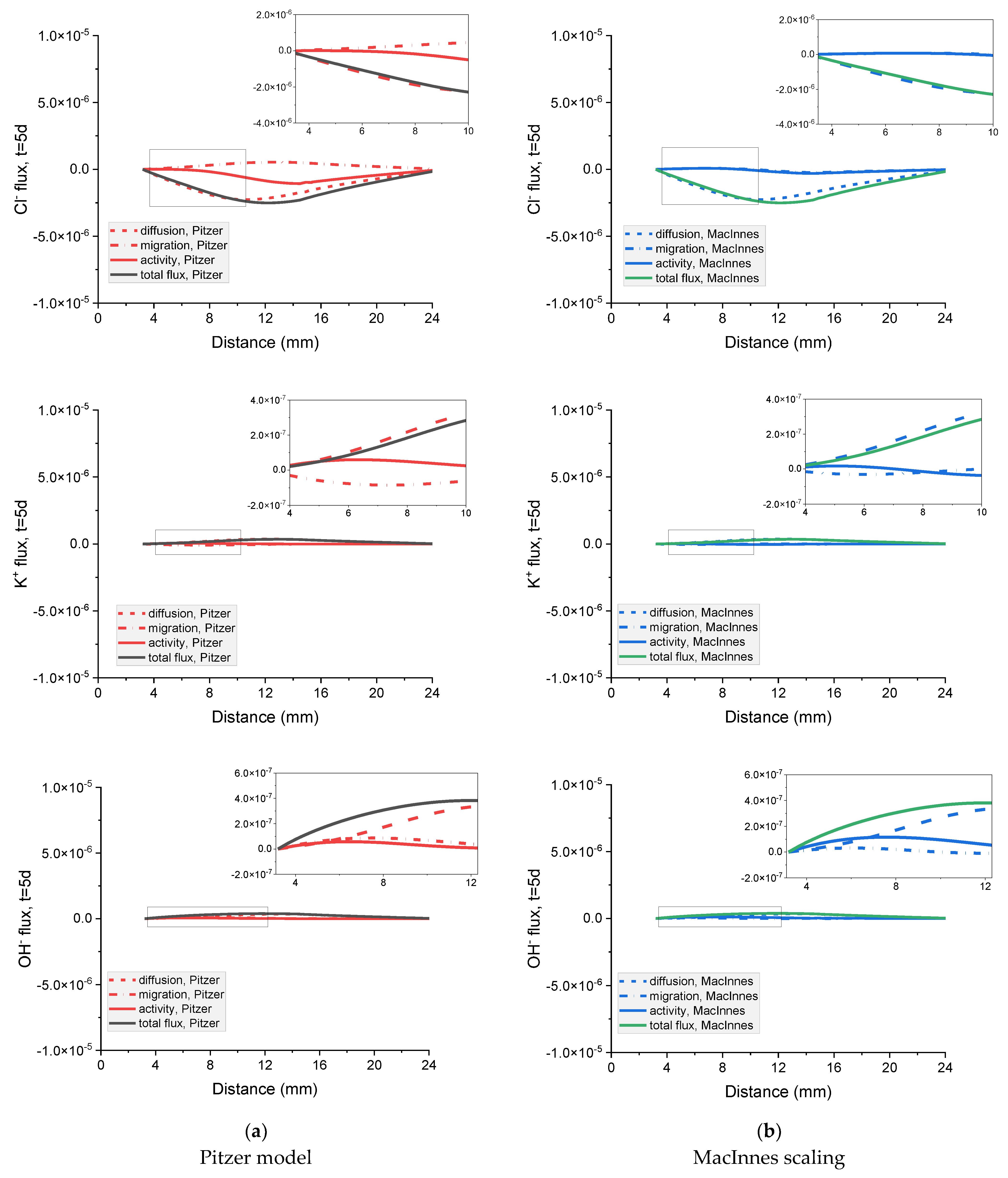
Figure 18.
Influence of diffusion, migration, and activity terms on the total flux of Na+, Cl− Cl−, K+, and OH− ions in the mortar after 5 days immersion in 20 wt% NaCl water solution for (a) Pitzer and (b) MacInnes scaling.
Figure 18.
Influence of diffusion, migration, and activity terms on the total flux of Na+, Cl− Cl−, K+, and OH− ions in the mortar after 5 days immersion in 20 wt% NaCl water solution for (a) Pitzer and (b) MacInnes scaling.
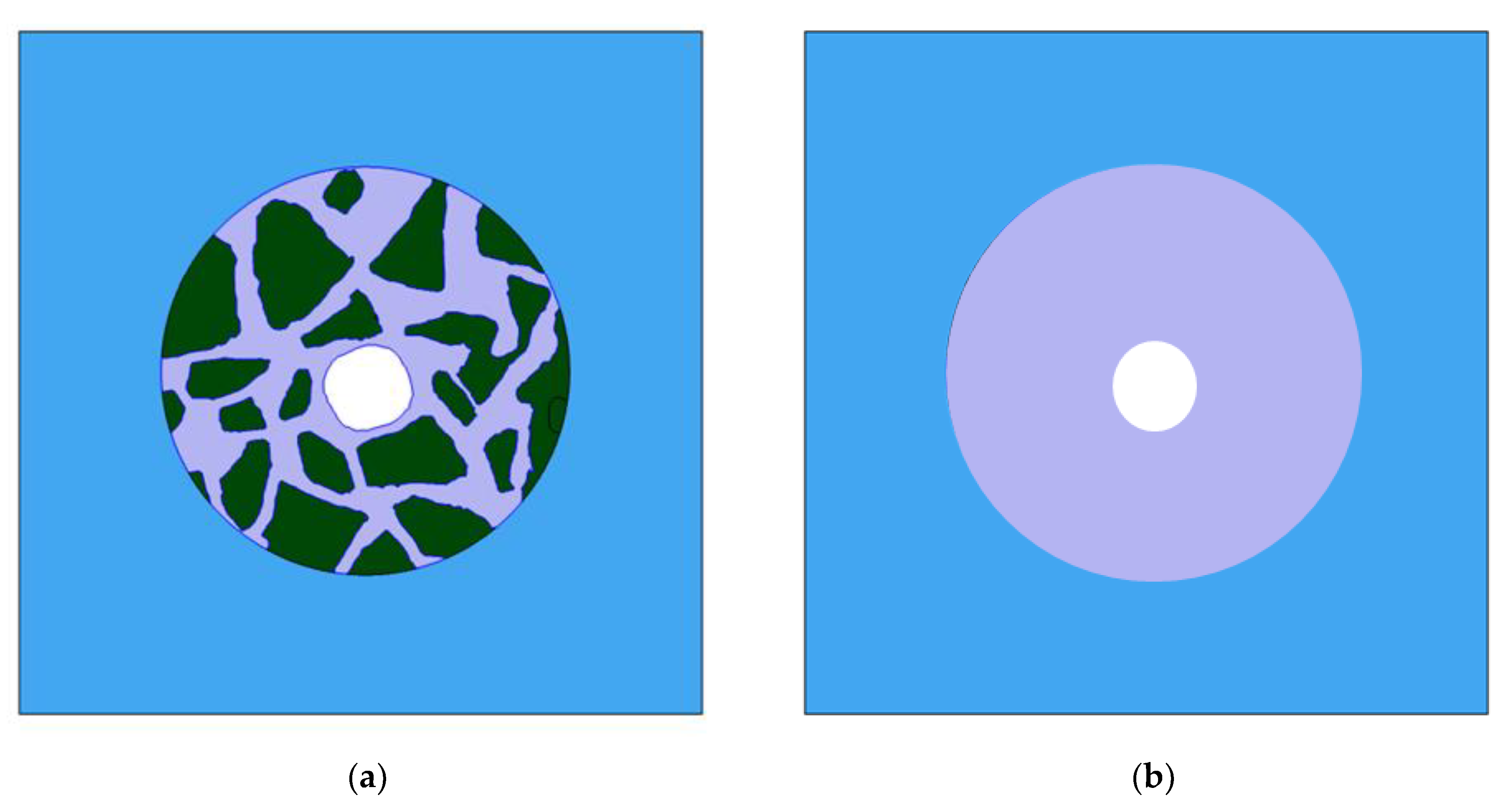
Figure 19.
Simulation domains for concrete (a) and mortar (b) samples. Four regions can be identified: electrolyte (blue), liquid in pores of cement (dark grey), aggregates (dark green), and central rebar (white).
Figure 19.
Simulation domains for concrete (a) and mortar (b) samples. Four regions can be identified: electrolyte (blue), liquid in pores of cement (dark grey), aggregates (dark green), and central rebar (white).
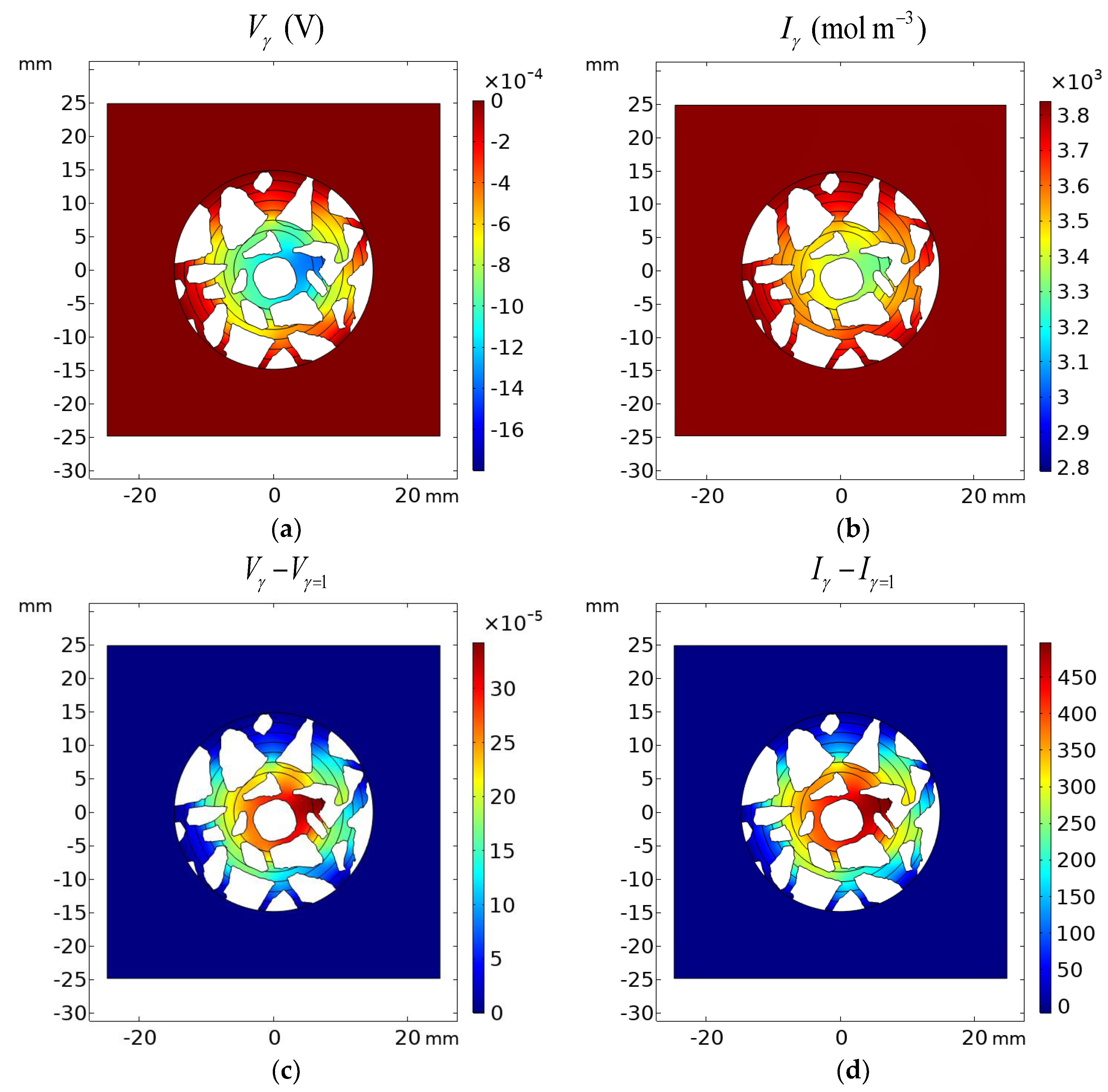
Figure 20.
Results of calculations: (a) potential distribution Vγ and (b) ionic strength I in the cement sample after 1200 h of immersion in 20% NaCl water solution assuming the Pitzer activity model; (c) deviation of the Pitzer activity model solution from the ideal solution approximation (γ = 1) of potential Vγ − Vγ=1 and (d) ionic strength Iγ − Iγ=1.
Figure 20.
Results of calculations: (a) potential distribution Vγ and (b) ionic strength I in the cement sample after 1200 h of immersion in 20% NaCl water solution assuming the Pitzer activity model; (c) deviation of the Pitzer activity model solution from the ideal solution approximation (γ = 1) of potential Vγ − Vγ=1 and (d) ionic strength Iγ − Iγ=1.
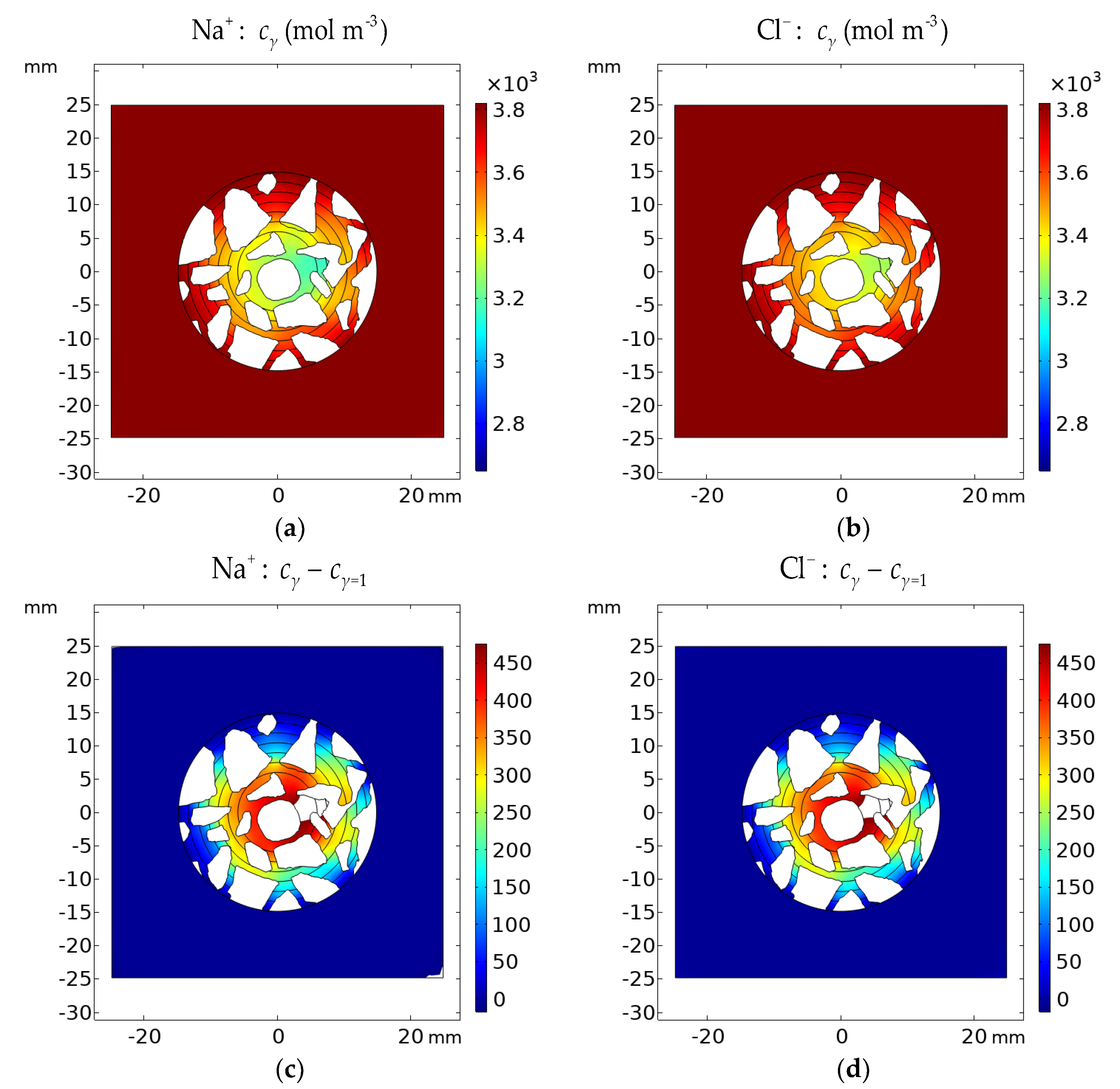
Figure 21.
Calculated concentration distribution cγ of (a) Na+ and (b) Cl− in the cement sample after 1200 h of immersion in 20% NaCl water solution assuming the Pitzer activity model. Deviation of the Pitzer activity model solution from the ideal solution approximation (γ = 1) cγ − cγ=1 for (c) Na+ and (d) Cl−.
Figure 21.
Calculated concentration distribution cγ of (a) Na+ and (b) Cl− in the cement sample after 1200 h of immersion in 20% NaCl water solution assuming the Pitzer activity model. Deviation of the Pitzer activity model solution from the ideal solution approximation (γ = 1) cγ − cγ=1 for (c) Na+ and (d) Cl−.
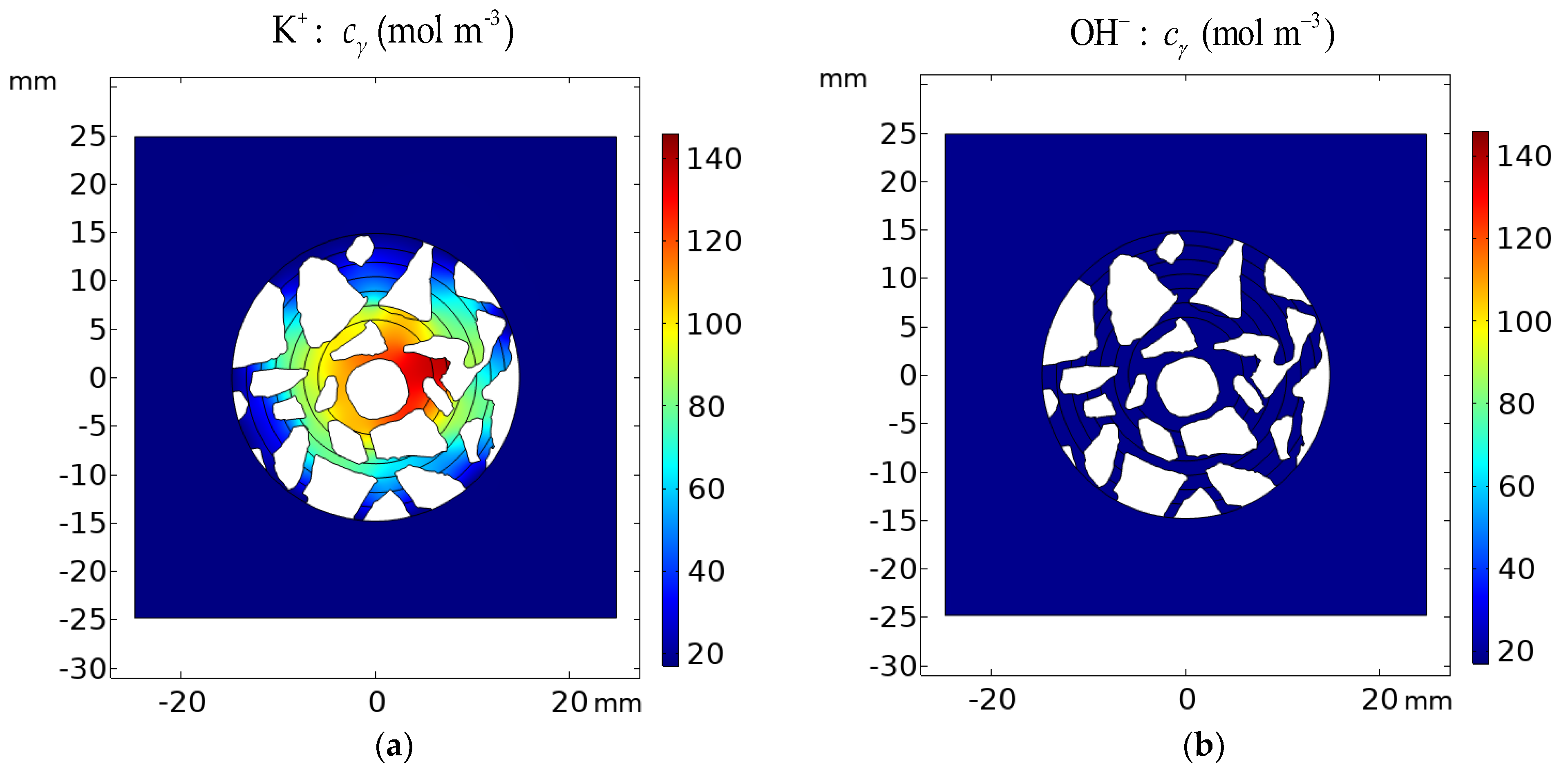
Figure 22.
Calculated concentration distribution cγ of (a) K+ and (b) OH− in the cement sample after 1200 h of immersion in 20% NaCl from the ideal solution approximation (γ = 1) cγ − cγ=1 for (c) K+ and (d) OH−.
Figure 22.
Calculated concentration distribution cγ of (a) K+ and (b) OH− in the cement sample after 1200 h of immersion in 20% NaCl from the ideal solution approximation (γ = 1) cγ − cγ=1 for (c) K+ and (d) OH−.
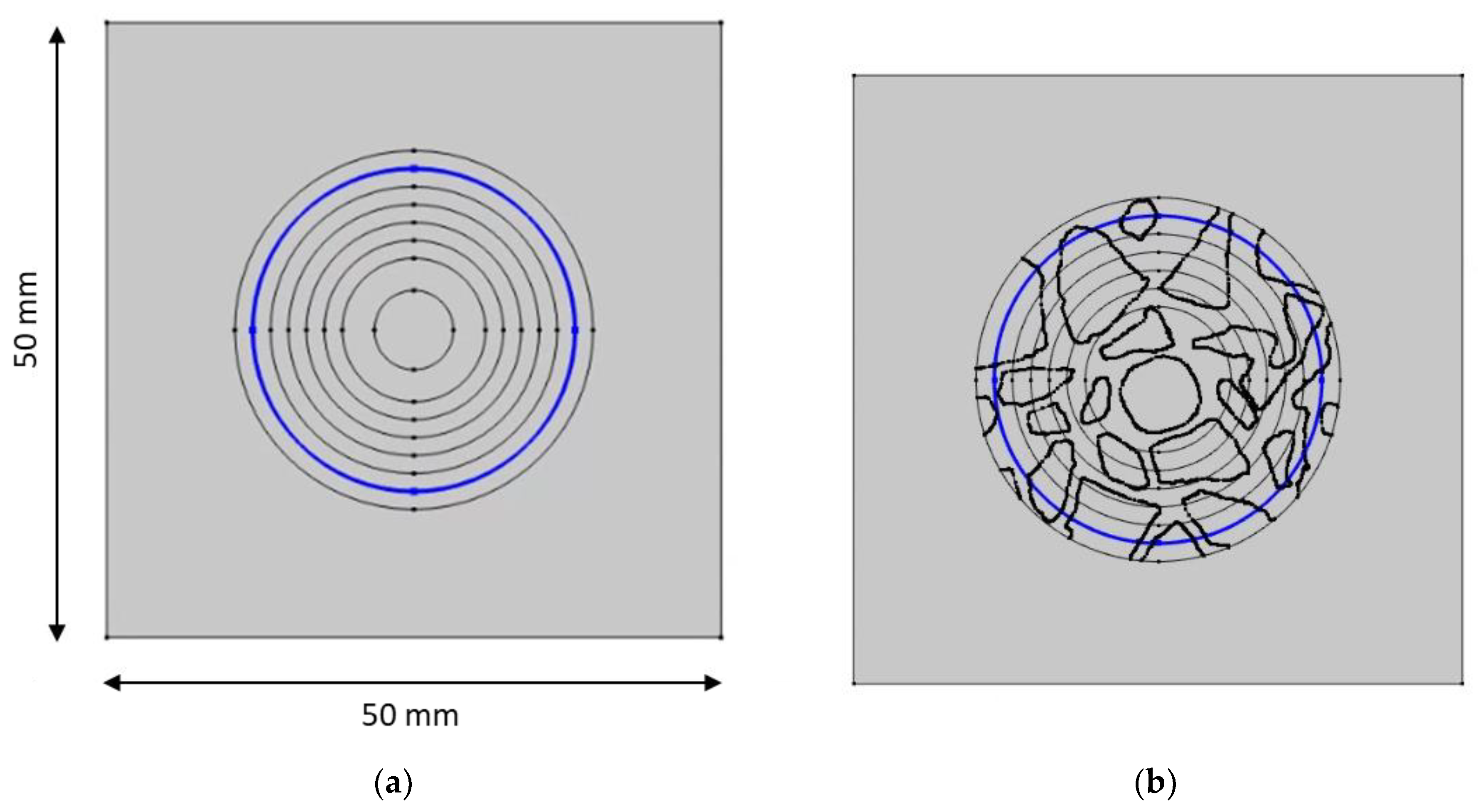
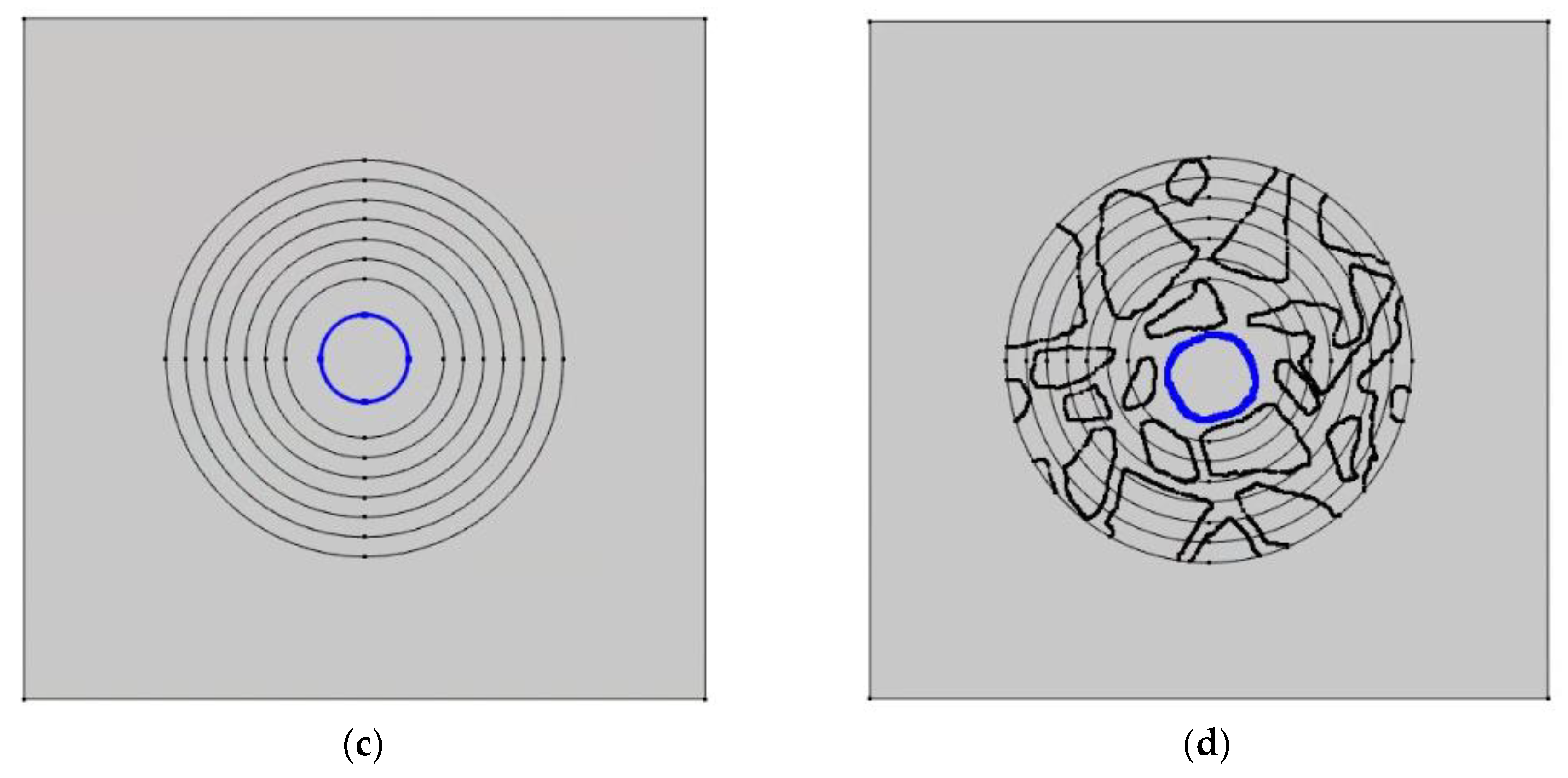
Figure 23.
Nonhomogeneous—concrete sample—and homogeneous—mortar sample—with lines (blue) 13 mm from the center and on the surface of the rod. (a) mortar sample—13 mm from the center. (b) concrete sample—13 mm from the center. (c) mortar sample—the surface of the rod. (d) concrete sample—the surface of the rod.
Figure 23.
Nonhomogeneous—concrete sample—and homogeneous—mortar sample—with lines (blue) 13 mm from the center and on the surface of the rod. (a) mortar sample—13 mm from the center. (b) concrete sample—13 mm from the center. (c) mortar sample—the surface of the rod. (d) concrete sample—the surface of the rod.
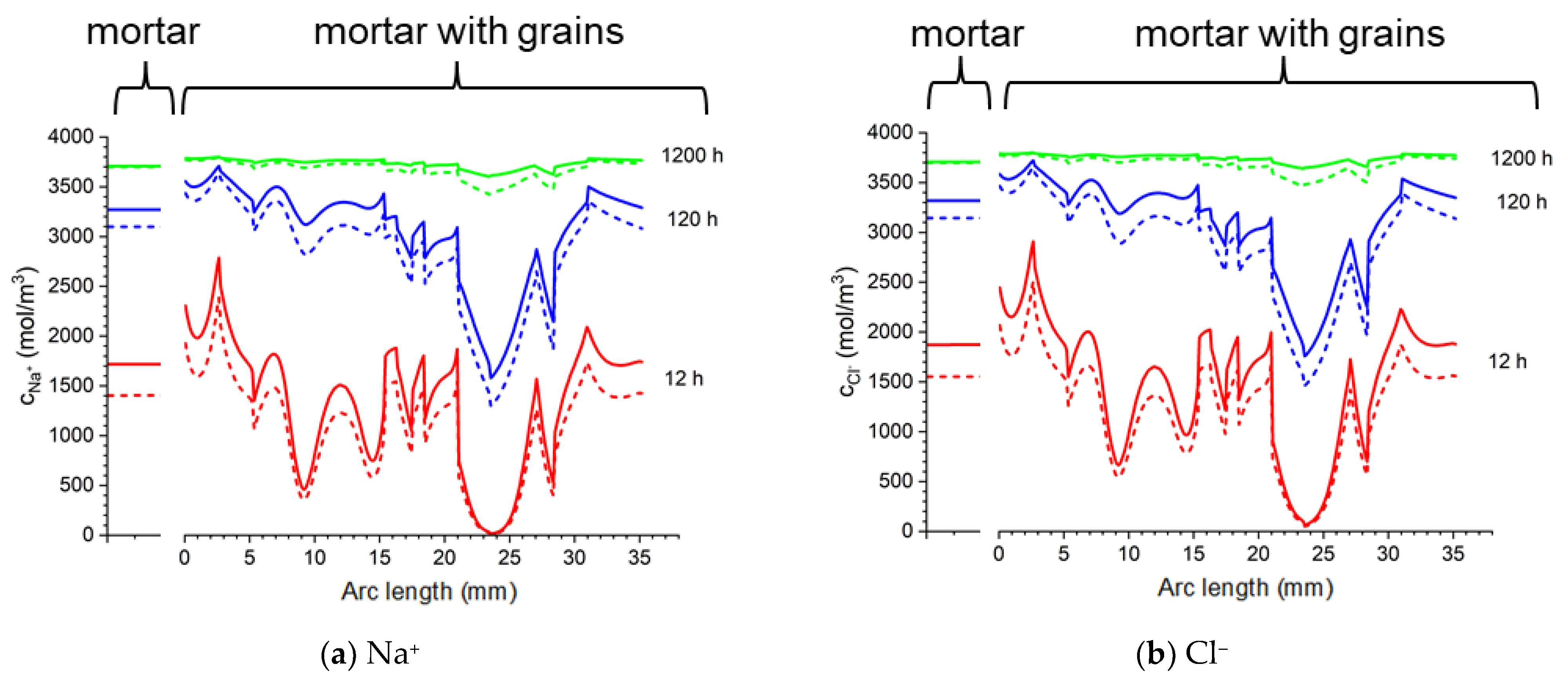
Figure 24.
Calculated: ion concentrations: (a) Na+, (b) Cl−, (c) K+, (d) OH−, (e) potential (ϕ), and (f) ionic strength in the mortar and concrete samples at the distance 13 mm from the center of the sample in the sample in 20% NaCl water solution (along a blue line). Solid lines correspond to the solution for the Pitzer activity model and dashed lines are the solution neglecting activities .
Figure 24.
Calculated: ion concentrations: (a) Na+, (b) Cl−, (c) K+, (d) OH−, (e) potential (ϕ), and (f) ionic strength in the mortar and concrete samples at the distance 13 mm from the center of the sample in the sample in 20% NaCl water solution (along a blue line). Solid lines correspond to the solution for the Pitzer activity model and dashed lines are the solution neglecting activities .
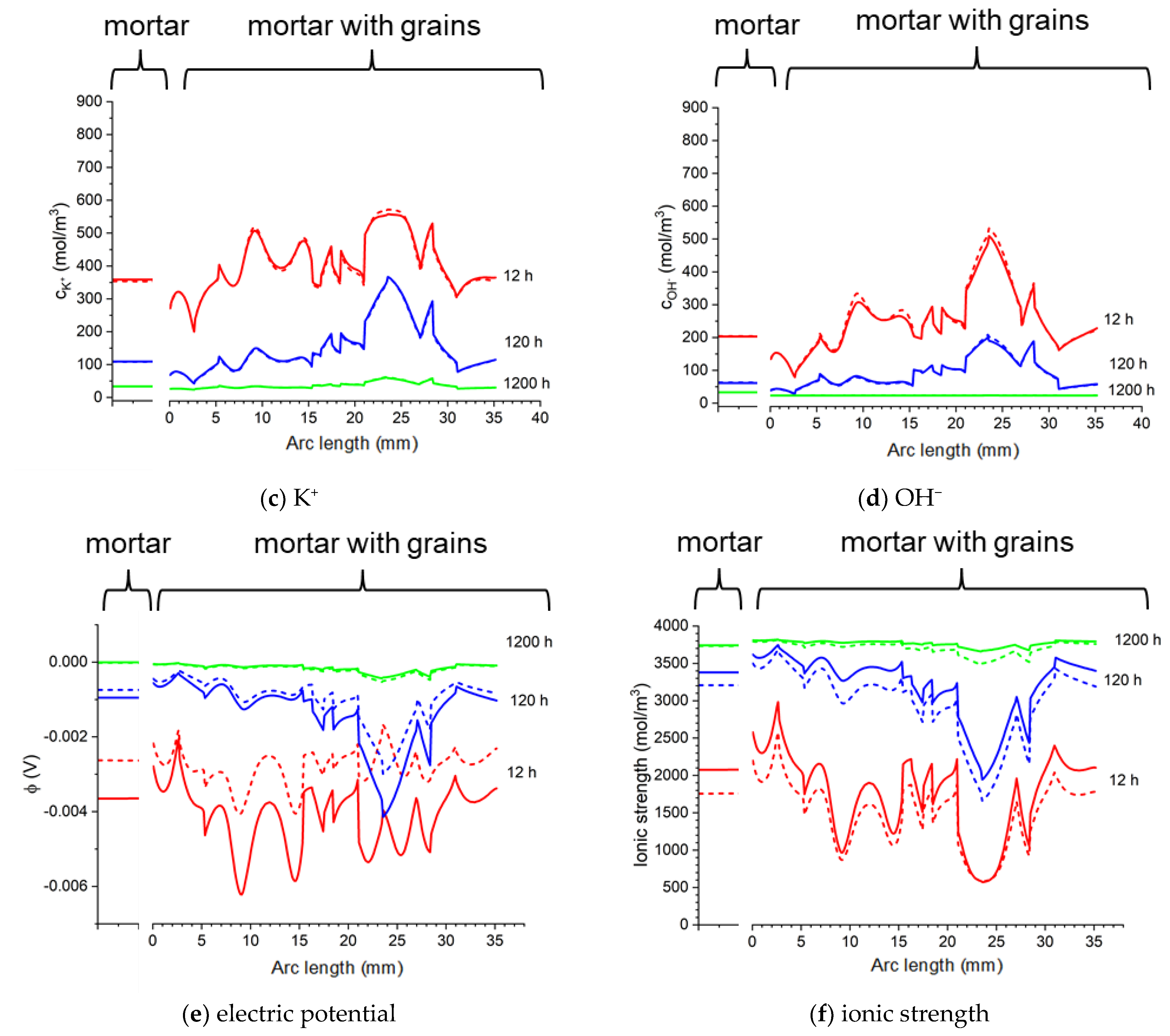
Figure 25.
Calculated: ion concentrations: (a) Na+, (b) Cl−, (c) K+, (d) OH−, (e) potential (ϕ), and (f) ionic strength in the mortar and concrete samples at the surface of the rod in 20% NaCl water solution (along a blue line). Solid lines correspond to the solution for the Pitzer activity model and dashed lines are the solution neglecting activities ().
Figure 25.
Calculated: ion concentrations: (a) Na+, (b) Cl−, (c) K+, (d) OH−, (e) potential (ϕ), and (f) ionic strength in the mortar and concrete samples at the surface of the rod in 20% NaCl water solution (along a blue line). Solid lines correspond to the solution for the Pitzer activity model and dashed lines are the solution neglecting activities ().
Table 1.
Initial concentrations of ions in liquid in pores of cementitious material (mol dm−3). The symbol I denotes molar ionic strength of the solution; (concentration of Cl− is zero).
Table 1.
Initial concentrations of ions in liquid in pores of cementitious material (mol dm−3). The symbol I denotes molar ionic strength of the solution; (concentration of Cl− is zero).
| Ion 1: Na+ | Ion 3: K+ | Ion 4: OH− | I (mol m−3) |
|---|
| Case 1 | 0 | 590 | 590 | 590 |
| Case 2 | 120 | 470 | 590 | 590 |
Table 2.
Iinitial concentrations of ions in the external solution (mol dm−3) for six cases studied (1, 3, 5, 10, 15, and 20% NaCl water solution). I denotes the molar ionic strength of the solution.
Table 2.
Iinitial concentrations of ions in the external solution (mol dm−3) for six cases studied (1, 3, 5, 10, 15, and 20% NaCl water solution). I denotes the molar ionic strength of the solution.
| | NaCl wt % | Ion 1: Na+ (mol m−3) | Ion 2: Cl− (mol m−3) | I (mol m−3) |
|---|
| Case 1 | 1 | 170 | 170 | 170 |
| Case 2 | 3 | 510 | 510 | 510 |
| Case 3 | 5 | 860 | 860 | 860 |
| Case 4 | 10 | 1710 | 1710 | 1710 |
| Case 5 | 15 | 2570 | 2570 | 2570 |
| Case 6 | 20 | 3420 | 3420 | 3420 |
Table 3.
The usable ranges of the most popular models of activity coefficient [
14], quoted after [
15].
Table 3.
The usable ranges of the most popular models of activity coefficient [
14], quoted after [
15].
| Activity Coefficient Model | Ionic Strength (mol m−3) Range of Application |
|---|
| Extended Debye–Hückel | 0–100 |
| Davies | 0–600 |
| Truesdell–Jones | 0–2000 |
| Specific Ion Interaction Theory | 0–4000 |
| Pitzer model | 0–6000 |
Table 4.
The parameters of the Truesdell–Jones model (see (11)) used in this work (based on [
14]).
Table 4.
The parameters of the Truesdell–Jones model (see (11)) used in this work (based on [
14]).
| Ion i | | |
|---|
| Na | 4.32 | 0.06 |
| Cl | 3.71 | 0.01 |
| K | 3.71 | 0.01 |
| OH (case #1) | 10.65 | 0.21 |
| OH (case #2) | 3.5 * | 0.21 |
Table 5.
Effective ionic radii
used in Equation (12) [
16].
Table 5.
Effective ionic radii
used in Equation (12) [
16].
| ai (Å) |
|---|
| Case | Ion 1: Na+ | Ion 2: Cl− | Ion 3: K+ | Ion 4: OH− |
|---|
| #1 | 3.0 | 3.0 | 3.0 | 3.0 |
| #2 | 3.0 * | 2.0 * | 3.3 * | 3.0 * |
Table 6.
Mesh parameters used in calculations of ions concentration and potential distributions in the concrete sample with the corresponding time of calculations.
Table 6.
Mesh parameters used in calculations of ions concentration and potential distributions in the concrete sample with the corresponding time of calculations.
| Mesh | No. of Elements | Avg. Element Quality | Time of Calculations |
|---|
| coarse | 45,911 | 0.828 | 1 h 13 min |
| fine | 71,745 | 0.828 | 1 h 47 min |
| finer | 94,588 | 0.838 | 2 h 19 min |
| extra fine | 126,652 | 0.850 | 3 h 33 min |
Table 7.
Calculated chloride ion concentration and electrical potential average absolute and relative errors for representative time 660 h of the process, for different meshes (see
Table 6).
Table 7.
Calculated chloride ion concentration and electrical potential average absolute and relative errors for representative time 660 h of the process, for different meshes (see
Table 6).
| Mesh | Chloride Ion Concentration | Electric Potential |
|---|
| Average Absolute Error [mol m−3] | Average Relative Error [%] | Average Absolute Error [V] | Average Relative Error [%] |
|---|
| (fine)—(coarse) * | 1.2 | 0.04 | 1·10−6 | 0.3 |
| (finer)—(fine) | 0.3 | 0.01 | 2·10−7 | 0.07 |
| (extra fine)—(finer) | 0.4 | 0.013 | 1.6·10−7 | 0.05 |
Table 8.
Parameters in Equation (23) adjusted for two-component systems [
59] using the Excel solver.
Table 8.
Parameters in Equation (23) adjusted for two-component systems [
59] using the Excel solver.
| Electrolyte | a | b |
|---|
| NaCl | 0.0409 | 0.0008 |
| NaOH | 0.0433 | 0.0015 |
| KOH | 0.0479 | 0.0013 |
| KCl | 0.0467 | 0.0009 |
Table 9.
Charge numbers, diffusion coefficients of ions in electrolyte
and ions effective diffusion coefficients
in the liquid in pores of cement at 25 °C [
36].
Table 9.
Charge numbers, diffusion coefficients of ions in electrolyte
and ions effective diffusion coefficients
in the liquid in pores of cement at 25 °C [
36].
| | Ion 1: Na+ | Ion 2: Cl− | Ion 3: K+ | Ion 4: OH− |
|---|
| zi | +1 | −1 | +1 | −1 |
| 1.356·10−9 | 2.011·10−9 | 1.983·10−9 | 5.27·10−9 |
| 3.932·10−12 | 6.0·10−12 | 5.751·10−12 | 1.528·10−11 |