Influence of Corrosion on the Bond–Slip Behaviour between Corroded Bars and Concrete
Abstract
:1. Introduction
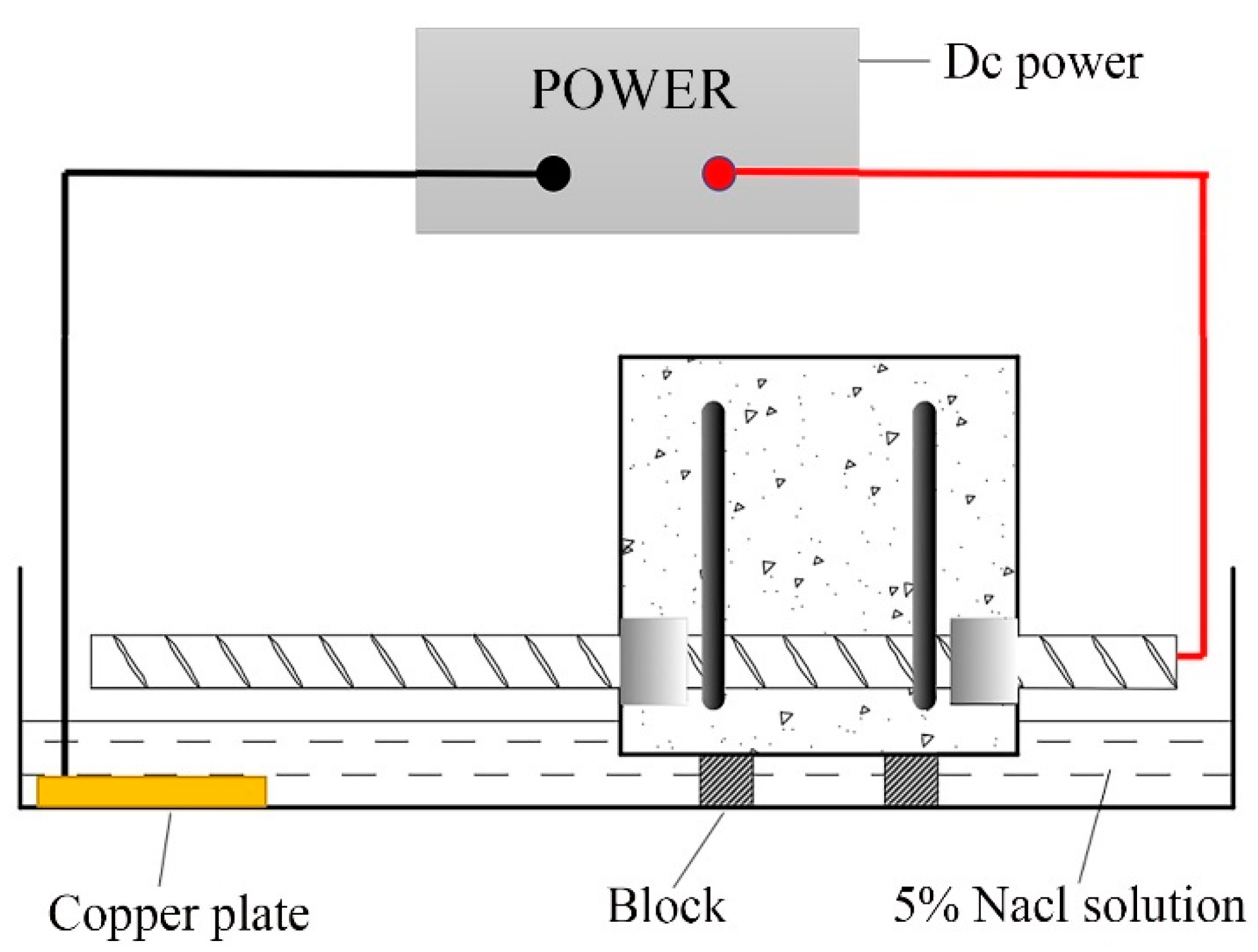
2. Overview of the Test
2.1. Experimental Design
2.2. Preparation of Test Piece
2.3. Loading of the Specimens
3. Results and Discussion
3.1. Analysis of Corrosion Test Results
3.2. The Influence of Longitudinal Bar Rust on the Ultimate Bonding Strength
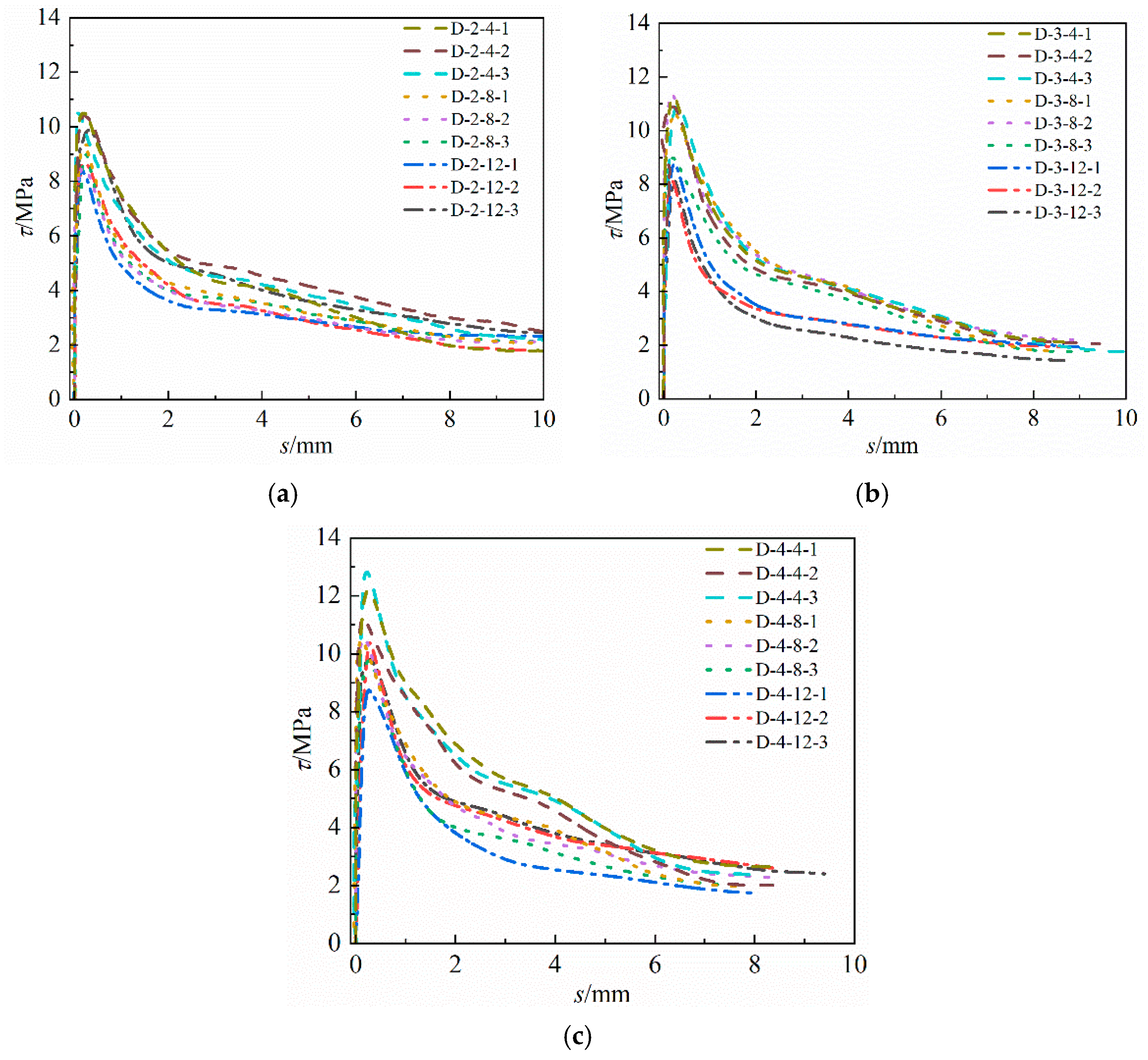
3.3. The Influence of Stirrup Corrosion on the Ultimate Bonding Strength
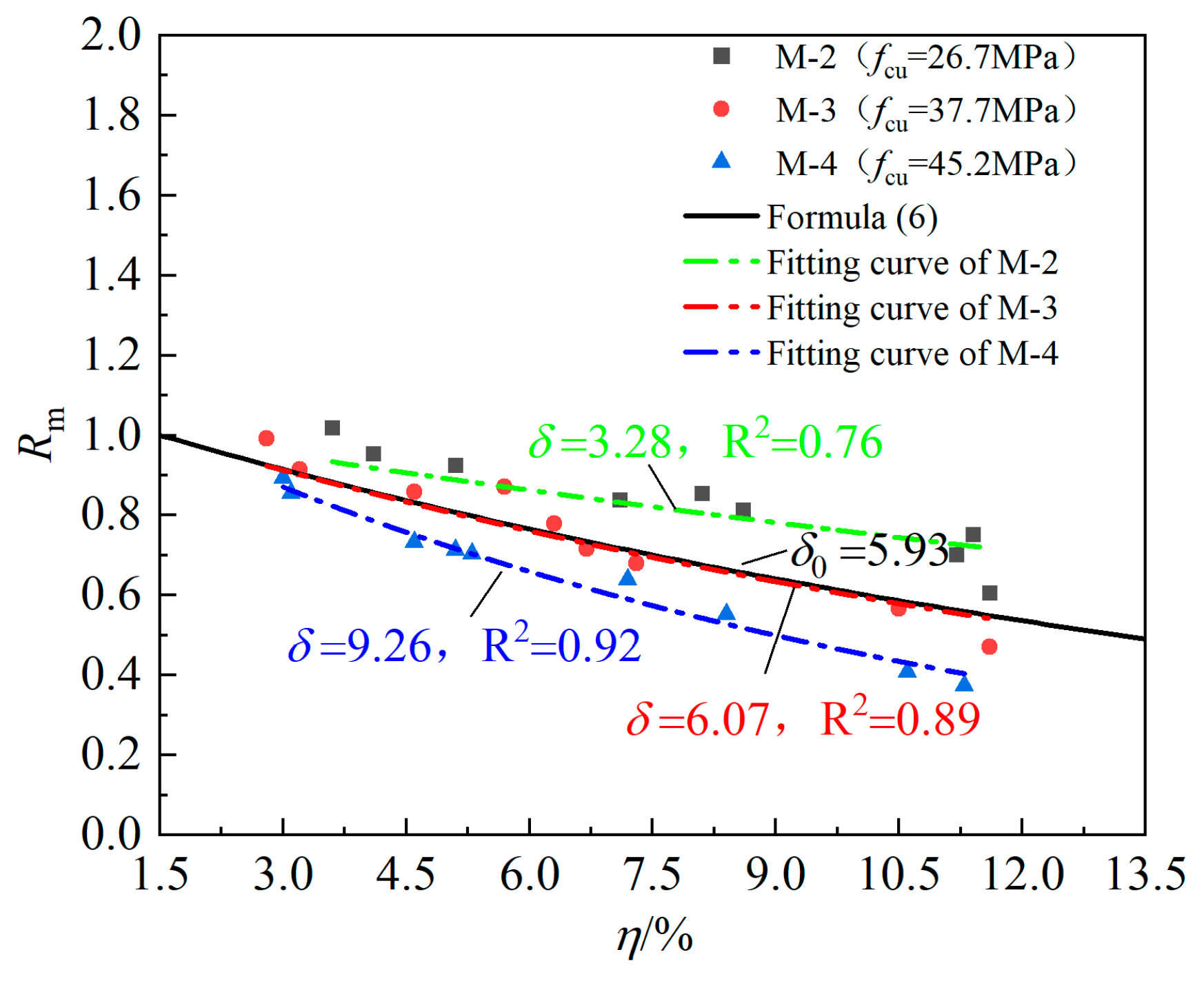
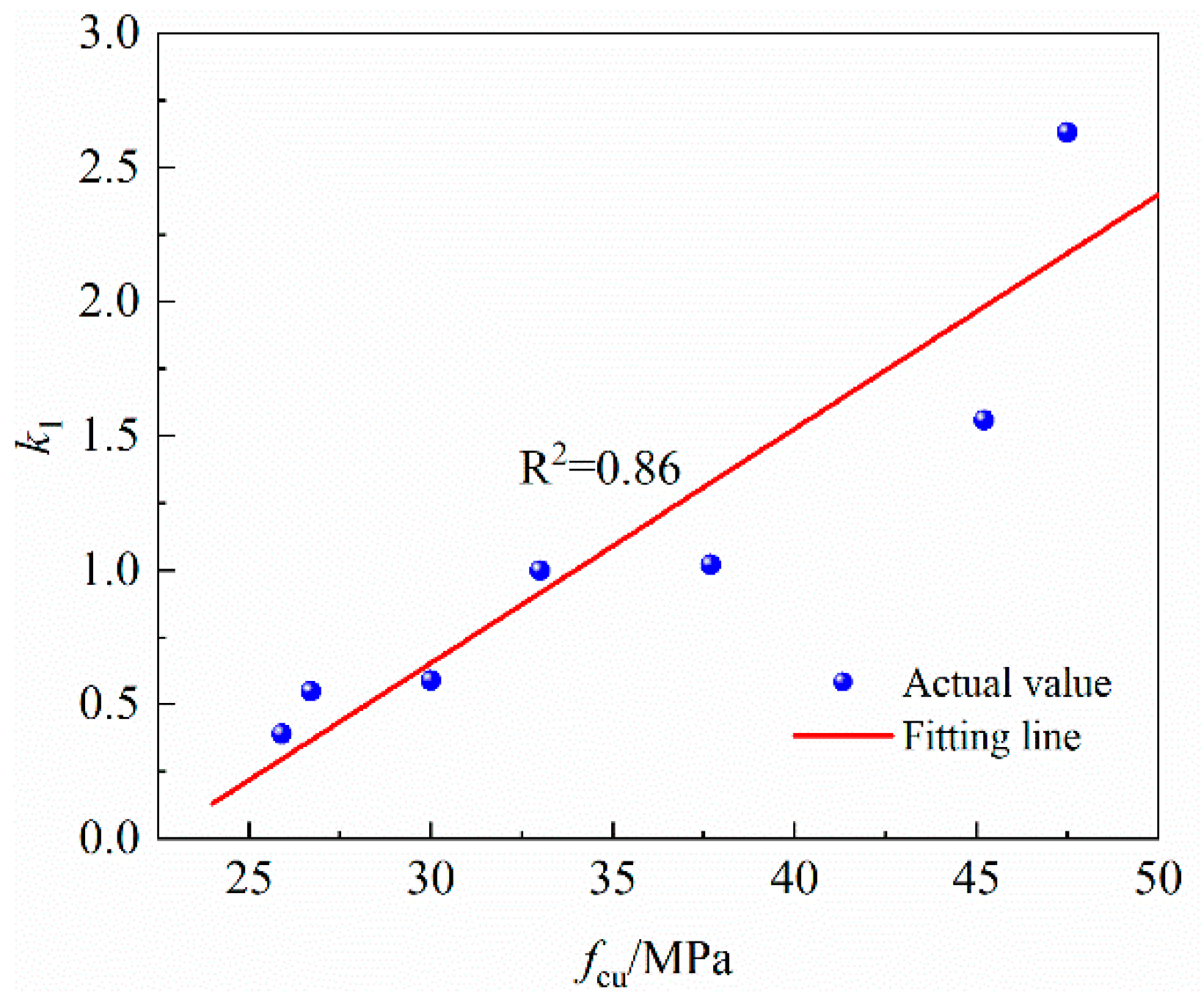
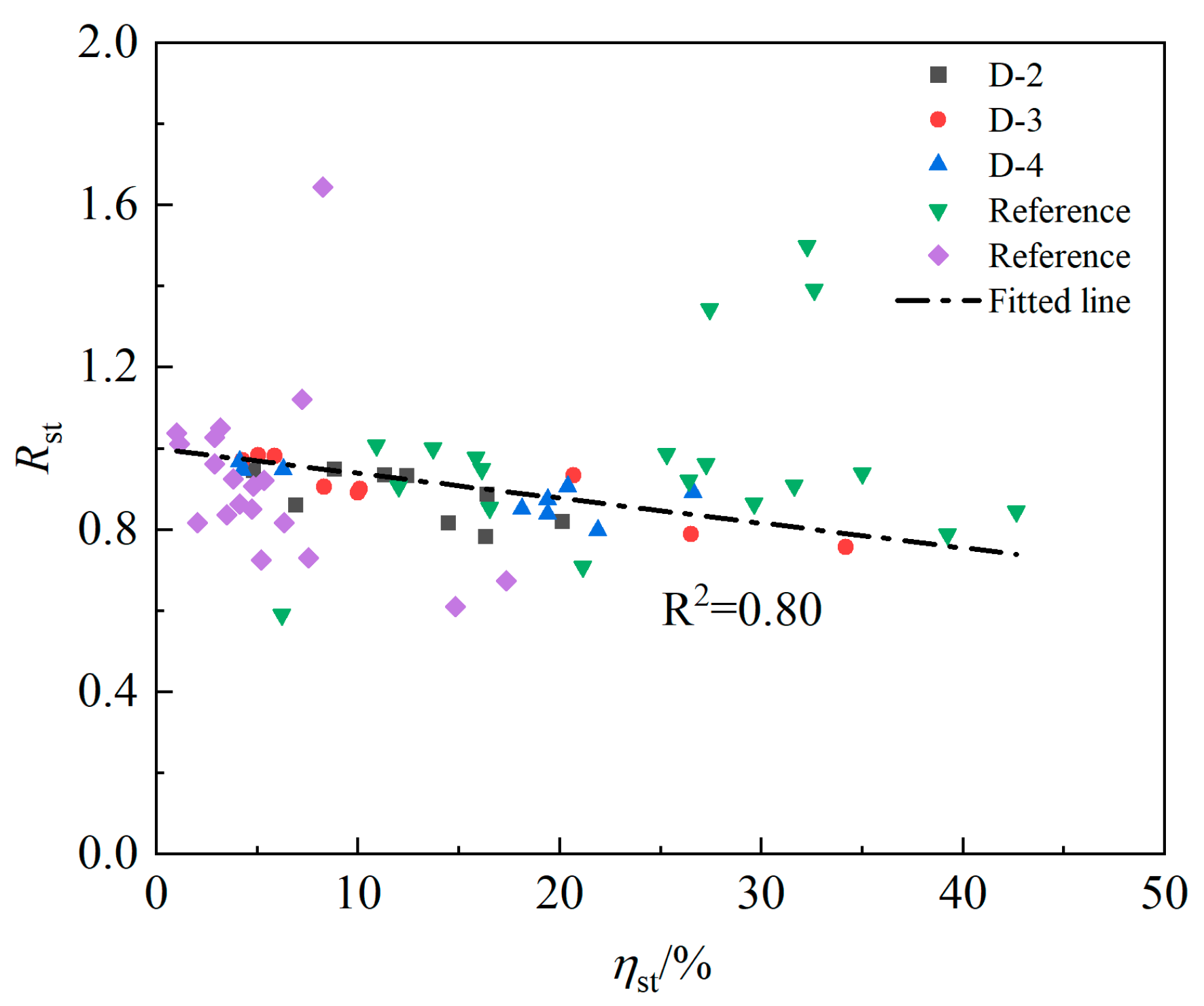
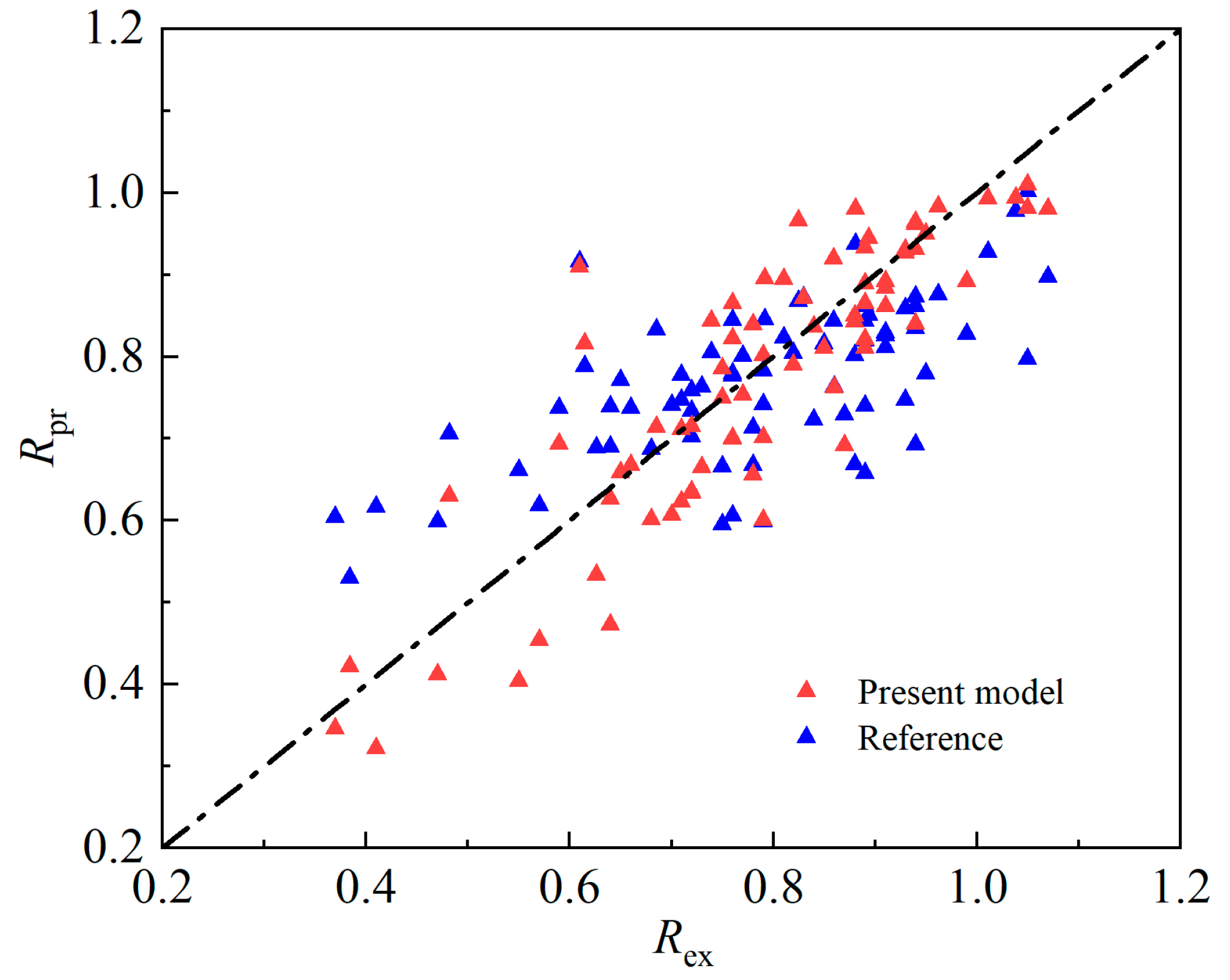
3.4. An Improved Formula for Calculating Relative Bonding Strength
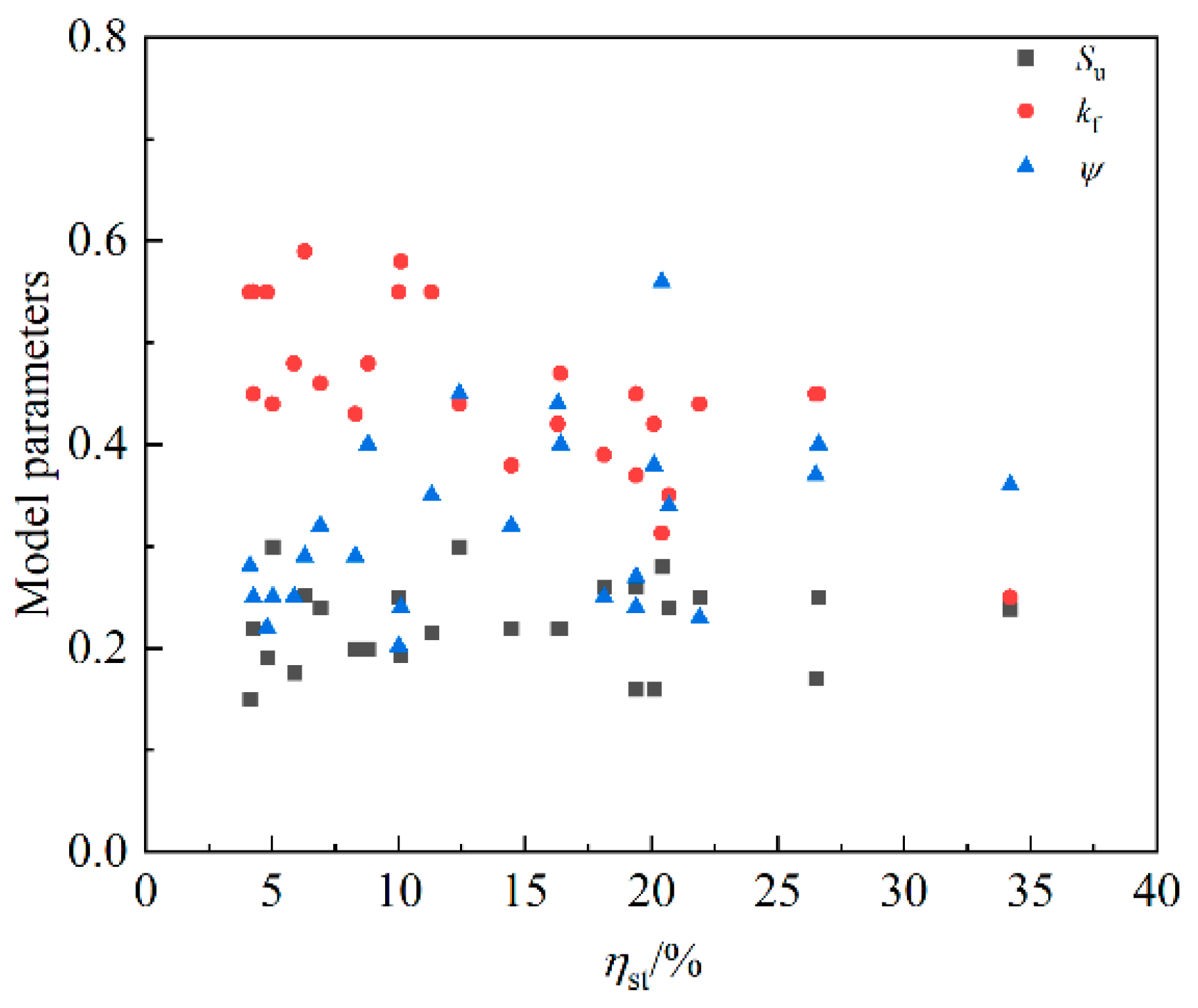
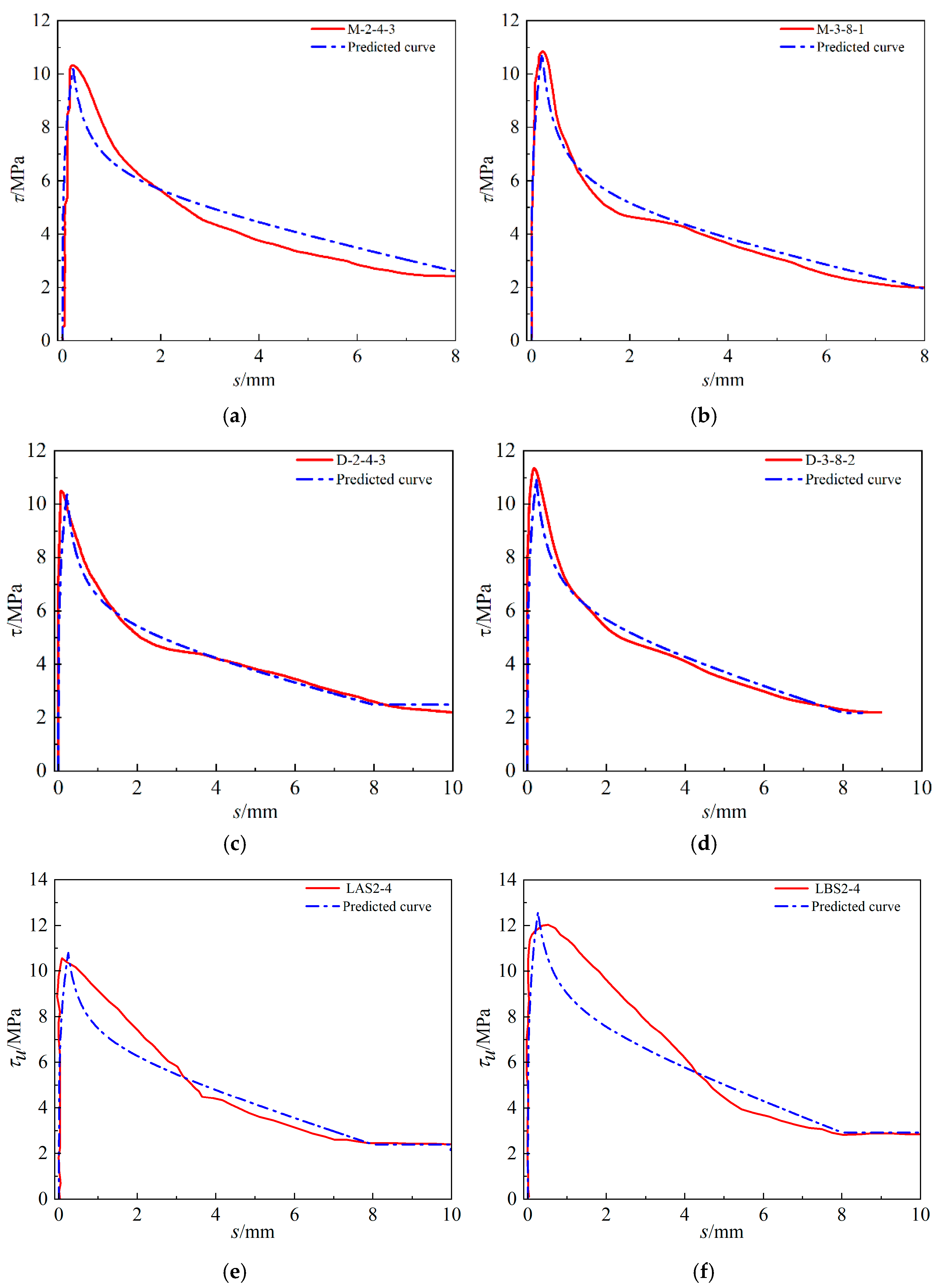
3.5. The Improved Bond–Slip Constitutive Model
4. Conclusions
- (1)
- With increasing corrosion time, different degrees of pitting and regional corrosion of the longitudinal bars are observed. The corrosion of the inner stirrup of a specimen with both longitudinal bar and stirrup corrosion is generally more serious than that of the longitudinal reinforcement, and the distribution of surface cracks is more complex than that of a specimen with only longitudinal reinforcement corrosion, showing a pattern of interlacing cracks, and the phenomenon of rusting during the corrosion process is more serious.
- (2)
- Steel bar corrosion in a specimen will reduce the bonding strength of the specimen. The higher the concrete strength grade of the specimen is, the faster the bonding strength deteriorates with increasing corrosion loss. In addition, under the same longitudinal reinforcement corrosion loss, the bonding strength of the longitudinal reinforcement- and stirrup-corroded specimens is significantly lower than that of the longitudinal reinforcement-corroded specimens only. In severe cases, the bonding strength of the longitudinal reinforcement-corroded specimens is only 75% of that of the longitudinal reinforcement- and stirrup-corroded specimens. Moreover, the reduction effect caused by stirrup corrosion can change approximately linearly with stirrup corrosion loss.
- (3)
- Based on the experimental results and previous work, a relative bonding strength degradation model and a bond–slip constitutive model of corroded reinforced concrete are established, accounting for many factors, such as concrete strength and longitudinal bar and stirrup rust. The empirical formula of peak slip and the values of each parameter are given, and the constitutive model is in good agreement with the relevant experimental results.
- (4)
- The model proposed in this paper is only applicable to the case of steel bars that do not yield. In future research, the bond–slip constitutive model of corroded reinforced concrete under the yield state of steel bars could be explored.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Naser, M.Z.; Hawileh, R.A.; Abdalla, J.A. Fiber-reinforced polymer composites in strengthening reinforced concrete structures: A critical review. Eng. Struct. 2019, 198, 109542. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Zheng, B.W.; Zhao, D.B.; Dang, L.J.; Sui, L.L.; Li, D.W.; Xing, F. Cyclic bond behaviors between corroded steel bar and concrete under the coupling effects of hoop FRP confinement and sustained loading. Compos. Struct. 2019, 224, 110991. [Google Scholar] [CrossRef]
- Kazemi, H.; Yekrangnia, M.; Shakiba, M.; Bazli, M.; Oskouei, A.V. Bond-slip behaviour between GFRP/steel bars and seawater concrete after exposure to environmental conditions. Eng. Struct. 2022, 268, 114796. [Google Scholar] [CrossRef]
- Ge, W.; Han, M.Y.; Guan, Z.; Zhang, P.; Yao, S. Tension and bonding behaviour of steel-FRP composite bars subjected to the coupling effects of chloride corrosion and load. Constr. Build. Mater. 2021, 296, 123641. [Google Scholar] [CrossRef]
- Wang, J.Z.; Xiao, F.D.; Yang, J.L. Experimental study on bond behavior between epoxy-coated reinforcement (ECR) and seawater sea-sand concrete (SSC) under FRP-steel confinement. Constr. Build. Mater. 2023, 385, 131426. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Lu, Z. Bond property test of reinforced concrete with all soaking and impressed current method corrosion. Trans. Tianjin Univ. 2013, 19, 366–371. [Google Scholar] [CrossRef]
- Fu, C.Q.; Fang, D.M.; Ye, H.L.; Huang, L.; Wang, J.D. Bond degradation of non-uniformly corroded steel rebars in concrete. Eng. Struct. 2021, 226, 111392. [Google Scholar] [CrossRef]
- Yalciner, H.; Eren, O.; Sensoy, S. An experimental study on the bond strength between reinforcement bars and concrete as a function of concrete cover, strength and corrosion level. Cem. Concr. Res. 2012, 42, 643–655. [Google Scholar] [CrossRef]
- Yin, S.P.; Hu, C.S.; Lv, H.L. Interfacial properties and bond strength model of TRC-confined concrete and deformed reinforcement under corrosion. Compos. Interface 2019, 26, 551–569. [Google Scholar] [CrossRef]
- Feng, Q.; Zhang, Y.P.; Visintin, P.; Xu, R.Q. Stirrup effects on the bond properties of corroded reinforced concrete. Mag. Concr. Res. 2021, 73, 1151–1166. [Google Scholar] [CrossRef]
- Zhou, H.J.; Qiao, M.D.; Du, Y.; Liu, J.; Zhou, Y.F.; Mo, Y.Q.; Feng, X.; Zhao, Y.P. Bond degradation behavior of rebar and reinforced concrete confined with corroded stirrups in a marine environment: Effects of concrete grade and casting position. Mag. Concr. Res. 2022, 74, 1039–1055. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y.; Yang, J.-Q.; Feng, P.; Ozbolt, J.; Ye, H. Effects of the corrosion of main bar and stirrups on the bond behavior of reinforcing steel bar. Constr. Build. Mater. 2019, 225, 13–28. [Google Scholar] [CrossRef]
- Koteš, P.; Vičan, J. Influence of reinforcement corrosion on moment and shear resistance in time of RC bridge girder. In Proceedings of the Conference IABMAS 2016 “Maintenance, Monitoring, Safety, Risk and Resilience of Bridges and Bridge Networks”, Paraná, Brazil, 26–30 June 2016; pp. 484–491. [Google Scholar]
- Zheng, Y.; Fang, Y.L.; Ma, H.Q. Bond-Slip Model of Corroded Reinforced Concrete and Its Application in Members. J. Earthq. Eng. 2023, 27, 3490–3517. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, G.Y.; Ye, H.L.; Zeng, Q.Z.; Zhang, Z.Z.; Tian, Z.S.; Jin, X.Y.; Jin, N.G.; Chen, Z.G.; Wang, J.X. Corrosion of steel rebar in concrete induced by chloride ions under natural environments. Constr. Build. Mater. 2023, 369, 130504. [Google Scholar] [CrossRef]
- Lin, H.W.; Zhao, Y.X. Effects of confinements on the bond strength between concrete and corroded steel bars. Constr. Build. Mater. 2016, 118, 127–138. [Google Scholar] [CrossRef]
- Li, F.H.; Jin, H.S.; Hu, D.H.; Zhang, G.B.; Li, X.Y. Experimental Study on Bond-Slip Performance of Corroded Reinforced Concrete. J. China Railw. Soc. 2018, 40, 154–159. (In Chinese) [Google Scholar]
- Gao, Z.Y.; Zhu, J.S. Monitoring of reinforcement corrosion within concrete and research on bond slip performance. Ind. Constr. 2016, 46, 95–99. (In Chinese) [Google Scholar]
- Wang, C.Y.; Zhou, Q.; Yang, O.; Huo, J.S.; Wang, H.T. Effect of Corrosion Rate of Steel Bar on Bond Performance Between Steel Bar and Concrete. Mater. Rep. 2019, 33, 309–316. (In Chinese) [Google Scholar]
- Zheng, Y.; Zheng, S.S.; Yang, L.; Dong, L.G.; Zhang, Y.B. Experimental study and analytical model of the bond behavior of corroded reinforcing steel bars in concrete. Constr. Build. Mater. 2022, 327, 126991. [Google Scholar] [CrossRef]
- Lin, H.W.; Zhao, Y.X.; Ozbolt, J.; Hans-Wolf, R. The bond behavior between concrete and corroded steel bar under repeated loading. Eng. Struct. 2017, 140, 390–405. [Google Scholar] [CrossRef]








| Specimen Name | Stirrup Insulation | Concrete Strength | Expected Corrosion Loss | Number of Specimens |
|---|---|---|---|---|
| A-25 | Y | C25 | 0% | 3 |
| M-2-4/8/12 | Y | C25 | 4%/8%/12% | 3/3/3 |
| D-2-4/8/12 | N | C25 | 4%/8%/12% | 3/3/3 |
| A-35 | Y | C35 | 0% | 3 |
| M-3-4/8/12 | Y | C35 | 4%/8%/12% | 3/3/3 |
| D-3-4/8/12 | N | C35 | 4%/8%/12% | 3/3/3 |
| A-45 | Y | C45 | 0% | 3 |
| M-4-4/8/12 | Y | C45 | 4%/8%/12% | 3/3/3 |
| D-4-4/8/12 | N | C45 | 4%/8%/12% | 3/3/3 |
| Specimen Name | Expected Corrosion Loss/% | Actual Corrosion Loss/% | Ultimate Bonding Strength/MPa | Relative Bonding Strength |
|---|---|---|---|---|
| A-25-1 | 0.00 | 0.00 | 10.80 | 1.00 |
| A-25-2 | 0.00 | 0.00 | 11.74 | 1.00 |
| A-25-3 | 0.00 | 0.00 | 10.92 | 1.00 |
| M-2-4-1 | 4.00 | 4.10 | 10.63 | 0.95 |
| M-2-4-2 | 4.00 | 3.60 | 11.35 | 1.01 |
| M-2-4-3 | 4.00 | 5.10 | 10.32 | 0.93 |
| M-2-8-1 | 8.00 | 7.10 | 9.37 | 0.84 |
| M-2-8-2 | 8.00 | 8.60 | 9.03 | 0.81 |
| M-2-8-3 | 8.00 | 8.10 | 9.48 | 0.85 |
| M-2-12-1 | 12.00 | 11.20 | 7.80 | 0.70 |
| M-2-12-2 | 12.00 | 11.40 | 8.36 | 0.75 |
| M-2-12-3 | 12.00 | 11.60 | 6.69 | 0.60 |
| A-35-1 | 0.00 | 0.00 | 12.32 | 1.00 |
| A-35-2 | 0.00 | 0.00 | 12.74 | 1.00 |
| A-35-3 | 0.00 | 0.00 | 12.17 | 1.00 |
| M-3-4-1 | 4.00 | 2.80 | 12.31 | 0.99 |
| M-3-4-2 | 4.00 | 3.20 | 11.34 | 0.91 |
| M-3-4-3 | 4.00 | 4.60 | 10.65 | 0.86 |
| M-3-8-1 | 8.00 | 5.70 | 10.80 | 0.87 |
| M-3-8-2 | 8.00 | 6.30 | 9.67 | 0.78 |
| M-3-8-3 | 8.00 | 6.70 | 8.88 | 0.72 |
| M-3-12-1 | 12.00 | 7.30 | 8.44 | 0.68 |
| M-3-12-2 | 12.00 | 10.50 | 7.02 | 0.57 |
| M-3-12-3 | 12.00 | 11.60 | 5.85 | 0.47 |
| A-45-1 | 0.00 | 0.00 | 13.83 | 1.00 |
| A-45-2 | 0.00 | 0.00 | 13.68 | 1.00 |
| A-45-3 | 0.00 | 0.00 | 13.53 | 1.00 |
| M-4-4-1 | 4.00 | 3.00 | 12.22 | 0.89 |
| M-4-4-2 | 4.00 | 3.10 | 11.70 | 0.85 |
| M-4-4-3 | 4.00 | 4.60 | 11.39 | 0.73 |
| M-4-8-1 | 8.00 | 5.30 | 9.63 | 0.70 |
| M-4-8-2 | 8.00 | 5.10 | 10.85 | 0.71 |
| M-4-8-3 | 8.00 | 7.20 | 8.73 | 0.64 |
| M-4-12-1 | 12.00 | 8.40 | 7.54 | 0.55 |
| M-4-12-2 | 12.00 | 10.60 | 5.97 | 0.41 |
| M-4-12-3 | 12.00 | 11.30 | 5.10 | 0.37 |
| Data Source | Concrete Strength/MPa | |||
|---|---|---|---|---|
| Ref. [17] | 25.9 | 12.60 | 4.87 | 0.39 |
| Ref. [18] | 30.0 | 14.49 | 8.61 | 0.59 |
| Ref. [19] | 47.5 | 4.99 | 12.98 | 2.60 |
| M-2 | 26.7 | 5.93 | 3.28 | 0.55 |
| M-3 | 37.7 | 5.93 | 6.07 | 1.02 |
| M-4 | 45.2 | 5.93 | 9.26 | 1.56 |
| Specimen Name | Longitudinal Bar Corrosion Loss/% | Stirrup Corrosion Loss/% | Ultimate Bonding Strength/MPa | Relative Bonding Strength |
|---|---|---|---|---|
| D-2-4-1 | 1.80 | 4.78 | 10.50 | 0.94 |
| D-2-4-2 | 1.70 | 11.30 | 10.40 | 0.93 |
| D-2-4-3 | 2.20 | 8.80 | 10.44 | 0.94 |
| D-2-8-1 | 4.60 | 16.40 | 9.33 | 0.84 |
| D-2-8-2 | 3.20 | 16.30 | 8.47 | 0.76 |
| D-2-8-3 | 2.30 | 14.47 | 8.98 | 0.81 |
| D-2-12-1 | 6.20 | 20.10 | 8.37 | 0.75 |
| D-2-12-2 | 7.10 | 6.90 | 8.63 | 0.78 |
| D-2-12-3 | 4.30 | 12.40 | 9.87 | 0.89 |
| D-3-4-1 | 2.50 | 4.27 | 11.24 | 0.91 |
| D-3-4-2 | 1.70 | 8.30 | 11.08 | 0.89 |
| D-3-4-3 | 3.10 | 5.03 | 10.90 | 0.88 |
| D-3-8-1 | 3.30 | 10.00 | 9.76 | 0.79 |
| D-3-8-2 | 2.50 | 5.86 | 11.35 | 0.91 |
| D-3-8-3 | 4.60 | 10.08 | 8.98 | 0.72 |
| D-3-12-1 | 4.00 | 20.70 | 8.74 | 0.79 |
| D-3-12-2 | 4.10 | 26.50 | 8.16 | 0.66 |
| D-3-12-3 | 3.60 | 34.20 | 8.11 | 0.65 |
| D-4-4-1 | 2.10 | 6.28 | 12.18 | 0.89 |
| D-4-4-2 | 3.10 | 4.12 | 11.21 | 0.82 |
| D-4-4-3 | 1.60 | 4.27 | 12.81 | 0.94 |
| D-4-8-1 | 1.90 | 21.90 | 10.46 | 0.76 |
| D-4-8-2 | 2.70 | 19.40 | 10.54 | 0.77 |
| D-4-8-3 | 3.20 | 18.12 | 9.75 | 0.71 |
| D-4-12-1 | 4.10 | 19.40 | 8.74 | 0.64 |
| D-4-12-2 | 3.20 | 20.40 | 10.37 | 0.76 |
| D-4-12-3 | 3.60 | 26.60 | 9.79 | 0.72 |
| Series | ||
|---|---|---|
| A | 0.45 | 0.27 |
| M | 0.51 | 0.41 |
| D | 0.46 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Ying, Z.; Du, C.; Yang, S.; Liu, H. Influence of Corrosion on the Bond–Slip Behaviour between Corroded Bars and Concrete. Materials 2023, 16, 7366. https://doi.org/10.3390/ma16237366
Zhao C, Ying Z, Du C, Yang S, Liu H. Influence of Corrosion on the Bond–Slip Behaviour between Corroded Bars and Concrete. Materials. 2023; 16(23):7366. https://doi.org/10.3390/ma16237366
Chicago/Turabian StyleZhao, Chenxu, Zongquan Ying, Chengbin Du, Shuai Yang, and Hansheng Liu. 2023. "Influence of Corrosion on the Bond–Slip Behaviour between Corroded Bars and Concrete" Materials 16, no. 23: 7366. https://doi.org/10.3390/ma16237366
APA StyleZhao, C., Ying, Z., Du, C., Yang, S., & Liu, H. (2023). Influence of Corrosion on the Bond–Slip Behaviour between Corroded Bars and Concrete. Materials, 16(23), 7366. https://doi.org/10.3390/ma16237366






