Next Article in Journal
Ab Initio Simulation of Structure and Properties in Ni-Based Superalloys: Haynes282 and Inconel740
Next Article in Special Issue
Single Crystals of EuScCuSe3: Synthesis, Experimental and DFT Investigations
Previous Article in Journal
Indirect Induction Sintering of Metal Parts Produced through Material Extrusion Additive Manufacturing
Previous Article in Special Issue
Phonon Structure, Infra-Red and Raman Spectra of Li2MnO3 by First-Principles Calculations
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 16
Issue 2
10.3390/ma16020886
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Prediction of Novel Ultrahard Phases in the B–C–N System from First Principles: Progress and Problems

by
Vladimir L. Solozhenko
1,* and
Samir F. Matar
2
1
LSPM–CNRS, Université Sorbonne Paris Nord, 93430 Villetaneuse, France
2
CMMS (Computational Materials & Molecular Science), Lebanese German University (LGU), Jounieh P.O. Box 206, Lebanon
*
Author to whom correspondence should be addressed.
Materials 2023, 16(2), 886; https://doi.org/10.3390/ma16020886
Submission received: 9 December 2022 / Revised: 9 January 2023 / Accepted: 13 January 2023 / Published: 16 January 2023
(This article belongs to the Special Issue Advances in Density Functional Theory (DFT) Studies of Solids (Second Volume))
Browse Figures
Versions Notes

Abstract

The modern synthesis of superhard and, especially, ultrahard phases is a fascinating area of research that could lead to the design of new, industrially important materials. Computational methods built within the well-established quantum mechanics framework of density functional theory (DFT) play an important role in the search for these advanced materials and the prediction of their properties. The close relationship between the physical properties of carbon and boron nitride has led to particular interest in the B–C–N ternary system, characterized by the small radii of the elements, resulting in short interatomic distances and reduced volumes—the parameters being ‘recipes’ for very high hardness in three-dimensional structures. The purpose of this review is to provide a brief outline of recent developments and problems in predicting novel ultrahard carbon allotropes as well as binary and ternary compounds of the B–C–N system with particular emphasis on the analysis of the models used to evaluate the hardness of the theoretically predicted structures.

1. Introduction

Historically, research in the field of ultrahard materials (usually defined as having Vickers hardness HV ≥ 80 GPa) was initiated a century ago, triggered by the increasing industrial application of diamond, the hardest (HV up to 120 GPa) known material. However, the use of diamond in mining and tooling raised problems due to the high cost of natural diamond, on the one hand, and its relatively low stability at even moderate operating temperatures, on the other hand. The first problem was solved by the development of the high-pressure synthesis of diamond [1], but its high reactivity with oxygen and ferrous metals remained a problem that required further efforts to find reliable substitutes for diamond.
An interim solution was the synthesis of cubic boron nitride (cBN) [2], which is half as hard as diamond, but has much higher thermal and chemical stability. It should be noted that in terms of electronic structure, BN is equivalent to 2C (vide infra). The close relationship between the physical properties of carbon allotropes and BN polymorphs has facilitated the search for ultrahard phases in the B–C–N ternary system constituted by light elements with small radii, resulting in short interatomic distances and reduced volumes—all the parameters being ‘recipes’ for high strength and hardness.
Until very recently, diamond was the only known material that was ultrahard. However, in 2001, cubic BC2N, a ternary compound that is halfway between diamond and BN in composition, was synthesized [3]. Vickers hardness of 76(4) GPa [4] makes it the second member of the ultrahard phases family. In 2009, the third ultrahard phase, diamond-like BC5, was discovered [5], which possesses Vickers hardness of 71(8) GPa, an unusually high for superhard materials fracture toughness (~10 MPa·m½), and very high (up to 1900 K) thermal stability. Both novel ultrahard phases have been synthesized at very high pressures and temperatures with in situ control using synchrotron X-ray diffraction, which indicates that the experimental search for such phases is a challenging task [6].
Since experimental material discovery is suffering from the high labor costs and limitations inherent to trial-and-error methods, theoretical approaches for predicting the mechanical properties of solids have been developed, from empirical models of hardness [7,8,9,10] to the ab initio calculation of elastic constants [11,12] and computational discovery of superhard materials [13,14,15]. Thus, modern algorithms and powerful computers can be used to search for materials with exceptional mechanical properties.
Studies within the B–C–N ternary system are a growing area of exploration, complementing the competence of experimenters using modern low- and high-pressure techniques, well adapted to light elements with high-purity sources, and theorists employing structure research tools such as CALYPSO [16] and USPEX [17,18] to access accurate characterizations of electronic structures and energy-related quantities such as mechanical and dynamic signatures from quantum mechanics software built in the framework of density functional theory (DFT) (cf. Appendix A). Calculation results serve as both interpretive and predictive tools for new materials with desired properties.
Since the present paper is not intended to be a comprehensive and exhaustive review, we aim to focus on the presentation of the recent developments and problems in this emerging research field, and illustrate the subject using examples from our own studies (both published and unpublished) (Figure 1). To highlight the structural and physical properties in the main body of review, we present the computational framework in Appendix A.

2. Elements

Carbon and boron (in particular, their dense allotropes, i.e., diamond and γ-B12 [19]) are the hardest elements. We shall not discuss boron here (the problem of searching for its superhard forms was already addressed in a recent review [20]), but will rather concentrate on carbon. The main research efforts with respect to carbon are focused on the search for new, dense allotropes with mechanical properties close to those of diamond. Diamond is known to exist in two forms: the cubic one that belongs to space group Fm−3m (No. 227), and a rare hexagonal form called ‘lonsdaleite’ (space group P63/mmc, No. 194). Recently, however, the existence of lonsdaleite as a discrete phase has been questioned, and it has been interpreted as a cubic diamond dominated by extensive twins and stacking faults [21].
It should be noted that information on 3-periodic carbon allotropes extracted from the scientific literature is gathered and indexed in the “SACADA” database [22]. Currently, it counts 524 unique carbon allotropes. From the structural point of view, and using chemistry terms, diamond is characterized by tetrahedral (sp3) carbon, as in the methane gas molecule CH4, and its crystal structure demonstrates three-dimensional stacking of corner-sharing C4 tetrahedra. In contrast, graphite is characterized by a layered structure where carbon is sp2 hybridized, as in the ethene gas molecule C2H4. While diamond is a large-band-gap insulator with Egap ≈ 5 eV, graphite is a semiconductor with a very small gap. Mixed sp2-sp3 hybridizations carbon was recently reported for a new, stable metallic allotrope, hex-C18 (called 18H carbon), which belongs to space group P6/mmm (No. 191) [23].
Carbon in a linear triatomic C–C–C arrangement is found in carbon suboxide C3O2, where carbon is sp2 hybridized. In the solid state, the linear configuration is kept for carbon suboxide, which is a molecular solid where weak (van-der-Waals-like) interactions prevail between separate molecules. The rarely occurring tricarbon C3 molecule was observed in interstellar space, mainly in the tails of comets (e.g., Hale-Bopp, C/1995O1), and experimentally identified by spectroscopic measurements [24]. Recently [25], we considered linear C–C–C in two novel structures: (i) rh-C3 (or hex-C9) (space group R−3m, No. 166) based on rhombohedral sodium azide characterized by the presence of a linear N3 fragment (Figure 2a), and (ii) hex-C6 (space group P63/mmc, No. 194) derived from lonsdaleite through the insertion of one extra carbon atom along the c-axis at 2d (2/3,1/3,¼) Wyckoff position (Figure 2b). From geometry optimization to the energy ground state within DFT (cf. Appendix A), energies and the energy-derived quantities were found within the range of diamond and lonsdaleite.
The elastic properties of ‘tricarbon’ allotropes rh-C3 and hex-C6 were determined by performing finite distortions of their lattices. The elastic constants Cij were derived from the strain–stress relationship. Indexes i and j represent directions: when i = j, the elastic constants correspond to the application of unidirectional stress (as in the case of C33 elastic constant discussed below), and when i ≠ j, the elastic constants are relevant to applying shear stress. For both allotropes, all calculated Cij values are positive, and their combinations obey the rules pertaining to the mechanical stability of the phases. The bulk (BV) and shear (GV) moduli were calculated from the elastic constants following the Voigt method [26], based on a uniform strain.
The Vickers hardness of the new carbon allotropes was predicted using four modern theoretical models [8,19,27,28]. The thermodynamic model [27] is based on the thermodynamic properties and crystal structure, the empirical Chen–Niu [8] and Mazhnik–Oganov [10] models use the elastic properties, and the Lyakhov–Oganov approach [28] considers the topology of the crystal structure, strength of covalent bonding, degree of ionicity and directionality. The fracture toughness (KIc) was evaluated within the Mazhnik–Oganov model [10]. Table 1 and Table 2 present the hardness values calculated using all four models, and other mechanical properties such as the bulk (B), shear (G) and Young’s (E) moduli, the Poisson’s ratio (ν) and the fracture toughness (KIc).
As has been reported earlier [36], in the case of ultrahard compounds of light elements, the thermodynamic model shows surprising agreement with available experimental data. Moreover, its use is preferable in the case of hybrid dense carbon allotropes, for which the Lyakhov–Oganov model gives underestimated hardness values, whereas the empirical models are not reliable. For this reason, both new ‘tricarbon’ allotropes should be considered as ultrahard phases.
Although the hardness and elastic moduli of rh-C3 and hex-C6 are somewhat lower than those of diamond, strong anisotropy was found for both ‘tricarbon’ allotropes, with exceptionally large C33 values along the hexagonal c-axis, i.e., C33 = 1636 GPa for rh-C3 (Figure 2a) and C33 = 1610 GPa for hex-C6 (Figure 2b), exceeding the corresponding value for lonsdaleite, C33 = 1380 GPa. The Vickers hardness predicted using four theoretical models (Table 1 and Table 2) points to slightly lower HV values for these new carbon allotropes compared to diamond (both cubic and hexagonal), but much higher than the hardness of the vast majority of recently predicted carbon allotropes, such as C14, C16, C24, C36, etc. [42,43,44,45]. Thus, both rh-C3 and hex-C6 have exceptional mechanical properties and can be considered as prospective ultrahard phases [46].
The dynamic stability of the ‘tricarbon’ allotropes was confirmed by phonon calculations. All frequencies are positive, with the particular feature of a gap in the highest-frequency optical phonon domain, not observed in lonsdaleite, and caused by the rigidly aligned C3 unit. A remarkable consequence of the presence of two carbon hybridizations (sp2 and sp3) is the occurrence of a metallic character in the electronic band structure of both ‘tricarbon’ allotropes, similar to that previously observed for hexagonal C18 [23] and monoclinic C12 [47] characterized by mixed sp2-sp3 and sp1-sp2 hybridizations, respectively.
Another novel ultrahard carbon allotrope, body-centered tetragonal C6 (space group I−4m2, No. 119) presenting mixed sp2/sp3 hybridizations, has been proposed very recently via a crystal chemistry approach and studied for the ground state structure and stability using DFT calculations [29]. Since C4 tetrahedra are in-plane stacked with corner-sharing and connected out-of-plane with C–C trigonal carbon (Figure 2c), a close relationship with so-called ‘glitter’, a hypothetical dense carbon network invented in 1994 [48], is apparent, and thus the new allotrope was named ‘neoglitter’. Besides the mechanical stability (positive values of elastic constants and their combinations), ‘neoglitter’ is also dynamically stable, as it follows from its phonon band structure. The novel allotrope reveals exceptional mechanical properties, i.e., very high hardness and elastic moduli (see Table 1 and Table 2), being conductive due to the metallic-like electronic structure, which is mainly caused by the itinerant role of trigonal carbon π-electrons.
Since the Vickers hardness calculated in the framework of the thermodynamic model exceeds 80 Gpa for the three novel carbon allotropes described above, they all should be attributed to the family of ultrahard phases.

3. Binary Compounds

The hardness of dense compounds of the binary B–N system—cubic BN [2], rhombohedral B13N2 [49,50] and tetragonal B50N2 [51]—does not exceed HV = 62 Gpa for single-crystal cBN [4], i.e., they all belong to the group of superhard phases. Special mention should be given to nanocrystalline cBN [52], with Vickers hardness up to 85 Gpa [53], mainly due to the Hall–Petch effect, i.e., nanosize effect, which restricts dislocation propagation through the material.
We will focus in more detail on two other binary systems, i.e., C–N and B–C, in which compounds with very high hardness have been predicted.

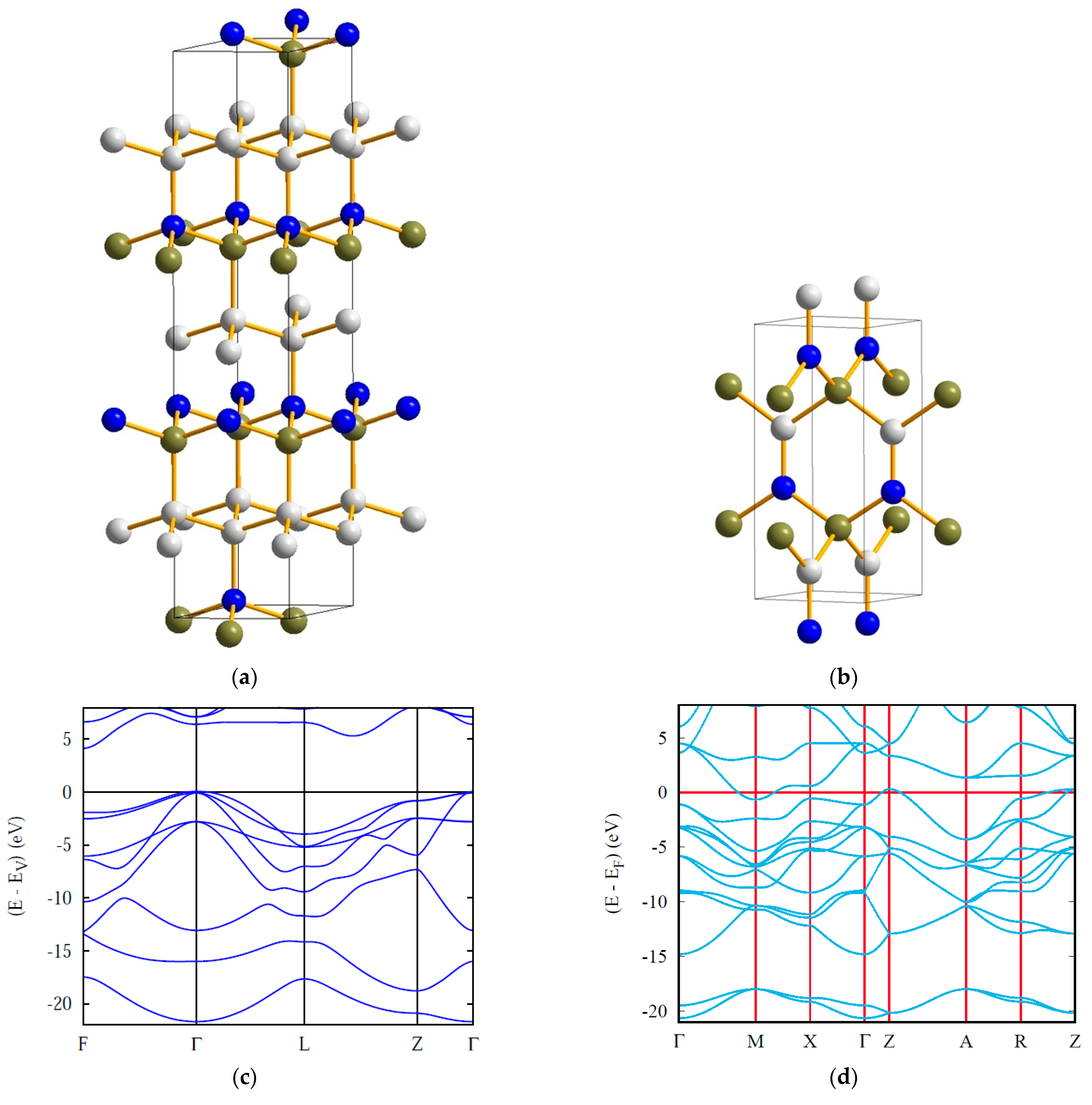
3.1. Carbon Nitrides

The main interest in studying the C–N system is a result of numerous (but unsuccessful) attempts to synthesize hypothetical ultrahard C3N4. In the 1990s, Liu et al. [30,54] and Teter and Hemley [31] predicted a number of dense low-compressibility carbon nitrides of C3N4 stoichiometry that were claimed to exhibit bulk moduli and hardness higher than those of diamond because of the short length and high covalence of the C–N bonds. However, our analysis in the framework of the thermodynamic model of hardness reveals that the Vickers hardness of the densest hypothetical cubic (P−43m [30] and I−43d [31]) and pseudocubic (P−42m [31]) polymorphs of C3N4 does not exceed 73 GPa.
Besides the carbon nitrides of C3N4 stoichiometry that are isoelectronic with diamond [55], carbon subnitrides of C11N4 stoichiometry were also studied [56] as they allow the modeling of CNx films with less than 30 at% N, which usually form when vapor phase deposition techniques are used [57]. In this context, structural models of C11N4 phases accounting for the low nitrogen content were derived from diamond being isoelectronic with it, through creating defects. Indeed, diamond expressed as 2C in primitive cells has eight valence electrons, and C11N4 has 11 × 4 + 4 × 5 = 64 = 8 × 8 electrons, i.e., an integer multiple of 8.
In the present paper, a novel (ultra)hard tetragonal C11N4 (space group P−4m2, No. 115) was derived from C16, a 2 × 2 × 1 cell of body-centered tetragonal C4 diamond-like structure [58] (Figure 3a). In this template, a defect was created at the center of the tetragonal cell by removal of the yellow carbon atom (see Figure 3a) and replacing the four surrounding carbon atoms with nitrogen (blue spheres in Figure 3b). The resulting fully relaxed carbon subnitride C11N4 was analyzed for the cohesive energy Ecoh obtained from subtracting the atomic energies of 11 C and 4 N atoms from the calculated total energy. C11N4 was found to be cohesive, with Ecoh = −1.93 eV/atom, which is lower than the corresponding value for pristine C16 (Ecoh = −2.49 eV/atom, the value identifying diamond). This is quite expected, since C11N4 results from the defect diamond-like structure of C16. Such observations are also valid for other binary compounds resulting from the perturbation of the diamond lattice.
The lattice parameters of C11N4 are a = b = 4.952 Å and c = 3.520 Å, with a nitrogen atom occupying the 4k site (0.50000, 0.24200, 0.72825) and four inequivalent carbon atoms located at the 1a (0.00000, 0.00000, 0.00000), 2g (0.50000, 0.00000, 0.97312), 4i (0.25368, 0.25368, 0.50000) and 4j (0.24974, 0.00000, 0.23750) sites. Besides being cohesive, C11N4 was found to be mechanically stable, with the whole set of elastic constants being positive, as well as being dynamically stable, with positive acoustic and optic phonon frequencies.
Calculated values of the hardness and elastic moduli of tet-C11N4 are listed in Table 1 and Table 2. Although the bulk and shear moduli of the novel carbon subnitride are lower than the corresponding values for high-density C3N4, its Vickers hardness HV = 76 GPa is higher than that of all hypothetical high-density polymorphs of C3N4 [30,31,54].
The electronic band structure of the novel tetragonal C11N4 is shown in Figure 3c, characterizing an insulator with a gap value slightly below 5 eV, from Γ (valence band) to Z (conduction band), similar to that of diamond, as a result of both structures being isoelectronic, as mentioned above.

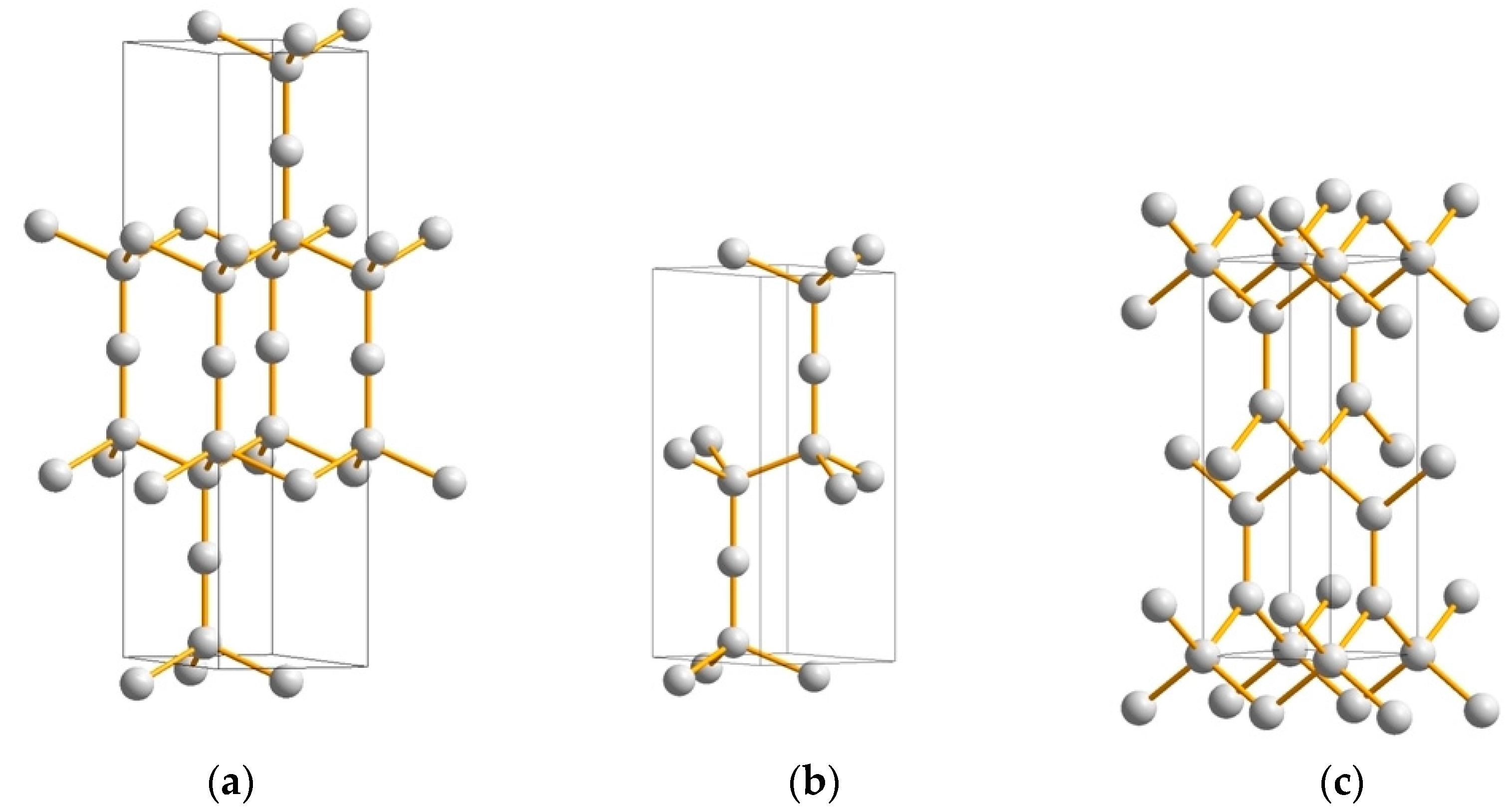
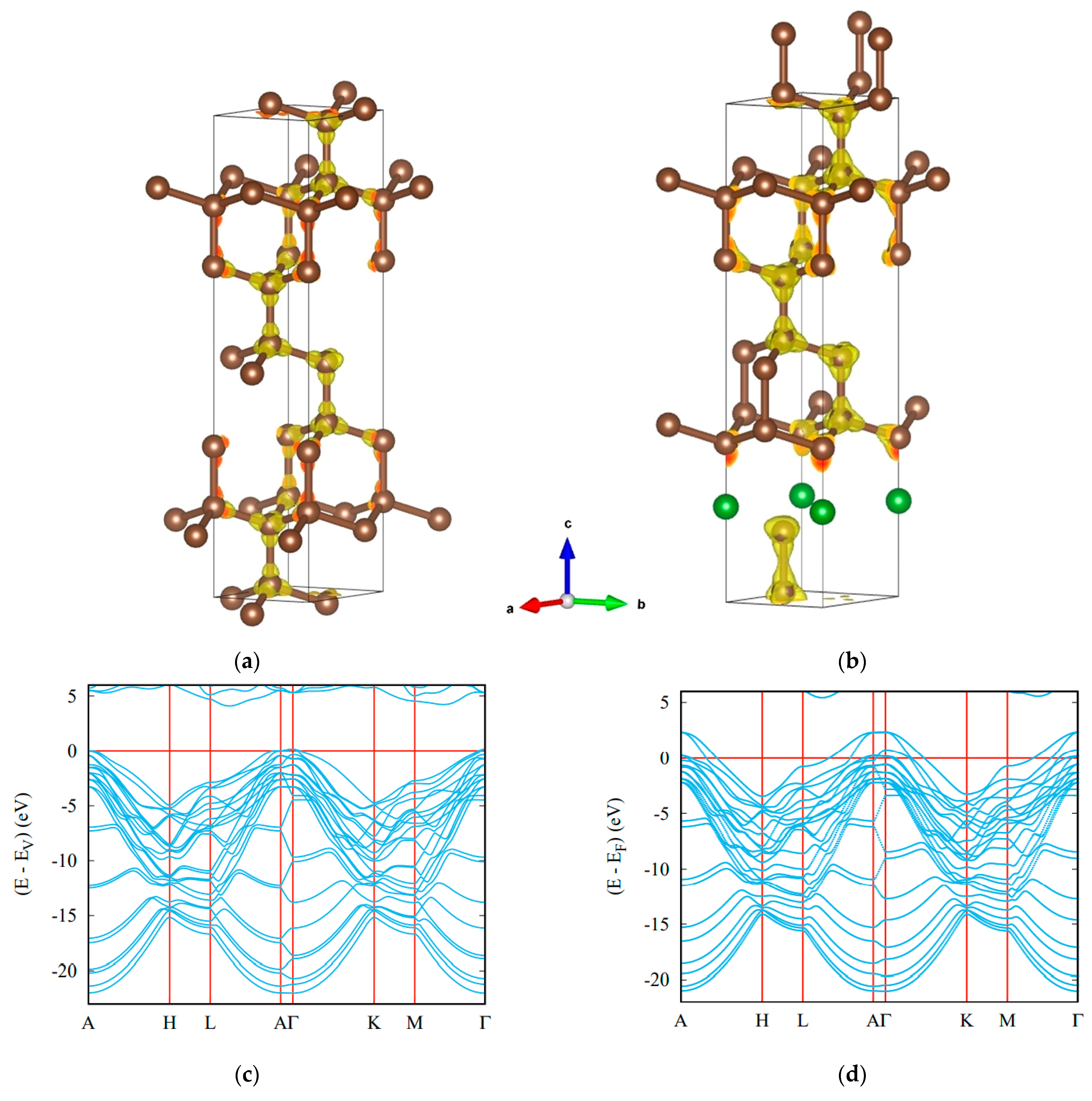
3.2. Boron Carbides

Rhombohedral boron carbide, B4C (B12C3), is the most important, well-studied and widely used compound of the B–C binary system; however, its Vickers hardness does not exceed 37 Gpa [59]. The synthesis of diamond-like BC5 with hardness above 70 GPa [5] has stimulated interest in the study of carbon-rich compounds of this system. Thus, four polymorphs of BC5 were predicted from first-principles structural optimizations [32], for two of which (tetragonal I−4m2 and triclinic P−1) Vickers hardness of approximately 80 Gpa was claimed. However, our assessments (the results for the densest tetragonal BC5 are presented in Table 1 and Table 2) showed that the hardness of all predicted phases was overestimated by ~15% as a result of the use of unreliable empirical correlations between the shear modulus and hardness.
A similar situation is observed in the case of five predicted BC7 polymorphs [33]: the claimed hardness values (e.g., 81 GPa for orthorhombic Pmm2 and 78 GPa for cubic P−43m phases) are also overestimated by 10–15% as a result of using the empirical microscopic hardness model (see our results for cubic BC7 in Table 1 and Table 2), and thus these phases, as well as BC5 polymorphs, cannot be considered ultrahard. However, one may expect that a further decrease in boron content will be accompanied by a hardness increase in the formed B-C binary compound(s).
Very recently, the latter has been confirmed by the prediction of trigonal BC11 (space group P3m1, No. 156) [34], produced by the substitution of carbon with boron in the diamond-like hex-C12 template [60], which led to the lowering of the crystal symmetry down to trigonal.
In the context of the energy criterion, it was interesting to position the novel carbon-rich BC11 among other B–C binary compounds. Comparison of trig-BC11’s cohesive energy with those reported for trig-BC5 [32] and trig-BC7 [33] shows a clear trend of decreasing Ecoh/atom with increasing boron content: −2.49 eV (diamond) < −2.33 eV (BC11: 8.3 at% B) < −2.24 eV (BC7: 12.5 at% B) < −2.16 eV (BC5: 16.7 at% B). Besides being more cohesive than the two other binary compounds, trig-BC11 was also found to be mechanically (elastic constants) and dynamically (phonon band structures) stable.
The crystal structures of template hex-C12 and trig-BC11 are shown in Figure 4. In hex-C12, the carbon network is perfectly covalent in all dimensions. Changes are observed for trig-BC11, featuring a large covalent part where the carbon networks remain as in hex-C12, but not in the surrounding area of boron atoms, whose charge density is transferred to carbon due to the larger electronegativity of carbon. Regarding its electronic band structure, bands belonging to boron states were found crossing the Fermi level EF, signaling a metallic character arising from one electron-less B (2s2,2p1) versus C (2s2,2p2) in the wide gap insulating diamond.
The hardness of trig-BC11 calculated using four models, as well as other mechanical properties, is given in Table 1 and Table 2. Although the introduction of boron atoms into the diamond crystal lattice predictably lowers the hardness, it remains high enough (>80 GPa) to consider trig-BC11 as an ultrahard phase, in contrast to other reported binary compounds of the B–C system [32,33,61].

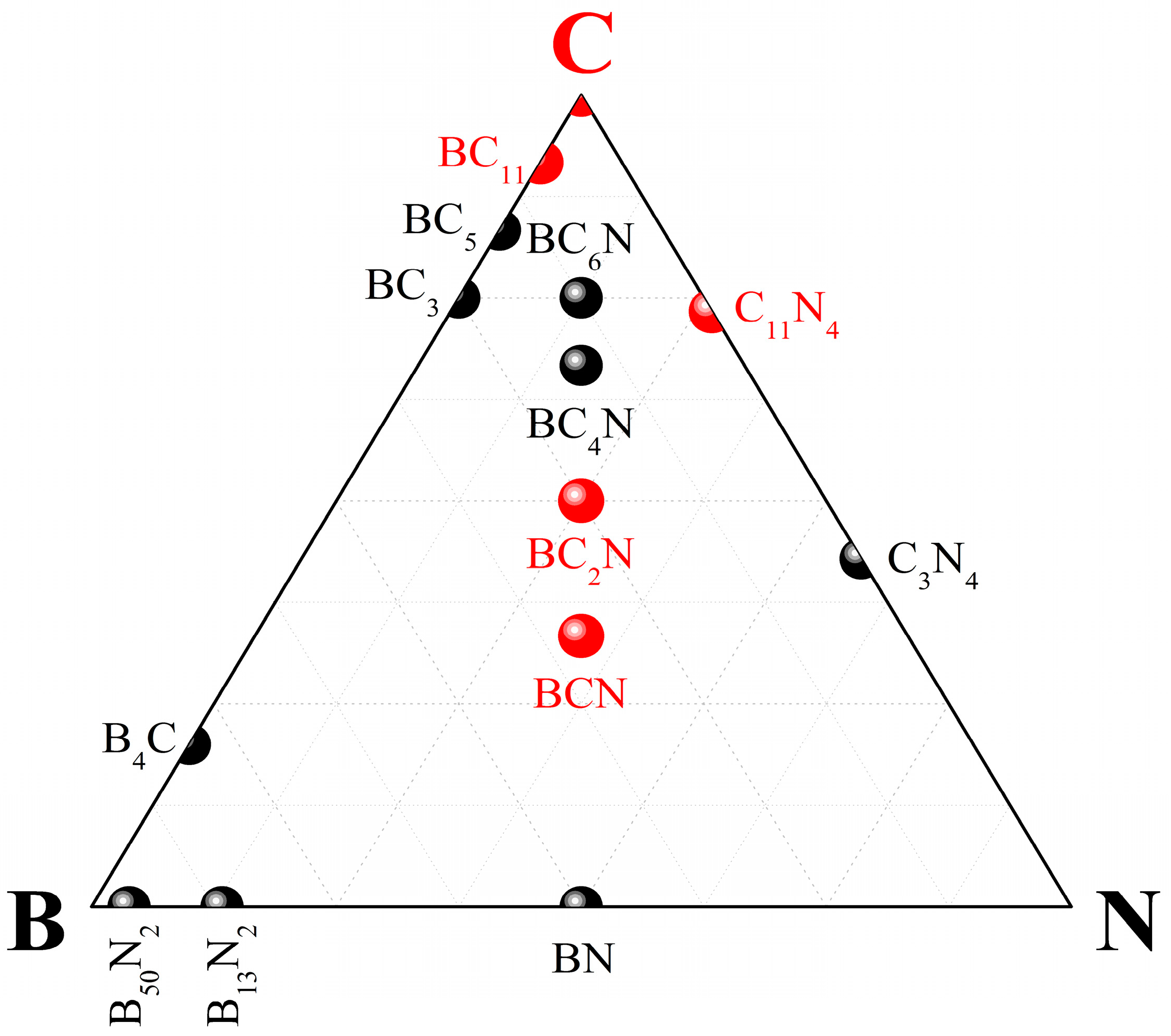
4. Ternary Compounds

Interest in the search for possible ‘hybrid’ structures of carbon and boron nitride and prediction of their properties (mechanical, in particular) has especially grown after the synthesis of ultrahard cubic BC2N [3]. Over the past 20 years, several dozen papers have been published on the subject, but here we will focus only on those that claim the ‘ultrahardness’ (HV ≥ 75 GPa) of the predicted phases. In addition to different BC2N structures [35,36,62,63], ultrahard phases of BCN [64], BC4N [65,66,67], BC6N [68,69] and BC10N [70] compositions have been reported.
Our assessments for orthorhombic (P2221) and trigonal (P3m1) BC2N [35], as well as for novel rhombohedral (R3m) BC2N [36] (Figure 5a), show that they all have Vickers hardness of the order of 75 GPa (see Table 1 and Table 2; the HV values calculated using the thermodynamic model are the most reliable), i.e., almost the same as experimental value 76(4) GPa for cubic BC2N [3,4]. As for the 79.7 GPa hardness claimed for the calculated low-energy zinc-blended BC2N [63], it seems to be overestimated due to the use of the empirical hardness model suggested by Gao et al. [71] (see Table 3).
A similar situation is observed for trigonal (P3m1) [65] and orthorhombic (Imm2) [66] BC4N, and tetragonal (P−42m) [68], rhombohedral (R3m) [68] and monoclinic (Pm and Cm) [69] BC6N. In all these cases, the use of Gao’s model results in a 4–11% hardness overestimation compared to the values that we obtained in the framework of the thermodynamic model of hardness (see Table 3).
The use of another empirical so-called ‘microscopic’ model of hardness suggested by Tian et al. [9] for trigonal BC4N [67] and BC10N [70] leads to even higher (15–20%) overestimations of hardness compared to the thermodynamic model (see Table 3).
In general, according to our estimates, the hardness of the dense ternary phases of the aforementioned compositions varies in the 72–76 GPa range, i.e., they all can be considered as (ultra)hard. Regarding possible equiatomic (B:C:N = 1:1:1) phases, their hardness should be even lower (~70 GPa); see, e.g., HV values for trigonal (P−3m1) and tetragonal (I41md) BCN [64] (Table 3).
The electronic band structure of rhombohedral BC2N [36] (Figure 5c) is characteristic of an insulator, similar to diamond. In fact, they both have a valence electron count multiple of 8 (C2), i.e., 16 (2 × 8) for BC2N and 32 (4 × 8) for diamond (C8).
Below, we discuss in more detail the tetragonal (P42mc) equiatomic boron carbonitride (Figure 5b) recently proposed by us using crystal chemistry rationale and DFT calculations [37].
Compounds containing CN− anions (such as ionic sodium cyanide Na1+CN1−) are called ‘cyanides’. Since boron is a metalloid (i.e., halfway between a metal and non-metal), its combination with nitrogen leads to the equiatomic boron nitride BN that could be expressed as ‘B3+N3−’ considering its ionic-like nature. However, BN is rather a polar covalent compound, as can be inferred from the Pauling electronegativity difference (Δχ). Considering the average electronegativity of CN, <χ(CN)> = (2.55 + 3.44)/2 ~ |3.0|, NaCN has Δχ = 0.9 − 3.0 = |2.1|, whereas BN is characterized by Δχ = 2.04 − 3.44 = |1.4|. For the presently proposed BCN, Δχ = 2.04 − 3.0 = |0.96|, which indicates a decrease in ionic character in the NaCN → BN → BCN row.
In the framework of the crystal chemistry approach, we considered three template structures for BCN: octahedral (CoCN), square-planar (NaCN) and linear (CuCN). The square-planar BC2N2 coordination was found to be the most stable among all three templates in terms of cohesive energy, but despite the relative stability, it remains a non-compact 2D-like structure. Therefore, as a 3D template allowing tetrahedral coordination for B with C and N, and connected BC2N2 tetrahedra, we used tetragonal hexacarbon C6, so-called ‘glitter’ [48], which possesses two types of carbon, tetrahedral C1 and trigonal C2, the latter forming C2–C2 pairs that separate the C1C24 tetrahedra. The structure shown in Figure 6a featuring the charge density projections reveals the two types of carbons in the ‘glitter’ structure, and the corresponding C1C24 tetrahedra (C1: sp3-like carbon). With appropriate substitutions of carbon for boron and nitrogen leading to BCN, the ground state energy configuration of the derived 3D structure was found to be more cohesive than the 2D-like candidate mentioned above.
The resulting BCN (B2C2N2) structure sketched in Figure 6b shows BC2N2 tetrahedra replacing the C1C24 tetrahedra in ‘glitter’ C6, and large differences in charge density distribution as compared to C6, with a charge density concentration skewed toward C–N bonds, and larger intensity on N versus C. Such B → C → N charge transfers are expected from the Pauling electronegativities: χ(B) = 2.04 < χ(C) = 2.55 < χ(N) = 3.44. In the case of BN, three electrons depart from B to N, leading to B3+N3−. In BCN, we equally observe B3+, but the negative ‘3-’ charge is now distributed between C and N, with a larger value on N due to its larger electronegativity versus C, and one obtains B3+C0.316−N2.684−. As follows from our results, cohesive tetragonal BCN is mechanically (elastic constant) and dynamically (phonon) stable. An interesting feature of this phase is that, at a relatively low density (2.783 g/cm3), it is characterized by very high hardness, HV = 65 GPa (i.e., harder than single-crystal cubic boron nitride, with density of 3.486 g/cm3 [72]), highly likely due to the presence of both tetrahedral (sp3) and trigonal (sp2) carbons in its crystal structure. Such mixed hybridizations in tetragonal BCN lead to its weakly metallic behavior, as illustrated by the electronic band structure in Figure 5d, exhibiting a few bands crossing the Fermi level EF.

5. Conclusions

The modern high-pressure synthesis of superhard and, especially, ultrahard phases is a fascinating area of research that could lead to the production of industrially important new materials. However, this field is still in its infancy, and a large number of new super- and ultrahard phases still remain to be discovered. Theoretical predictions play an important role in the present search for advanced materials with desired properties (mechanical, in particular). In this review, we have illustrated, with selected examples, the wealth of (ultra)hard allotropes and phases in the B–C–N ternary system, the theoretical (crystal chemistry considerations combined with quantum mechanics calculations) study of which is a very active area of research.
At the same time, precise calculations of the mechanical properties of superhard materials (hardness, in particular) often lie beyond the capabilities of the most advanced and modern techniques. Thus, we should state that neither widely used empirical models [7,8,9,10,71] nor machine learning [14,70,73] allow us to reliably estimate the hardness of newly predicted superhard and, especially, ultrahard phases. The only model that seems to work in these cases is the thermodynamic model [27]. Moreover, not all theoretically predicted structures exist or can be synthesized. A vivid illustration is the case of hypothetical cubic C3N4 with a bulk modulus claimed to be higher than that of diamond [31]. Despite enormous efforts (new attempts are still being undertaken), this phase has not been synthesized so far, and its expected ultrahardness has never been demonstrated.
Finally, it should be noted that the search for new ultrahard phases is indeed at the frontier of fundamental science and promises great prospects for the creation of new materials that are needed for existing and prospective applications. However, the recent advances in this field clearly show that phases with hardness exceeding that of diamond are highly unlikely, or even impossible [40].

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Computational Framework

Accurate energy-based studies are primarily achieved within the framework of quantum mechanics. The most successful framework is density functional theory (DFT), whose theoretical basis was presented by Hohenberg and Kohn in 1964 [74]. One year later, Kohn and Sham devised the so-called KS equations to efficiently solve the wave equation of the system [75] using computational codes based on DFT. Among the numerous programs, we used the plane-wave Vienna Ab Initio Simulation Package (VASP) code [76,77] with the projector augmented wave (PAW) method [77,78] for the atomic potentials with all valence states, especially in regard to light elements such as boron, carbon and nitrogen. The exchange-correlation effects inherent to DFT were considered with the generalized gradient approximation (GGA) following Perdew, Burke and Ernzerhof (PBE) [79]. The PBE scheme was affirmed by Kilmes et al. as the best suited for quantum calculations of carbon structures [80]. A conjugate-gradient algorithm [81] was used in this computational scheme to relax the atoms onto the ground state. The tetrahedron method with Blöchl et al. corrections [82] and the Methfessel–Paxton scheme [83] were applied for both geometry relaxation and total energy calculations, respectively. Brillouin-zone integrals were approximated using a special k-point sampling scheme by Monkhorst and Pack [84]. The optimization of the structural parameters was performed until the forces on the atoms were less than 0.02 eV/Å, and all stress components below 0.003 eV/Å3. The calculations were converged at an energy cut-off of 500 eV for the plane-wave basis set concerning the k-point integration in the Brillouin zone, with a starting mesh of 6 × 6 × 6 up to 12 × 12 × 12 for the best convergence and relaxation to zero strains. In the post-treatment process of the ground state electronic structures, the electron localization function and the electronic and phonon band structures were computed, visualized and assessed. Calculations of phonon dispersion curves were also carried out to verify the dynamic stability of the proposed structures. The phonon modes were computed via finite displacements of the atoms off their equilibrium positions to obtain the forces from the summation over different configurations. The phonon dispersion curves along the direction of the Brillouin zone were subsequently obtained using the “phonopy” code based on the Python language [85].
Further investigations of the electronic band structure and electron density of states were carried out with the full-potential DFT-built augmented spherical-wave ASW method [86]. Figure 4c,d show the results of band structure calculations for template diamond-like hex-C12 and the resulting trigonal BC11.

References

  1. Bundy, F.; Hall, H.; Strong, H.; Wentorf, R.H. Man-made diamonds. Nature 1955, 176, 51–55. [Google Scholar] [CrossRef]
  2. Wentorf, R.H. Cubic form of boron nitride. J. Chem. Phys. 1957, 26, 956. [Google Scholar] [CrossRef]
  3. Solozhenko, V.L.; Andrault, D.; Fiquet, G.; Mezouar, M.; Rubie, D. Synthesis of superhard cubic BC2N. Appl. Phys. Lett. 2001, 78, 1385–1387. [Google Scholar] [CrossRef]
  4. Solozhenko, V.L.; Dub, S.; Novikov, N. Mechanical properties of cubic BC2N, a new superhard phase. Diam. Relat. Mater. 2001, 10, 2228–2231. [Google Scholar] [CrossRef]
  5. Solozhenko, V.L.; Kurakevych, O.; Le Godec, D.A.Y.; Mezouar, M. Ultimate metastable solubility of boron in diamond: Synthesis of superhard diamondlike BC5. Phys. Rev. Lett. 2009, 102, 015506. [Google Scholar] [CrossRef]
  6. Le Godec, Y.; Courac, A.; Solozhenko, V.L. High-pressure synthesis of superhard and ultrahard materials. J. Appl. Phys. 2019, 126, 151102. [Google Scholar] [CrossRef]
  7. Gao, F. Theoretical model of intrinsic hardness. Phys Rev. B 2006, 73, 132104. [Google Scholar] [CrossRef]
  8. Chen, X.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
  9. Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
  10. Mazhnik, E.; Oganov, A. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. [Google Scholar] [CrossRef]
  11. Yao, H.; Ouyang, L.; Ching, W.-Y. Ab initio calculation of elastic constants of ceramic crystals. J. Am. Ceram. Soc. 2007, 90, 3194–3204. [Google Scholar] [CrossRef]
  12. Perger, W.; Criswell, J.; Civalleri, B.; Dovesi, R. Ab-initio calculation of elastic constants of crystalline systems with the CRYSTAL code. Comput. Phys. Commun. 2009, 180, 1753–1759. [Google Scholar] [CrossRef]
  13. Kvashnin, A.; Allahyari, Z.; Oganov, A. Computational discovery of hard and superhard materials. J. Appl. Phys. 2019, 126, 040901. [Google Scholar] [CrossRef]
  14. Avery, P.; Wang, X.; Oses, C.; Gossett, E.; Proserpio, D.; Toher, C.; Curtarolo, S.; Zurek, E. Predicting superhard materials via a machine learning informed evolutionary structure search. NPJ Comput. Mater. 2019, 5, 89. [Google Scholar] [CrossRef]
  15. Allahyari, Z.; Oganov, A. Coevolutionary search for optimal materials in the space of all possible compounds. NPJ Comput. Mater. 2020, 6, 55. [Google Scholar] [CrossRef]
  16. Zhang, S.; He, J.; Zhao, Z.; Yu, D.; Tian, Y. Discovery of superhard materials via CALYPSO methodology. Chin. Phys. B 2019, 28, 106104. [Google Scholar] [CrossRef]
  17. Oganov, A.; Glass, C. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
  18. Glass, C.; Oganov, A.; Hansen, N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Commun. 2006, 175, 713–720. [Google Scholar] [CrossRef]
  19. Oganov, A.; Chen, J.; Gatti, C.; Ma, Y.; Ma, Y.; Glass, C.; Liu, Z.; Yu, T.; Kurakevych, O.; Solozhenko, V.L. Ionic high-pressure form of elemental boron. Nature 2009, 457, 863–867. [Google Scholar] [CrossRef]
  20. Oganov, A.; Solozhenko, V.L. Boron: A hunt for superhard polymorphs. J. Superhard Mater. 2009, 31, 285–291. [Google Scholar] [CrossRef]
  21. Németh, P.; Garvie, L.; Aoki, T.; Dubrovinskaia, N.; Dubrovinsky, L.; Buseck, P. Lonsdaleite is faulted and twinned cubic diamond and does not exist as a discrete material. Nat. Commun. 2014, 5, 5447. [Google Scholar] [CrossRef] [PubMed]
  22. Hoffmann, R.; Kabanov, A.; Golov, A.; Proserpio, D. Homo Citans and carbon allotropes: For an ethics of citation. Angew. Chem. Int. Ed. 2016, 55, 10962–10976, Samara Carbon Allotrope Database. Available online: http://sacada.sctms.ru (accessed on 8 December 2022). [CrossRef] [PubMed]
  23. Zhao, C.-X.; Niu, C.-Y.; Qin, Z.-J.; Ren, X.; Wang, J.-T.; Cho, J.-H.; Jia, Y. H18 carbon: A new metallic phase with sp2-sp3 hybridized bonding network. Sci. Rep. 2016, 6, 21879. [Google Scholar] [CrossRef] [PubMed]
  24. Tennyson, J. Molecules in Space. In Handbook of Molecular Physics and Quantum Chemistry; John Wiley & Sons: Chichester, UK, 2003; Volume 3, part III, p. 358. [Google Scholar]
  25. Matar, S.F.; Etourneau, J.; Solozhenko, V.L. First-principles investigations of tricarbon: From the isolated C3 molecule to a novel ultra-hard anisotropic solid. Carbon Trends 2021, 6, 100132. [Google Scholar] [CrossRef]
  26. Voigt, W. Über die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annal. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
  27. Mukhanov, V.; Kurakevych, O.; Solozhenko, V.L. The interrelation between hardness and compressibility of substances and their structure and thermodynamic properties. J. Superhard Mater. 2008, 30, 368–378. [Google Scholar] [CrossRef]
  28. Lyakhov, A.; Oganov, A. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 2011, 84, 092103. [Google Scholar] [CrossRef]
  29. Matar, S.F.; Solozhenko, V.L. Novel ultrahard sp2/sp3 hybrid carbon allotrope from crystal chemistry and first principles: Body-centered tetragonal C6 (′neoglitter′). ChemRxiv 2022. [Google Scholar] [CrossRef]
  30. Liu, A.; Wentzcovitch, R. Stability of carbon nitride solids. Phys. Rev. B 1994, 50, 10362–10365. [Google Scholar] [CrossRef]
  31. Teter, D.; Hemley, R. Low-compressibility carbon nitrides. Science 1996, 271, 53–55. [Google Scholar] [CrossRef]
  32. Yao, Y.; Tse, J.; Klug, D. Crystal and electronic structure of superhard BC5: First-principles structural optimizations. Phys. Rev. B 2009, 80, 094106. [Google Scholar] [CrossRef]
  33. Liu, H.; Li, Q.; Zhu, L.; Ma, Y. Superhard polymorphs of diamond-like BC7. Solid State Comm. 2011, 151, 716–719. [Google Scholar] [CrossRef]
  34. Matar, S.F.F. Novel trigonal BC11 as model structure of heavily doped diamond: Crystal chemistry rationale and first principles characterizations. Diam. Relat. Mater. 2022, 123, 108842. [Google Scholar] [CrossRef]
  35. Mattesini, M.; Matar, S.F. First-principles characterization of new ternary heterodiamond BC2N phases. Comput. Mater. Sci. 2001, 20, 107–119. [Google Scholar] [CrossRef]
  36. Matar, S.F.; Solozhenko, V.L. Crystal chemistry and ab initio prediction of ultrahard rhombohedral B2N2 and BC2N. Solid State Sci. 2021, 118, 106667. [Google Scholar] [CrossRef]
  37. Matar, S.F.; Solozhenko, V.L. Novel superhard tetragonal BCN from crystal chemistry and first principles. Materialia 2022, 26, 101581. [Google Scholar] [CrossRef]
  38. Ownby, P.; Yang, X.; Liu, J. Calculated X-ray diffraction data for diamond polytypes. J. Am. Ceram. Soc. 1992, 75, 1876–1883. [Google Scholar] [CrossRef]
  39. Bindzus, N.; Straasø, T.; Wahlberg, N.; Becker, J.; Bjerg, L.; Lock, N.; Dippel, A.-C.; Iversen, B. Experimental determination of core electron deformation in diamond. Acta Cryst. A 2014, 70, 39–48. [Google Scholar] [CrossRef]
  40. Brazhkin, V.; Solozhenko, V.L. Myths about new ultrahard phases: Why materials that are significantly superior to diamond in elastic moduli and hardness are impossible. J. Appl. Phys. 2019, 125, 130901. [Google Scholar] [CrossRef]
  41. Manyali, G.; Warmbier, R.; Quandt, A.; Lowther, J. Ab initio study of elastic properties of super hard and graphitic structures of C3N4. Comput. Mater. Sci. 2013, 69, 299–303. [Google Scholar] [CrossRef]
  42. Yang, X.; Liu, S.; Qin, J.Z.J.; Du, M.; Yang, D.; Li, X.; Liu, B.; Shan, C.-X. Orthorhombic C14 carbon: A novel superhard sp3 carbon allotrope. Carbon 2020, 156, 309–312. [Google Scholar] [CrossRef]
  43. Fan, Q.; Liu, H.; Jiang, L.; Yu, X.; Zhang, W.; Yun, S. Two orthorhombic superhard carbon allotropes: C16 and C24. Diam. Relat. Mater. 2021, 116, 108426. [Google Scholar] [CrossRef]
  44. Fan, Q.; Liu, H.; Yang, R.; Yu, X.; Zhang, W.; Yun, S. An orthorhombic superhard carbon allotrope: Pmma C24. J. Solid State Chem. 2021, 300, 122260. [Google Scholar] [CrossRef]
  45. Chen, J.; Ying, P.; Gao, Y.; Wei, X.; Li, B.; Huan, Q.; Luo, K. Orthorhombic C36: A sp2–sp3 carbon with pressure-induced metallization and superconductivity. J. Mater. Sci. 2021, 56, 17665–17673. [Google Scholar] [CrossRef]
  46. Solozhenko, V.L.; Le Godec, Y. A hunt for ultrahard materials. J. Appl. Phys. 2019, 126, 230401. [Google Scholar] [CrossRef]
  47. Wei, Q.; Zhang, Q.; Zhang, M.-G.; Yan, H.-Y.; Guo, L.-X.; Wei, B. A novel hybrid sp-sp2 metallic carbon allotrope. Front. Phys. 2018, 13, 136105. [Google Scholar] [CrossRef]
  48. Bucknum, M.; Hoffmann, R. A hypothetical dense 3,4-connected carbon net and related B2C and CN2 nets built from 1,4-cyclohexadienoid units. J. Am. Chem. Soc. 1994, 116, 11456–11464. [Google Scholar] [CrossRef]
  49. Kurakevych, O.; Solozhenko, V.L. Rhombohedral boron subnitride, B13N2, by X-ray powder diffraction. Acta Crystallogr. C 2007, 63, i80–i82. [Google Scholar] [CrossRef]
  50. Solozhenko, V.L.; Bushlya, V. Mechanical properties of superhard boron subnitride B13N2. J. Superhard Mater. 2017, 39, 422–426. [Google Scholar] [CrossRef]
  51. Cherednichenko, K.; Solozhenko, V.L. Structure and equation of state of tetragonal boron subnitride B50N2. J. Appl. Phys. 2017, 122, 155901. [Google Scholar] [CrossRef]
  52. Solozhenko, V.L.; Kurakevych, O.; Le Godec, Y. Creation of nanostuctures by extreme conditions: High-pressure synthesis of ultrahard nanocrystalline cubic boron nitride. Adv. Mater. 2012, 24, 1540–1544. [Google Scholar] [CrossRef] [PubMed]
  53. Solozhenko, V.L.; Bushlya, V.; Zhou, J. Mechanical properties of ultra-hard nanocrystalline cubic boron nitride. J. Appl. Phys. 2019, 126, 075107. [Google Scholar] [CrossRef]
  54. Liu, A.; Cohen, M. Prediction of new low compressibility solids. Science 1989, 245, 841–842. [Google Scholar] [CrossRef] [PubMed]
  55. Matar, S.F.; Mattesini, M. Ab initio search of carbon nitrides, isoelectronic with diamond, likely to lead to new ultra-hard materials. Comptes Rendus De L’académie Des Sci. 2001, 4, 255–272. [Google Scholar] [CrossRef]
  56. Mattesini, M.; Matar, S.F. Density-functional theory investigation of hardness, stability, and electron-energy-loss spectra of carbon nitrides with C11N4 stoichiometry. Phys. Rev. B 2002, 65, 075110. [Google Scholar] [CrossRef]
  57. Betranhandy, E.; Matar, S.F. A model study for the breaking of cyanogen out of CNx within DFT. Diam. Relat. Mater. 2006, 15, 1609–1613. [Google Scholar] [CrossRef]
  58. Matar, S.F.; Solozhenko, V.L. The simplest dense carbon allotrope: Ultra-hard body-centered tetragonal C4. J. Solid State Chem. 2022, 314, 123424. [Google Scholar] [CrossRef]
  59. Werheit, H.; Leithe-Jasper, A.; Tanaka, T.; Rotter, H.; Schwetz, K. Some properties of single-crystal boron carbide. J. Solid State Chem. 2004, 177, 575–579. [Google Scholar] [CrossRef]
  60. Matar, S.F.; Solozhenko, V.L. Ultra-hard rhombohedral carbon by crystal chemistry and ab initio investigations. J. Solid State Chem. 2021, 302, 122354. [Google Scholar] [CrossRef]
  61. Liu, Z.; He, J.; Yang, J.; Guo, X.; Sun, H.; Wang, H.-T.; Wu, E.; Tian, Y. Prediction of a sandwichlike conducting superhard boron carbide: First-principles calculations. Phys. Rev. B 2006, 73, 172101. [Google Scholar] [CrossRef]
  62. Kim, E.; Pang, T.; Utsumi, W.; Solozhenko, V.L.; Zhao, Y. Cubic phases of BC2N: A first-principles study. Phys. Rev. B 2007, 75, 184115. [Google Scholar] [CrossRef]
  63. Fan, X.; Wu, H.; Shen, Z.; Kuo, J.-L. A first-principle study on the structure, stability and hardness of cubic BC2N. Diam. Relat. Mater. 2009, 18, 1278–1282. [Google Scholar] [CrossRef]
  64. Wang, H.; Qu, N.; Li, Q.; Li, Y.; Li, Z.; Gou, H.; Gao, F. First-principles calculations on two superhard BCN allotropes: P−3m1-BCN and I41md-BCN. Comput. Mater. Sci. 2020, 184, 109869. [Google Scholar] [CrossRef]
  65. Luo, X.; Zhou, X.-F.; Liu, Z.; He, J.; Xu, B.; Yu, D.; Wang, H.-T.; Tian, Y. Refined crystal structure and mechanical properties of superhard BC4N crystal: First-principles calculations. J. Phys. Chem. C 2008, 112, 9516–9519. [Google Scholar] [CrossRef]
  66. Qu, N.-R.; Wang, H.; Li, Q.; Li, Z.-P.; Gao, F.-M. An orthorhombic phase of superhard o-BC4N. Chin. Phys. Lett. 2019, 36, 036201. [Google Scholar] [CrossRef]
  67. Zhu, L.; Ma, M.; Gao, Q.; Li, B.; Wei, X.; Xiong, M.; Zhao, Z.; He, J. Prediction of a series of superhard BC4N structures. Diam. Relat. Mater. 2022, 127, 109192. [Google Scholar] [CrossRef]
  68. Luo, X.; Guo, X.; Liu, Z.; He, J.; Yu, D.; Tian, Y.; Wang, H.-T. Ground-state properties and hardness of high density BC6N phases originating from diamond structure. J. Appl. Phys. 2007, 101, 083505. [Google Scholar] [CrossRef]
  69. Qu, N.-R.; Wang, H.-C.; Li, Q.; Li, Y.-D.; Li, Z.-P.; Gou, H.-Y.; Gao, F.-M. Surperhard monoclinic BC6N allotropes: First-principles investigations. Chin. Phys. B 2019, 28, 096201. [Google Scholar] [CrossRef]
  70. Chen, W.-C.; Schmidt, J.; Yan, D.; Vohra, Y.; Chen, C.-C. Machine learning and evolutionary prediction of superhard B-C-N compounds. NPJ Comput. Mater. 2021, 7, 114. [Google Scholar] [CrossRef]
  71. Gao, F.; He, J.; Wu, E.; Liu, S.; Yu, D.; Li, D.; Zhang, S.; Tian, Y. Hardness of covalent crystals. Phys. Rev. Lett. 2003, 91, 015502. [Google Scholar] [CrossRef]
  72. Solozhenko, V.L.; Chernyshev, V.; Fetisov, G.; Rybakov, V.; Petrusha, I. Structure analysis of the cubic boron nitride crystals. J. Phys. Chem. Solids 1990, 51, 1011–1012. [Google Scholar] [CrossRef]
  73. Mazhnik, E.; Oganov, A. Application of machine learning methods for predicting new superhard materials. J. Appl. Phys. 2020, 128, 075102. [Google Scholar] [CrossRef]
  74. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
  75. Kohn, W.; Sham, L. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
  76. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
  77. Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented wave. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  78. Blöchl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  79. Perdew, J.; Burke, K.; Ernzerhof, M. The Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  80. Klimeš, J.; Bowler, D.A. Michaelides, Van der Waals density functionals applied to solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar] [CrossRef]
  81. Press, W.; Flannery, B.; Teukolsky, S.; Vetterling, W. Numerical Recipes, 2nd ed.; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
  82. Blöchl, P.; Jepsen, O.; Anderson, O. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
  83. Methfessel, M.; Paxton, A. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
  84. Monkhorst, H.; Pack, J. Special k-points for Brillouin Zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  85. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  86. Eyert, V. Basic notions and applications of the augmented spherical wave method. Int. J. Quantum Chem. 2000, 77, 1007–1031. [Google Scholar] [CrossRef]
Materials 16 00886 g001
Figure 1. Superhard phases of the B–C–N ternary system. Ultrahard phases discussed in the present paper are shown in red.
Figure 1. Superhard phases of the B–C–N ternary system. Ultrahard phases discussed in the present paper are shown in red.
Materials 16 00886 g001
Materials 16 00886 g002
Figure 2. Novel ultrahard carbon allotropes: ‘tricarbons’—rhombohedral C3 (a) and hexagonal C6 (b) (both structures are in hexagonal setting); and tetragonal C6 ‘neoglitter’ (c).
Figure 2. Novel ultrahard carbon allotropes: ‘tricarbons’—rhombohedral C3 (a) and hexagonal C6 (b) (both structures are in hexagonal setting); and tetragonal C6 ‘neoglitter’ (c).
Materials 16 00886 g002
Materials 16 00886 g003
Figure 3. Novel ultrahard carbon subnitride: crystal structures of template diamond-like C16 (a) and tetragonal C11N4 (b); electronic band structure of C11N4 (c).
Figure 3. Novel ultrahard carbon subnitride: crystal structures of template diamond-like C16 (a) and tetragonal C11N4 (b); electronic band structure of C11N4 (c).
Materials 16 00886 g003
Materials 16 00886 g004
Figure 4. Ultrahard carbon-rich boron carbide: crystal structures of template hexagonal C12 (a) and trigonal BC11 (b) with charge density distributions, and electronic band structures of insulating hex-C12 (c) and metallic BC11 (d). Boron atoms are shown by green spheres.
Figure 4. Ultrahard carbon-rich boron carbide: crystal structures of template hexagonal C12 (a) and trigonal BC11 (b) with charge density distributions, and electronic band structures of insulating hex-C12 (c) and metallic BC11 (d). Boron atoms are shown by green spheres.
Materials 16 00886 g004
Materials 16 00886 g005
Figure 5. Crystal structures (a,b) and electronic band structures (c,d) of rhombohedral BC2N and tetragonal BCN. Boron, carbon and nitrogen atoms are shown by olive, white and blue spheres, respectively.
Figure 5. Crystal structures (a,b) and electronic band structures (c,d) of rhombohedral BC2N and tetragonal BCN. Boron, carbon and nitrogen atoms are shown by olive, white and blue spheres, respectively.
Materials 16 00886 g005
Materials 16 00886 g006
Figure 6. Crystal structures of template ‘glitter’ C6 (a) and tetragonal BCN (b) with charge density distributions. Boron, carbon and nitrogen atoms are shown by green, brown and grey spheres, respectively.
Figure 6. Crystal structures of template ‘glitter’ C6 (a) and tetragonal BCN (b) with charge density distributions. Boron, carbon and nitrogen atoms are shown by green, brown and grey spheres, respectively.
Materials 16 00886 g006
Table 1. (Ultra)hard phases of the B–C–N system: lattice parameters, density (ρ), Vickers hardness (HV) and bulk moduli (B0) calculated in the framework of thermodynamic model of hardness [27].
Table 1. (Ultra)hard phases of the B–C–N system: lattice parameters, density (ρ), Vickers hardness (HV) and bulk moduli (B0) calculated in the framework of thermodynamic model of hardness [27].
Space Groupa = b (Å)c (Å)ρ (g/cm3)HV (GPa)B0 (GPa)
DiamondFd−3m3.56661 ‡3.51798 pw445 §
LonsdaleiteP63/mmc2.5221 †4.1186 †3.51697 pw443 pw
rh-C3#166 [25]R−3m2.490010.41003.21189406
hex-C6#194 [25]P63/mmc2.49506.96103.18987404
tet-C6#119 [29]I−4m22.46666.43203.05885385
c-C3N4#215 [30]P−43m3.43003.78871 pw421 pw
c-C3N4#220 [31]I−43d5.39733.88973 pw430 pw
tet-C11N4#115 [pw]P−4m24.95263.52023.61876408
tet-BC5#119 [32]I−4m22.525011.32303.26070 pw350 pw
c-BC7#215 [33]P−43m3.62053.32072 pw358 pw
trig-BC11#156 [34]P3m12.538112.59553.37883 pw395 pw
o-BC2N #17 [35]P22213.5536/3.59863.55283.57073 pw381 pw
trig-BC2N #156 [35]P3m12.49554.19233.58774 pw384 pw
rh-BC2N #160 [36]R3m2.538212.60543.46075426 pw
tet-BCN #105 [37]P42mc2.70476.00732.78365282
† Ref. [38]; ‡ Ref. [39]; § Ref. [40]; pw present work.
Table 2. Mechanical properties of (ultra)hard phases of the B–C–N system: Vickers hardness (HV), bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν) and fracture toughness (KIc).
Table 2. Mechanical properties of (ultra)hard phases of the B–C–N system: Vickers hardness (HV), bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν) and fracture toughness (KIc).
HVBGVE **ν **KIc‡
T *LO †MO ‡CN §B0 *BV
GPa MPa·m½
Diamond [pw]989010093445 ††530 ††11380.0746.4
Lonsdaleite [pw]9790999444343252111150.0706.2
rh-C3#166 [25]898373 pw65 pw4063944029000.1195.1
hex-C6#194 [25]878273 pw65 pw4043924008950.1195.1
tet-C6#119 [29]857868 pw633853663758390.1184.7
c-C3N4#215 [30]71 pw63 pw68 pw58 pw421 pw425397 ***908 pw0.144 pw7.1 pw
c-C3N4#220 [31]73 pw74 pw56 pw48 pw430 pw487 §§393 §§930 §§0.18 §§ 9.1 pw
tet-C11N4#115 [pw]7678878240840646110030.0885.5
tet-BC5#119 [32]70 pw62 pw68 pw62 pw350 pw376379851 pw0.123 pw4.9 pw
c-BC7#215 [33]72 pw59 pw75 pw70 pw358 pw375403890 pw0.104 pw4.8 pw
trig-BC11#156 [34]83 pw81 pw75 pw68395 pw405414926 pw0.119 pw5.3 pw
o-BC2N #17 [35]73 pw69 pw88 pw76 pw381 pw4594821071 pw0.111 pw6.4 pw
trig-BC2N #156 [35]74 pw58 pw––––384 pw420––––––––
rh-BC2N #160 [36]7574 pw9084426 pw41247610310.0835.7
tet-BCN #105 [37]656135 pw362822802325450.1754.2
* Thermodynamic model [27]; † Lyakhov–Oganov model [28]; ‡ Mazhnik–Oganov model [10]; § Chen–Niu model [8]; ** E and ν values calculated using isotropic approximation; †† Ref. [40]; *** Calculated from elastic moduli Cij [30] using Voigt’s approach [26]; §§ Ref. [41]; pw present work.
Table 3. Vickers hardness of hypothetical ternary B–C–N phases calculated using different models.
Table 3. Vickers hardness of hypothetical ternary B–C–N phases calculated using different models.
HV (GPa)
Gao’s Model *Tian’s Model †Thermodynamic Model ‡
c-BC2N [63]79.7–75 pw
trig-BC4N (P3m1) [65]84.3–76 pw
o-BC4N (Imm2) [66]78.7–73 pw
trig-BC4N [67]–87.573 pw
tet-BC6N (P−42m) [68]79.9–75 pw
rh-BC6N (R3m) [68]79.1–76 pw
m-BC6N (Pm) [69]77.4–72 pw
m-BC6N (Cm) [69]80.6–73 pw
trig-BC10N (P3m1) [70]–8775 pw
tet-BCN (I41md) [64]61.8–70 pw
trig-BCN (P−3m1) [64]68.5–69 pw
* Ref. [71]; † Ref. [9]; ‡ Ref. [27]; pw present work.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Solozhenko, V.L.; Matar, S.F. Prediction of Novel Ultrahard Phases in the B–C–N System from First Principles: Progress and Problems. Materials 2023, 16, 886. https://doi.org/10.3390/ma16020886

AMA Style

Solozhenko VL, Matar SF. Prediction of Novel Ultrahard Phases in the B–C–N System from First Principles: Progress and Problems. Materials. 2023; 16(2):886. https://doi.org/10.3390/ma16020886

Chicago/Turabian Style

Solozhenko, Vladimir L., and Samir F. Matar. 2023. "Prediction of Novel Ultrahard Phases in the B–C–N System from First Principles: Progress and Problems" Materials 16, no. 2: 886. https://doi.org/10.3390/ma16020886

APA Style

Solozhenko, V. L., & Matar, S. F. (2023). Prediction of Novel Ultrahard Phases in the B–C–N System from First Principles: Progress and Problems. Materials, 16(2), 886. https://doi.org/10.3390/ma16020886

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop