Phonon Structure, Infra-Red and Raman Spectra of Li2MnO3 by First-Principles Calculations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Synthesis and Characterization
2.2. Calculation Details
3. Results and Discussion
3.1. Characterization of the Li2MnO3 Powder Material
3.2. Optimized Crystal Structure and Electronic Properties of the Li2MnO3
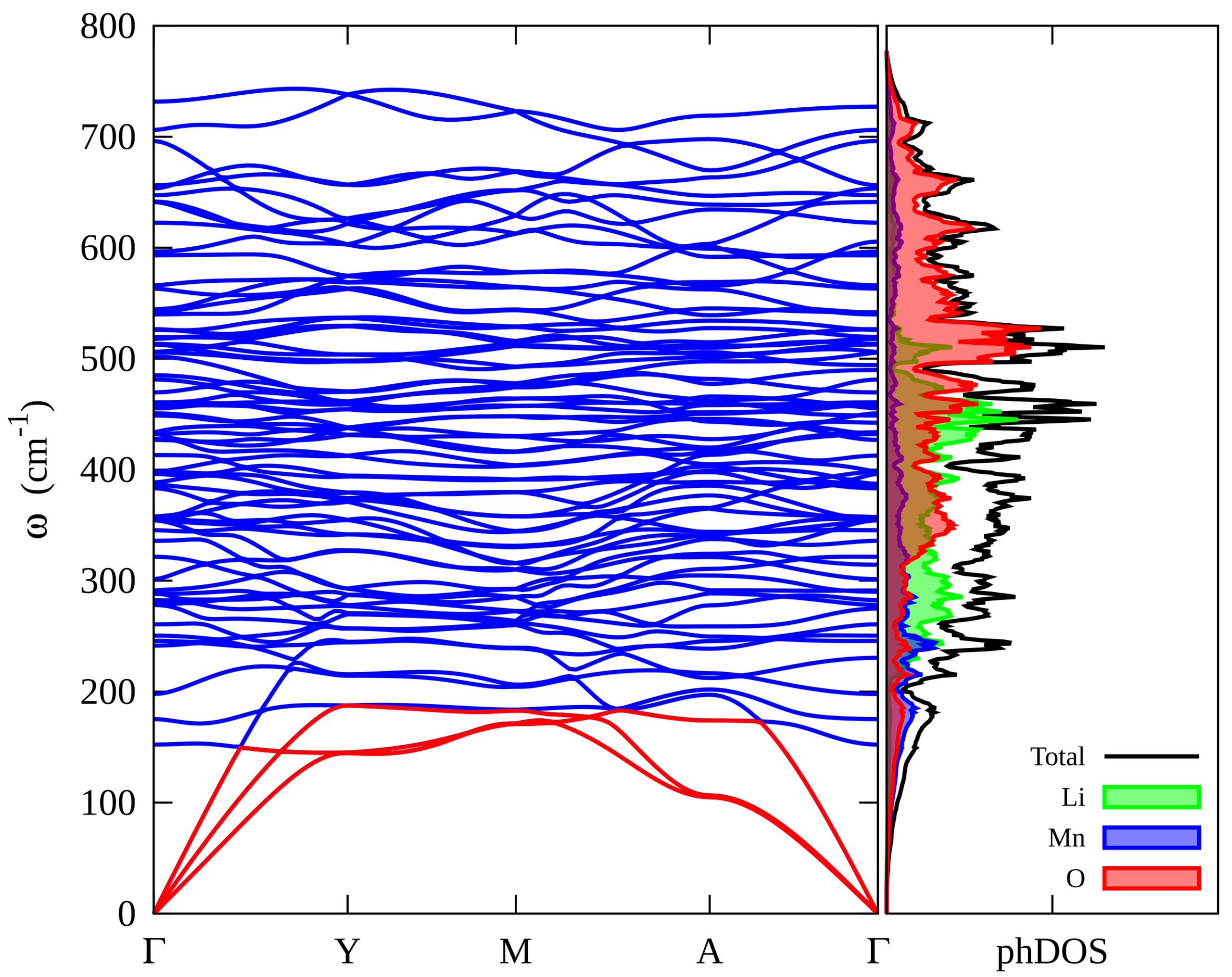
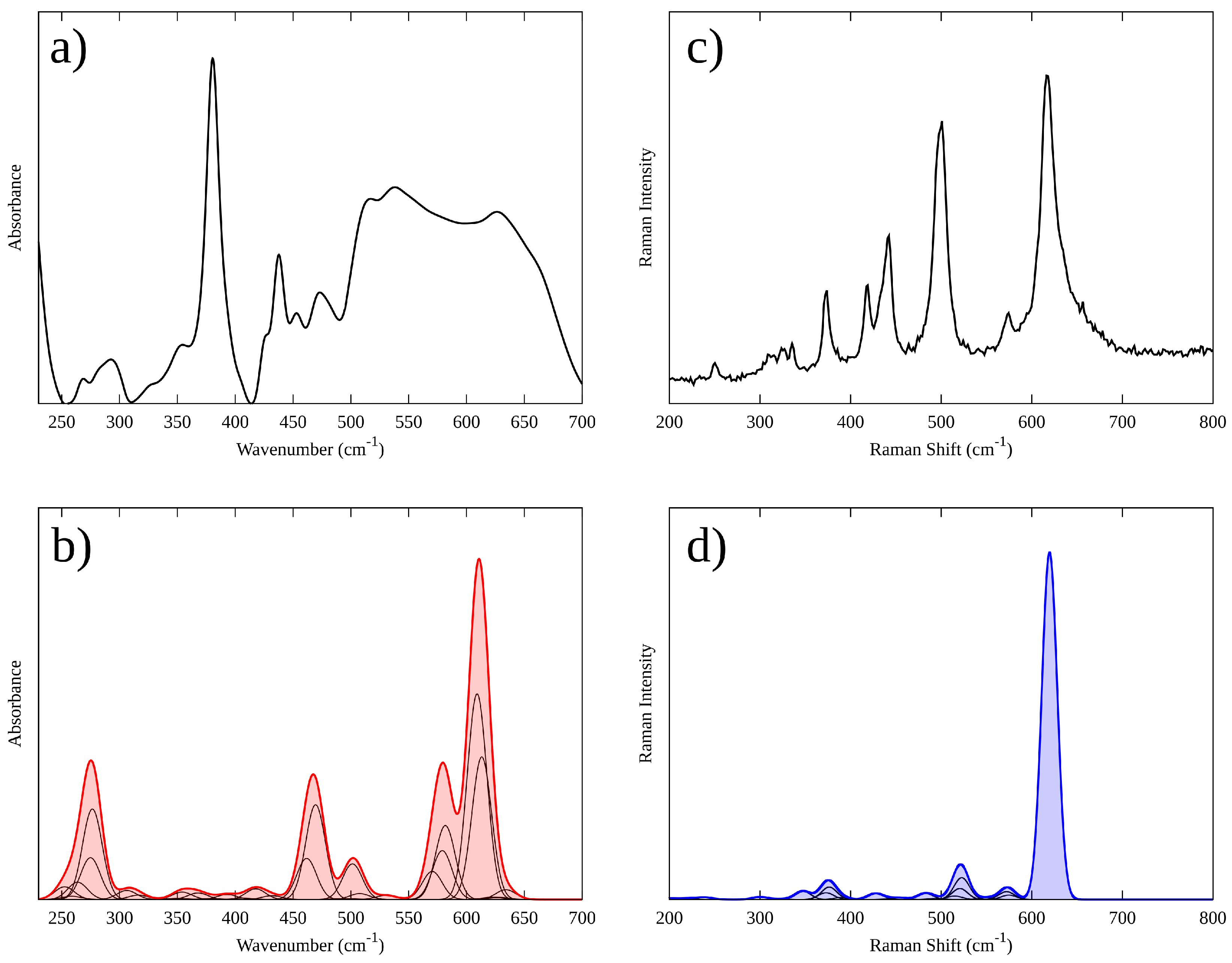
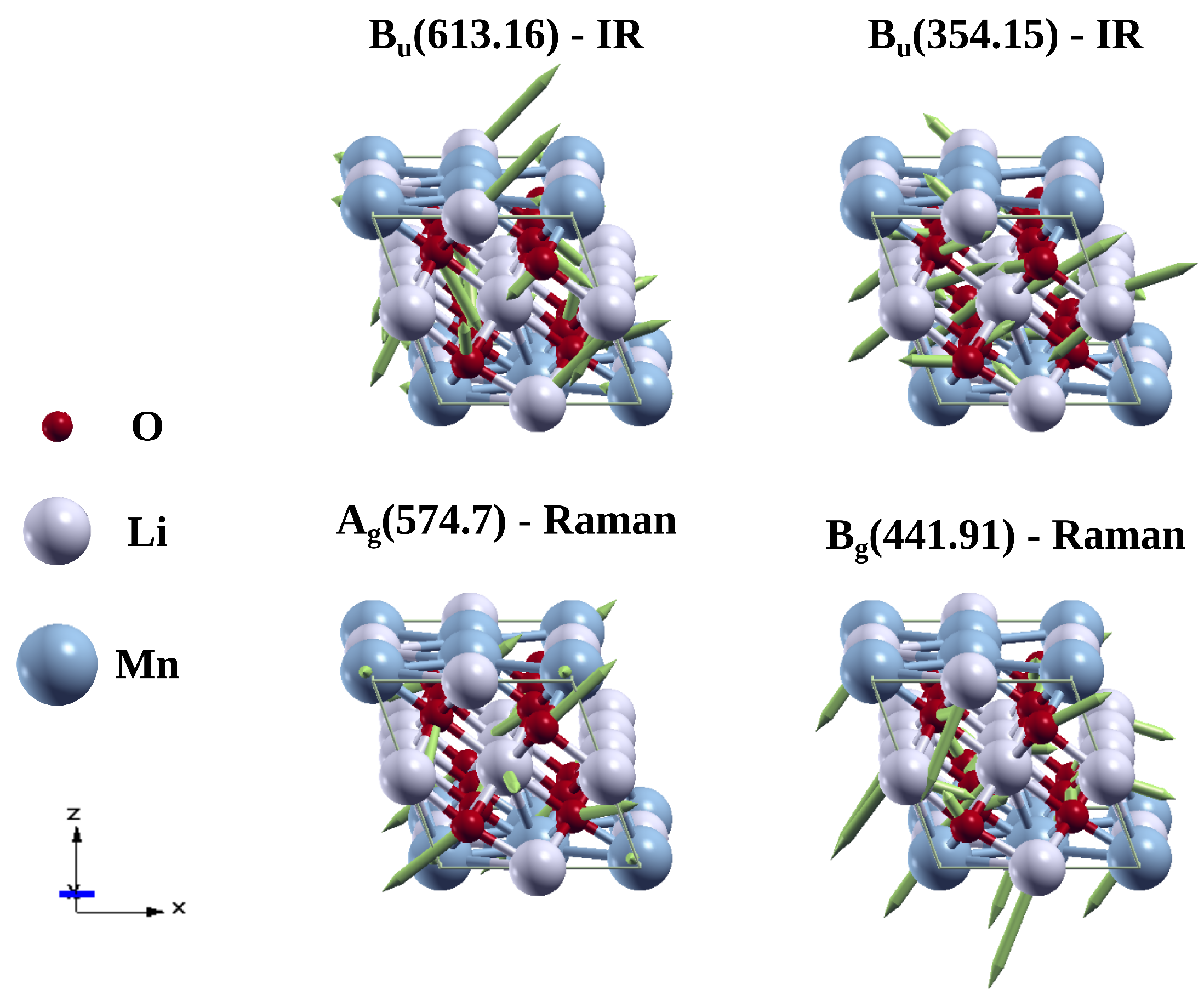
3.3. Vibrational Properties of Li2MnO3
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| DFPT | Density Functional Perturbation Theory |
| LMO | Lithium Manganese Oxide |
| LDA | Local Density Approximation |
| DOS | Density of States |
| IR | Infrared |
References
- Karrech, A.; Azadi, M.A.; Elchalakani, M.; Shahin, M.A.; Seibi, A.C. A review on methods for liberating lithium from pegmatities. Miner. Eng. 2020, 145, 106085. [Google Scholar] [CrossRef]
- Potapenko, A.V.; Kirillov, S.A. Lithium manganese spinel materials for high-rate electrochemical applications. J. Energy Chem. 2014, 23, 543–558. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, S.; Chen, J.; Gao, M.; Liu, Y.; Zhu, T.; Jiang, Y. Li- and Mn-rich layered oxide cathode materials for lithium-ion batteries: A review from fundamentals to research progress and applications. Mol. Syst. Des. Eng. 2018, 3, 748–803. [Google Scholar] [CrossRef]
- Yu, H.; Naidu, G.; Zhang, C.; Wang, C.; Razmjou, A.; Han, D.S.; He, T.; Shon, H. Metal-based adsorbents for lithium recovery from aqueous resources. Desalination 2022, 539, 115951. [Google Scholar] [CrossRef]
- Xu, X.; Chen, Y.; Wan, P.; Gasem, K.; Wang, K.; He, T.; Adidharma, H.; Fan, M. Extraction of lithium with functionalized lithium ion-sieves. Prog. Mater. Sci. 2016, 84, 276–313. [Google Scholar] [CrossRef]
- Marincaş, A.H.; Goga, F.; Dorneanu, S.; Ilea, P. Review on synthesis methods to obtain LiMn2O4-based cathode materials for Li-ion batteries. J. Solid State Electrochem. 2020, 24, 473–497. [Google Scholar] [CrossRef]
- Mabokela, T.; Nwanya, A.; Ndipingwi, M.; Kaba, S.; Ekwere, P.; Werry, S.; Ikpo, C.; Modibane, K.; Iwuoha, E. Review—Recent Advances on High-Capacity Li Ion-Rich Layered Manganese Oxide Cathodes. J. Electrochem. Soc. 2021, 168, 070530. [Google Scholar] [CrossRef]
- Pulido, R.; Naveas, N.; Graber, T.; Martin-Palma, R.J.; Agulló-Rueda, F.; Brito, I.; Morales, C.; Soriano, L.; Pascual, L.; Marini, C.; et al. Hydrothermal control of the lithium-rich Li2MnO3 phase in lithium manganese oxide nanocomposites and their application as precursors for lithium adsorbents. Dalton Trans. 2021, 50, 10765–10778. [Google Scholar] [CrossRef]
- Li, Y.; Makita, Y.; Lin, Z.; Lin, S.; Nagaoka, N.; Yang, X. Synthesis and characterization of lithium manganese oxides with core-shell Li4Mn5O12@Li2MnO3 structure as lithium battery electrode materials. Solid State Ionics 2011, 196, 34–40. [Google Scholar] [CrossRef]
- Johnson, C.; Li, N.; Vaughey, J.; Hackney, S.; Thackeray, M. Lithium–manganese oxide electrodes with layered–spinel composite structures xLi2MnO3·(1 − x)Li1+yMn2-yO4 (0 < x < 1, 0 ≤ y ≤ 0.33) for lithium batteries. Electrochem. Commun. 2005, 7, 528–536. [Google Scholar] [CrossRef]
- Pulido, R.; Naveas, N.; Martín-Palma, R.J.; Graber, T.; Brito, I.; Hernández-Montelongo, J.; Manso Silván, M. Experimental and density functional theory study of the Li+ desorption in spinel/layered lithium manganese oxide nanocomposites using HCl. Chem. Eng. J. 2022, 441, 136019. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, X.; Wang, C.; Bi, H.; Zhang, J.; Li, S.; Wang, M.; Che, R. Insight into the atomic structure of Li2MnO3 in Li-rich Mn-based cathode materials and the impact of its atomic arrangement on electrochemical performance. J. Mater. Chem. A 2017, 5, 11214–11223. [Google Scholar] [CrossRef]
- Xiao, R.; Li, H.; Chen, L. Density Functional Investigation on Li2MnO3. Chem. Mater. 2012, 24, 4242–4251. [Google Scholar] [CrossRef]
- Thackeray, M.M.; Johnson, C.S.; Vaughey, J.T.; Li, N.; Hackney, S.A. Advances in manganese-oxide ‘composite’ electrodes for lithium-ion batteries. J. Mater. Chem. 2005, 15, 2257–2267. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhuo, S. Nano layered-spinel 0.8Li2MnO3·0.2LiMn2O4 as high-performance cathode for Li-ion batteries. IOP Conf. Ser. Mater. Sci. Eng. 2020, 733, 012005. [Google Scholar] [CrossRef]
- Wei, Y.; Kim, K.B.; Chen, G. Evolution of the local structure and electrochemical properties of spinel LiNixMn2-xO4 (0 ≤ x ≤ 0.5). Electrochim. Acta 2006, 51, 3365–3373. [Google Scholar] [CrossRef]
- Zhao, W.; Xiong, L.; Xu, Y.; Xiao, X.; Wang, J.; Ren, Z. Magnesium substitution to improve the electrochemical performance of layered Li2MnO3 positive-electrode material. J. Power Sources 2016, 330, 37–44. [Google Scholar] [CrossRef]
- Kim, K.W.; Lee, S.W.; Han, K.S.; Chung, H.J.; Woo, S.I. Characterization of Al-doped spinel LiMn2O4 thin film cathode electrodes prepared by Liquid Source Misted Chemical Deposition (LSMCD) technique. Electrochim. Acta 2003, 48, 4223–4231. [Google Scholar] [CrossRef]
- Gao, A.; Hou, X.; Sun, Z.; Li, S.; Li, H.; Zhang, J. Lithium-desorption mechanism in LiMn2O4, Li1.33Mn1.67O4, and Li1.6Mn1.6O4 according to precisely controlled acid treatment and density functional theory calculations. J. Mater. Chem. A 2019, 7, 20878–20890. [Google Scholar] [CrossRef]
- Julien, C.M.; Massot, M. Lattice vibrations of materials for lithium rechargeable batteries III. Lithium manganese oxides. Mater. Sci. Eng. B 2003, 100, 69–78. [Google Scholar] [CrossRef]
- Julien, C. Local Environment in 4-Volt Cathode Materials for Li-Ion Batteries. In Materials for Lithium-Ion Batteries; Julien, C., Stoynov, Z., Eds.; Springer: Dordrecht, The Netherlands, 2000; pp. 309–326. [Google Scholar] [CrossRef]
- Julien, C.; Mauger, A. In situ Raman analyses of electrode materials for Li-ion batteries. AIMS Mater. Sci. 2018, 5, 650–698. [Google Scholar] [CrossRef]
- Julien, C.; Massot, M. Structural Transitions in Positive Electrodes for Li-Ion Batteries the Vibronic Approach. Ionics 2002, 8, 6–16. [Google Scholar] [CrossRef]
- Julien, C.M.; Massot, M. Raman spectroscopic studies of lithium manganates with spinel structure. J. Phys. Condens. Matter 2003, 15, 3151–3162. [Google Scholar] [CrossRef]
- Julien, C.M. Local structure of lithiated manganese oxides. Solid State Ionics 2006, 177, 11–19. [Google Scholar] [CrossRef]
- Julien, C.M.; Massot, M. Lattice vibrations of materials for lithium rechargeable batteries I. Lithium manganese oxide spinel. Mater. Sci. Eng. B 2003, 97, 217–230. [Google Scholar] [CrossRef]
- Cheng, M.; Tang, W.; Sun, Y.; Zhu, K. Electrochemical properties of Li2MnO3 nanocrystals synthesized using a hydrothermal method. RSC Adv. 2015, 5, 71088–71094. [Google Scholar] [CrossRef]
- Dheivamalar, S.; Silambarasan, V. DFT simulations and vibrational analysis of FTIR and FT-Raman spectra of 2-amino-4-methyl benzonitrile. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2012, 96, 480–484. [Google Scholar] [CrossRef]
- Ratnaparkhe, A.; Lambrecht, W.R.L. Calculated phonon modes, infrared, and Raman spectra in ZnGeGa2N4. J. Appl. Phys. 2020, 128, 075702. [Google Scholar] [CrossRef]
- Oreshonkov, A.S.; Sukhanova, E.V.; Popov, Z.I. Raman Spectroscopy of Janus MoSSe Monolayer Polymorph Modifications Using Density Functional Theory. Materials 2022, 15, 3988. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- van Setten, M.; Giantomassi, M.; Bousquet, E.; Verstraete, M.; Hamann, D.; Gonze, X.; Rignanese, G.M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Hoang, K. Defect Physics, Delithiation Mechanism, and Electronic and Ionic Conduction in Layered Lithium Manganese Oxide Cathode Materials. Phys. Rev. Appl. 2015, 3, 24013. [Google Scholar] [CrossRef]
- Chen, H.; Islam, M.S. Lithium Extraction Mechanism in Li-Rich Li2MnO3 Involving Oxygen Hole Formation and Dimerization. Chem. Mater. 2016, 28, 6656–6663. [Google Scholar] [CrossRef]
- Hoang, K. Doping Li-rich cathode material Li2MnO3: Interplay between lattice site preference, electronic structure, and delithiation mechanism. Phys. Rev. Mater. 2017, 1, 075404. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comput. Mater. Sci. 2003, 28, 155–168. [Google Scholar] [CrossRef]
- Nakao, Y.; Ozawa, K.; Nemoto, Y.; Uesugi, F.; Fujii, H.; Mochiku, T. Structural variation of Li2MnO3 during charge-discharge cycling. Nippon. Seramikkusu Kyokai Gakujutsu Ronbunshi/J. Ceram. Soc. Jpn. 2015, 123, 589–594. [Google Scholar] [CrossRef]
- Shimoda, K.; Oishi, M.; Matsunaga, T.; Murakami, M.; Yamanaka, K.; Arai, H.; Ukyo, Y.; Uchimoto, Y.; Ohta, T.; Matsubara, E.; et al. Direct observation of layered-to-spinel phase transformation in Li2MnO3 and the spinel structure stabilised after the activation process. J. Mater. Chem. A 2017, 5, 6695–6707. [Google Scholar] [CrossRef] [Green Version]
- Kaewmala, S.; Limphirat, W.; Yordsri, V.; Kim, H.; Muhammad, S.; Yoon, W.S.; Srilomsak, S.; Limthongkul, P.; Meethong, N. Structural and Electrochemical Kinetic Properties of 0.5Li2MnO3·0.5LiCoO2 Cathode Materials with Different Li2MnO3 Domain Sizes. Sci. Rep. 2019, 9, 427. [Google Scholar] [CrossRef]
- Boulineau, A.; Croguennec, L.; Delmas, C.; Weill, F. Structure of Li2MnO3 with different degrees of defects. Solid State Ionics 2010, 180, 1652–1659. [Google Scholar] [CrossRef]
- Boulineau, A.; Croguennec, L.; Delmas, C.; Weill, F. Reinvestigation of Li2MnO3 Structure: Electron Diffraction and High Resolution TEM. Chem. Mater. 2009, 21, 4216–4222. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, L.; Gao, M. Molecular dynamics study on the Li diffusion mechanism and delithiation process of Li2MnO3. Solid State Ionics 2020, 346, 115195. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, F.; Wu, S.; Zhu, Z. Identifying a Li-rich superionic conductor from charge–discharge structural evolution study: Li2MnO3. Phys. Chem. Chem. Phys. 2021, 23, 4829–4834. [Google Scholar] [CrossRef] [PubMed]
- Saraiva, G.; da Silva Filho, J.; Saraiva-Souza, A.; de Castro, A.R.; Teixeira, A.; Luz-Lima, C.; Oliveira, F.; Neto, V.S.; Freire, P.; de Sousa, F. Temperature dependence Raman spectroscopy and DFT calculations of Bi2(MoO4)3. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 224, 117340. [Google Scholar] [CrossRef]
- Moura, J.; Silveira, J.; da Silva Filho, J.; Souza Filho, A.; Luz-Lima, C.; Freire, P. Temperature-induced phase transition in h-MoO3: Stability loss mechanism uncovered by Raman spectroscopy and DFT calculations. Vib. Spectrosc. 2018, 98, 98–104. [Google Scholar] [CrossRef]
- Post, J.; Mckeown, D.; Heaney, P. Raman spectroscopy study of manganese oxides: Tunnel structures. Am. Mineral. 2020, 105, 1175–1190. [Google Scholar] [CrossRef]
- Yu, D.Y.W.; Yanagida, K. Structural Analysis of Li2MnO3 and Related Li-Mn-O Materials. J. Electrochem. Soc. 2011, 158, A1015. [Google Scholar] [CrossRef]
- Ruther, R.E.; Dixit, H.; Pezeshki, A.M.; Sacci, R.L.; Cooper, V.R.; Nanda, J.; Veith, G.M. Correlating Local Structure with Electrochemical Activity in Li2MnO3. J. Phys. Chem. C 2015, 119, 18022–18029. [Google Scholar] [CrossRef]
- Torres-Castro, L.; Shojan, J.; Julien, C.M.; Huq, A.; Dhital, C.; Paranthaman, M.P.; Katiyar, R.S.; Manivannan, A. Synthesis, characterization and electrochemical performance of Al-substituted Li2MnO3. Mater. Sci. Eng. B 2015, 201, 13–22. [Google Scholar] [CrossRef] [Green Version]
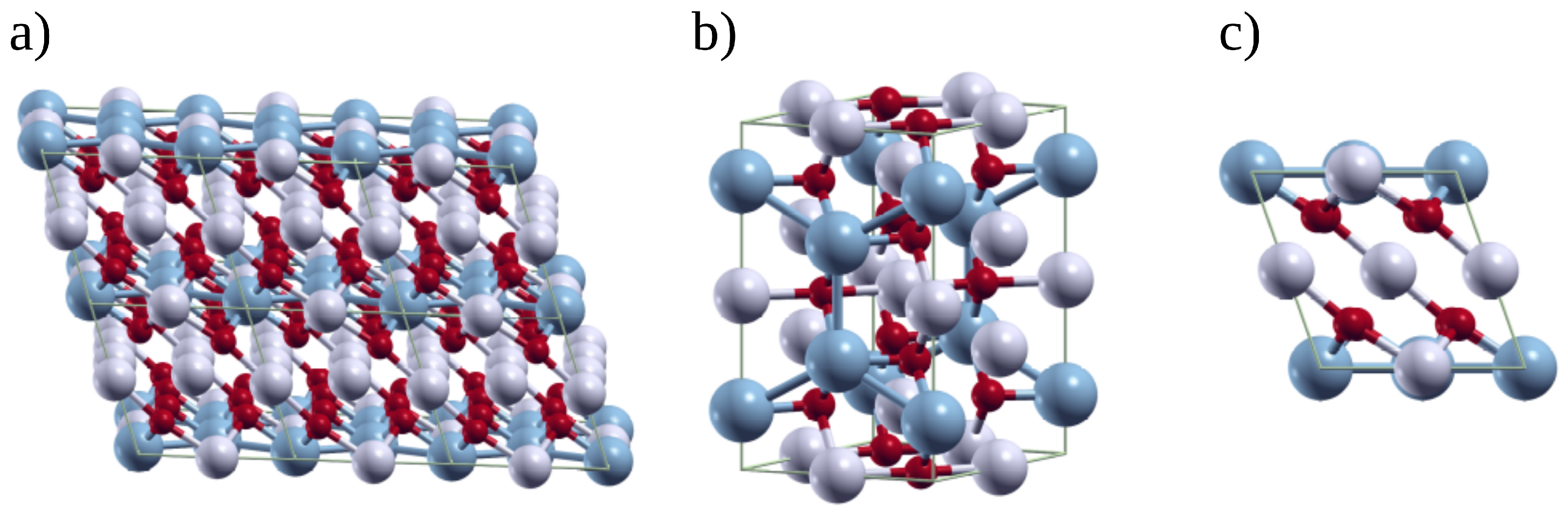
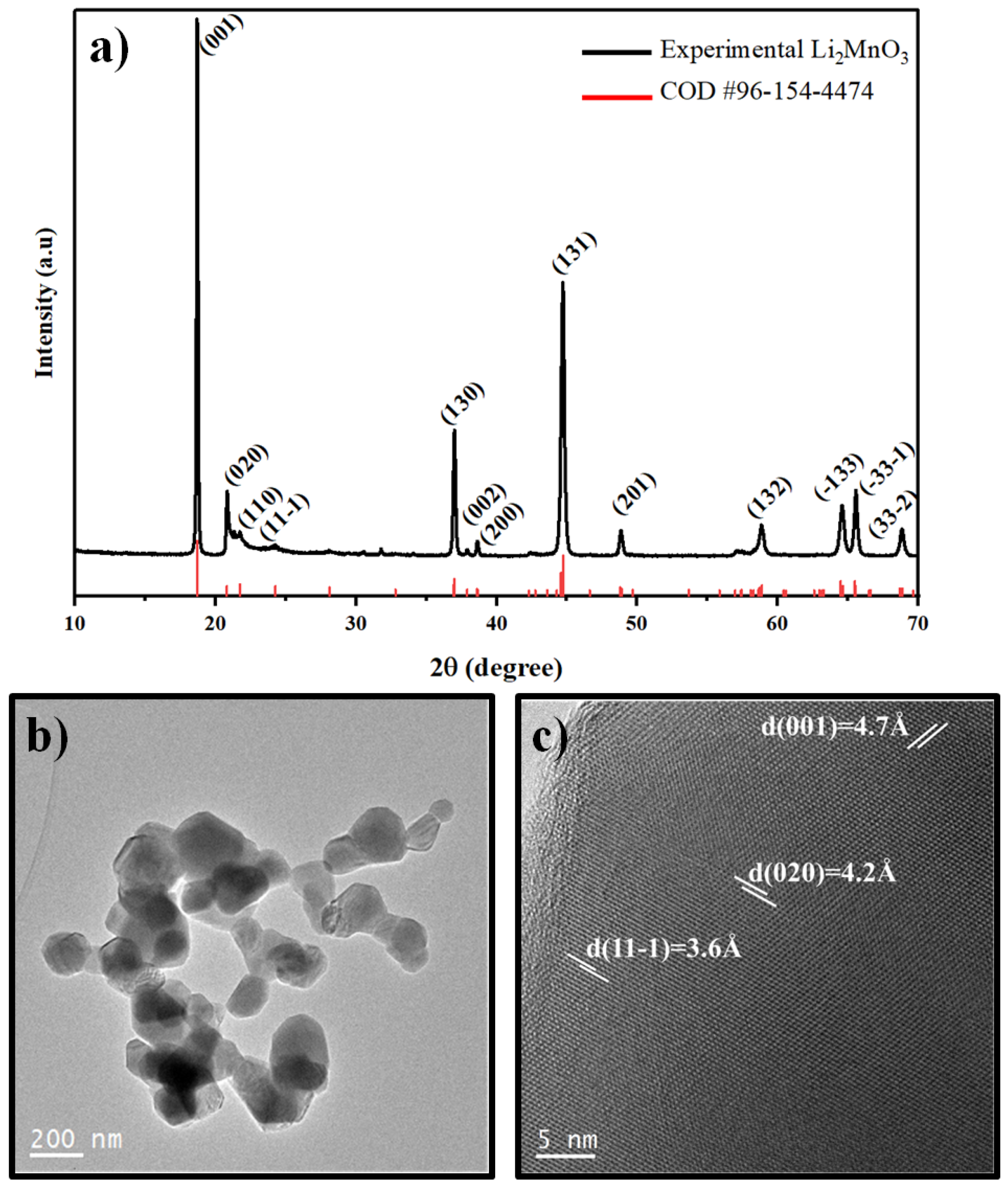

| a (Å) | b (Å) | c (Å) | (°) | Volume (ų) | |
|---|---|---|---|---|---|
| LDA | 4.805 | 8.308 | 4.854 | 109.628 | 182.494 |
| Experimental | 4.933 | 8.535 | 5.026 | 109.314 | 211.608 |
| Exp. IR freq.(cm−1) | Calc. IR freq.(cm−1) | Symmetry | Exp. IR freq.(cm−1) | Calc. IR freq.(cm−1) | Symmetry |
|---|---|---|---|---|---|
| 173.38 | 417.7 | ||||
| 181.89 | 425 | 431.79 | |||
| 184.75 | 439.87 | ||||
| 208.99 | 437.8 | 461.78 | |||
| 226.19 | 437.8 | 469.48 | |||
| 252.46 | 489.38 | ||||
| 258.53 | 498.5 | ||||
| 268 | 263.69 | 501.37 | |||
| 282 | 274.87 | 514 | 507.57 | ||
| 282 | 276.48 | 530.38 | |||
| 292 | 306.25 | 543.95 | |||
| 327 | 316.27 | 537 | 570.37 | ||
| 334.01 | 537 | 579.04 | |||
| 352 | 350.02 | 537 | 581.66 | ||
| 352 | 354.15 | 627 | 609.12 | ||
| 367.76 | 627 | 613.16 | |||
| 380 | 378.5 | 627 | 622.42 | ||
| 393 | 627 | 628.49 | |||
| 401.78 | 627 | 633.94 | |||
| 407.29 |
| Exp. Raman freq.(cm−1) | Calc. Raman freq.(cm−1) | Symmetry | Exp. Raman freq.(cm−1) | Calc. Raman freq.(cm−1) | Symmetry |
|---|---|---|---|---|---|
| 201.07 | 482.56 | ||||
| 218.24 | 501 | 493.99 | |||
| 224.08 | 501 | 514.9 | |||
| 250 | 238.84 | 501 | 520.66 | ||
| 309 | 300.07 | 501 | 522.63 | ||
| 324 | 322.81 | 549.63 | |||
| 335 | 347.34 | 552.83 | |||
| 374 | 372.87 | 565.07 | |||
| 374 | 376.47 | 574 | 572.2 | ||
| 390.11 | 574 | 574.7 | |||
| 419 | 427.5 | 616 | 619.61 | ||
| 435.11 | 623.26 | ||||
| 442 | 441.91 | 668.64 | |||
| 454.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pulido, R.; Naveas, N.; Martin-Palma, R.J.; Agulló-Rueda, F.; Ferró, V.R.; Hernández-Montelongo, J.; Recio-Sánchez, G.; Brito, I.; Manso-Silván, M. Phonon Structure, Infra-Red and Raman Spectra of Li2MnO3 by First-Principles Calculations. Materials 2022, 15, 6237. https://doi.org/10.3390/ma15186237
Pulido R, Naveas N, Martin-Palma RJ, Agulló-Rueda F, Ferró VR, Hernández-Montelongo J, Recio-Sánchez G, Brito I, Manso-Silván M. Phonon Structure, Infra-Red and Raman Spectra of Li2MnO3 by First-Principles Calculations. Materials. 2022; 15(18):6237. https://doi.org/10.3390/ma15186237
Chicago/Turabian StylePulido, Ruth, Nelson Naveas, Raúl J. Martin-Palma, Fernando Agulló-Rueda, Victor R. Ferró, Jacobo Hernández-Montelongo, Gonzalo Recio-Sánchez, Ivan Brito, and Miguel Manso-Silván. 2022. "Phonon Structure, Infra-Red and Raman Spectra of Li2MnO3 by First-Principles Calculations" Materials 15, no. 18: 6237. https://doi.org/10.3390/ma15186237
APA StylePulido, R., Naveas, N., Martin-Palma, R. J., Agulló-Rueda, F., Ferró, V. R., Hernández-Montelongo, J., Recio-Sánchez, G., Brito, I., & Manso-Silván, M. (2022). Phonon Structure, Infra-Red and Raman Spectra of Li2MnO3 by First-Principles Calculations. Materials, 15(18), 6237. https://doi.org/10.3390/ma15186237










