Impact of Bismuth Incorporation into (Ga,Mn)As Dilute Ferromagnetic Semiconductor on Its Magnetic Properties and Magnetoresistance
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
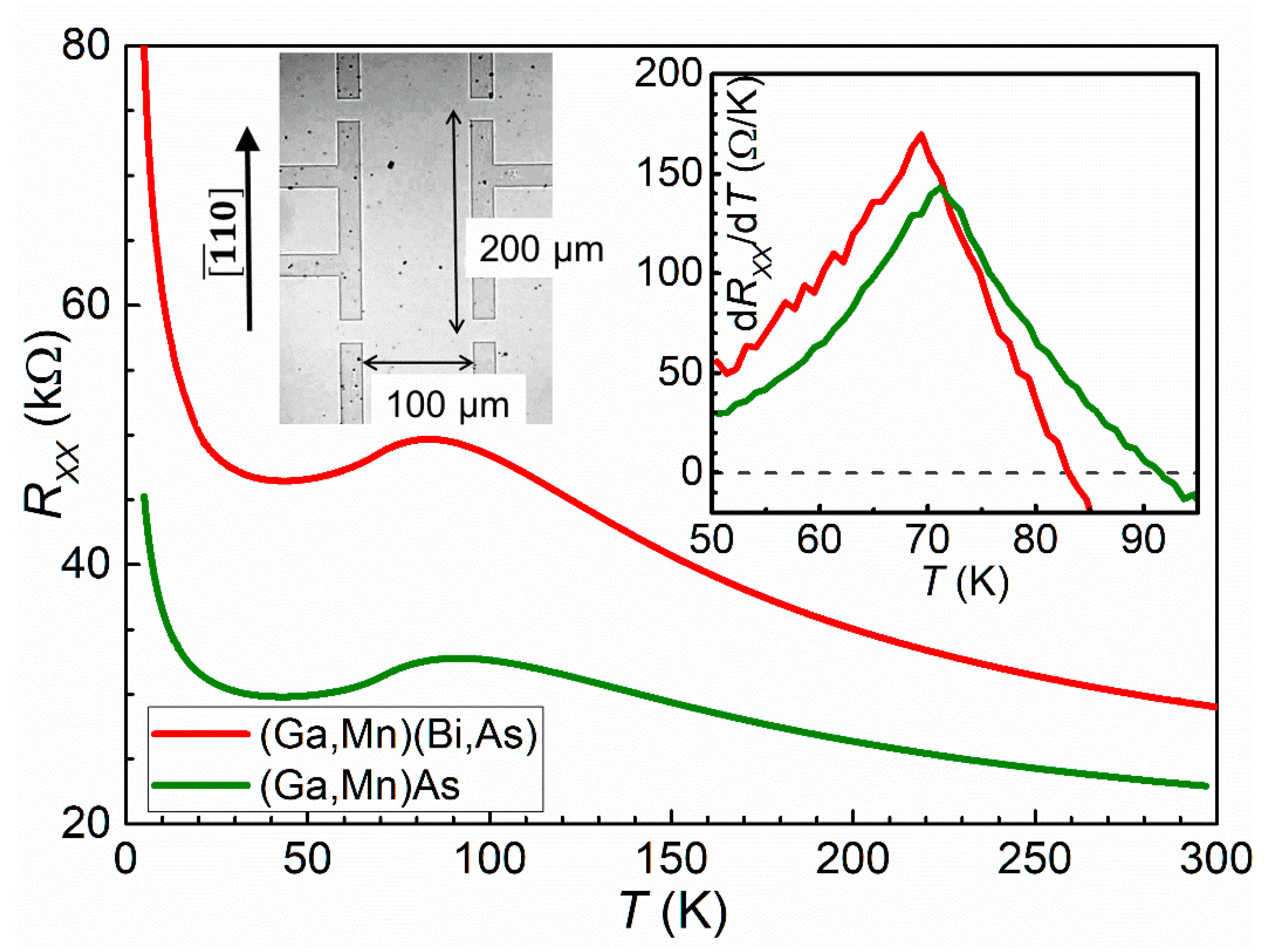
3.1. Electrical Characterization
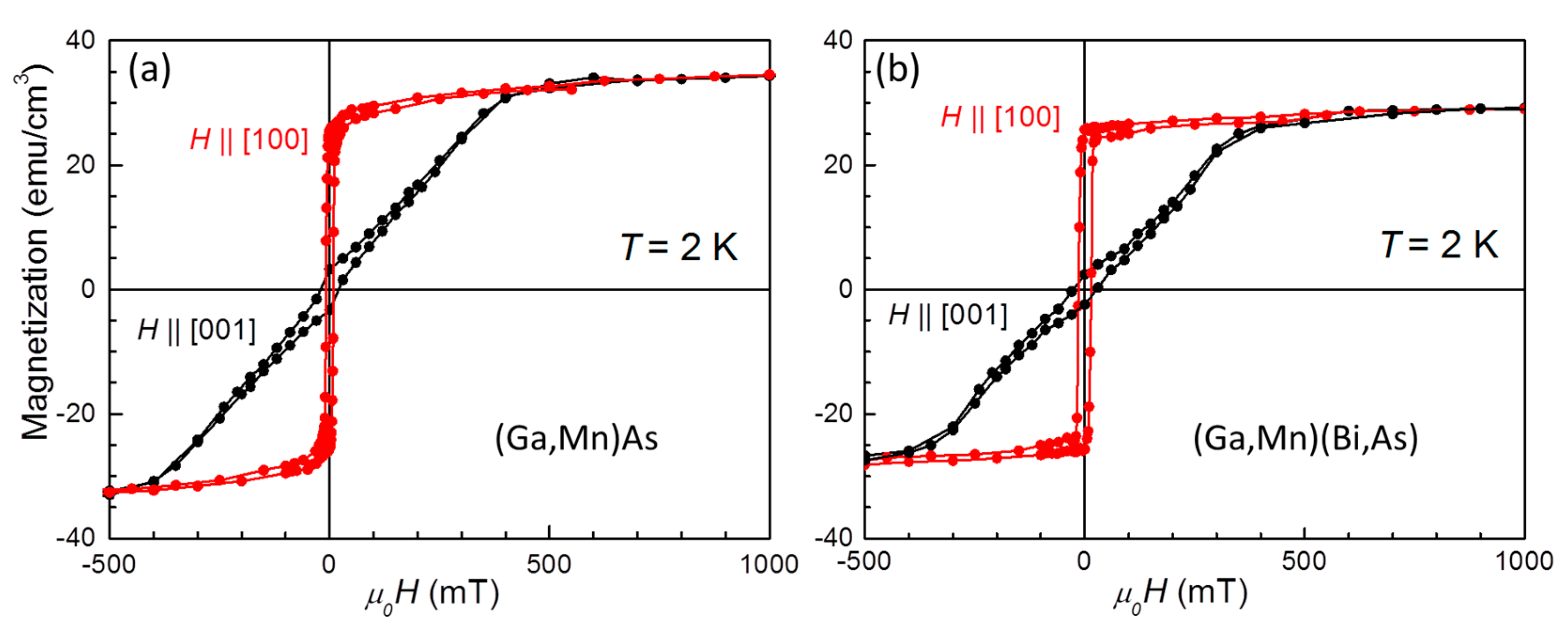
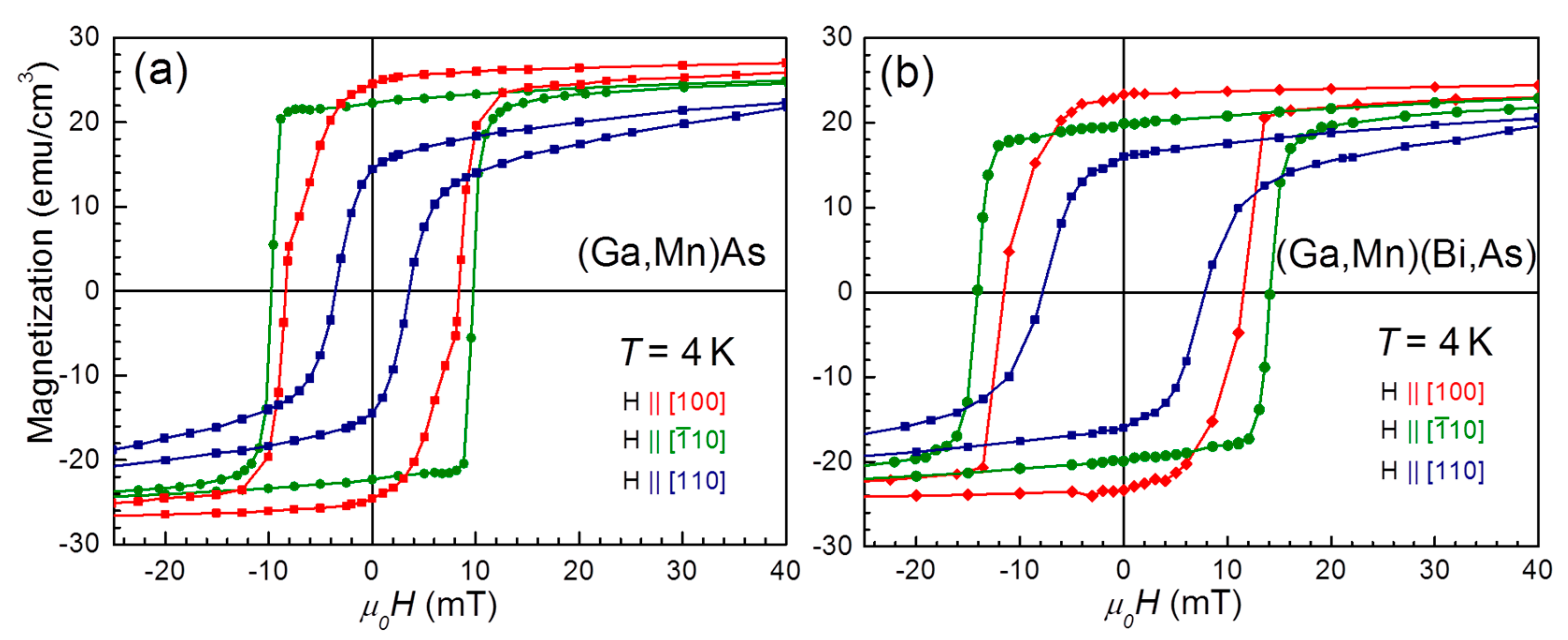
3.2. Magnetic Properties
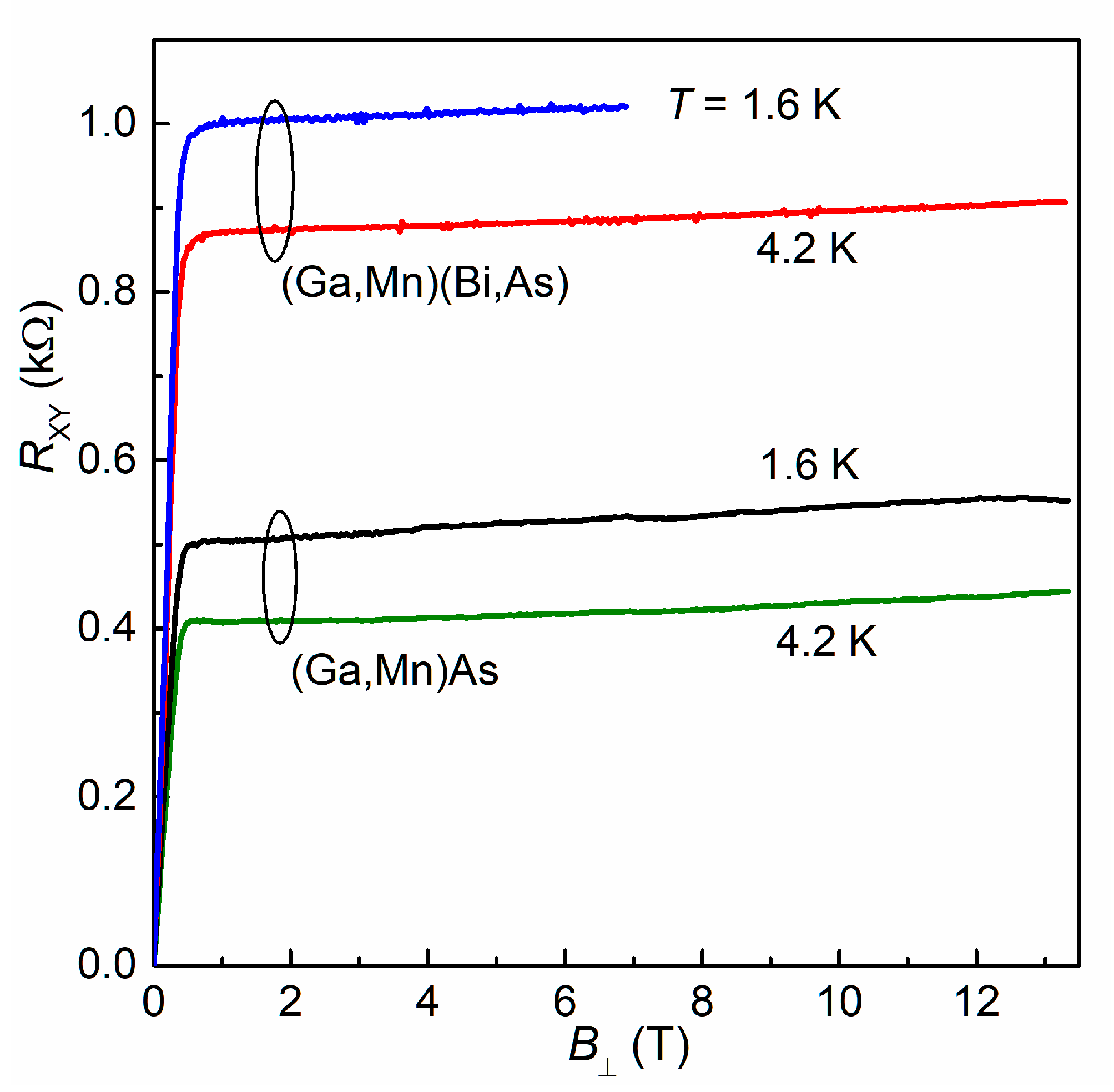
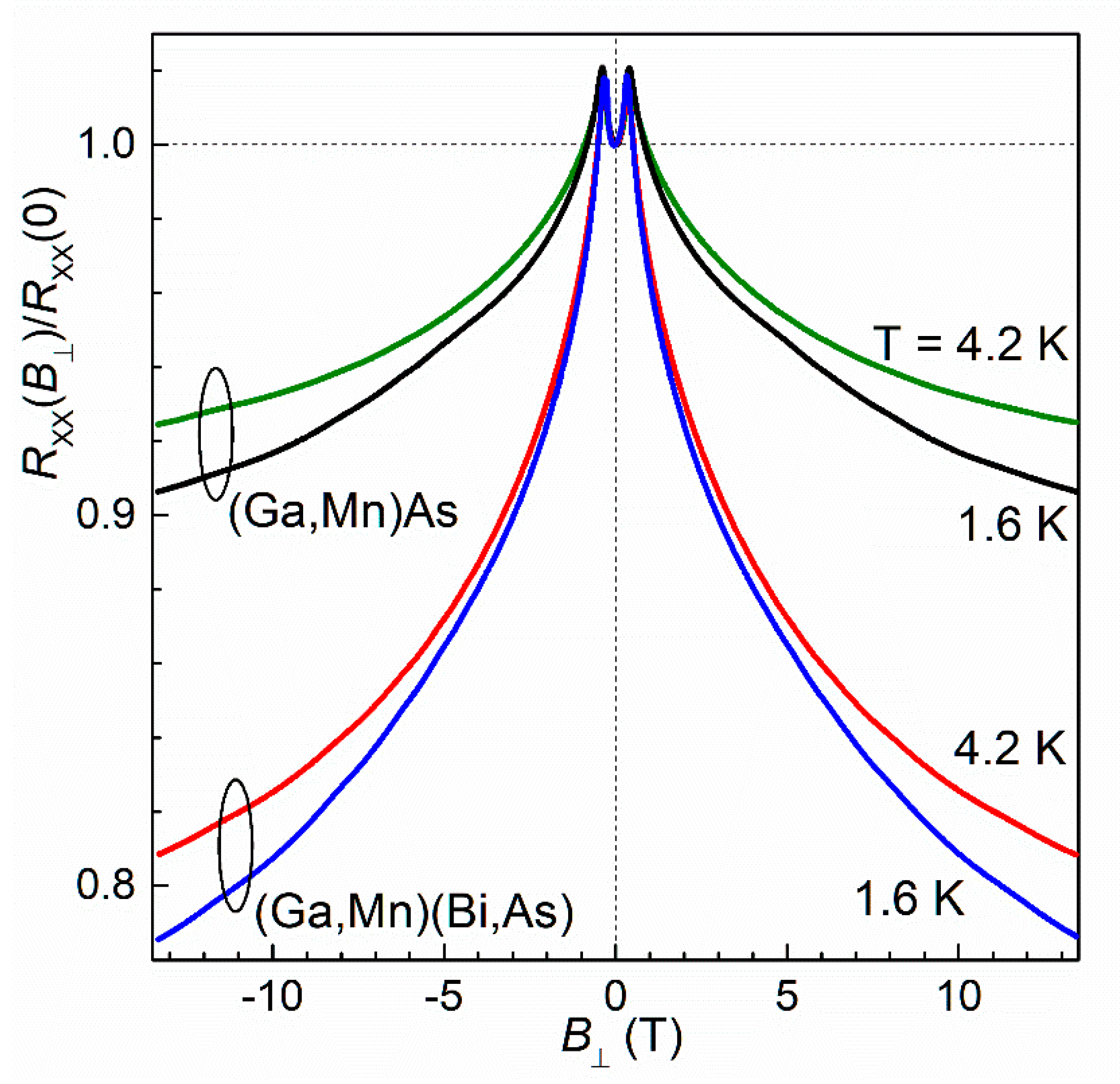
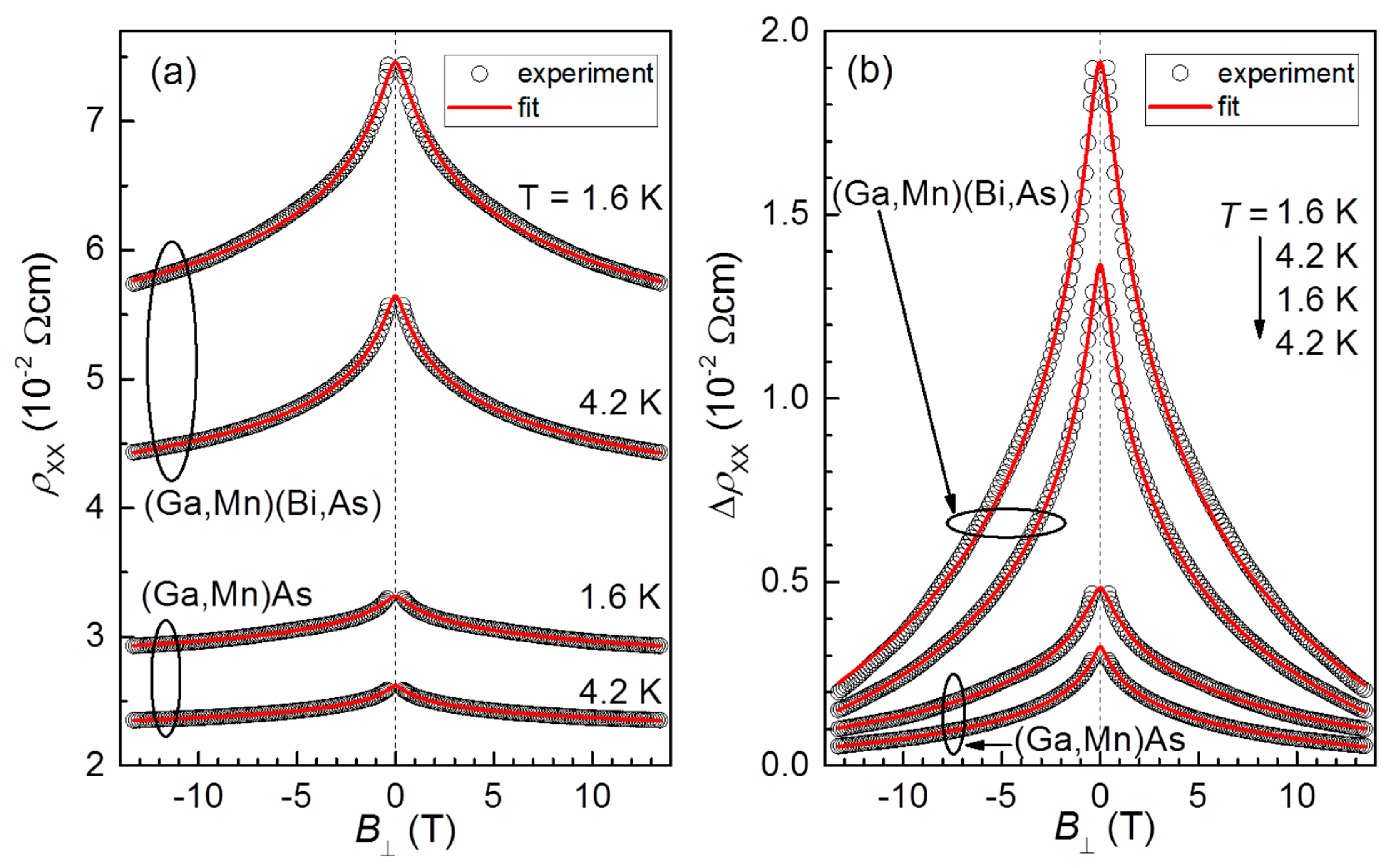
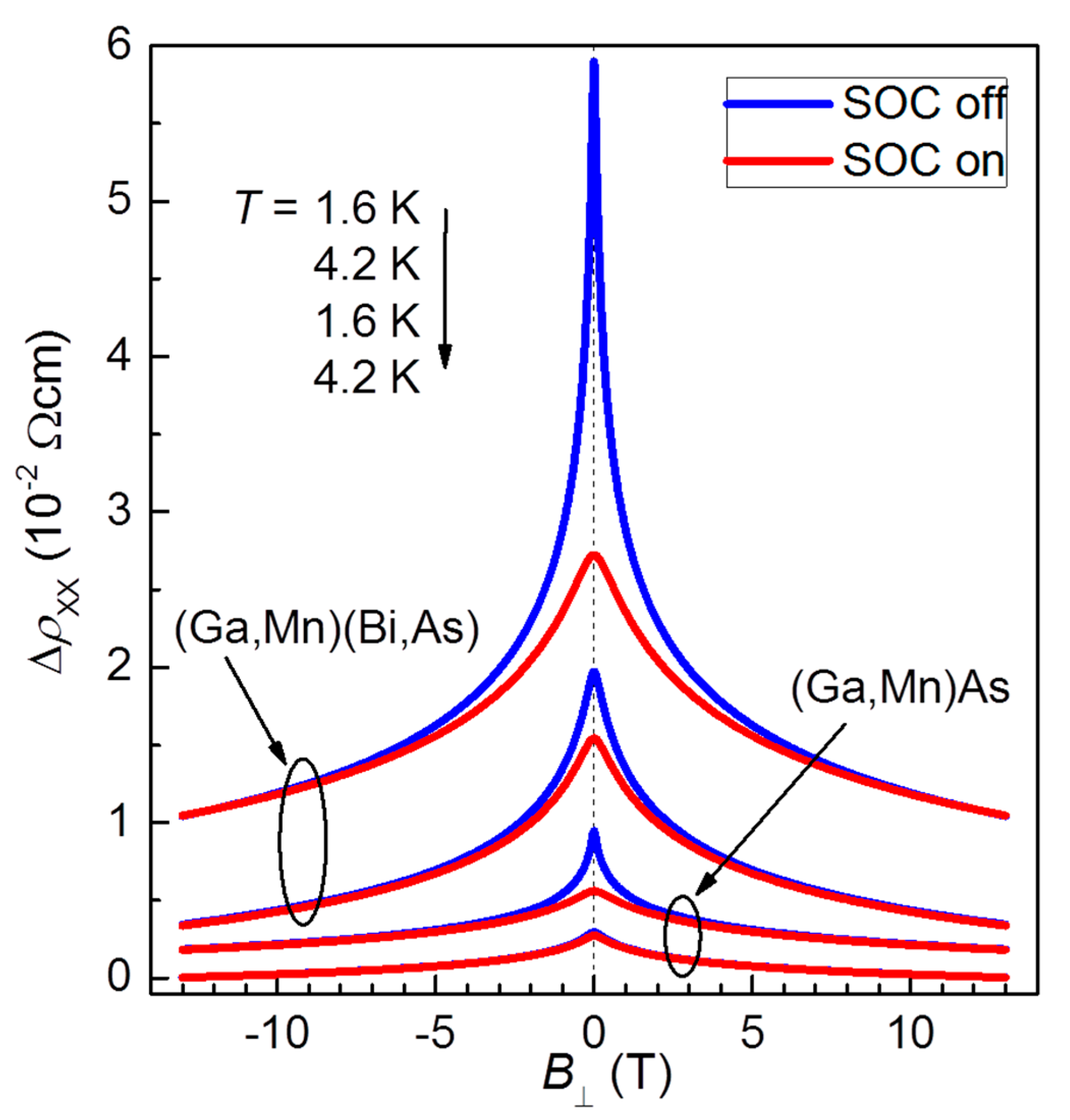
3.3. Magnetoresistance and Weak Localization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MacDonald, A.H.; Schiffer, P.; Samarth, N. Ferromagnetic semiconductors: Moving beyond (Ga,Mn)As. Nat. Mater. 2005, 4, 195–202. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H. Dilute ferromagnetic semiconductors: Physics and spintronic structures. Rev. Mod. Phys. 2014, 86, 187–251. [Google Scholar] [CrossRef]
- Jungwirth, T.; Wunderlich, J.; Novak, V.; Olejnik, K.; Gallagher, B.L.; Campion, R.P.; Edmonds, K.W.; Rushforth, A.W.; Ferguson, A.J.; Nemec, P. Spin-dependent phenomena and device concepts explored in (Ga,Mn)As. Rev. Mod. Phys. 2014, 86, 855–896. [Google Scholar] [CrossRef]
- Ramaswany, R.; Lee, J.M.; Cai, K.; Yang, H. Recent advances in spin-orbit torques: Moving towards device applications. Appl. Phys. Rev. 2018, 5, 031107. [Google Scholar] [CrossRef]
- Yang, H.; Valenzuela, S.; Chshiev, M.; Couet, S.; Dieny, B.; Dlubak, B.; Fert, A.; Garello, K.; Jamet, M.; Jeong, D.-E.; et al. Two-dimensional materials prospects for non-volatile spintronic memories. Nature 2022, 606, 663–673. [Google Scholar] [CrossRef]
- Chernyshov, A.; Overby, M.; Liu, X.; Furdyna, J.K.; Lyanda-Geller, Y.; Rokhinson, L.P. Evidence for reversible control of magnetization in a ferromagnetic material by means of spin-orbit magnetic field. Nat. Phys. 2009, 5, 656–659. [Google Scholar] [CrossRef]
- Miron, I.M.; Garello, K.; Gaudin, G.; Zermatten, P.-J.; Costache, M.V.; Auffret, S.; Bandiera, S.; Rodmacq, B.; Schuhl, A.; Gambardella, P. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 2011, 476, 189–194. [Google Scholar] [CrossRef]
- Fukami, S.; Anekawa, T.; Zhang, C.; Ohno, H. A spin-orbit torque switching scheme with collinear magnetic easy axis and current configuration. Nat. Nanotechnol. 2016, 11, 621–625. [Google Scholar] [CrossRef]
- Dresselhaus, G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 1955, 100, 580–586. [Google Scholar] [CrossRef]
- Bychkov, Y.A.; Rashba, E.I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 1984, 39, 78–81. [Google Scholar]
- Garate, I.; Sinova, J.; Jungwirth, T.; MacDonald, A.H. Theory of weak localization in ferromagnetic (Ga,Mn)As. Phys. Rev. B 2009, 79, 155207. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
- Yastrubchak, O.; Sadowski, J.; Gluba, L.; Domagala, J.Z.; Rawski, M.; Żuk, J.; Kulik, M.; Andrearczyk, T.; Wosinski, T. Ferromagnetism and the electronic band structure in (Ga,Mn)(Bi,As) epitaxial layers. Appl. Phys. Lett. 2014, 105, 072402. [Google Scholar] [CrossRef]
- Levchenko, K.; Andrearczyk, T.; Domagala, J.Z.; Sadowski, J.; Kowalczyk, L.; Szot, M.; Kuna, R.; Figielski, T.; Wosinski, T. Novel quaternary dilute magnetic semiconductor (Ga,Mn)(Bi,As): Magnetic and magneto-transport investigations. J. Supercond. Nov. Magn. 2017, 30, 825–829. [Google Scholar] [CrossRef]
- Fluegel, B.; Francoeur, S.; Mascarenhas, A.; Tixier, S.; Young, E.C.; Tiedje, T. Giant spin-orbit bowing in GaAs1-xBix. Phys. Rev. Lett. 2006, 97, 067205. [Google Scholar] [CrossRef]
- Alberi, K.; Wu, J.; Walukiewicz, W.; Yu, K.M.; Dubon, O.D.; Watkins, S.P.; Wang, C.X.; Liu, X.; Cho, Y.-J.; Furdyna, J. Valence band anticrossing in mismatched III-V semiconductor alloys. Phys. Rev. B 2007, 75, 045203. [Google Scholar] [CrossRef]
- Andrearczyk, T.; Levchenko, K.; Sadowski, J.; Domagala, J.Z.; Kaleta, A.; Dłużewski, P.; Wróbel, J.; Figielski, T.; Wosinski, T. Structural quality and magnetotransport properties of epitaxial layers of the (Ga,Mn)(Bi,As) dilute magnetic semiconductor. Materials 2020, 13, 5507. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, K.; Prokscha, T.; Sadowski, J.; Radelytskyi, I.; Jakiela, R.; Trzyna, M.; Andrearczyk, T.; Figielski, T.; Wosinski, T. Evidence for the homogeneous ferromagnetic phase in (Ga,Mn)(Bi,As) epitaxial layers from muon spin relaxation spectroscopy. Sci. Rep. 2019, 9, 3394. [Google Scholar] [CrossRef] [PubMed]
- Andrearczyk, T.; Sadowski, J.; Wróbel, J.; Figielski, T.; Wosinski, T. Tunable planar Hall effect in (Ga,Mn)(Bi,As) epitaxial layers. Materials 2021, 14, 4483. [Google Scholar] [CrossRef]
- Andrearczyk, T.; Sadowski, J.; Dybko, K.; Figielski, T.; Wosinski, T. Current-induced magnetization reversal in (Ga,Mn)(Bi,As) epitaxial layer with perpendicular magnetic anisotropy. Appl. Phys. Lett. 2022, 121, 242401. [Google Scholar] [CrossRef]
- Kasuya, T. Electrical resistance of ferromagnetic metals. Prog. Theor. Phys. 1956, 16, 58–63. [Google Scholar] [CrossRef]
- Dugaev, V.K.; Bruno, P.; Barnaś, J. Weak localization in ferromagnets with spin-orbit interaction. Phys. Rev. B 2001, 64, 144423. [Google Scholar] [CrossRef]
- Matsukura, F.; Sawicki, M.; Dietl, T.; Chiba, D.; Ohno, H. Magnetotranport properties of metallic (Ga,Mn)As films with compressive and tensile strain. Phys. E 2004, 21, 1032–1036. [Google Scholar] [CrossRef]
- Dietl, T. Interplay between carrier localization and magnetism in diluted magnetic and ferromagnetic semiconductors. J. Phys. Soc. Jpn. 2008, 77, 031005. [Google Scholar] [CrossRef]
- Gluba, L.; Yastrubchak, O.; Domagala, J.Z.; Jakiela, R.; Andrearczyk, T.; Żuk, J.; Wosinski, T.; Sadowski, J.; Sawicki, M. Band structure evolution and the origin of magnetism in (Ga,Mn)As: From paramagnetic through superparamagnetic to ferromagnetic phase. Phys. Rev. B 2018, 97, 115201. [Google Scholar] [CrossRef]
- Wang, K.Y.; Edmonds, K.W.; Campion, R.P.; Gallagher, B.L.; Farley, N.R.S.; Foxon, C.T.; Sawicki, M.; Bogusławski, P.; Dietl, T. Influence of the Mn Interstitial on the Magnetic and Transport Properties of (Ga,Mn)As. J. Appl. Phys. 2004, 95, 6512. [Google Scholar] [CrossRef]
- Edmonds, K.W.; Bogusławski, P.; Wang, K.Y.; Campion, R.P.; Novikov, S.V.; Farley, N.R.S.; Gallagher, B.L.; Foxon, C.T.; Sawicki, M.; Dietl, T.; et al. Mn interstitial diffusion in (Ga,Mn)As. Phys. Rev. Lett. 2004, 92, 037201. [Google Scholar] [CrossRef]
- Gas, K.; Sadowski, J.; Sawicki, M. Magnetic Properties of Wurtzite (Ga,Mn)As. J. Mag. Magn. Mater. 2021, 533, 168012. [Google Scholar] [CrossRef]
- Sawicki, M.; Stefanowicz, W.; Ney, A. Sensitive SQUID Magnetometry for Studying Nanomagnetism. Semicond. Sci. Technol. 2011, 26, 064006. [Google Scholar] [CrossRef]
- Von Molnár, S.; Kasuya, T. Evidence of band conduction and critical scattering in dilute Eu-chalcogenide alloys. Phys. Rev. Lett. 1968, 21, 1757–1761. [Google Scholar] [CrossRef]
- Novák, V.; Olejnik, K.; Wunderlich, J.; Cukr, M.; Vyborny, K.; Rushforth, A.W.; Edmonds, K.W.; Campion, R.P.; Gallagher, B.L.; Sinova, J.; et al. Curie point singularity in the temperature derivative of resistivity in (Ga,Mn)As. Phys. Rev. Lett. 2008, 101, 077201. [Google Scholar] [CrossRef] [PubMed]
- Kwiatkowski, A.; Gryglas-Borysiewicz, M.; Juszynski, P.; Przybytek, J.; Sawicki, M.; Sadowski, J.; Wasik, D.; Baj, M. Determining Curie temperature of (Ga,Mn)As samples based on electrical transport measurements: Low Curie temperature case. Appl. Phys. Lett. 2016, 108, 242103. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H.; Matsukura, F. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors. Phys. Rev. B 2001, 63, 195205. [Google Scholar] [CrossRef]
- Sawicki, M. Magnetic properties of (Ga,Mn)As. J. Mag. Magn. Mater. 2006, 300, 1. [Google Scholar] [CrossRef]
- Sawicki, M.; Matsukura, F.; Idziaszek, A.; Dietl, T.; Schott, G.M.; Ruester, C.; Gould, C.; Karczewski, G.; Schmidt, G.; Molenkamp, L.W. Temperature dependent magnetic anisotropy in (Ga,Mn)As layers. Phys. Rev. B 2004, 70, 245325. [Google Scholar] [CrossRef]
- Liu, X.; Sasaki, Y.; Furdyna, J.K. Ferromagnetic resonance in Ga1-xMnxAs: Effects of magnetic anisotropy. Phys. Rev. B 2003, 67, 205204. [Google Scholar] [CrossRef]
- Tang, H.X.; Kawakami, R.K.; Awschalom, D.D.; Roukes, M.L. Giant planar Hall effect in epitaxial (Ga,Mn)As devices. Phys. Rev. Lett. 2003, 90, 107201. [Google Scholar] [CrossRef]
- Hrabovsky, D.; Vanelle, E.; Fert, A.R.; Yee, D.S.; Redoules, J.P.; Sadowski, J.; Kanski, J.; Ilver, L. Magnetization reversal in GaMnAs layers studied by Kerr effect. Appl. Phys. Lett. 2002, 81, 2806–2808. [Google Scholar] [CrossRef]
- Welp, U.; Vlasko-Vlasov, V.K.; Liu, X.; Furdyna, J.K.; Wojtowicz, T. Magnetic domain structure and magnetic anisotropy in Ga1-xMnxAs. Phys. Rev. Lett. 2003, 90, 167206. [Google Scholar] [CrossRef]
- Sawicki, M.; Proselkov, O.; Sliwa, C.; Aleshkevych, P.; Domagala, J.Z.; Sadowski, J.; Dietl, T. Cubic anisotropy in (Ga, Mn)As layers: Experiment and theory. Phys. Rev. B 2018, 97, 184403. [Google Scholar] [CrossRef]
- Gould, C.; Rüster, C.; Jungwirth, T.; Girgis, E.; Schott, G.M.; Giraud, R.; Brunner, K.; Schmidt, G.; Molenkamp, L.W. Tunneling anisotropic magnetoresistance: A spin-valve-like tunnel magnetoresistance using a single magnetic layer. Phys. Rev. Lett. 2004, 93, 117203. [Google Scholar] [CrossRef] [PubMed]
- Pappert, K.; Gould, C.; Sawicki, M.; Wenisch, J.; Brunner, K.; Schmidt, G.; Molenkamp, L.W. Detailed transport investigation of the magnetic anisotropy of (Ga,Mn)As. New J. Phys. 2007, 9, 354. [Google Scholar] [CrossRef]
- Wang, K.-Y.; Sawicki, M.; Edmonds, K.W.; Campion, R.P.; Maat, S.; Foxon, C.T.; Gallagher, B.L.; Dietl, T. Spin Reorientation Transition in Single-Domain (Ga,Mn)As. Phys. Rev. Lett. 2005, 95, 217204. [Google Scholar] [CrossRef]
- Shen, A.; Ohno, H.; Matsukura, F.; Sugawara, Y.; Akiba, N.; Kuroiwa, T.; Oiwa, A.; Endo, A.; Katsumoto, S.; Iye, Y. Epitaxy of (Ga,Mn)As, a new diluted magnetic semiconductor based on GaAs. J. Cryst. Growth 1997, 175/176, 1069–1074. [Google Scholar] [CrossRef]
- Sawicki, M.; Matsukura, F.; Dietl, T.; Schott, G.M.; Rüster, C.; Schmidt, G.; Molenkamp, L.W.; Karczewski, G. Temperature peculiarities of magnetic anisotropy in (Ga,Mn)As: The role of the hole concentration. J. Supercond. Novel Magn. 2003, 16, 7. [Google Scholar] [CrossRef]
- McGuire, T.R.; Potter, R.I. Anisotropic magnetoresistance in ferromagnetic 3d alloys. IEEE Trans. Magn. 1975, 11, 1018–1038. [Google Scholar] [CrossRef]
- Figielski, T.; Wosiński, T.; Pelya, O.; Sadowski, J.; Morawski, A.; Mąkosa, A.; Dobrowolski, W.; Szymczak, R.; Wróbel, J. Magnetotransport through nanoconstriction in ferromagnetic (Ga,Mn)As epilayers. In Physics, Chemistry and Applications of Nanostructures, Proceedings of the Nanomeeting-2005, Minsk, Belarus, 24–27 May 2005; Borisenko, V.E., Gaponenko, S.V., Gurin, V.S., Eds.; World Scientific: Singapore, 2005; pp. 289–292. [Google Scholar]
- Neumaier, D.; Wagner, K.; Geißler, S.; Wurstbauer, U.; . Sadowski, J.; Wegscheider, W.; Weiss, D. Weak Localization in Ferromagnetic (Ga,Mn)As Nanostructures. Phys. Rev. Lett. 2007, 99, 116803. [Google Scholar] [CrossRef]
- Andrearczyk, T.; Jaroszyński, J.; Grabecki, G.; Dietl, T.; Fukumura, T.; Kawasaki, M. Spin-related magnetoresistance of n-type ZnO:Al and Zn1−xMnxO:Al thin films. Phys. Rev. B 2005, 72, 121309(R). [Google Scholar] [CrossRef]

| Layer | T (K) | ρc (10−2 Ωcm) | Fσ | Lso (nm) |
|---|---|---|---|---|
| (Ga,Mn)(Bi,As) | 1.6 | 3.0 | 0.13 | 44 |
| 4.2 | 2.5 | 0.15 | 70 | |
| (Ga,Mn)As | 1.6 | 2.1 | 0.12 | 52 |
| 4.2 | 1.8 | 0.11 | 140 |
| Layer | T (K) | µ (cm2/(Vs)) | kFl |
|---|---|---|---|
| (Ga,Mn)(Bi,As) | 1.6 | 1.0 | 0.23 |
| 4.2 | 1.2 | 0.27 | |
| (Ga,Mn)As | 1.6 | 1.5 | 0.32 |
| 4.2 | 1.7 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrearczyk, T.; Levchenko, K.; Sadowski, J.; Gas, K.; Avdonin, A.; Wróbel, J.; Figielski, T.; Sawicki, M.; Wosinski, T. Impact of Bismuth Incorporation into (Ga,Mn)As Dilute Ferromagnetic Semiconductor on Its Magnetic Properties and Magnetoresistance. Materials 2023, 16, 788. https://doi.org/10.3390/ma16020788
Andrearczyk T, Levchenko K, Sadowski J, Gas K, Avdonin A, Wróbel J, Figielski T, Sawicki M, Wosinski T. Impact of Bismuth Incorporation into (Ga,Mn)As Dilute Ferromagnetic Semiconductor on Its Magnetic Properties and Magnetoresistance. Materials. 2023; 16(2):788. https://doi.org/10.3390/ma16020788
Chicago/Turabian StyleAndrearczyk, Tomasz, Khrystyna Levchenko, Janusz Sadowski, Katarzyna Gas, Andrei Avdonin, Jerzy Wróbel, Tadeusz Figielski, Maciej Sawicki, and Tadeusz Wosinski. 2023. "Impact of Bismuth Incorporation into (Ga,Mn)As Dilute Ferromagnetic Semiconductor on Its Magnetic Properties and Magnetoresistance" Materials 16, no. 2: 788. https://doi.org/10.3390/ma16020788
APA StyleAndrearczyk, T., Levchenko, K., Sadowski, J., Gas, K., Avdonin, A., Wróbel, J., Figielski, T., Sawicki, M., & Wosinski, T. (2023). Impact of Bismuth Incorporation into (Ga,Mn)As Dilute Ferromagnetic Semiconductor on Its Magnetic Properties and Magnetoresistance. Materials, 16(2), 788. https://doi.org/10.3390/ma16020788







