The Origin of Anomalous Density Behavior of Silica Glass
Abstract
:1. Introduction
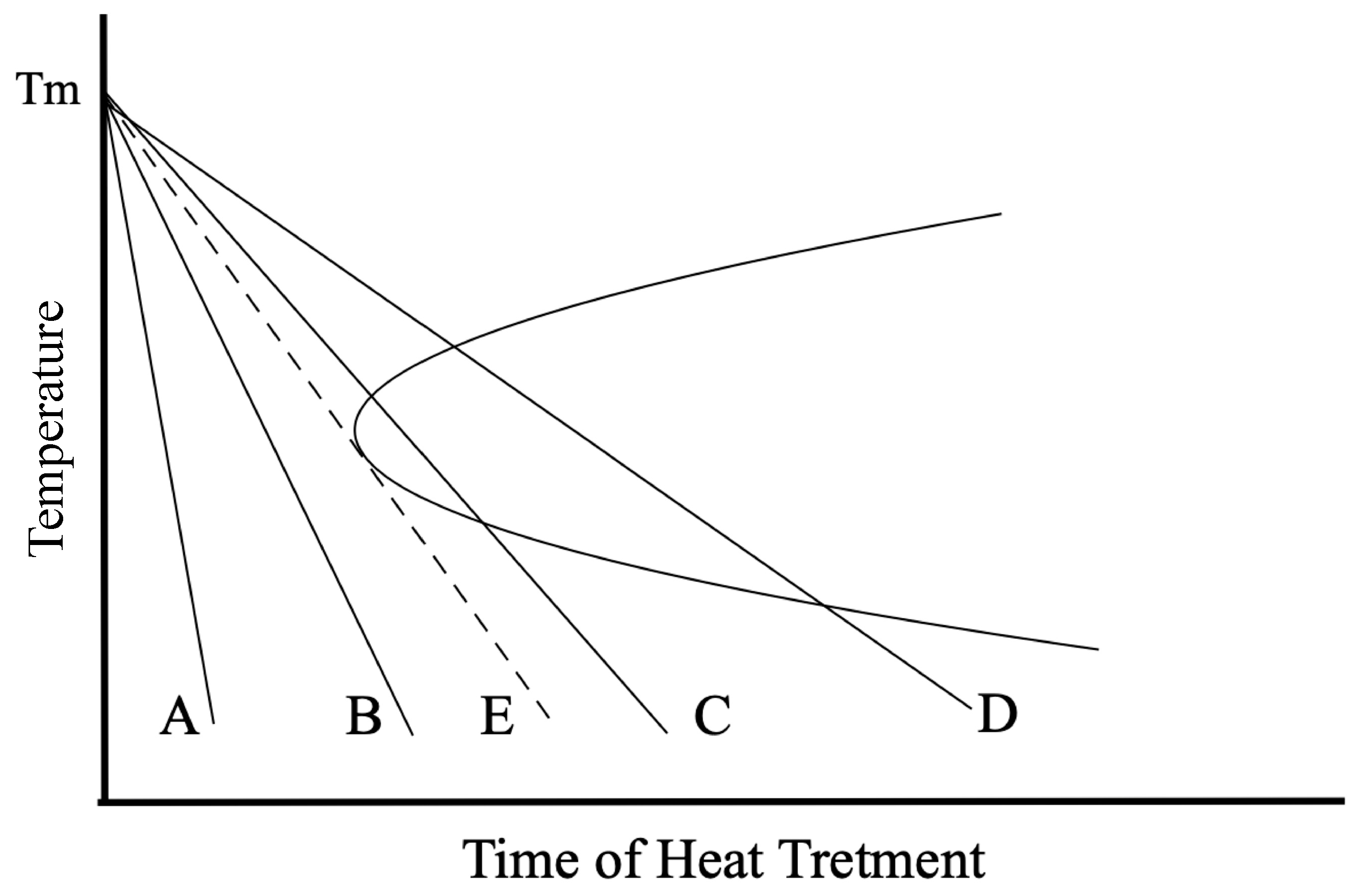
2. Anomalies of the Density–Temperature Relation of Silica Glass
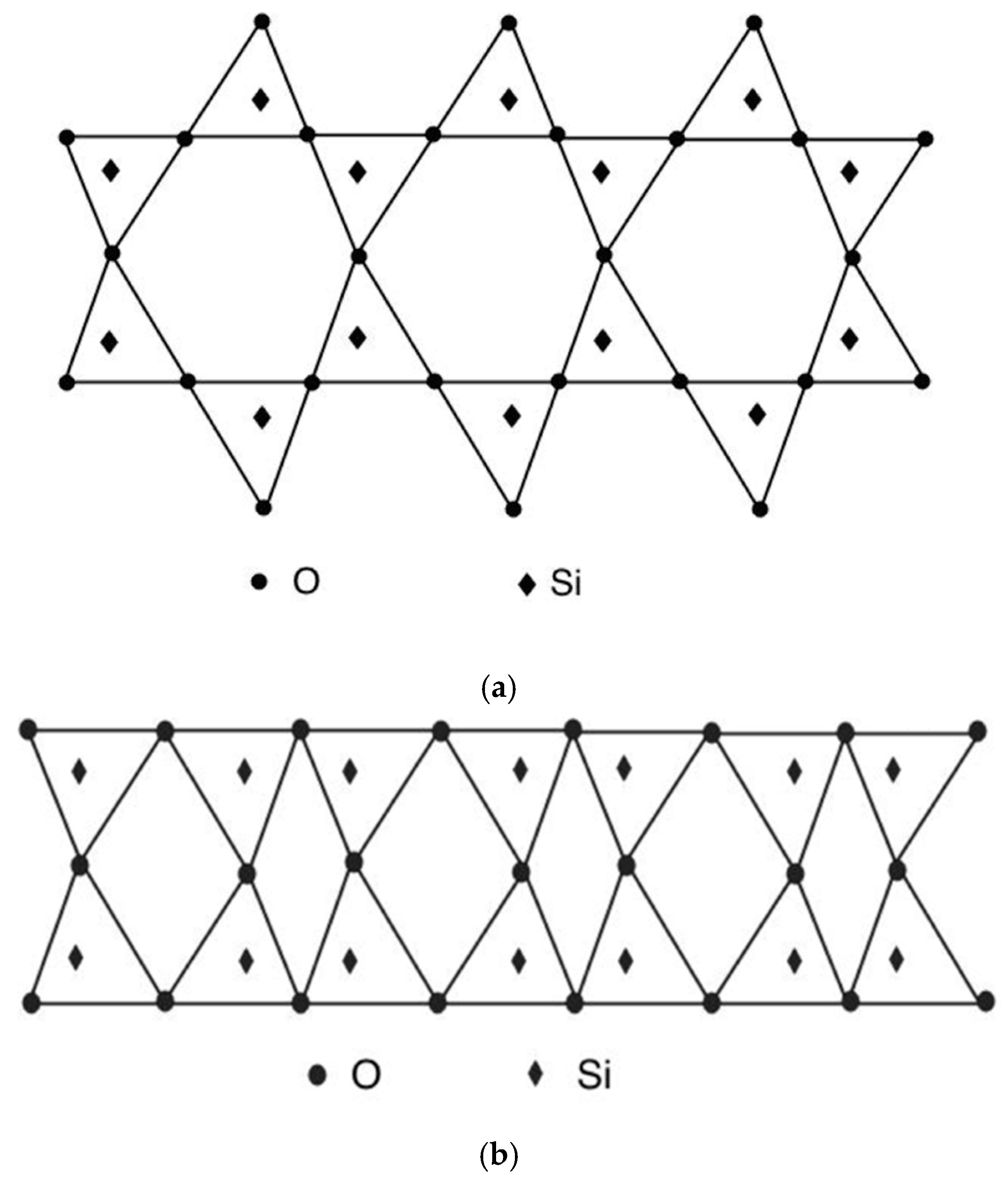
3. Nanoflake Model for the Silica Glass’s Structure in the Medium Range
4. Explanation of Density Anomaly of Silica Glass
5. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brückner, R. Properties and structure of vitreous silica 1. J. Non-Cryst. Solids 1970, 5, 123–175. [Google Scholar] [CrossRef]
- Brückner, R. Metastable equilibrium density of hydroxyl-free synthetic vitreous silica. J. Non-Cryst. Solids 1971, 5, 281–285. [Google Scholar] [CrossRef]
- Sen, S.; Andrus, R.L.; Baker, D.E.; Murtagh, M.T. Observation of an Anomalous Density Minimum in Vitreous Silica. Phys. Rev. Lett. 2004, 93, 125902. [Google Scholar] [CrossRef] [PubMed]
- Shelby, J.E. Density of vitreous silica. J. Non-Cryst. Solids 2004, 349, 331–336. [Google Scholar] [CrossRef]
- Skinner, L.B.; Benmore, C.J.; Weber, J.K.R.; Wilding, M.C.; Tumber, S.K.; Parise, J.B. A time resolved high energy X-ray diffraction study of cooling liquid SiO2. Phys. Chem. Chem. Phys. 2013, 15, 8566–8572. [Google Scholar] [CrossRef] [PubMed]
- Champagnon, B.; Martinez, V.; Martinet, C.; Le Parc, R.; Levelut, C. Density and density fluctuations of SiO2 glass: Comparison and light-scattering study. Phil. Mag. 2007, 87, 691–695. [Google Scholar] [CrossRef]
- Clark, A.N.; Lesher, C.E.; Jacobsen, S.D.; Sen, S. Mechanisms of anomalous compressibility of vitreous silica. Phys. Rev. B 2014, 90, 174110. [Google Scholar] [CrossRef]
- Tirelli, A.; Nakano, K. Topological Data Analysis for Revealing the Structural Origin of Density Anomalies in Silica Glass. J. Phys. Chem. B 2023, 127, 3302–3311. [Google Scholar] [CrossRef] [PubMed]
- Jabes, B.S.; Agarwal, M.; Chakravarty, C. Tetrahedral order, pair correlation entropy, and waterlike liquid state anomalies: Comparison of GeO2 with BeF2, SiO2, and H2O. J. Chem. Phys. 2010, 132, 234507. [Google Scholar] [CrossRef] [PubMed]
- Shih, Y.; Sundararaman, S.; Huang, L. Structural origin of the anomalous density maximum in silica and alkali silicate glasses. J. Am. Ceram. Soc. 2020, 103, 3942–3953. [Google Scholar] [CrossRef]
- Tan, A.R.; Urata, S.; Yamada, M.; Gómez-Bombarelli, R. Graph theory-based structural analysis on density anomaly of silica glass. Comput. Mater. Sci. 2023, 225, 112190. [Google Scholar] [CrossRef]
- Tanaka, H.; Tong, H.; Shi, R.; Russo, J. Revealing key structural features hidden in liquids and glasses. Nat. Rev. Phys. 2019, 1, 333–348. [Google Scholar] [CrossRef]
- Ojovan, I.; Lee, E. Topologically disordered systems at the glass transition. J. Phys. Condens. Matter 2006, 18, 11507–11520. [Google Scholar] [CrossRef]
- Cheng, S. A nano-flake model for the medium range structure in vitreous silica. Phys. Chem. Glas. Eur. J. Glas. Sci. Technol. Part B 2017, 58, 33–40. [Google Scholar] [CrossRef]
- Cheng, S. New Interpretation of X-ray Diffraction Pattern of Vitreous Silica. Ceramics 2021, 4, 83–96. [Google Scholar] [CrossRef]
- Cheng, S. Research Advancements in the Field of Materials Science; Index of Sciences Ltd.: London, UK, 2022; pp. 30+39+46. [Google Scholar]
- Hlavac, J. The Technology of Glass and Ceramics: An Introduction; Elsevier: Amsterdam, The Netherlands, 1983; p. 12. [Google Scholar]
- Brazhkin, V.V.; Lyapin, A.G.; Popova, S.V.; Voloshin, R.N. New Kinds of Phase Transitions: Transformations in Disordered Substances; NATO Science Series II; Brazhkin, V.V., Buldyrev, S.V., Ryzhov, V.N., Stanley, H.E., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; Volume 81, pp. 15–27. [Google Scholar]
- Zachariasen, W.H. The Atomic arrangement in glass. J. Am. Chem. Soc. 1932, 54, 3841–3851. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray determination of the structure of glass. J. Am. Ceram. Soc. 1934, 17, 249–254. [Google Scholar] [CrossRef]
- Warren, B.E.; Biscoe, J. Fourier analysis of X-ray patterns of soda-silica glass. J. Am. Ceram. Soc. 1938, 21, 259–265. [Google Scholar] [CrossRef]
- Israelachvili, J.S. The forces between surfaces. Philos. Mag. A 1981, 43, 753–770. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S. The Origin of Anomalous Density Behavior of Silica Glass. Materials 2023, 16, 6218. https://doi.org/10.3390/ma16186218
Cheng S. The Origin of Anomalous Density Behavior of Silica Glass. Materials. 2023; 16(18):6218. https://doi.org/10.3390/ma16186218
Chicago/Turabian StyleCheng, Shangcong. 2023. "The Origin of Anomalous Density Behavior of Silica Glass" Materials 16, no. 18: 6218. https://doi.org/10.3390/ma16186218
APA StyleCheng, S. (2023). The Origin of Anomalous Density Behavior of Silica Glass. Materials, 16(18), 6218. https://doi.org/10.3390/ma16186218





