Abstract
This work assesses the flexural performance of prestressed concrete beams with external carbon fiber-reinforced polymer (CFRP) tendons, focusing on tendon-related variables. A finite element analysis (FEA) method is verified. A numerical parametric analysis of prestressed concrete beams with external CFRP tendons is carried out. Four tendon-related variables are considered, namely, the area, initial prestress, depth and elastic modulus of tendons. The analysis shows that flexural ductility decreases as the tendon area, initial prestress or elastic modulus increases but is insensitive to the tendon depth. The ultimate tendon stress increment (Δσp) is influenced by all of the four variables investigated. JGJ 92-2016 (Chinese technical specification for concrete structures prestressed with unbonded tendons) significantly underestimates Δσp and, hence, is over-conservative for the strength design of these beams. An equation is proposed for calculating Δσp, taking into account all four variables investigated. An analytical model is then developed to estimate the flexural strength (Mu) of prestressed concrete beams with external CFRP tendons. The proposed analytical model shows good agreement with FEA, i.e., the mean discrepancy for Δσp is 0.9% with a standard deviation of 11.1%; and the mean discrepancy for Mu is −1.6% with a standard deviation of 2.1%.
1. Introduction
External prestressing is a powerful technique for structural rehabilitation and construction [1,2]. The major concern for this technique is the corrosive damage of external tendons made of conventional prestressing steel. The utilization of fiber-reinforced polymer (FRP) reinforcement in engineering is widespread [3,4]. The composite reinforcement may be made of glass fiber-reinforced polymer (GFRP) [5], aramid fiber-reinforced polymer (AFRP) [6], basalt fiber-reinforced polymer (BFRP) [7] or carbon fiber-reinforced polymer (CFRP) [8]. Of various FRP composites, carbon fiber-reinforced polymer (CFRP) possesses the best resistance to creep, namely, it can sustain around 80% of the tensile strength without experiencing creep rupture [9,10]. Therefore, CFRP is recognized to be ideal for prestressing applications [11,12,13]. This non-corrosive composite material is particularly suitable for external tendons in lieu of conventional prestressing steel in overcoming the corrosive problem [14,15], as these tendons are exposed to harsh conditions.
Researchers have paid much attention to prestressed concrete beams with external CFRP tendons. Grace et al. [16] performed a set of laboratory tests including one reference box-specimen without external tendons, one box-specimen prestressed by external CFRP tendons and one box-specimen with external CFRP tendons without prestressing. Their tests showed that the prestressing of girders by external CFRP tendons significantly increased the ultimate load-carrying capacities but reduced the ultimate deflection and flexural ductility. Bennitz et al. [17] tested seven reinforced concrete T-beams including one reference specimen without external prestressing and six specimens prestressed with external CFRP tendons. The main investigated variables were the deviator configuration (no deviators or one deviator at midspan), initial tendon depth and initial prestress level. Some of the specimens were designed based on the specimens that were prestressed with external steel tendons and tested by Tan and Ng [18] (i.e., using CFRP tendons instead of steel tendons). Similar to the findings concluded by Grace et al. [16], the test results demonstrated that beams with external CFRP tendons experienced higher flexural strength and lower ductility than the reference beam. In addition, beams with external CFRP tendons exhibited similar behavior compared to the counterparts with external steel tendons. The slight performance difference between beams with external CFRP and steel tendons was attributed to their difference in the tendon modulus of elasticity. This observation was later confirmed by a numerical work in terms of comprehensive aspects of behavior, including deformation, neutral axis evolution, tendon stress and flexural strength [19]. Contrary to the limited influence of the external tendon type, a numerical study performed by Pang et al. [20] showed that using FRP rebars instead of steel rebars significantly affected the structural behavior of concrete beams prestressed with external CFRP tendons.
Although much investigation has been performed, knowledge about externally CFRP prestressed beams has yet to be further developed. For example, the prestressing tendons are the primary material controlling the overall behavior of externally post-tensioned beams. Variables related to CFRP tendons include the tendon area, prestress level, tendon depth and modulus of elasticity. Note that the CFRP modulus of elasticity covers a large range and may vary from 80 to 500 GPa according to [10]. So far, the effects of these variables on the flexural response have not been fully addressed.
In this paper, a finite element analysis (FEA) method is verified with experimental data. A numerical study is carried out to examine the effects of various tendon-related variables. Based on the results of numerical parametric analysis, an analytical model is developed to predict the ultimate tendon stress and the flexural strength of prestressed concrete beams with external CFRP tendons.
2. Materials, Method and Verification
2.1. Materials and Method
According to [21], the stress–strain (σc–εc) law for compressive concrete is represented by
where fck is the cylinder compressive strength; k is a coefficient and εc0 is the strain corresponding to peak stress.
According to [22], the stress–strain law for tensile concrete is represented by
where Ec is the concrete elastic modulus; ft is the tensile strength; εcr is the cracking strain and εt0 = 10εcr.
The stress–strain (σp–εp) law for CFRP prestressing tendons [10] is represented by
where Ep is the tendon elastic modulus and εpu is the ultimate tendon strain.
It is assumed that the stress–strain (σs–εs) law for steel bars [10] is represented by
where Es is the steel elastic modulus and εy is the yield strain.
An FEA method for prestressed beams with external tendons was developed [23]. The following assumptions are adopted: (1) plane section remaining plane (excluding external tendons due to their unbonded nature [24]); (2) negligible bond-slip for internal steel bars; (3) negligible shear deformation (given that prestressed concrete beams generally have a high slenderness); (4) negligible frictional loss between external tendons and deviators (this assumption is reasonable in practice but may lead to a bit of an overestimation of the tendon stress). The Euler–Bernoulli beam theory is employed. The material laws for concrete and steel bars are introduced by applying the layered method. External prestressing is transformed into equivalent loads. The analysis consists of two steps. The first step is to determine the stress and deformation at self-weight only. The second step is to perform the full-range analysis from zero loads up to failure. During the analysis, as long as concrete crushing or reinforcement rupture occurs, the beam fails. Details of the FEA method were reported in [23].
2.2. Verification
Two beam specimens (B4 and B5) are selected herein [17]. The T-beams had a clear span of 3000 mm, subjected to two concentrated loads at third points, as illustrated in Figure 1. External tendons were attached with one deviator at the midspan. The specimens were designed to be identical except for the prestress level, i.e., the initial prestress was 396 MPa for B4 and 889 MPa for B5. CFRP tendons had an area of 100.5 mm2, an elastic modulus of 158 GPa and a rupture strength of 2790 MPa. The bottom steel bars had an area of 402 mm2, an elastic modulus of 172 GPa and a yield strength of 560 MPa. The top steel bars had an area of 201 mm2, an elastic modulus of 187 GPa and a yield strength of 510 MPa. The targeted fck was 30 MPa.
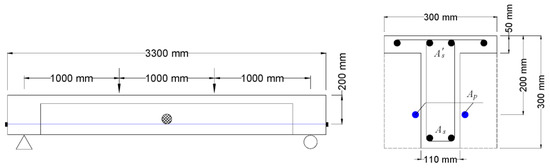
Figure 1.
Specimens prestressed with external CFRP tendons [17].
A comparison between the test and FEA results regarding the load versus deflection and load versus tendon force for two specimens is illustrated in Figure 2. It is seen that the FEA is able to reasonably capture the key response characteristics of the specimens during the complete loading stages, including the cracking, yielding and ultimate limit states. In addition, both test and FEA results demonstrate that Specimen B5 exhibits higher cracking and ultimate loads but a lower ultimate deflection and an increase in the tendon force compared to Specimen B4. This observation indicates the importance of the prestress level. In the following section, this variable is analyzed in more detail along with other important variables related to CFRP tendons (tendon area, depth and elastic modulus)
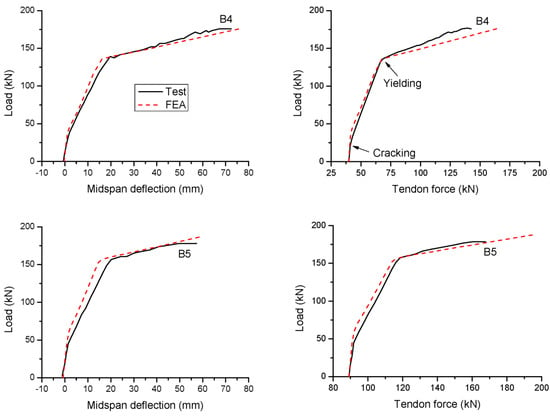
Figure 2.
Comparison with FEA results for test specimens.
3. Numerical Study
Figure 3 shows an externally prestressed concrete reference beam for numerical parametric study. The fck is 60 MPa. The tendon area is 1100 mm2. CFRP tendons have a rupture strength of 1840 MPa, an elastic modulus of 150 GPa and an initial prestress of 1104 MPa. Either the bottom or top steel bars have a cross-sectional area of 360 mm2, yield strength of 450 MPa and elastic modulus of 200 GPa.
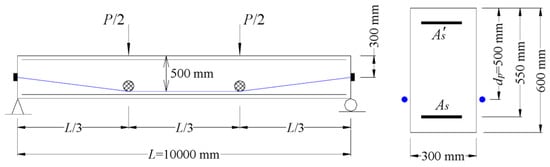
Figure 3.
Externally prestressed concrete reference beam for investigation.
3.1. Effect of Tendon Area
The tendon area, Ap, varies between 200 and 2000 mm2 to examine its effect on the structural response. Figure 4a shows that, at a small area of 200 mm2, the prestressing effect is not prominent, just counteracting the effect of the self-weight, i.e., the initial deflection prior to the live load is around zero. At Ap = 650 mm2 or above, the prestressing effect becomes pronounced, leading to an upward deflection at the initial state. However, at high areas of 1550 and 2000 mm2, there occur excessive prestressing effects. In these cases, the top face of the critical section has cracked prior to load application, and the upward deflection is rather big (13.5 and 18.3 mm). It is observed in Figure 4a that as the tendon area increases, the cracking and ultimate loads significantly increase, while the ultimate deflection obviously decreases. In this analysis, increasing the tendon area from 200 to 2000 mm2 leads to an increase in the ultimate load by 528.5% and a decrease in the ultimate deflection by 18.3%. Figure 4b shows that, at the initial state, the self-weight moment is 56 kN·m. A higher tendon area causes substantially higher flexural stiffness and flexural strength but a markedly smaller ultimate curvature.
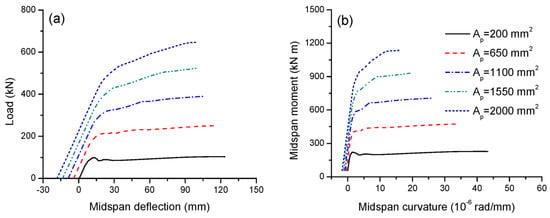
Figure 4.
Effect of tendon area on the deformation development. (a) Load-deflection; (b) moment-curvature.
The flexural ductility can be expressed by either deflection or curvature ductility, defined as the ratio of deflection or curvature at ultimate to that at yielding. Table 1 presents the data for the flexural ductility of beams with different tendon areas. It is seen that the flexural ductility quickly deceases as the tendon area increases, i.e., increasing the tendon area from 200 to 2000 mm2 leads to a decrease in deflection ductility by 70.8% and curvature ductility by 73.9%.

Table 1.
Effect of tendon area on flexural ductility.
Figure 5a,b illustrate the tendon stress versus midspan moment and deflection for beams with various tendon areas, respectively. In the initial range of loading up to tensile cracking, the rate of increase in tendon stress with the moment is independent of the tendon area, as demonstrated in Figure 5a. A higher tendon area causes a higher cracking moment and, correspondingly, a larger increase in tendon stress at cracking. Moreover, the ultimate stress increase in tendons decreases as the tendon area increases. In this analysis, increasing the tendon area from 200 to 2000 mm2 reduces the ultimate stress increase in external tendons by 24.4%. Figure 5b demonstrates that, for the same deflection, a high tendon area causes a small increase in tendon stress. The slopes of the stress–deflection relationship for beams with Ap = 200, 650, 1100, 1550 and 2000 mm2 are 2.54, 2.50, 2.45, 2.39 and 2.35 MPa/mm, respectively.
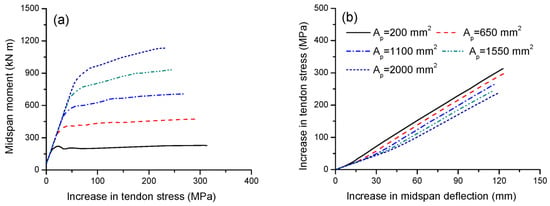
Figure 5.
Effect of tendon area on tendon stress development. (a) Moment versus increase in tendon stress; (b) increase in deflection versus increase in tendon stress.
3.2. Effect of Prestress Level
Five initial prestress levels are considered, i.e., 0, 20, 40, 60 and 80% of the rupture strength, or, equivalently, the initial prestress, σp0, corresponds to 0, 368, 736, 1104 and 1472 MPa. Figure 6a,b show the load-deflection and moment-curvature behavior of beams with various prestress levels.
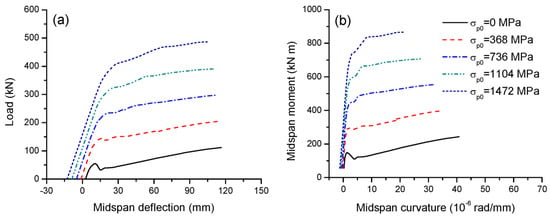
Figure 6.
Effect of initial prestress on the deformation development. (a) Load-deflection; (b) moment-curvature.
The initial deflection is highly dependent on the prestress level, i.e., a higher prestress level corresponds to a larger upward deflection. At a prestress level of zero, there is a downward deflection due to the self-weight effect, as expected. In addition, a higher prestress level effectively improves not only the cracking load and moment but also the ultimate load and flexural strength. It is worth mentioning that this observation is different from the case using bonded tendons. Generally, bonded FRP tendons rupture at failure, and therefore, the prestress level has practically no influence on the ultimate load or flexural strength of the beams [25]. On the other hand, the stress increase in external tendons is much slower than that in bonded tendons due to strain incompatibility between external tendons and the adjacent concrete and also the second-order effects [26]. Therefore, the ultimate stress in external tendons is generally below their rupture strength. The ultimate load or flexural strength is controlled by the tendon stress and is therefore strongly dependent on the prestress level in external tendons. Moreover, a higher prestress level results in a substantially higher flexural stiffness and lower ultimate curvature, while this variable appears to have a marginal effect on the ultimate deflection. Table 2 presents the data for flexural ductility for beams with different prestress levels. It is seen that as the prestress level increases, the flexural ductility quickly decreases. Increasing the initial prestress from 0 to 1472 MPa leads to a decrease in deflection ductility by 70.3% and in curvature ductility by 60.9%.

Table 2.
Effect of initial prestress on flexural ductility.
Figure 7a,b illustrate the effect of the initial prestress on the tendon stress versus midspan moment and deflection, respectively. Over the elastic range, the initial prestress has no impact on the increase in tendon stress as the moment develops, as shown in Figure 7a. A higher initial prestress corresponds to a higher increment in tendon stress at cracking but, generally, a lower one at ultimate. In this analysis, increasing the prestress level from 20 to 80% causes a reduction in the ultimate stress increase in external tendons by 10.7%. It is seen in Figure 7b that, when deflecting, the greater the initial prestress, the slower the increase in tendon stress.
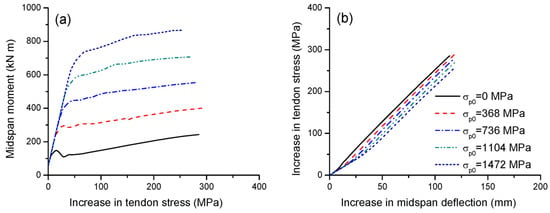
Figure 7.
Effect of initial prestress on tendon stress development. (a) Moment versus increase in tendon stress; (b) increase in deflection versus increase in tendon stress.
3.3. Effect of Tendon Depth
The initial tendon depth (maximum depth), dp, ranging from 400 to 600 mm, is used to investigate its effect on the structural response. The load-deflection and moment-curvature behavior are shown in Figure 8a,b, respectively. From Figure 8, it is seen that a larger tendon depth registers a larger upward deflection prior to load application. In addition, the cracking and ultimate loads or moments substantially increase as the tendon depth increases. In this analysis, increasing the tendon depth from 400 to 600 mm2 causes an increase in the ultimate load by 74.2%. However, the ultimate deflection, curvatures and flexural ductility are insensitive to the tendon depth, as presented in Table 3.
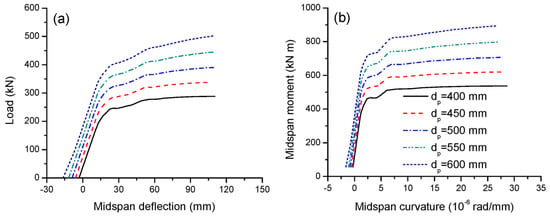
Figure 8.
Effect of tendon depth on the deformation development. (a) Load-deflection; (b) moment-curvature.

Table 3.
Effect of tendon depth on flexural ductility.
Figure 9a,b illustrate the tendon stress versus midspan moment and deflection for beams with various tendon depths, respectively. As the tendon depth increases, the ultimate tendon stress increases substantially. As mentioned previously, the beams with different tendon depths exhibit approximately the same deformation at ultimate, implying there are approximately the same concrete strain distributions along the depth of the sections of these beams. Therefore, the larger the tendon depth, the larger the average change in the concrete strain at the same level of the external tendons and, thereby, the larger the tendon stress increase. Due to a lower reduction in the effective tendon depth, a larger tendon depth assumes relatively less significant second-order effects, which would reduce relatively less tendon stresses. In this analysis, increasing the tendon depth from 400 to 600 mm causes an increase in the ultimate tendon stress increment by 93.2%. For the same deflection, the greater the tendon depth, the greater the tendon stress increase. The slopes of the stress–deflection relationship for beams with dp = 400, 450, 500, 550 and 600 mm are 1.70, 1.96, 2.45, 2.86 and 3.30 MPa/mm, respectively.
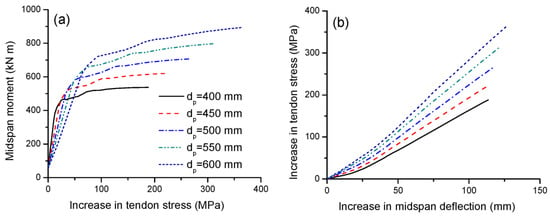
Figure 9.
Effect of tendon depth on tendon stress development. (a) Moment versus increase in tendon stress; (b) increase in deflection versus increase in tendon stress.
3.4. Effect of Tendon Elastic Modulus
The elastic modulus of CFRP tendons, Ep, ranges from 80 to 500 GPa [10]. Figure 10a,b show the effect of the tendon elastic modulus on the load-deflection and moment-curvature behavior, respectively. The beams exhibit identical behavior up to cracking. After that, the behaviors differ because the contribution of the external tendon becomes increasingly important. A higher tendon modulus of elasticity mobilizes stiffer behavior of the beams. As the tendon modulus of elasticity increases, the ultimate load and flexural strength increase, while the ultimate deflection and curvature tend to decrease. As presented in Table 4, increasing the tendon elastic modulus from 80 to 500 GPa leads to a decrease in deflection ductility by 11.1% and in curvature ductility by 31.4%.
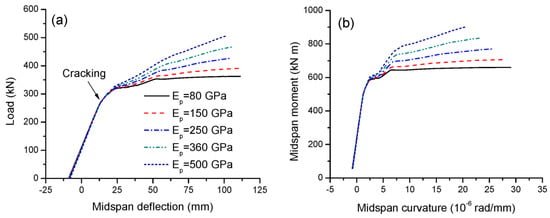
Figure 10.
Effect of tendon elastic modulus on the deformation development. (a) Load-deflection; (b) moment-curvature.

Table 4.
Effect of tendon elastic modulus on flexural ductility.
Figure 11a,b show the effect of the tendon elastic modulus on the tendon stress versus midspan moment and deflection, respectively. At a given moment or deflection level, a high tendon elastic modulus corresponds to a significantly higher tendon stress. The ultimate stress increase in external tendons with an elastic modulus of 500 GPa is 5.17 times that of 80 GPa. It should be noted that the stress ratio of 5.17 is smaller than the modulus ratio of 6.25, as a higher tendon elastic modulus would lead to a smaller ultimate tendon strain. The slopes of the stress–deflection relationship for beams with Ep = 80, 150, 250, 360 and 500 GPa are 1.33, 2.45, 3.98, 5.57 and 7.43 MPa/mm, respectively.
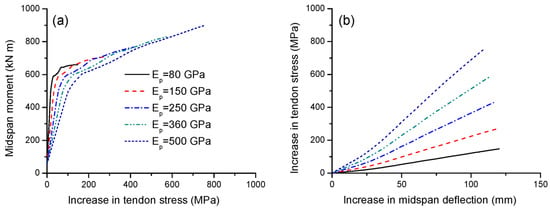
Figure 11.
Effect of tendon elastic modulus on tendon stress development. (a) Moment versus increase in tendon stress; (b) increase in deflection versus increase in tendon stress.
4. Analytical Study
4.1. Method
In externally post-tensioned members, the ultimate tendon stress, σpu, depends on the whole member deformation, and therefore, its accurate predictions are complicated. The calculation of σpu is essential for the flexural strength design of externally prestressed members [27,28,29,30,31,32]. The stress σpu is commonly expressed by
where Δσp is the ultimate stress increment and σpe is the effective prestress.
JGJ 92-2016 [33] recommended the following equation for predicting Δσp:
where ω0 is the combined reinforcing index; h is the section height; L is the span and k1 is a coefficient associated with the pattern of loading on continuous beams. For the simply supported beams considered in this study, k1 = 1.0. The ω0 is expressed by
where b is the section width and As and fy are the tensile steel bar area and yield strength, respectively.
Figure 12 shows the Δσp–ω0 relationships for the beams with different tendon-related variables obtained by FEA along with the JGJ 92-2016 curve. By adopting the key parameter ω0, JGJ 92-2016 takes into account the effect of the tendon area, prestress level and tendon depth but neglects the effect of the tendon modulus of elasticity. In addition, JGJ 92-2016 significantly underestimates the value of Δσp, except for the beam with Ep = 80 GPa.
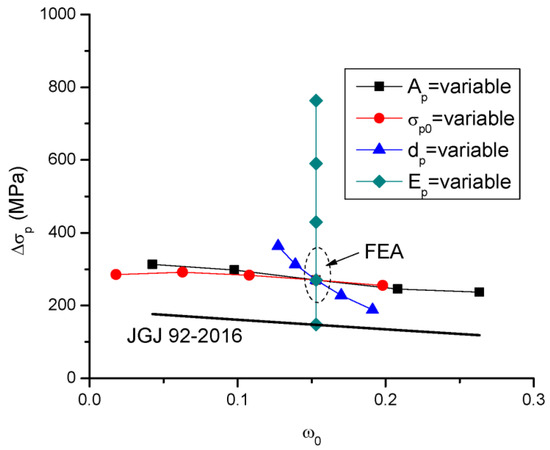
Figure 12.
Relationships between Δσp and ω0 according to FEA and JGJ 92-2016.
The numerical analysis demonstrates that the ultimate tendon stress is affected by all four tendon-related variables, i.e., the tendon area, prestress level, tendon depth and modulus of elasticity. As the parameter ω0 involves three of the tendon-related variables (i.e., Ap, dp and σpe), this parameter is adopted in a new equation to be developed herein for the prediction of Δσp. As illustrated in Figure 13, fitting to the FEA data about the Δσp–ω0 relationship of beams with various tendon areas leads to the following expression:
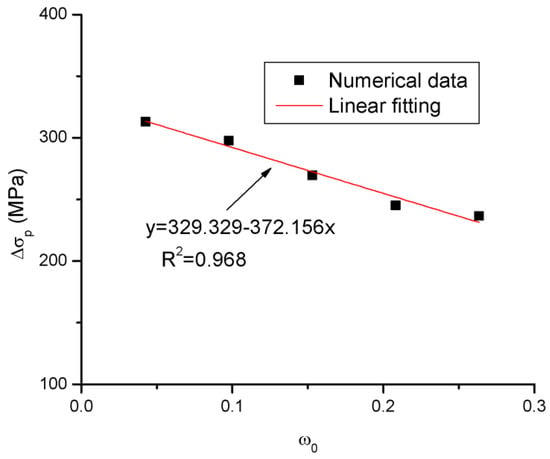
Figure 13.
Fitting to FEA data about the Δσp–ω0 relationship.
Note that the above equation does not consider the tendon modulus of elasticity, which has been demonstrated to be crucial for Δσp. In order to include the effect of the tendon elastic modulus, Equation (8) is modified by introducing a coefficient as follows:
where λE is a coefficient related with the tendon elastic modulus Ep. The FEA data regarding the variation in λE against Ep/Eps is presented in Figure 14, where Eps is the elastic modulus of prestressing steel, taken to be equal to 195 GPa. According to the fit curve, λE is expressed by
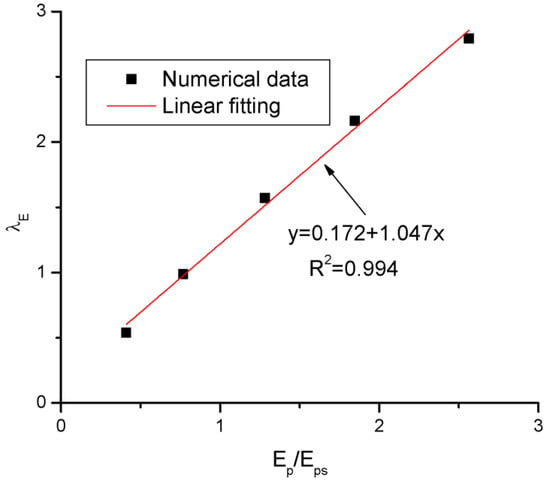
Figure 14.
Fitting to FEA data about the λE versus EP/Eps relationship.
The axial equilibrium of beams is given by the following equation [34]:
where β1 = 0.85; and are the compressive steel bar area and yield strength, respectively and cu is the neutral axis depth. According to Equation (11), cu is calculated by
The flexural strength is determined by the following equation [34]:
where ds and are the depths of tensile and compressive bars, respectively, and de is the effective depth of external tendons, which is given by
where Rd is a reduction coefficient due to second-order effects. According to [35], for third-point loading, the value of Rd is calculated from
4.2. Results
A comparison of Δσp and Mu for beams with different tendon-related variables predicted by the simplified models and FEA is presented in Table 5 and Figure 15 and Figure 16. It is seen that JGJ 92-2016 leads to significant underestimation in Δσp, and, therefore, this code underestimates the flexural strength of the beams. The predicted Δσp is 53.5% of the FEA data, on average, with a standard deviation of 16.2%, while the predicted Mu is 88.6% of the FEA data, on average, with a standard deviation of 6.9%. The proposed simplified model shows much better predictions than JGJ 92-2016. According to the proposed model, the mean discrepancy for Δσp is 0.9%, with a standard deviation of 11.1%, while the mean discrepancy for Mu is −1.6%, with a standard deviation of 2.1%.

Table 5.
Comparison of Δσp and Mu by simplified models with FEA data.
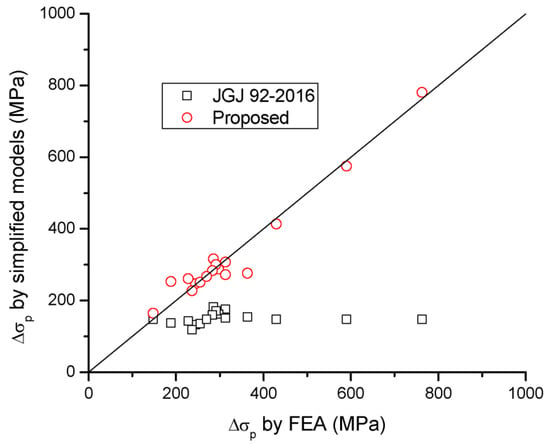
Figure 15.
Correlation of Δσp by simplified models to FEA data.
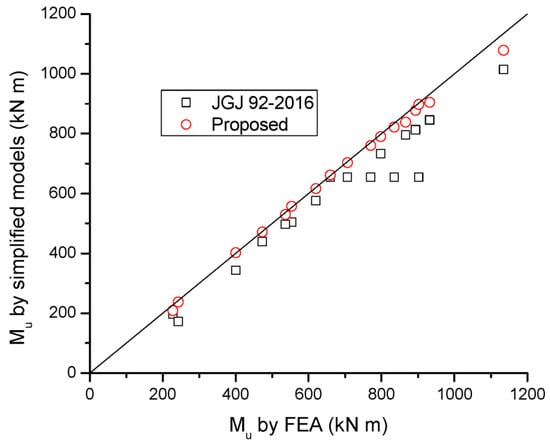
Figure 16.
Correlation of Mu by simplified models to FEA data.
5. Conclusions
By applying a validated FEA method, a numerical study is carried out to examine the flexural behavior of concrete beams prestressed with external CFRP tendons. Particular focus is placed on variables related to CFRP tendons, i.e., the area, prestress level, depth and elastic modulus of the tendons. An analytical model is also developed. The main conclusions are:
- CFRP tendons play a crucial role in the structural performance of externally prestressed beams, including the flexural stiffness, ultimate load-carrying capacity, stress increase in external tendons, deformation and ductility. A higher tendon area, initial prestress or elastic modulus causes a lower flexural ductility. The Δσp decreases as the tendon area or initial prestress level increases or as the tendon depth or elastic modulus increases.
- JGJ 92-2016 significantly underestimates the ultimate tendon stress, and hence, this code is over-conservative for flexural strength predictions of externally CFRP prestressed beams. The predicted Δσp and Mu by JGJ 92-2016 are 53.5% and 88.6% of the FEA data, on average, respectively.
- An equation is proposed to calculate Δσp, considering the influence of the tendon area, effective prestress, tendon depth and modulus of elasticity. The proposed analytical model shows excellent predictions of tendon stress and flexural strength, i.e., the mean discrepancy for Δσp is 0.9% with a standard deviation of 11.1%, while the mean discrepancy for Mu is −1.6% with a standard deviation of 2.1%.
Author Contributions
Conceptualization, M.P. and T.L.; methodology, M.P.; software, H.H.; validation, T.L.; formal analysis, H.H.; investigation, H.H.; resources, T.L.; data curation, H.H.; writing—original draft preparation, H.H. and T.L.; writing—review and editing, M.P.; visualization, M.P.; supervision, T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Portuguese Foundation for Science and Technology, grant numbers 2022.04729.CEECIND, UIDB/00285/2020 and LA/P/0112/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Recupero, A.; Spinella, N.; Colajanni, P.; Scilipoti, C.D. Increasing the capacity of existing bridges by using unbonded prestressing technology: A case study. Adv. Civil Eng. 2014, 2014, 840902. [Google Scholar] [CrossRef]
- Santarsiero, G.; Picciano, V. Durability enhancement of half-joints in RC bridges through external prestressed tendons: The Musmeci Bridge’s case study. Case Stud. Constr. Mater. 2023, 18, e01813. [Google Scholar] [CrossRef]
- Panahi, M.; Zareei, S.A.; Izadi, A. Flexural strengthening of reinforced concrete beams through externally bonded FRP sheets and near surface mounted FRP bars. Case Stud. Constr. Mater. 2021, 15, e00601. [Google Scholar] [CrossRef]
- Abdallah, M.; Al Mahmoud, F.; Khelil, A.; Mercier, J.; Almassri, B. Assessment of the flexural behavior of continuous RC beams strengthened with NSM-FRP bars, experimental and analytical study. Compos. Struct. 2020, 242, 112127. [Google Scholar] [CrossRef]
- Barris, C.; Torres, L.; Vilanova, I.; Mias, C.; Llorens, M. Experimental study on crack width and crack spacing for Glass-FRP reinforced concrete beams. Eng. Struct. 2017, 131, 231–242. [Google Scholar] [CrossRef]
- Efe, S.; Shokouhian, M.; Head, M.; Chinaka, E. Numerical study on the cyclic response of AFRP reinforced columns with externally unbonded energy dissipaters. Struct. Infrastruct. Eng. 2018, 14, 218–231. [Google Scholar] [CrossRef]
- Alkhraisha, H.; Mhanna, H.; Tello, N.; Abed, F. Serviceability and flexural behavior of concrete beams reinforced with basalt fiber-reinforced polymer (BFRP) bars exposed to harsh conditions. Polymers 2020, 12, 2110. [Google Scholar] [CrossRef]
- Alam, M.S.; Hussein, A. Relationship between the shear capacity and the flexural cracking load of FRP reinforced concrete beams. Constr. Build. Mater. 2017, 154, 819–828. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars; ACI 440.1R-15; American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- FIB Model Code 2010; Bulletins 55 and 56; International Federation for Structural Concrete: Lausanne, Switzerland, 2012.
- Zhuge, P.; Tao, G.; Wang, B.; Jie, Z.; Zhang, Z. Effects of high temperatures on the performance of carbon fiber reinforced polymer (CFRP) composite cables protected with fire-retardant materials. Materials 2022, 15, 4696. [Google Scholar] [CrossRef]
- Xia, J.; Xu, Z.; Zhuge, P.; Wang, B.; Cai, W.; Fu, J. Testing and evaluation of flexural tensile strength of prestressed CFRP cables. Materials 2022, 15, 7065. [Google Scholar] [CrossRef]
- Elbelbisi, A.H.; El-Sisi, A.A.; Hassan, H.A.; Salim, H.A.; Shabaan, H.F. Parametric study on steel-concrete composite beams strengthened with post-tensioned CFRP tendons. Sustainability 2022, 14, 15792. [Google Scholar] [CrossRef]
- Jia, L.; Fang, Z.; Hu, R.; Pilakoutas, K.; Huang, Z. Fatigue behavior of UHPC beams prestressed with external CFRP tendons. ASCE J. Compos. Constr. 2022, 26, 04022066. [Google Scholar] [CrossRef]
- Abdel Aziz, M.; Abdel-Sayed, G.; Ghrib, F.; Grace, N.F.; Madugula, M.K.S. Analysis of concrete beams prestressed and post-tensioned with externally unbonded carbon fiber reinforced polymer tendons. Can. J. Civ. Eng. 2005, 31, 1138–1151. [Google Scholar] [CrossRef]
- Grace, N.F.; Singh, S.B.; Puravankara, S.; Sachidanandan, S. Behavior of prestressed concrete box-beam bridges using CFRP tendons. PCI J. 2006, 51, 26–41. [Google Scholar] [CrossRef]
- Bennitz, A.; Schmidt, J.W.; Nilimaa, J.; Taljsten, B.; Goltermann, P.; Ravn, D.L. Reinforced concrete T-beams externally prestressed with unbonded carbon fiber-reinforced polymer tendons. ACI Struct. J. 2012, 109, 521–530. [Google Scholar]
- Tan, K.H.; Ng, C.K. Effects of Deviators and tendon configuration on behavior of externally prestressed beams. ACI Struct. J. 1997, 94, 13–21. [Google Scholar]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Numerical analysis of behaviour of concrete beams with external FRP tendons. Constr. Build. Mater. 2012, 35, 970–978. [Google Scholar] [CrossRef]
- Pang, M.; Li, Z.; Lou, T. Numerical study of using FRP and steel rebars in simply supported prestressed concrete beams with external FRP tendons. Polymers 2020, 12, 2773. [Google Scholar] [CrossRef]
- EN 1992-1-1; CEN Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Kwak, H.G.; Kim, S.P. Nonlinear analysis of RC beams based on moment-curvature relation. Comput. Struct. 2002, 80, 615–628. [Google Scholar] [CrossRef]
- Lou, T.; Xiang, Y. Finite element modeling of concrete beams prestressed with external tendons. Eng. Struct. 2006, 28, 1919–1926. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.C.; Tullini, N. Vibration of prestressed beams: Experimental and finite-element analysis of post-tensioned thin-walled box-girders. J. Constr. Steel Res. 2023, 205, 107854. [Google Scholar] [CrossRef]
- Kim, Y.J. Flexural response of concrete beams prestressed with AFRP tendons: Numerical investigation. ASCE J. Compos. Constr. 2010, 14, 647–658. [Google Scholar] [CrossRef]
- Lou, T.; Karavasilis, T.L.; Chen, B. Assessment of second-order effect in externally prestessed steel-concrete composite beams. ASCE J. Bridge Eng. 2021, 26, 04021024. [Google Scholar] [CrossRef]
- Lou, T.; Li, Z.; Pang, M. Behavior of externally prestressed continuous beams with FRP/steel rebars under symmetrical/unsymmetrical loading: Numerical study. Case Stud. Constr. Mater. 2022, 17, e01196. [Google Scholar] [CrossRef]
- Alqam, M.; Alkhairi, F.; Naaman, A. An improved methodology for the prediction of the stress at ultimate in unbonded internal and external steel tendons. Arab. J. Sci. Eng. 2020, 45, 7915–7954. [Google Scholar] [CrossRef]
- Ghallab, A. Calculating ultimate tendon stress in externally prestressed continuous concrete beams using simplified formulas. Eng. Struct. 2013, 46, 417–430. [Google Scholar] [CrossRef]
- He, Z.Q.; Liu, Z. Stresses in external and internal unbonded tendons: Unified methodology and design equations. ASCE J. Struct. Eng. 2010, 136, 1055–1065. [Google Scholar] [CrossRef]
- Roberts-Wollmann, C.L.; Kreger, M.E.; Rogowsky, D.M.; Breen, J.E. Stresses in external tendons at ultimate. ACI Struct. J. 2005, 102, 206–213. [Google Scholar]
- Maguire, M.; Chang, M.; Collins, W.; Sun, Y. Stress increase of unbonded tendons in continuous posttensioned members. ASCE J. Bridge Eng. 2017, 22, 04016115. [Google Scholar] [CrossRef]
- JGJ 92-2016; Technical Specification for Concrete Structures Prestressed with Unbonded Tendons. China Architecture & Building Press: Beijing, China, 2016.
- Hu, H.; Lopes, S.M.R.; Lopes, A.V.; Lou, T. Flexural response of axially restricted RC beams: Numerical and theoretical study. Materials 2022, 15, 6052. [Google Scholar] [CrossRef]
- ACI Committee 440. Prestressing Concrete Structures with FRP Tendons; ACI 440.4R-04; American Concrete Institute: Farmington Hills, MI, USA, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).