Non-Fourier Heat Conduction of Nano-Films under Ultra-Fast Laser
Abstract
1. Introduction
2. Method
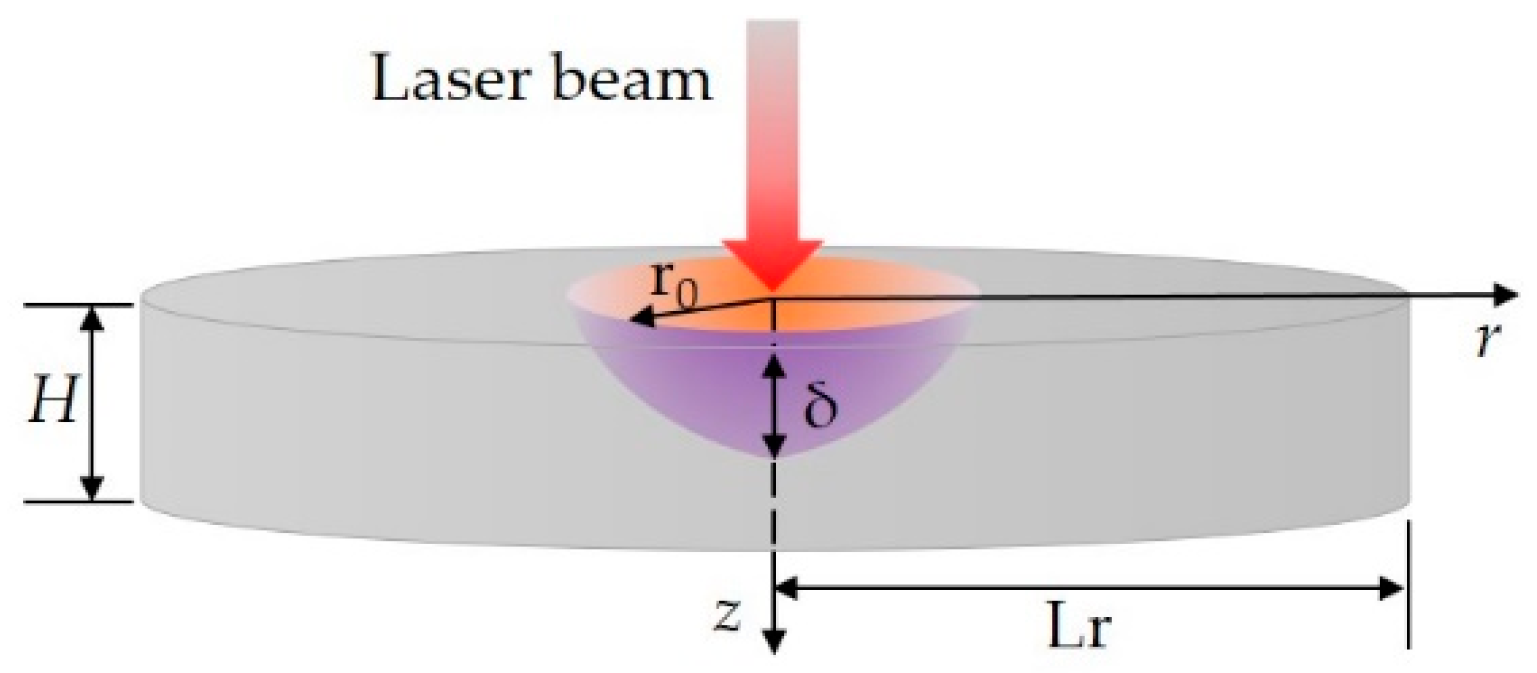
2.1. Physical Model
2.2. Mathematical Model
2.3. Cases Descriptions
3. Analysis of Results
3.1. Authentication
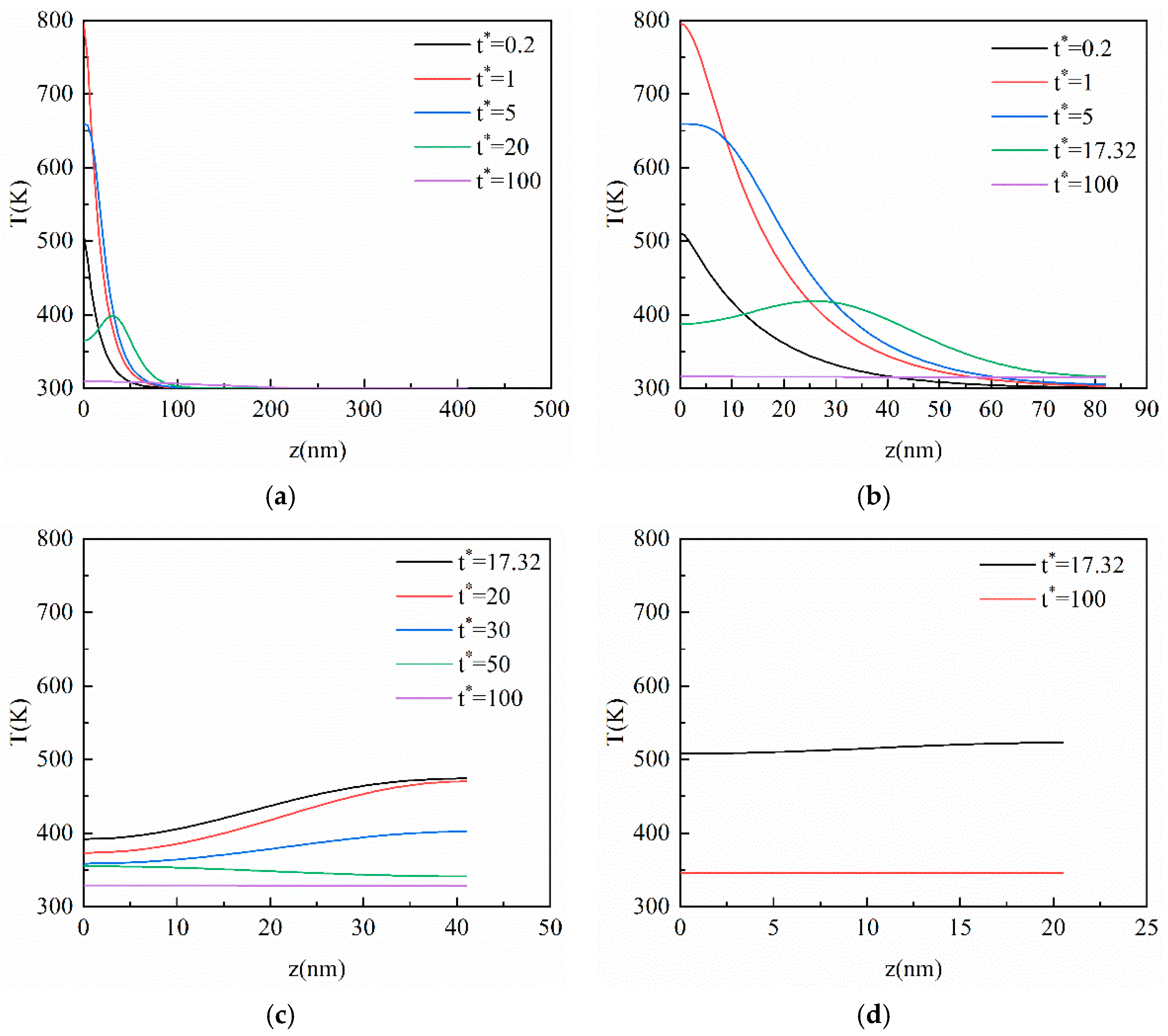
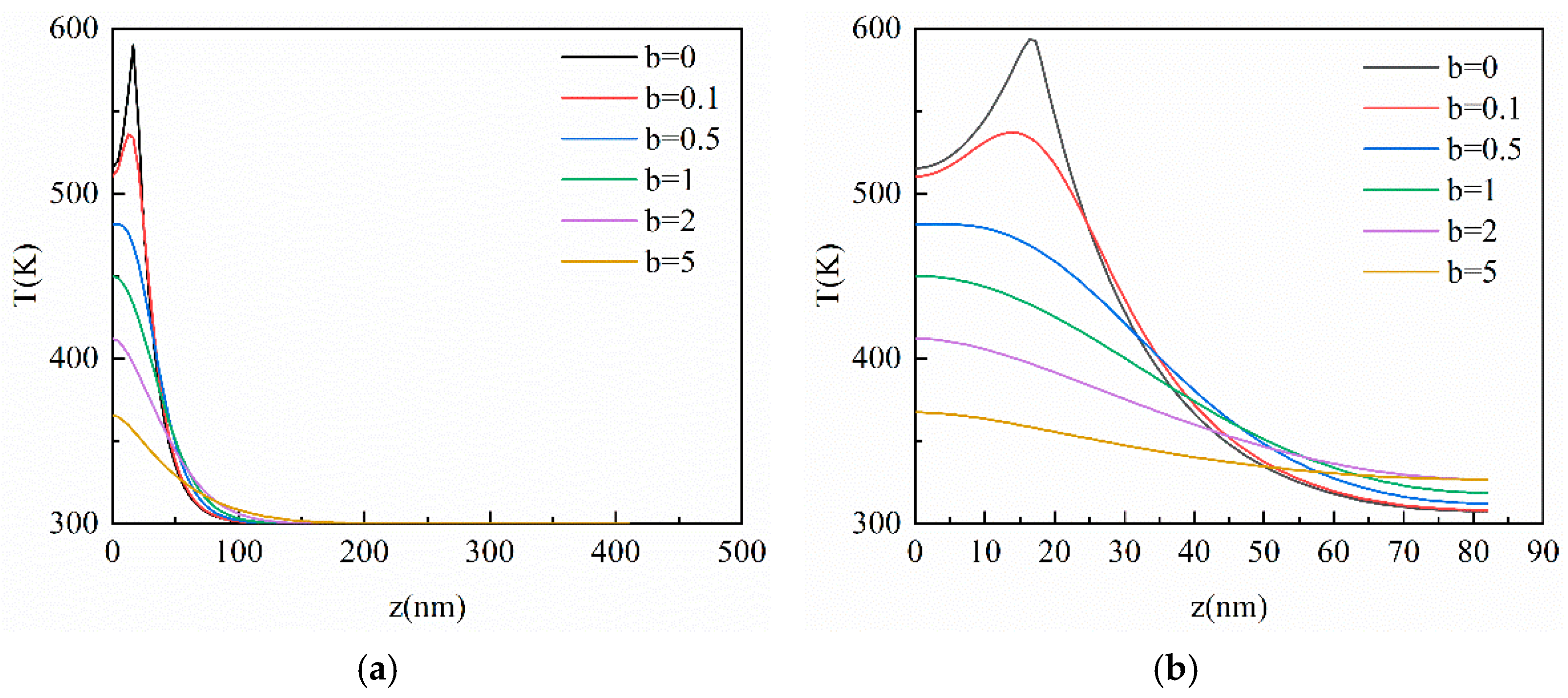
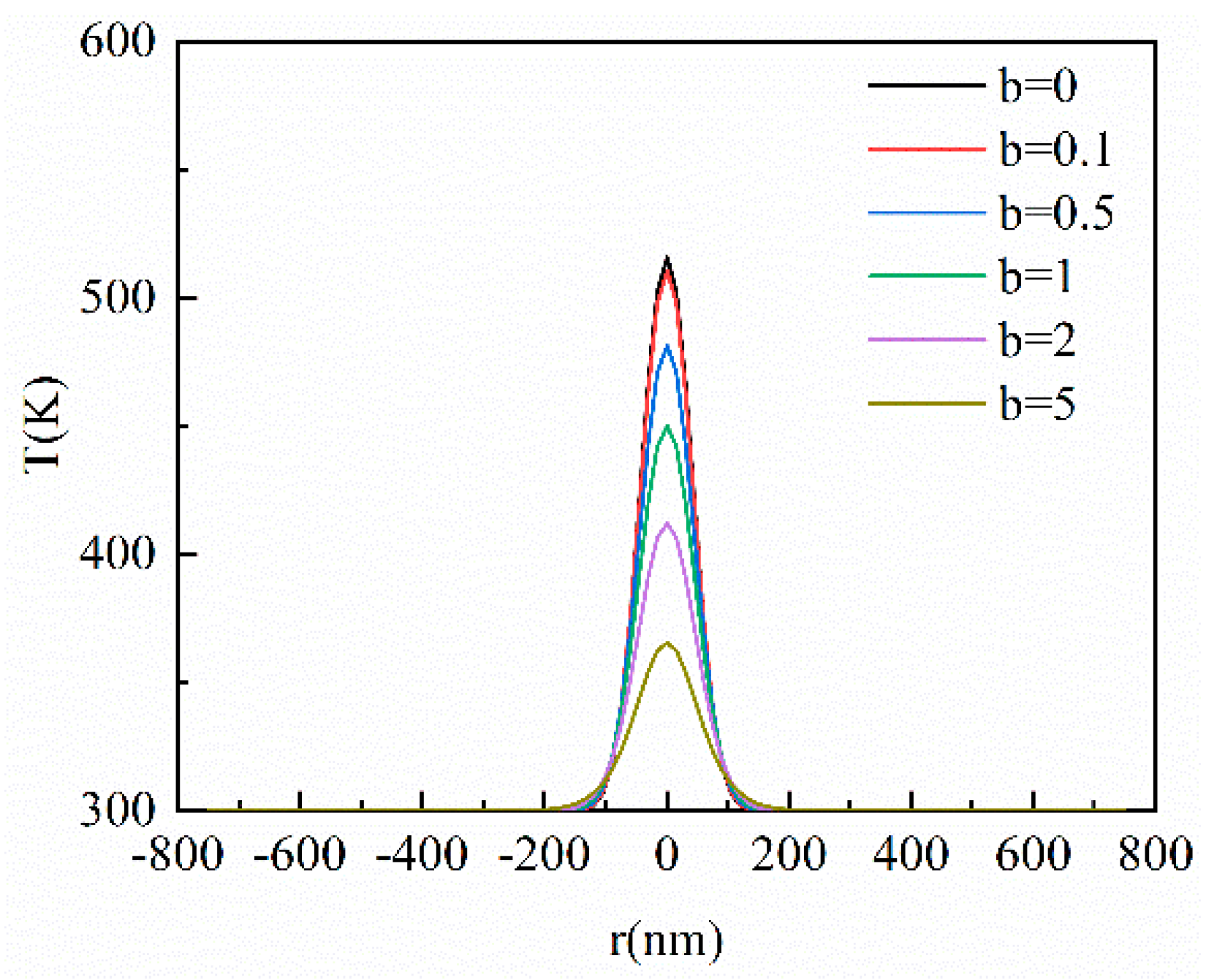
3.2. Result of the CV Model
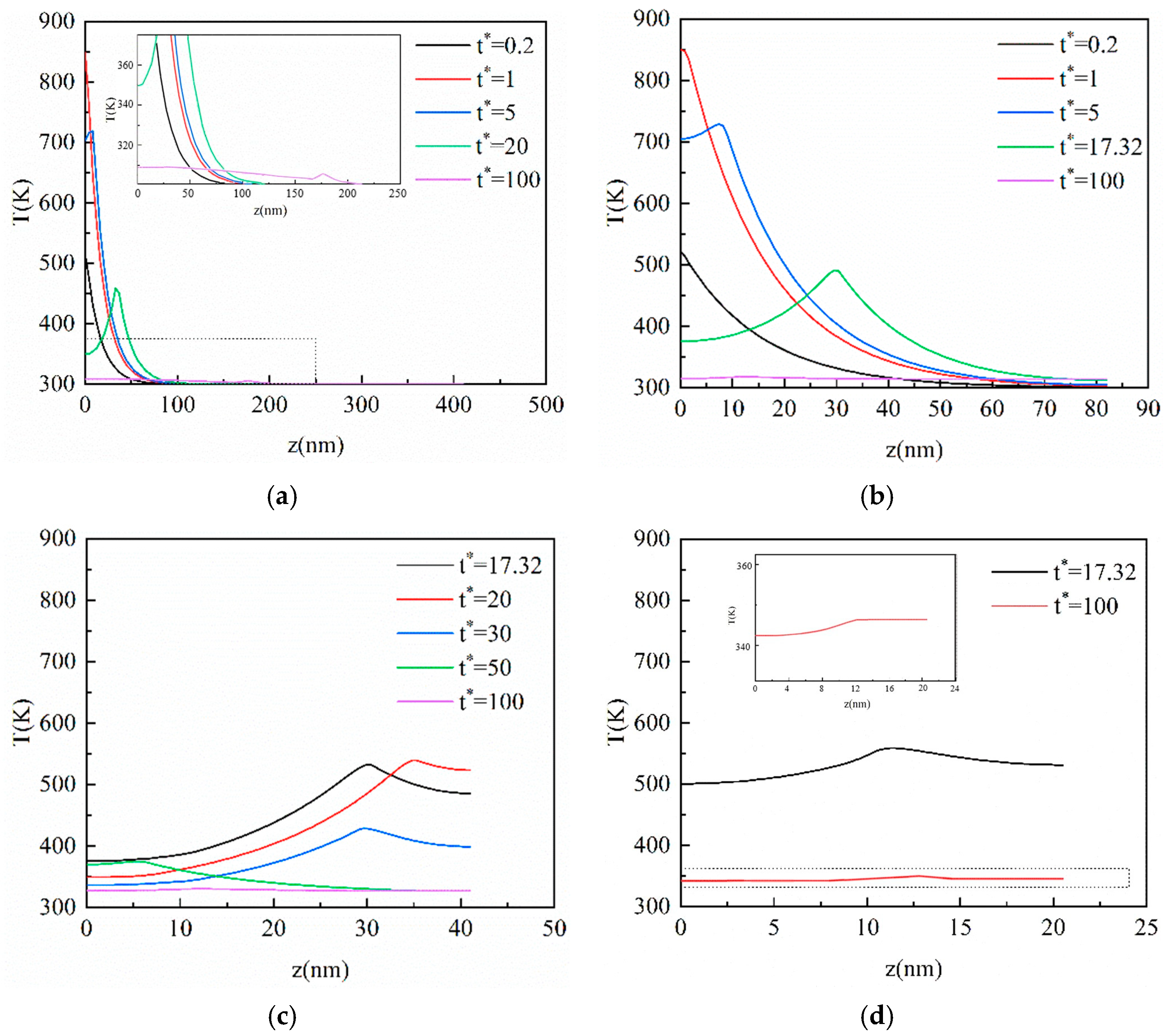
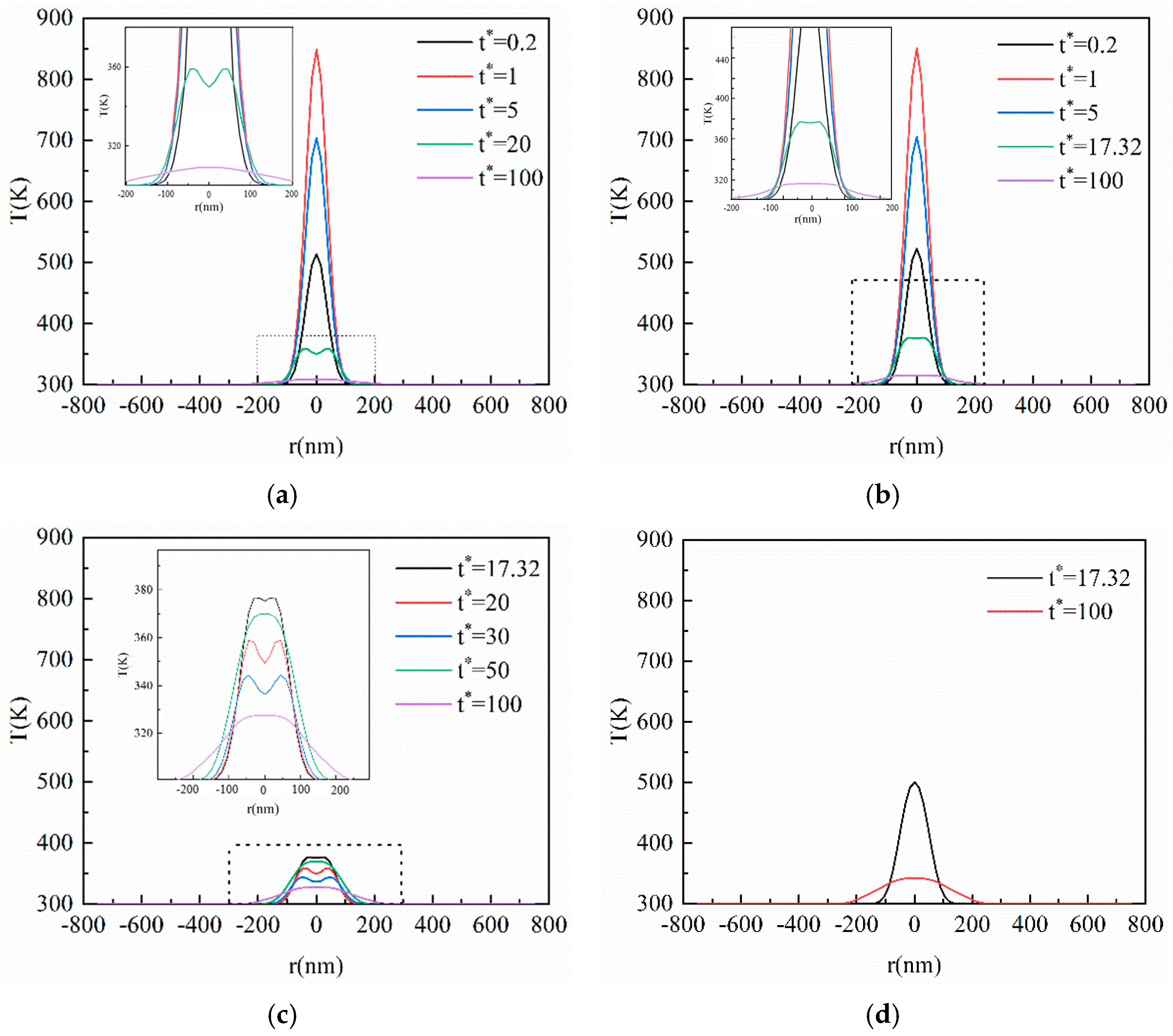
3.3. Result of the DPL Model
3.4. Influence of the Hysteresis Time of the Temperature Gradient
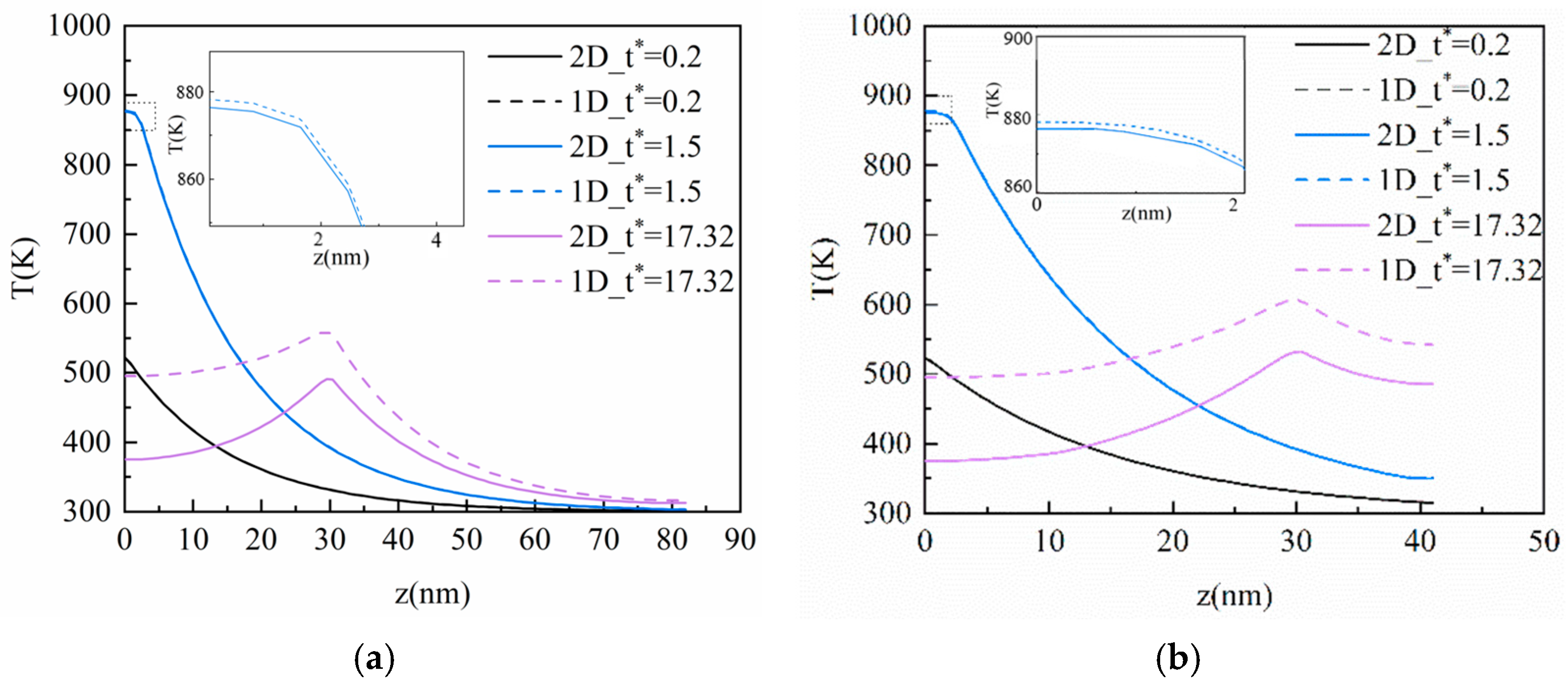
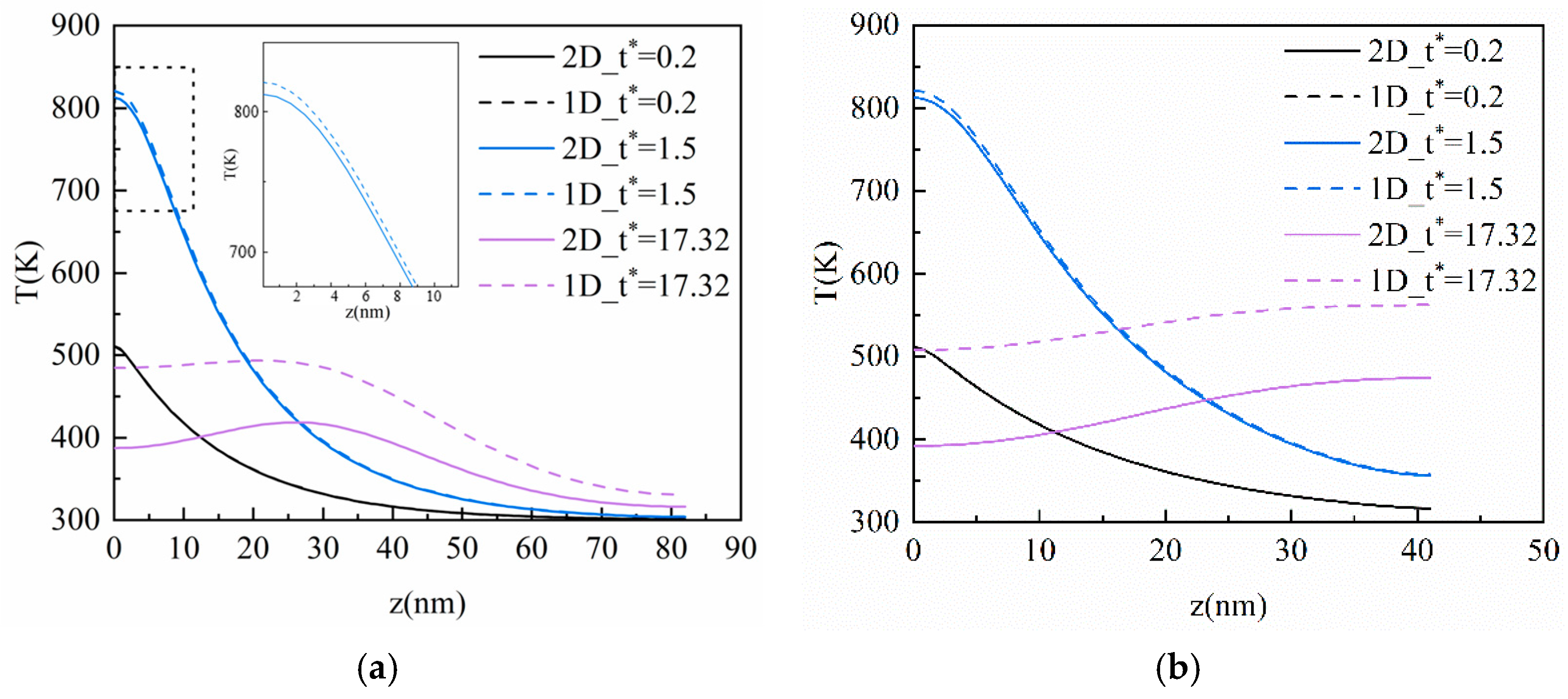
3.5. Comparative between 2-D and 1-D Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Catania, F.; Oliveira, H.; Lugoda, P. Thin-film electronics on active substrates: Review of materials, technologies and applications. J. Phys. D Appl. Phys. 2022, 55, 323002. [Google Scholar] [CrossRef]
- Abhik, S.; Sudip, M.; Kanoria, M. Effect of nonlocality in the vibration of a microscale ribbon due to laser pulse. Waves Random Complex Media 2020, 32, 2751–2775. [Google Scholar]
- Badgujar, A.C.; Dusane, R.O.; Dhage, S.R. Solution-processed CIGS thin film solar cell by controlled selenization process. Mater. Today Proc. 2022, 52, 829–833. [Google Scholar] [CrossRef]
- Abouabassi, K.; Sala, A.; Atourki, L. Electrodeposited CuSbSe2 thin films based solar cells on various substrates. J. Nanopart. Res. 2022, 24, 221. [Google Scholar] [CrossRef]
- Al-Qaissi, H.; Al-qarni, Y.; Al-Aniezi, A. Optical characterizations of synthetic nano PcGaCl thin film. In vitro, hemocompatibility, cytotoxicity, and PDT evaluation. Dig. J. Nanomater. Biostruct. 2022, 17, 861–869. [Google Scholar] [CrossRef]
- Asgar, A.; Barman, A.; Sanatan, D. Electromagnetic phenomena in cilia actuated peristaltic transport of hybrid nano-blood with Jeffrey model through an artery sustaining regnant magnetic field. Waves Random Complex Media 2022, 1–32. [Google Scholar]
- He, S.Q.; He, T.H. Investigation on the transient response of a porous half-space with strain and thermal relaxations due to laser pulse heating. Waves Random Complex Media 2021, 1–25. [Google Scholar] [CrossRef]
- Joseph, D.D.; Preziosi, L. Addendum to the Paper Thermal waves. Rev. Mod. Phys. 1990, 62, 375–391. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Ghazanfarian, J.; Shomali, Z.; Abbassi, A. Macro-to nanoscale heat and mass transfer: The lagging behavior. Int. J. Thermophys. 2015, 36, 1416–1467. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.D.; Zhang, J.J. An analytical solution for two-dimensional modeling of repetitive long pulse laser heating material. Int. J. Heat Mass Transf. 2017, 104, 503–509. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An analytic parametric study of rounded laser pulse heating. Optik 2021, 240, 167001. [Google Scholar] [CrossRef]
- Mishra, S.C.; Sahai, H. Analyses of non-Fourier heat conduction in 1-D cylindrical and spherical geometry—An application of the lattice Boltzmannmethod. Int. J. Heat Mass Transf. 2012, 55, 7015–7023. [Google Scholar] [CrossRef]
- Frankel, J.I.; Vick, B.; Özisik, M.N. General formulation and analysis of hyperbolic heat conduction in composite media. Int. J. Heat Mass Transf. 1987, 30, 1293–1305. [Google Scholar] [CrossRef]
- Cattaneo, C. A form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compte Rendus 1958, 247, 431–435. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. In Atti del Seminario matematico e Fisico dell’Università di Modena; Società tipografica Modenese: Modena, Italy, 1948; Volume 3, pp. 83–101. [Google Scholar]
- Vernotte, P. Some possible complications in the phenomena of thermal conduction. Compte Rendus 1961, 252, 2190–2193. [Google Scholar]
- Liu, Y.; Li, L.; Lou, Q. A hyperbolic lattice Boltzmann method for simulating non-Fourier heat conduction. Int. J. Heat Mass Transf. 2019, 131, 772–780. [Google Scholar] [CrossRef]
- Lin, S.M.; Li, C.Y. Analytical solutions of non-Fourier bio-heat conductions for skin subjected to pulsed laser heating. Int. J. Therm. Sci. 2016, 110, 146–158. [Google Scholar] [CrossRef]
- Xu, G.Y.; Wang, J.B. Analytical solution of time fractional Cattaneo heat equation for finite slab under pulse heat flux. Appl. Math. Mech. 2018, 39, 1465–1476. [Google Scholar] [CrossRef]
- Lenarczyk, M.; Domanski, R. Non-Fourier effects in the thermal protection against high-power ultra-fast laser pulses. HTRSE-2018 2018, 70, 03008. [Google Scholar] [CrossRef]
- Faouzi, N.; Hichem, G.; Mohamed, F.B.A. Influence of Joule effect on thermal response of nano FinFET transistors. Superlattices Microstruct. 2021, 156, 106980. [Google Scholar]
- Nasri, F.; Ben Aissa, M.F.; Belmabrouk, H. Microscale thermal conduction based on Cattaneo-Vernotte model in Silicon On Insulator and Double Gate MOSFETs. Appl. Therm. Eng. 2015, 76, 206–211. [Google Scholar] [CrossRef]
- Zhang, X.M.; Peng, S.; Zhang, L. Variational equation of non-fourier heat conduction. Heat Transf. Res. 2018, 49, 275–285. [Google Scholar] [CrossRef]
- Noroozi, M.J.; Saedodin, S.; Ganji, D.D. A new approximate-analytical method to solve non-Fourier heat conduction problems. Kuwait J. Sci. 2017, 44, 87–96. [Google Scholar]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Rubin, M.B. Hyperbolic heat conduction and the second law. Int. J. Eng. Sci. 1992, 30, 1665–1676. [Google Scholar] [CrossRef]
- Yang, Z.B.; Wang, Z.K.; Tian, S.H. Analysis and Modelling of Non-Fourier Heat Behavior Using the Wavelet Finite Element Method. Materials 2019, 12, 1337. [Google Scholar] [CrossRef] [PubMed]
- Tzou, D.Y. The generalized lagging response in small-scale and high-rate heating. Int. J. Heat. Mass Transf. 1995, 38, 3231–3234. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro-to Microscale Heat Transfer: The Lagging Behavior; Taylor & Francis: Washington, DC, USA, 1997. [Google Scholar]
- Xu, M.; Wang, L. Thermal oscillation and resonance in dual-phase-lagging heat conduction. Int. J. Heat Mass Transf. 2002, 45, 1055–1061. [Google Scholar] [CrossRef]
- Majchrzak, E.; Mochnacki, B. Numerical Simulation of Thermal Processes in a Domain of Thin Metal Film Subjected to an Ultrashort Laser Pulse. Materials 2018, 11, 2116. [Google Scholar] [CrossRef]
- Xu, B.B.; Gao, X.W.; Cui, M. High precision simulation and analysis of non-Fourier heat transfer during laser processing. Int. J. Heat Mass Transf. 2021, 17, 121574. [Google Scholar] [CrossRef]
- Van der Merwe, A.J.; Van Rensburg, N.F.J.; Sieberhagen, R.H. Comparing the dual phase lag, Cattaneo-Vernotte and Fourier heat conduction models using modal analysis. Appl. Math. Comput. 2021, 698, 125934. [Google Scholar] [CrossRef]
- Chen, B.Q.; Kan, A.K.; Chen, Z.F. Investigation on Effective Thermal Conductivity of Fibrous Porous Materials as Vacuum Insulation Panels’ Core Using Lattice Boltzmann Method. Energies 2023, 19, 3692. [Google Scholar] [CrossRef]
- Escobar, R. Lattice Boltzmann Modeling of Phonon Transport in Silicon Films. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2005. [Google Scholar]
- Chen, J.; Zhang, G.; Li, B.W. Molecular Dynamics Simulations of Heat Conduction in Nanostructures: Effect of Heat Bath. J. Phys. Soc. Jpn. 2010, 79, 074604. [Google Scholar] [CrossRef]
- Kumar, S.R.; Reddy, B.K.; Balaji, C.A. Application of Hybrid Monte Carlo Algorithm in Heat Transfer. J. Heat Transf. 2017, 139, 082004. [Google Scholar] [CrossRef]
- Palluotto, L.; Dumont, N.; Rodrigues, P. Assessment of randomized Quasi-Monte Carlo method efficiency in radiative heat transfer simulations. J. Quant. Specteosc. Radiat. Transf. 2019, 236, 106570. [Google Scholar] [CrossRef]
- Mao, Y.D.; Xu, M.T. Lattice Boltzmann numerical analysis of heat transfer in nano-scale silicon films induced by ultra-fast laser heating. Int. J. Therm. Sci. 2015, 89, 210–221. [Google Scholar] [CrossRef]



| T0 = 300 K | l = 41 nm | J = 732 J/m2 |
| K = 148 W/(m·K) | τq = 6.5 ps | = 15.3 nm |
| Cv = 2.3 × 106 J/(m3·K) | tp = 0.65 ps | R = 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Y.; Liu, S.; Liu, J.; Yu, M.; Li, X.; Yang, K. Non-Fourier Heat Conduction of Nano-Films under Ultra-Fast Laser. Materials 2023, 16, 4988. https://doi.org/10.3390/ma16144988
Mao Y, Liu S, Liu J, Yu M, Li X, Yang K. Non-Fourier Heat Conduction of Nano-Films under Ultra-Fast Laser. Materials. 2023; 16(14):4988. https://doi.org/10.3390/ma16144988
Chicago/Turabian StyleMao, Yudong, Shouyu Liu, Jiying Liu, Mingzhi Yu, Xinwei Li, and Kaimin Yang. 2023. "Non-Fourier Heat Conduction of Nano-Films under Ultra-Fast Laser" Materials 16, no. 14: 4988. https://doi.org/10.3390/ma16144988
APA StyleMao, Y., Liu, S., Liu, J., Yu, M., Li, X., & Yang, K. (2023). Non-Fourier Heat Conduction of Nano-Films under Ultra-Fast Laser. Materials, 16(14), 4988. https://doi.org/10.3390/ma16144988







