Study on Load Transfer Mechanism of Local Curved Prestressed Hollow-Core Slab Bridge
Abstract
1. Introduction
2. Finite Element Analysis Method
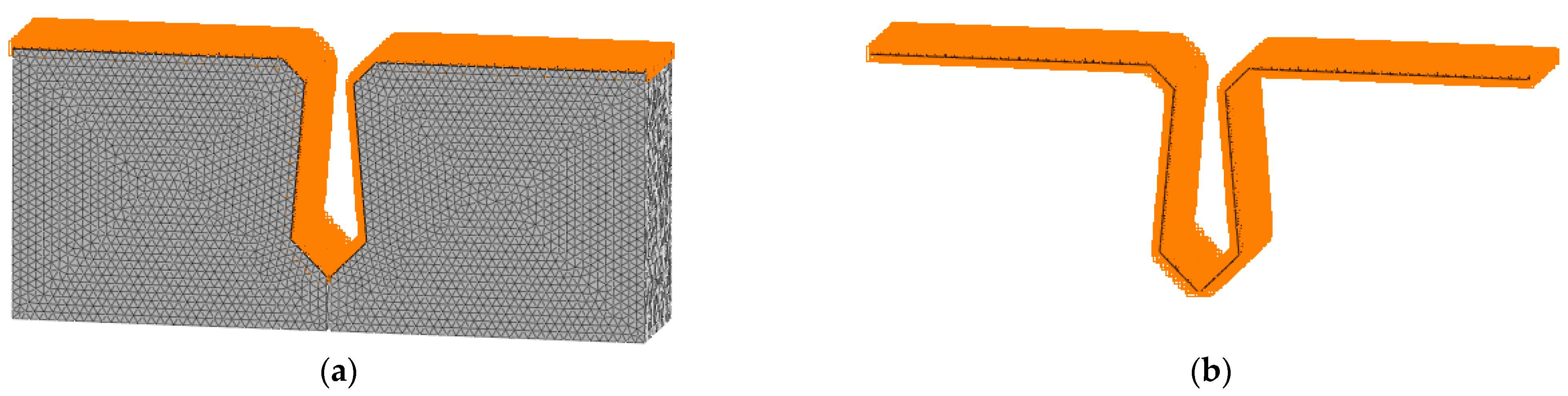
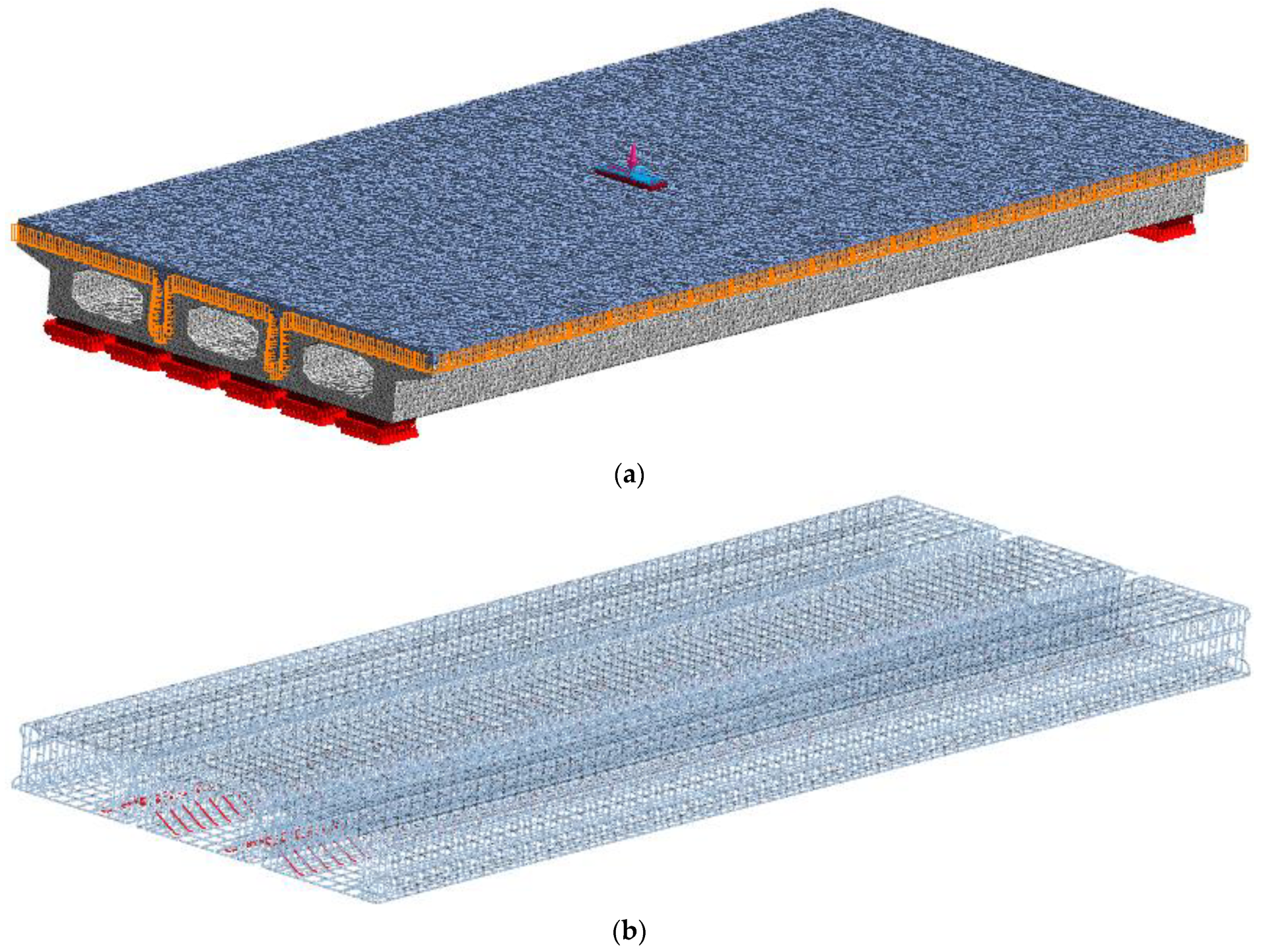
2.1. Finite Element Model of Beam with Joint
2.1.1. Concrete Setting
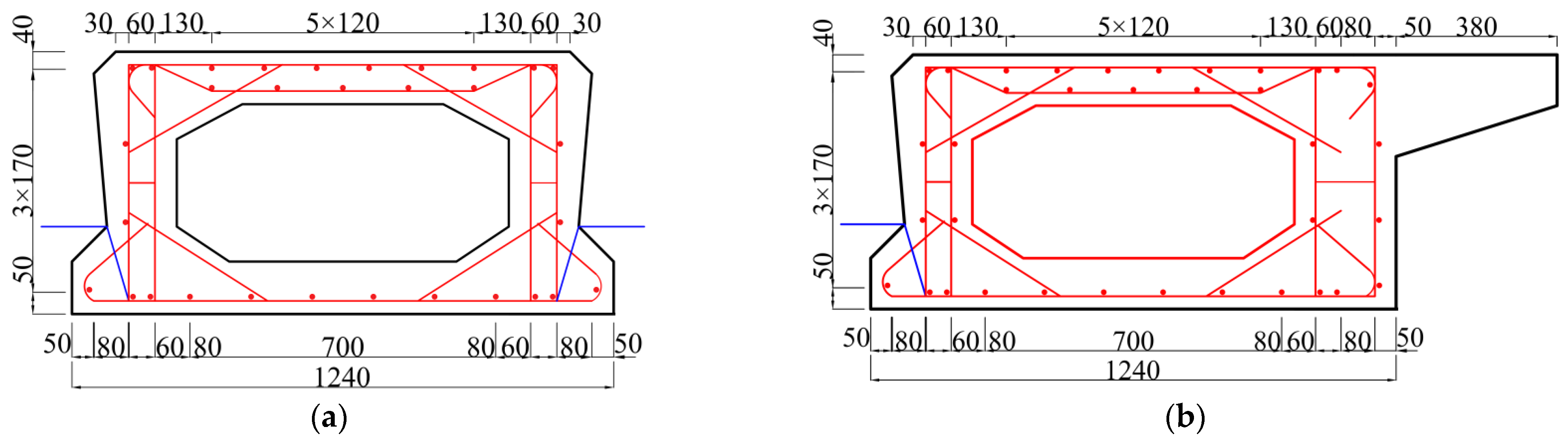
2.1.2. Rebar Setting
2.1.3. Interface Setting of New-to-Old Concrete
2.1.4. Setting of Unbonded Prestressed Tendons
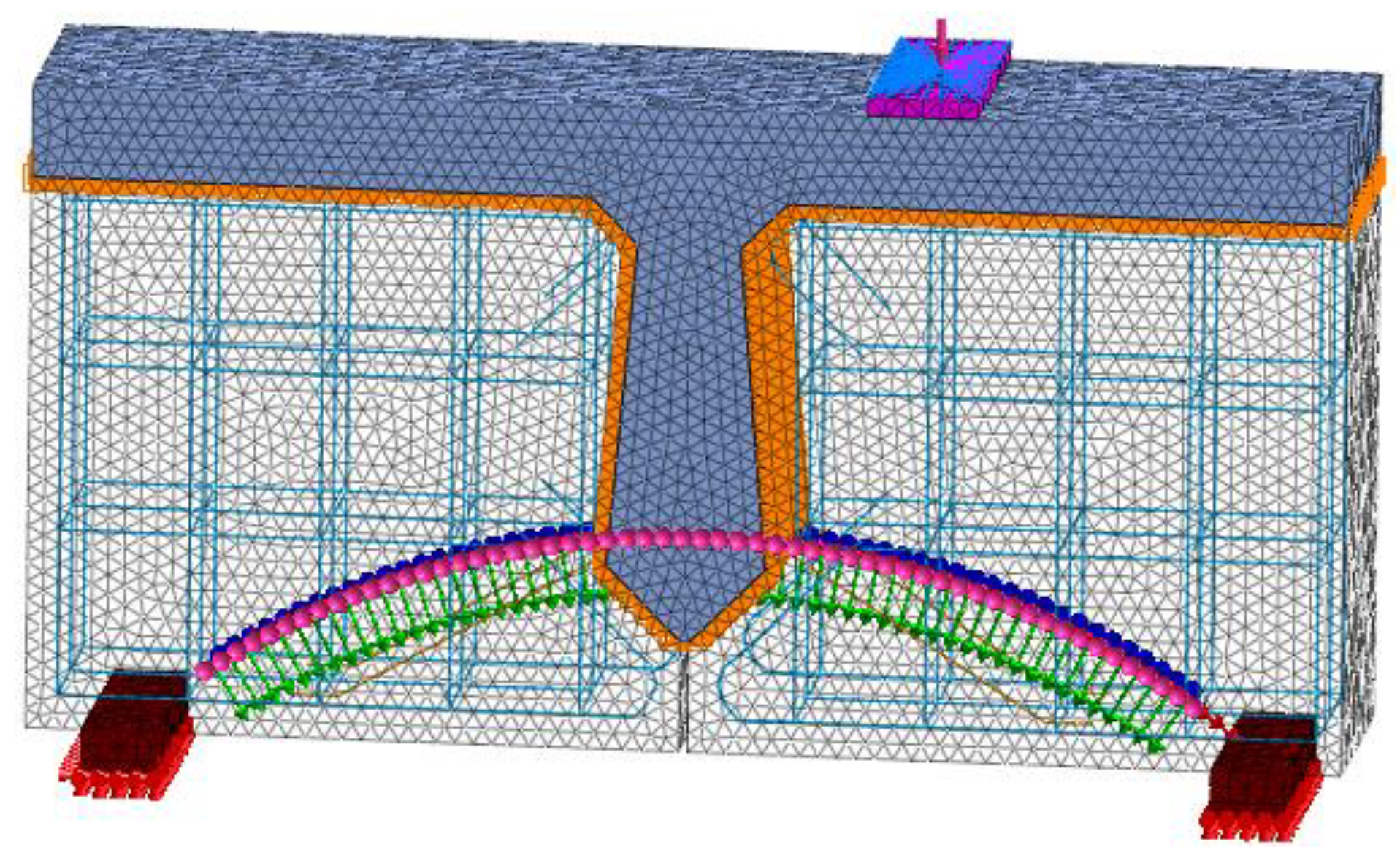
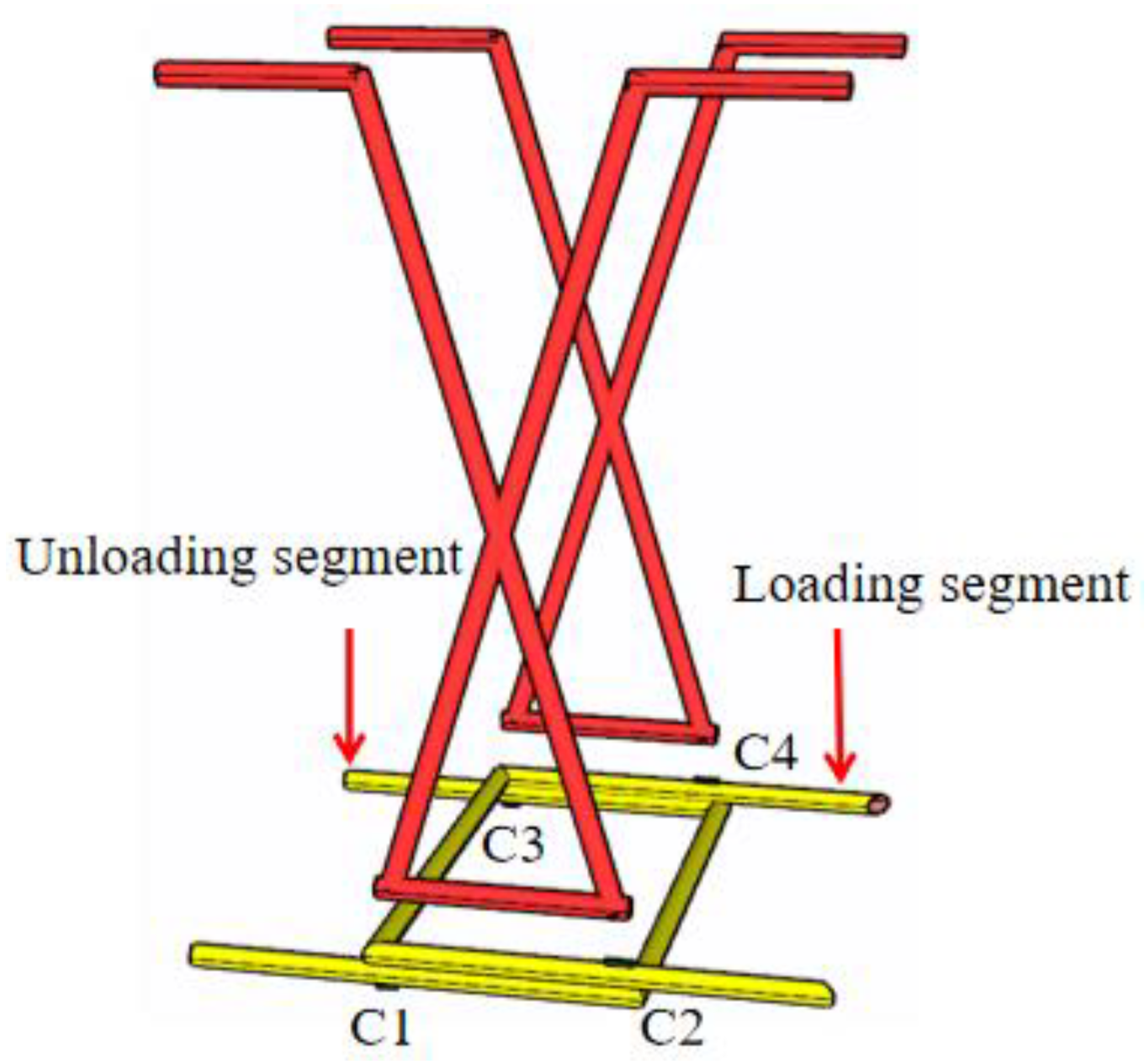
2.1.5. Bearing and Constraint Setting
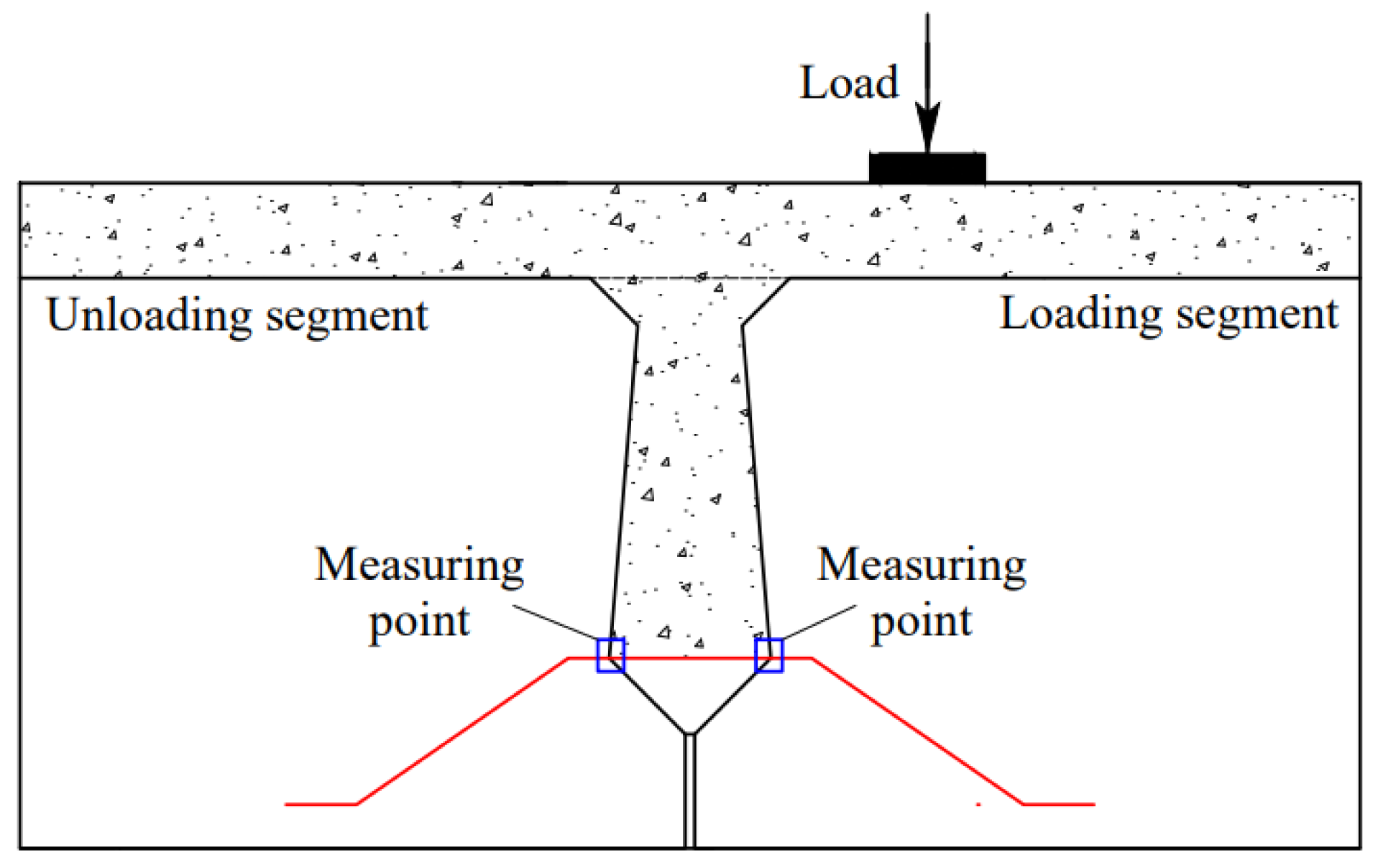
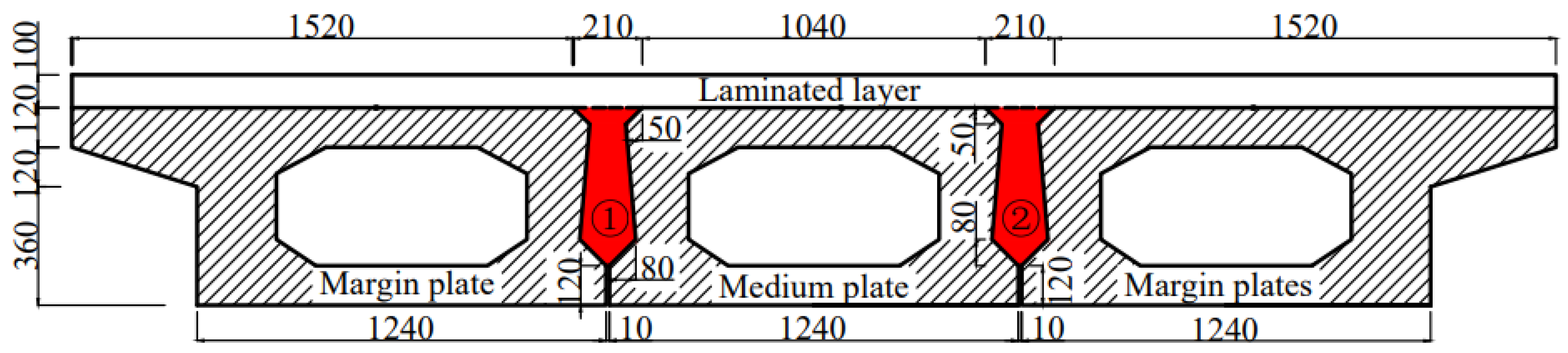
2.2. Hollow-Core Slab Bridge Model and Loading
3. Model Verification and Result Analysis
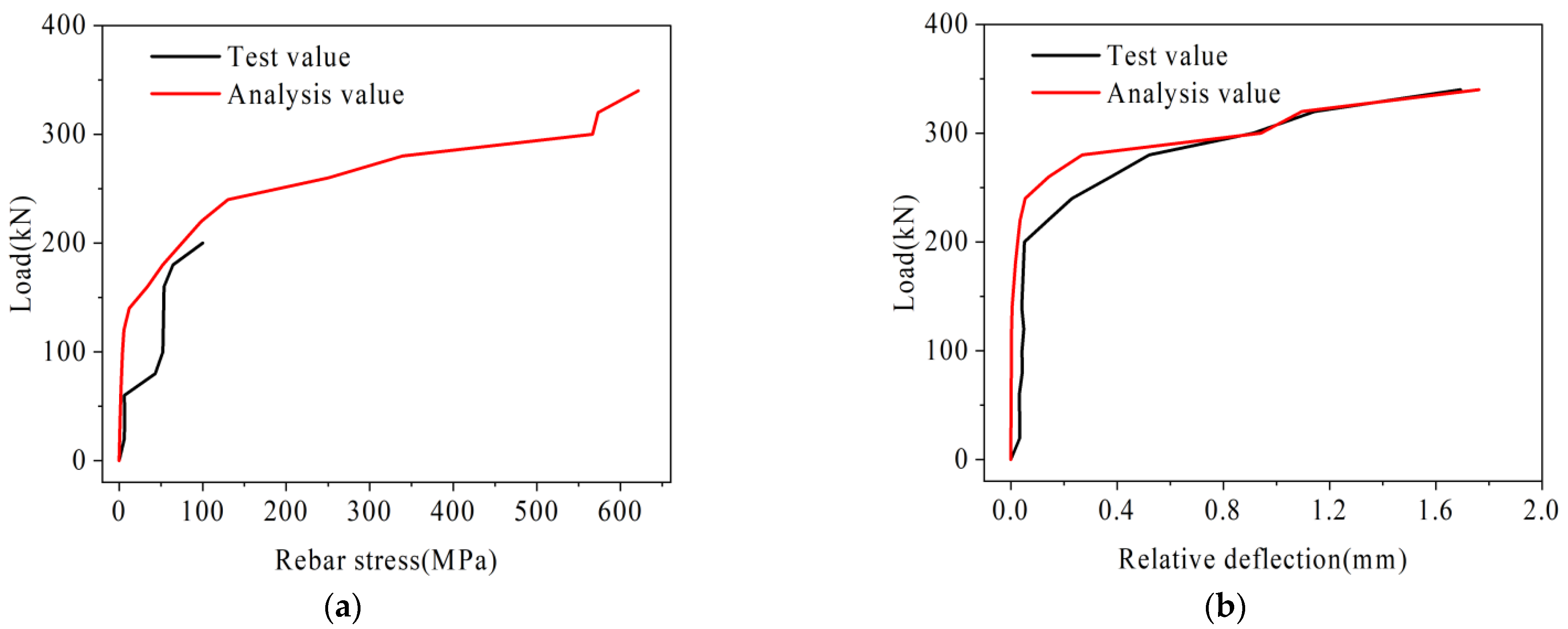
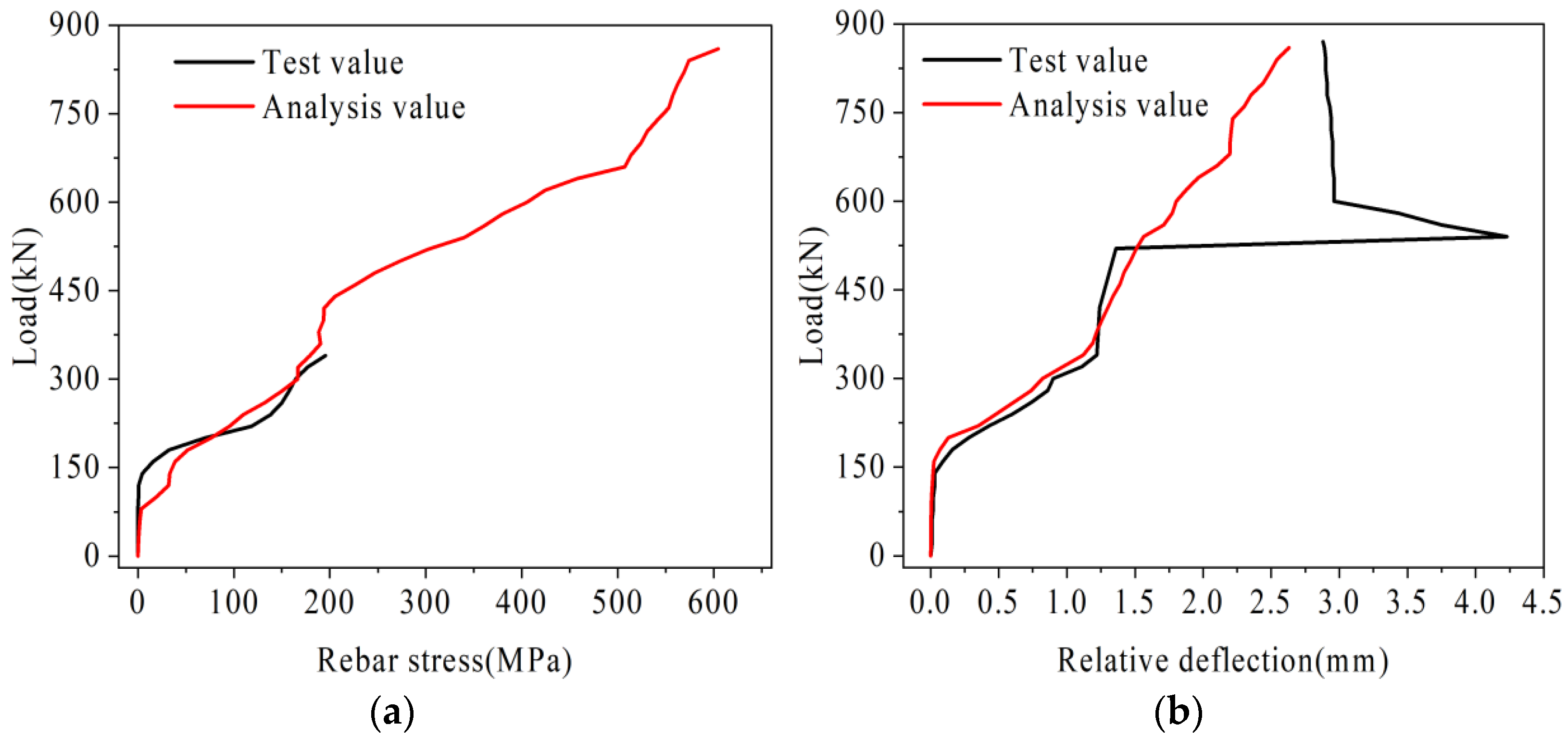
3.1. Model Verification
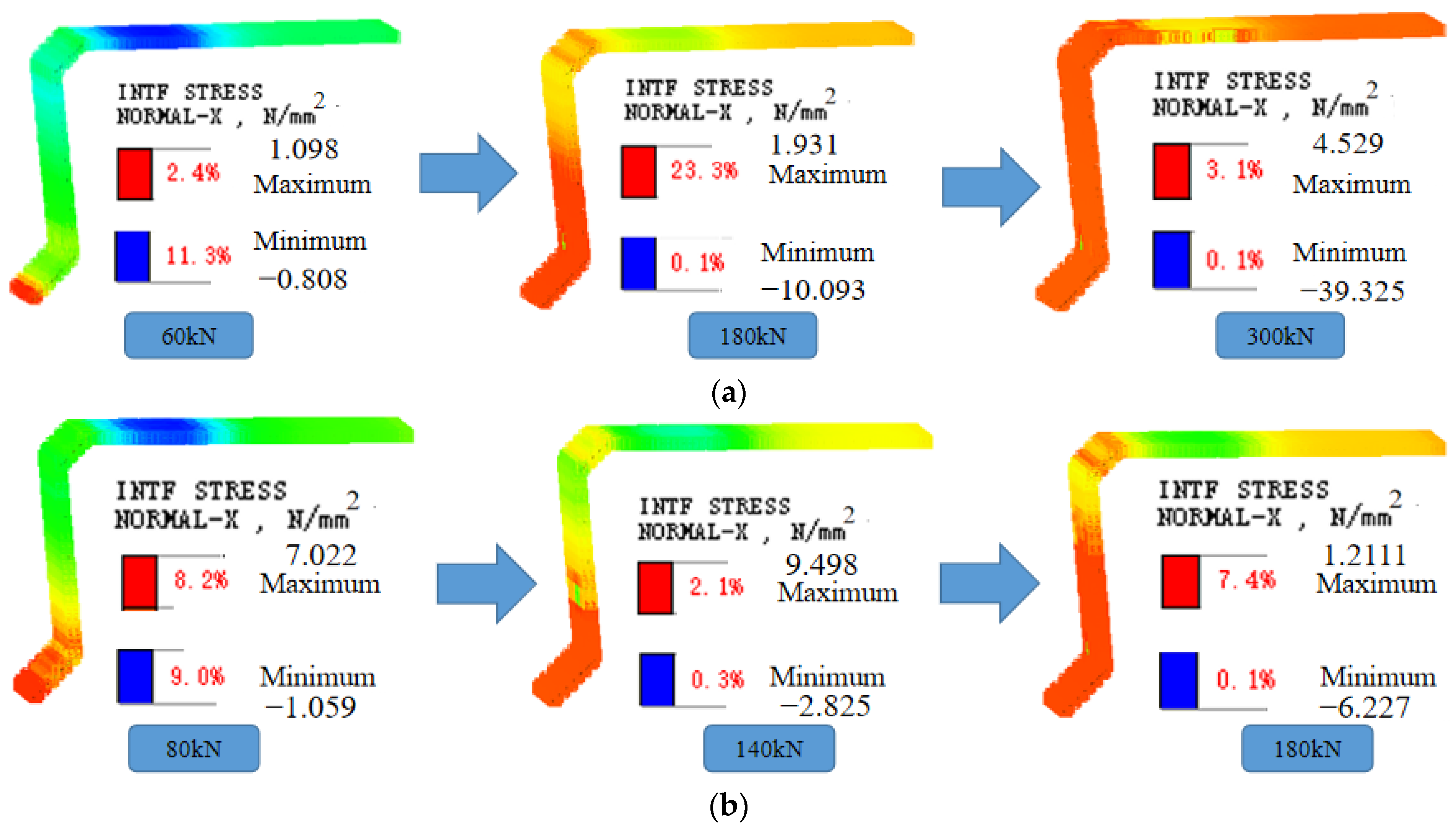
3.2. Interface Stress Analysis
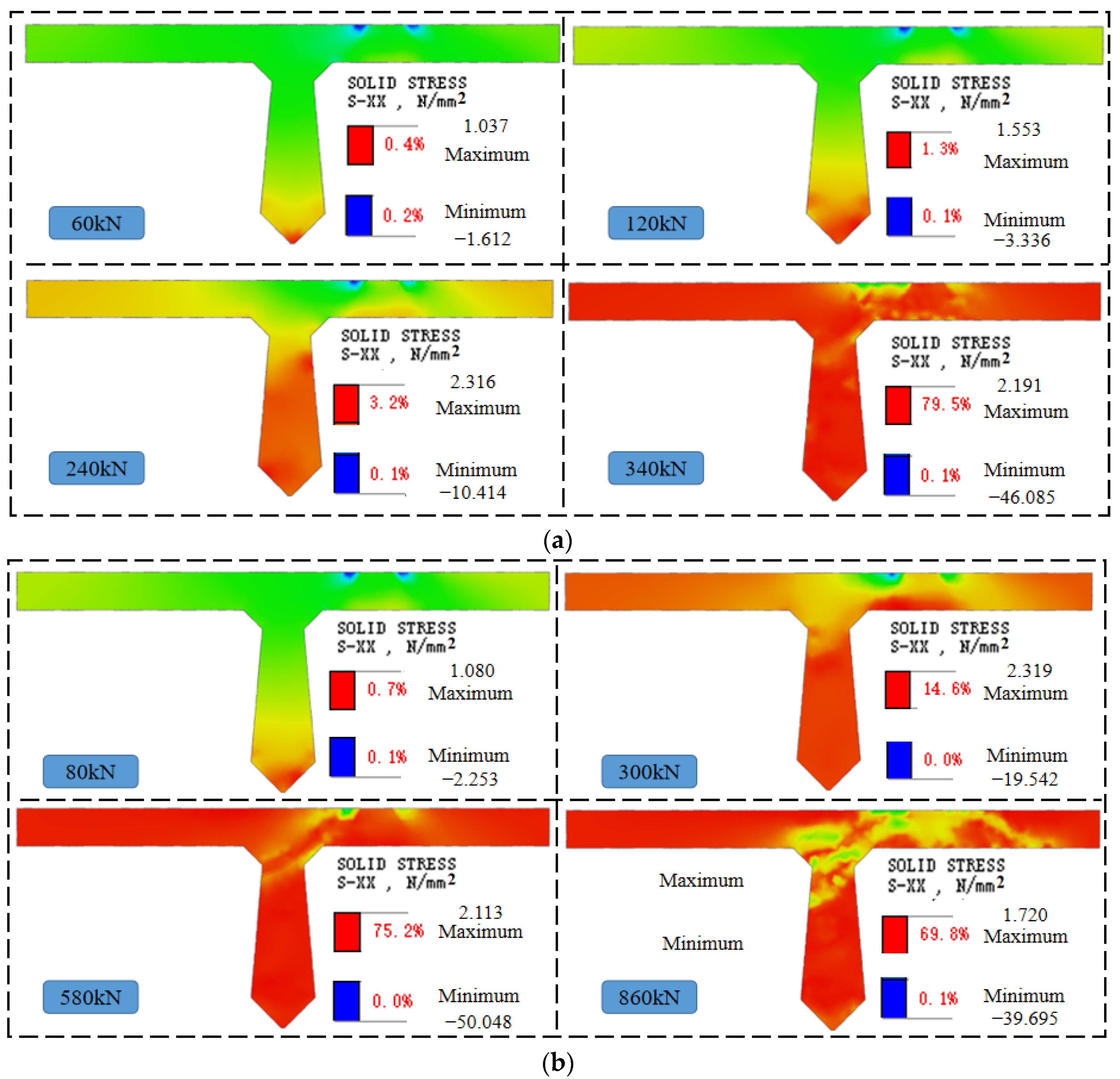
3.3. Stress Analysis of Joint and Laminated Layer
4. Hollow-Core Slab Bridge Results Analysis
4.1. Failure Process Analysis of Traditional Hollow-Core Slab Bridge
4.2. Failure Process Analysis of Prestressed Hollow-Core Slab Bridge
4.3. Comparative Analysis of Results
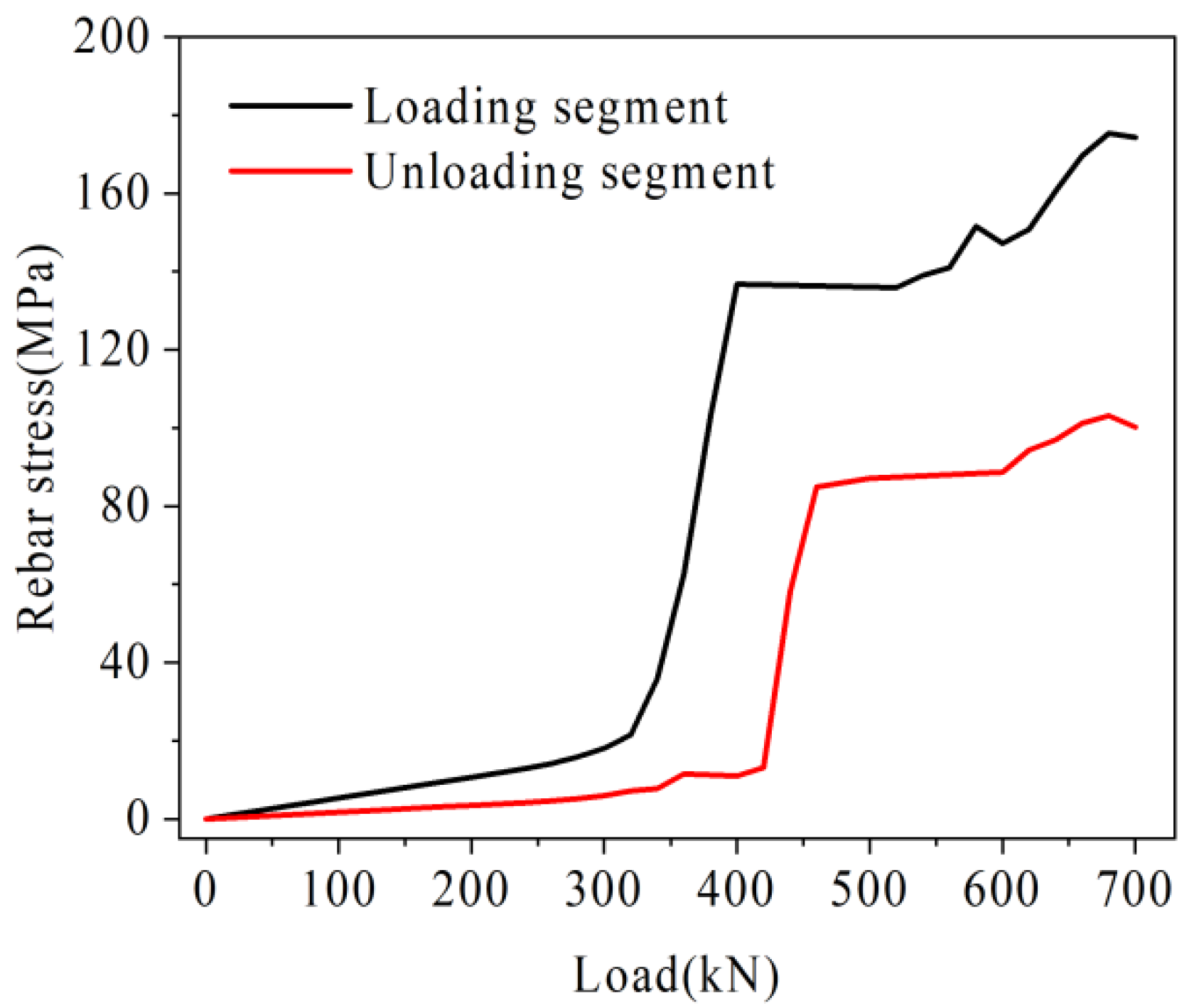
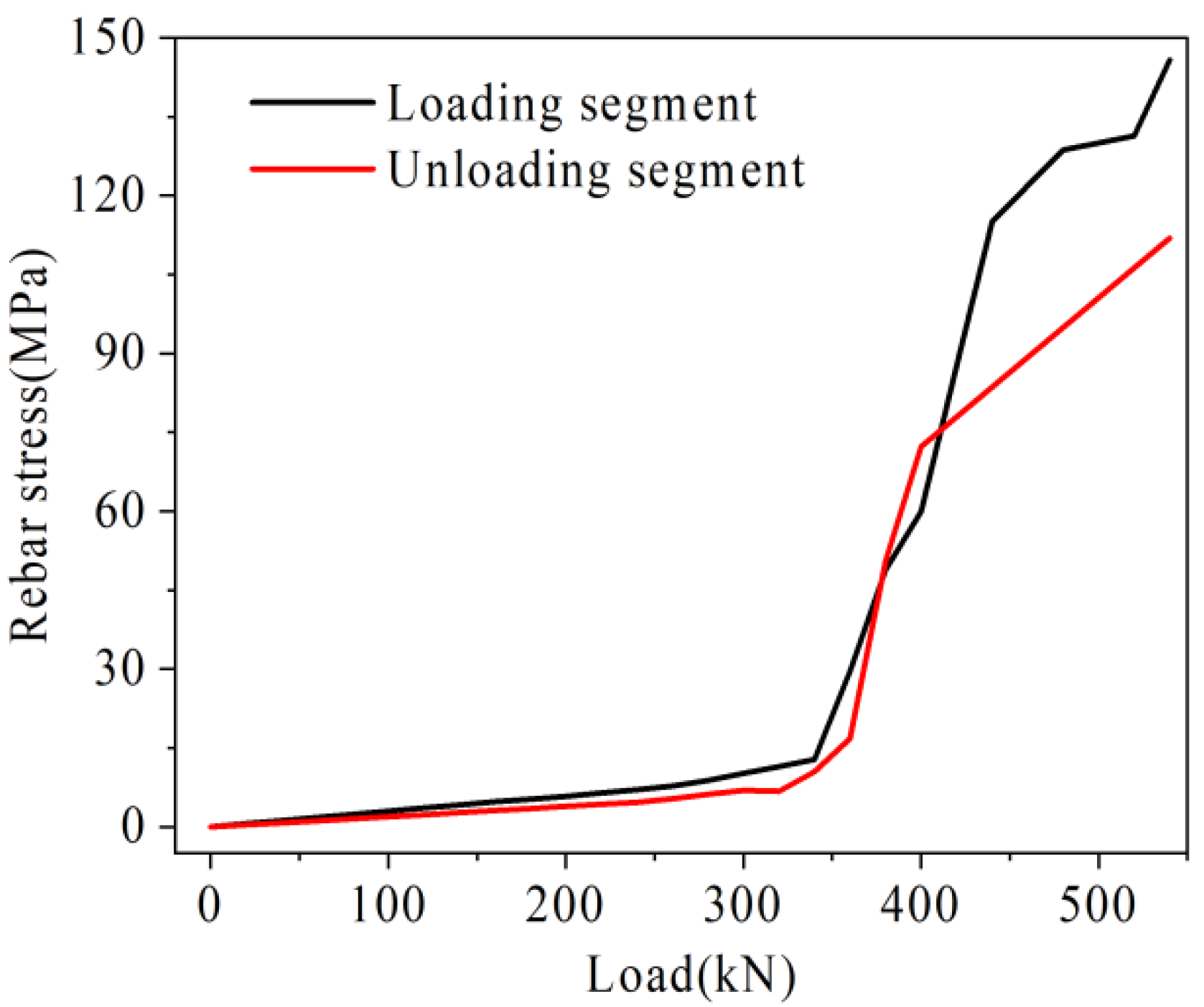
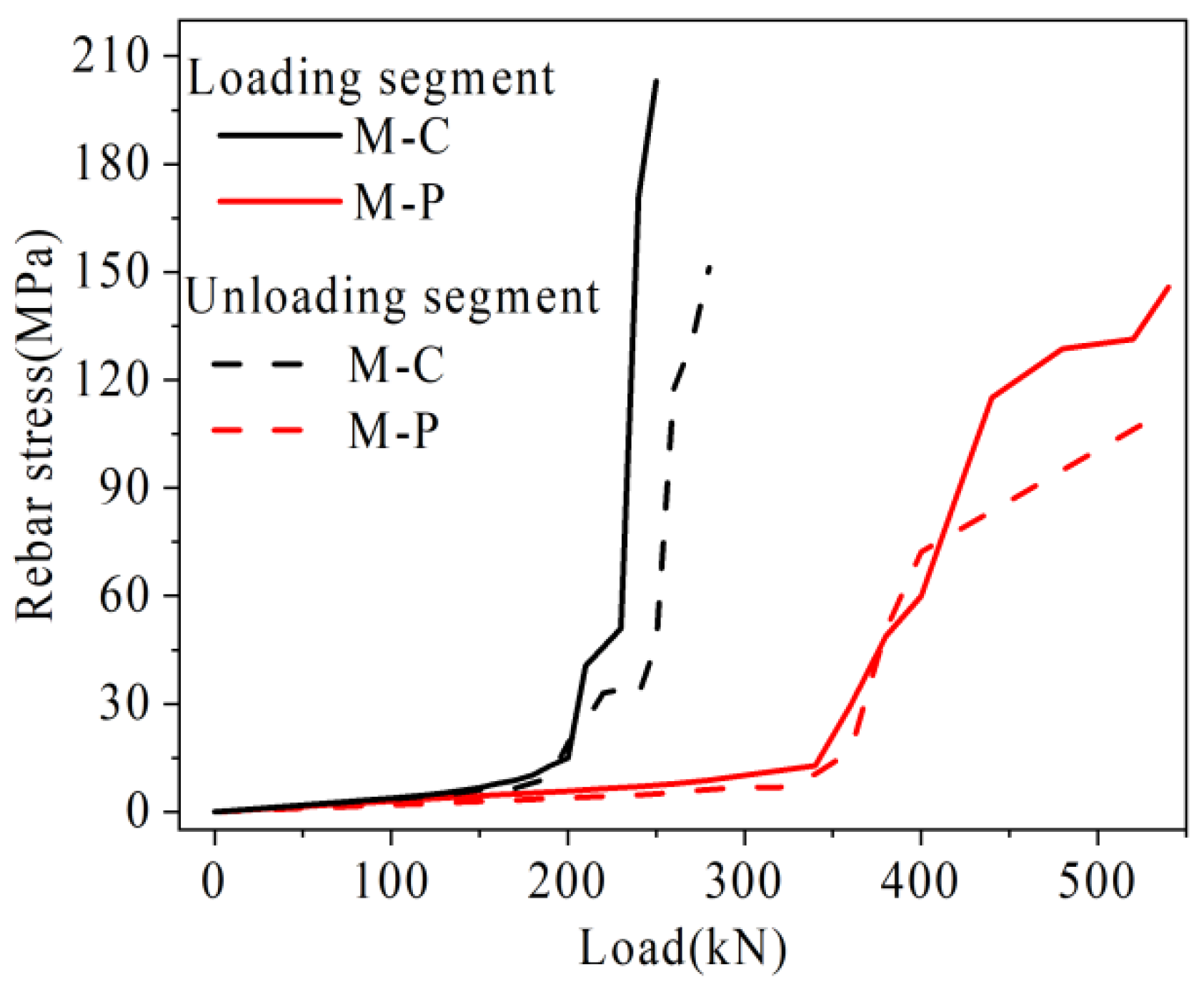
4.3.1. Analysis of Rebar Stress
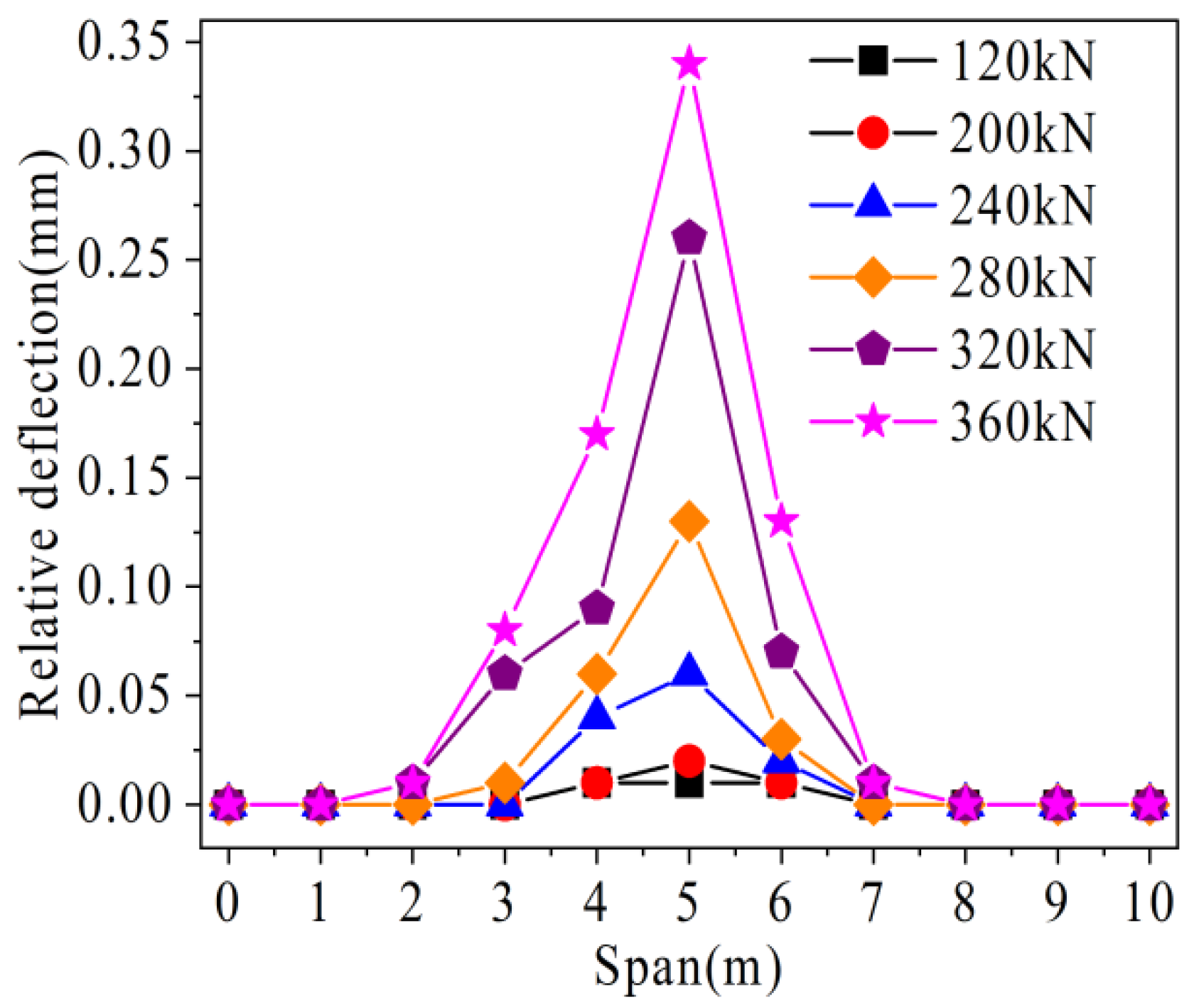
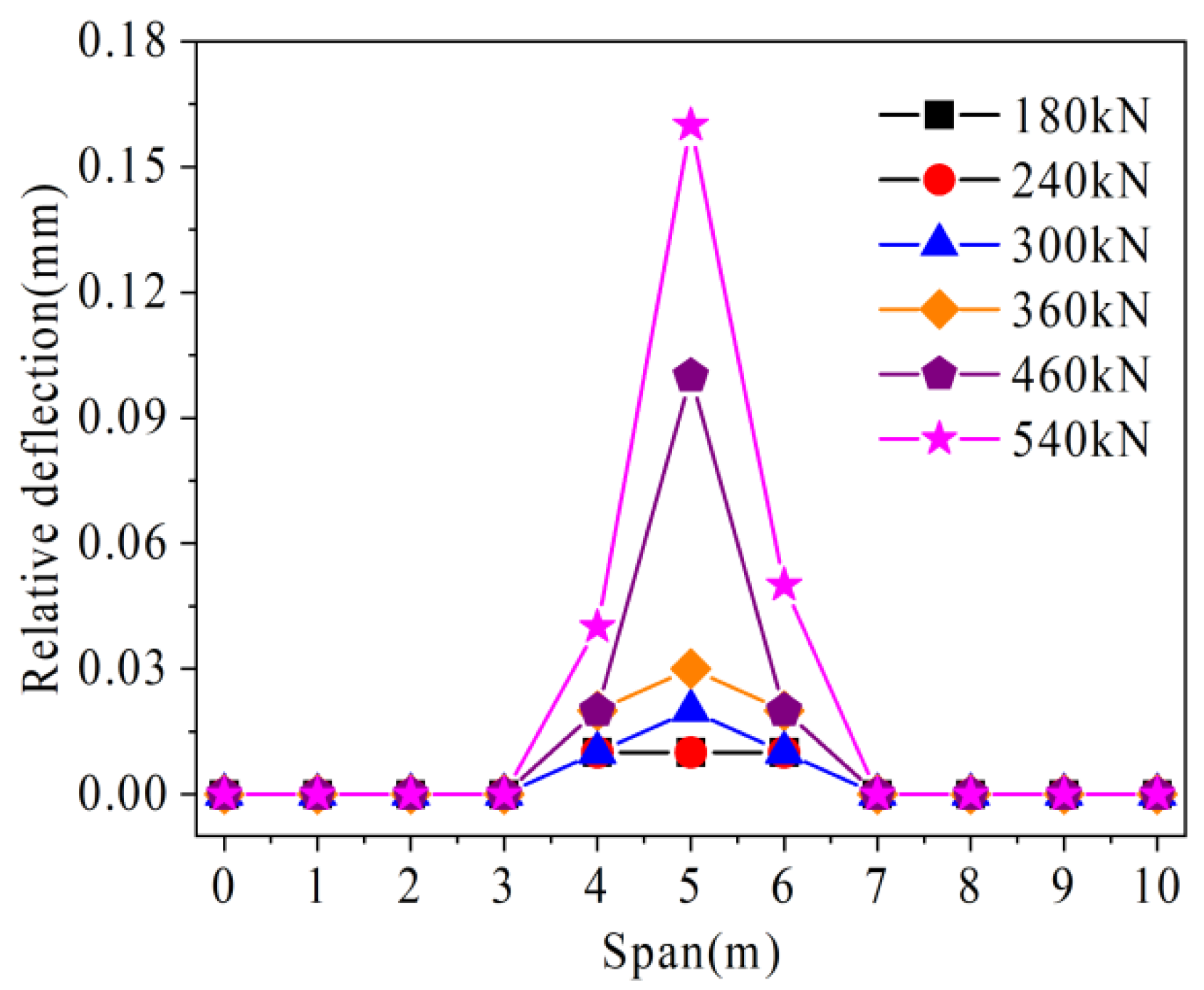
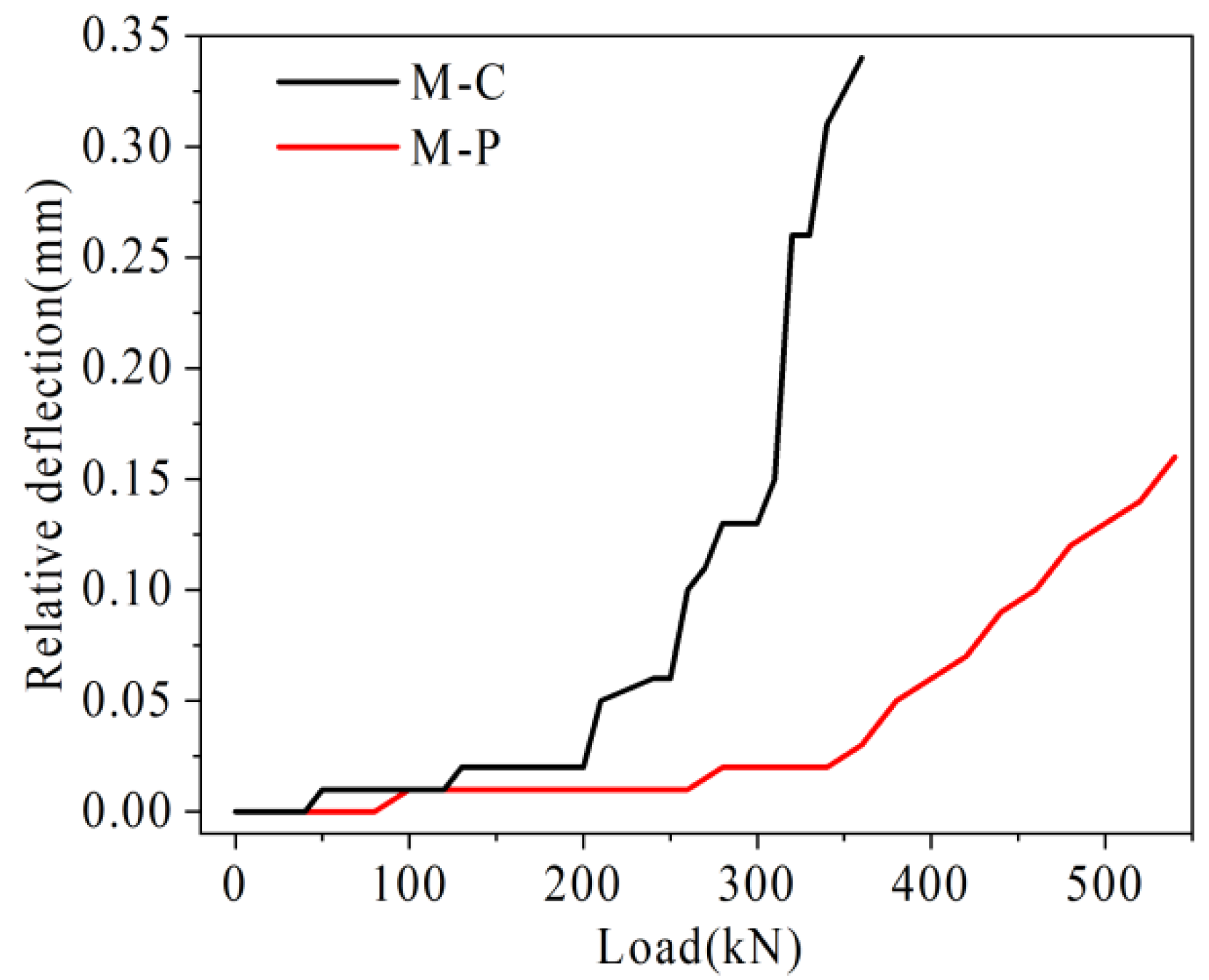
4.3.2. Relative Deflection Analysis
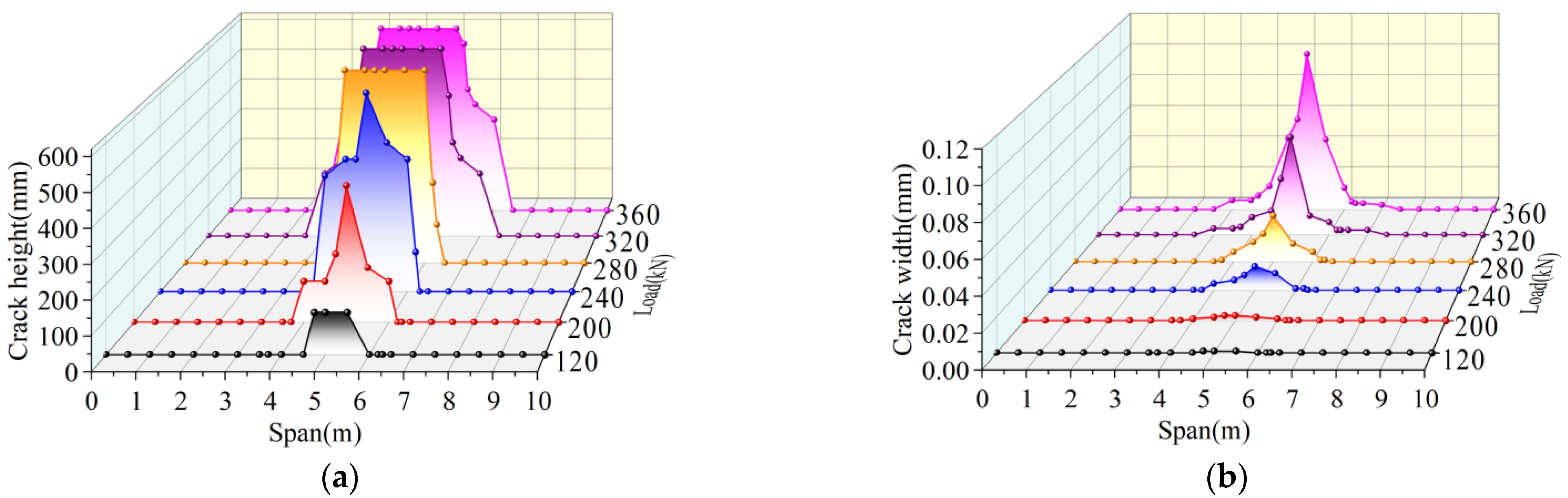
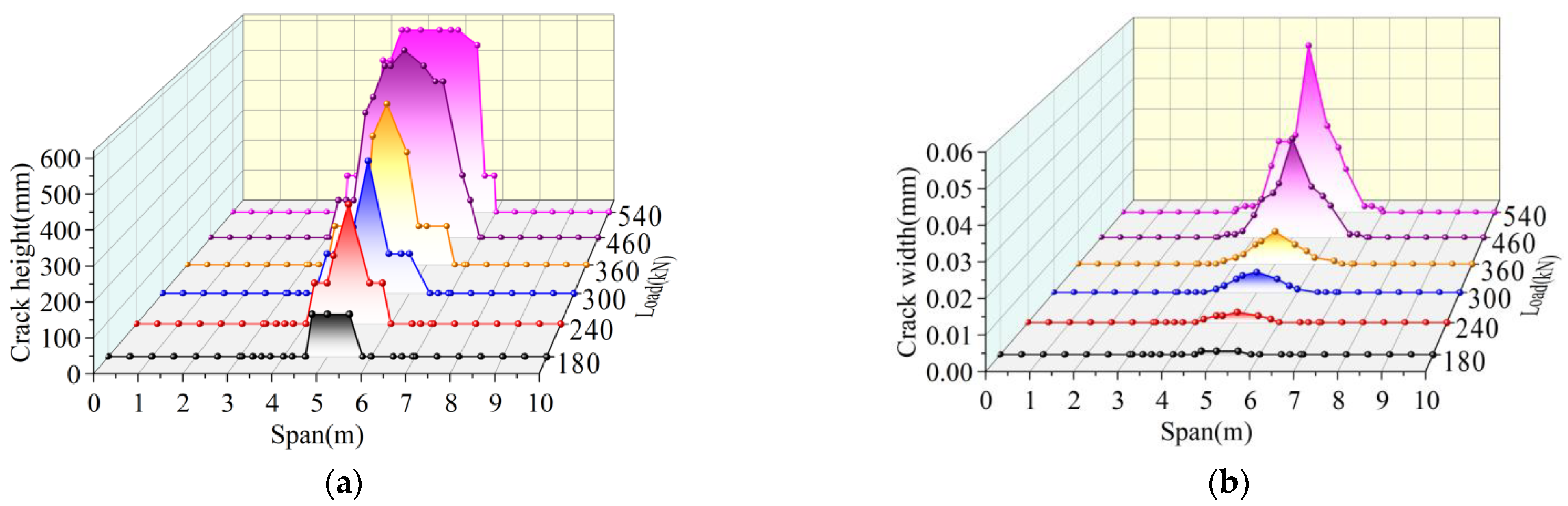
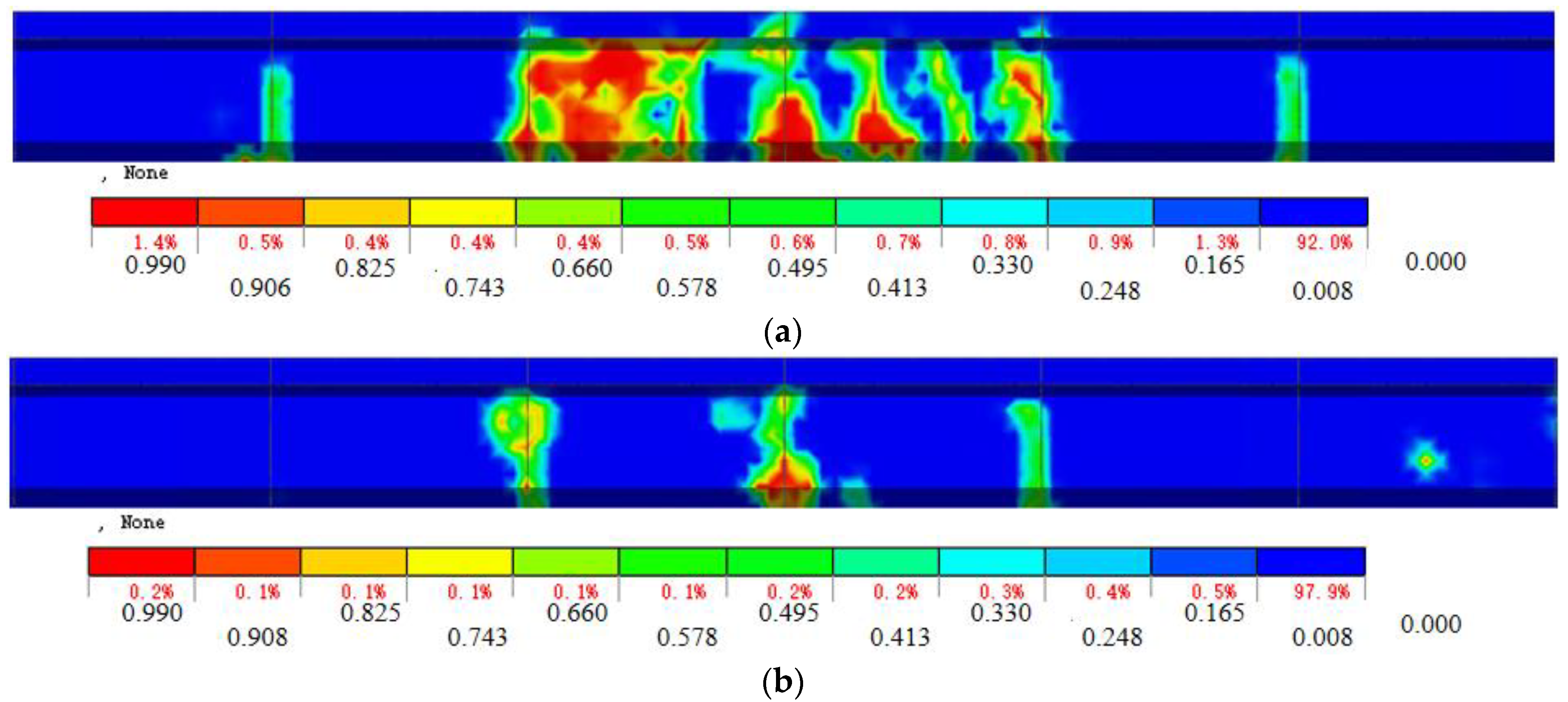
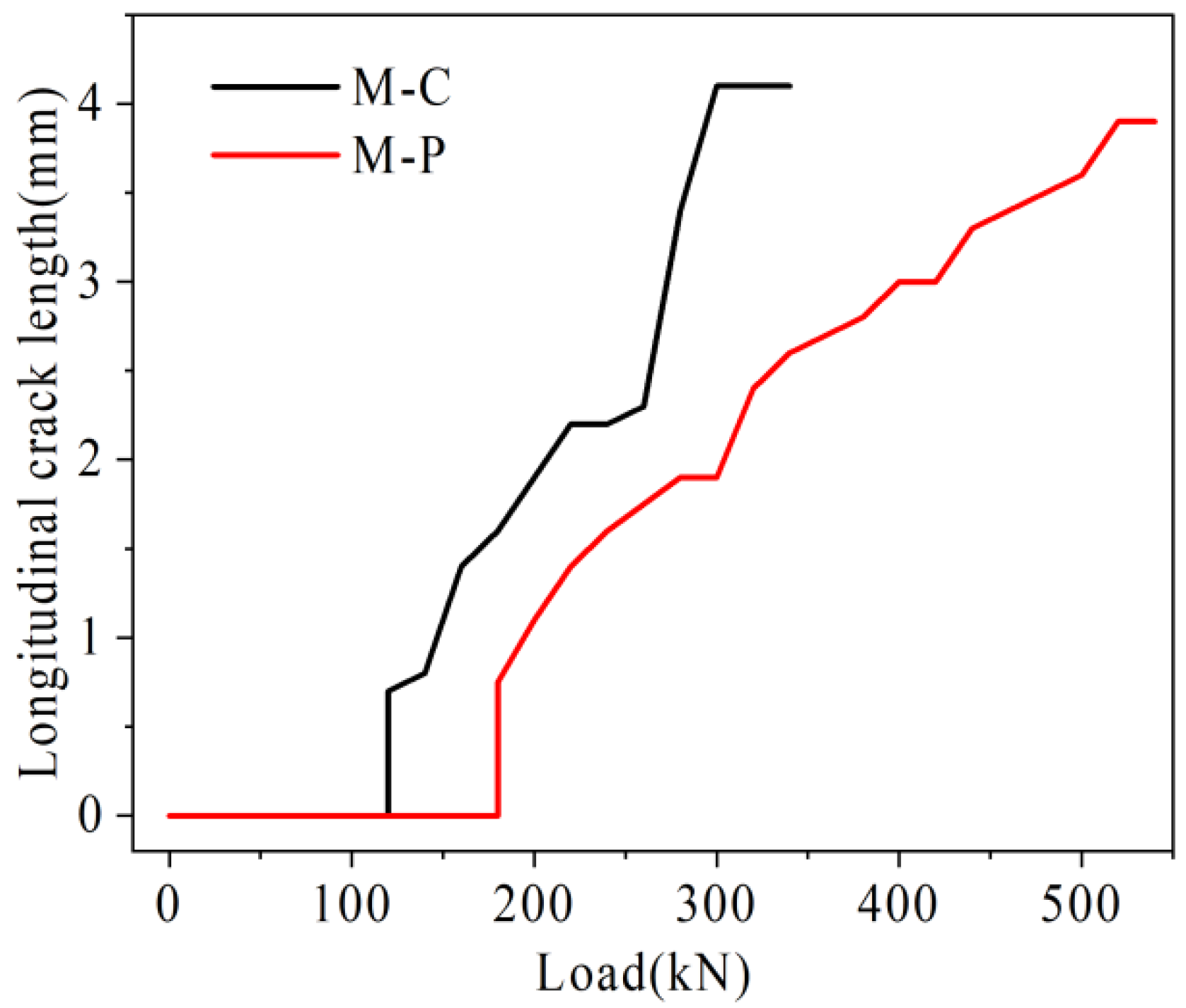
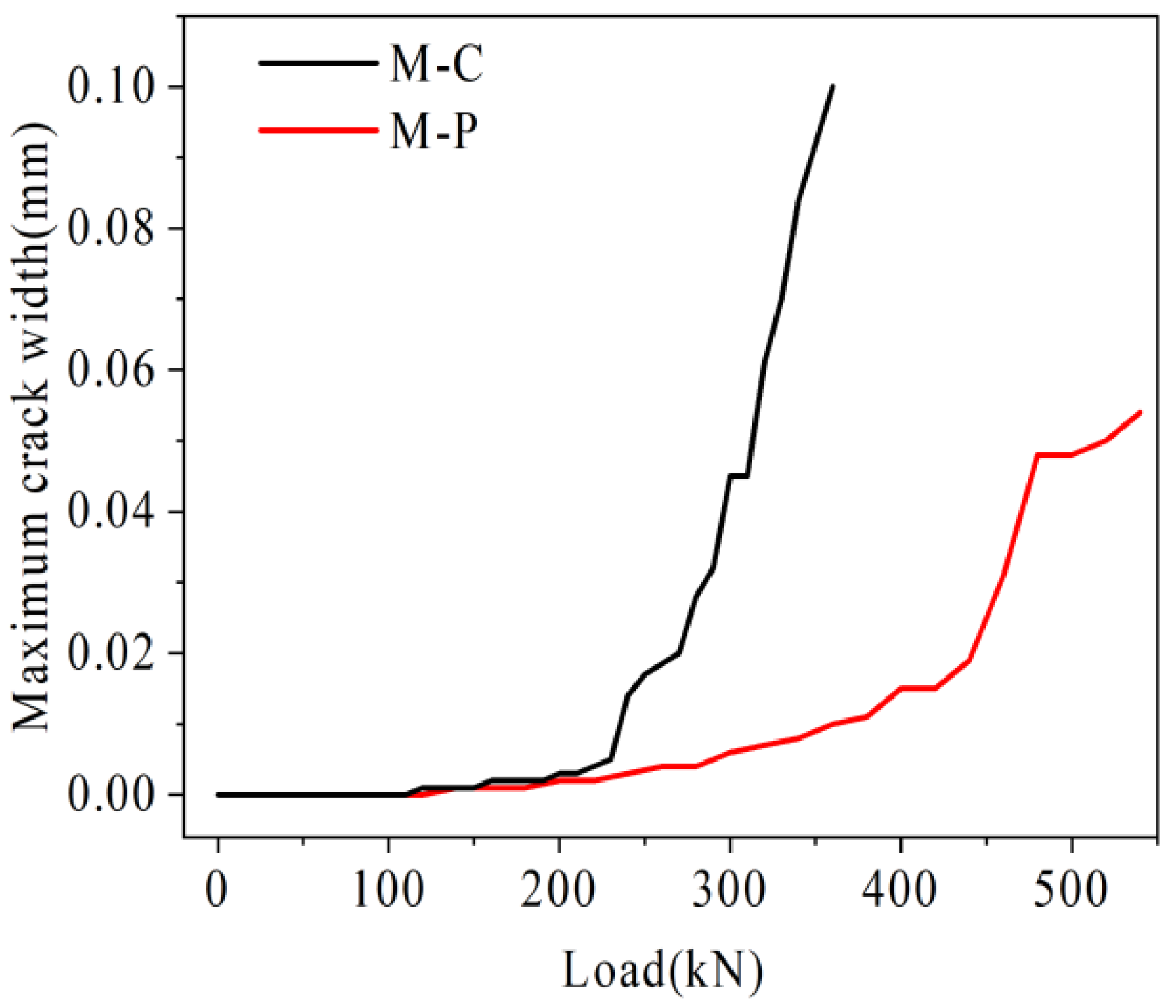
4.3.3. Analysis of Longitudinal Crack Length and Maximum Crack Width
4.4. Force Transmission Mechanism
- (1)
- Uncracked stage: At this stage, no cracks are generated in the hollow-core slab bridge and the force performance of the joints is good. In this stage, with the load increases, the U-bar stress value, the relative deflection values on both sides of the joints, and the maximum crack width values grow slowly, and the load is mainly transferred by the interface unit.
- (2)
- Working stage with cracks: At this stage, cracks are generated in the hollow-core slab bridge. With the increase of load, longitudinal cracks gradually extend to both sides of the hollow-core slab bridge, and the height of cracks gradually rises. With the increase of load, the stress value of the U-bar, the relative deflection value on both sides of the joint, and the maximum crack width increase faster than that in the uncracked stage. In this stage, in the traditional hollow-core slab bridge, the load is mainly transmitted by U-bars and interface units. In the prestressed hollow-core slab bridge, the load is mainly transmitted by U-bars, prestressed tendons, and interface units.
- (3)
- Failure stage: At this stage, the cracks in the hollow-core slab bridge have reached the bottom of the laminated layer. With the increase of load, the stress value of the U-bar, the relative deflection value on both sides of the joint, and the maximum crack width value increase rapidly. In this stage, the interface unit in the hollow-core slab bridge exits to transfer load. In the traditional hollow-core slab bridge, the load is only transmitted by U-bars. In the prestressed hollow-core slab bridge, the U-bars and prestressed tendons jointly transfer the load.
5. Conclusions
- (1)
- The interface normal stiffness of the traditional and prestressed hinge joint finite element models is 12,000 MPa and 20,000 MPa, respectively, and the interface tensile strength is 1 MPa and 0.6 MPa, respectively. The error between the finite element analysis results and the static load test results is basically within 15%.
- (2)
- The total failure process of the prestressed hollow-core slab bridge is cracking near the mid-span under 33.3% ultimate load. Under 44.4% ultimate load, the longitudinal crack length reaches 1.6 m. Under 85.2% ultimate load, the longitudinal crack length reaches 3.4 m. Under 100% ultimate load, the longitudinal crack length reaches 3.9 m. With the increase of load, the longitudinal cracks extend to both sides and the width of cracks increases.
- (3)
- Compared with the traditional hollow-core slab bridge, the cracking load, through-joint load, and ultimate load of the prestressed hollow-core slab bridge are increased by 50.0%, 91.7%, and 66.7%, respectively. The durability and bearing capacity of the prestressed hollow-core slab bridge have been improved.
- (4)
- Under the same load, the U-bar stress, the relative deflection on both sides of joint, and the maximum width of joint of the prestressed hollow-core slab bridge are smaller than those of the traditional hollow-core slab bridge. Under the ultimate load, the longitudinal crack span of the traditional hollow-core slab bridge is 0.22–0.7 L, and that of the prestressed hollow-core slab bridge is 0.3–0.7 L. Prestressed tendons can share the transfer load and restrain the deterioration of a hollow-core slab bridge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Cao, X.Z.; Zhou, Y.J.; Wang, G.; Tian, R. Lateral Load Distribution for Hollow Slab Bridge: Field Test Investigation. Int. J. Concr. Struct. Mater. 2020, 14, 22. [Google Scholar] [CrossRef]
- Zhang, J.; Yi, T.H.; Qu, C.X.; Li, H. Determining Orders of Modes Sensitive to Hinge Joint Damage in Assembled Hollow Slab Bridges. J. Bridge Eng. 2022, 27, 04022001. [Google Scholar] [CrossRef]
- Liu, H.B.; Wang, X.R.; Tan, G.J.; He, X.; Luo, G. System Reliability Evaluation of Prefabricated RC Hollow Slab Bridges Considering Hinge Joint Damage Based on Modified AHP. Appl. Sci. 2019, 9, 4841. [Google Scholar] [CrossRef]
- Zhu, H.; Yang, Y.; Fan, W. External prestressing bridge reinforcement technology review: MATEC Web of Conferences. EDP Sci. 2015, 22, 04028. [Google Scholar]
- Wang, G.; Shen, Y.G.; Xie, X. Force Transfer Mechanism of the Hinge Joint of Multi-Adjacent Hollow Slab Precast Bridge. Adv. Mater. Res. 2013, 658, 311–317. [Google Scholar] [CrossRef]
- Du, Y.T.; Wang, J.P.; Peng, B. Analysis of Influence of Hinge Condition on Overall Mechanical Performance of Hollow Slab Beam. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 042018. [Google Scholar]
- Du, J.S.; Au, F.T.; Chan, E.K.; Liu, L. Deflection of unbonded partially prestressed concrete continuous beams. Eng. Struct. 2016, 118, 89–96. [Google Scholar] [CrossRef]
- Knight, D.; Visintin, P.; Oehlers, D.; Ali, M.M. Simulating RC beams with unbonded FRP and steel prestressing tendons. Compos. Part B Eng. 2014, 60, 392–399. [Google Scholar] [CrossRef]
- He, Z.; Liu, Z. Stresses in external and internal unbonded tendons: Unified methodology and design equations. J. Struct. Eng. 2010, 136, 1055–1065. [Google Scholar] [CrossRef]
- Alkhairi, F.M.; Naaman, A.E. Analysis of beams prestressed with unbonded internal or external tendons. J. Struct. Eng. 1993, 119, 2680–2700. [Google Scholar] [CrossRef]
- Barbieri, R.A.; de Paula Simões Lopes Gastal, F.; Filho, A.C. Numerical model for the analysis of unbonded prestressed members. J. Struct. Eng. 2006, 132, 34–42. [Google Scholar] [CrossRef]
- Chen, J.-H.; Wang, Y.-X.; Zhu, Q.; Guo, M.-Z.; Fan, B.-Q. Mechanical properties and reinforcement technology of deep joints under static and fatigue loads. Structures 2023, 47, 1182–1195. [Google Scholar] [CrossRef]
- Kaneko, Y.; Connor, J.J.; Triantafillou, T.C.; Leung, C.K. Fracture Mechanics Approach for Failure of Concrete Shear Key. I: Theory. J. Eng. Mech. 1993, 119, 681–700. [Google Scholar] [CrossRef]
- Kaneko, Y.; Connor, J.J.; Triantafillou, T.C.; Leung, C.K. Fracture Mechanics Approach for Failure of Concrete Shear Key. II: Verification. J. Eng. Mech. 1993, 119, 701–719. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, J.M.; Kim, H.Y.; Song, J.-J. Analytical Study on a Longitudinal Joints of the Slab-Type Modular Bridges. Int. J. Civ. Environ. Eng. 2012, 6, 164–169. [Google Scholar]
- Reginato, L.; Dos Santos, D.P.; Neto, J.A.D.F.; dos Santos, R.C. Influence of geometry on the strength of shear keys based on numerical analysis. In Proceedings of the CILAMCE 2022—XLIII Ibero-Latin American Congress on Computational Methods in Engineering, Foz do Iguaçu, Brazil, 21–25 November 2022. [Google Scholar]
- Kim, Y.; Chin, W.; Jeon, S. Interface shear strength at joints of ultra-high performance concrete structures. Int. J. Concr. Struct. Mater. 2018, 12, 59. [Google Scholar] [CrossRef]
- Sangkhon, A.; Pisitpaibool, C. Shear strength test of joint with different geometric shapes of shear keys between segments of precast segmental bridge. Int. Trans. J. Eng. Manag. Appl. Sci. Technol. 2017, 8, 23–37. [Google Scholar]
- Yi, H.; Li, C.; Dai, L. Experimental study on the shear performance of shallow hinge joints for prefabricated hollow slab bridges. Adv. Civ. Eng. 2018, 2018, 3962942. [Google Scholar] [CrossRef]
- Di, J.; Sun, Y.; Yu, K.; Liu, L.; Qin, F. Experimental investigation of shear performance of existing PC hollow slab. Eng. Struct. 2020, 211, 110451. [Google Scholar] [CrossRef]
- Zou, L.L.; Cai, R.; Wu, Y.H. Study on Reinforcement of Transverse Prestressed Carbon Fiber Slab for Assembled Skew Hollow Slab Bridge. IOP Conf. Ser. Mater. Sci. Eng. 2019, 563, 022044. [Google Scholar] [CrossRef]
- Xiang, Y.Q.; Xing, C.; Shao, L.H.; Xing, Y. Lateral Load Distribution of Articulated Hollow Slab Beam Bridge Strengthened by Transverse Prestressed Force: Advanced Materials Research. Trans. Tech. Publ. 2012, 446–449, 1653–1656. [Google Scholar]
- Liang, D.; Li, P.F. Effects of Transverse Prestressed Tendons (TPTS) on the Mechanical Performance of Hollow Slab Bridge. Adv. Mater. Res. 2014, 889–890, 1358–1361. [Google Scholar] [CrossRef]
- Li, X.L.; Wang, F.M.; Li, X.N.; Zhong, Y. Reinforcement Experiment of a Hollow Slab Bridge by External Prestressing. Appl. Mech. Mater. 2012, 1802, 178–181. [Google Scholar] [CrossRef]
- Jin, H.; Xu, Y.; Zheng, Q.C.; Shao, G.T. Application of Shaped Steel and Concrete Composite Reinforcement Technique to Hollow Slab Bridge. Bridge Constr. 2017, 47, 114–118. [Google Scholar]
- Wang, F.M.; Kang, S.Z.; Li, X.L.; Cai, Y. Strengthening Experiment of a Hollow Slab Bridge by External Transverse Prestressing. Adv. Mater. Res. 2011, 243–249, 1561–1566. [Google Scholar] [CrossRef]
- Ni, H.J.; Ni, Y.S.; Tian, J. Contrastive Analysis on Hinge Joint Reinforcement Measures of Hollow Plate and Deduction Design Parameter. Appl. Mech. Mater. 2014, 578–579, 1379–1395. [Google Scholar] [CrossRef]
- Li, X.; Hu, Z.; Shah, Y.I. Transverse Connection Performance of Prefabricated PC Box Girder Bridge with Transverse Prestress. Int. J. Civ. Eng. 2022, 20, 957–966. [Google Scholar] [CrossRef]
- Jia, L.; Tao, L.; Hong, H.; Jian, J.; Zhi, H. Experimental Test on Bridge Reinforcement by Enlarging Section-Prestress Method. E3S Web Conf. 2020, 165, 4015. [Google Scholar] [CrossRef]
- Kim, T.-K.; Jung, W.-T.; Park, J.-S.; Park, H.-B. Experimental Study on Effects of Additional Prestressing Using Fiber Reinforced Polymers and Strands on Deterioration of PSC Bridge Structure. Polymers 2022, 14, 1115. [Google Scholar] [CrossRef] [PubMed]
- Wells, Z.B.; Barr, P.J.; James, P.H. Performance of post-tensioned curved-strand connections in transverse joints of precast bridge decks. J. Bridge Eng. 2013, 18, 1062–1073. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Building Industry Press: Beijing, China, 2011.
- Zhang, Y.; Zhao, B.; Li, R.; Du, X. Monotonic and low cycle fatigue testing and research for HRB400. Eng. Mech. 2016, 33, 121–129. [Google Scholar]
- Guo, Q.Y.; Jia, C.H.; Xu, H.F. Experimental study and numerical analysis of flexural performance of large-span unbonded prestressed HSFRC beam. Build. Struct. 2022, 52, 69–75. [Google Scholar]

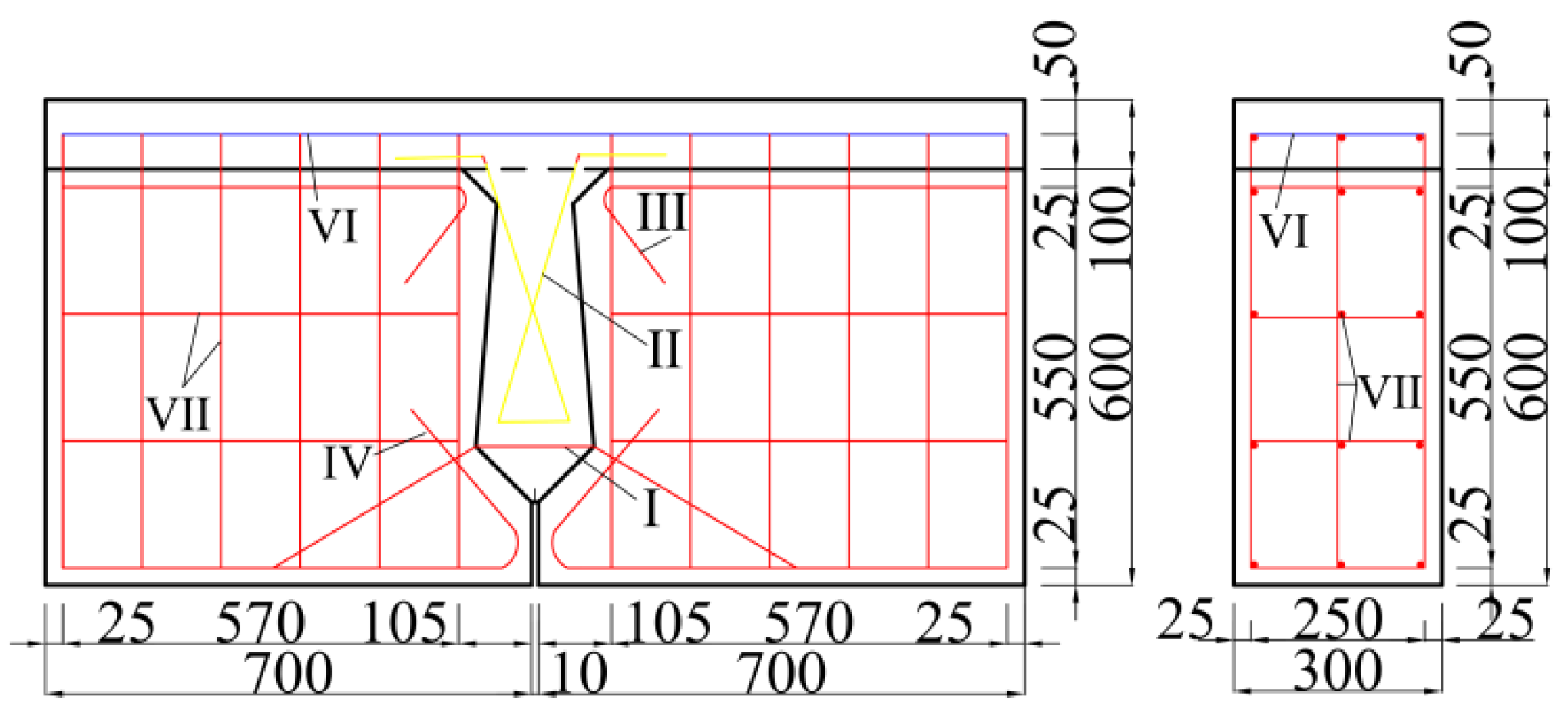
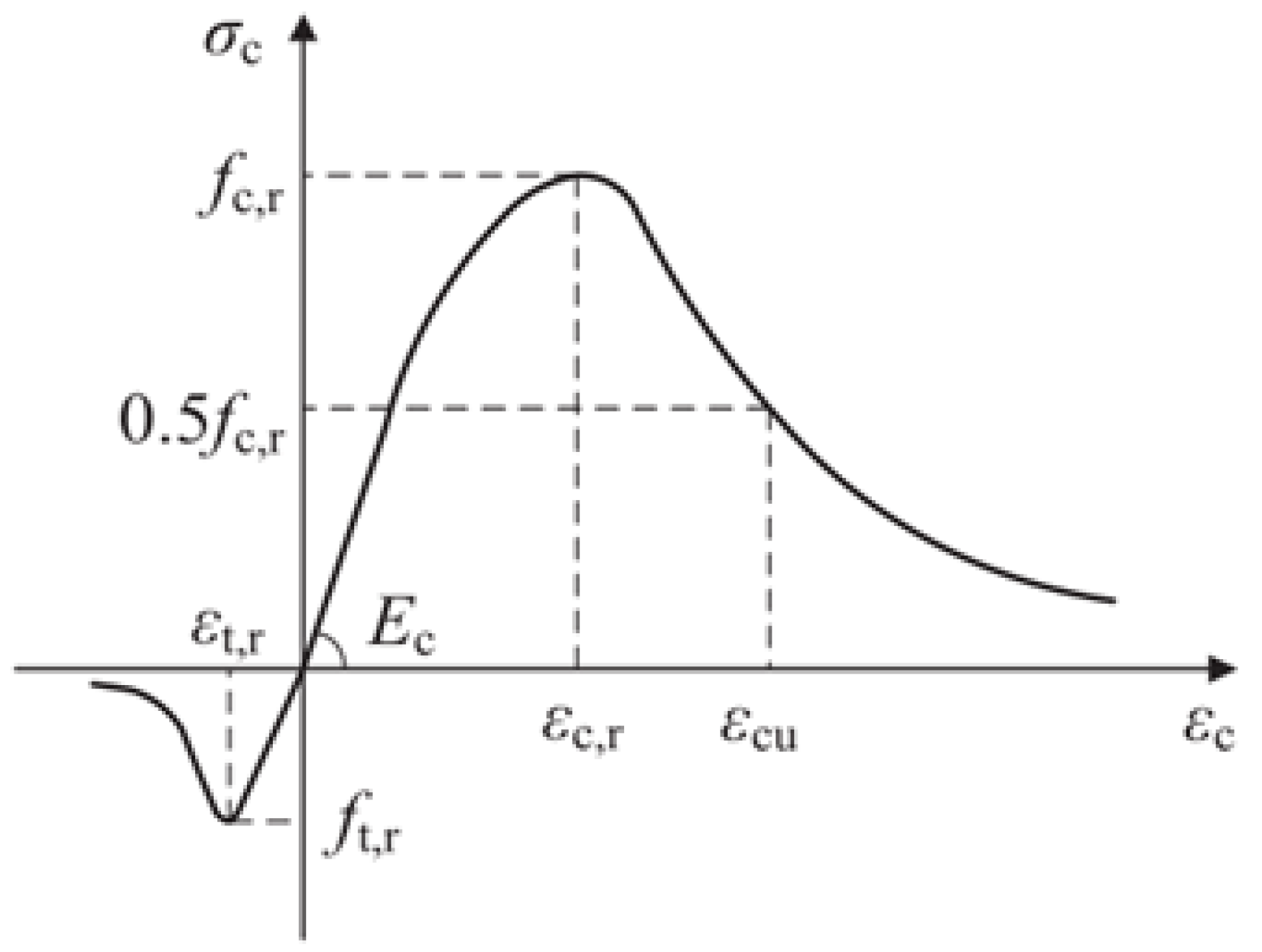

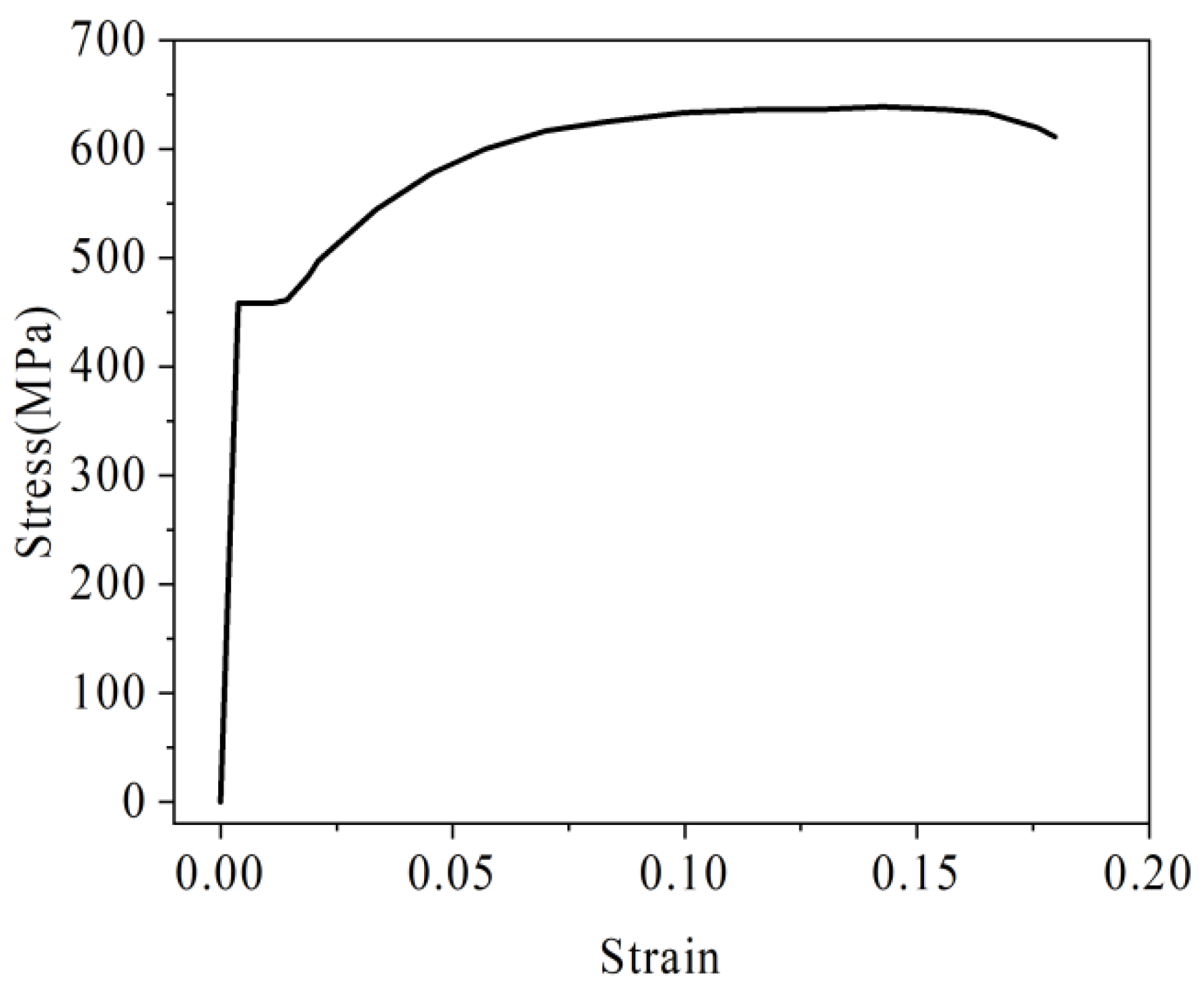
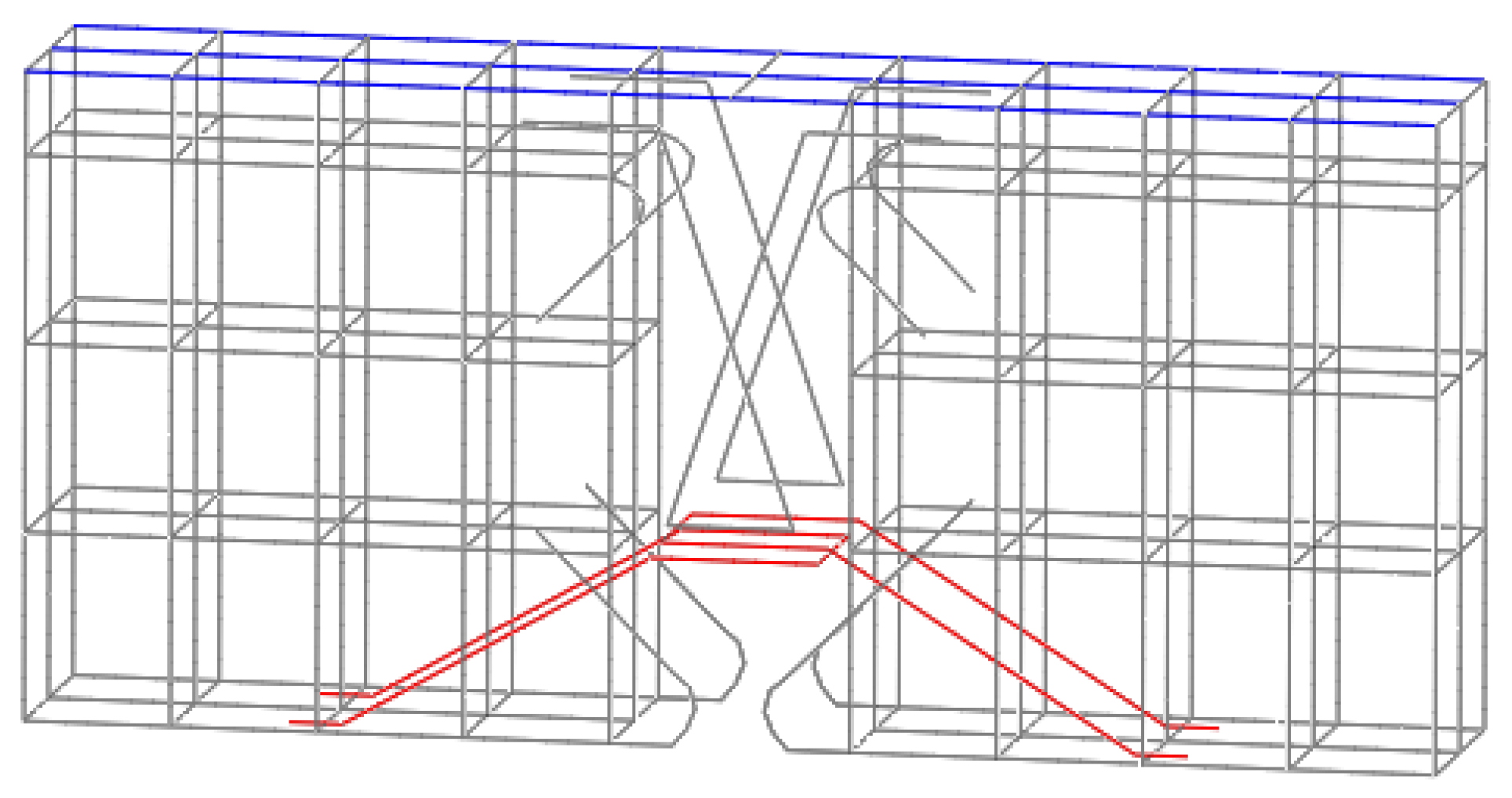


| Number | Moulded Dimensions | Enhancement Mode | Model Use |
|---|---|---|---|
| B-C | Scale model | Unreinforced | Finite element model verification |
| B-P | Scale model | local prestress | Finite element model verification |
| M-C | Hollow-core slab bridge model | Unreinforced | Finite element result analysis |
| M-P | Hollow-core slab bridge model | local prestress | Finite element result analysis |
| Number | Cracking Load (kN) | Through-Joint Load (kN) | Ultimate Load (kN) | |||
|---|---|---|---|---|---|---|
| Test Value | Analysis Value | Test Value | Analysis Value | Test Value | Analysis Value | |
| B-C | 60 | 70 | 280 | 300 | 340 | 340 |
| B-P | 130 | 100 | 180 | 200 | 870 | 860 |
| Number | Cracking Load (kN) | Through-Joint Load (kN) | Ultimate Load (kN) |
|---|---|---|---|
| M-C | 120 | 240 | 360 |
| M-P | 180 | 460 | 540 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, Y.; Zhu, Q. Study on Load Transfer Mechanism of Local Curved Prestressed Hollow-Core Slab Bridge. Materials 2023, 16, 4708. https://doi.org/10.3390/ma16134708
Chen J, Wang Y, Zhu Q. Study on Load Transfer Mechanism of Local Curved Prestressed Hollow-Core Slab Bridge. Materials. 2023; 16(13):4708. https://doi.org/10.3390/ma16134708
Chicago/Turabian StyleChen, Jihao, Yuxin Wang, and Qian Zhu. 2023. "Study on Load Transfer Mechanism of Local Curved Prestressed Hollow-Core Slab Bridge" Materials 16, no. 13: 4708. https://doi.org/10.3390/ma16134708
APA StyleChen, J., Wang, Y., & Zhu, Q. (2023). Study on Load Transfer Mechanism of Local Curved Prestressed Hollow-Core Slab Bridge. Materials, 16(13), 4708. https://doi.org/10.3390/ma16134708






