Abstract
Concrete compressive strength (CCS) is among the most important mechanical characteristics of this widely used material. This study develops a novel integrative method for efficient prediction of CCS. The suggested method is an artificial neural network (ANN) favorably tuned by electromagnetic field optimization (EFO). The EFO simulates a physics-based strategy, which in this work is employed to find the best contribution of the concrete parameters (i.e., cement (C), blast furnace slag (), fly ash (), water (W), superplasticizer (SP), coarse aggregate (), fine aggregate (), and the age of testing ()) to the CCS. The same effort is carried out by three benchmark optimizers, namely the water cycle algorithm (WCA), sine cosine algorithm (SCA), and cuttlefish optimization algorithm (CFOA) to be compared with the EFO. The results show that hybridizing the ANN using the mentioned algorithms led to reliable approaches for predicting the CCS. However, comparative analysis indicates that there are appreciable distinctions between the prediction capacity of the ANNs created by the EFO and WCA vs. the SCA and CFOA. For example, the mean absolute error calculated for the testing phase of the ANN-WCA, ANN-SCA, ANN-CFOA, and ANN-EFO was 5.8363, 7.8248, 7.6538, and 5.6236, respectively. Moreover, the EFO was considerably faster than the other strategies. In short, the ANN-EFO is a highly efficient hybrid model, and can be recommended for the early prediction of the CCS. A user-friendly explainable and explicit predictive formula is also derived for the convenient estimation of the CCS.
1. Introduction
Analyzing buildings from different perspectives is of great importance for safe design [1,2,3]. Concrete is among the most widely used materials for construction purposes [4,5,6]. It is used for building various structural elements, from foundations to columns and beams [7,8]. Hereupon, engineers have conducted studies to analyze the behavior of concrete in terms of various parameters, such as ion penetration resistance [9], seismic behavior [10], load-bearing capacity [11], slump and workability [12], etc.
High-performance concrete (HPC) is a strong and durable type of concrete that has gained significant popularity for many construction projects all over the world [13,14,15]. In concrete, compressive strength is the main design parameter [16,17]. Therefore, evaluating this parameter is of great importance to structural and geotechnical engineers. It is an essential yet difficult task [18,19]. With that said, the non-linear abilities of machine learning methods make them a suitable solution to such issues [20,21,22]. They can effectively explore the influence of various key factors on concrete compressive strength (CCS).
Data-mining techniques, such as gene expression programming [23], support vector machine (SVM) [24], and artificial neural network (ANN) [25], have broadly served as the approximators of CCS. Dao et al. [26] examined the efficiency of ANN and a Gaussian process regression (GPR) developed using various kernels for predicting the strength of HPC. In this way, they also used Monte Carlo simulation to investigate the sensitivity of the models. Evaluation of the accuracy of the implemented models showed that the GPR with Matern32 function yields the best prediction. Shahmansouri et al. [27] modeled the CCS of pozzolanic geopolymer concrete based on ground granulated blast-furnace slag. High agreement between the products of the ANN and expected CCSs confirmed the reliability of the proposed technique. Jalal et al. [28] proved the applicability of an adaptive neuro-fuzzy inference system (ANFIS), which is a powerful approximator for estimating the strength of rubberized concrete measured at four different ages (3, 7, 28, and 42 days). Dao et al. [29] studied the suitability of the ANN for CCS prediction in foamed concrete. Based on 97.2% testing correlation obtained for the optimized structure, they introduced the ANN as an efficient predictor of this parameter. Additionally, the executed sensitivity analysis revealed the largest impact for the dry density factor. Simsek et al. [30] incorporated a decision support method with extreme gradient boosting (XGB) to create an efficient predictor for the strength of HPC. Regarding the root mean square errors (RMSEs) of 4.36, 7.15, 10.47, and 6.71 calculated for the XGB, MLR, R-MLR, and ANN, the XGB was the superior model. Further studies with a focus on utilizing machine learning models in this field can be found in [31,32,33,34].
In more recent studies, scholars have realized that metaheuristic algorithms can be used for design aims [35,36,37]. Ulusoy et al. [38], for example, employed metaheuristic algorithms such as bat algorithm and harmony search for the optimal design of reinforced concrete beams. Moreover, metaheuristic strategies have excellent search capacities for attaining optimal solutions to a problem. Converting the prediction tasks (using data-mining techniques) to an optimization problem, these algorithms are capable of finding the optimal situation for the processor [39,40]. Hoang et al. [41] optimized a least squares support vector regression (LSSVR) using a differential flower pollination algorithm for simulating concrete bond strength. The RMSE = 2.39 and R2 = 0.84 indicated a high accuracy for the proposed model and its superiority over conventional tools such as ANN. Mai et al. [42] were able to enhance the accuracy of the radial basis function ANN using a firefly algorithm (FFA) for predicting the axial compression capacity of concrete-filled steel columns. Two other metaheuristic techniques, namely genetic algorithm (GA) and differential evolution (DE), which were relatively weaker than FFA, were also used. Ma et al. [43] evaluated the efficiency of four metaheuristic optimizers, namely a salp swarm algorithm (SSA), grasshopper optimization algorithm (GOA), artificial bee colony (ABC), and shuffled frog leaping algorithm (SFLA), to tune the ANN for predicting the CCS. Considering the time and accuracy measures, the SSA and GOA were introduced as the strongest algorithms. In this regard, a notable distinction was observed for the correlation between these two algorithms (around 0.97%) and ABC (70.60%) and SFLA (88.90%). The predictive formula of the SSA and GOA was lastly derived. Notably, ABC emerged as a time-consuming technique. The use of the whale optimization algorithm (WOA) for the same purpose (i.e., neural network tuning for the CCS modeling) was recommended by Bui et al. [44]. The dragonfly algorithm and ant colony optimization were two other optimizers that presented a weaker performance relative to the WOA. A hybrid of the random forest and beetle antennae search (BAS) algorithm was proposed by Zhang et al. [45] for simulating the uniaxial compressive strength of oil palm shell concrete. Due to the high correlation (>95%) obtained for the testing process, the suggested model is a reliable and effective approach to the aforementioned simulation.
As we have argued, diverse efforts concerning the accuracy improvement of conventional approaches illustrate the importance of this task in civil engineering. On the other hand, benefiting from optimization strategies (e.g., grey wolf optimizer [46], symbiotic organism searches [47], teaching learning-based optimization [48], etc.) has been regarded an effective idea for this purpose. Hence, this study is concerned with the evaluation of an innovative hybrid method for predicting the CCS of HPC. To this end, electromagnetic field optimization (EFO) is combined with an ANN model to offer an optimal predictor. Moreover, the EFO is validated through comparing the results with three other optimizers, namely the water cycle algorithm (WCA), sine cosine algorithm (SCA), and cuttlefish optimization algorithm (CFOA).
2. Materials and Methods
2.1. Data Provision
The used dataset consists of compressive strength records of 1133 HPC samples [49]. It was originally created by Yeh [50], and has also been used in earlier studies [51,52]. Observing these data, the CCS is affected by the present amounts of seven ingredients: cement (C), blast furnace slag (), fly ash (), water (W), superplasticizer (SP), coarse aggregate (), fine aggregate (), and the age of testing (). Figure A1 shows a histogram of the data.
Table A1 illustrates the dataset statistically. Regarding values, the specimens are 1, 3, 7, 14, 28, 56, 90, 91, 100, 120, 180, 270, 360, and 365 day(s) old. The weakest and strongest specimens are distinguished by the minimum and maximum CCSs, 2.33 and 82.60 MPa, respectively. The average CCS of the whole dataset is 35.84 MPa. Likewise, the mean value for C, , , W, SP, , , and is 276.50 kg/m3, 74.27 kg/m3, 62.81 kg/m3, 182.98 kg/m3, 6.42 kg/m3, 964.83 kg/m3, 770.49 kg/m3, and 44.06 days, respectively.
Of these 1133 samples, first, 906 samples are randomly selected to feed the networks. They use these data for learning the relationship between the target parameter (i.e., the CCS) and the inputs (i.e., C, , , W, SP, , , and ). More clearly for the metaheuristic hybrids used in this study, the WCA, SCA, CFOA, and EFO assign a multiplying weight to each input factor, and a bias term to each neuron of the ANN. The same process is carried out for the subsequent neurons to create a non-linear model. The acquired pattern is then exposed to the rest of the data, which comprises 227 samples, to predict the CCS for unfamiliar specimens. In this way, the versatility of the models is assessed.
2.2. EFO Algorithm
The EFO is considered a physics-based technique because the developers, Abedinpourshotorban et al. [53], used electromagnetics rules for designing it. The population of this algorithm is cooperative, and aims to improve the position for the betterment of the solution. Attraction–repulsion forces affect individuals called electromagnet particles (EMPs). Famously, opposite, and similar polarities cause attraction and repulsion forces, respectively. For EMPs, there is more power in the attraction forces (5–10% higher than the repulsion forces). In the EFO, a golden value is sought for the ration between these forces. During the implementation, the EMPs in the neutral field maintain distance from those of the negative field (i.e., the poorly fitted ones) because of the repulsion interaction, and conversely, they approach those of the positive field (i.e., nicely fitted ones) because of the attraction interaction.
First, a population is initialized, evaluated, and sorted according to the individuals’ fitness. They are classified into three groups, namely the positive field (best individuals), negative field (weak individuals), and neutral field (the rest). In the neutral field, there are small negative polarities close to zero, where
where , , and symbolize the population of the negative, positive, and neutral groups. Likewise, stands for the whole population. Additionally, and are the EFO parameters.
In the subsequent step, a new individual is created, and after comparing its fitness with existing ones, it finds the appropriate place, and the polarity is accordingly determined. Remarkably, the weakest individual is removed from the population. The generation of the new individual can be modeled as follows:
where is the golden ration, rand is a random value in ♥0, 1♥, m = 1, 2, 3, …, and N_var, , , and give random integers where and [54]. Further sources for learning about the EFO mechanism are [55,56,57].
2.3. Benchmarks Optimizers
As previously mentioned, the EFO is validated by comparing its performance with three other algorithms, namely WCA, SCA, and CFOA. These techniques were designed by Eskandar et al. [58], Mirjalili [59], and Eesa et al. [60], respectively. As a generic measure in population-based optimizers, the algorithms go through certain steps (e.g., initializing the population, fitness evaluation, updating the situation, and monitoring stopping criteria) to perform the optimization task.
For example, the water cycle (and the movements of rivers and streams toward a sea) is the inspiration for the WCA algorithm. After it has rained, the raindrops are evaluated and based on their goodness, and they form streams, rivers, and one sea so that the most accurate solution is held in the sea. Other components update their positions to improve themselves and replace the sea. This is while the SCA is based on mathematical rules including sine and cosine functions. Utilizing some random values, the position of the population is improved to obtain a more promising solution. Unlike the WCA and SCA, the CFOA is a bio-inspired method that simulates the camouflage action of the cuttlefish. Over two stages, namely reflection and visibility, which mimic the light reflection and pattern matching procedures, respectively, this animal is able to enact an optimal change in its color. Detailed descriptions of the WCA, SCA, and CFOA can be found in references [61,62,63,64,65,66], respectively.
2.4. Quality Measures
In comparable earlier studies, accuracy is the most important determinant factor in the efficiency evaluation of the models. Therefore, proper measures should be deployed for reporting accuracy. In this paper, the errors of both learning and prediction are measured using two well-known criteria, namely the root mean square error (RMSE) and mean absolute error (MAE), where the error indicates the differences between the laboratory and estimated CCSs (i.e., Error = ). As the names connote, they give a rooted value of the squared average of the errors, and the average of the absolute errors, respectively. Calculations of the RMSE and MAE are shown in Equations (7) and (8).
where Z stands for the size (i.e., the number) of the assessed data.
The Pearson correlation coefficient (PCC) is a correlation evaluative index that is used herein to report the agreement between the . and for all Z samples. The PCC is formulated as follows:
3. Results and Discussion
3.1. Optimization and Training Assessment
As was mentioned earlier, this study offers various metaheuristic trained ANNs for predicting CCS. The training process is detailed in this section. First, a general structure of the ANN with adjustable parameters was coded and given to the WCA, SCA, CFOA, and EFO as the problem function. In each iteration of implementing the ANN-WCA, ANN-SCA, ANN-CFOA, and ANN-EFO, the algorithm aims to minimize the RMSE of training. In other words, this criterion is deemed the objective function. This is how the optimal ANN is achieved by each optimizer [67,68].
The number of the iterations (NIter) and population size (SPop) are two important parameters of all metaheuristic algorithms that need to be selected carefully. Both parameters can be completely different for two algorithms, due to the specific behaviors and strategies executed by them. For the EFO, five SPops (25, 30, 35, 40, and 45) were tested, where the NIter equals 30,000, while the WCA, SCA, and CFOA were tested using SPops of 100, 200, 300, 400, and 500, with NIter = 1000 [69,70]. In this way, the sensitivity of the algorithms to SPop can be monitored, and the best network configuration can be selected. Figure 1 shows the convergence curves obtained after this process. According to this figure and based on the error reduction steps, the optimization proceedings of the algorithms are different from each other. The CFOA, for example, reduced the objective function in the initial iterations more effectively, while the SCA reduced it more gently, in several steps, and the EFO and WCA reduced it by following a smooth trajectory.
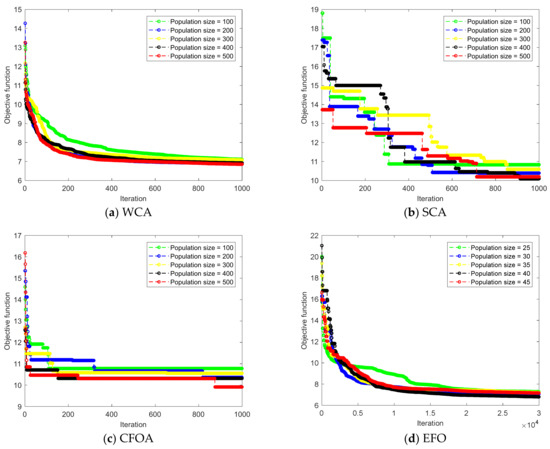
Figure 1.
Optimizing the ANN using different metaheuristic configurations.
This figure also shows that the best ANN training (i.e., the smallest RMSEs) was attained by the SPop of 500, 400, 500, and 40 for the WCA, SCA, CFOA, and EFO, respectively. The obtained RMSEs of ANN-WCA, ANN-SCA, ANN-CFOA, and ANN-EFO were 6.8558, 10.0972, 9.9135, and 6.7992. The magnitude of the error was calculated for all 906 training specimens, and their frequencies are depicted in Figure 2. It is shown that all four models have suitable error histograms, meaning that compared to large errors, much larger frequencies can be observed for small errors. This reliability can be also proven by tolerable MAEs 5.2712, 7.9139, 7.6845, and 5.2653, as well as the PCCs of 0.90493, 0.79004, 0.79200, and 0.90659.
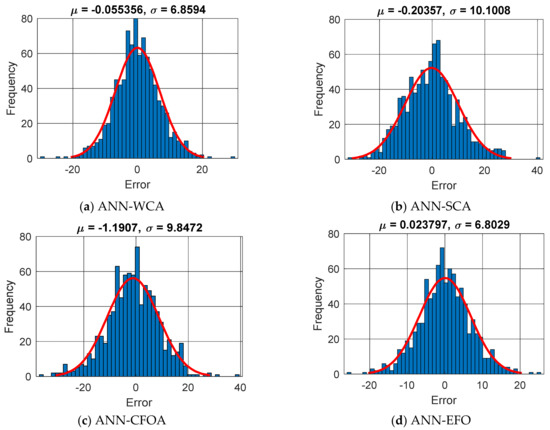
Figure 2.
The frequency of errors in the training process (Error = ).
According to the above results, although all algorithms could tune the ANN properly, the search strategies of the WCA and EFO were more successful than those of the SCA and CFOA. This can be deduced from the lower errors and the higher PCC values obtained for the ANN-WCA and ANN-EFO. For the same reason, the accuracy of the EFO was slightly more promising than that of the WCA. The ANN network optimized by this algorithm is presented in the form of the below equations:
Given that is the skeleton of Equations (10)–(16), they yield the outputs of the middle layer of the ANN. These parameters are obtained by processing the input factors (i.e., C, , , W, SP, , , and ), and themselves play the role of inputs for the next layer. The final calculation is carried out using Equation (17) for releasing the predicted CCS.
3.2. Testing Performance
As explained earlier, once the hybrids acquire a satisfying understanding from the training data, they are asked to predict the CCS for 227 stranger specimens. This work, which is referred to as the testing phase, reflects the competency of the models in dealing with new concrete mixtures. Similar to the training phase, the accuracy of prediction is examined by means of the RMSE, MAE, and PCC. Figure 3 shows the error values in this dataset. The RMSEs were 7.8044, 10.0340, 9.8392, and 7.4895, which along with the MAEs of 5.8363, 7.8248, 7.6538, and 5.6236 indicate the promising prediction potential of the used models. However, in accordance with training results, the ANNs designed by the WCA and EFO can predict the CCS with a considerably smaller error compared to those tuned with the SCA and CFOA.
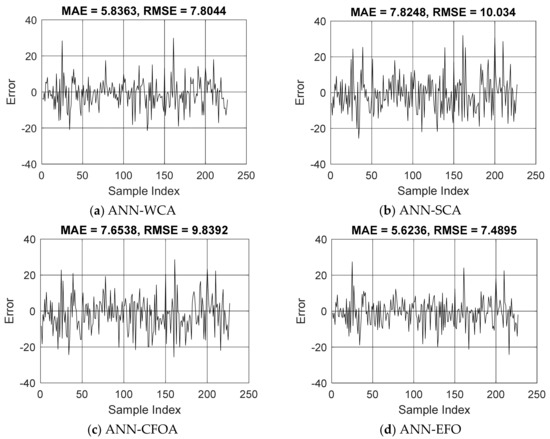
Figure 3.
The trend of errors over the testing dataset (Error = ).
Moreover, the consistency of the testing results is graphically shown in Figure 4. Accordingly, the predicted CCSs are in a very good agreement with the values recorded in the laboratory. By comparison, the results of the ANN-SCA and ANN-CFOA are more scattered than the ANN-WCA and ANN-EFO. This excellence can also be demonstrated numerically in the PCCs of 0.87666, 0.80249, 0.79832, and 0.88633.
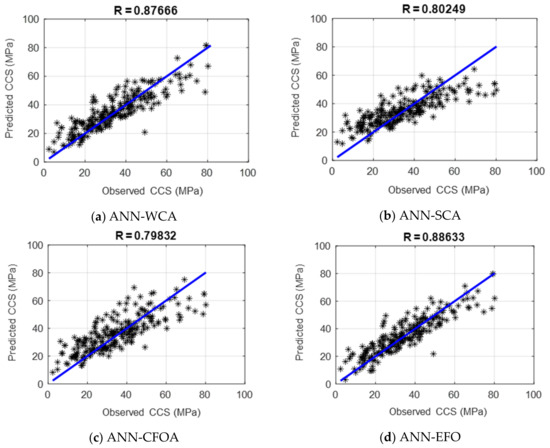
Figure 4.
The correlation of the testing results (R = ).
3.3. Discussion and More Evaluation
Civil engineering comprises a wide range of subjects from geotechnical to structural engineering, each exploring concrete from a different perspective [71,72]. Structural engineers have long considered concrete as a potential versatile material for different projects. Hence, significant attention has been paid to analyzing the behavior of concrete-based elements [73,74]. The main motivation of this research was to develop a predictive framework for analyzing the CCS of concrete. Different intelligent models were used and assessed using three accuracy indicators. Table 1 summarizes the calculated accucracy criteria.

Table 1.
Statistics of the data.
Evaluating the accuracy pointed out the superiority of the WCA and the proposed EFO in solving the given CCS problem. Since the ANNs tuned by these two algorithms were of higher potential than the SCA and CFOA, it can be inferred that the computational biases and weights offered by the WCA and EFO are more suitable. Therefore, these techniques enjoy excellent search abilities.
Moreover, assessing the computation times revealed that optimizing the ANN using WCA, SCA, CFOA, and EFO takes around 7520, 17443, 6430, and 314 s. In spite of the huge number of iterations considered for the EFO, it is much faster than other tested algorithms. Therefore, it may be an effective optimizer for engineering tasks in which time is a critical parameter.
Similar metaheuristic algorithms have been used in some previous studies with compatible datasets similar to the present work. These studies have proven that the tested hybrid ANNs were more accurate than conventional ANN. For instance, Hu et al. [75] were able to optimize the ANN using a multi-verse optimizer (MVO), shuffled complex evolution (SCE), and beetle antennae search (BAS). The calculated testing RMSEs were 8.3540, 7.8965, and 7.5401 for the SCE, MVO, and BAS, which are higher than the RMSEs achieved in this study by the WCA and EFO. Likewise, Moayedi et al. [76] were able to improve the accuracy of the ANN using metaheuristic models, and when comparing the accuracy, the outstanding models of the present study are more reliable than the equilibrium optimizer (RMSE = 7.8720 and MAE = 5.9869) used in the cited work. Further comparisons can be considered by referring to similar studies such as that of Li and Wu [77] (the improved sparrow algorithm), and Bui et al. [44] (the ant colony optimization and dragonfly algorithm).
From a practical point of view, there are various benefits of using the proposed models in the concrete and construction industries. These predictive models can estimate the performance of different concrete mixtures, and engineers can quickly explore a wide range of design options and select the most promising ones. Optimizing the composition of concrete materials through identifying the relationships between proportions, material components, and desired properties is another viable use; this may also be helpful in minimizing costs and environmental impacts. The EFO algorithm proposed in this work is among the quickest optimizers, and is recommended for practical estimations in cases wherein time is a critical resource. In the context of concrete and structural design, quality control, structural performance prediction, and developing decision support systems are other feasible applications of these inexpensive and time-effective metaheuristic models.
4. Conclusions
As the primary aim of many civil engineers, accurate simulation of CCS is of great importance for optimizing the construction process. In this work, an efficient novel predictive model was developed for this problem. Electromagnetic field optimization was synthesized with an ANN model for predicting CCS using a comprehensive and robust dataset. The sufficient learning of the CCS pattern was reflected by the MAE of 5.2653. Among the tested benchmarks, the WCA could train the ANN with superior accuracy (MAE = 5.2712). Applying the proposed model to new data revealed that the ANN-EFO can produce a reliable prediction of the CCS. The MAE in this phase was 5.6236, which is lower than those obtained for the WCA (5.8363), SCA (7.8248), and CFOA (7.6538). Apart from the accuracy, assessing the complexity of the models showed that the EFO needed a very smaller number of individuals (i.e., SPop of 40 vs. 500, 400, and 500) for optimizing the ANN. Moreover, despite the EFO being implemented with a NIters 30 times that of other algorithms, it was the fastest algorithm. Therefore, the ANN-EFO may be a potent indirect method for evaluating CCS. Comparisons with some previous studies demonstrated the superiority of the models offered in this work. Additionally, recommendations were presented for practical usages of the models in the concrete and construction industries. However, the authors believe that this work can be built upon by extending the methodologies, optimizing the dataset, and performing cross-validation with real-world concrete data.
Author Contributions
Conceptualization, M.L.N.; Methodology, M.L.N.; Software, M.R.A. and H.G.; Validation, A.A.; Formal analysis, M.R.A., H.G. and A.A.; Investigation, M.R.A., H.G., A.A. and R.P.; Resources, R.P.; Data curation, M.R.A., H.G. and R.P.; Writing—original draft, M.R.A., H.G., A.A. and R.P.; Writing—review & editing, M.L.N.; Visualization, M.R.A., H.G., A.A. and R.P.; Supervision, M.L.N.; Project administration, M.L.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The used data is available from the resources given in Section 2.1.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
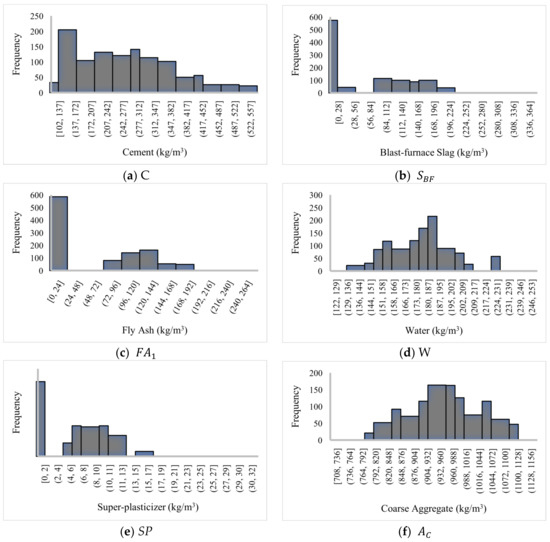
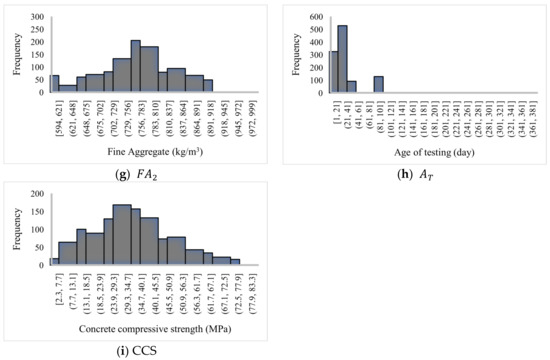
Figure A1.
Histogram of the dataset.

Table A1.
Statistics of the data.
Table A1.
Statistics of the data.
| Parameter | Unit | Mean | Standard Error | Standard Deviation | Sample Variance | Skewness | Minimum | Maximum |
|---|---|---|---|---|---|---|---|---|
| C | kg/m3 | 276.50 | 3.07 | 103.47 | 10,706.03 | 0.53 | 102.00 | 540.00 |
| 74.27 | 2.50 | 84.25 | 7097.52 | 0.77 | 0.00 | 359.40 | ||
| 62.81 | 2.13 | 71.58 | 5124.15 | 0.61 | 0.00 | 260.00 | ||
| W | 182.98 | 0.65 | 21.71 | 471.49 | 0.09 | 121.75 | 247.00 | |
| SP | 6.42 | 0.17 | 5.80 | 33.60 | 0.84 | 0.00 | 32.20 | |
| 964.83 | 2.46 | 82.79 | 6853.89 | −0.17 | 708.00 | 1145.00 | ||
| 770.49 | 2.36 | 79.37 | 6300.21 | −0.19 | 594.00 | 992.60 | ||
| Day | 44.06 | 1.80 | 60.44 | 3653.15 | 3.47 | 1.00 | 365.00 | |
| CCS | MPa | 35.84 | 0.48 | 16.10 | 259.23 | 0.42 | 2.33 | 82.60 |
References
- Dang, P.; Cui, J.; Liu, Q.; Li, Y. Influence of source uncertainty on stochastic ground motion simulation: A case study of the 2022 Mw 6.6 Luding, China, earthquake. Stoch. Environ. Res. Risk Assess. 2023, 1–18. [Google Scholar] [CrossRef]
- Wu, M.; Ba, Z.; Liang, J. A procedure for 3D simulation of seismic wave propagation considering source-path-site effects: Theory, verification and application. Earthq. Eng. Struct. Dyn. 2022, 51, 2925–2955. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Yang, J. Analysis of stochastic process to model safety risk in construction industry. J. Civ. Eng. Manag. 2021, 27, 87–99. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Z.; Liu, Y.; Chen, Y.; Du, Y.; Zhou, F. Interfacial debonding detection for CFST structures using an ultrasonic phased array: Application to the Shenzhen SEG building. Mech. Syst. Signal Process. 2023, 192, 110214. [Google Scholar] [CrossRef]
- Qi, B.; Gao, S.; Xu, P. The Application of Rubber Aggregate-Combined Permeable Concrete Mixture in Sponge City Construction. Coatings 2023, 13, 87. [Google Scholar] [CrossRef]
- Qi, B.; Gao, S.; Xu, P. The Application of Recycled Epoxy Plastic Sheets Waste to Replace Concrete in Urban Construction and Building. Processes 2023, 11, 201. [Google Scholar] [CrossRef]
- Guo, M.; Huang, H.; Zhang, W.; Xue, C.; Huang, M. Assessment of RC Frame Capacity Subjected to a Loss of Corner Column. J. Struct. Eng. 2022, 148, 04022122. [Google Scholar] [CrossRef]
- Wang, M.; Yang, X.; Wang, W. Establishing a 3D aggregates database from X-ray CT scans of bulk concrete. Constr. Build. Mater. 2022, 315, 125740. [Google Scholar] [CrossRef]
- Han, Y.; Shao, S.; Fang, B.; Shi, T.; Zhang, B.; Wang, X.; Zhao, X. Chloride ion penetration resistance of matrix and interfacial transition zone of multi-walled carbon nanotube-reinforced concrete. J. Build. Eng. 2023, 72, 106587. [Google Scholar] [CrossRef]
- Huang, H.; Yuan, Y.; Zhang, W.; Li, M. Seismic behavior of a replaceable artificial controllable plastic hinge for precast concrete beam-column joint. Eng. Struct. 2021, 245, 112848. [Google Scholar] [CrossRef]
- Huang, H.; Guo, M.; Zhang, W.; Zeng, J.; Yang, K.; Bai, H. Numerical investigation on the bearing capacity of RC columns strengthened by HPFL-BSP under combined loadings. J. Build. Eng. 2021, 39, 102266. [Google Scholar] [CrossRef]
- Safayenikoo, H.; Khajehzadeh, M.; Nehdi, M.L. Novel evolutionary-optimized neural network for predicting fresh concrete slump. Sustainability 2022, 14, 4934. [Google Scholar] [CrossRef]
- Yin, W.; Li, X.; Sun, T.; Wang, J.; Chen, Y.; Yan, G. Experimental investigation on the mechanical and rheological properties of high-performance concrete (HPC) incorporating sinking bead. Constr. Build. Mater. 2020, 243, 118293. [Google Scholar] [CrossRef]
- Sabet, F.A.; Libre, N.A.; Shekarchi, M. Mechanical and durability properties of self consolidating high performance concrete incorporating natural zeolite, silica fume and fly ash. Constr. Build. Mater. 2013, 44, 175–184. [Google Scholar] [CrossRef]
- Lu, D.; Tang, Z.; Zhang, L.; Zhou, J.; Gong, Y.; Tian, Y.; Zhong, J. Effects of combined usage of supplementary cementitious materials on the thermal properties and microstructure of high-performance concrete at high temperatures. Materials 2020, 13, 1833. [Google Scholar] [CrossRef]
- Rashid, K.; Yazdanbakhsh, A.; Rehman, M.U. Sustainable selection of the concrete incorporating recycled tire aggregate to be used as medium to low strength material. J. Clean. Prod. 2019, 224, 396–410. [Google Scholar] [CrossRef]
- Alizadeh, V. Finite element analysis of controlled low strength materials. Front. Struct. Civ. Eng. 2019, 13, 1243–1250. [Google Scholar] [CrossRef]
- Alencar, D.; Carvalho, D.; Koenders, E.; Mourão, F.; Rocha, L. Devising a computational model based on data mining techniques to predict concrete compressive strength. Procedia Comput. Sci. 2017, 108, 455–464. [Google Scholar] [CrossRef]
- Khademi, F.; Jamal, S.M. Estimating the compressive strength of concrete using multiple linear regression and adaptive neuro-fuzzy inference system. Int. J. Struct. Eng. 2017, 8, 20–31. [Google Scholar] [CrossRef]
- Omran, B.A.; Chen, Q.; Jin, R. Comparison of data mining techniques for predicting compressive strength of environmentally friendly concrete. J. Comput. Civ. Eng. 2016, 30, 04016029. [Google Scholar] [CrossRef]
- Chopra, P.; Sharma, R.K.; Kumar, M. Prediction of compressive strength of concrete using artificial neural network and genetic programming. Adv. Mater. Sci. Eng. 2016, 2016, 7648467. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Chen, Y. Inverse design of materials by machine learning. Materials 2022, 15, 1811. [Google Scholar] [CrossRef] [PubMed]
- Ashrafian, A.; Gandomi, A.H.; Rezaie-Balf, M.; Emadi, M. An evolutionary approach to formulate the compressive strength of roller compacted concrete pavement. Measurement 2020, 152, 107309. [Google Scholar] [CrossRef]
- Yu, Y.; Li, W.; Li, J.; Nguyen, T.N. A novel optimised self-learning method for compressive strength prediction of high performance concrete. Constr. Build. Mater. 2018, 184, 229–247. [Google Scholar] [CrossRef]
- Asteris, P.G.; Argyropoulos, I.; Cavaleri, L.; Rodrigues, H.; Varum, H.; Thomas, J.; Lourenço, P.B. Masonry Compressive Strength Prediction Using Artificial Neural Networks. In Proceedings of the International Conference on Transdisciplinary Multispectral Modeling and Cooperation for the Preservation of Cultural Heritage, Athens, Greece, 10–13 October 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 200–224. [Google Scholar]
- Dao, D.V.; Adeli, H.; Ly, H.-B.; Le, L.M.; Le, V.M.; Le, T.-T.; Pham, B.T. A sensitivity and robustness analysis of GPR and ANN for high-performance concrete compressive strength prediction using a Monte Carlo simulation. Sustainability 2020, 12, 830. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Yazdani, M.; Ghanbari, S.; Bengar, H.A.; Jafari, A.; Ghatte, H.F. Artificial neural network model to predict the compressive strength of eco-friendly geopolymer concrete incorporating silica fume and natural zeolite. J. Clean. Prod. 2020, 279, 123697. [Google Scholar] [CrossRef]
- Jalal, M.; Arabali, P.; Grasley, Z.; Bullard, J.W. Application of adaptive neuro-fuzzy inference system for strength prediction of rubberized concrete containing silica fume and zeolite. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 438–451. [Google Scholar] [CrossRef]
- Dao, D.V.; Ly, H.-B.; Vu, H.-L.T.; Le, T.-T.; Pham, B.T. Investigation and Optimization of the C-ANN Structure in Predicting the Compressive Strength of Foamed Concrete. Materials 2020, 13, 1072. [Google Scholar] [CrossRef]
- Simsek, S.; Gumus, M.; Khalafalla, M.; Issa, T.B. A hybrid data analytics approach for high-performance concrete compressive strength prediction. J. Bus. Anal. 2020, 3, 158–168. [Google Scholar] [CrossRef]
- Asteris, P.G.; Apostolopoulou, M.; Skentou, A.D.; Moropoulou, A. Application of artificial neural networks for the prediction of the compressive strength of cement-based mortars. Comput. Concr. 2019, 24, 329–345. [Google Scholar]
- Deng, F.; He, Y.; Zhou, S.; Yu, Y.; Cheng, H.; Wu, X. Compressive strength prediction of recycled concrete based on deep learning. Constr. Build. Mater. 2018, 175, 562–569. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Keshavarz, Z.; Torkian, H. Application of ANN and ANFIS models in determining compressive strength of concrete. J. Soft Comput. Civ. Eng. 2018, 2, 62–70. [Google Scholar]
- Zhang, J.; Huang, Y.; Wang, Y.; Ma, G. Multi-objective optimization of concrete mixture proportions using machine learning and metaheuristic algorithms. Constr. Build. Mater. 2020, 253, 119208. [Google Scholar] [CrossRef]
- Sarir, P.; Armaghani, D.J.; Jiang, H.; Sabri, M.M.S.; He, B.; Ulrikh, D.V. Prediction of Bearing Capacity of the Square Concrete-Filled Steel Tube Columns: An Application of Metaheuristic-Based Neural Network Models. Materials 2022, 15, 3309. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Nguyen, H.M.; Naderi Bakhtiyari, A.; Asadi, A. Feasibility of ANFIS-PSO and ANFIS-GA models in predicting thermophysical properties of Al2O3-MWCNT/oil hybrid nanofluid. Materials 2019, 12, 3628. [Google Scholar] [CrossRef]
- Ulusoy, S.; Kayabekir, A.E.; Bekdaş, G.; Niğdeli, S. Metaheuristic Algorithms in Optimum Design of Reinforced Concrete Beam by Investigating Strength of Concrete. Chall. J. Concr. Res. Lett. 2020, 11, 33–37. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.A.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2019, 35, 967–984. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Kalantar, B.; Mu’Azu, M.A.; Rashid, A.S.A.; Foong, L.K.; Nguyen, H. Novel hybrids of adaptive neuro-fuzzy inference system (ANFIS) with several metaheuristic algorithms for spatial susceptibility assessment of seismic-induced landslide. Geomat. Nat. Hazards Risk 2019, 10, 1879–1911. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Tran, X.-L.; Nguyen, H. Predicting ultimate bond strength of corroded reinforcement and surrounding concrete using a metaheuristic optimized least squares support vector regression model. Neural Comput. Appl. 2020, 32, 7289–7309. [Google Scholar] [CrossRef]
- Mai, S.H.; Seghier, M.E.A.B.; Nguyen, P.L.; Jafari-Asl, J.; Thai, D.-K. A hybrid model for predicting the axial compression capacity of square concrete-filled steel tubular columns. Eng. Comput. 2020, 30, 1205–1222. [Google Scholar] [CrossRef]
- Ma, X.; Foong, L.K.; Morasaei, A.; Ghabussi, A.; Lyu, Z. Swarm-based hybridizations of neural network for predicting the concrete strength. Smart Struct. Syst. 2020, 26, 241–251. [Google Scholar]
- Bui, D.T.; Ghareh, S.; Moayedi, H.; Nguyen, H. Fine-tuning of neural computing using whale optimization algorithm for predicting compressive strength of concrete. Eng. Comput. 2019, 37, 701–712. [Google Scholar]
- Zhang, J.; Li, D.; Wang, Y. Predicting uniaxial compressive strength of oil palm shell concrete using a hybrid artificial intelligence model. J. Build. Eng. 2020, 30, 101282. [Google Scholar] [CrossRef]
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 202, 54–64. [Google Scholar] [CrossRef]
- Prayogo, D.; Cheng, M.; Widjaja, J.; Ongkowijoyo, H.; Prayogo, H. Prediction of Concrete Compressive Strength from Early Age Test Result Using an Advanced Metaheuristic-Based Machine Learning Technique. In Proceedings of the International Symposium on Automation and Robotics in Construction (ISARC), Taipei, China, 28 June–1 July 2017; IAARC Publications: Taipei, China, 2017. [Google Scholar]
- Ly, H.-B.; Pham, B.T.; Dao, D.V.; Le, V.M.; Le, L.M.; Le, T.-T. Improvement of ANFIS model for prediction of compressive strength of manufactured sand concrete. Appl. Sci. 2019, 9, 3841. [Google Scholar] [CrossRef]
- Nguyen, T.; Ngo, T. Compressive Strength Dataset of Foamed/Normal Concrete for Prediction Model; University of Melbourne: Melbourne, Australia, 2018. [Google Scholar]
- Yeh, I.-C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Nguyen, T.; Kashani, A.; Ngo, T.; Bordas, S. Deep neural network with high-order neuron for the prediction of foamed concrete strength. Comput. -Aided Civ. Infrastruct. Eng. 2019, 34, 316–332. [Google Scholar] [CrossRef]
- Bui, D.-K.; Nguyen, T.; Chou, J.-S.; Nguyen-Xuan, H.; Ngo, T.D. A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr. Build. Mater. 2018, 180, 320–333. [Google Scholar] [CrossRef]
- Abedinpourshotorban, H.; Shamsuddin, S.M.; Beheshti, Z.; Jawawi, D.N. Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm. Swarm Evol. Comput. 2016, 26, 8–22. [Google Scholar] [CrossRef]
- AbouOmar, M.S.; Su, Y.-X.; Zhang, H.-J. Hybrid Feedback-Feedforward Fuzzy Control of PEM Fuel Cell Air Feed System with Electromagnetic Field Optimization. IETE J. Res. 2019, 68, 575–591. [Google Scholar] [CrossRef]
- Song, S.; Jia, H.; Ma, J. A chaotic electromagnetic field optimization algorithm based on fuzzy entropy for multilevel thresholding color image segmentation. Entropy 2019, 21, 398. [Google Scholar] [CrossRef] [PubMed]
- Talebi, B.; Dehkordi, M.N. Sensitive association rules hiding using electromagnetic field optimization algorithm. Expert Syst. Appl. 2018, 114, 155–172. [Google Scholar] [CrossRef]
- Bouchekara, H.; Zellagui, M.; Abido, M.A. Optimal coordination of directional overcurrent relays using a modified electromagnetic field optimization algorithm. Appl. Soft Comput. 2017, 54, 267–283. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. -Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Eesa, A.S.; Brifcani, A.M.A.; Orman, Z. Cuttlefish algorithm-a novel bio-inspired optimization algorithm. Int. J. Sci. Eng. Res. 2013, 4, 1978–1986. [Google Scholar]
- Nasir, M.; Sadollah, A.; Choi, Y.H.; Kim, J.H. A comprehensive review on water cycle algorithm and its applications. Neural Comput. Appl. 2020, 32, 17433–17488. [Google Scholar] [CrossRef]
- Foong, L.K.; Moayedi, H.; Lyu, Z. Computational modification of neural systems using a novel stochastic search scheme, namely evaporation rate-based water cycle algorithm: An application in geotechnical issues. Eng. Comput. 2020, 37, 3347–3358. [Google Scholar] [CrossRef]
- Wang, J.; Yang, W.; Du, P.; Niu, T. A novel hybrid forecasting system of wind speed based on a newly developed multi-objective sine cosine algorithm. Energy Convers. Manag. 2018, 163, 134–150. [Google Scholar] [CrossRef]
- Mirjalili, S.M.; Mirjalili, S.Z.; Saremi, S.; Mirjalili, S. Sine cosine algorithm: Theory, literature review, and application in designing bend photonic crystal waveguides. In Nature-Inspired Optimizers; Springer: Berlin/Heidelberg, Germany, 2020; pp. 201–217. [Google Scholar]
- Giernacki, W.; Fraire, T.E.; Kozierski, P. Cuttlefish Optimization Algorithm in Autotuning of Altitude Controller of Unmanned Aerial Vehicle (UAV). In Proceedings of the Iberian Robotics Conference, Sevilla, Spain, 22–24 November 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 841–852. [Google Scholar]
- Eesa, A.S.; Orman, Z. A new clustering method based on the bio-inspired cuttlefish optimization algorithm. Expert Syst. 2020, 37, e12478. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef] [PubMed]
- Mehrabi, M.; Pradhan, B.; Moayedi, H.; Alamri, A. Optimizing an adaptive neuro-fuzzy inference system for spatial prediction of landslide susceptibility using four state-of-the-art metaheuristic techniques. Sensors 2020, 20, 1723. [Google Scholar] [CrossRef] [PubMed]
- Mehrabi, M.; Moayedi, H. Landslide susceptibility mapping using artificial neural network tuned by metaheuristic algorithms. Environ. Earth Sci. 2021, 80, 804. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrabi, M.; Kalantar, B.; Moayedi, H.; Abdullahi, M.A.M. Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2019, 10, 1667–1693. [Google Scholar] [CrossRef]
- Yuan, J.; Gan, Y.; Chen, J.; Tan, S.; Zhao, J. Experimental research on consolidation creep characteristics and microstructure evolution of soft soil. Phys. Mech. Prop. Treat. Technol. Hazard. Geomater. 2023, 10, 1137324. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, G.; Wu, B.; Kong, X. A study on mechanical properties and permeability of steam-cured mortar with iron-copper tailings. Constr. Build. Mater. 2023, 383, 131372. [Google Scholar] [CrossRef]
- Huang, H.; Huang, M.; Zhang, W.; Guo, M.; Chen, Z.; Li, M. Progressive collapse resistance of multistory RC frame strengthened with HPFL-BSP. J. Build. Eng. 2021, 43, 103123. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zhang, C.; Khorshidi, H.; Zhu, L.; Hsiao, P.-C. Seismic upgrading of existing RC frames with displacement-restraint cable bracing. Eng. Struct. 2023, 282, 115764. [Google Scholar] [CrossRef]
- Hu, P.; Moradi, Z.; Ali, H.E.; Foong, L.K. Metaheuristic-reinforced neural network for predicting the compressive strength of concrete. Smart Struct. Syst. 2022, 30, 195–207. [Google Scholar]
- Moayedi, H.; Eghtesad, A.; Khajehzadeh, M.; Keawsawasvong, S.; Al-Amidi, M.M.; Le Van, B. Optimized ANNs for predicting compressive strength of high-performance concrete. Steel Compos. Struct. 2022, 44, 853–868. [Google Scholar]
- Li, J.; Wu, Y. Improved Sparrow Search Algorithm with the Extreme Learning Machine and Its Application for Prediction. Neural Process. Lett. 2022, 54, 4189–4209. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).