Recent Advances in the Analytical Stress Field Solutions for Radiused Notches in Orthotropic Solids
Abstract
1. Introduction
- In Section 2, the fundamentals of complex potentials for orthotropic elasticity are discussed, with reference to plane stress or strain and antiplane shear problems.
- Section 3Sections toSection 6 present the analytical expressions for the mode 1, 2, and 3 stress fields related to different notch geometries, i.e., elliptical hole (Section 3), hyperbolic lateral notches (Section 4), parabolic notches, i.e., blunt cracks, (Section 5), and lateral radiused V-notches (Section 6).
- Eventually, Section 7 reports some examples of application, comparing the presented analytical solutions to the results from numerical analyses related to relevant cases.
2. Fundamentals of Complex Potential for Orthotropic Elasticity
2.1. Plane Stress or Plane Strain Problems
2.2. Antiplane Shear Deformation Problems
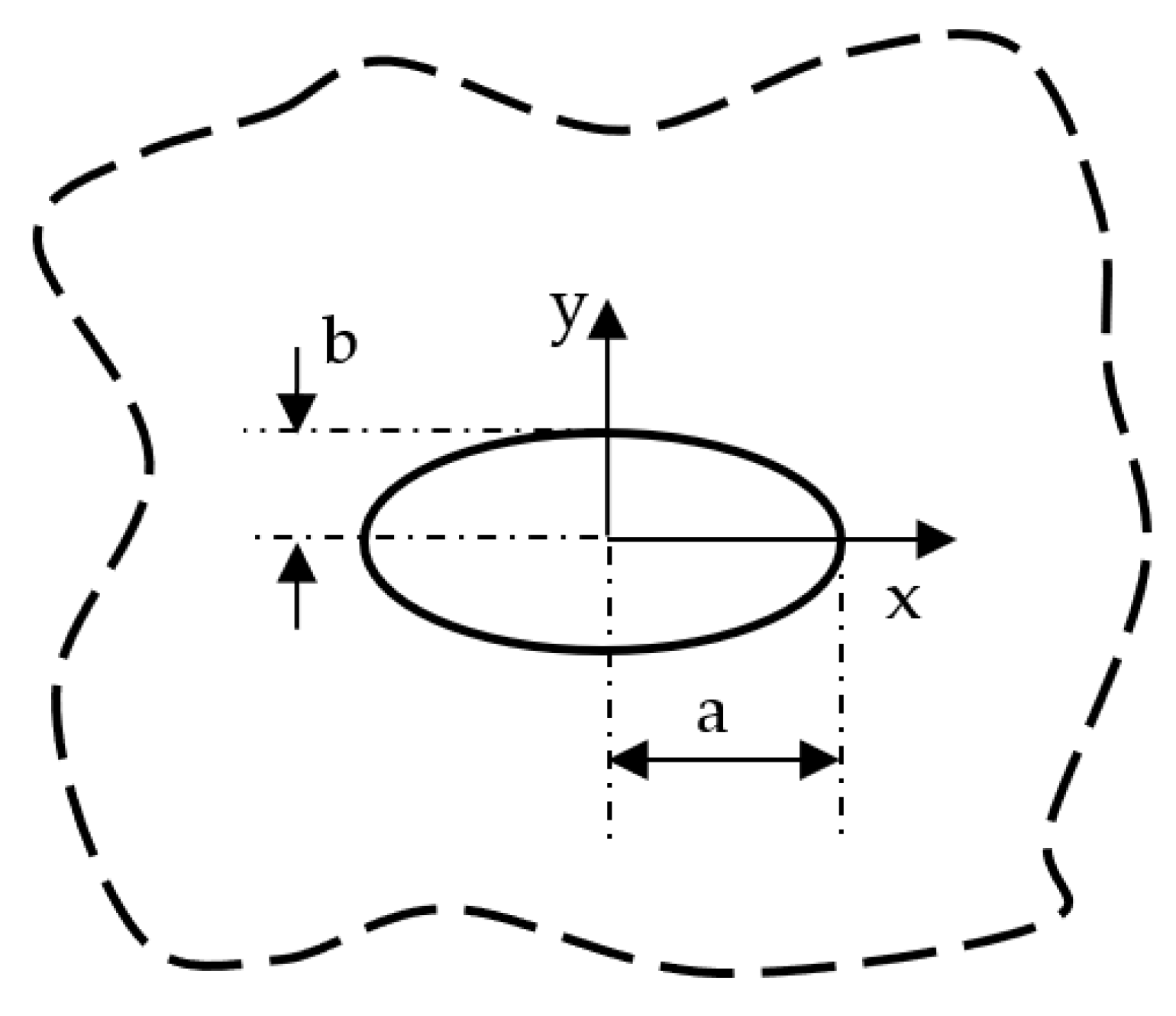
3. Stress Fields for an Infinite Orthotropic Plate with an Elliptical Hole
3.1. Mode 1 Loadings
3.2. Mode 2 Loadings
3.3. Mode 3 Loadings
4. Stress Fields for an Orthotropic Finite Plate with Two Symmetric Hyperbolic Notches
4.1. Mode 1 Loadings
4.2. Mode 2 Loadings
4.3. Mode 3 Loadings
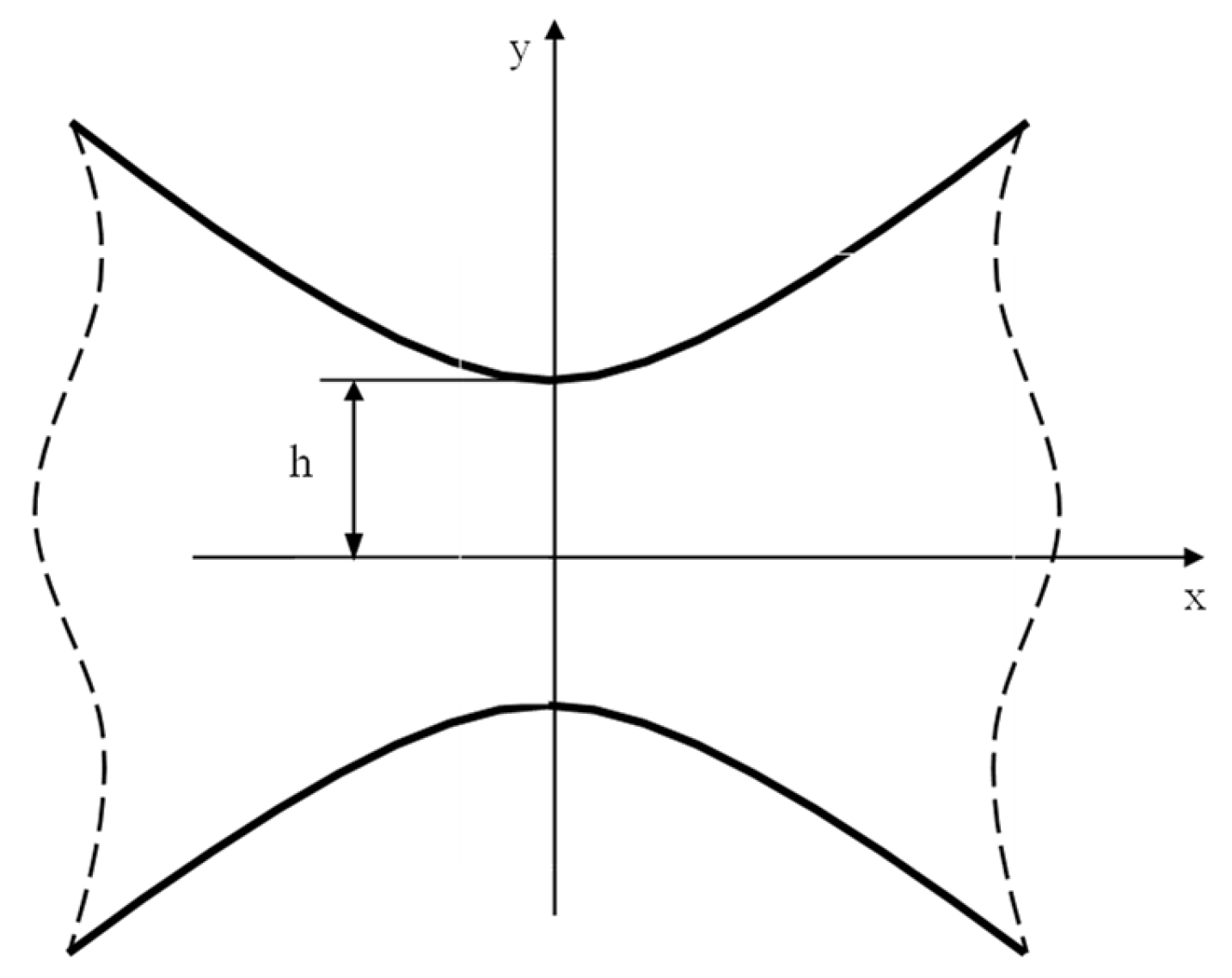
5. Stress Fields for Orthotropic Plate with a Deep Parabolic Notch
5.1. Mode 1 Problem
5.2. Mode 2 Problem
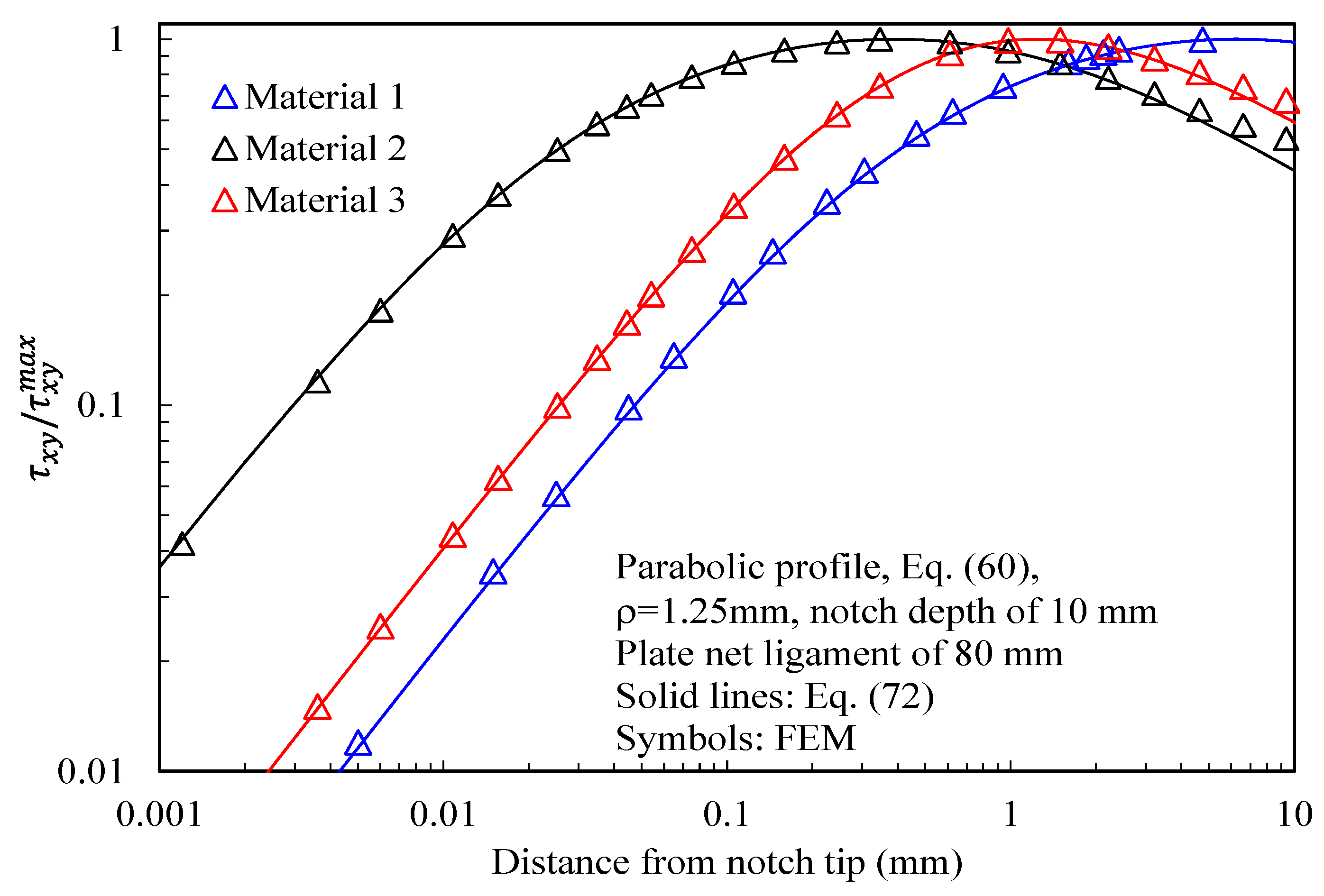
- As a function of the maximum shear stress along the bisector of the notch:where represents the distance from the notch tip corresponding to the maximum value for the shear stress, τxy.
- It can be linked to the maximum value of the normal stress, σvv, along the notch boundary:where:and is the solution of the following equation:
- It can be linked to a generalized stress intensity factor, K2ρ. Indeed, at a proper distance from the notch tip:where is the mode 2 generalized stress intensity factor for the orthotropic blunt crack [50].
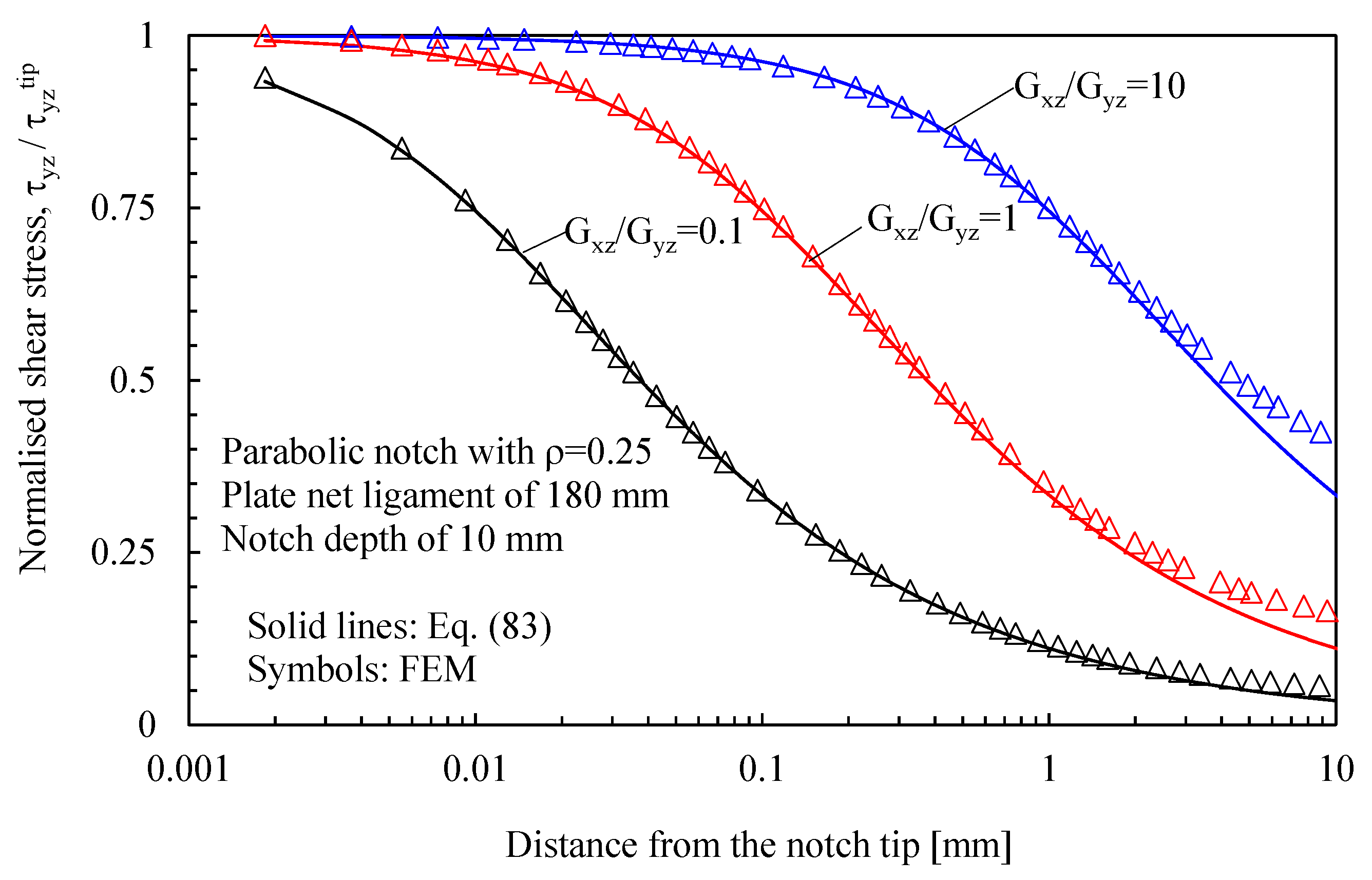
5.3. Mode 3 Problem
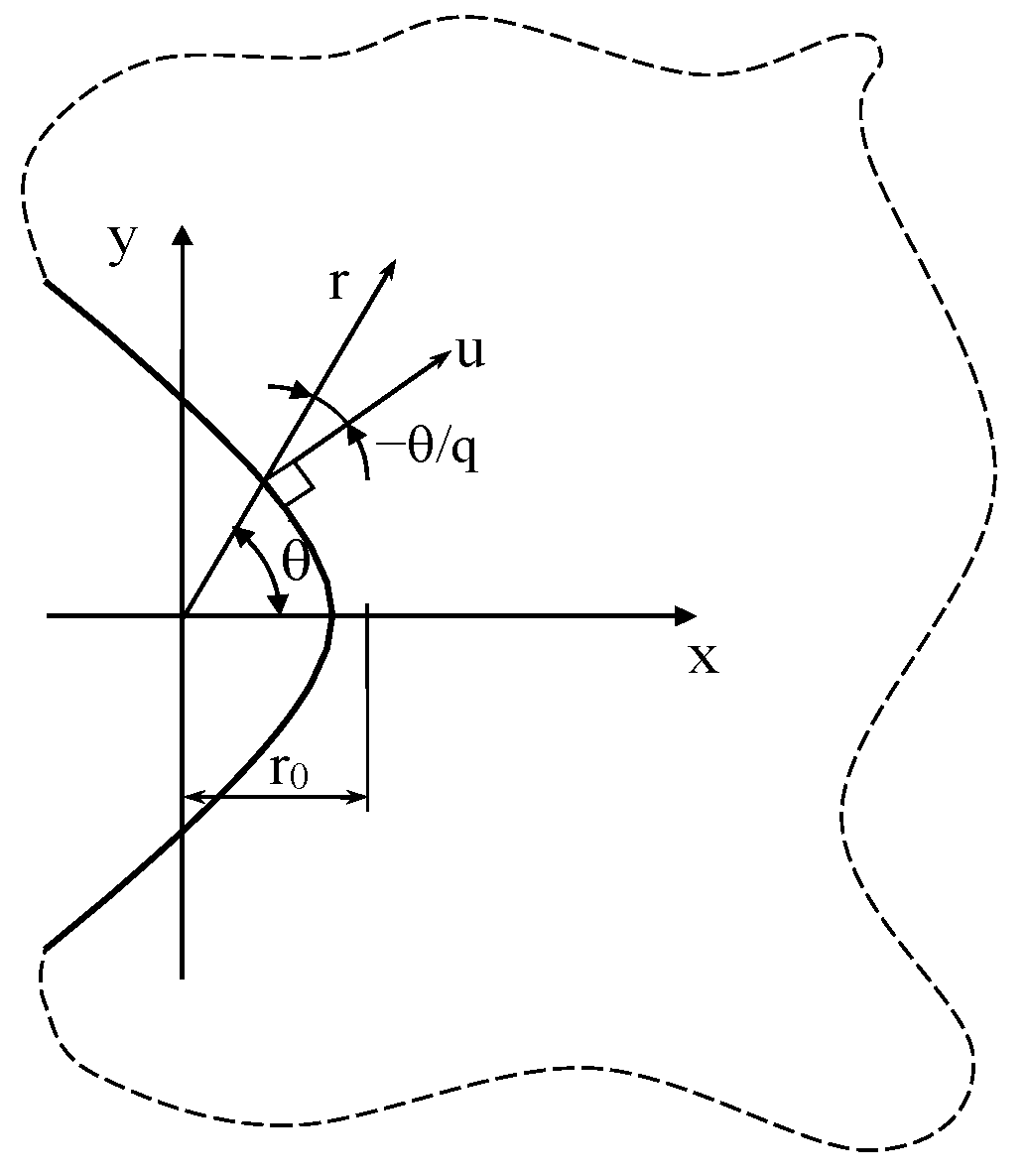
6. Lateral Radiused V-Shaped Notches
6.1. Mode 1 Loadings
6.2. Mode 2 Loadings
6.3. Mode 3 Loadings
7. Examples of Application
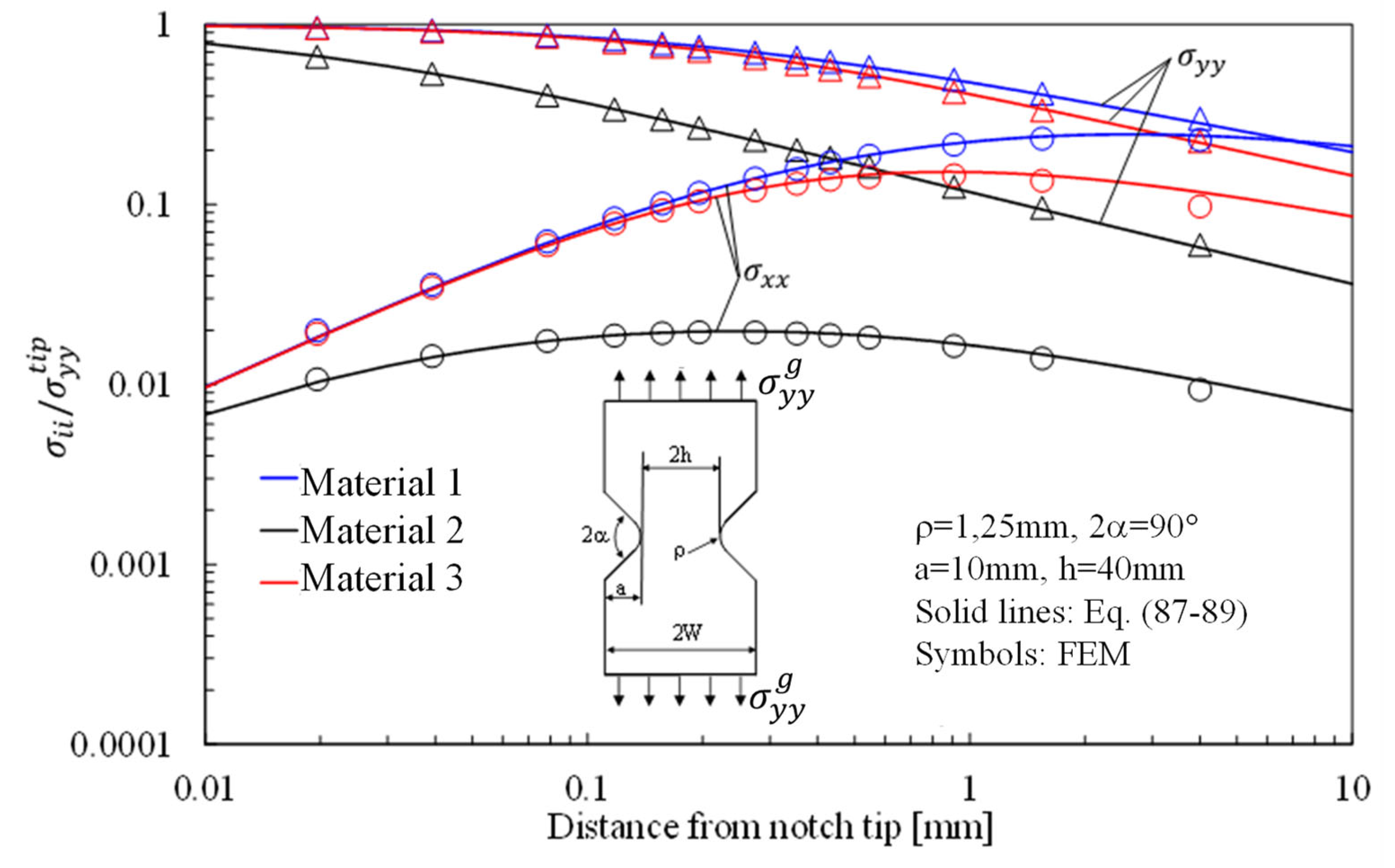
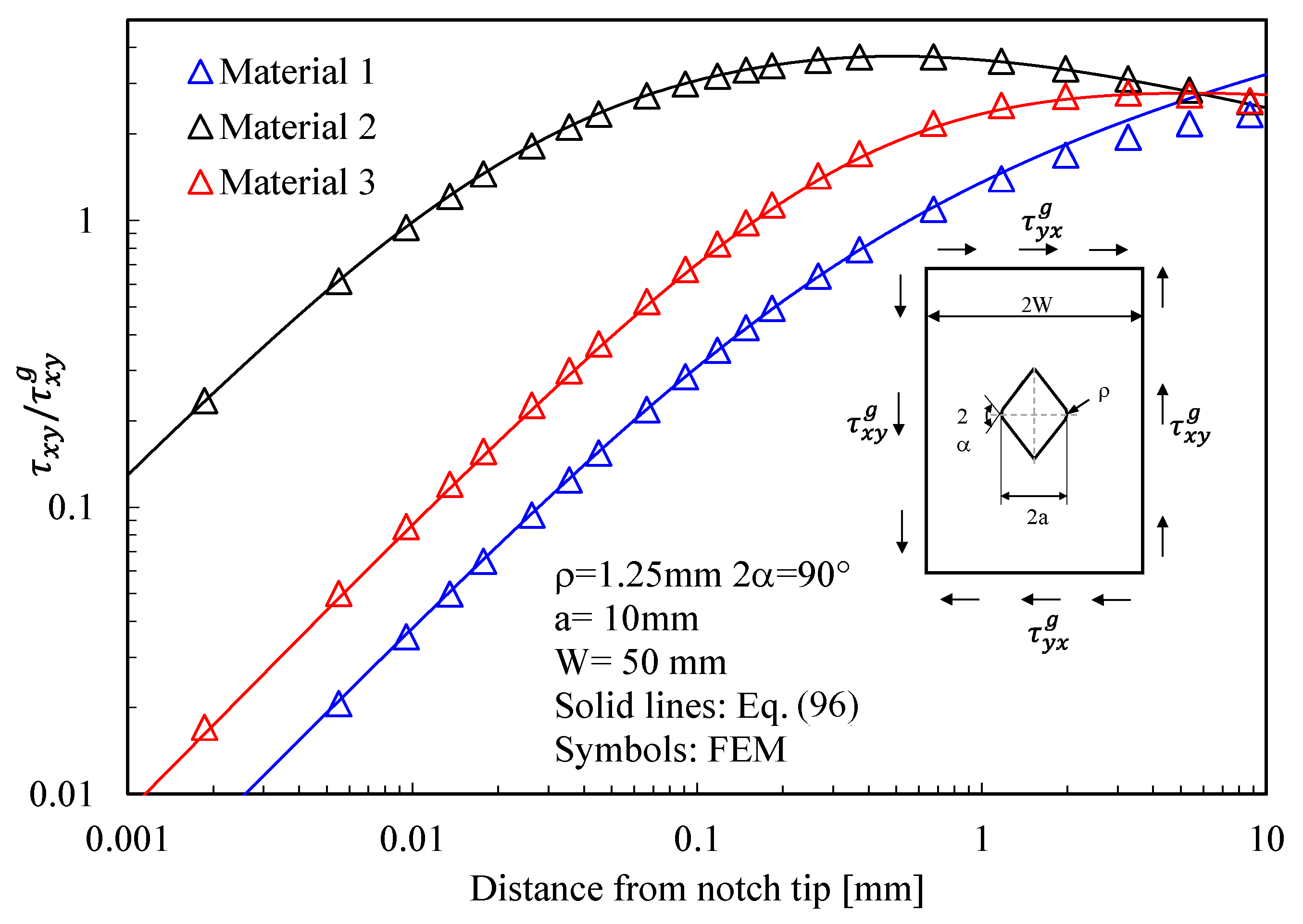
- Material 1 with the following properties: Ex = 160 GPa, Ey = 10 GPa, Gxy = 5 GPa, νxy = 0.30 so that β1 = 0.7198, β2 = 5.5572, representative of a unidirectional Carbon-Fiber Reinforced Epoxy laminate with fibers oriented along the notch bisector line;
- Material 2 with the following properties: Ex = 10 GPa, Ey = 160 GPa, Gxy = 5 GPa, νxy = 0.01875 so that β1 = 0.1799, β2 = 1.3893, representative of a unidirectional Carbon-Fiber Reinforced Epoxy laminate with fibers oriented along the direction normal to the notch bisector line;
- Material 3 with the following properties: Ex = 10 GPa, Ey = 10 GPa, Gxy = 3.846 GPa, νxy = 0.3 so that β1 = 0.9904, β2 = 1.0095, representative of a symmetric quasi-isotropic glass fib laminate.
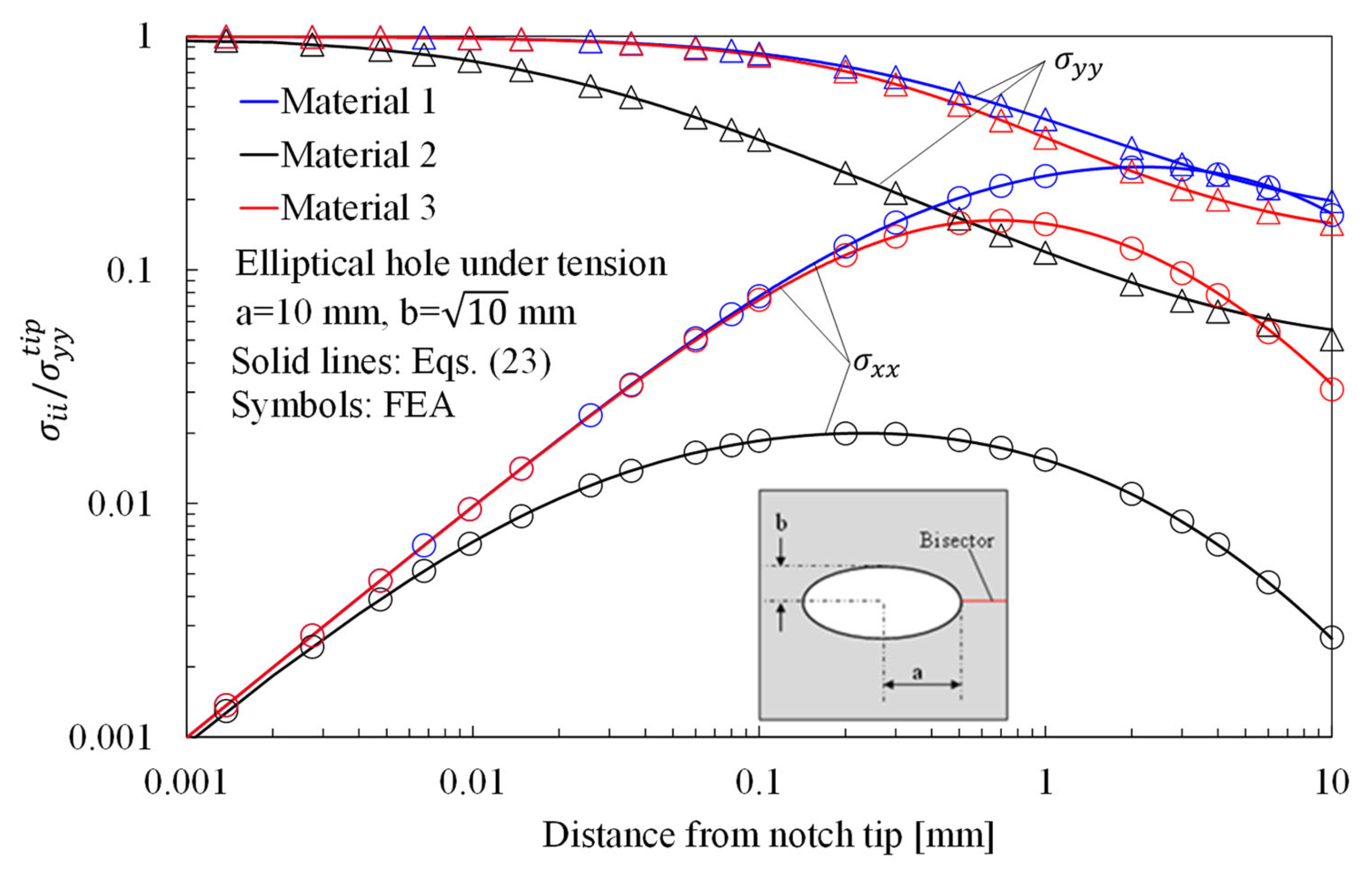
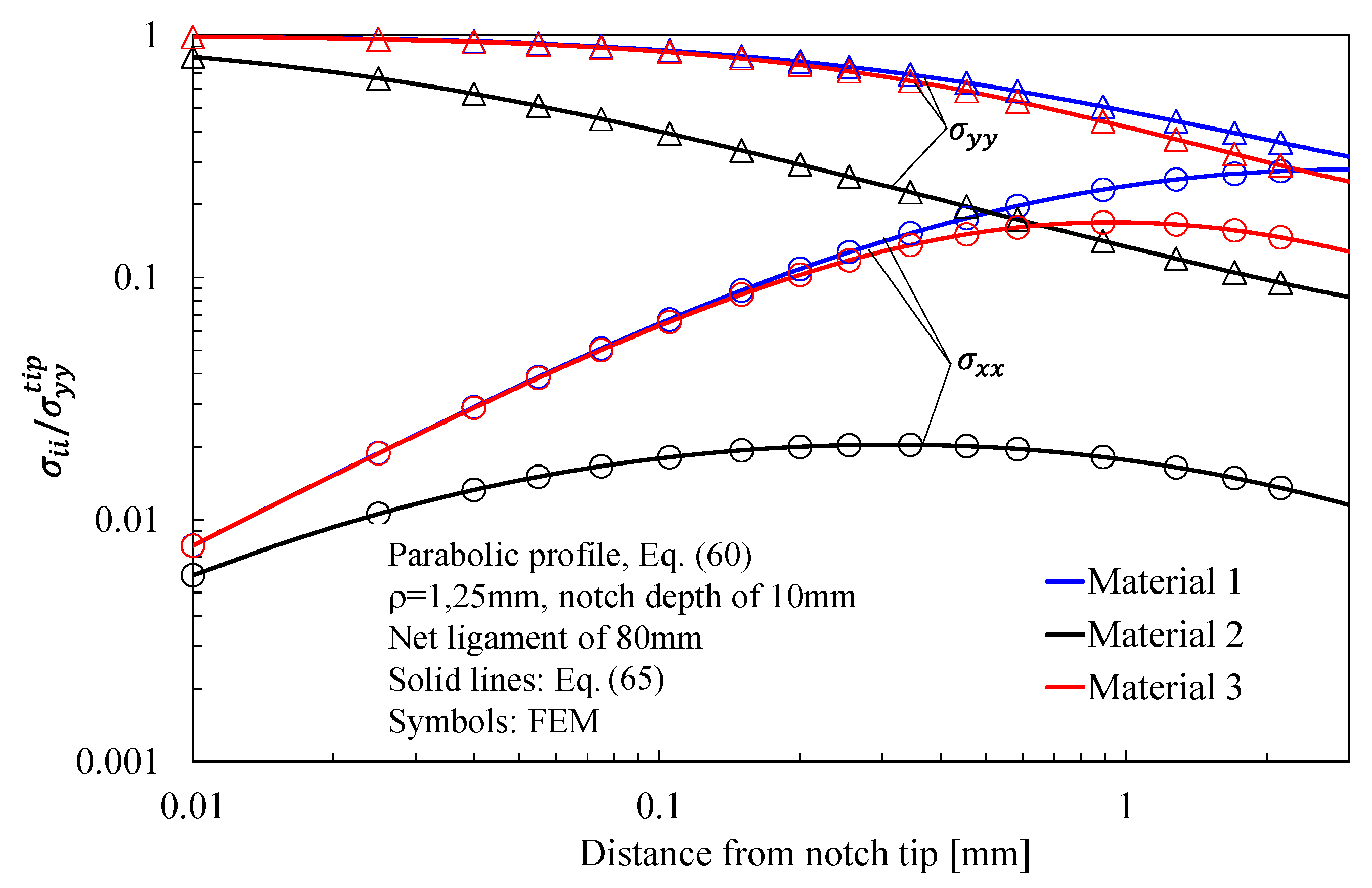
- With regards to Mode 1 loadings, Figure 5, Figure 8, Figure 11 and Figure 14 make it evident that when the material is very stiff along the loading direction (Material 2), the stress gradient is high, and the distribution of the maximum principal stress along the notch bisector line (i.e., the normal stress orthogonal to the notch bisector line) is very steep. Conversely, in the case of a material very stiff along the notch bisector line (Material 1), the stress gradient is much lower, and the distribution of the maximum principal stress along the notch bisector line (i.e., the normal stress orthogonal to the notch bisector line) is mild. As evident, this behavior is general and does not depend on the particular notch geometry under investigation.
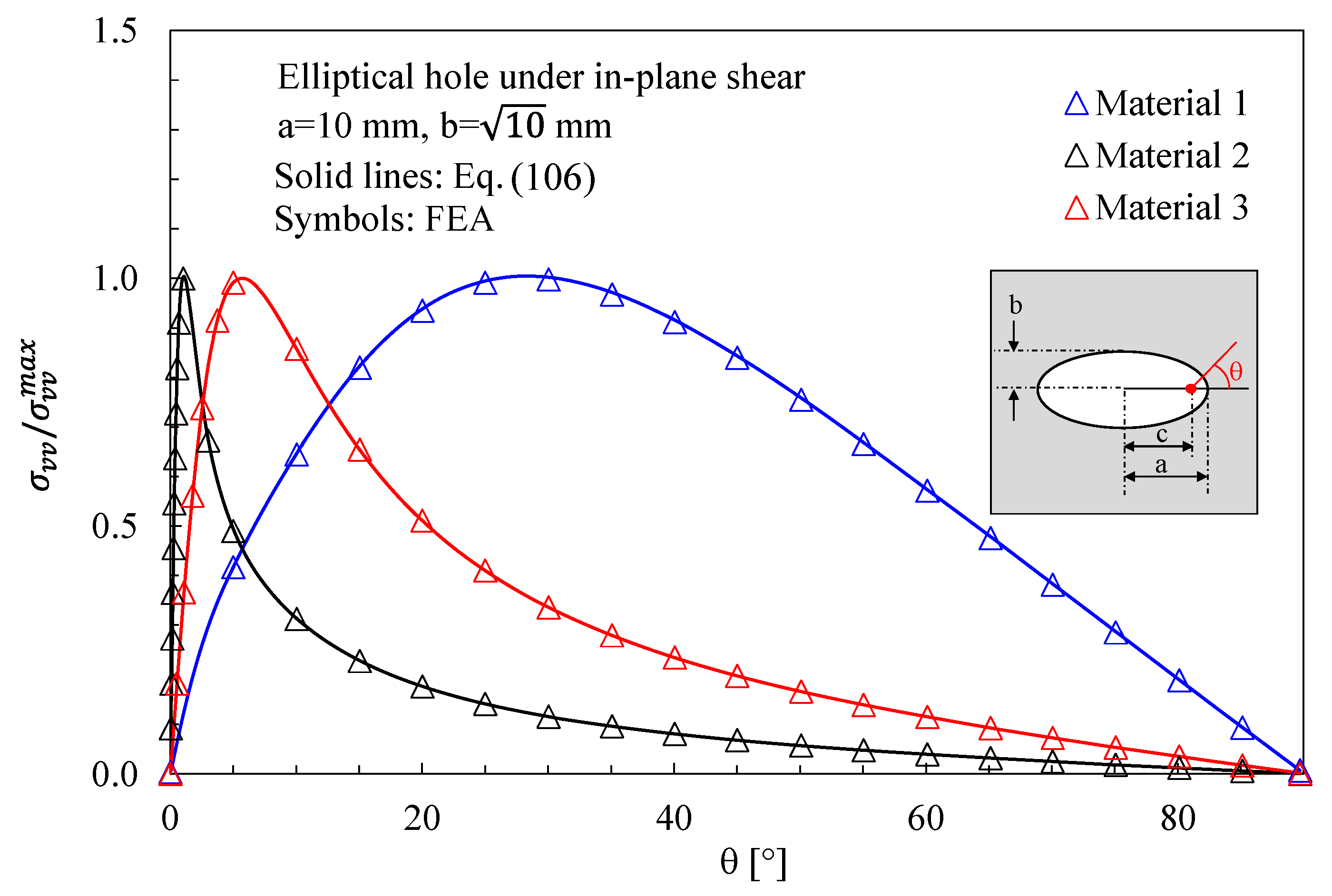
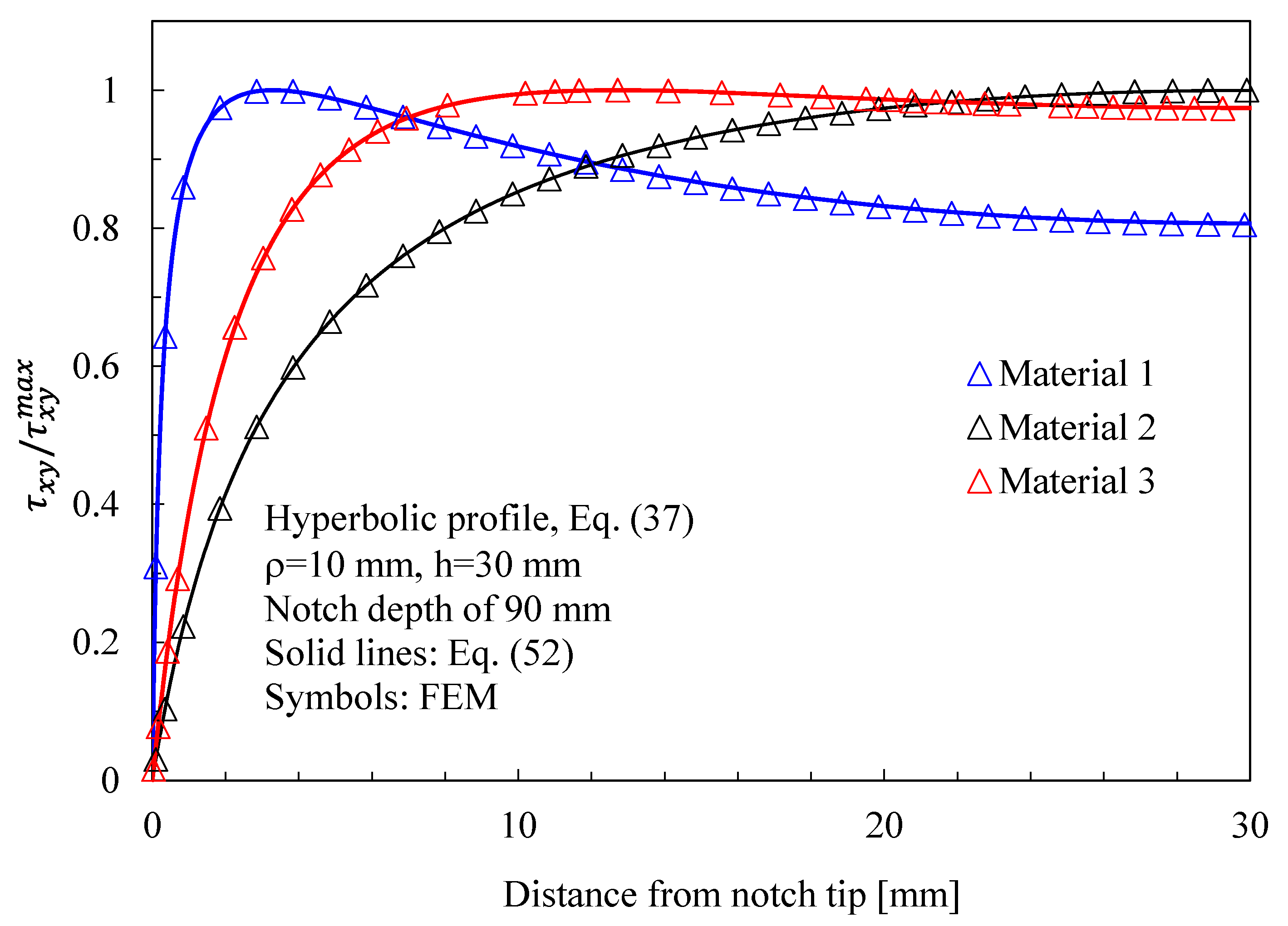
- With regards to Mode 2 loadings, from Figure 6, Figure 9, Figure 12 and Figure 15, it is evident that when the material is very stiff along the direction normal to the bisector line (Material 2), the stress gradient is high, and the point, along the notch bisector line, exhibiting the maximum shear stress is very close to the notch tip. This behavior is general and does not depend on the particular notch geometry under investigation.
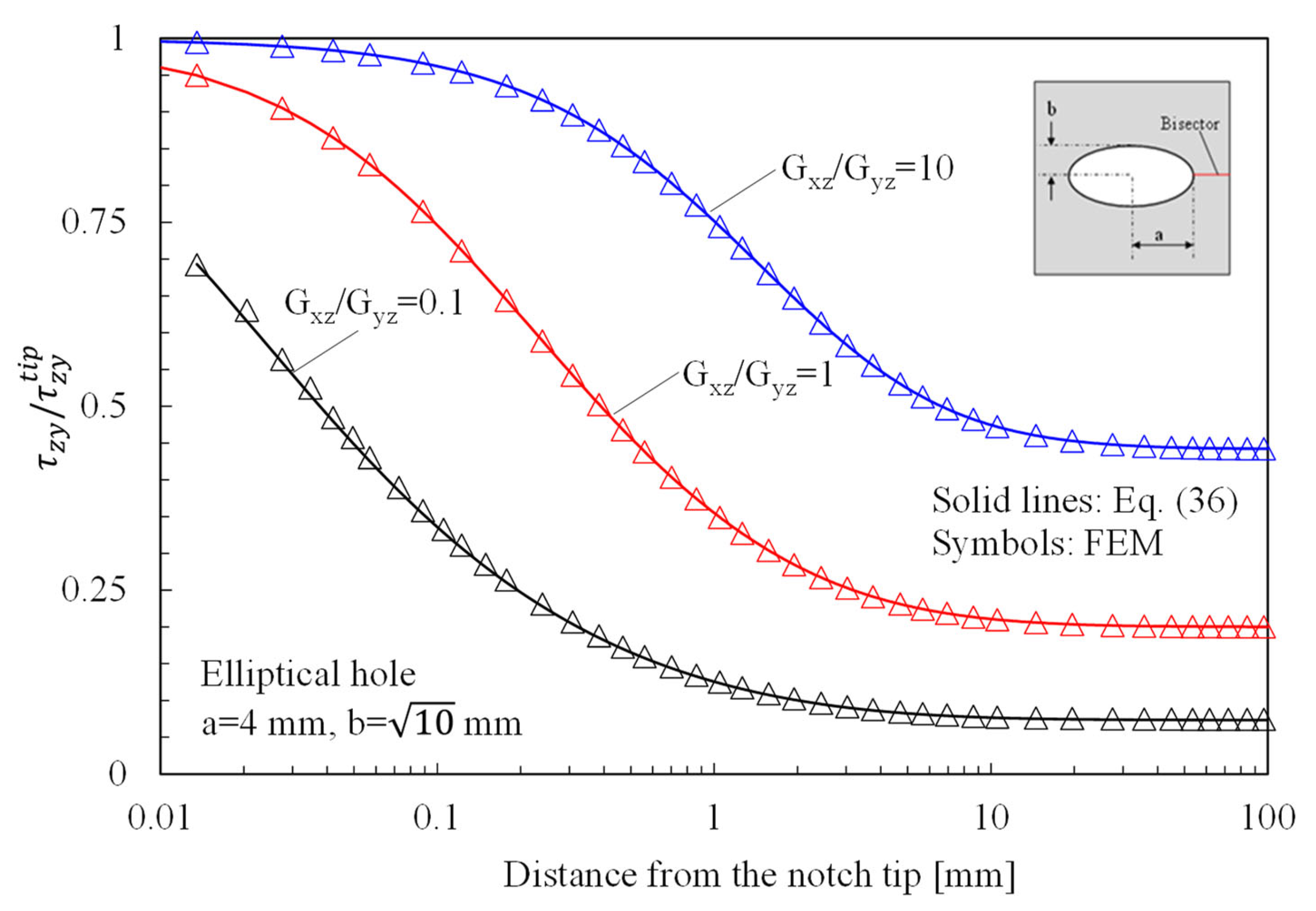
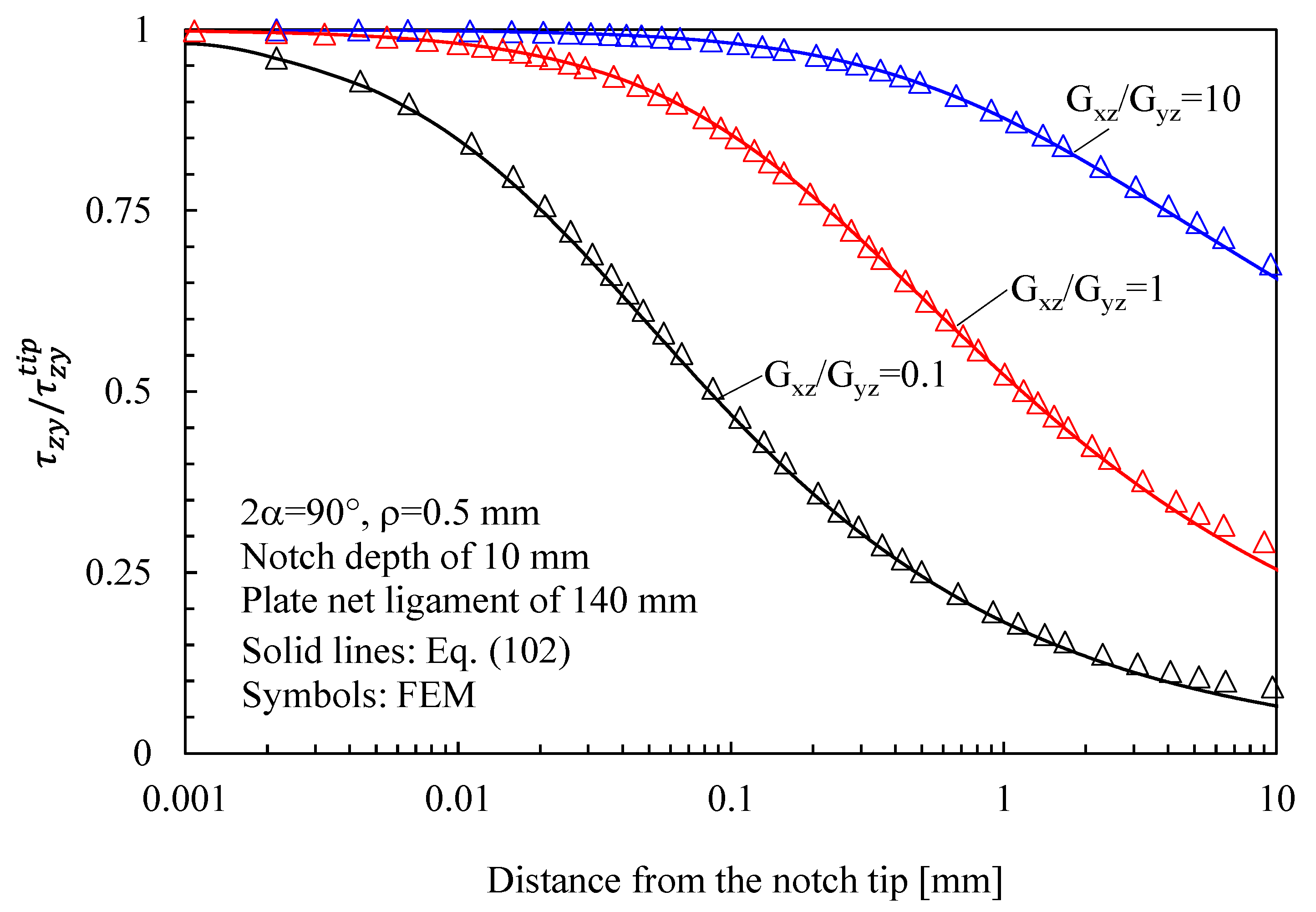
- Eventually, with reference to Mode 3 loadings, from Figure 7, Figure 10, Figure 13 and Figure 16, it is evident that when Giz is much larger than Gjz, where j is the direction of the notch bisector line, the stress gradient is high, and the distribution of the maximum antiplane shear stress along the notch bisector line is very steep, independent of the considered notched geometry. Vice versa, when Giz is smaller than Gjz, the stress gradient is mild.
8. Conclusions and Final Remarks
- With regards to Mode 1 loadings, when the material is very stiff along the traction direction, the stress gradient is high, and the distribution of the maximum principal stress along the notch bisector line (i.e., the normal stress orthogonal to the notch bisector line) is very steep. Conversely, in the case of a material very stiff along the notch bisector line, the stress gradient is much lower, and the distribution of the maximum principal stress along the notch bisector line is mild.
- With regards to Mode 2 loadings, when the material is very stiff along the direction normal to the bisector line, the stress gradient is high, and the point, along the notch bisector line, exhibiting the maximum shear stress is very close to the notch tip.
- With reference to Mode 3 loadings, when Giz is much larger than Gjz, where j is the direction of the notch bisector line, the stress gradient is high, and the distribution of the maximum antiplane shear stress along the notch bisector line is very steep. Vice versa, when Giz is smaller than Gjz, the stress gradient is mild.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kirsch, E.G. Die Theorie Der Elastizität Und Die Bedürfnisse Der Festigkeitslehre. Z. Des. Ver. Dtsch. Ing. 1898, 42, 10020157230. [Google Scholar]
- Filon, L.N.G. On the Resistance to Torsion of Certain Forms of Shafting, with Special Reference to the Effect of Keyways. Philos. Trans. R. Soc. Lond. 1900, 193, 309–352. [Google Scholar] [CrossRef]
- Wieghardt, K. Über Das Spalten Und Zerreißen Elastischer Körper. Z. Math. Phys. 1907, 55, 60–103. [Google Scholar]
- Inglis, C.E. Stresses in a Plate Due to the Presence of Cracks and Sharp Corners. Trans. Inst. Nav. Arch. 1913, 55, 219–241. [Google Scholar]
- Williams, M.L. Stress Singularities Resulting From Various Boundary Conditions in Angular Corners of Plates in Extension. J. Appl. Mech. 1952, 19, 526–528. [Google Scholar] [CrossRef]
- Irwin, B.R. Analysis of Stresses and Strains Near the End of a Crack Traversing a Plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Creager, M.; Paris, P.C. Elastic Field Equations for Blunt Cracks with Reference to Stress Corrosion Cracking. Int. J. Fract. Mech. 1967, 3, 247–252. [Google Scholar] [CrossRef]
- Neuber, H. Kerbspannungslehre; Springer: Berlin/Heidelberg, Germany, 1958. [Google Scholar]
- Lazzarin, P.; Tovo, R. A Unified Approach to the Evaluation of Linear Elastic Stress Fields in the Neighborhood of Cracks and Notches. Int. J. Fract. 1996, 78, 3–19. [Google Scholar] [CrossRef]
- Filippi, S.; Lazzarin, P.; Tovo, R. Developments of Some Explicit Formulas Useful to Describe Elastic Stress Fields Ahead of Notches in Plates. Int. J. Solids Struct. 2002, 39, 4543–4565. [Google Scholar] [CrossRef]
- Filippi, S.; Lazzarin, P. Distributions of the Elastic Principal Stress Due to Notches in Finite Size Plates and Rounded Bars Uniaxially Loaded. Int. J. Fatigue 2004, 26, 377–391. [Google Scholar] [CrossRef]
- Zappalorto, M.; Lazzarin, P. In-Plane and out-of-Plane Stress Field Solutions for V-Notches with End Holes. Int. J. Fract. 2011, 168, 167–180. [Google Scholar] [CrossRef]
- Zappalorto, M.; Lazzarin, P. Stress Fields Due to Inclined Notches and Shoulder Fillets in Shafts under Torsion. J. Strain Anal. Eng. Des. 2011, 46, 187–199. [Google Scholar] [CrossRef]
- Salviato, M.; Zappalorto, M. A Unified Solution Approach for a Large Variety of Antiplane Shear and Torsion Notch Problems: Theory and Examples. Int. J. Solids Struct. 2016, 102–103, 10–20. [Google Scholar] [CrossRef]
- Savin, G. Stress Concentration around Holes; Pergamon Press: Oxford, UK, 1961. [Google Scholar]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotropic Elastic Body; AIP Publishing: Melville, NY, USA, 1964. [Google Scholar]
- Sih, G.C.; Paris, P.C.; Irwin, G.R. On Cracks in Rectilinearly Anisotropic Bodies. Int. J. Fract. Mech. 1965, 1, 189–203. [Google Scholar] [CrossRef]
- Bogy, D.B. The Plane Solution for Anisotropic Elastic Wedges Under Normal and Shear Loading. J. Appl. Mech. 1972, 39, 1103–1109. [Google Scholar] [CrossRef]
- Kuo, M.C.; Bogy, D.B. Plane Solutions for Traction Problems on Orthotropic Unsymmetrical Wedges and Symmetrically Twinned Wedges. J. Appl. Mech. 1974, 41, 203–208. [Google Scholar] [CrossRef]
- Ting, T.C.T.; Chou, S.C. Edge Singularities in Anisotropic Composites. Int. J. Solids Struct. 1981, 17, 1057–1068. [Google Scholar] [CrossRef]
- Chien-Ching, M.; Bao-Luh, H. Analysis of Dissimilar Anisotropic Wedges Subjected to Antiplane Shear Deformation. Int. J. Solids Struct. 1989, 25, 1295–1309. [Google Scholar] [CrossRef]
- Wu, K.C.; Chen, C.T. Stress Analysis of Anisotropic Elastic V-Notched Bodies. Int. J. Solids Struct. 1996, 33, 2403–2416. [Google Scholar] [CrossRef]
- Chue, C.H.; Liu, C. Stress Singularities in a Bimaterial Anisotropic Wedge with Arbitrary Fiber Orientation. Compos. Struct. 2002, 58, 49–56. [Google Scholar] [CrossRef]
- Chue, C.H.; Liu, C.I. A General Solution on Stress Singularities in an Anisotropic Wedge. Int. J. Solids Struct. 2001, 38, 6889–6906. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G.; Rao, D.K.N. Stress Distribution around Triangular Holes in Anisotropic Plates. Compos. Struct. 1999, 45, 171–183. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G.; Rao, D.K.N. A General Solution for Stresses around Holes in Symmetric Laminates under Inplane Loading. Compos. Struct. 2000, 49, 339–354. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G.; Kakhandki, V. Stress Analysis for an Orthotropic Plate with an Irregular Shaped Hole for Different In-Plane Loading Conditions—Part 1. Compos. Struct. 2005, 70, 255–274. [Google Scholar] [CrossRef]
- Zappalorto, M.; Carraro, P.A. Stress Fields at Sharp Angular Corners in Thick Anisotropic Composite Plates. Compos. Struct. 2014, 117, 346–353. [Google Scholar] [CrossRef]
- Hasebe, N. Stress Analysis for an Orthotropic Elastic Half Plane with an Oblique Edge Crack and Stress Intensity Factors. Acta Mech. 2021, 232, 967–982. [Google Scholar] [CrossRef]
- Hasebe, N. Stress Analysis of an Orthotropic Elastic Infinite Plane with a Hole. ZAMM J. Appl. Math. Mech. Z. Für Angew. Math. Und Mech. 2021, 101, e202000184. [Google Scholar] [CrossRef]
- Fil’shtyns’kyi, L.A.; Nosov, D.M.; Eremenko, H.A. Plane Problem of Magnetoelasticity for a Piezomagnetic Medium with Cracks. Mater. Sci. 2015, 51, 267–275. [Google Scholar] [CrossRef]
- Bonora, N.; Costanzi, M.; Marchetti, M. On Closed Form Solution for the Elastic Stress Field around Holes in Orthotropic Composite Plates under In-Plane Stress Conditions. Compos. Struct. 1993, 25, 139–156. [Google Scholar] [CrossRef]
- Bonora, N.; Costanzi, M.; Marchetti, M. A Computational Procedure to Calculate Stress-Strain Field around Simple Shape Holes in Composite Laminates. Comput. Struct. 1994, 53, 1167–1179. [Google Scholar] [CrossRef]
- Chiang, C.R. The Stress Field for a Blunt Crack in an Anisotropic Material. Int. J. Fract. 1993, 68, R41–R46. [Google Scholar] [CrossRef]
- Wang, H. An Analytical Solution for the Stress Distribution around the Cased Borehole in the Orthotropic Formation. Int. J. Rock. Mech. Min. Sci. 2021, 142, 104770. [Google Scholar] [CrossRef]
- Hsieh, M.L.; Hwu, C. A Full Field Solution for an Anisotropic Elastic Plate with a Hole Perturbed from an Ellipse. Eur. J. Mech. A Solids 2023, 97, 104823. [Google Scholar] [CrossRef]
- Nguyen-Hoang, M.; Becker, W. Open Holes in Composite Laminates with Finite Dimensions: Structural Assessment by Analytical Methods. Arch. Appl. Mech. 2022, 92, 1101–1125. [Google Scholar] [CrossRef]
- Khechai, A.; Tati, A.; Guettala, A.; Mohite, P.M. A General Solution for Stress Resultants around a Circular Cutout in Laminate Plates under Different In-Plane Loadings: Analytical and Experimental Investigations. Arch. Appl. Mech. 2018, 88, 1187–1208. [Google Scholar] [CrossRef]
- Huang, Z.Q.; He, X.Q.; Liew, K.M. A Sensitive Interval of Imperfect Interface Parameters Based on the Analysis of General Solution for Anisotropic Matrix Containing an Elliptic Inhomogeneity. Int. J. Solids Struct. 2015, 73–74, 67–77. [Google Scholar] [CrossRef]
- Kazberuk, A.; Savruk, M.P.; Chornenkyi, A.B. Stress Distribution at Sharp and Rounded V-Notches in Quasi-Orthotropic Plane. Int. J. Solids Struct. 2016, 85–86, 134–143. [Google Scholar] [CrossRef]
- Savruk, M.P.; Kazberuk, A. Stress Concentration near Sharp and Rounded V-Notches in Orthotropic and Quasi-Orthotropic Bodies. Theor. Appl. Fract. Mech. 2016, 84, 166–176. [Google Scholar] [CrossRef]
- Chen, C. De Singular Stress Analysis near Sharp Corners in Anisotropic Notched Plates Subjected to Bending Loads. Appl. Math. Model. 2018, 55, 183–204. [Google Scholar] [CrossRef]
- Savruk, M.P.; Kazberuk, A.; Onyshko, L.I. Influence of the Anisotropy of Materials on the Distribution of Stresses Near Parabolic Notches. Mater. Sci. 2016, 51, 773–784. [Google Scholar] [CrossRef]
- Zappalorto, M.; Carraro, P.A. Stress Distributions for Blunt Cracks and Radiused Slits in Anisotropic Plates under In-Plane Loadings. Int. J. Solids Struct. 2015, 56–57, 136–141. [Google Scholar] [CrossRef]
- Zappalorto, M.; Carraro, P.A. Two-Dimensional Stress Distributions in Tensioned Orthotropic Plates Weakened by Blunt V-Shaped Notches. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 804–819. [Google Scholar] [CrossRef]
- Pastrello, M.; Pontefisso, A.; Zappalorto, M. A New Explicit Solution for the Mode I Stress Fields in Notched Orthotropic Solids. Eur. J. Mech. A Solids 2023, 97, 104819. [Google Scholar] [CrossRef]
- Pastrello, M.; Salviato, M.; Zappalorto, M. Stress Distributions in Orthotropic Solids with Blunt Notches under In-Plane Shear Loadings. Eur. J. Mech. A Solids 2022, 92, 104436. [Google Scholar] [CrossRef]
- Zappalorto, M.; Salviato, M. Antiplane Shear Stresses in Orthotropic Plates with Lateral Blunt Notches. Eur. J. Mech. A Solids 2019, 77, 103815. [Google Scholar] [CrossRef]
- Stevenson, A.C. Complex Potentials in Two-Dimensional Elasticity. Proc. R. Soc. Lond. 1945, 184, 129–179. [Google Scholar] [CrossRef]
- Zappalorto, M. Mode I Generalised Stress Intensity Factors for Rounded Notches in Orthotropic Plates. Theor. Appl. Fract. Mech. 2019, 101, 356–364. [Google Scholar] [CrossRef]
- Zappalorto, M.; Lazzarin, P. A Unified Approach to the Analysis of Nonlinear Stress and Strain Fields Ahead of Mode III-Loaded Notches and Cracks. Int. J. Solids Struct. 2010, 47, 851–864. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pontefisso, A.; Pastrello, M.; Zappalorto, M. Recent Advances in the Analytical Stress Field Solutions for Radiused Notches in Orthotropic Solids. Materials 2023, 16, 3915. https://doi.org/10.3390/ma16113915
Pontefisso A, Pastrello M, Zappalorto M. Recent Advances in the Analytical Stress Field Solutions for Radiused Notches in Orthotropic Solids. Materials. 2023; 16(11):3915. https://doi.org/10.3390/ma16113915
Chicago/Turabian StylePontefisso, Alessandro, Matteo Pastrello, and Michele Zappalorto. 2023. "Recent Advances in the Analytical Stress Field Solutions for Radiused Notches in Orthotropic Solids" Materials 16, no. 11: 3915. https://doi.org/10.3390/ma16113915
APA StylePontefisso, A., Pastrello, M., & Zappalorto, M. (2023). Recent Advances in the Analytical Stress Field Solutions for Radiused Notches in Orthotropic Solids. Materials, 16(11), 3915. https://doi.org/10.3390/ma16113915






