Numerical and Experimental Investigation of Quasi-Static Crushing Behaviors of Steel Tubular Structures
Abstract
1. Introduction
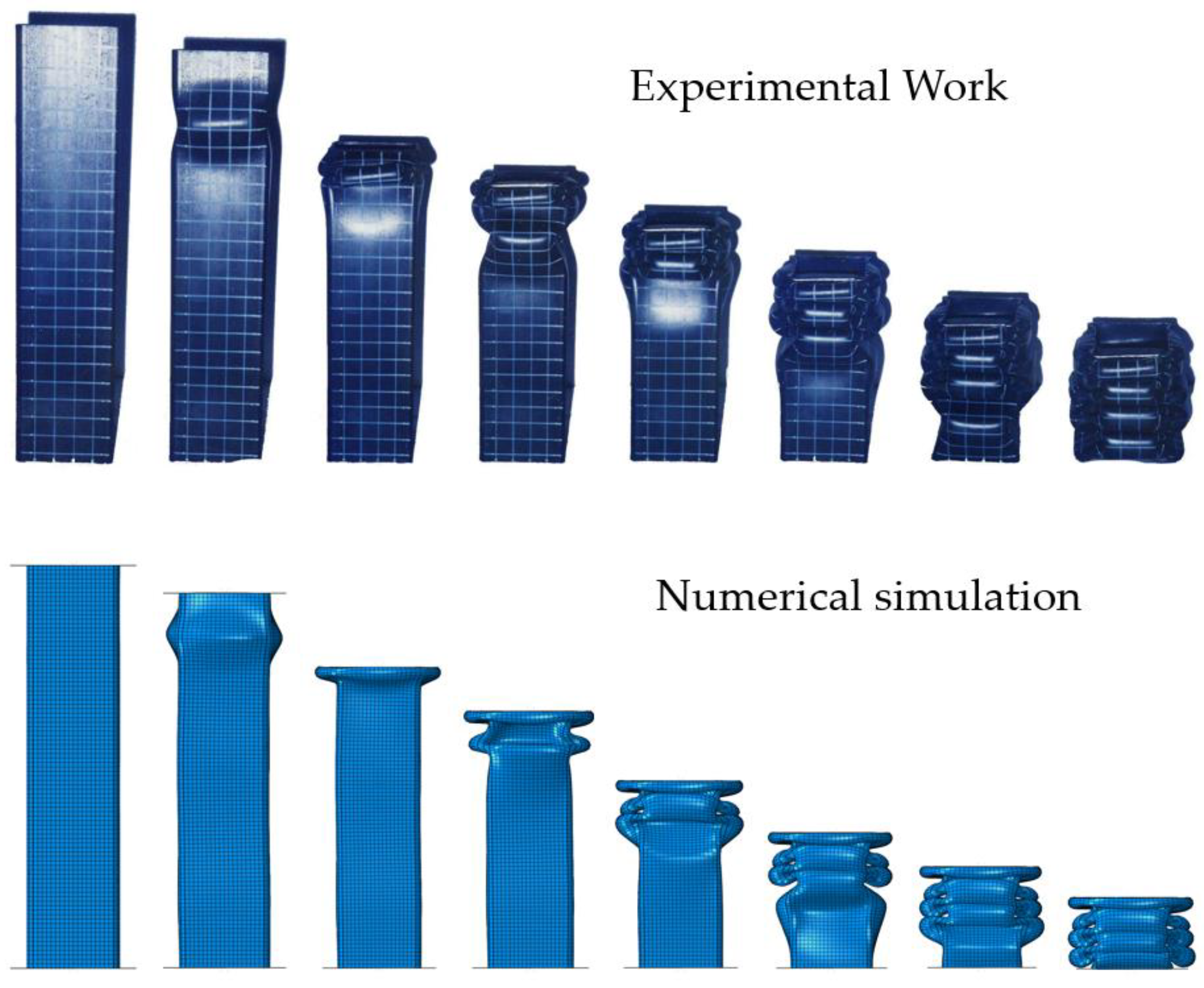
2. Experimental Works
3. Finite Element Analysis
3.1. Specifications of the Finite Element Analyses
- (1)
- Boundary condition;
- (2)
- Geometrical imperfection;
- (3)
- Friction coefficient;
- (4)
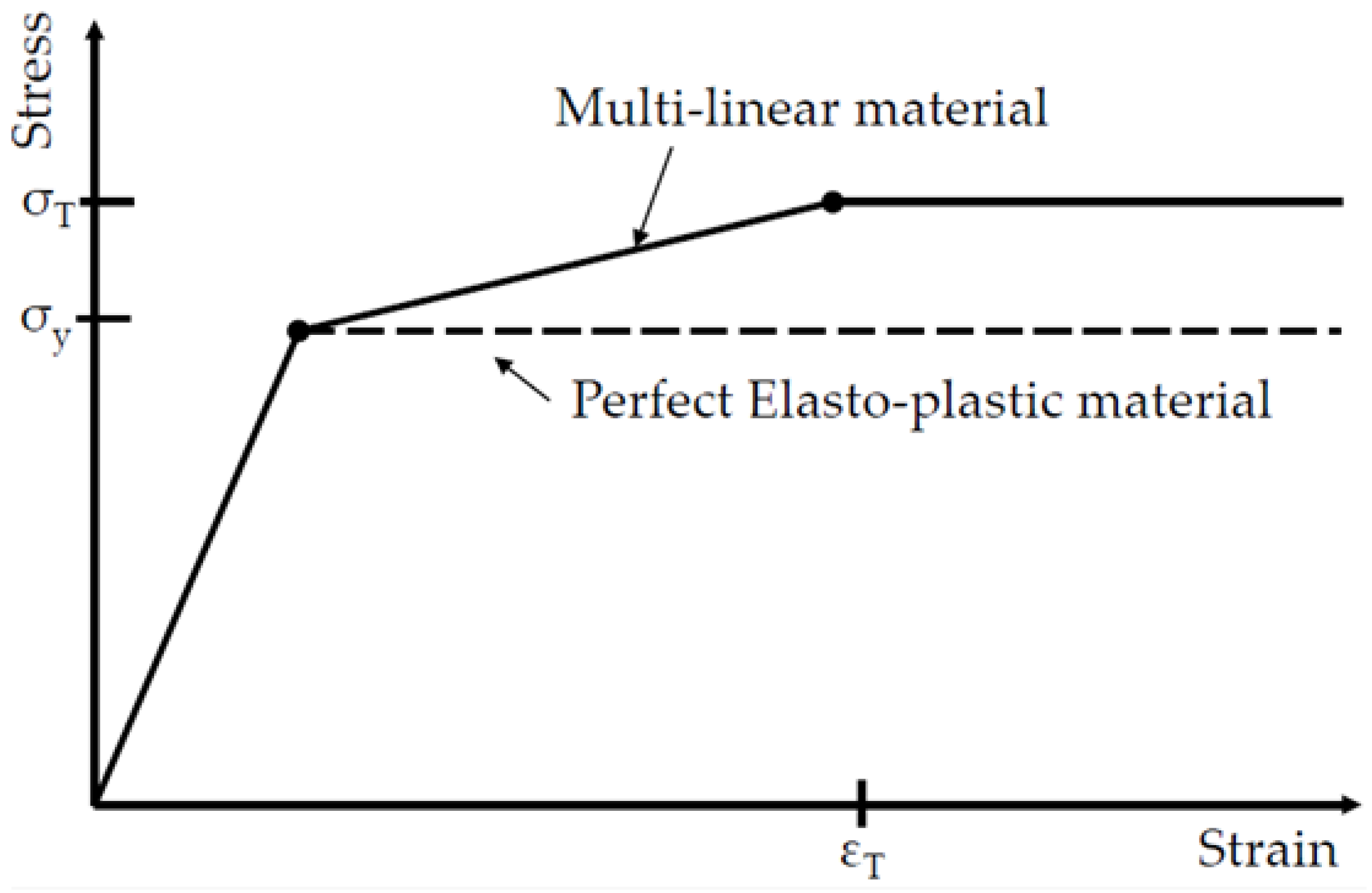
- Material nonlinearity model (perfect elasto-plastic model vs. multilinear plastic model);
- (5)
- Element size;
- (6)
- Element type (full integration vs. reduced integration shell).
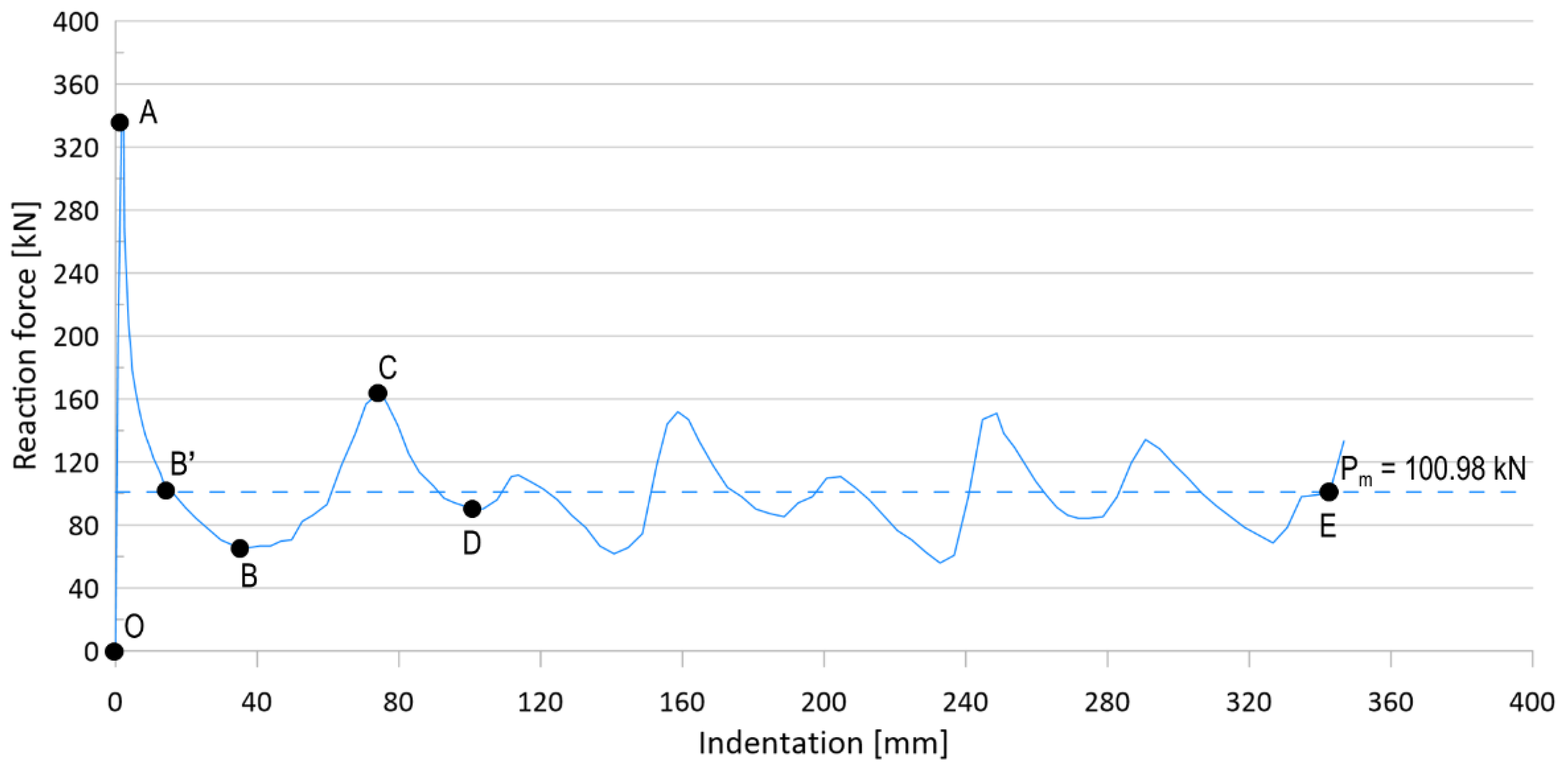
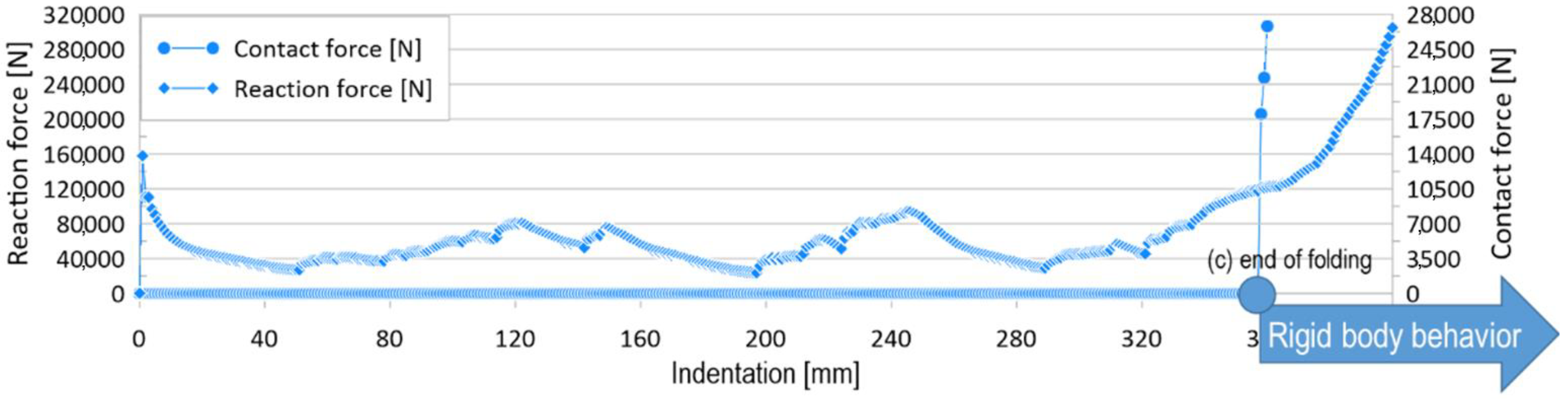
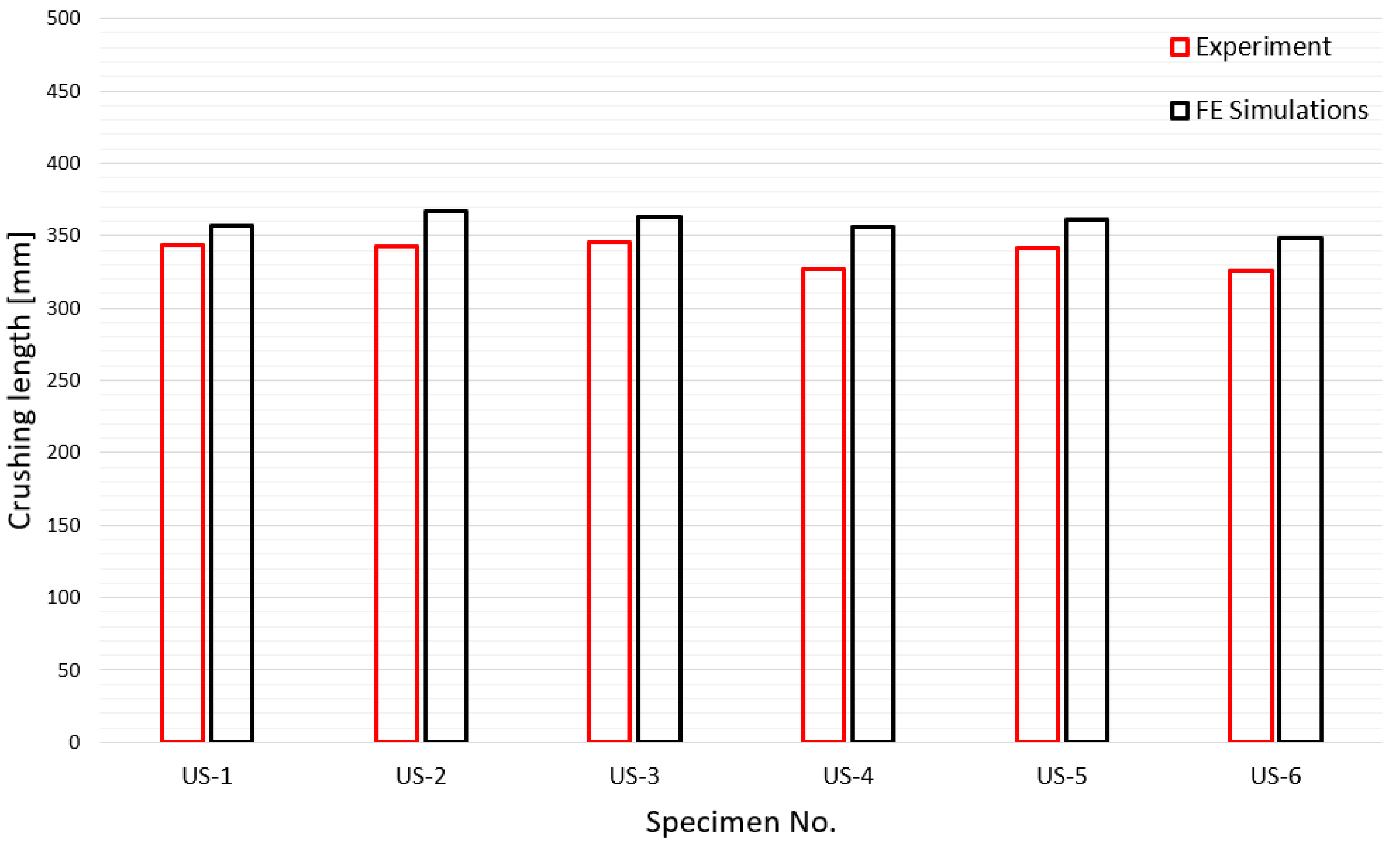
3.2. Crushing Length
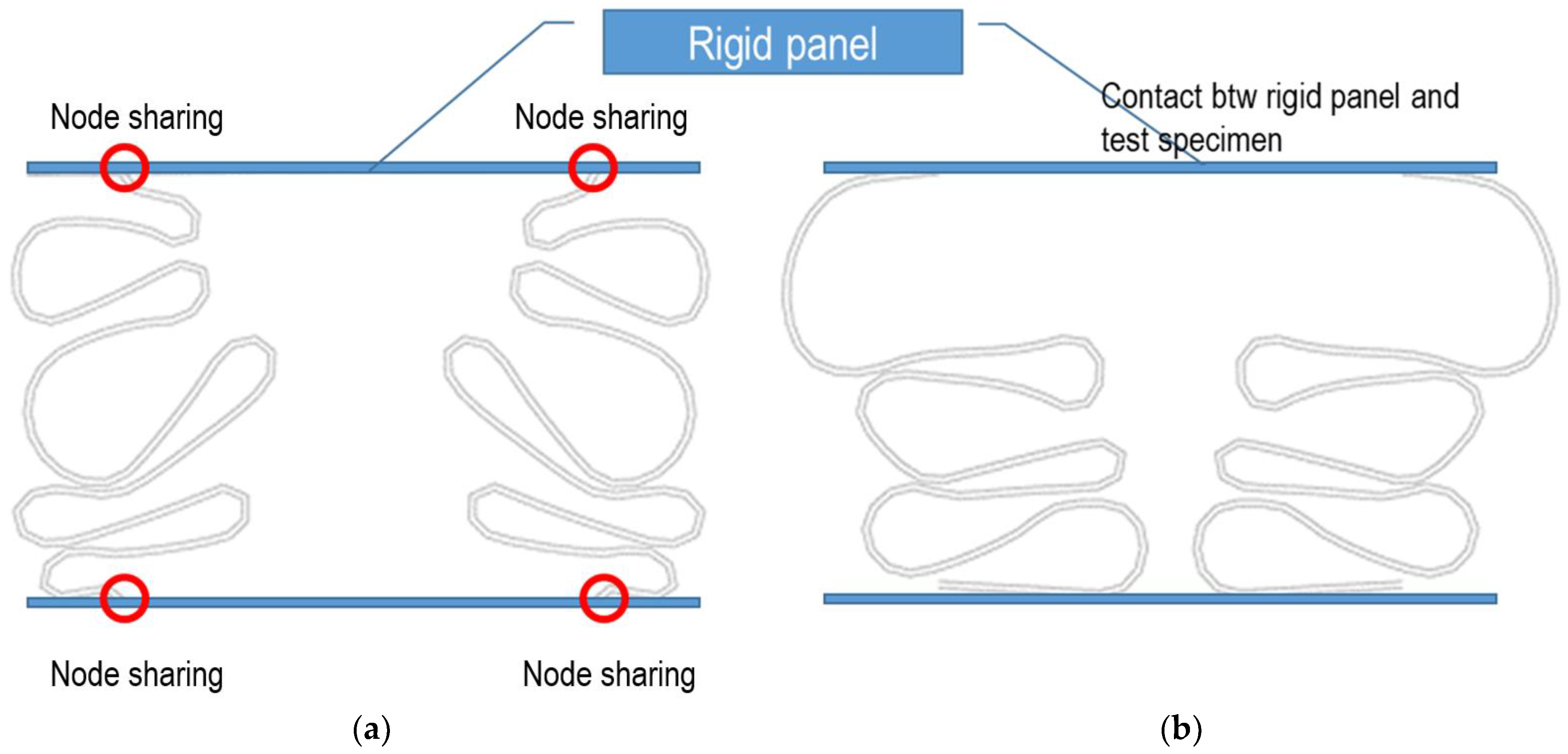
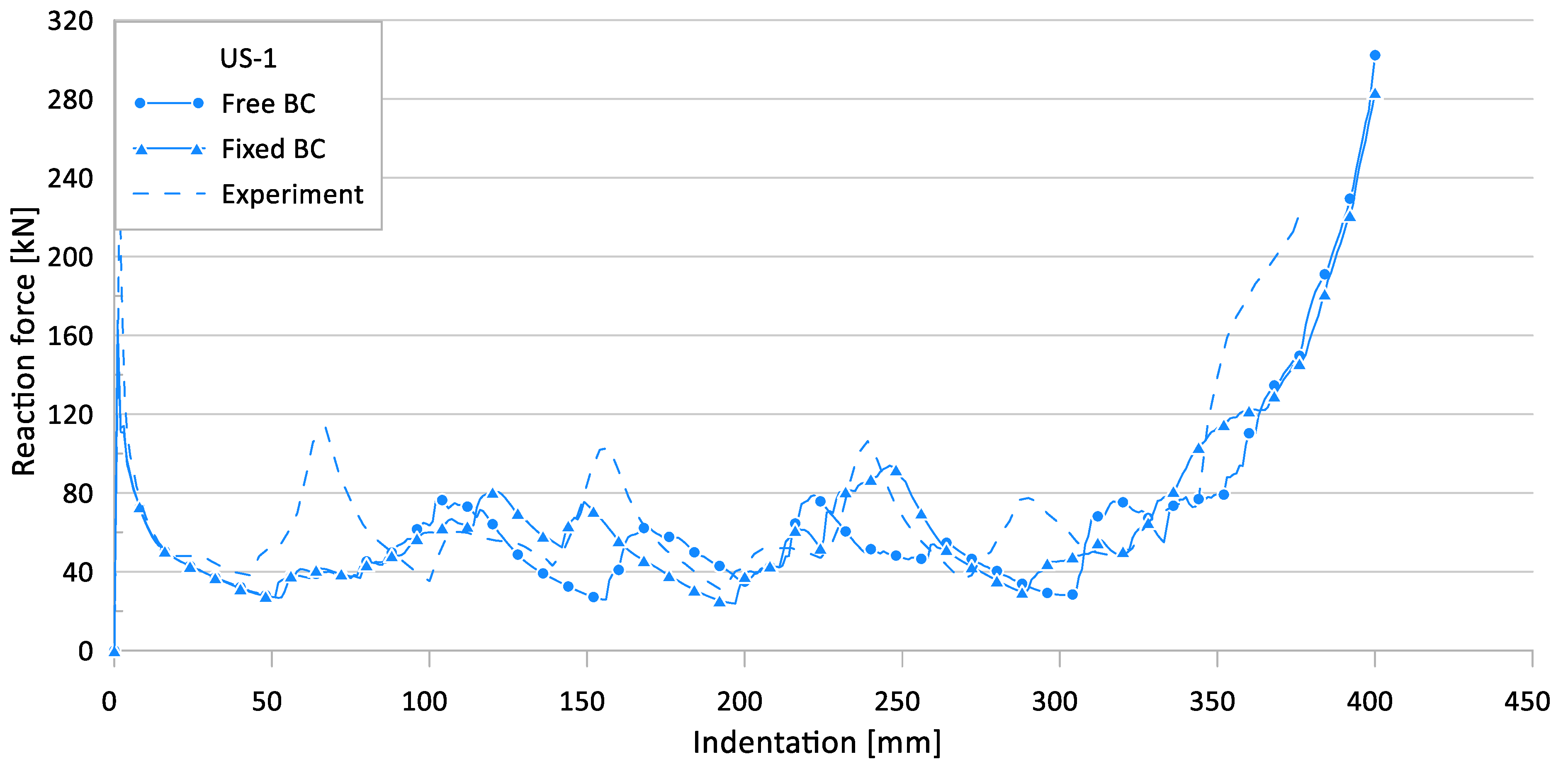
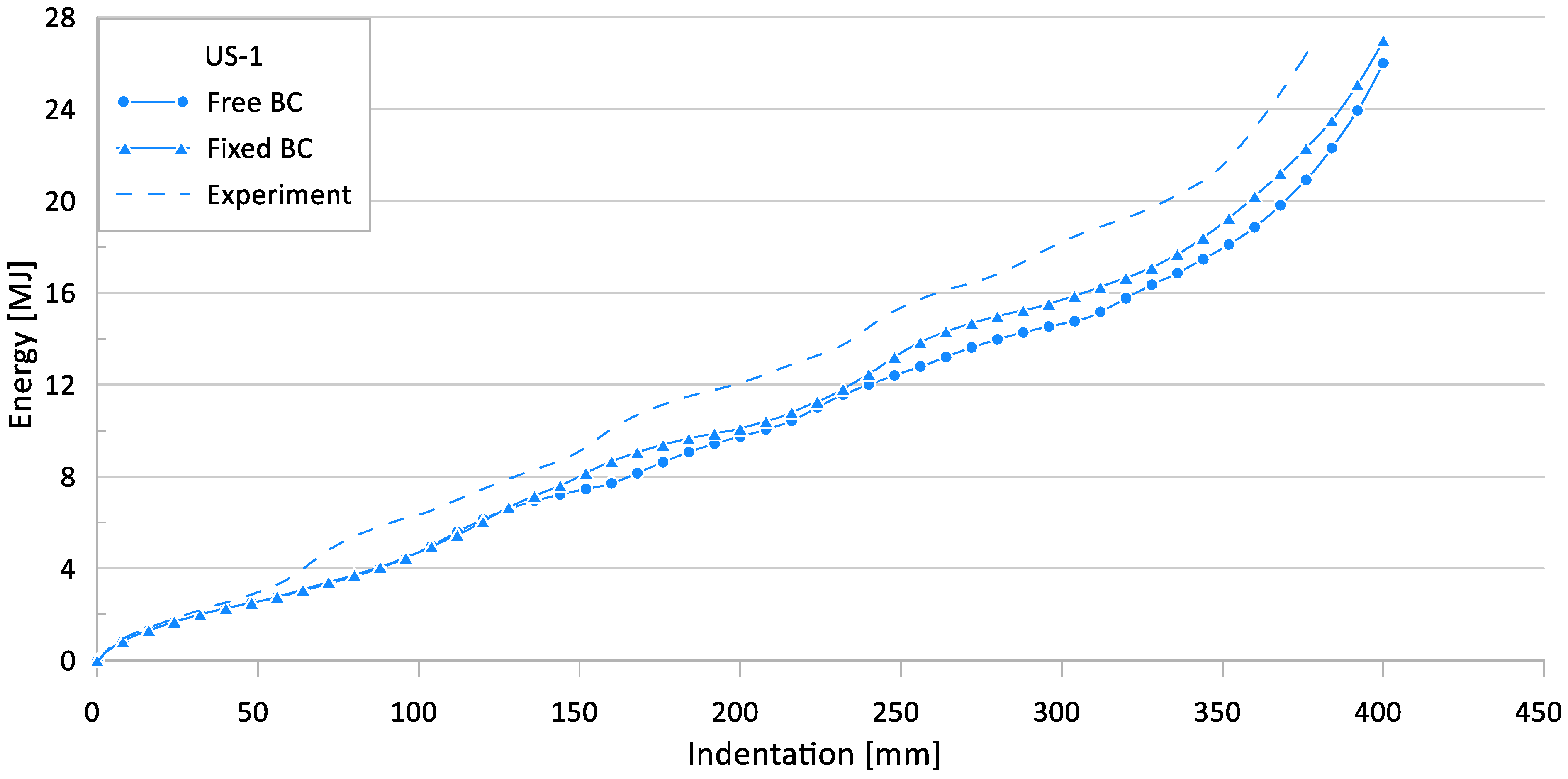
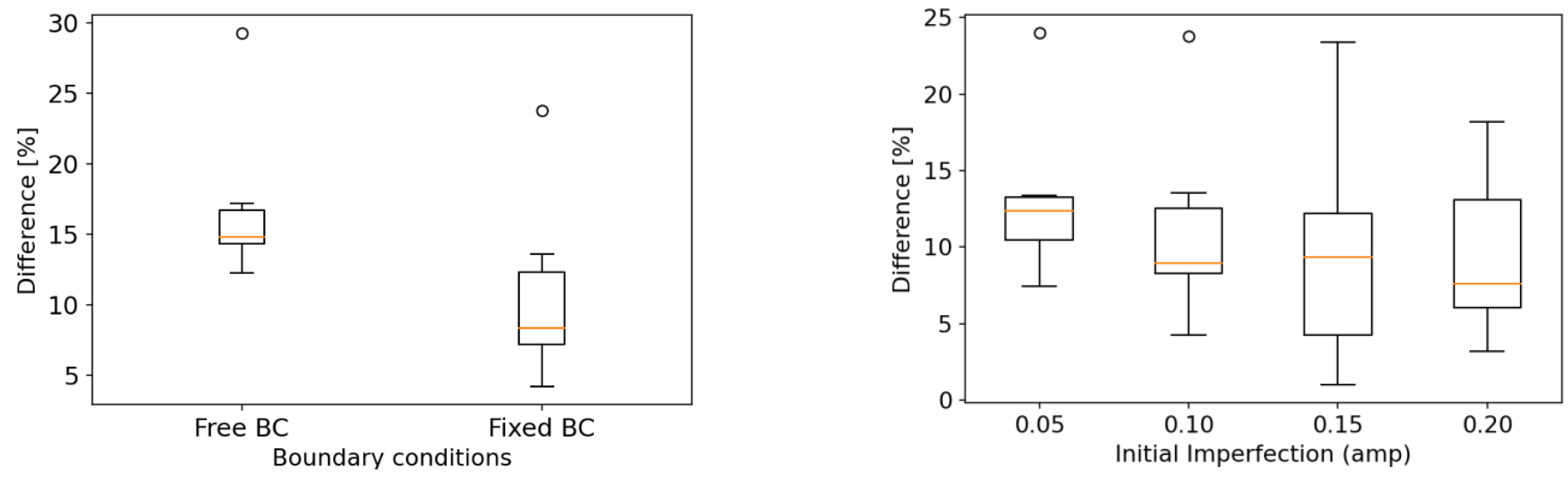
3.3. Parameter #1: Boundary Condition
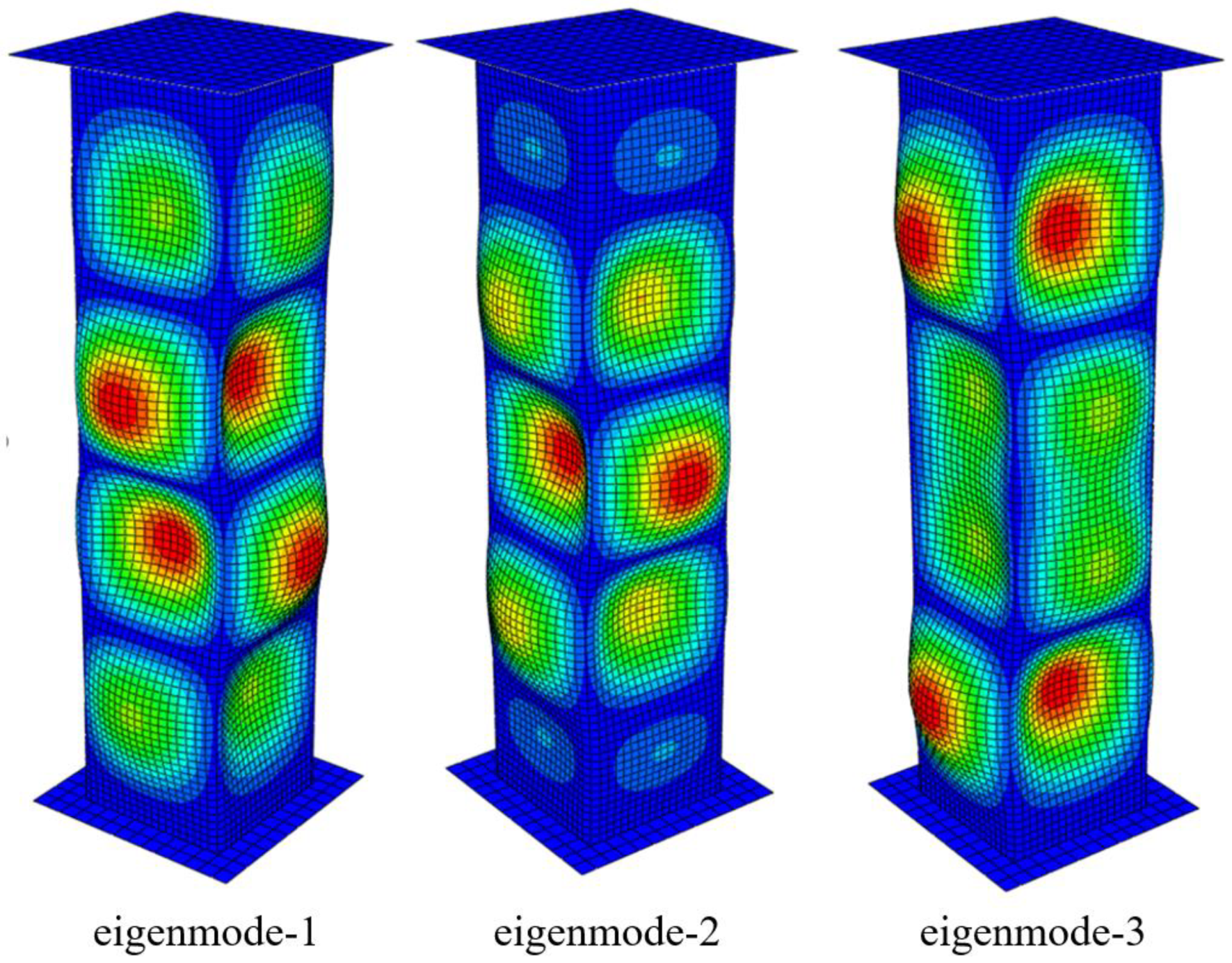
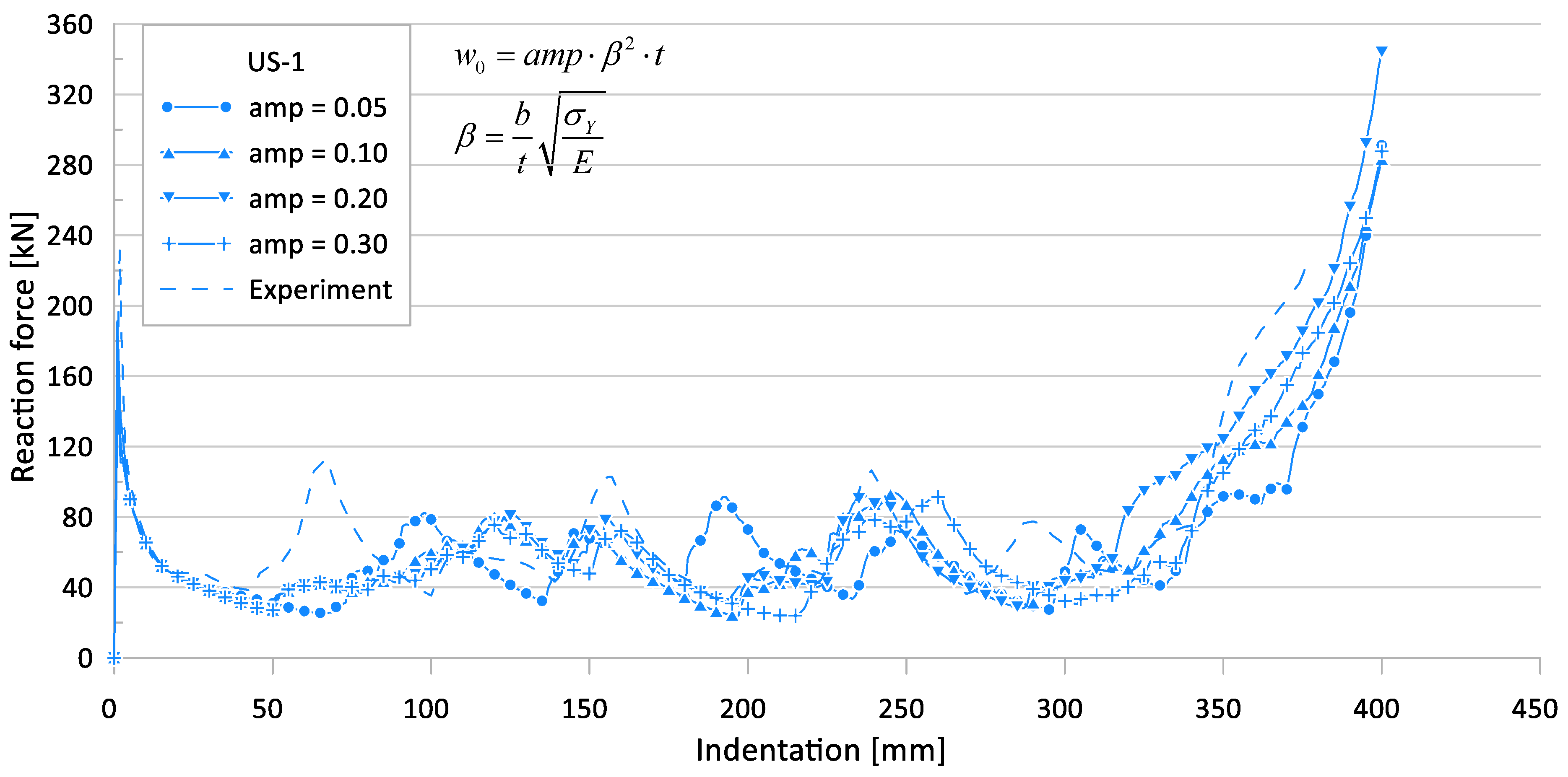
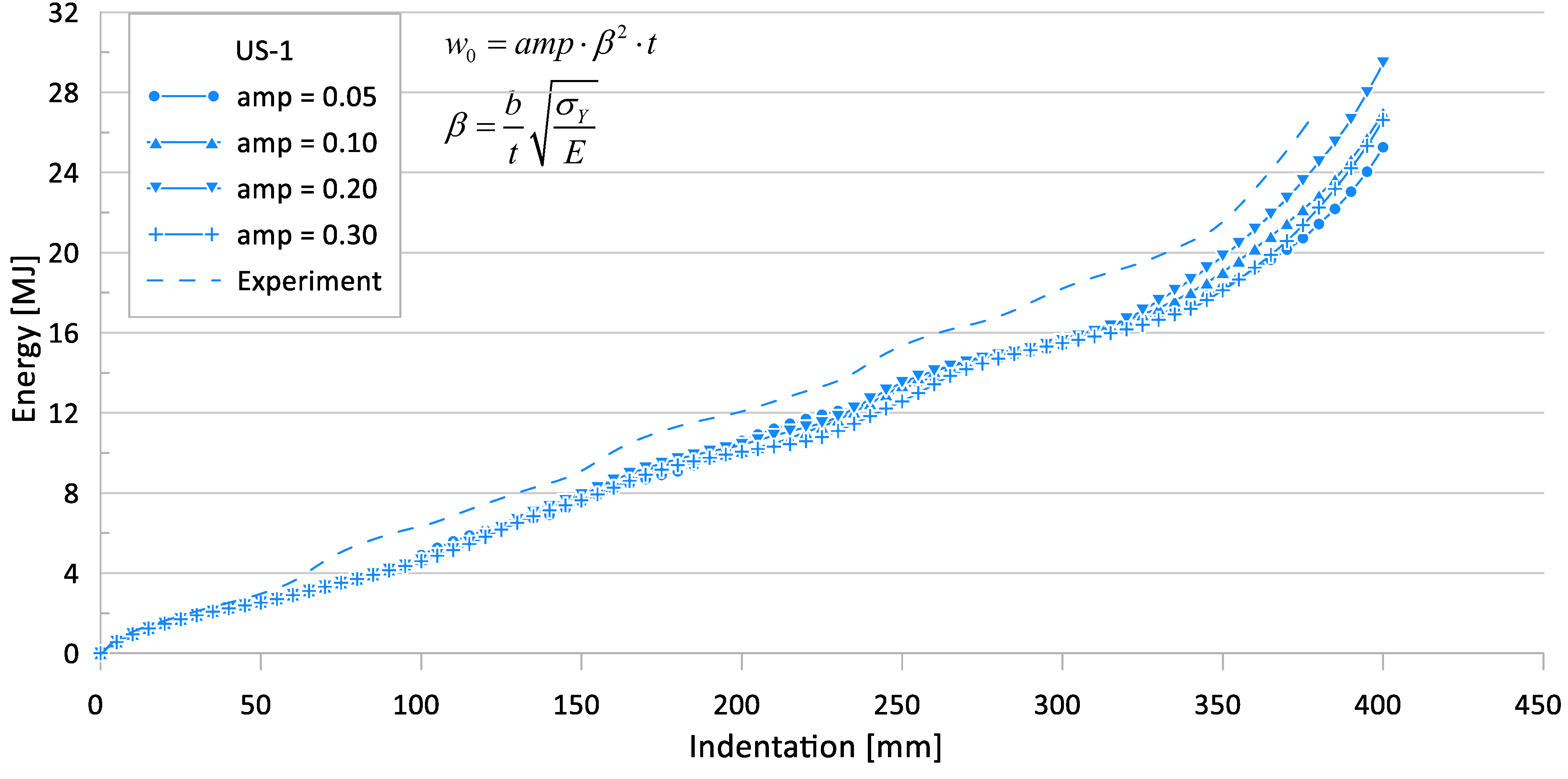
3.4. Parameter #2: Initial Imperfection
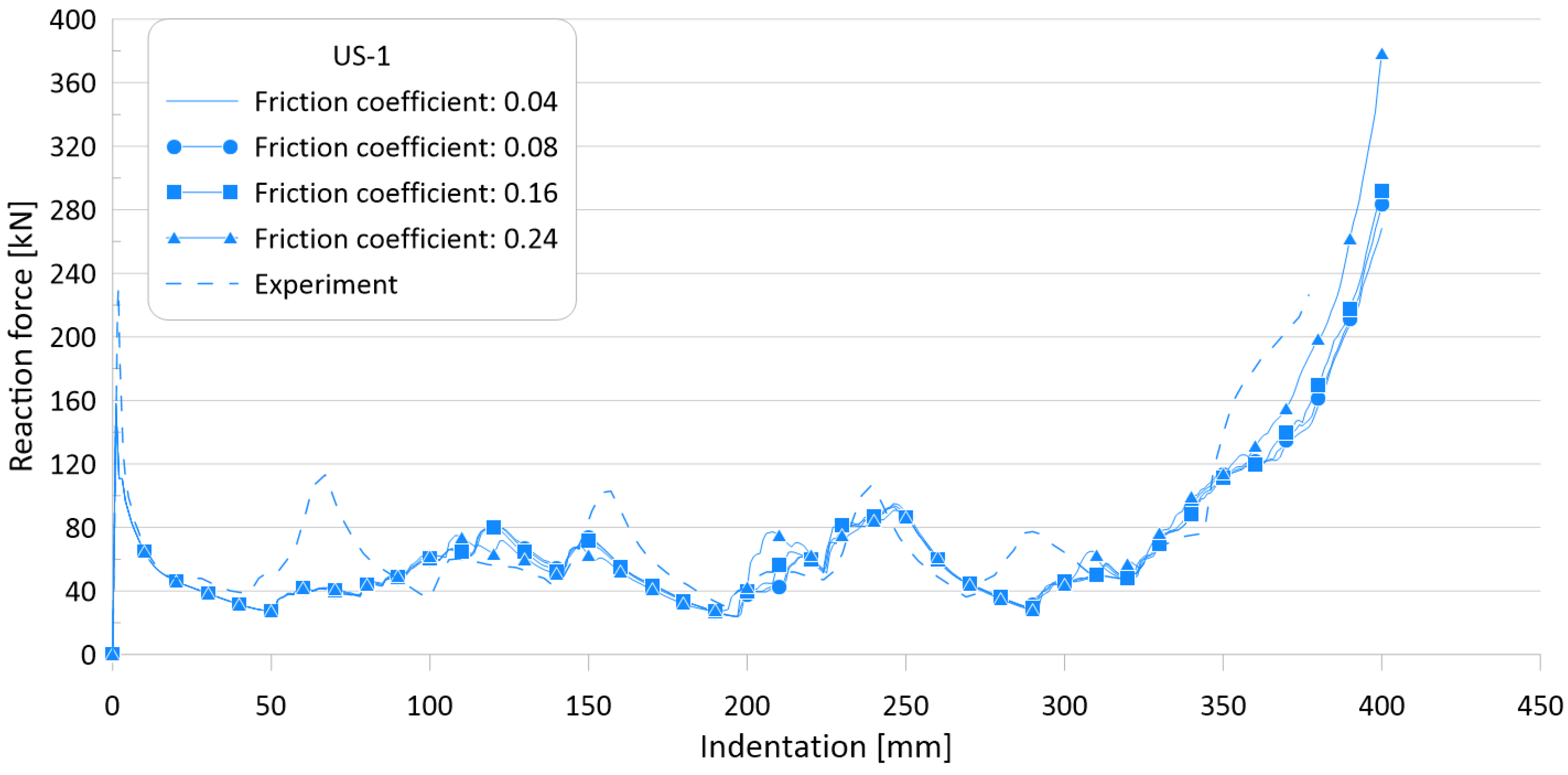
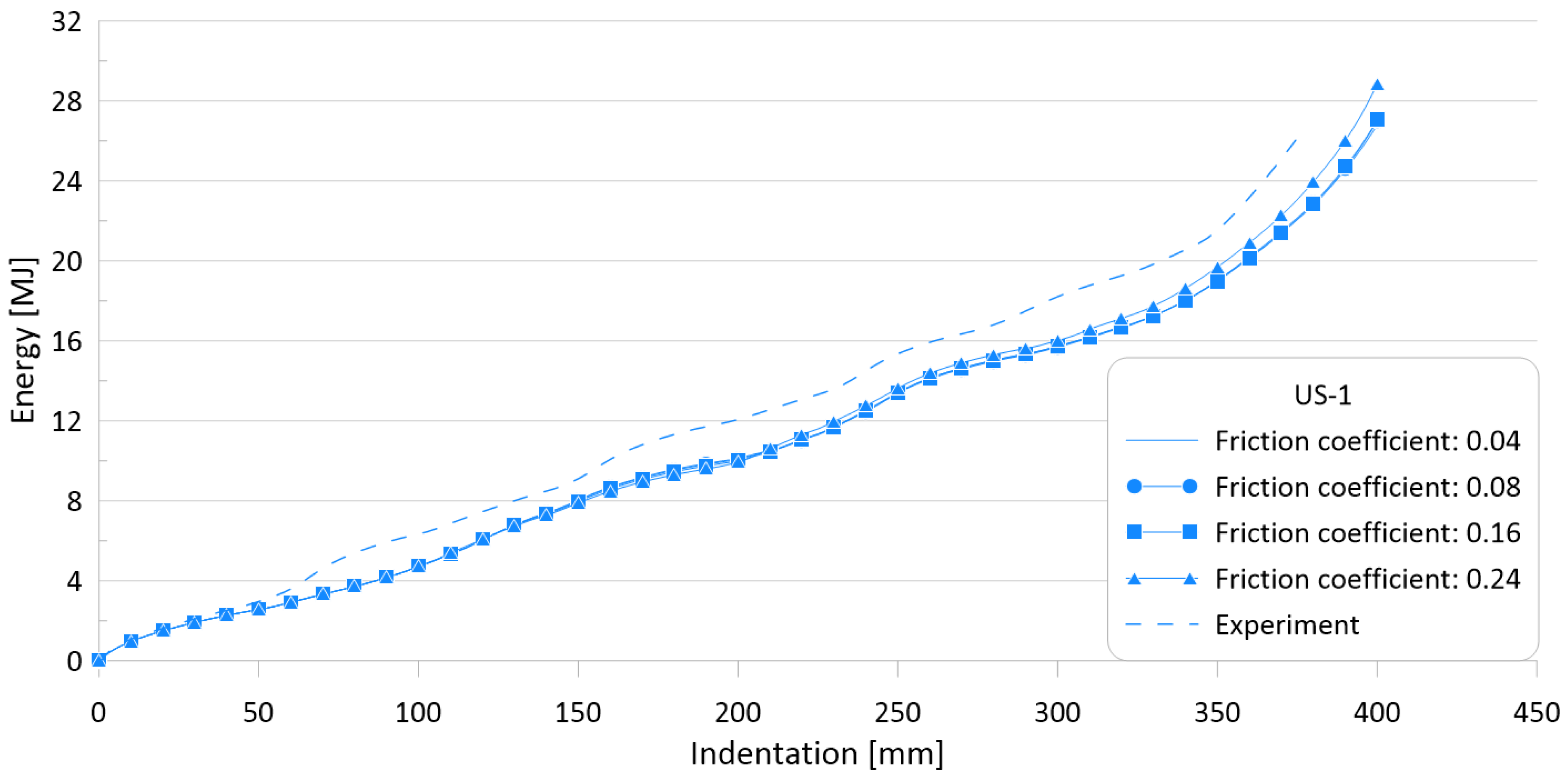
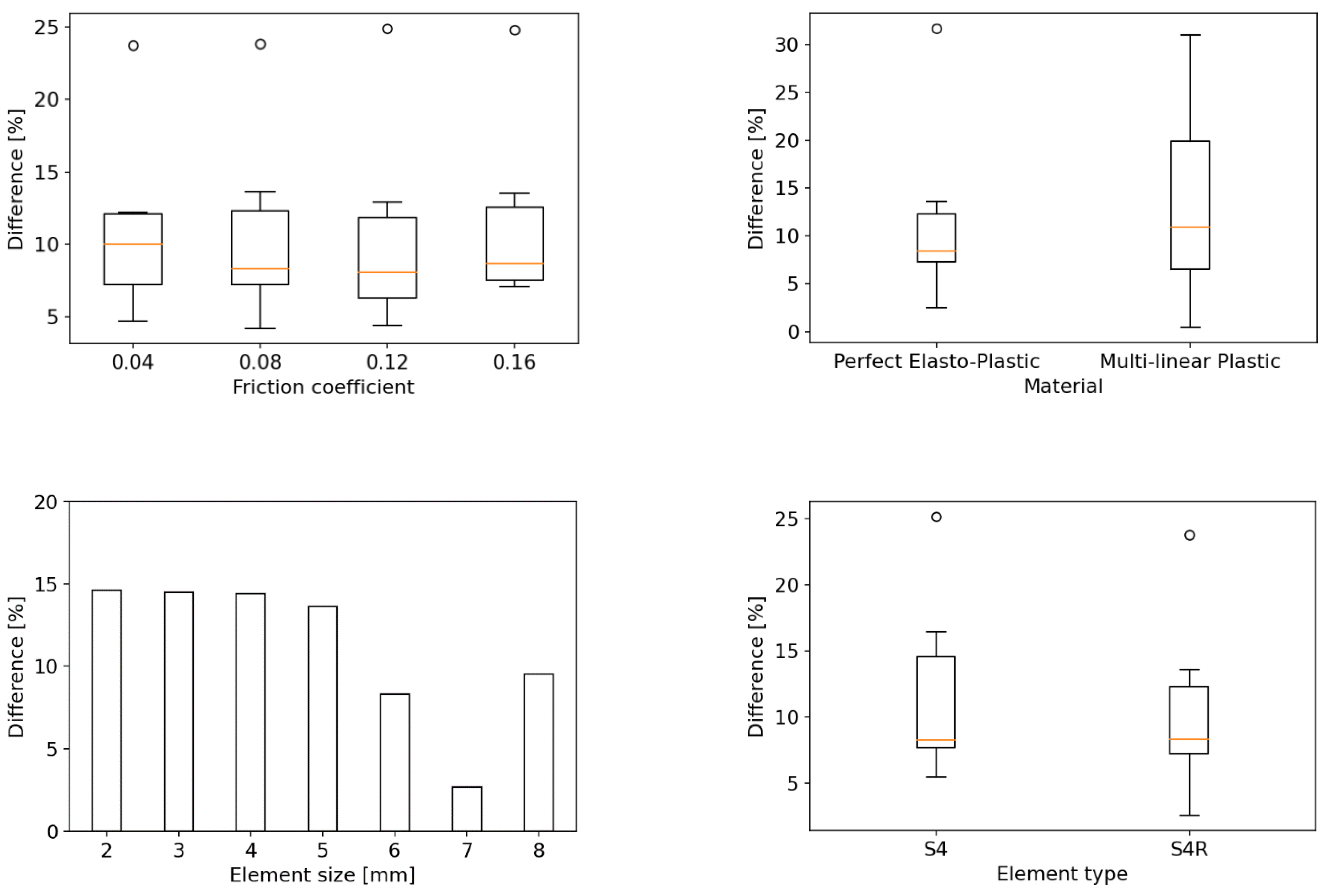
3.5. Parameter #3: Friction Coefficient
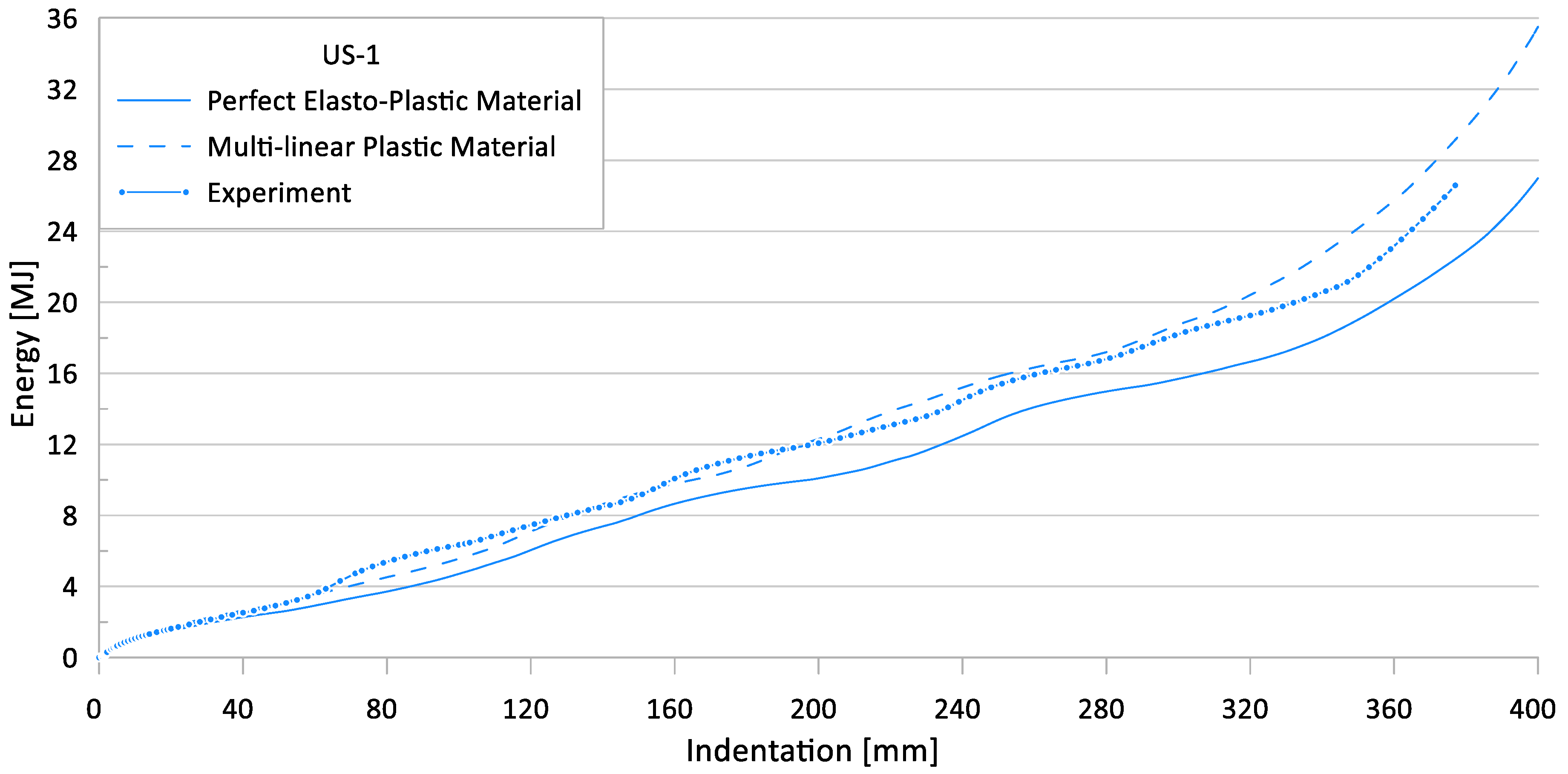
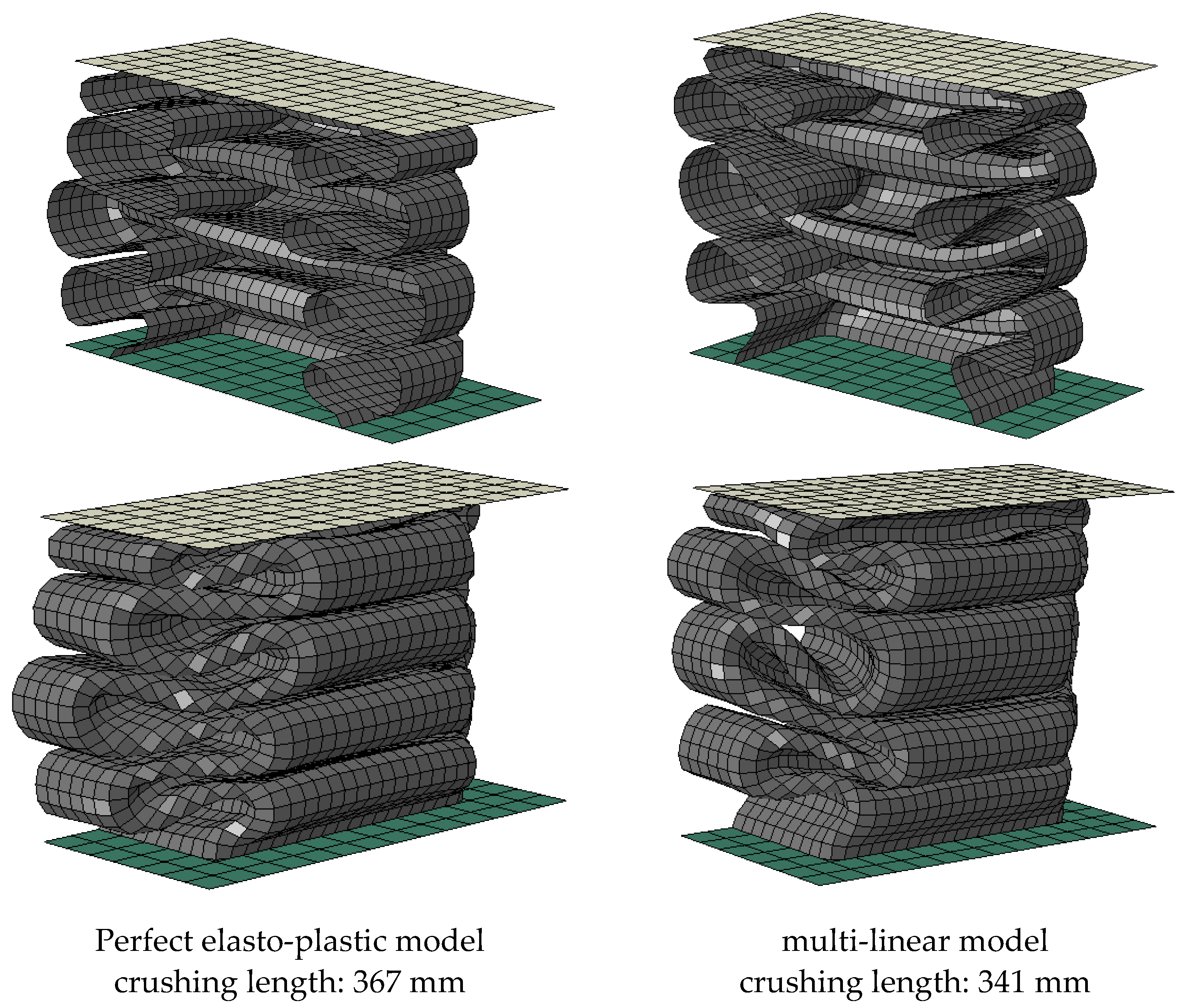
3.6. Parameter #4: Material Property Model
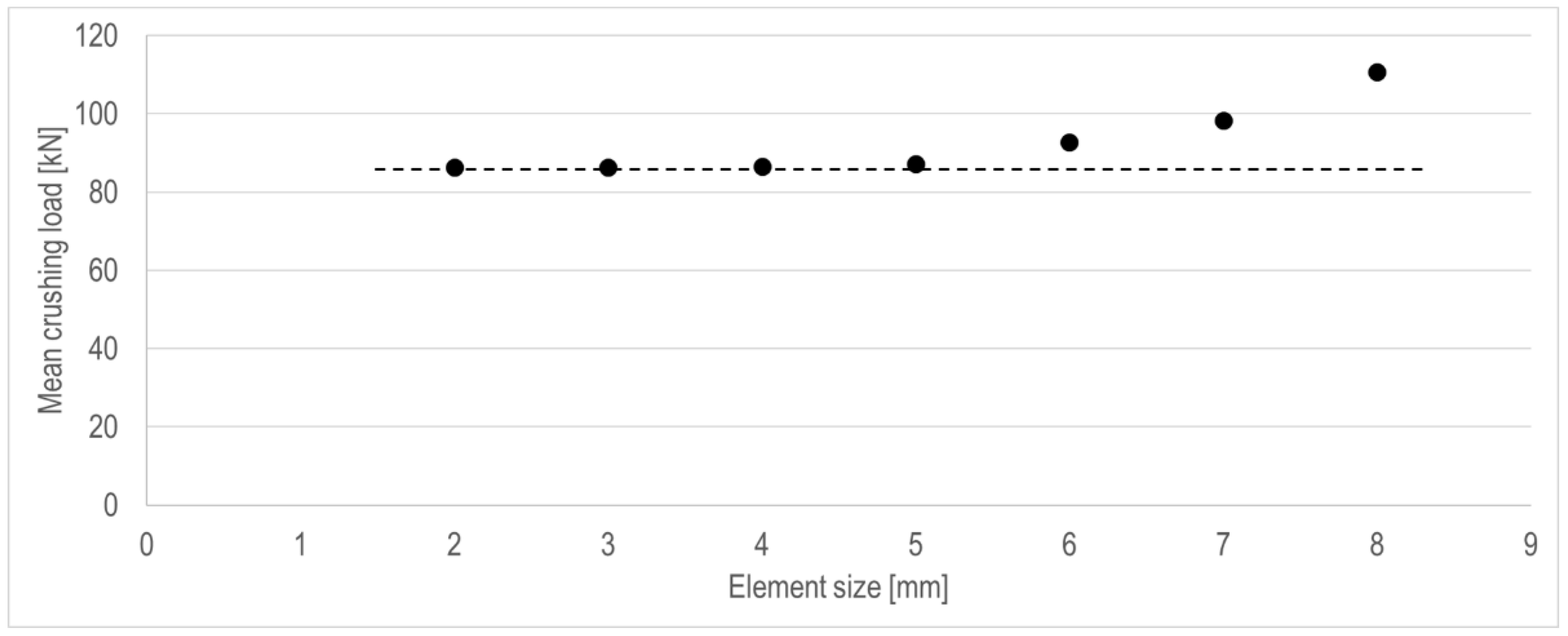
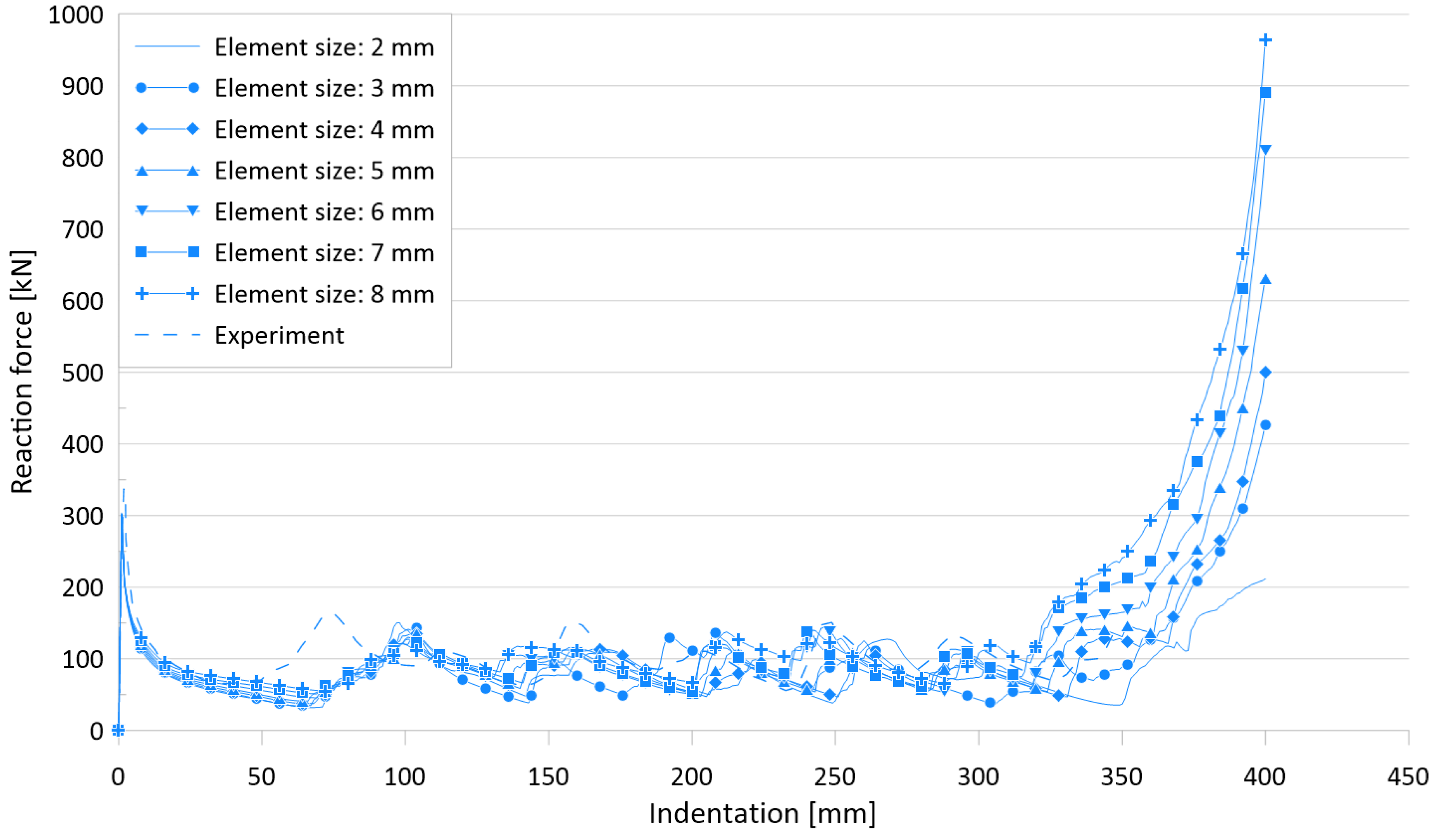
3.7. Parameter #5: Finite Element Mesh Size
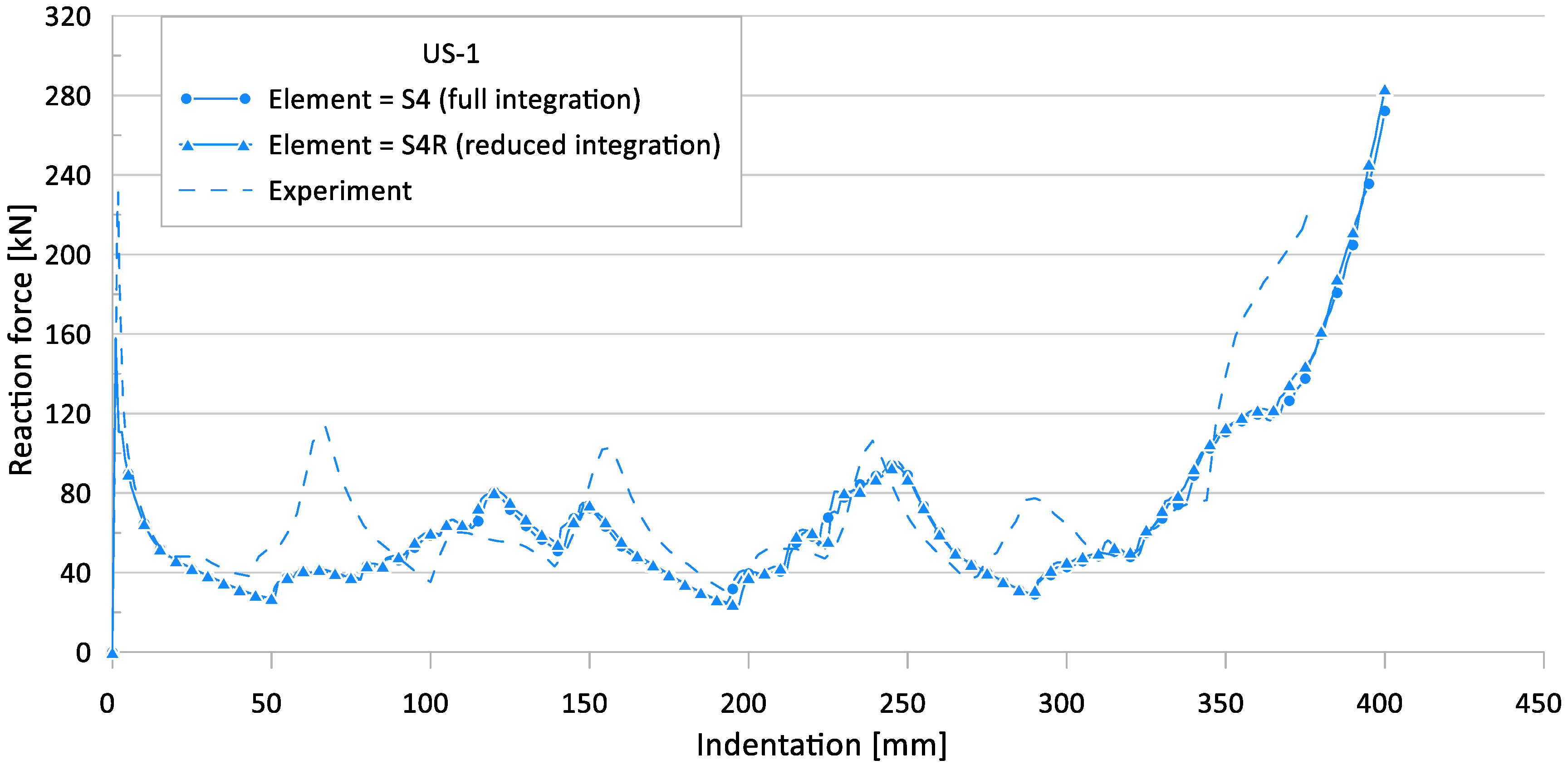
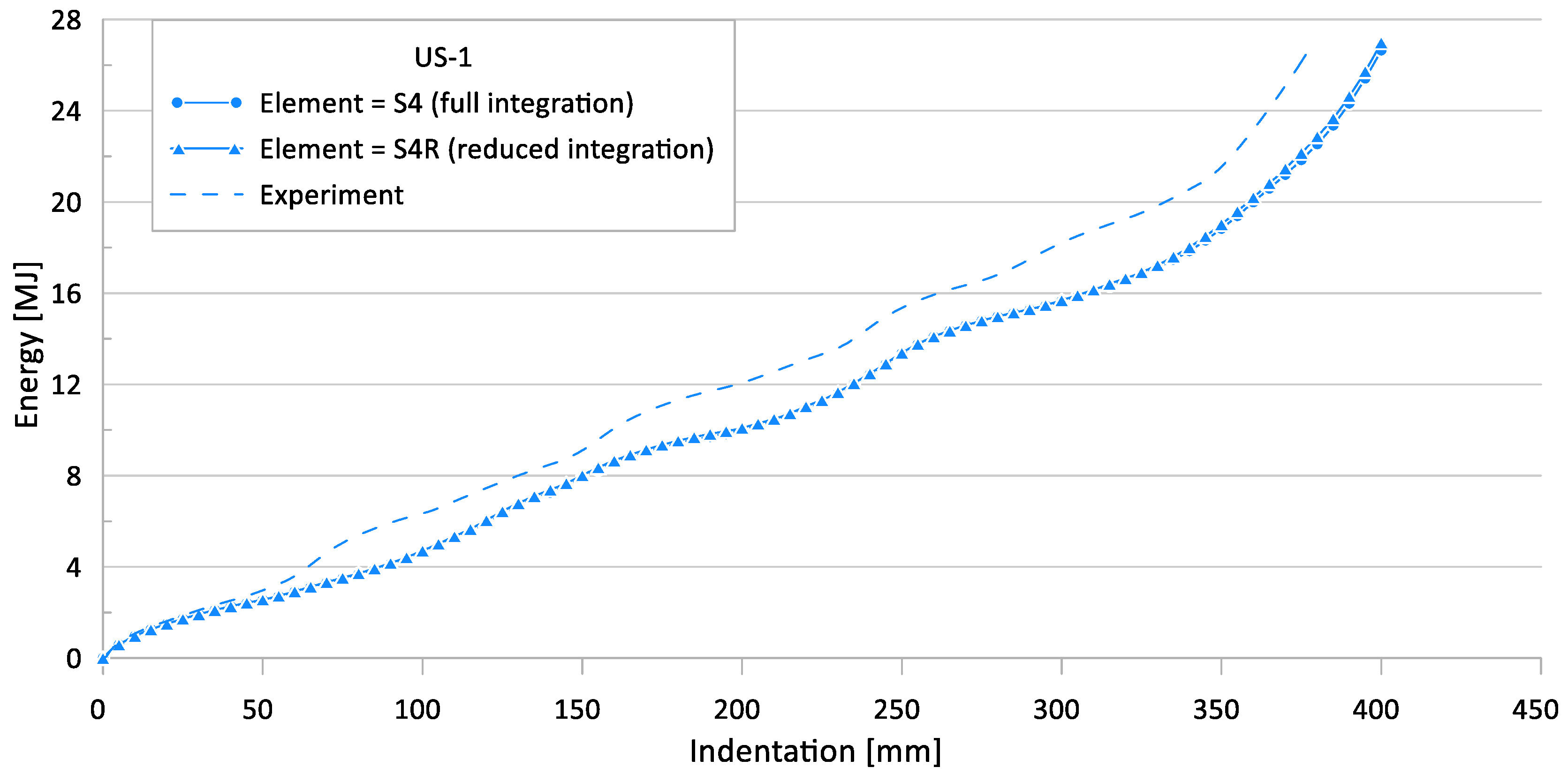
3.8. Parameter #6: Element Type (Reduced Integration vs. Full Integration)
4. Discussion
4.1. Determination of the Parameters for Finite Element Simulation
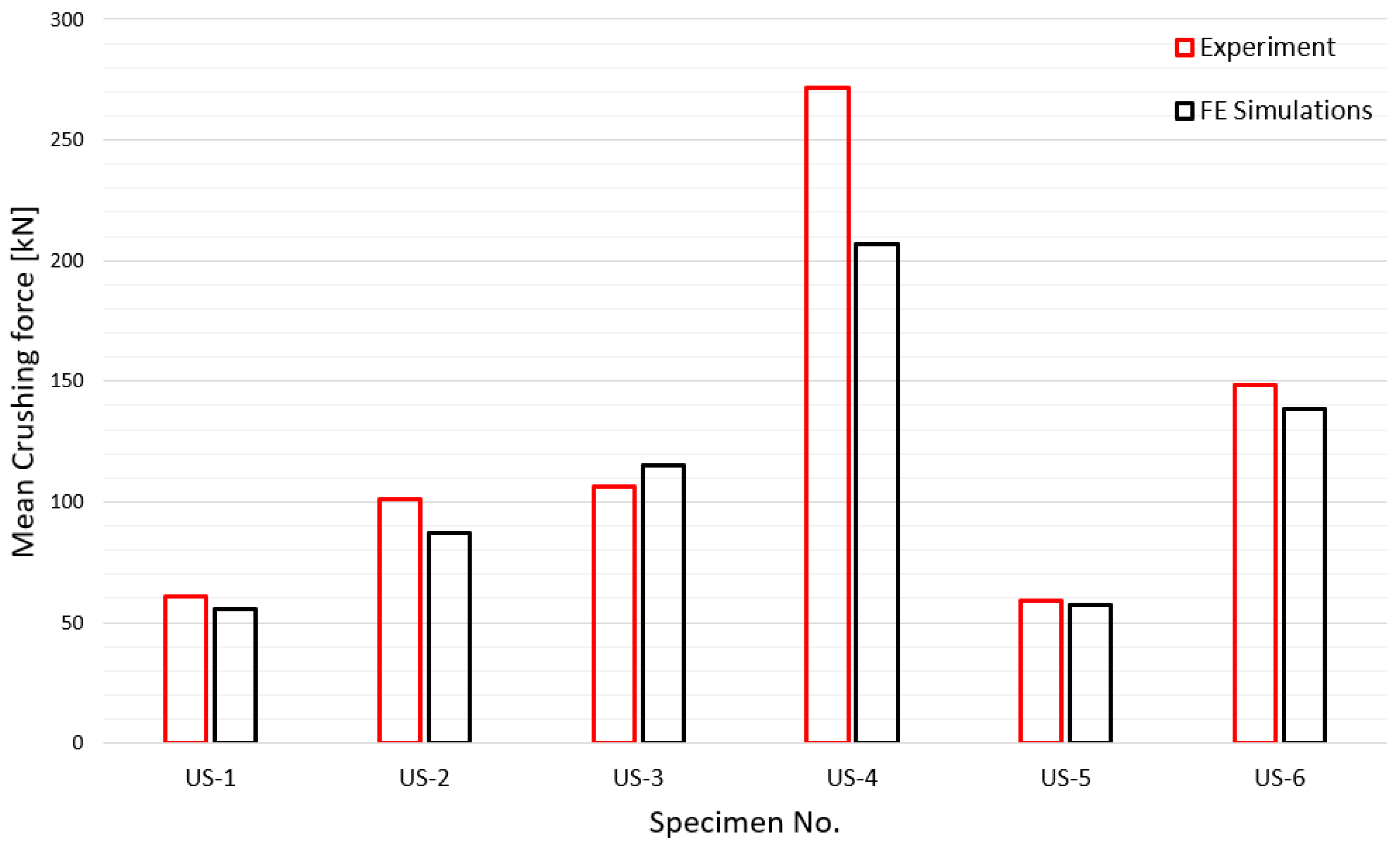
4.2. Comparison between Numerical Simulation and Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xin, X.; Lui, K.; Yang, Z.; Zhang, J.; Wu, X. A probabilistic risk approach for the collision detection of multi-ships under spatiotemporal movement uncertainty. Reliab. Eng. Syst. Saf. 2021, 215, 107772. [Google Scholar] [CrossRef]
- Viswabrahmana, M.; Suresh, A.V. Experimental investigation of tubular crushing and tubular bending of TWB application in automotive vehicles for frontal crash. Mater. Today Proc. 2021, in press. [Google Scholar] [CrossRef]
- Ataabadi, P.B.; Karagiozova, D.; Alves, M. Finite element modeling of crushing of CFRP cylindrical tubes under low-velocity axial impact. Compos. Struct. 2022, 280, 114902. [Google Scholar] [CrossRef]
- Dong, J.; Fan, U. Crushing behaviors of buckling-oriented hexagonal lattice structures. Mech. Mater. 2022, 165, 104160. [Google Scholar] [CrossRef]
- Paik, J.K.; Kim, B.J.; Park, D.K.; Jang, B.S. On quasi-static crushing of thin-walled steel structures in cold temperature: Experimental and numerical studies. Int. J. Impact Eng. 2011, 38, 13–28. [Google Scholar] [CrossRef]
- Paik, J.K.; Thayamballi, A.K.; Kim, G.S. The strength characteristics of aluminum honeycomb sandwich panels. Thin-Walled Struct. 1999, 35, 205–231. [Google Scholar] [CrossRef]
- Wang, G.; Suzuki, K. The crushing mechanics of bow structure in head on collision (2nd Report). J. Soc. Nav. Archit. Jpn. 1995, 177, 357–363. [Google Scholar] [CrossRef]
- Paik, J.K.; Pedersen, P.T. On design of double hull tankers against collisions. In Proceedings of the International Symposium on Practical Design of Ships and Mobile Units (PRADS), Seoul, Korea, 17–22 September 1995. [Google Scholar]
- Paik, J.K.; Pedersen, P.T. Collision strength analysis of double hull tanker. J. Soc. Nav. Archit. Korea 1995, 32, 103–117. [Google Scholar]
- Ohtsubo, H.; Suzuki, K. The crushing mechanics of bow structure in head on collision (1st Report). J. Soc. Nav. Archit. Jpn. 1994, 176, 301–308. [Google Scholar] [CrossRef]
- Jones, N.; Birch, R.S. Dynamic and static axial crushing of axially stiffened square tubes. Proc. Inst. Mech. Eng. 1990, 204, 293–310. [Google Scholar] [CrossRef]
- Pugsley, A.G. The crumpling of tubular structures under impact conditions. In Proceedings of the a Symposium on the Use of Aluminum in Railway Rolling Stock, Institution of Locomotive Engineers, London, UK, 27 May 1960; pp. 22–41. [Google Scholar]
- Macaulay, M.A.; Redwood, R.G. Small scale model railway coaches under impact. Engineer 1964, 25, 1041–1046. [Google Scholar]
- Lowe, W.T.; Al-Hassani, S.T.S.; Johnson, W. Impact behavior of small scale model motor coaches. Proc. Inst. Mech. Eng. 1972, 186, 409–419. [Google Scholar] [CrossRef]
- Nagasawa, H.; Arita, K.; Tani, M.; Oka, S. A study on the collapse of ship structure in collision with bridge piers. J. Soc. Nav. Archit. Jpn. 1977, 142, 323–332. [Google Scholar] [CrossRef]
- Nagasawa, H.; Arita, K.; Tani, M.; Oka, S. A study on the collapse of ship structure in collision with bridge piers (2nd Report). J. Soc. Nav. Archit. Jpn. 1979, 146, 329–337. [Google Scholar] [CrossRef]
- Nagasawa, H.; Arita, K.; Tani, M.; Oka, S. A study on the collapse of ship structure in collision with bridge piers (3rd Report). J. Soc. Nav. Archit. Jpn. 1980, 148, 153–161. [Google Scholar] [CrossRef][Green Version]
- Ohnishi, T.; Kawakami, H.; Yasukawa, W.; Nagasawa, H. On the ultimate strength of bow construction. J. Soc. Nav. Archit. Jpn. 1982, 151, 174–186. [Google Scholar] [CrossRef]
- Lee, J.W. The crushing behavior of thin plates subjected to compression. J. Soc. Nav. Archit. Korea 1982, 19, 33–39. [Google Scholar]
- Lee, J.W. On the optimization design of soft bow structure. In Proceedings of the International Symposium on Practical Design in Shipbuilding, Tokyo, Japan; Seoul, Korea, 17–22 October 1983; pp. 429–435. [Google Scholar]
- Meng, Q.; Al-Hassani, S.T.S.; Soden, P.D. Axial crushing of square tubes. Int. J. Mech. Sci. 1983, 25, 747–773. [Google Scholar] [CrossRef]
- Wierzbicki, T. Crushing behavior of plate intersections. In Proceedings of the First International Symposium on Structural Crashworthiness; University of Liverpool: Liverpool, UK, 1983; pp. 66–95. [Google Scholar]
- Amdahl, J. Energy absorption in ship-platform impacts. In Division of Marine Structures; Report No. UR-83-34; University of Trondheim: Trondheim, Norway, 1983. [Google Scholar]
- Abramowicz, W. The effective crushing distance in axially compressed thin-walled metal columns. Int. J. Impact Eng. 1983, 1, 309–317. [Google Scholar] [CrossRef]
- Abramowicz, W.; Jones, N. Dynamic axial crushing of square tubes. Int. J. Impact Eng. 1984, 2, 179–208. [Google Scholar] [CrossRef]
- Kawai, T.; Toi, Y.; Suzuki, N. Numerical simulations on the crushing behavior of structural members. J. Soc. Nav. Archit. Jpn. 1985, 158, 435–443. [Google Scholar] [CrossRef]
- Yang, P.D.C.; Caldwell, J.B. Collision energy absorption of ship’s bow structures. Int. J. Impact Eng. 1988, 7, 181–196. [Google Scholar] [CrossRef]
- Toi, Y.; Yuge, K.; Nagawama, T.; Obata, K. Numerical and experimental studies on the crushworthiness of structural members. Nav. Archit. Ocean. Eng. 1988, 26, 91–101. [Google Scholar]
- Jung, J.Y. On the Collision Strength of Ship’s Bow. Ph.D. Thesis, Pusan National University, Busan, Korea, 1997. [Google Scholar]
- Lindholm, U.S. Dynamic deformation of metals. In Behavior of Materials under Dynamic Loading; ASME: New York, NY, USA, 1965; p. 42. [Google Scholar]
- Dassault Systèmes Simulia Corp. Abaqus 6.14 Theory Manual; Dassault Systèmes Simulia Corp: Irving, TX, USA, 2014. [Google Scholar]
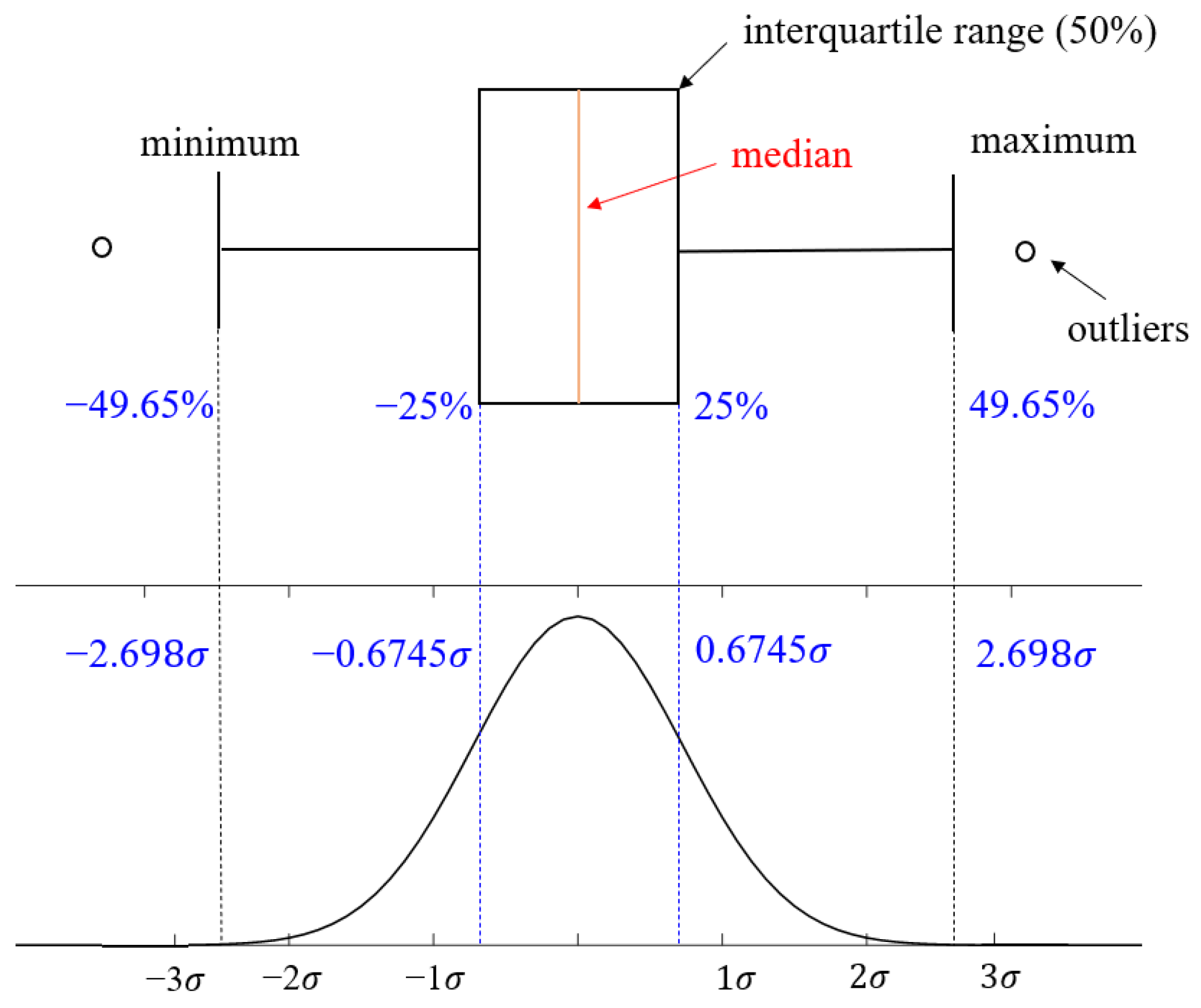
- Kotz, S.; Johnson, H.L.; Read, C.B. Encyclopedia of Statistical Sciences; No. 519.5 E5; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar]
- Tarigopula, V.; Langseth, M.; Hopperstad, O.S.; Clausen, A.H. Axial crushing of thin-walled high-strength steel sections. Int. J. Impact Eng. 2006, 32, 847–882. [Google Scholar] [CrossRef]

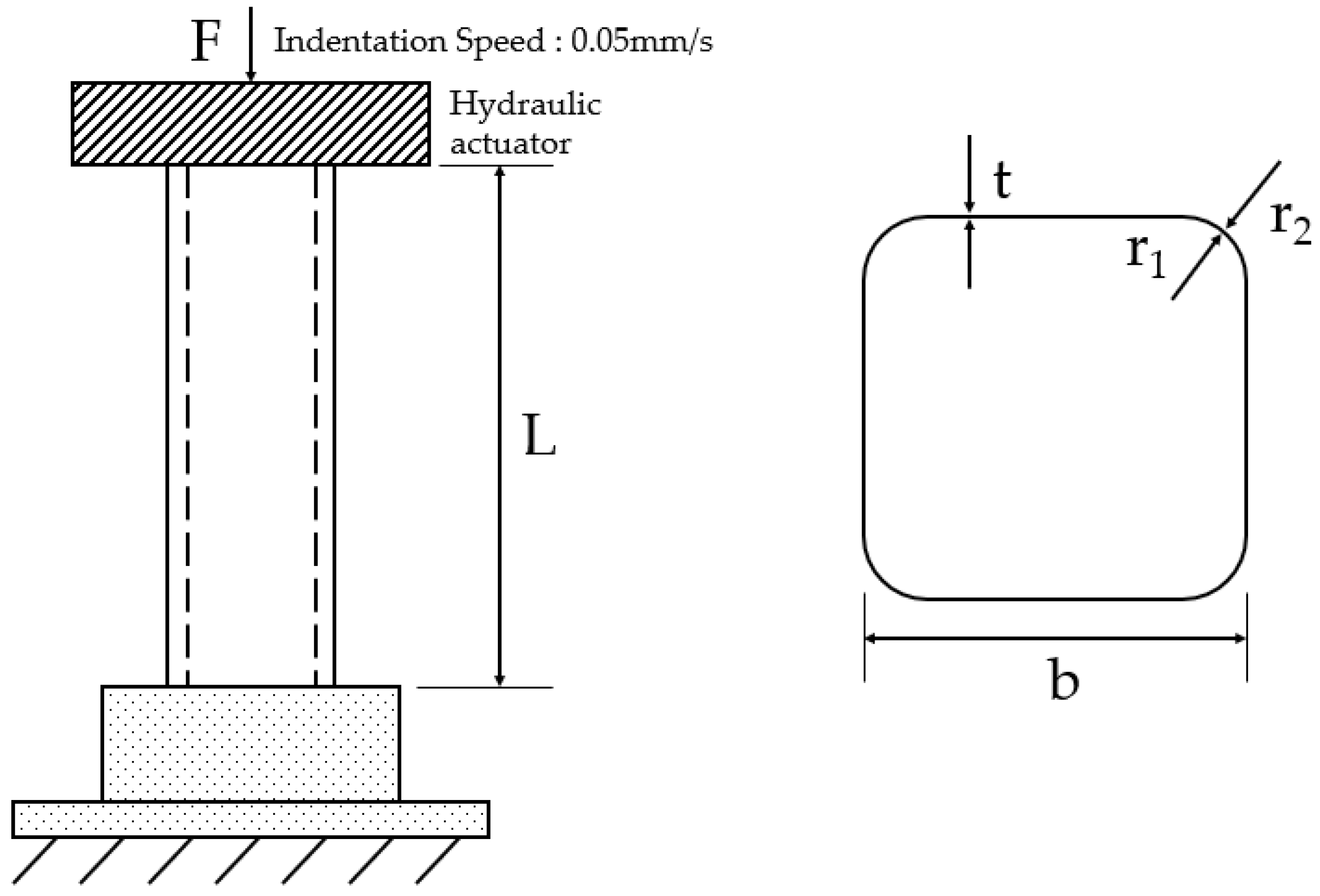

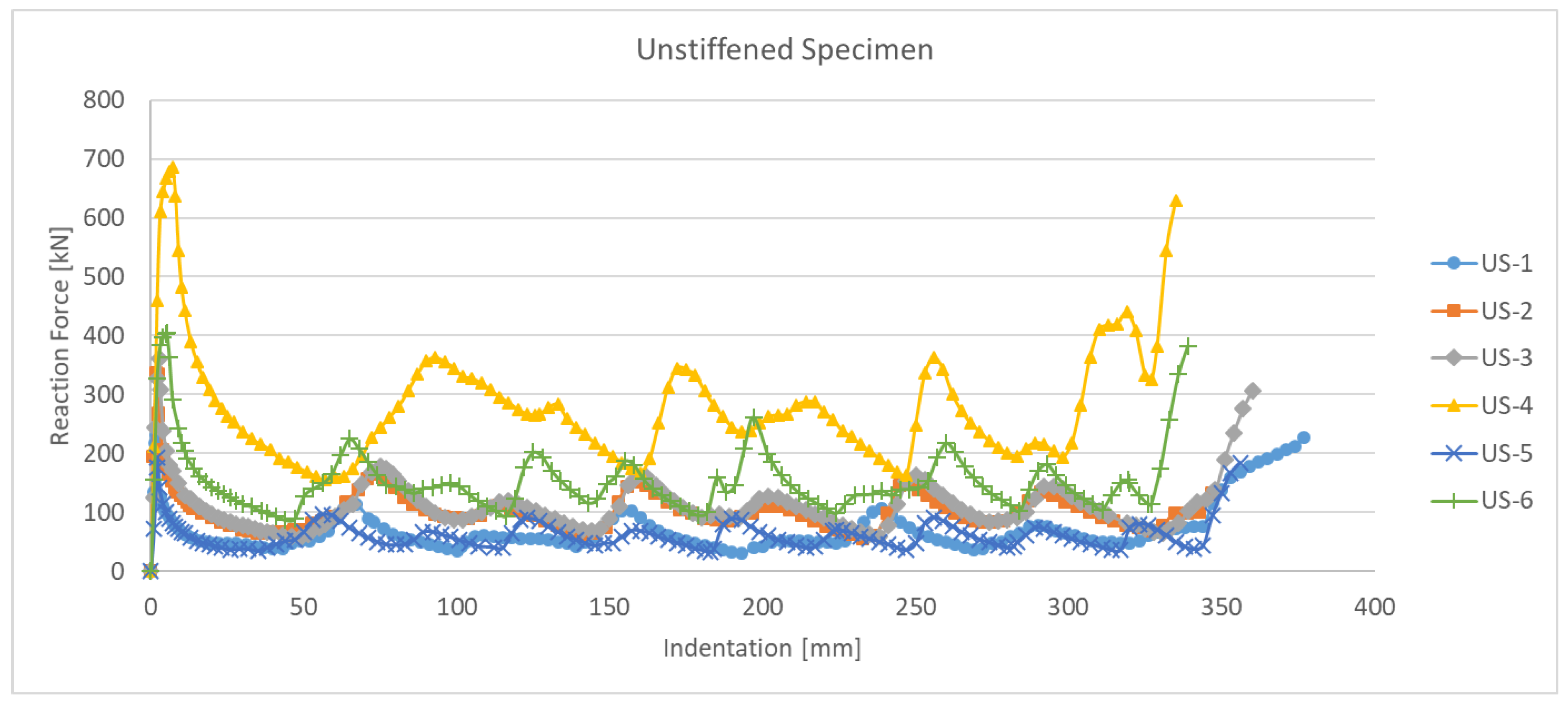




| Specimen Type | Specimen ID | L 1 [mm] | b 1 [mm] | t 1 [mm] |
|---|---|---|---|---|
| Unstiffened specimen | US-1 | 450 | 100 | 2.2 |
| US-2 | 100 | 2.8 | ||
| US-3 | 100 | 3.0 | ||
| US-4 | 100 | 4.2 | ||
| US-5 | 75 | 2.1 | ||
| US-6 | 75 | 3.2 |
| Specimen ID | Elongation [%] | E [GPa] | σy [MPa] (0.2% Proof Stress) | σT [MPa] | εT |
|---|---|---|---|---|---|
| US-1 | 41.9 | 199.2 | 286.1 | 351.9 | 0.210 |
| US-2 | 35.4 | 205.8 | 310.8 | 363.3 | 0.177 |
| US-3 | 35.6 | 207.8 | 299.3 | 351.2 | 0.178 |
| US-4 | 36.5 | 199.9 | 366.8 | 450.8 | 0.183 |
| US-5 | 37.4 | 200.1 | 328.5 | 399.4 | 0.187 |
| US-6 | 24.9 | 209.7 | 427.6 | 477.2 | 0.125 |
| Item | Note | |
|---|---|---|
| Finite element solver | ABAQUS standard ABAQUS explicit | For eigenvalue buckling assessment For nonlinear crushing simulation |
| Material type | Homogeneous isotropic material | |
| Boundary condition | Fixed type Simply supported type | |
| Surface contact | Kinematic hard contact option | |
| Elastic modulus | 205,800 MPa | |
| Poisson’s ratio | 0.3 | |
| Yield strength | From the experimental tests | |
| Specimen ID | Experimental Works [kN] | Finite Element Simulations [kN] | Difference [%] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Free | Fixed | Free | Fixed | |||||||
| Pu (1) | Pm (2) | Pu (3) | Pm (4) | Pu (5) | Pm (6) | ((1) − (3))/(1) | ((2) − (4))/(2) | ((1) − (5))/(1) | ((2) − (6))/(2) | |
| US-1 | 231.3 | 60.6 | 167.5 | 51.4 | 157.9 | 55.6 | 27.6 | 15.2 | 31.7 | 8.2 |
| US-2 | 337.1 | 101.0 | 305.7 | 83.7 | 302.3 | 87.3 | 9.3 | 17.2 | 10.3 | 13.6 |
| US-3 | 361.6 | 106.2 | 310.1 | 90.9 | 315.3 | 115.2 | 14.3 | 14.4 | 12.8 | 8.5 |
| US-4 | 626.0 | 271.6 | 583.5 | 192.0 | 588.7 | 207.0 | 6.8 | 29.3 | 6.0 | 23.8 |
| US-5 | 193.1 | 59.0 | 175.7 | 50.6 | 174.9 | 57.5 | 9.0 | 14.3 | 9.4 | 4.2 |
| US-6 | 404.7 | 148.4 | 390.4 | 130.2 | 388.4 | 138.2 | 3.5 | 12.3 | 4.0 | 6.9 |
| Specimen ID | Experimental Works | FE Simulations | Difference [%] | ||||
|---|---|---|---|---|---|---|---|
| Pu (1) [kN] | Pm (2) [kN] | amp | Pu (3) [kN]) | Pm (4) [kN] | ((1) − (3))/(1) [%] | ((2) − (4))/(2) [%] | |
| US-1 | 231.3 | 60.6 | 0.05 | 191.2 | 54.5 | 17 | 10 |
| 0.10 | 157.9 | 55.6 | 32 | 8 | |||
| 0.20 | 157.2 | 61.2 | 32 | 1 | |||
| 0.30 | 144.9 | 51.6 | 37 | 15 | |||
| US-2 | 337.1 | 101.0 | 0.05 | 327.3 | 87.5 | 3 | 13 |
| 0.10 | 302.3 | 87.3 | 10 | 14 | |||
| 0.20 | 256.9 | 88.2 | 24 | 13 | |||
| 0.30 | 227.7 | 97.8 | 32 | 3 | |||
| US-3 | 361.6 | 106.2 | 0.05 | 335.5 | 118.6 | 7 | 12 |
| 0.10 | 315.3 | 115.2 | 13 | 8 | |||
| 0.20 | 264.4 | 114.5 | 27 | 8 | |||
| 0.30 | 234.2 | 113.9 | 35 | 7 | |||
| US-4 | 626.0 | 271.6 | 0.05 | 593.9 | 206.3 | 5 | 24 |
| 0.10 | 588.7 | 207.0 | 6 | 24 | |||
| 0.20 | 576.4 | 208.1 | 8 | 23 | |||
| 0.30 | 546.4 | 222.1 | 13 | 18 | |||
| US-5 | 193.1 | 59.0 | 0.05 | 194.2 | 51.3 | 1 | 13 |
| 0.10 | 174.9 | 57.5 | 9 | 4 | |||
| 0.20 | 142.7 | 52.6 | 26 | 11 | |||
| 0.30 | 134.5 | 54.3 | 30 | 8 | |||
| US-6 | 404.7 | 148.4 | 0.05 | 398.0 | 140.3 | 2 | 5 |
| 0.10 | 388.4 | 138.2 | 4 | 7 | |||
| 0.20 | 364.7 | 145.1 | 10 | 2 | |||
| 0.30 | 339.6 | 142.3 | 16 | 4 | |||
| Specimen ID | Experimental Works | FE Simulations | Difference | ||||
|---|---|---|---|---|---|---|---|
| Pu (1) [kN] | Pm (2) [kN] | Friction Coefficient | Pu (3) [kN] | Pm (4) [kN] | ((1) − (3))/(1) [%] | ((2) − (4))/(2) [%] | |
| US-1 | 231.3 | 60.6 | 0.04 | 157.9 | 55.6 | 31.7 | 8.2 |
| 0.08 | 157.9 | 55.6 | 31.7 | 8.2 | |||
| 0.16 | 157.9 | 55.3 | 31.7 | 8.7 | |||
| 0.24 | 157.9 | 54.6 | 31.7 | 9.8 | |||
| US-2 | 337.1 | 101.0 | 0.04 | 302.3 | 88.7 | 10.3 | 12.2 |
| 0.08 | 302.3 | 87.3 | 10.3 | 13.6 | |||
| 0.16 | 302.3 | 87.9 | 10.3 | 12.9 | |||
| 0.24 | 302.3 | 87.4 | 10.3 | 13.5 | |||
| US-3 | 361.6 | 106.2 | 0.04 | 343.6 | 118.8 | 5.0 | 11.8 |
| 0.08 | 343.6 | 115.2 | 5.0 | 8.5 | |||
| 0.16 | 343.6 | 112.5 | 5.0 | 5.9 | |||
| 0.24 | 343.6 | 114.1 | 5.0 | 7.5 | |||
| US-4 | 626.0 | 271.6 | 0.04 | 588.7 | 207.3 | 6.0 | 23.7 |
| 0.08 | 588.7 | 207.0 | 6.0 | 23.8 | |||
| 0.16 | 588.7 | 204.0 | 6.0 | 24.9 | |||
| 0.24 | 588.7 | 204.3 | 6.0 | 24.8 | |||
| US-5 | 193.1 | 59.0 | 0.04 | 174.9 | 56.2 | 9.4 | 4.7 |
| 0.08 | 174.9 | 57.5 | 9.4 | 4.2 | |||
| 0.16 | 174.9 | 56.4 | 9.4 | 4.4 | |||
| 0.24 | 174.9 | 54.5 | 9.4 | 7.6 | |||
| US-6 | 404.7 | 148.4 | 0.04 | 388.4 | 138.2 | 4.0 | 6.9 |
| 0.08 | 388.4 | 138.2 | 4.0 | 6.9 | |||
| 0.16 | 388.4 | 137.3 | 4.0 | 7.5 | |||
| 0.24 | 388.4 | 137.9 | 4.0 | 7.1 | |||
| Specimen No. | Pu [kN] | Pm [kN] | Difference [%] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pu | Pm | |||||||||
| Exp. | PE | MLM | Exp. | PE | MLM | PE | MLM | PE | MLM | |
| US-1 | 231.3 | 157.9 | 159.5 | 60.6 | 55.6 | 68.7 | 31.7 | 31.0 | 8.3 | 13.4 |
| US-2 | 337.1 | 302.3 | 304.1 | 101.0 | 87.3 | 100.6 | 10.3 | 9.8 | 13.6 | 0.4 |
| US-3 | 361.6 | 343.6 | 344.8 | 106.2 | 115.2 | 129.7 | 5.0 | 4.6 | 8.5 | 22.1 |
| US-4 | 626.0 | 588.7 | 589.6 | 271.6 | 207.0 | 252.6 | 6.0 | 5.8 | 31.7 | 31.0 |
| US-5 | 193.1 | 174.9 | 176.4 | 59.0 | 57.5 | 64.0 | 9.4 | 8.6 | 2.5 | 8.5 |
| US-6 | 404.7 | 388.4 | 388.8 | 148.4 | 138.2 | 157.0 | 4.0 | 3.9 | 6.9 | 5.8 |
| Size | Deformed Shape—Edge Line | Deformed Shape—Half of the Specimen | No. of Elements for Each Folding |
|---|---|---|---|
| 2 mm |  | 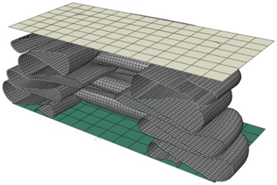 | 63 |
| 3 mm |  | 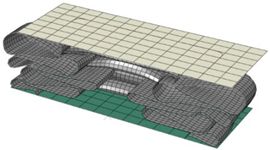 | 41 |
| 4 mm |  | 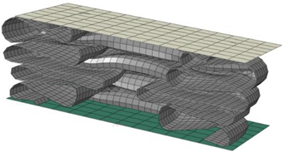 | 31 |
| 5 mm | 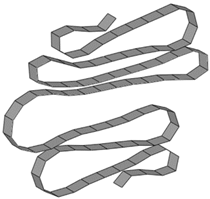 | 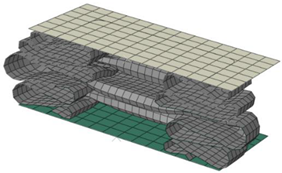 | 24 |
| 6 mm | 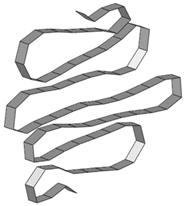 | 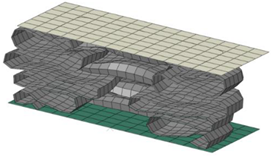 | 20 |
| 7 mm | 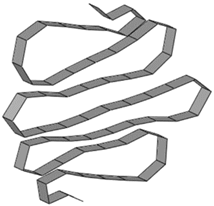 | 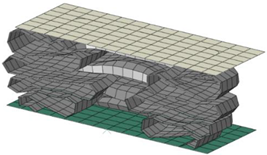 | 19 |
| 8 mm | 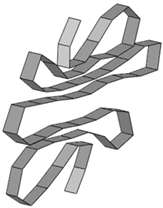 | 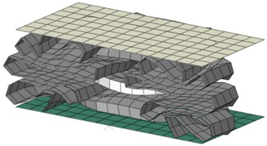 | 17 |
| Experiment | FE Simulations | Difference | ||||
|---|---|---|---|---|---|---|
| Pu [kN] | Pm [kN] | Element Size [mm] | Pu [kN] | Pm [kN] | Pu [%] | Pm [%] |
| 337.1 | 101.1 | 2 | 300.2 | 86.3 | 10.9 | 14.6 |
| 3 | 300.5 | 86.4 | 10.9 | 14.5 | ||
| 4 | 301.3 | 86.5 | 10.6 | 14.4 | ||
| 5 | 302.3 | 87.3 | 10.3 | 13.6 | ||
| 6 | 302.3 | 92.7 | 10.3 | 8.3 | ||
| 7 | 301.8 | 98.4 | 10.5 | 2.7 | ||
| 8 | 303.7 | 110.7 | 9.9 | 9.5 | ||
| Specimen No. | Experiment [kN] | FEM [kN] | Difference [%] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S4 1 | S4R 1 | ((3) − (5))/(3) | ((4) − (6))/(4) | ((1) − (3))/(1) | ((2) − (4))/(2) | ((1) − (5))/(1) | ((2) − (6))/(2) | |||||
| Pu (1) | Pm (2) | Pu (3) | Pm (4) | Pu (5) | Pm (6) | Pu | Pm | Pu | Pm | Pu | Pm | |
| US-1 | 231.3 | 60.6 | 157.8 | 55.9 | 157.9 | 55.6 | 0.06 | 0.54 | 31.78 | 7.76 | 31.73 | 8.25 |
| US-2 | 337.1 | 101.0 | 301.9 | 84.4 | 302.3 | 87.3 | 0.13 | 3.44 | 10.44 | 16.44 | 10.32 | 13.56 |
| US-3 | 361.6 | 106.2 | 343.7 | 112.0 | 343.6 | 115.2 | 0.03 | 2.86 | 4.95 | 5.46 | 4.98 | 8.47 |
| US-4 | 626.0 | 271.6 | 588.9 | 203.2 | 588.7 | 207.0 | 0.03 | 1.87 | 5.93 | 25.18 | 5.96 | 23.78 |
| US-5 | 193.1 | 59.0 | 174.9 | 54.5 | 174.9 | 57.5 | 0.00 | 5.50 | 9.43 | 7.63 | 9.43 | 2.54 |
| US-6 | 404.7 | 148.4 | 388.7 | 135.4 | 388.4 | 138.2 | 0.08 | 2.07 | 3.95 | 8.76 | 4.03 | 6.87 |
| Parameter | Selected Case |
|---|---|
| Boundary condition | Fix |
| Initial imperfection | |
| Friction coefficient | 0.08 |
| Material property model | perfect elasto-plastic material |
| Finite element mesh size | 5 mm |
| Element type | S4R (reduced integration four-node shell element) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.I.; Cho, J.-S.; Kim, J.-H. Numerical and Experimental Investigation of Quasi-Static Crushing Behaviors of Steel Tubular Structures. Materials 2022, 15, 2107. https://doi.org/10.3390/ma15062107
Park YI, Cho J-S, Kim J-H. Numerical and Experimental Investigation of Quasi-Static Crushing Behaviors of Steel Tubular Structures. Materials. 2022; 15(6):2107. https://doi.org/10.3390/ma15062107
Chicago/Turabian StylePark, Young IL, Jin-Seong Cho, and Jeong-Hwan Kim. 2022. "Numerical and Experimental Investigation of Quasi-Static Crushing Behaviors of Steel Tubular Structures" Materials 15, no. 6: 2107. https://doi.org/10.3390/ma15062107
APA StylePark, Y. I., Cho, J.-S., & Kim, J.-H. (2022). Numerical and Experimental Investigation of Quasi-Static Crushing Behaviors of Steel Tubular Structures. Materials, 15(6), 2107. https://doi.org/10.3390/ma15062107






