Reorientation of Suspended Ceramic Particles in Robocasted Green Filaments during Drying
Abstract
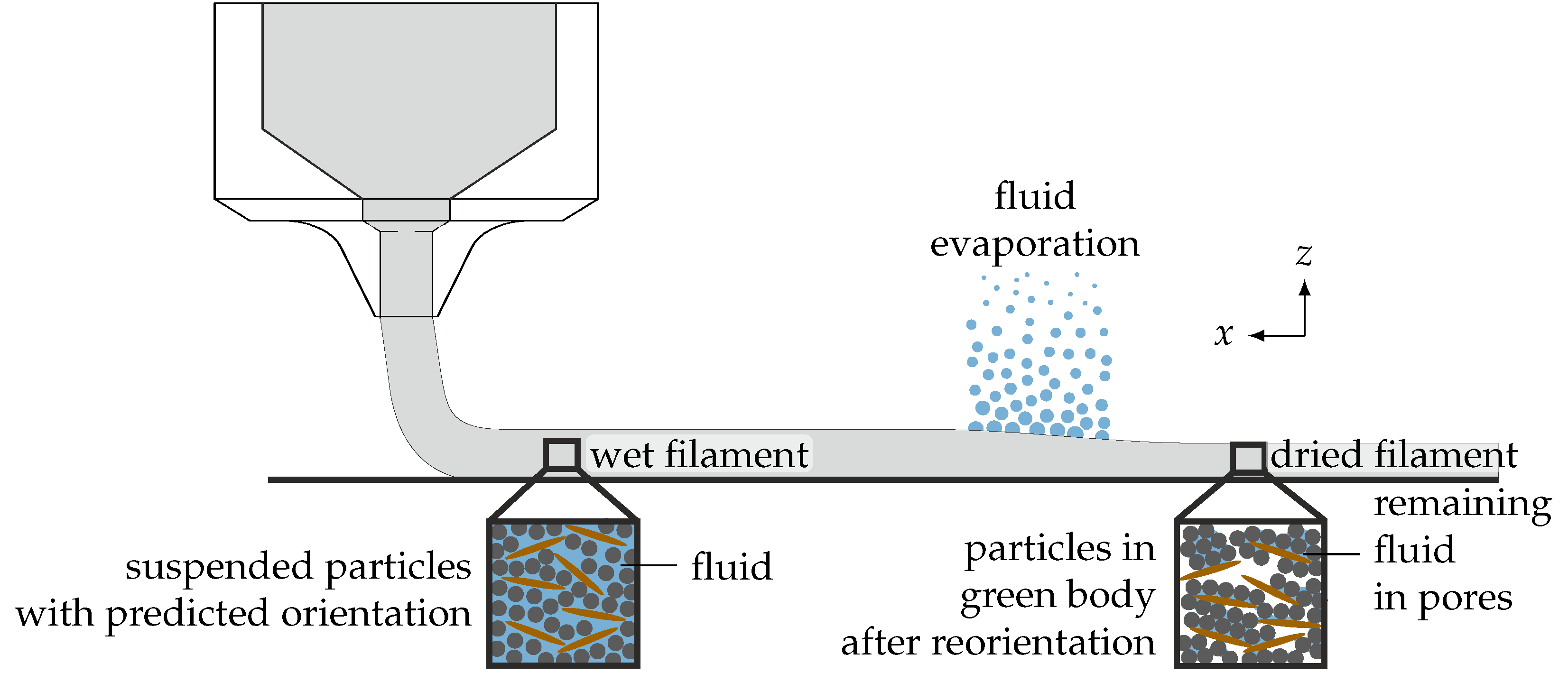
:1. Introduction
2. Method
2.1. Experimental Robocasting and Measurement of Drying Shrinkage
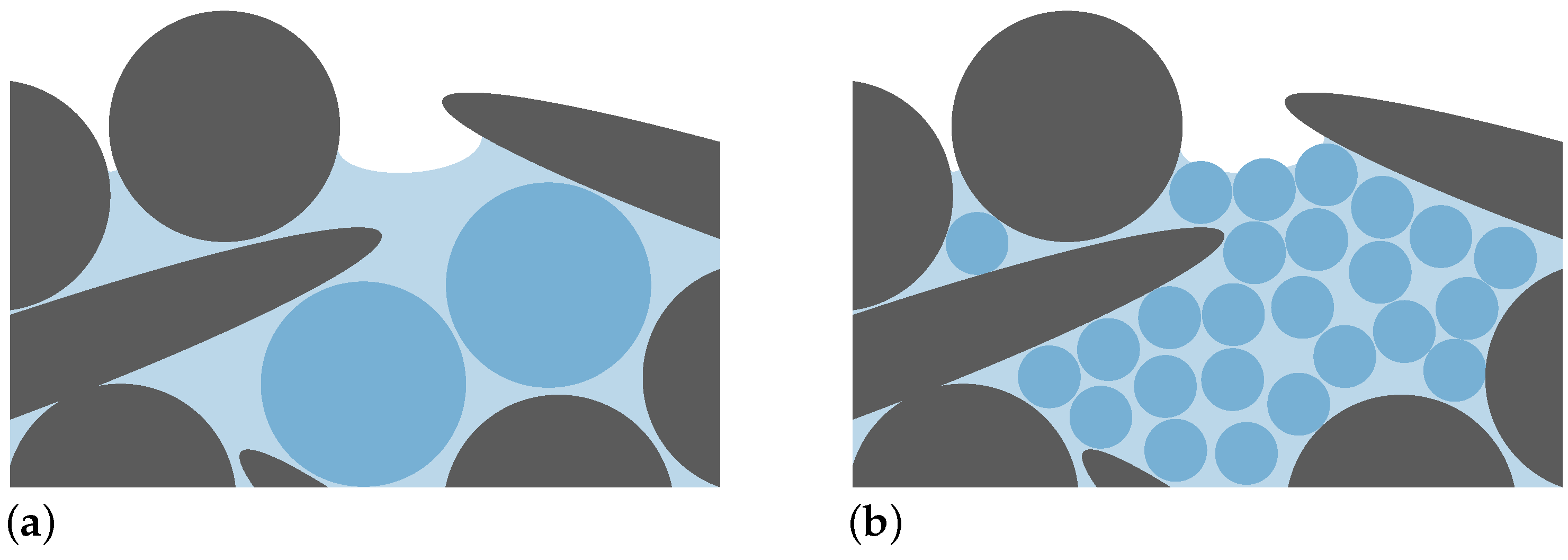
2.2. Applying the DEM to Model Particle Reorientation during Drying
2.2.1. Contact Forces
2.2.2. Liquid Bridge Model
2.2.3. Neighbor Independent Forces
2.2.4. Discretization of Experimental Particles by Rigid Bodies
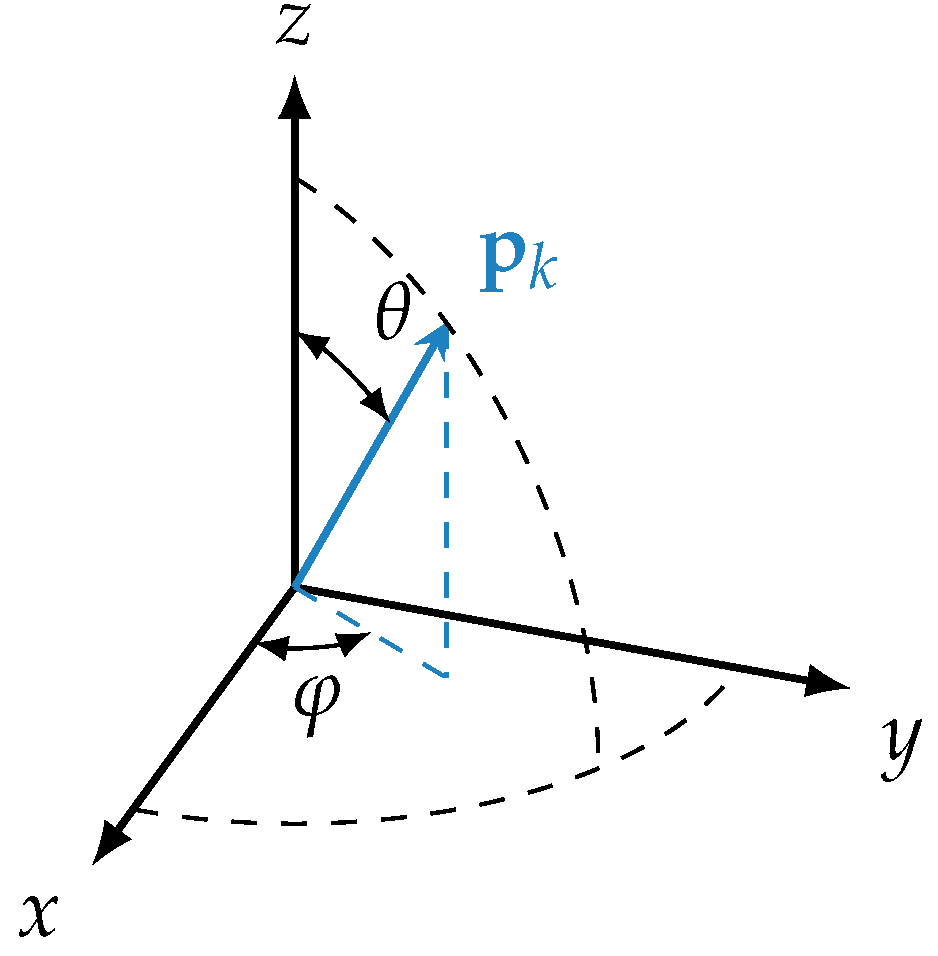
2.3. Mean Orientation Description by Orientation Tensors
2.4. Start Configuration and Initial Orientation within the Wet Filament
2.5. Modeling of the Drying Process
3. Results
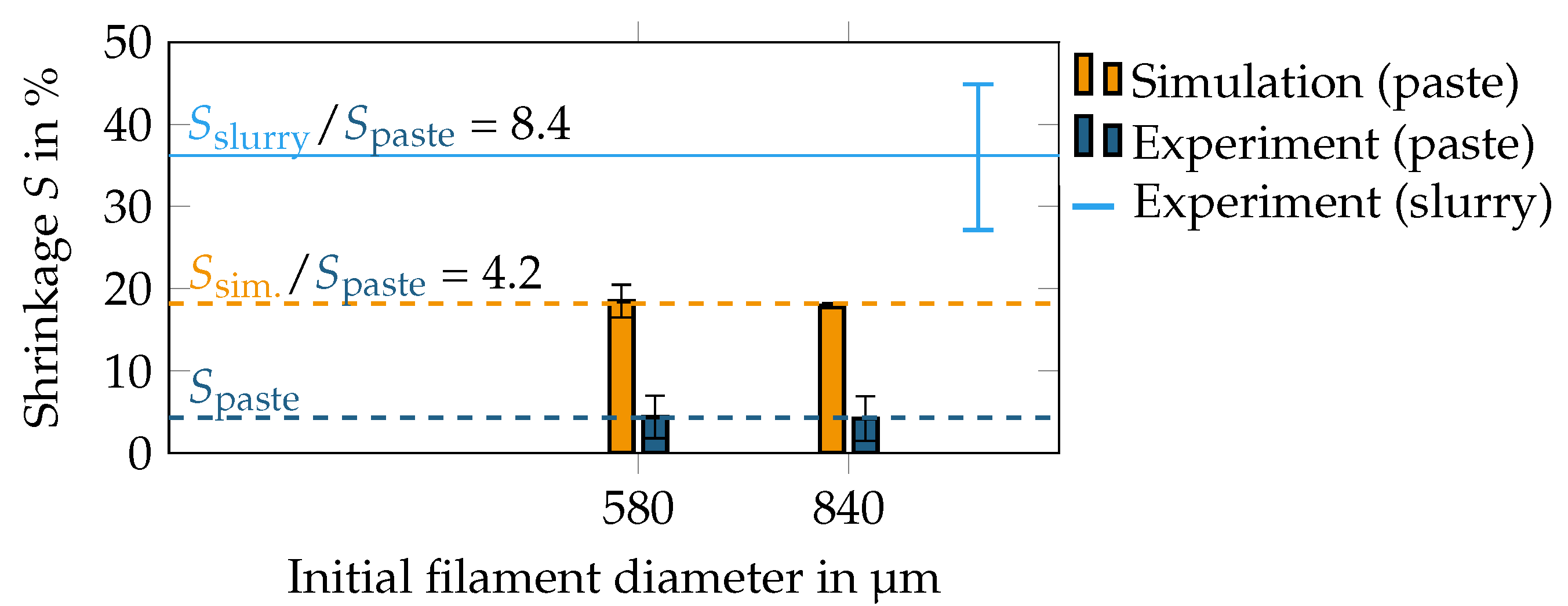
3.1. Experimental and Numerical Filament Shrinkage during Drying
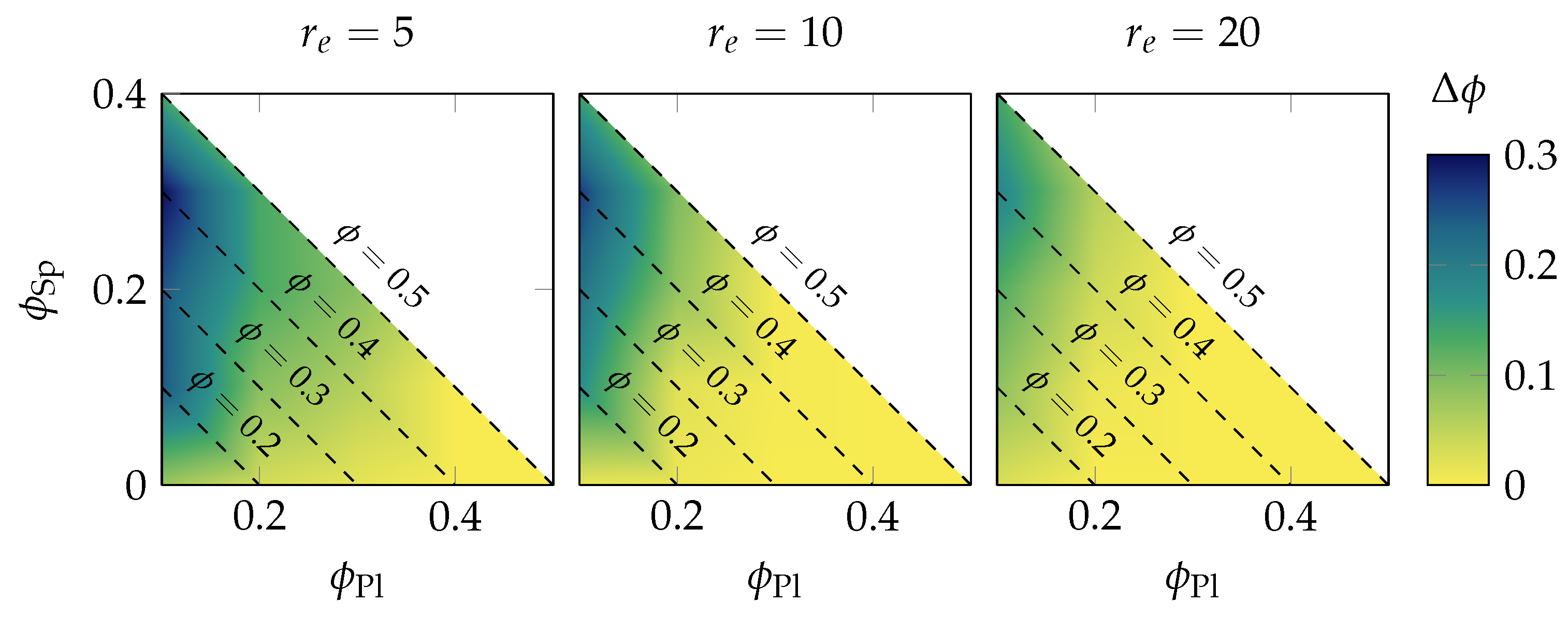
3.2. Increase of the Filling Fraction during Drying
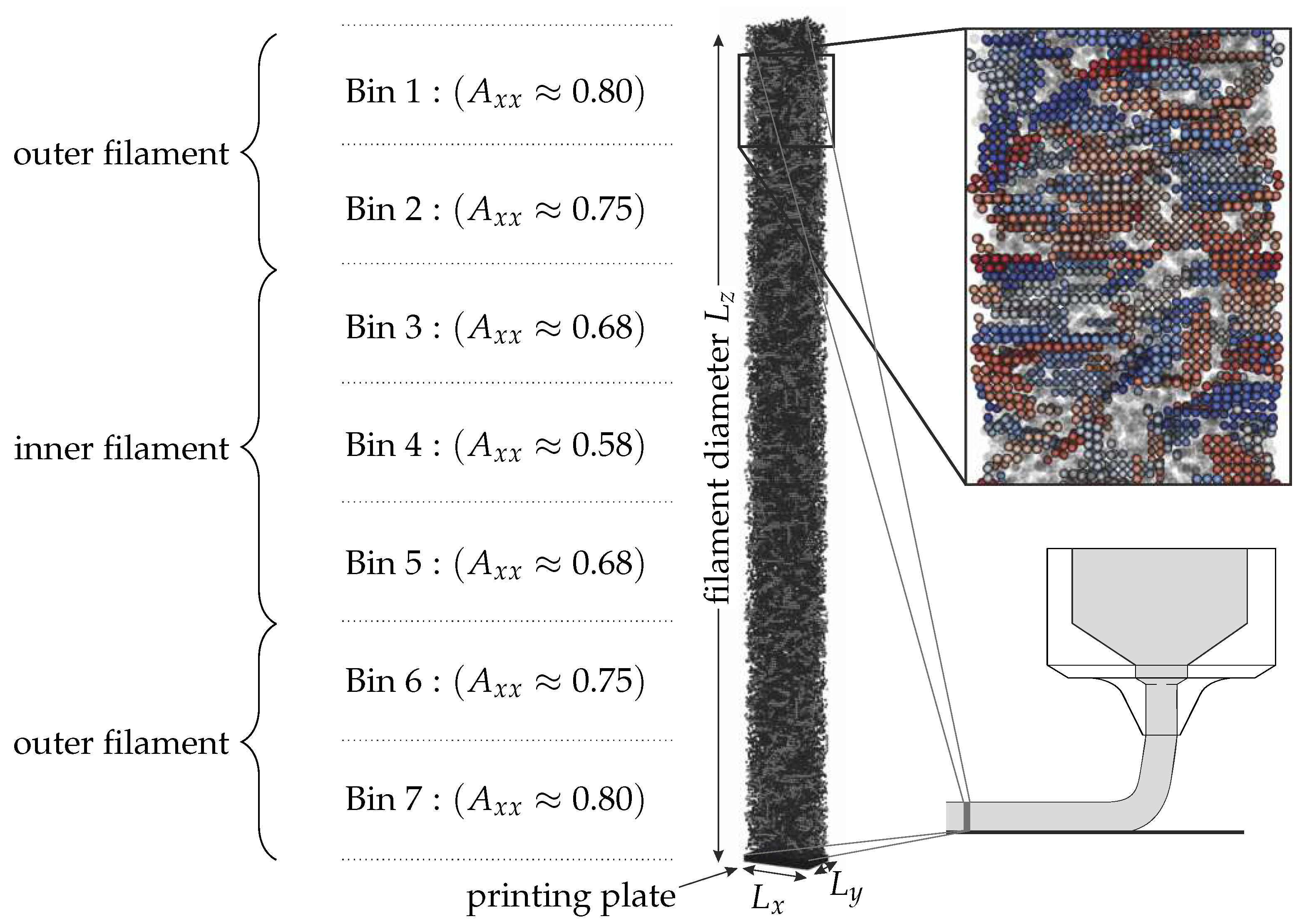
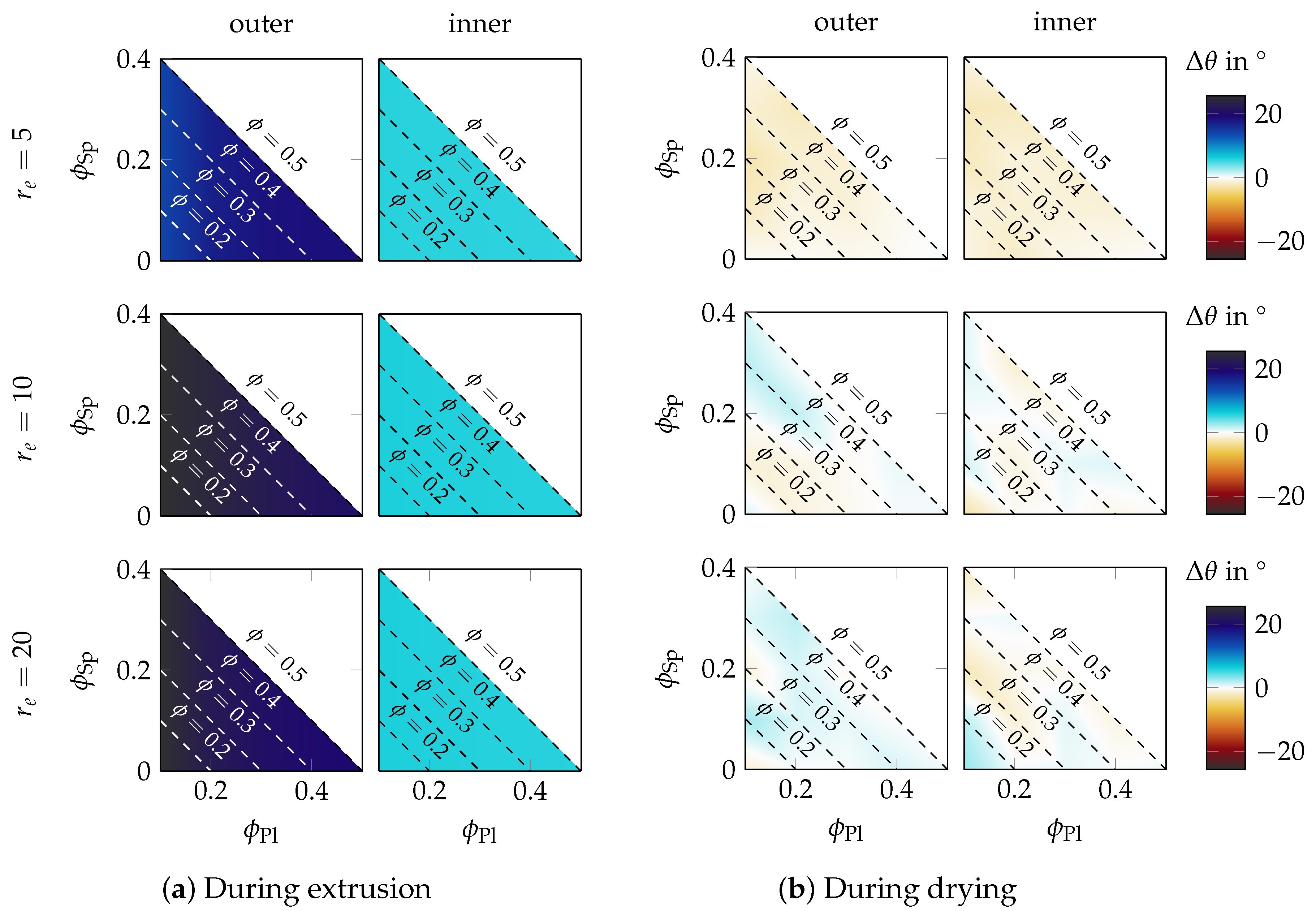
3.3. Orientation Change during Drying
3.3.1. Influence of the Composition and Platelet Aspect Ratio
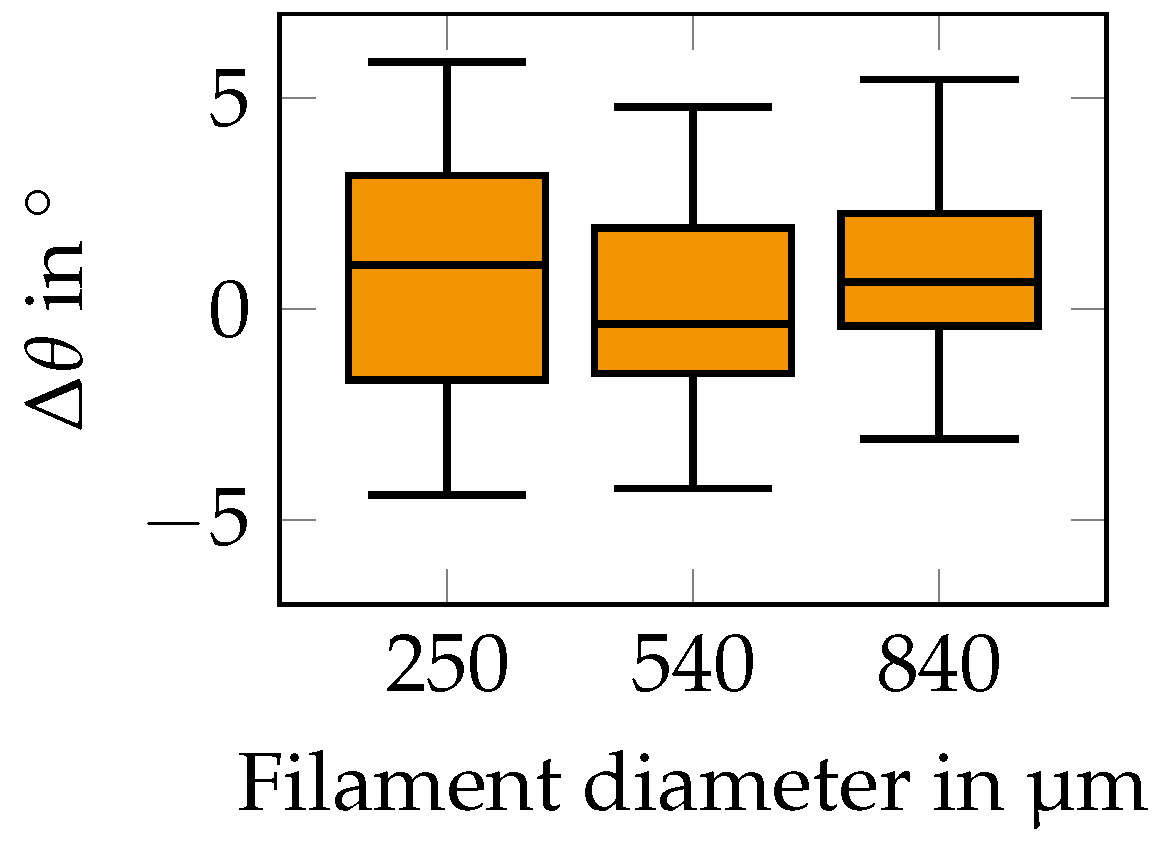
3.3.2. Influence of Filament Diameter
4. Discussion
4.1. Discussion of the Model
4.2. Discussion of Results
4.3. Limitations of This Work
4.4. Consequences for Orientation Prediction Models and Homogenization Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | three-dimensional |
| CFD | computational fluid dynamic |
| EAM | material-extrusion-based additive manufacturing |
| ODF | orientation distribution function |
| OPM | orientation prediction model |
| PBC | periodic boundary condition |
| RVE | representative volume element |
| SEM | scanning electron microscopy |
References
- Wang, Z.; Smith, D.E. Rheology Effects on Predicted Fiber Orientation and Elastic Properties in Large Scale Polymer Composite Additive Manufacturing. J. Compos. Sci. 2018, 2, 10. [Google Scholar] [CrossRef] [Green Version]
- Simon, S.A.; Bechara, A.; Osswald, T.A. Experimental Validation of a Direct Fiber Model for Orientation Prediction. J. Compos. Sci. 2020, 4, 59. [Google Scholar] [CrossRef]
- Jeffery, G.B. The Motion of Ellipsoidal Particles Immersed in a Viscous Fluid. Proc. R. Soc. Math. Phys. Eng. Sci. 1922, 102, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Folgar, F.; Tucker, C.L. Orientation Behavior of Fibers in Concentrated Suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Wang, J.; O’Gara, J.F.; Tucker, C.L. An objective model for slow orientation kinetics in concentrated fiber suspensions: Theory and rheological evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Phenomenological improvements to predictive models of fiber orientation in concentrated suspensions. J. Rheol. 2013, 57, 1597–1631. [Google Scholar] [CrossRef]
- Bakharev, A. (Ed.) Using New Anisotropic Rotational Diffusion Model to Improve Prediction of Short Fibers in Thermoplastic Injection Molding; Society of Plastics Engineers: Danbury, CT, USA, 2018. [Google Scholar]
- Phelps, J.H.; Tucker, C.L. An anisotropic rotary diffusion model for fiber orientation in short- and long-fiber thermoplastics. J. Non-Newton. Fluid Mech. 2009, 156, 165–176. [Google Scholar] [CrossRef]
- Dietemann, B.; Bosna, F.; Lorenz, M.; Travitzky, N.; Kruggel-Emden, H.; Kraft, T.; Bierwisch, C. Numerical study of texture in material extrusion: Orientation in a multicomponent system of spheres and ellipsoids. J. Non-Newton. Fluid Mech. 2021, 291, 104532. [Google Scholar] [CrossRef]
- Sasayama, T.; Inagaki, M. Efficient bead-chain model for predicting fiber motion during molding of fiber-reinforced thermoplastics. J. Non-Newton. Fluid Mech. 2019, 264, 135–143. [Google Scholar] [CrossRef]
- Sasayama, T.; Sato, N.; Katagiri, Y.; Murayama, Y. Particle-level simulation for the prediction of short fiber orientation in injection molding. Compos. Part Appl. Sci. Manuf. 2020, 139, 106115. [Google Scholar] [CrossRef]
- Scherer, G.W. Theory of Drying. J. Am. Ceram. Soc. 1990, 73, 3–14. [Google Scholar] [CrossRef]
- Strumiłło, C.; Kudra, T. Drying: Principles, applications and design. In Topics in Chemical Engineering; Gordon and Breach Science Publ: New York, NY, USA, 1986; Volume 3. [Google Scholar]
- Sherwood, T.K. The Drying of Solids—I. Ind. Eng. Chem. 1929, 21, 12–16. [Google Scholar] [CrossRef]
- Sherwood, T.K. The Drying of solids—II. Ind. Eng. Chem. 1929, 21, 976–980. [Google Scholar] [CrossRef]
- Sherwood, T.K. The Drying of Solids—III Mechanism of the Drying of Pulp and Paper. Ind. Eng. Chem. 1930, 22, 132–136. [Google Scholar] [CrossRef]
- Gilliland, E.R.; Sherwood, T.K. The Drying of Solids. VI. Diffusion Equations for the Period of Constant Drying Rate. Ind. Eng. Chem. 1933, 25, 1134–1136. [Google Scholar] [CrossRef]
- Briscoe, B.J.; Lo Biundo, G.; Özkan, N. Drying kinetics of water-based ceramic suspensions for tape casting. Ceram. Int. 1998, 24, 347–357. [Google Scholar] [CrossRef]
- Oummadi, S.; Nait-Ali, B.; Alzina, A.; Victor, J.L.; Launay, Y.; Mirdrikvand, M.; Dreher, W.; Rezwan, K.; Smith, D.S. Distribution of water in ceramic green bodies during drying. J. Eur. Ceram. Soc. 2019, 39, 3164–3172. [Google Scholar] [CrossRef]
- Fu, Z.; Polfer, P.; Kraft, T.; Roosen, A. Correlation Between Anisotropic Green Microstructure of Spherical-Shaped Alumina Particles and Their Shrinkage Behavior. J. Am. Ceram. Soc. 2015, 98, 3438–3444. [Google Scholar] [CrossRef]
- Keita, E.; Faure, P.; Rodts, S.; Coussot, P. MRI evidence for a receding-front effect in drying porous media. Phys. Rev. E 2013, 87, 62303. [Google Scholar] [CrossRef]
- Mezhericher, M.; Levy, A.; Borde, I. Modelling of particle breakage during drying. Chem. Eng. Process. Process. Intensif. 2008, 47, 1404–1411. [Google Scholar] [CrossRef]
- Elhalwagy, M.M.; Straatman, A.G. Dynamic coupling of phase-heat and mass transfer in porous media and conjugate fluid/porous domains. Int. J. Heat Mass Transf. 2017, 106, 1270–1286. [Google Scholar] [CrossRef]
- Ghosal, S.; Emami-Naeini, A.; Harn, Y.P.; Draskovich, B.S.; Pollinger, J.P. A Physical Model for the Drying of Gelcast Ceramics. J. Am. Ceram. Soc. 1999, 82, 513–520. [Google Scholar] [CrossRef]
- Harun, Z.; Gethin, D.T.; Lewis, J.A. Combined heat and mass transfer for drying ceramic (shell) body. Int. J. Multiphys. 2008, 2, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Harun, Z.; Ong, T.C.; Matsuura, T.; Hubadillah, S.K.; Othman, M.H.D.; Ismail, A.F. Modelling of transport mechanisms and drying shrinkage for multilayer ceramic membrane structure. Chem. Eng. Res. Des. 2018, 133, 111–125. [Google Scholar] [CrossRef]
- Teixeira de Brito, M.K.; Teixeira de Almeida, D.B.; Barbosa de Lima, A.G.; Almeida Rocha, L.; Santana de Lima, E.; Barbosa de Oliveira, V.A. Heat and Mass Transfer during Drying of Clay Ceramic Materials: A Three-Dimensional Analytical Study. Diffus. Found. 2017, 10, 93–106. [Google Scholar] [CrossRef]
- Yang, X.; Kong, S.C. A smoothed particle hydrodynamics method for evaporating multiphase flows. Phys. Rev. E 2017, 96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barati, A.; Kokabi, M.; Famili, N. Modeling of liquid desiccant drying method for gelcast ceramic parts. Ceram. Int. 2003, 29, 199–207. [Google Scholar] [CrossRef]
- Breinlinger, T.; Polfer, P.; Hashibon, A.; Kraft, T. Surface tension and wetting effects with smoothed particle hydrodynamics. J. Comput. Phys. 2013, 243, 14–27. [Google Scholar] [CrossRef]
- Fujita, M.; Koike, O.; Yamaguchi, Y. Direct simulation of drying colloidal suspension on substrate using immersed free surface model. J. Comput. Phys. 2015, 281, 421–448. [Google Scholar] [CrossRef] [Green Version]
- Khalili, K.; Bagherian, M.; Khisheh, S. Numerical Simulation of Drying Ceramic Using Finite Element and Machine Vision. Procedia Technol. 2014, 12, 388–393. [Google Scholar] [CrossRef] [Green Version]
- Keum, Y.T.; Jeong, J.H.; Auh, K.H. Finite-element simulation of ceramic drying processes. Model. Simul. Mater. Sci. Eng. 2000, 8, 541–556. [Google Scholar] [CrossRef]
- Keum, Y.T.; Oh, J.W. Finite element simulation of a ceramic drying process considering pore shape and porosity. Model. Simul. Mater. Sci. Eng. 2005, 13, 225–237. [Google Scholar] [CrossRef]
- Luikov, A.V. Heat and Mass Transfer in Capillary-Porous Bodies. Adv. Heat Transf. 1964, 1, 123–184. [Google Scholar] [CrossRef]
- Whitaker, S. Simultaneous Heat, Mass, and Momentum Transfer in Porous Media: A Theory of Drying. Adv. Heat Transf. 1977, 13, 119–203. [Google Scholar] [CrossRef]
- Silva, F.R.; Gonçalves, G.; Lenzi, M.K.; Lenzi, E.K. An extension of the linear Luikov system equations of heat and mass transfer. Int. J. Heat Mass Transf. 2013, 63, 233–238. [Google Scholar] [CrossRef]
- Liao, Q.; Chen, L.; Qu, X.; Jin, X. Brownian Dynamics Simulation of Film Formation of Mixed Polymer Latex in the Water Evaporation Stage. J. Colloid Interface Sci. 2000, 227, 84–94. [Google Scholar] [CrossRef]
- Reyes, Y.; Duda, Y. Modeling of drying in films of colloidal particles. Langmuir 2005, 21, 7057–7060. [Google Scholar] [CrossRef]
- Reyes, Y.; Campos-Terán, J.; Vázquez, F.; Duda, Y. Properties of films obtained from aqueous polymer dispersions: Study of drying rate and particle polydispersity effects. J. Phys. Condens. Matter 2007, 15, 355–368. [Google Scholar] [CrossRef]
- Fortini, A.; Martín-Fabiani, I.; de La Haye, J.L.; Dugas, P.Y.; Lansalot, M.; D’Agosto, F.; Bourgeat-Lami, E.; Keddie, J.L.; Sear, R.P. Dynamic Stratification in Drying Films of Colloidal Mixtures. Phys. Rev. Lett. 2016, 116, 118301. [Google Scholar] [CrossRef] [Green Version]
- Lebovka, N.I.; Vygornitskii, N.V.; Gigiberiya, V.A.; Tarasevich, Y.Y. Monte Carlo simulation of evaporation-driven self-assembly in suspensions of colloidal rods. Phys. Rev. E 2016, 94, 62803. [Google Scholar] [CrossRef] [Green Version]
- Lebovka, N.I.; Tarasevich, Y.Y.; Vygornitskii, N.V. Vertical drying of a suspension of sticks: Monte Carlo simulation for continuous two-dimensional problem. Phys. Rev. E 2018, 97, 022136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Y.; Grest, G.S.; Cheng, S. Stratification of drying particle suspensions: Comparison of implicit and explicit solvent simulations. J. Chem. Phys. 2019, 150, 224901. [Google Scholar] [CrossRef] [PubMed]
- Dietemann, B.; Bosna, F.; Kruggel-Emden, H.; Kraft, T.; Bierwisch, C. Assessment of Analytical Orientation Prediction Models for Suspensions Containing Fibers and Spheres. J. Compos. Sci. 2021, 5, 107. [Google Scholar] [CrossRef]
- Lorenz, M.; Dietemann, B.; Wahl, L.; Bierwisch, C.; Kraft, T.; Kruggel-Emden, H.; Travitzky, N. Influence of platelet content on the fabrication of colloidal gels for robocasting: Experimental analysis and numerical simulation. J. Eur. Ceram. Soc. 2020, 40, 811–825. [Google Scholar] [CrossRef]
- Rasband, W.S. imageJ. 2020. Available online: https://imagej.nih.gov/ij/ (accessed on 30 April 2020).
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford Science Publications; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angew. Math. 1881, 92, 156–171. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity: Second Revised and Enlarged Edition, 2nd ed.; Pergamon Press: Elmsford, NY, USA, 1970. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. An improved integral non-linear model for the contact of particles in distinct element simulations. Chem. Eng. Sci. 2005, 60, 1303–1312. [Google Scholar] [CrossRef]
- Luding, S. Shear flow modeling of cohesive and frictional fine powder. Powder Technol. 2005, 158, 45–50. [Google Scholar] [CrossRef]
- Luding, S. About contact force-laws for cohesive frictional materials in 2D and 3D. Behav. Granul. Media 2006, 9, 137–147. [Google Scholar]
- Zhou, Y.C.; Xu, B.H.; Yu, A.B.; Zulli, P. An experimental and numerical study of the angle of repos of coarse spheres. Powder Technol. 2002, 125, 45–54. [Google Scholar] [CrossRef]
- Richefeu, V.; Radjaï, F.; El Youssoufi, M.S. Stress transmission in wet granular materials. Eur. Phys. J. Soft Matter 2006, 21, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Dortmund Data Bank. Surface Tension of Water. Available online: http://www.ddbst.com/en/EED/PCP/SFT_C174.php (accessed on 30 March 2021).
- Vo, T.T.; Nezamabadi, S.; Mutabaruka, P.; Delenne, J.Y.; Radjai, F. Additive rheology of complex granular flows. Nat. Commun. 2020, 11, 1476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarray, A.; Magnanimo, V.; Luding, S. Wet granular flow control through liquid induced cohesion. Powder Technol. 2019, 341, 126–139. [Google Scholar] [CrossRef]
- Willett, C.D.; Adams, M.J.; Johnson, S.A.; Seville, J.P.K. Capillary Bridges between Two Spherical Bodies. Langmuir 2000, 16, 9396–9405. [Google Scholar] [CrossRef]
- Lian, G.; Thornton, C.; Adams, M.J. A Theoretical Study of the Liquid Bridge Forces between Two Rigid Spherical Bodies. J. Colloid Interface Sci. 1993, 161, 138–147. [Google Scholar] [CrossRef]
- Omelyan, I.P. On the numerical integration of motion for rigid polyatomics: The modified quaternion approach. J. Comput. Phys. 1998, 12, 97–103. [Google Scholar] [CrossRef] [Green Version]
- Omelyan, I.P. Algorithm for numerical integration of the rigid-body equations of motion. Phys. Rev. E 1998, 58, 1169–1172. [Google Scholar] [CrossRef] [Green Version]
- Dietemann, B.; Kraft, T.; Kruggel-Emden, H.; Bierwisch, C. A Smoothed Particle Hydrodynamics scheme for arbitrarily shaped rigid bodies within highly viscous fluids. J. Comput. Phys. X 2020, 8, 100068. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Kech, A.; Kugler, S.K.; Osswald, T.A. Significance of Model Parameter Variations in the pARD-RSC Model. J. Compos. Sci. 2020, 4, 109. [Google Scholar] [CrossRef]
- Kugler, S.K.; Dey, A.P.; Saad, S.; Cruz, C.; Kech, A.; Osswald, T.A. A Flow-Dependent Fiber Orientation Model. J. Compos. Sci. 2020, 4, 96. [Google Scholar] [CrossRef]
- Willems, F.; Reitinger, P.; Bonten, C. Calibration of Fiber Orientation Simulations for LFT—A New Approach. J. Compos. Sci. 2020, 4, 163. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Dalmont: Paris, France, 1856. [Google Scholar]
- Fu, Z.; Eckstein, U.; Dellert, A.; Roosen, A. In situ study of mass loss, shrinkage and stress development during drying of cast colloidal films. J. Eur. Ceram. Soc. 2015, 35, 2883–2893. [Google Scholar] [CrossRef]
- Fu, Z.; Roosen, A. Shrinkage of Tape Cast Products During Binder Burnout. J. Am. Ceram. Soc. 2015, 98, 20–29. [Google Scholar] [CrossRef]
- Fu, Z.; Polfer, P.; Kraft, T.; Roosen, A. Three-dimensional shrinkage behavior of green tapes derived from spherical-shaped powders: Experimental studies and numerical simulations. J. Eur. Ceram. Soc. 2015, 35, 2413–2425. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dietemann, B.; Wahl, L.; Travitzky, N.; Kruggel-Emden, H.; Kraft, T.; Bierwisch, C. Reorientation of Suspended Ceramic Particles in Robocasted Green Filaments during Drying. Materials 2022, 15, 2100. https://doi.org/10.3390/ma15062100
Dietemann B, Wahl L, Travitzky N, Kruggel-Emden H, Kraft T, Bierwisch C. Reorientation of Suspended Ceramic Particles in Robocasted Green Filaments during Drying. Materials. 2022; 15(6):2100. https://doi.org/10.3390/ma15062100
Chicago/Turabian StyleDietemann, Bastien, Larissa Wahl, Nahum Travitzky, Harald Kruggel-Emden, Torsten Kraft, and Claas Bierwisch. 2022. "Reorientation of Suspended Ceramic Particles in Robocasted Green Filaments during Drying" Materials 15, no. 6: 2100. https://doi.org/10.3390/ma15062100
APA StyleDietemann, B., Wahl, L., Travitzky, N., Kruggel-Emden, H., Kraft, T., & Bierwisch, C. (2022). Reorientation of Suspended Ceramic Particles in Robocasted Green Filaments during Drying. Materials, 15(6), 2100. https://doi.org/10.3390/ma15062100





