Correlation of Load-Bearing Behavior of Reinforced Concrete Members and Velocity Changes of Coda Waves
Abstract
:1. Introduction
2. Methods
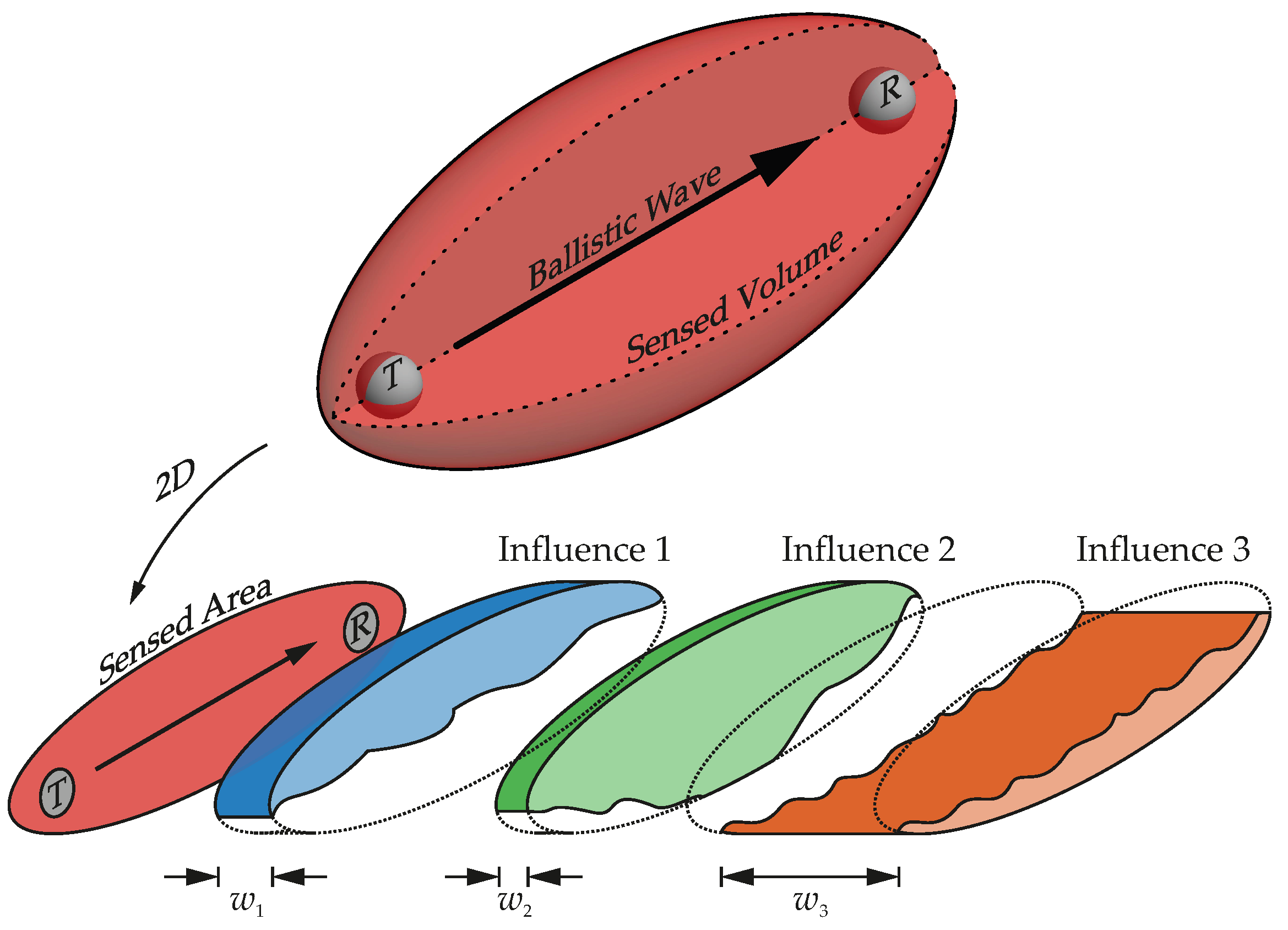
2.1. Sensing Structures with Ultrasound
2.1.1. General Aspects
- 1
- The low frequency range and stationary wave regime, where the wavelength is greater than the specimen itself. This regime is typically limited to .
- 2
- The single scattering regime where the wavelength is longer than the grains but smaller than the macroscopic size of the structure (). In this regime and , intrinsic absorption can be neglected since .
- 3
- The multiple scattering regime ( where but intrinsic absorption does not dominate signal spreading).
- 4
- The attenuative regime with where scattering and intrinsic absorption prevent elastic waves from significant spreading.
2.1.2. The CWI-Method
2.2. Load-Bearing Behavior of Flexural RC Members
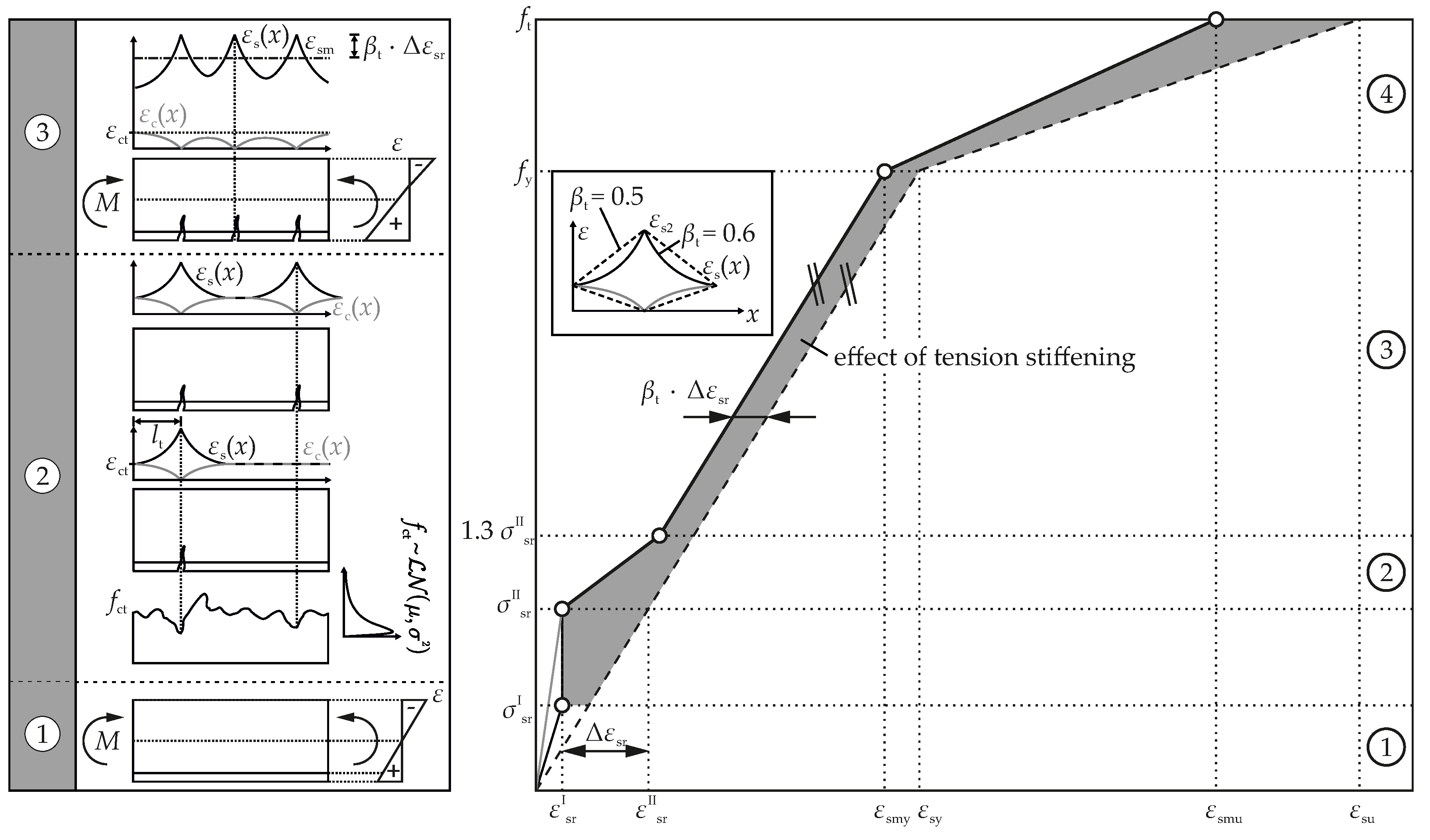
2.2.1. Phenomenological Characterization of RC
2.2.2. Intermediate Resume
2.2.3. Computational Approach
3. Experiments
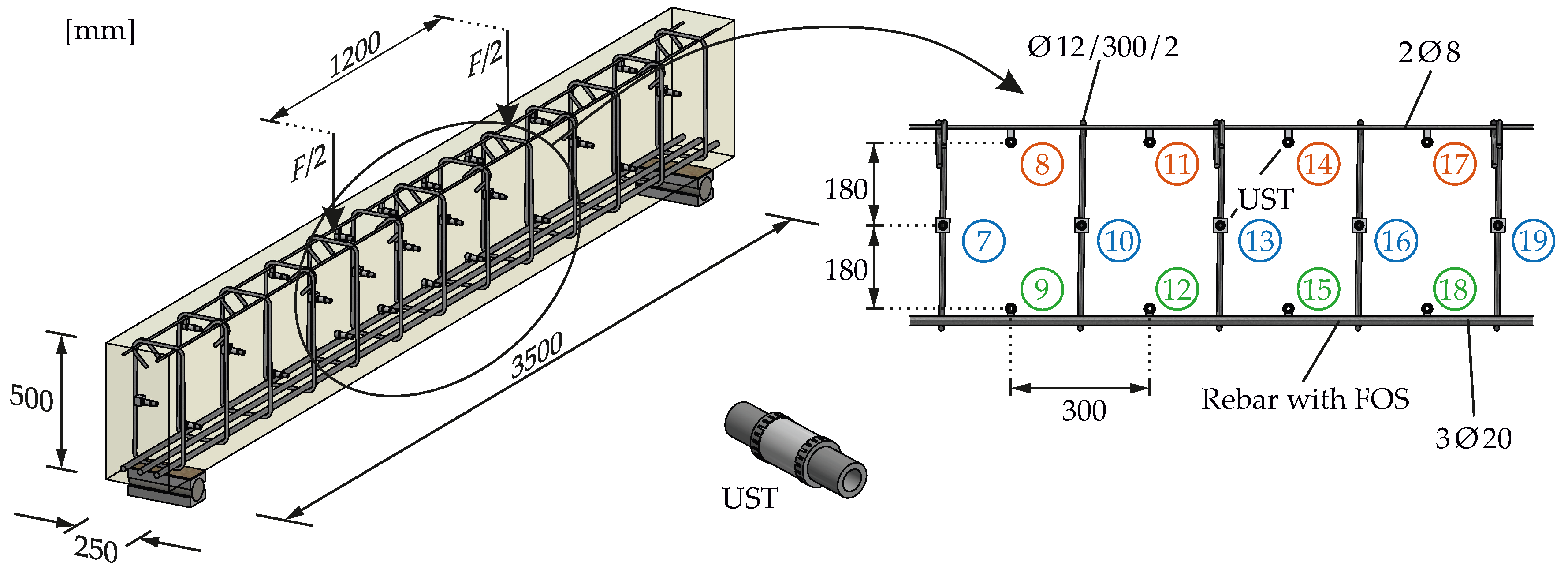
3.1. Experimental Setup
3.2. Placement of Measuring Equipment
3.3. Concreting and Curing
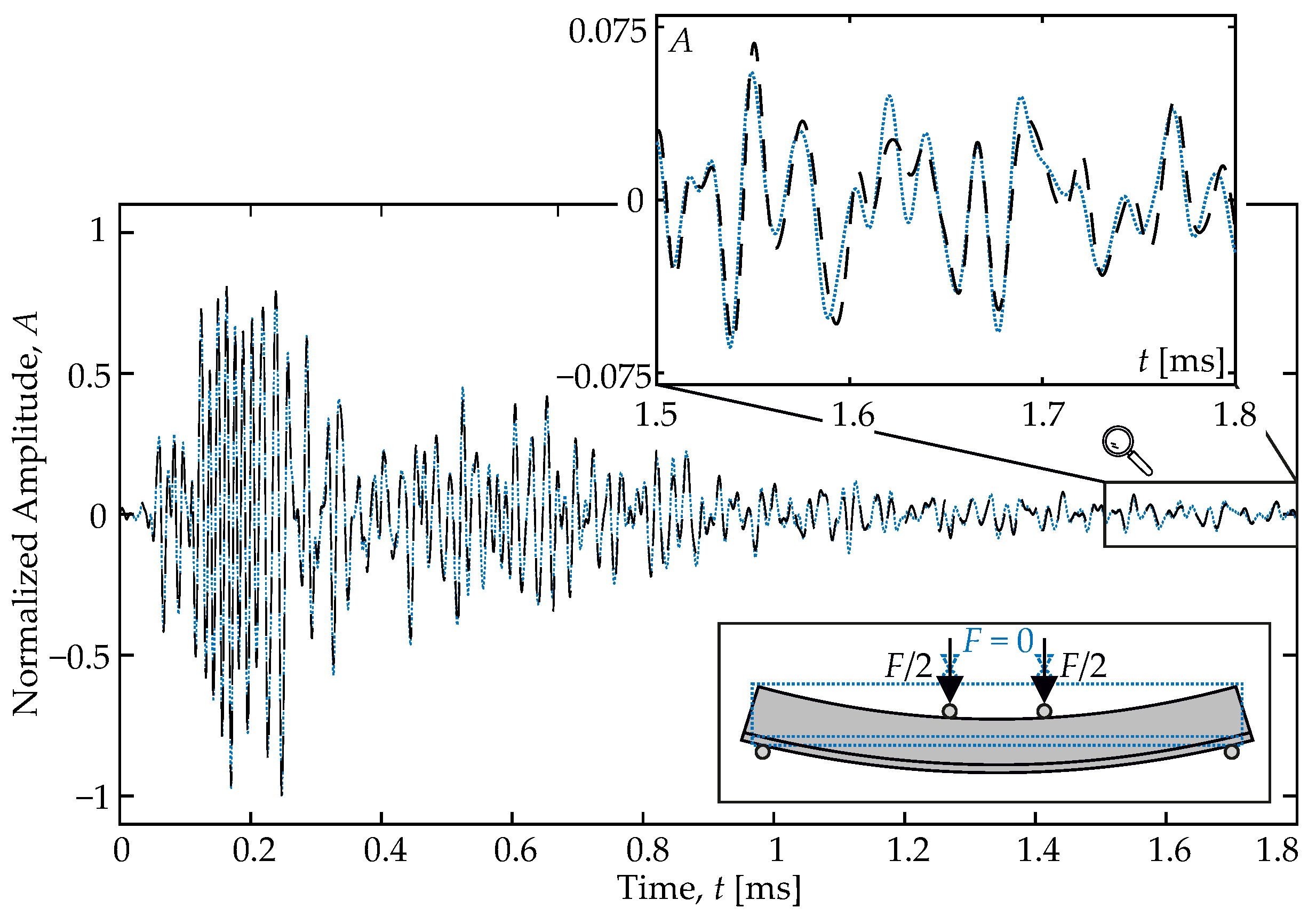
3.4. Load Control
3.5. Proof of Concept
4. Results and Discussion
4.1. Development of the Relative Velocity Change with Time and Load
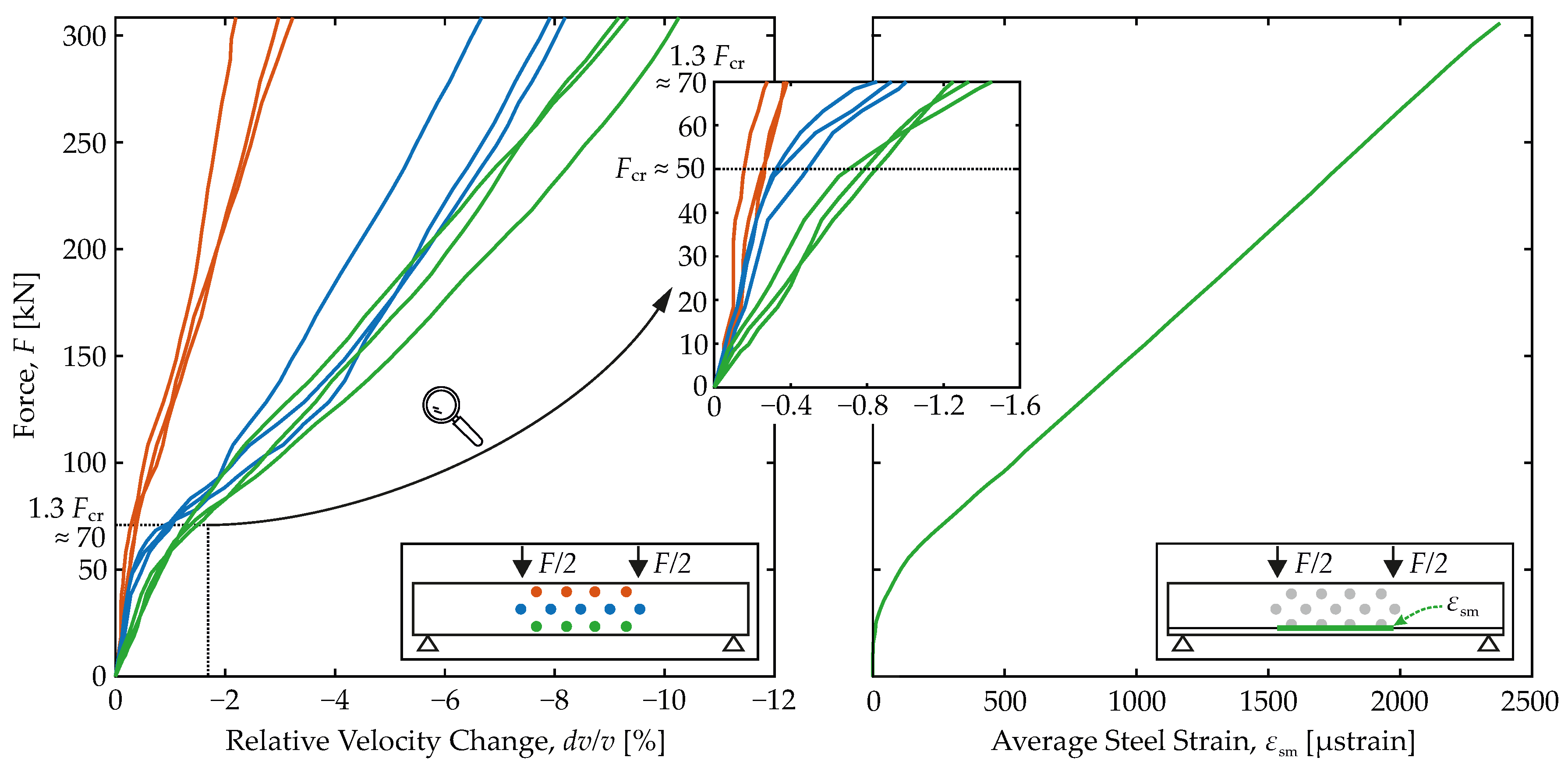
- 1
- Cracking strongly affects the US signal and the key quantities computed with CWI, the correlation coefficient and the relative velocity change .
- 2
- The relative velocity change is always negative.
- 3
- Characteristic points associated with significant changes in the material response and can be identified in the F- relation, too.
- 4
- A fundamental change of the load-bearing behavior happens in the range of cracking ➁ and is also predicted by the F- relation.
- 5
- In agreement with the decreasing slope of the - relation, the slope of the F- relation decreases in transition from the non-cracked to the cracked state.
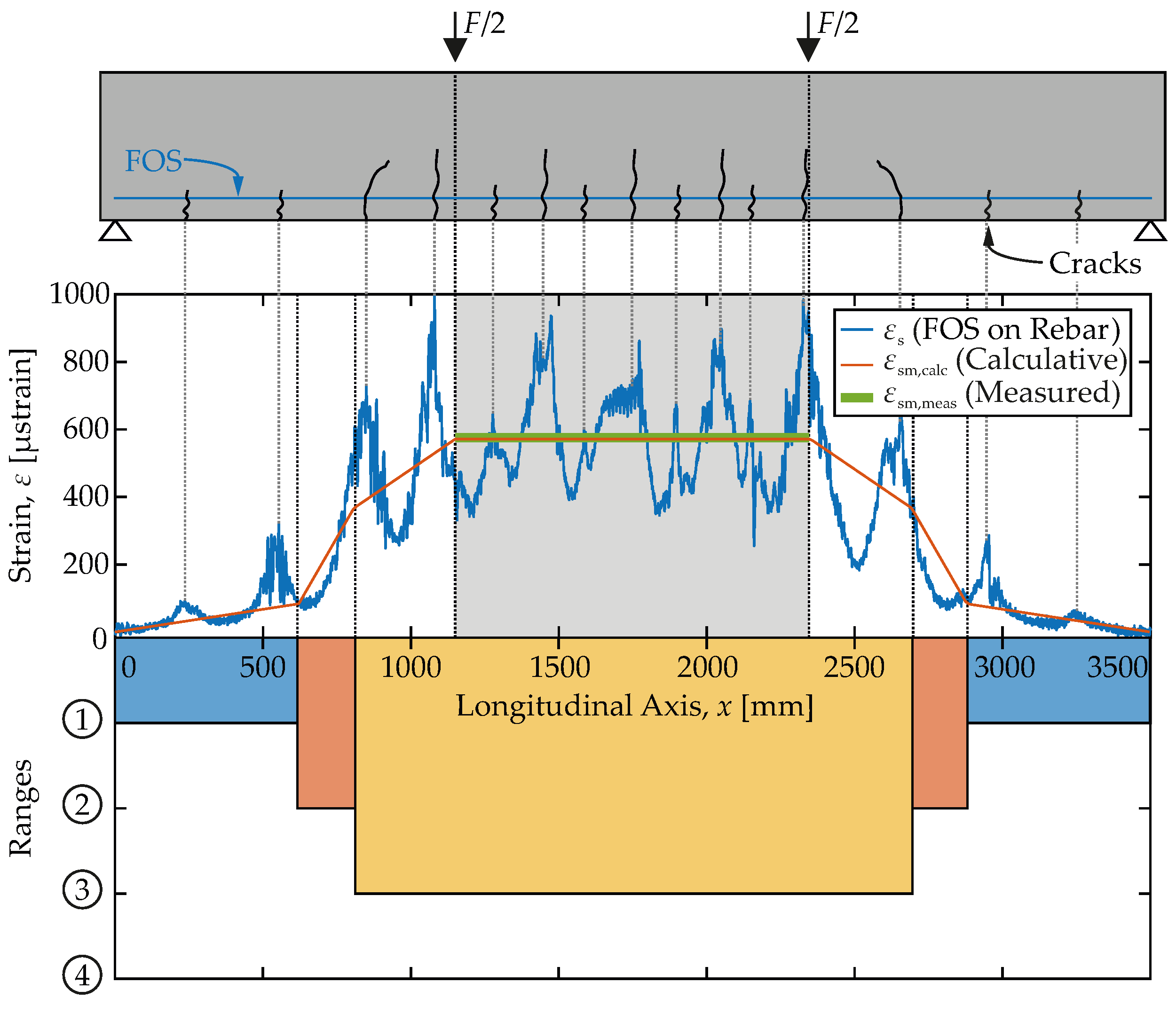
- 1
- The closer a sensor pair is located to the tensile zone, the more the relative velocity change drops.
- 2
- With load increase, cracks gradually grow towards the compressive zone at top. This is well-reflected by the trend of the central axis’ gradient towards the tensile one. As the cracks approach the centerline transducers, the US signal is affected more like the signal in the tensile zone.
- 3
- Not even in the non-cracked state with linear elastic material behavior, the central trend is the average of compressive and tensile trends. Thus, the relative velocity change develops non-linear with the load.
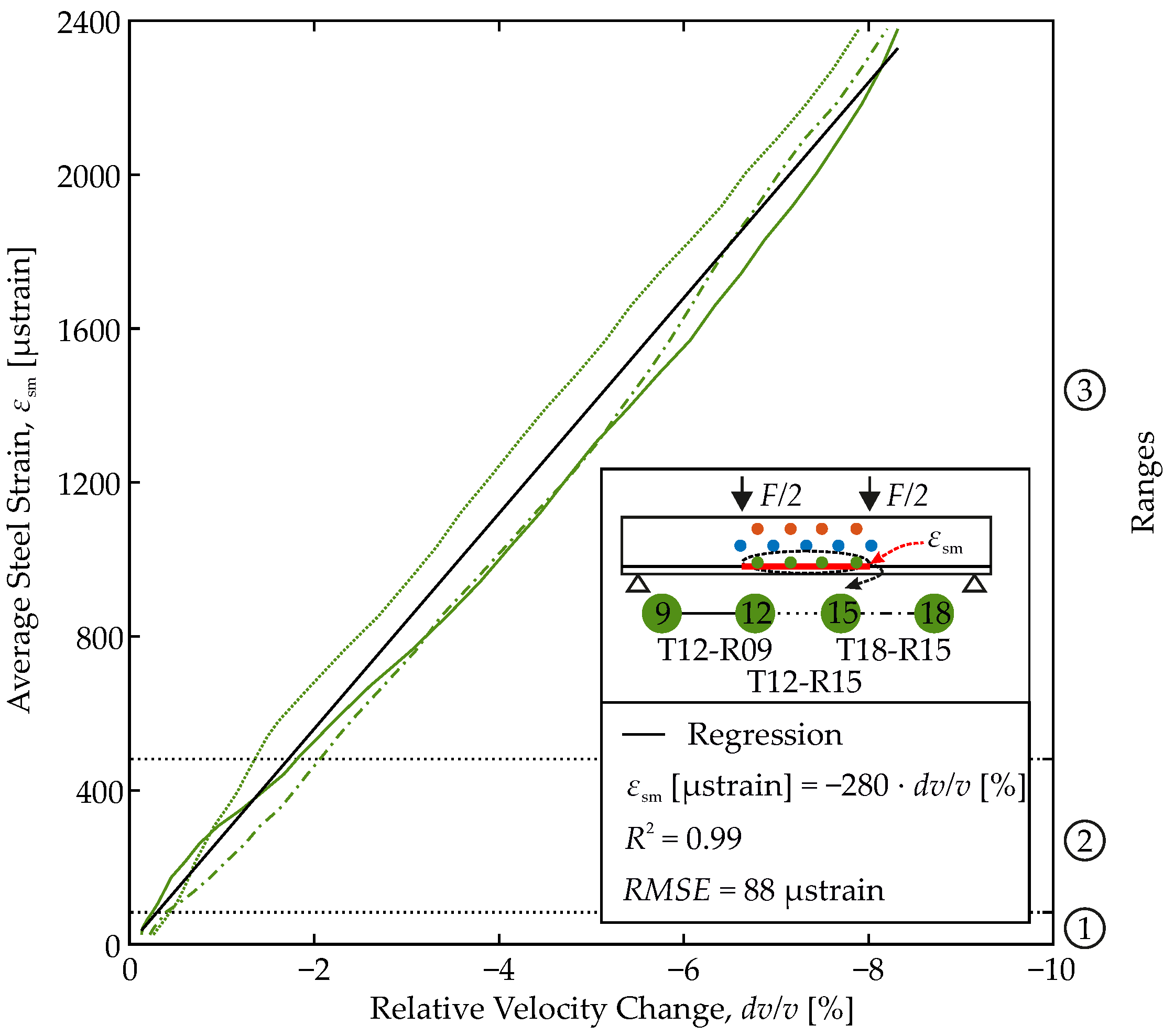
4.2. Establishing a Correlation Function
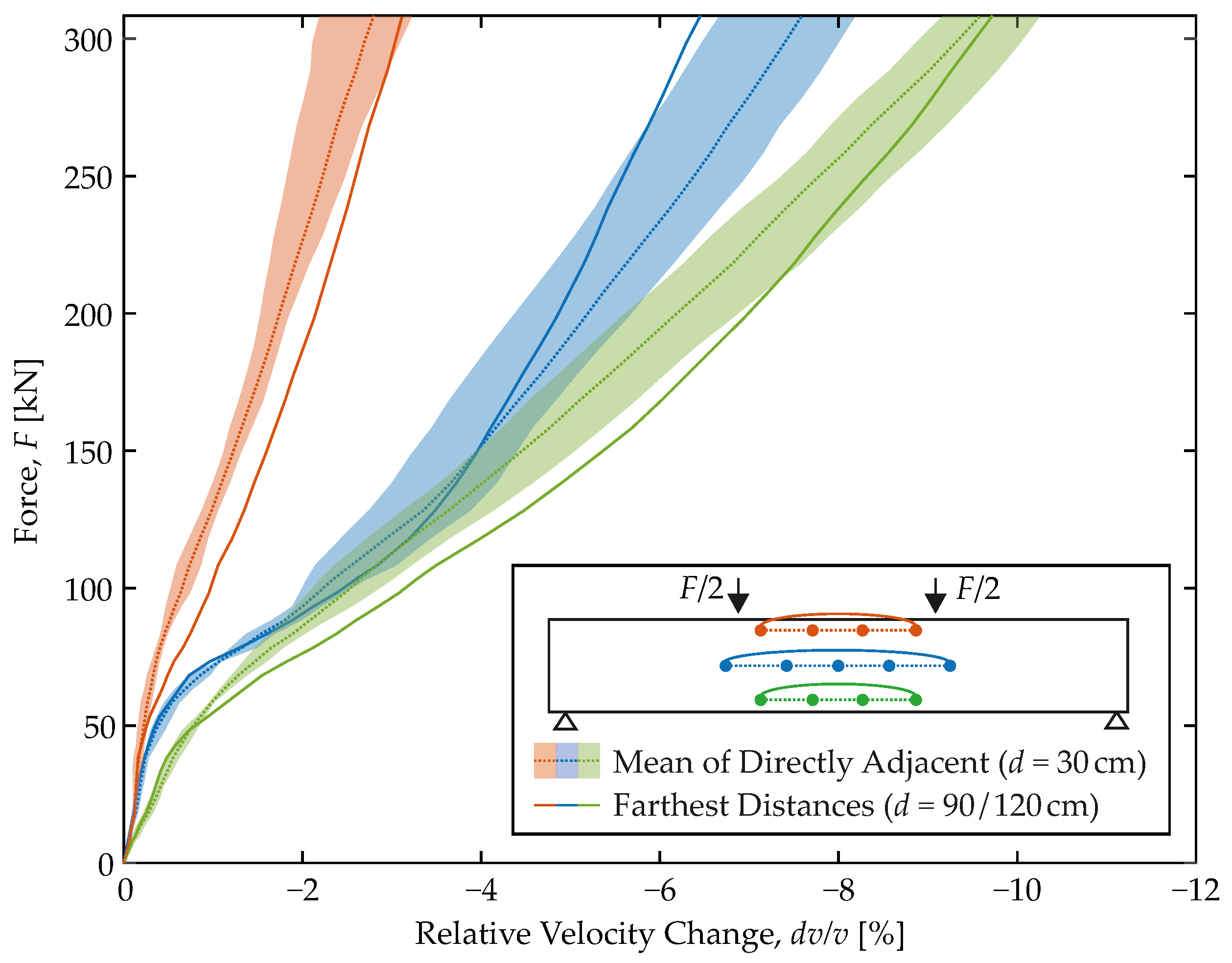
4.3. Impact of the Transducer Distance
5. Conclusions
- For the first time, a correlation between a key parameter of ultrasound and a structural state variable is established that covers 90% of the complex load-bearing behavior of RC members. It integrates load-dependent stiffness and concrete cracking.
- For the beam and a sensor distance of 30 cm, a linear model is established with great confidence: with: strain.
- Tripled sensor distances do not impair the proposed correlation function much.
- Whether in compression or tension, obtained from step-wise CWI is found to be negative throughout.
- The closer a sensor pair is located to the tensile zone, the more drops.
- Although always integrates elastic effects as well as micro- and macro-cracking, the latter seems to dominate. Compared to the compressive zone, is more sensitive to changes in the tensile zone.
- Conversely, changes in the compressive zone are more difficult to detect because they are easily superimposed by tension.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FOS | Fiber Optic Sensor |
| US | Ultrasonic |
| RC | Reinforced Concrete |
| NDT | Non-Destructive Testing |
| CWI | Coda Wave Interferometry |
References
- Deutsches Institut für Normung e.V. DIN 1076:1999-11: Engineering Structures in Connection with Roads—Inspection and Test; Beuth Verlag: Berlin, Germany, 1999. [Google Scholar] [CrossRef]
- Stojić, D.; Nestorović, T.; Marković, N.; Marjanović, M. Experimental and numerical research on damage localization in plate-like concrete structures using hybrid approach. Struct. Control. Health Monit. 2018, 25. [Google Scholar] [CrossRef]
- Naraniecki, H.; Hartung, R.; Marx, S.; Klemt-Albert, K. Condition state prediction of engineering structures based on digital twins and inspection data. Bautechnik 2021. [Google Scholar] [CrossRef]
- Zhong, B.; Zhu, J.; Morcous, G. Measuring acoustoelastic coefficients for stress evaluation in concrete. Constr. Build. Mater. 2021, 309, 125127. [Google Scholar] [CrossRef]
- Bayoumi, A.; Minten, T.; Mueller, I. Determination of Detection Probability and Localization Accuracy for a Guided Wave-Based Structural Health Monitoring System on a Composite Structure. Appl. Mech. 2021, 2, 996–1008. [Google Scholar] [CrossRef]
- Fischer, O.; Müller, A.; Lechner, T.; Wild, M.; Kessner, K. Findings and insights concerning the results of re-analyzed concrete bridges in Germany. Beton- Stahlbetonbau 2014, 109, 107–127. [Google Scholar] [CrossRef]
- Wiggenhauser, H.; Niederleithinger, E.; Milmann, B. Nondestructive testing of thick and highly reinforced concrete structures with ultrasound. Bautechnik 2017, 94, 682–688. [Google Scholar] [CrossRef]
- Zeman, O.; Schwenn, M.; Granig, M.; Bergmeister, K. Assessment of the Deterioration State of Post-Installed Bonded Anchors Using Ultrasonic. Materials 2021, 14, 2077. [Google Scholar] [CrossRef] [PubMed]
- Larose, É.; Hall, S.A. Monitoring stress related velocity variation in concrete with a 2.10-5 relative resolution using diffuse ultrasound. J. Acoust. Soc. Am. 2009, 125, 1853–1856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lillamand, I.; Chaix, J.F.; Ploix, M.A.; Garnier, V. Acoustoelastic effect in concrete material under uni-axial compressive loading. NDT E Int. 2010, 43, 655–660. [Google Scholar] [CrossRef]
- Stähler, S.C.; Sens-Schönfelder, C.; Niederleithinger, E. Monitoring stress changes in a concrete bridge with coda wave interferometry. J. Acoust. Soc. Am. 2011, 129, 1945–1952. [Google Scholar] [CrossRef] [Green Version]
- Planès, T.; Larose, E. A review of ultrasonic Coda Wave Interferometry in concrete. Cem. Concr. Res. 2013, 53, 248–255. [Google Scholar] [CrossRef]
- Niederleithinger, E.; Sens-Schönfelder, C.; Grothe, S.; Wiggenhauser, H. Coda Wave Interferometry Used to Localize Compressional Load Effects in a Concrete Specimen. In Proceedings of the EWSHM—7th European Workshop on Structural Health Monitoring, Nntes, France, 8–11 July 2014; Le Cam, V., Mevel, L., Schoefs, F., Eds.; IFFSTTAR; Inria; Université de Nantes: Nntes, France, 2014. [Google Scholar]
- Hafiz, A.; Schumacher, T. Monitoring of Stresses in Concrete Using Ultrasonic Coda Wave Comparison Technique. J. Nondestruct. Eval. 2018, 37, 1691. [Google Scholar] [CrossRef]
- Zhang, Y.; Abraham, O.; Grondin, F.; Loukili, A.; Tournat, V.; Le Duff, A.; Lascoup, B.; Durand, O. Study of stress-induced velocity variation in concrete under direct tensile force and monitoring of the damage level by using thermally-compensated Coda Wave Interferometry. Ultrasonics 2012, 52, 1038–1045. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Abraham, O.; Tournat, V.; Le Duff, A.; Lascoup, B.; Loukili, A.; Grondin, F.; Durand, O. Validation of a thermal bias control technique for Coda Wave Interferometry (CWI). Ultrasonics 2013, 53, 658–664. [Google Scholar] [CrossRef] [Green Version]
- Niederleithinger, E.; Wunderlich, C. Influence of small temperature variations on the ultrasonic velocity in concrete. AIP Conf. Proc. 2013, 1511, 390–397. [Google Scholar] [CrossRef]
- Epple, N.; Barroso, D.F.; Niederleithinger, E. Towards Monitoring of Concrete Structures with Embedded Ultrasound Sensors and Coda Waves—First Results of DFG for CoDA. In Proceedings of the European Workshop on Structural Health Monitoring, EWSHM 2020, Palermo, Italy, 6–9 July 2020; Volume 127, pp. 266–275. [Google Scholar] [CrossRef]
- Grêt, A.; Snieder, R.; Scales, J. Time-lapse monitoring of rock properties with coda wave interferometry. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Ju, T.; Li, S.; Achenbach, J.; Qu, J. Effects of moisture on ultrasound propagation in cement mortar. AIP Conf. Proc. 2015, 1650, 1409–1414. [Google Scholar] [CrossRef]
- Legland, J.B.; Théry, R.; Abraham, O.; Villain, G.; Durnad, O.; Larose, E.; Tournat, V. Influence of moisture on the estimation of nonlinear parameters in concrete with Nonlinear ultrasonic Coda Wave Interferometry. In Proceedings of the 12th European Conference on Non-Destructive Testing (ECNDT 2018), Gothenburg, Sweden, 11–15 June 2019. [Google Scholar]
- Masera, D.; Bocca, P.; Grazzini, A. Coda Wave Interferometry Method Applied in Structural Monitoring to Assess Damage Evolution in Masonry and Concrete Structures. J. Phys. Conf. Ser. 2011, 305, 012108. [Google Scholar] [CrossRef] [Green Version]
- Schurr, D.P.; Kim, J.Y.; Sabra, K.G.; Jacobs, L.J. Damage detection in concrete using coda wave interferometry. NDT E Int. 2011, 44, 728–735. [Google Scholar] [CrossRef]
- Larose, E.; Obermann, A.; Digulescu, A.; Planès, T.; Chaix, J.F.; Mazerolle, F.; Moreau, G. Locating and characterizing a crack in concrete with diffuse ultrasound: A four-point bending test. J. Acoust. Soc. Am. 2015, 138, 232–241. [Google Scholar] [CrossRef] [PubMed]
- Niederleithinger, E.; Herbrand, M.; Müller, M. Monitoring of shear tests on prestressed concrete continuous beams using ultrasound and coda wave interferometry. Bauingenieur 2017, 92, 474–481. [Google Scholar] [CrossRef]
- Grabke, S.; Clauß, F.; Bletzinger, K.U.; Ahrens, M.A.; Mark, P.; Wüchner, R. Damage Detection at a Reinforced Concrete Specimen with Coda Wave Interferometry. Materials 2021, 14, 5013. [Google Scholar] [CrossRef] [PubMed]
- Mark, P.; Schnütgen, B. Limits of Elastic Material Behaviour of Concrete. Beton- Stahlbetonbau 2001, 96, 373–378. [Google Scholar] [CrossRef]
- Clauß, F.; Epple, N.; Ahrens, M.A.; Niederleithinger, E.; Mark, P. Comparison of Experimentally Determined Two-Dimensional Strain Fields and Mapped Ultrasonic Data Processed by Coda Wave Interferometry. Sensors 2020, 20, 4023. [Google Scholar] [CrossRef]
- Quast, U. Zur Mitwirkung des Betons in der Zugzone. Beton- Stahlbetonbau 1981, 76, 247–250. [Google Scholar] [CrossRef]
- Pfeiffer, U. Die Nichtlineare Berechnung Ebener Rahmen aus Stahl- oder Spannbeton mit Berücksichtigung der Durch das Aufreißen Bedingten Achsendehnung. Ph.D. Thesis, Technische Universität Hamburg-Harburg, Hamburg, Germany, 2004. (In German). [Google Scholar]
- DAfStb. DAfStb-Heft 630 Bemessung nach DIN EN 1992 in den Grenzzuständen der Tragfähigkeit und der Gebrauchstauglichkeit; DAfStb-Heft; Beuth Verlag: Berlin, Germany, 2018. (In German) [Google Scholar]
- Zilch, K.; Zehetmaier, G. Bemessung im Konstruktiven Betonbau; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Scherr, J.F.; Grosse, C.U. Delamination detection on a concrete bridge deck using impact echo scanning. Struct. Concr. 2021, 22, 806–812. [Google Scholar] [CrossRef]
- Carino, N.J. The Impact-Echo Method: An Overview; Structures 2001; Chang, P.C., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 1–18. [Google Scholar] [CrossRef] [Green Version]
- Committee, A. Report on Nondestructive Test Methods for Evaluation of Concrete in Structures; American Concrete Institute: Farming Hills, MI, USA, 2013. [Google Scholar]
- Agency, I.A.E. Guidebook on Non-Destructive Testing of Concrete Structures; IAEA: Vienna, Austria, 2002. [Google Scholar]
- Schabowicz, K. Non-Destructive Testing of Materials in Civil Engineering. Materials 2019, 12, 3237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aki, K. Correlogram Analyses of Seismograms by Means of a Simple Automatic Computer. J. Phys. Earth 1956, 4, 71–79. [Google Scholar] [CrossRef]
- Poupinet, G.; Ellsworth, W.; Frechet, J. Monitoring velocity variations in the crust using earthquake doublets: An application to the Calaveras Fault, California. J. Geophys. Res. Solid Earth 1984, 89, 5719–5731. [Google Scholar] [CrossRef] [Green Version]
- Snieder, R. Coda wave interferometry and the equilibration of energy in elastic media. Phys. Rev. E 2002, 66, 046615. [Google Scholar] [CrossRef] [Green Version]
- Larose, E.; de Rosny, J.; Margerin, L.; Anache, D.; Gouedard, P.; Campillo, M.; van Tiggelen, B. Observation of multiple scattering of kHz vibrations in a concrete structure and application to monitoring weak changes. Phys. Rev. E 2006, 73, 016609. [Google Scholar] [CrossRef]
- Zhang, Y.; Planès, T.; Larose, E.; Obermann, A.; Rospars, C.; Moreau, G. Diffuse ultrasound monitoring of stress and damage development on a 15-ton concrete beam. J. Acoust. Soc. Am. 2016, 139, 1691–1701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niederleithinger, E.; Wang, X.; Herbrand, M.; Müller, M. Processing Ultrasonic Data by Coda Wave Interferometry to Monitor Load Tests of Concrete Beams. Sensors 2018, 18, 1971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Chakraborty, J.; Bassil, A.; Niederleithinger, E. Detection of Multiple Cracks in Four-Point Bending Tests Using the Coda Wave Interferometry Method. Sensors 2020, 20, 1986. [Google Scholar] [CrossRef] [Green Version]
- Xue, Q.; Larose, E.; Moreau, L.; Thery, R.; Abraham, O.; Jean-Marie, H. Ultrasonic monitoring of stress and cracks of the 1/3 scale mock-up of nuclear reactor concrete containment structure. Struct. Health Monit. 2021. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite Deformations of an Elastic Solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
- Toupin, R.; Bernstein, B. Sound waves in deformed perfectly elastic materials. Acoustoelastic effect. J. Acoust. Soc. Am. 1961, 33, 216–225. [Google Scholar] [CrossRef]
- Zilch, K.; Rogge, A. Bemessung von Stahlbeton- und Spannbetonbauteilen im Brücken- und Hochbau. In Beton-Kalender; Volume 2; Ernst & Sohn: Berlin, Germany. (In German)
- Joint Commitee On Structural Safety. JCSS Probabilistic Model Code.
- Heek, P. Modellbildung und Numerische Analysen zur Ermüdung von Stahlfaserbeton. Ph.D. Thesis, Shaker Verlag, Aachen, Germany, 2018. (In German). [Google Scholar]
- König, G.; Tue, N.V. Grundlagen und Bemessungshilfen für die Rißbreitenbeschränkung im Stahlbeton und Spannbeton sowie Kommentare, Hintergrundinformationen und Anwendungsbeispiele zu den Regelungen nach DIN 1045, EC2 und Model Code 90. In Deutscher Ausschuß für Stahlbeton; Beuth: Berlin, Germany, 1996; Volume 466. (In German) [Google Scholar]
- Winkler, K.; Mark, P.; Heek, P.; Rohländer, S.; Sommer, S. Punching shear tests on symmetrically reduced slab quarters. Struct. Concr. 2014, 15, 484–496. [Google Scholar] [CrossRef]
- Löschmann, J.; Clauß, F.; Mark, P. Strengthening of reinforced concrete structures with temperature induction. Beton- Stahlbetonbau 2020, 115, 746–757. [Google Scholar] [CrossRef]
- Löschmann, J.; Stolzuoli, N.; Ahrens, M.A.; Mark, P. Steering of continuity stresses in beam structures by temperature induction. Eng. Struct. 2021, 229, 111621. [Google Scholar] [CrossRef]
- Henke, V.; Empelmann, M. Crack Width Limitation for Combined Reinforcement. Beton- Stahlbetonbau 2007, 102, 66–79. (In German) [Google Scholar] [CrossRef]
- Heek, P.; Tkocz, J.; Mark, P. A thermo-mechanical model for SFRC beams or slabs at elevated temperatures. Mater. Struct. 2018, 51, 78. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung e.V. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; German Version EN 1992-1-1:2004 + AC:2010; Beuth Verlag: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Wolf, J.; Niederleithinger, E.; Mielentz, F.; Grothe, S.; Wiggenhauser, H. Monitoring of concrete constructions by embedded ultrasonic sensors. Bautechnik 2014, 91, 783–796. [Google Scholar] [CrossRef]
- Niederleithinger, E.; Wolf, J.; Mielentz, F.; Wiggenhauser, H.; Pirskawetz, S. Embedded ultrasonic transducers for active and passive concrete monitoring. Sensors 2015, 15, 9756. [Google Scholar] [CrossRef] [Green Version]
- Clauß, F.; Ahrens, M.A.; Mark, P. A Comparative Evaluation of Strain Measurement Techniques in Reinforced Concrete Structures—A Discussion of Assembly, Application, and Accuracy. Struct. Concr. 2021, 22, 2992–3007. [Google Scholar] [CrossRef]
- Konertz, D.; Löschmann, J.; Clauß, F.; Mark, P. Fiber optic sensing of strain and temperature fields. Bauingenieur 2019, 94, 292–300. [Google Scholar] [CrossRef]

| 33.0 | 2.8 | 28,800 | 552.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clauß, F.; Epple, N.; Ahrens, M.A.; Niederleithinger, E.; Mark, P. Correlation of Load-Bearing Behavior of Reinforced Concrete Members and Velocity Changes of Coda Waves. Materials 2022, 15, 738. https://doi.org/10.3390/ma15030738
Clauß F, Epple N, Ahrens MA, Niederleithinger E, Mark P. Correlation of Load-Bearing Behavior of Reinforced Concrete Members and Velocity Changes of Coda Waves. Materials. 2022; 15(3):738. https://doi.org/10.3390/ma15030738
Chicago/Turabian StyleClauß, Felix, Niklas Epple, Mark Alexander Ahrens, Ernst Niederleithinger, and Peter Mark. 2022. "Correlation of Load-Bearing Behavior of Reinforced Concrete Members and Velocity Changes of Coda Waves" Materials 15, no. 3: 738. https://doi.org/10.3390/ma15030738
APA StyleClauß, F., Epple, N., Ahrens, M. A., Niederleithinger, E., & Mark, P. (2022). Correlation of Load-Bearing Behavior of Reinforced Concrete Members and Velocity Changes of Coda Waves. Materials, 15(3), 738. https://doi.org/10.3390/ma15030738






