Thermal Insulation and Compressive Performances of 3D Printing Flexible Load-Bearing and Thermal Insulation Integrated Lattice
Abstract
1. Introduction
2. Materials and Methods
2.1. BWR Lattice Structures
2.2. Materials
2.3. Additive Manufacturing Process
2.4. Characterizations
3. Results
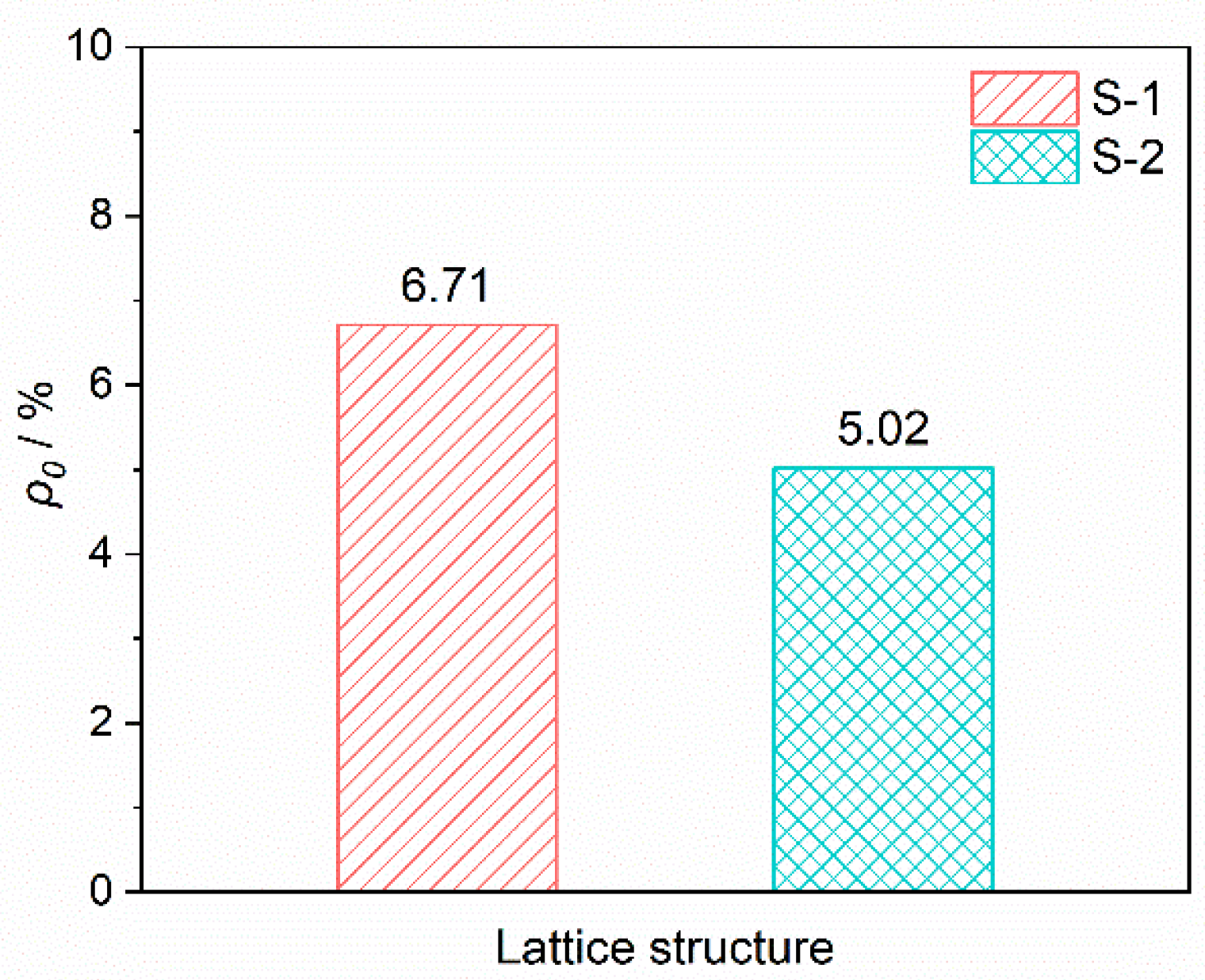
3.1. Relative Density
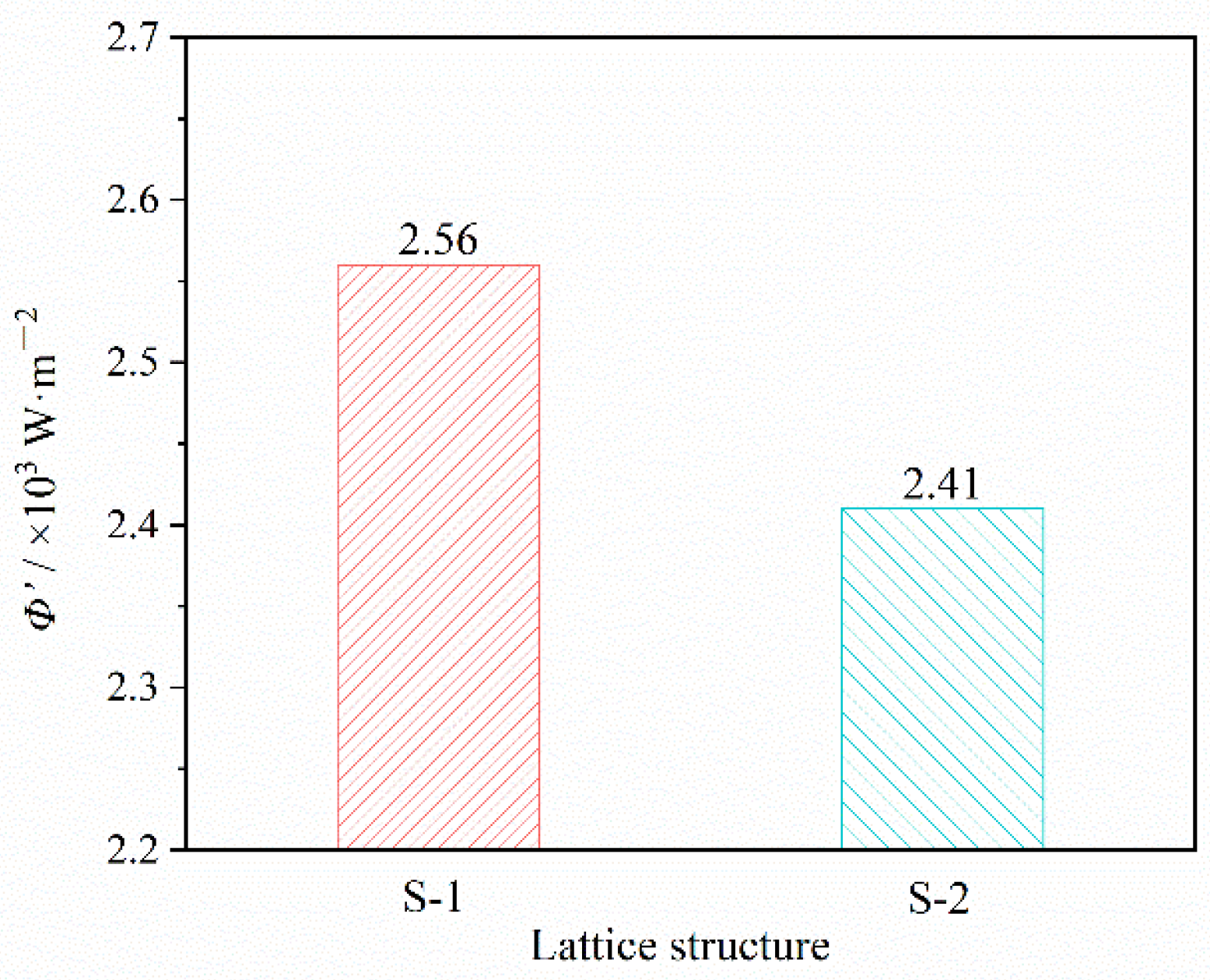
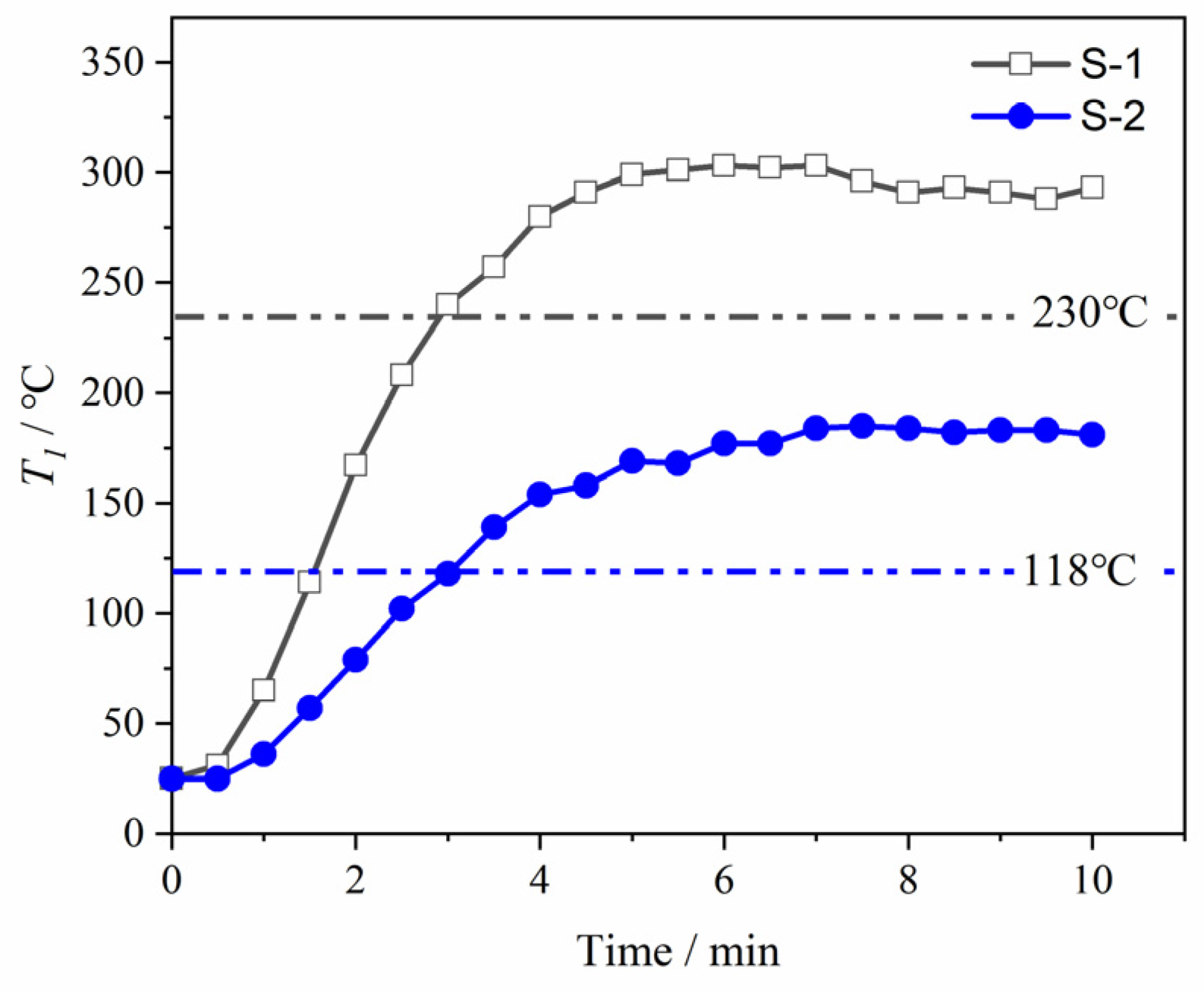
3.2. Thermal Insulation Performance
3.3. Compressive Performance
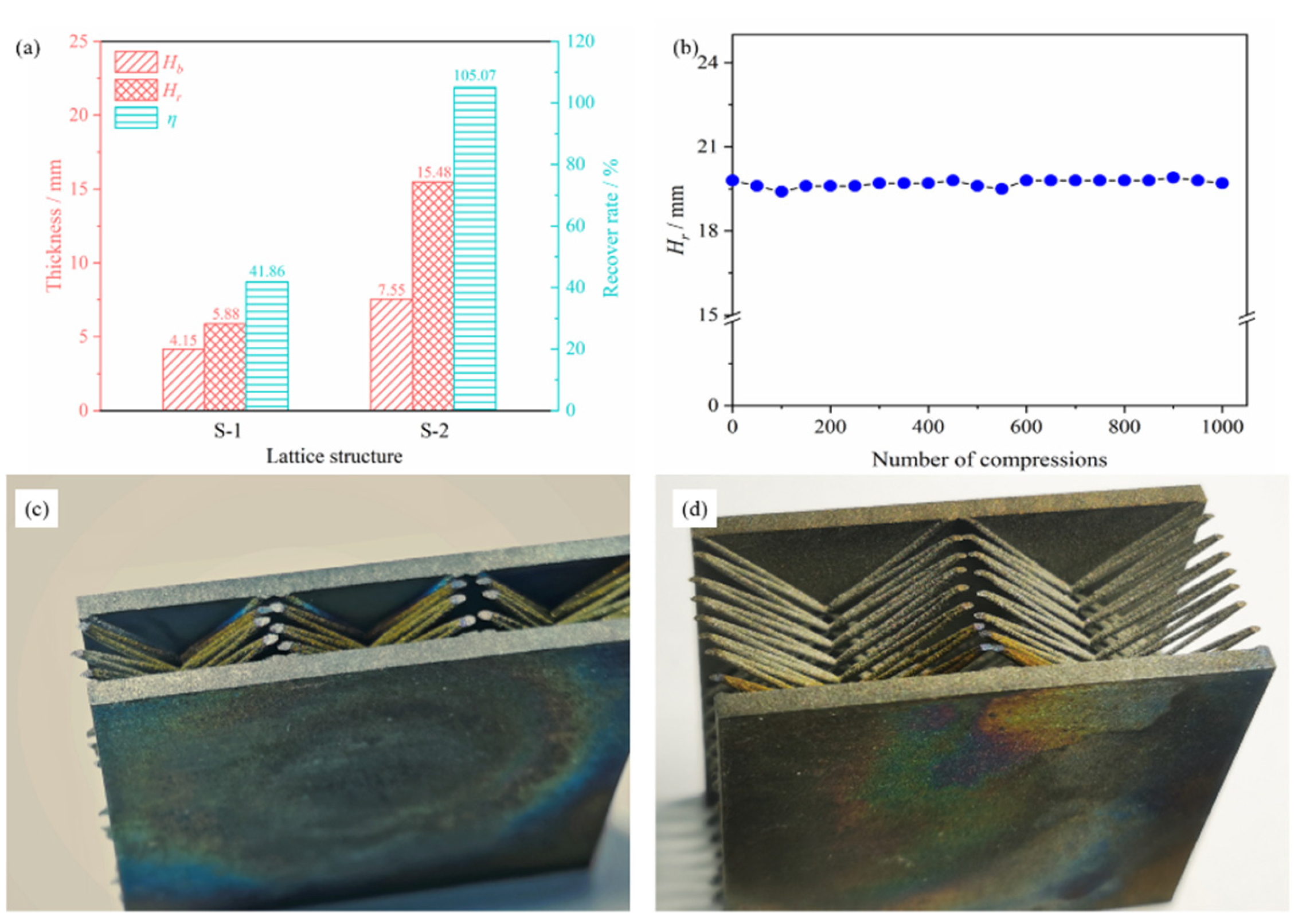
3.4. Cycle Resilient Performance
4. Discussions
4.1. Thermal Transfer Process of the BWR Lattice
4.1.1. Calculations of Thermal Flow and Equivalent Coefficient of Thermal Conductivity
4.1.2. Analysis of Thermal Insulation Performance
4.2. Resilient Performance of the BWR Lattice
4.2.1. Resilient Mechanism
4.2.2. Influence of Compressive Failure on Thermal Insulation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, D.; Yue, K.; Cheng, L.; Yang, X.; Zhang, X. Measurement of the thermophysical properties of anisotropic insulation materials with consideration of the effect of thermal contact resistance. Materials 2020, 13, 1353. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Wang, Y.; Gao, Z.; Yang, J. Insulation performance of heat-resistant material for high-speed aircraft under thermal environments. J. Mater. Eng. Perform. 2015, 24, 3373–3385. [Google Scholar] [CrossRef]
- Huang, Y.; Azarmi, F.; Jazi, M.S. Innovative insulations for spacecraft on-surface monitoring system in harsh environments. In Proceedings of the Conference on Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, SPIE, San Diego, CA, USA, 8–12 March 2015. [Google Scholar]
- Hou, C.; Yang, G.; Wan, X.; Chen, J. Study of thermo-fluidic characteristics for geometric-anisotropy Kagome truss-cored lattice. Chin. J. Aeronaut. 2019, 32, 1635–1645. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, Z.; Yan, N. Effect of insulation core type on thermal conductivity of sandwich structure. J. Compos. Mater. 2017, 52, 2273–2280. [Google Scholar] [CrossRef]
- Wang, X.; Wei, K.; Tao, Y.; Yang, X.; Zhou, H.; He, R.; Fang, D. Thermal protection system integrating graded insulation materials and multilayer ceramic matrix composite cellular sandwich panels. Compos. Struct. 2019, 209, 523–534. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Trupiano, S.; Vivio, F. Multiscale analysis and mechanical characterization of open-cell foams by simplified FE modeling. Eur. J. Mech.-A Solids 2021, 89, 104291. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; McMillan, M.; Elambasseril, J.; Brandt, M. SLM additive manufacture of H13 tool steel with conformal cooling and structural lattices. Rapid Prototyp. J. 2016, 22, 504–518. [Google Scholar] [CrossRef]
- Evans, A.; Hutchinson, J.; Ashby, M. Multifunctionality of cellular metal systems. Prog. Mater. Sci. 1998, 43, 171–221. [Google Scholar] [CrossRef]
- Wicks, N.; Hutchinson, J.W. Optimal truss plates. Int. J. Solids Struct. 2001, 38, 5165–5183. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Zhao, Y.; He, R.; Ai, S.; Tang, L.; Fang, D. Mechanical behaviors of C/SiC pyramidal lattice core sandwich panel under in-plane compression. Compos. Struct. 2019, 214, 103–113. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Liu, F.; Li, Z.H.; Ma, Z.B.; Ren, Z.H. Mechanical and energy absorption characteristics of additively manufactured functionally graded sheet lattice structures with minimal surfaces. Int. J. Mech. Sci. 2020, 167, 105262. [Google Scholar] [CrossRef]
- Liu, J.; Kanwal, H.; Tang, C.; Hao, W. Study on flexural properties of 3D printed lattice-reinforced concrete structures using acoustic emission and digital image correlation. Constr. Build. Mater. 2022, 333, 127418. [Google Scholar] [CrossRef]
- Tao, Y.; Li, P.; Zhang, H.; Shi, S.Q.; Zhang, J.; Yin, Q. Compression and flexural properties of rigid polyurethane foam composites reinforced with 3D-printed polylactic acid lattice structures. Compos. Struct. 2022, 279, 114866. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, N.; Zhang, W.; Zhu, J. A multi-layer integrated thermal protection system with C/SiC composite and Ti alloy lattice sandwich. Compos. Struct. 2019, 230, 111507. [Google Scholar] [CrossRef]
- Lv, T.; Liu, M.; Zhu, D.; Gan, L.; Chen, T. Nanocarbon-Based Materials for Flexible All-Solid-State Supercapacitors. Adv. Mater. 2018, 30, e1705489. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, L.; Shi, X.; Shi, X.; Chen, L.; Dargusch, M.; Zou, J.; Chen, Z.-G. Flexible Thermoelectric Materials and Generators: Challenges and Innovations. Adv. Mater. 2019, 31, e1807916. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, F.; Liu, J. Direct 3D printing of low melting point alloy via adhesion mechanism. Rapid Prototyp. J. 2017, 23, 642–650. [Google Scholar] [CrossRef]
- Guo, J.; Fu, S.; Deng, Y.; Xu, X.; Laima, S.; Liu, D.; Zhang, P.; Zhou, J.; Zhao, H.; Yu, H.; et al. Hypocrystalline ceramic aerogels for thermal insulation at extreme conditions. Nature 2022, 606, 909–916. [Google Scholar] [CrossRef]
- Xiao, L.; Song, W. Additively-manufactured functionally graded Ti-6Al-4V lattice structures with high strength under static and dynamic loading: Experiments. Int. J. Impact Eng. 2018, 111, 255–272. [Google Scholar] [CrossRef]
- Liang, D.; He, G.; Chen, W.; Chen, Y.; Chyu, M.K. Fluid flow and heat transfer performance for micro-lattice structures fabricated by Selective Laser Melting. Int. J. Therm. Sci. 2022, 172, 107312. [Google Scholar] [CrossRef]
- Bai, X.; Zheng, Z.; Nakayama, A. Heat transfer performance analysis on lattice core sandwich panel structures. Int. J. Heat Mass Transf. 2019, 143, 118525. [Google Scholar] [CrossRef]
- Yang, M.; Tao, W. Heat Transfer, 4th ed.; Higher Education Press: Beijing, China, 2006; pp. 1–457. [Google Scholar]
- Caogen, Y.; Hongjun, L.; Zhonghua, J.; Xinchao, J.; Yan, L.; Haigang, L. A study on metallic thermal protection system panel for Reusable Launch Vehicle. Acta Astronaut. 2008, 63, 280–284. [Google Scholar] [CrossRef]
- Wei, K.; He, R.; Cheng, X.; Pei, Y.; Zhang, R.; Fang, D. Fabrication and heat transfer characteristics of C/SiC pyramidal core lattice sandwich panel. Appl. Therm. Eng. 2015, 81, 10–17. [Google Scholar] [CrossRef]
- De Arrieta, I.G.; González-Fernández, L.; Risueño, E.; Echániz, T.; Tello, M. Isothermal oxidation kinetics of nitrided Ti-6Al-4V studied by infrared emissivity. Corros. Sci. 2020, 173, 108723. [Google Scholar] [CrossRef]
- Gao, G.; Li, Y.; Hu, D.; Wu, Z.; Li, C.; Li, Z.; Xi, Z. Effect of voltage on infrared emissivity of MAO coatings on TC4 titanium alloys. Titan. Ind. Prog. 2018, 35, 32–37. [Google Scholar]
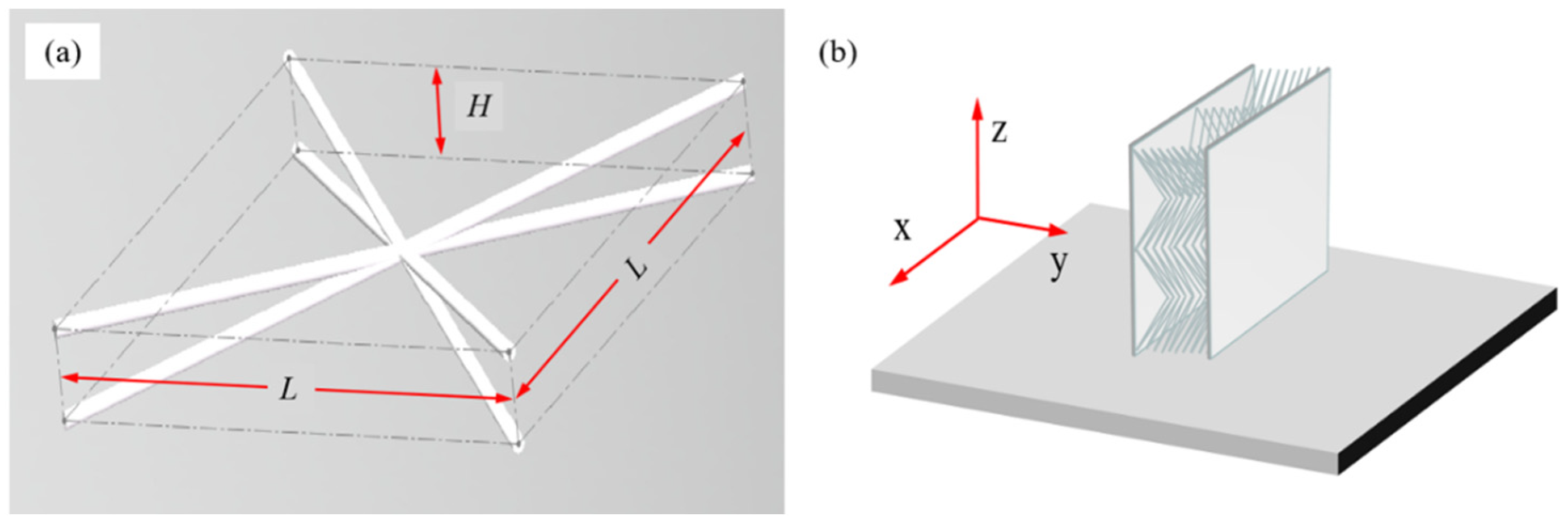






| k | Designed Structure | Printed Structure | Truss Diameter /mm | Cell Size /mm | Lattice Size /mm | |
|---|---|---|---|---|---|---|
| S-1 | 6 |  |  | 0.75 | 15 × 15 × 2.5 | 45 × 45 × 10 |
| S-2 | 8 |  |  | 0.75 | 20 × 20 × 2.5 | 40 × 40 × 20 |
| Element | Al | V | Fe | O | N | Ti |
|---|---|---|---|---|---|---|
| Component (wt.%) | 6.16 | 4.3 | 0.163 | 0.0924 | 0.0104 | Bal. |
| Scan Strategy | Scan Speed /mm·s−1 | Laser Power /W | Hatch Spacing /μm | Layer Thickness /μm | |
|---|---|---|---|---|---|
| Parameters | S type | 900 | 95 | 60 | 30 |
| λ0 /W·m−1·°C−1 | H /mm | L /mm | D /mm | n | m | |
|---|---|---|---|---|---|---|
| S-1 | 7.96 | 2.5 | 15 | 0.75 | 9 | 4 |
| S-2 | 7.96 | 2.5 | 20 | 0.75 | 4 | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, A.; Liu, X.; Wan, X. Thermal Insulation and Compressive Performances of 3D Printing Flexible Load-Bearing and Thermal Insulation Integrated Lattice. Materials 2022, 15, 8625. https://doi.org/10.3390/ma15238625
Wang X, Li A, Liu X, Wan X. Thermal Insulation and Compressive Performances of 3D Printing Flexible Load-Bearing and Thermal Insulation Integrated Lattice. Materials. 2022; 15(23):8625. https://doi.org/10.3390/ma15238625
Chicago/Turabian StyleWang, Xin, Ang Li, Xuefeng Liu, and Xiangrui Wan. 2022. "Thermal Insulation and Compressive Performances of 3D Printing Flexible Load-Bearing and Thermal Insulation Integrated Lattice" Materials 15, no. 23: 8625. https://doi.org/10.3390/ma15238625
APA StyleWang, X., Li, A., Liu, X., & Wan, X. (2022). Thermal Insulation and Compressive Performances of 3D Printing Flexible Load-Bearing and Thermal Insulation Integrated Lattice. Materials, 15(23), 8625. https://doi.org/10.3390/ma15238625






