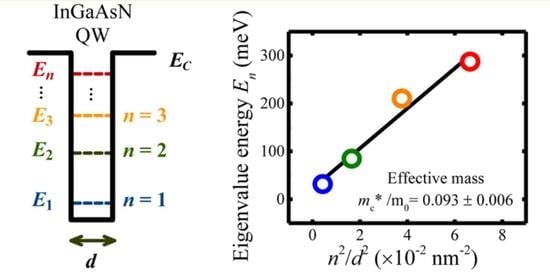
Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
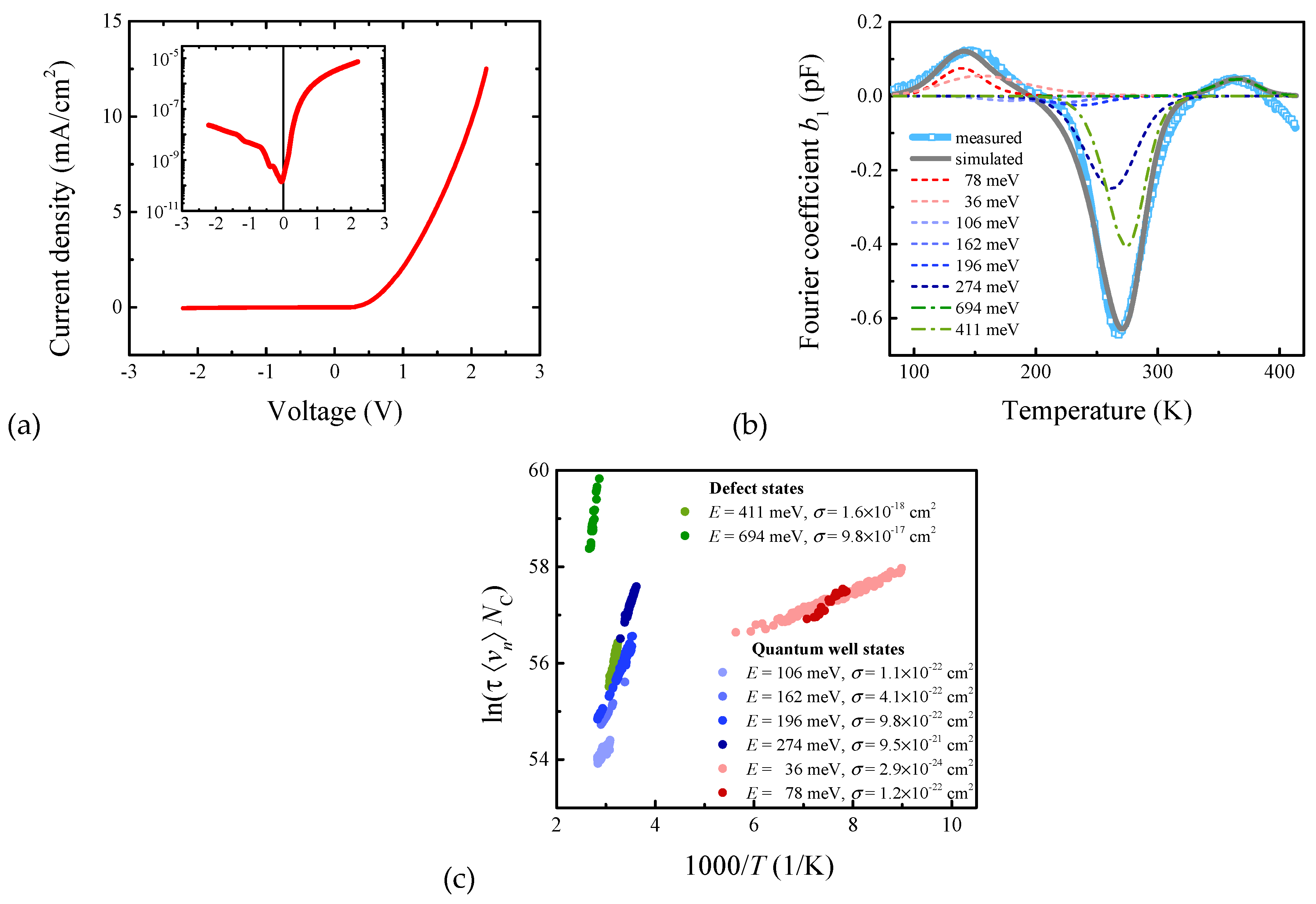
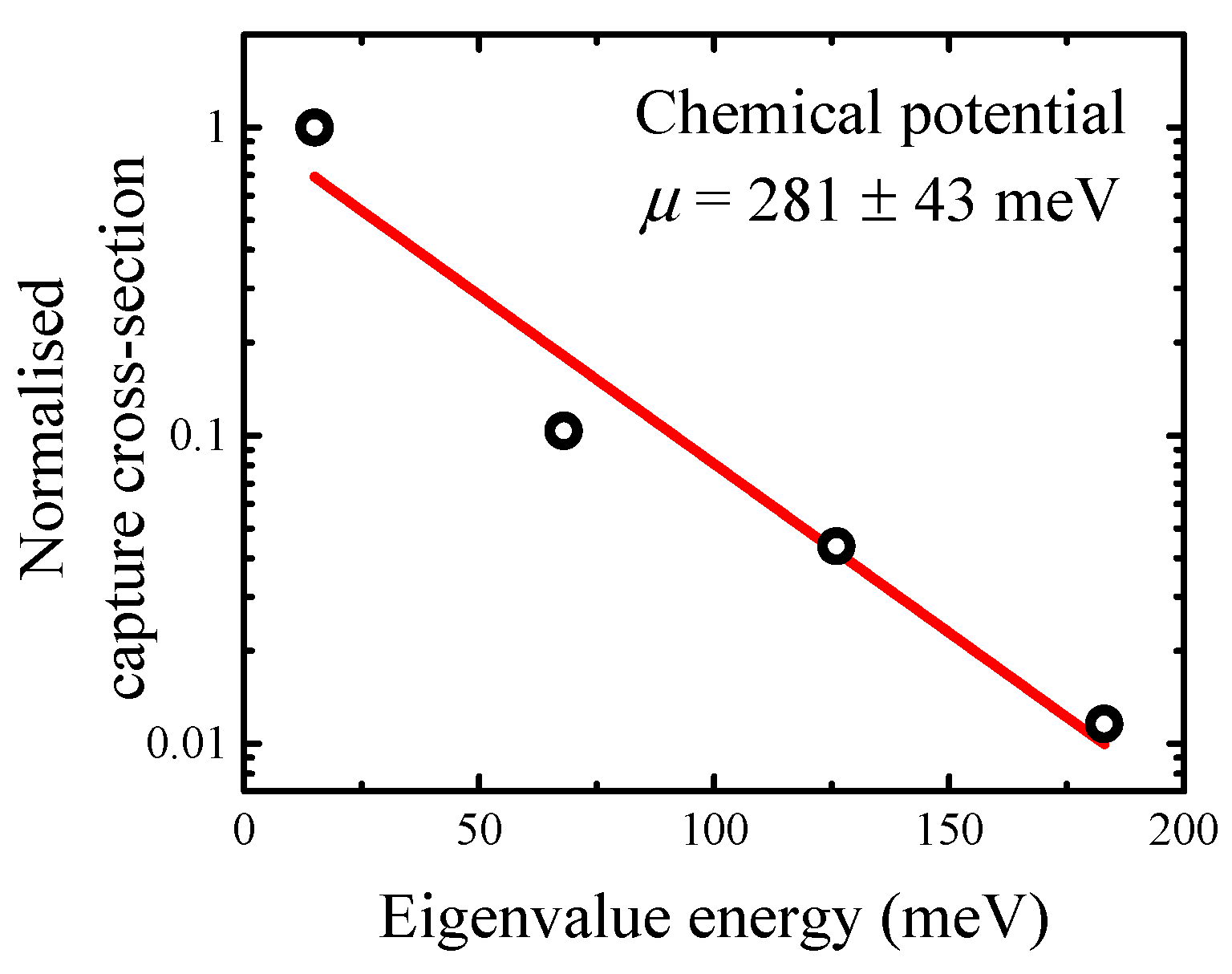
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Hinken, D.; Rauer, M.; Hao, X. Solar cell efficiency tables (Version 60). Prog. Photovolt. Res. Appl. 2022, 30, 687–701. [Google Scholar] [CrossRef]
- Pastuszak, J.; Węgierek, P. Photovoltaic Cell Generations and Current Research Directions for Their Development. Materials 2022, 15, 5542. [Google Scholar] [CrossRef] [PubMed]
- Barnham, K.; Ballard, I.; Barnes, J.; Connolly, J.; Griffin, P.; Kluftinger, B.; Nelson, J.; Tsui, E.; Zachariou, A. Quantum well solar cells. Appl. Surf. Sci. 1997, 113, 722–733. [Google Scholar] [CrossRef]
- Klemmer, P.S.; Mityagin, Y.A.; Telenkov, M.P.; Nagaraja, K.K.; Elantsev, D.A.; Amiri, S. Resonant tunneling in GaAs/AlGaAs quantum well system for solar photovoltaics. Superlattices Microstruct. 2020, 140, 106472. [Google Scholar] [CrossRef]
- Rein, S. Lifetime Spectroscopy: A Method of Defect Characterisation in Silicon for Photovoltaic Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Balcioglu, A.; Ahrenkiel, R.K.; Hasoon, F. Deep-level impurities in CdTe/CdS thin-film solar cells. J. Appl. Phys. 2000, 88, 7175–7178. [Google Scholar]
- Kim, J.W.; Song, G.H.; Lee, J.W. Observation of minority-carrier traps in In Ga N/Ga N multiple-quantum-well light-emitting diodes during deep-level transient spectroscopy measurements. Appl. Phys. Lett. 2006, 88, 182103. [Google Scholar] [CrossRef]
- Letartre, X.; Stievenard, D.; Lannoo, M.; Barbier, E. Tunnel deep level transient spectroscopy on a single quantum well. J. Appl. Phys. 1991, 69, 7336–7338. [Google Scholar] [CrossRef]
- Letartre, X.; Stievenard, D.; Barbier, E. Accurate determination of the conduction-band offset of a single quantum well using deep level transient spectroscopy. Appl. Phys. Lett. 1991, 58, 1047–1049. [Google Scholar] [CrossRef]
- Colakerol, L.; Veal, T.D.; Jeong, H.K.; Plucinski, L.; DeMasi, A.; Learmonth, T.; Glans, P.A.; Wang, S.; Zhang, Y.; Piper, L.F.; et al. Quantized electron accumulation states in indium nitride studied by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2006, 97, 237601. [Google Scholar] [CrossRef]
- Warburton, R.J.; Michels, J.G.; Nicholas, R.J.; Harris, J.J.; Foxon, C.T. Optically detected cyclotron resonance of GaAs quantum wells: Effective-mass measurements and offset effects. Phys. Rev. B 1992, 46, 13394. [Google Scholar] [CrossRef]
- Pan, Z.; Li, L.H.; Lin, Y.W.; Sun, B.Q.; Jiang, D.S.; Ge, W.K. Conduction band offset and electron effective mass in GaInNAs/GaAs quantum-well structures with low nitrogen concentration. Appl. Phys. Lett. 2001, 78, 2217–2219. [Google Scholar] [CrossRef]
- Knolle, J.; Cooper, N.R. Anomalous de Haas–van Alphen effect in InAs/GaSb quantum wells. Phys. Rev. Lett. 2017, 118, 176801. [Google Scholar] [CrossRef] [PubMed]
- Hatke, A.T.; Zudov, M.A.; Pfeiffer, L.N.; West, K.W. Shubnikov–de Haas oscillations in GaAs quantum wells in tilted magnetic fields. Phys. Rev. B. 2012, 85, 241305. [Google Scholar] [CrossRef]
- Failla, M.; Keller, J.; Scalari, G.; Maissen, C.; Faist, J.; Reichl, C.; Wegscheider, W.; Newell, O.J.; Leadley, D.R.; Myronov, M.; et al. Terahertz quantum Hall effect for spin-split heavy-hole gases in strained Ge quantum wells. New J. Phys. 2016, 18, 113036. [Google Scholar] [CrossRef]
- Gass, M.H.; Papworth, A.J.; Joyce, T.B.; Bullough, T.J.; Chalker, P.R. Measurement of the effective electron mass in GaInNAs by energy-loss spectroscopy. Appl. Phys. Lett. 2004, 84, 1453–1455. [Google Scholar] [CrossRef]
- Papež, N.; Dallaev, R.; Ţălu, Ş.; Kaštyl, J. Overview of the Current State of Gallium Arsenide-Based Solar Cells. Materials 2021, 14, 3075. [Google Scholar] [CrossRef]
- Wartak, M.S.; Weetman, P. Numerical analysis of the effective masses in InGaAsN quantum-well structures with self-consistent effects. J. Phys Cond. Matter 2005, 17, 6539. [Google Scholar] [CrossRef]
- Wartak, M.S.; Weetman, P. Characterisation of effective masses in InGaAsN quantum well structures by computer simulations. J. Appl. Phys. 2005, 98, 113705. [Google Scholar] [CrossRef]
- Skierbiszewski, C.; Łepkowski, S.P.; Perlin, P.; Suski, T.; Jantsch, W.; Geisz, J. Effective mass and conduction band dispersion of GaAsN/GaAs quantum wells. Phys. E 2002, 13, 1078–1081. [Google Scholar] [CrossRef]
- Shan, W.; Walukiewicz, W.; Yu, K.M.; Ager Iii, J.W.; Haller, E.E.; Geisz, J.F.; Friedman, D.J.; Olson, J.M.; Kurtz, S.R.; Xin, H.P.; et al. Band anticrossing in III–N–V alloys. Phys. Status Solidi B 2001, 223, 75–85. [Google Scholar] [CrossRef]
- Ściana, B.; Radziewicz, D.; Pucicki, D.; Serafińczuk, J.; Dawidowski, W.; Bielak, K.; Badura, M.; Gelczuk, Ł.; Tłaczała, M.; Latkowska, M.; et al. Influence of the AP MOVPE process parameters on properties of (In, Ga)(As, N)/GaAs heterostructures for photovoltaic applications. Electron Technol. Conf. 2013 2013, 8902, 136–143. [Google Scholar]
- Weiss, S.; Kassing, R. Deep Level Transient Fourier Spectroscopy (DLTFS)—A technique for the analysis of deep level properties. Solid-State Electron. 1988, 31, 1733–1742. [Google Scholar] [CrossRef]
- Yakimova, R.; Paskova, T.; Hardalov, C. Behavior of an EL5-like defect in metalorganic vapor-phase epitaxial GaAs: Sb. J. Appl. Phys. 1993, 74, 6170–6173. [Google Scholar] [CrossRef]
- Shiraki, H.; Tokuda, Y.; Sassa, K. Bistable behavior of a medium-deep center related to EL5 and EL6 in n-type bulk GaAs. J. Appl. Phys. 1998, 84, 3167–3174. [Google Scholar] [CrossRef]
- Weiss, S.; Beckmann, R.; Kassing, R. The Electrical Properties of Zinc in Silicon. Appl. Phys. A 1990, 50, 151–156. [Google Scholar] [CrossRef]
- Galluppi, M.; Geelhaar, L.; Riechert, H. Nitrogen and indium dependence of the band offsets in InGaAsN quantum wells. Appl. Phys. Lett. 2005, 86, 131925. [Google Scholar] [CrossRef]
- Nag, B.R. Physics of Quantum Well Devices; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Soma, T.; Satoh, J.; Matsuo, H. Thermal expansion coefficient of GaAs and InP. Solid State Commun. 1982, 42, 889–892. [Google Scholar] [CrossRef]
- Héroux, J.B.; Yang, X.; Wang, W.I. Optical characterization of strained InGaAsN/GaAs multiple quantum wells. Vac. Sci. Technol. B 2002, 20, 1154–1157. [Google Scholar] [CrossRef]
- Ardali, S.; Tiras, E.; Erol, A. Integer quantum Hall effect measurement analysis in Ga0. 68In0. 32N0. 017As/GaAs quantum wells with various annealing time. Phys. B Condens. Matter 2021, 621, 413305. [Google Scholar] [CrossRef]
- Sarcan, F.; Donmez, O.; Erol, A.; Gunes, M.; Arikan, M.C.; Puustinen, J.; Guina, M. Influence of nitrogen on hole effective mass and hole mobility in p-type modulation doped GaInNAs/GaAs quantum well structures. Appl. Phys. Lett. 2013, 103, 082121. [Google Scholar] [CrossRef]
- Baranov, P.G.; Romanov, N.G.; Preobrazhenski, V.L.; Egorova, A.Y.; Ustinov, V.M.; Sobolev, M.M. Optically-detected microwave resonance in InGaAsN/GaAs quantum wells and InAs/GaAs quantum dots emitting around 1.3 μm. Int. J. Nanosci. 2003, 2, 469–478. [Google Scholar] [CrossRef]

| Technique | Reference | |
|---|---|---|
| 0.05 ~ 0.09 (n) | RTOP | [12] |
| 0.06 ~ 0.08 (n) | RTOP | [30] |
| 0.077 ~ 0.078 (n) | QHE, SdH | [31] |
| 0.07 ~ 0.12 (p) | SdH | [32] |
| 0.07 (n) | ODCR | [33] |
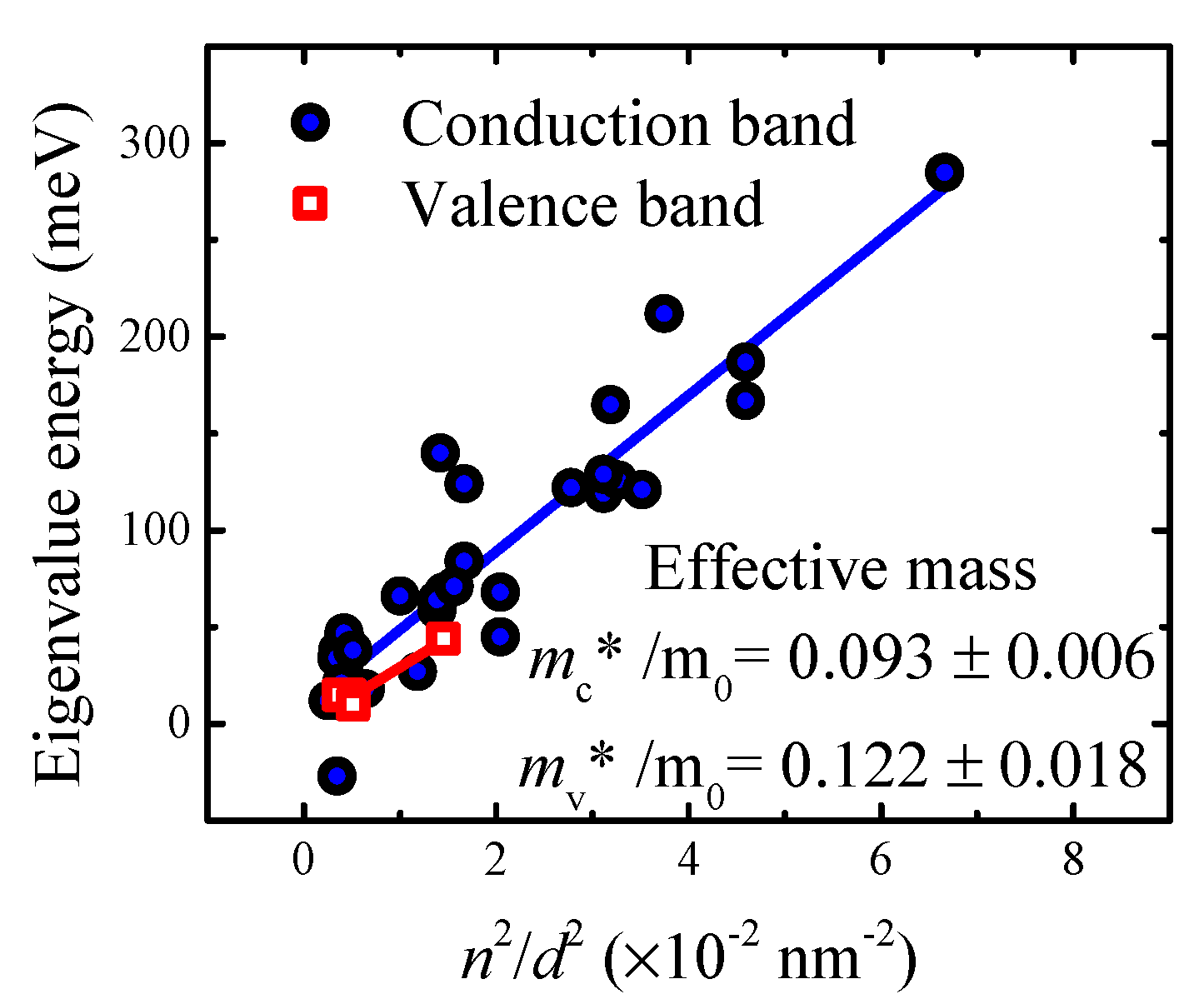
| 0.093 ± 0.006 (n) | Transient spectroscopy | This work |
| 0.122 ± 0.018 (p) | Transient spectroscopy | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stuchlikova, L.; Sciana, B.; Kosa, A.; Matus, M.; Benko, P.; Marek, J.; Donoval, M.; Dawidowski, W.; Radziewicz, D.; Weis, M. Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy. Materials 2022, 15, 7621. https://doi.org/10.3390/ma15217621
Stuchlikova L, Sciana B, Kosa A, Matus M, Benko P, Marek J, Donoval M, Dawidowski W, Radziewicz D, Weis M. Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy. Materials. 2022; 15(21):7621. https://doi.org/10.3390/ma15217621
Chicago/Turabian StyleStuchlikova, Lubica, Beata Sciana, Arpad Kosa, Matej Matus, Peter Benko, Juraj Marek, Martin Donoval, Wojciech Dawidowski, Damian Radziewicz, and Martin Weis. 2022. "Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy" Materials 15, no. 21: 7621. https://doi.org/10.3390/ma15217621
APA StyleStuchlikova, L., Sciana, B., Kosa, A., Matus, M., Benko, P., Marek, J., Donoval, M., Dawidowski, W., Radziewicz, D., & Weis, M. (2022). Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy. Materials, 15(21), 7621. https://doi.org/10.3390/ma15217621