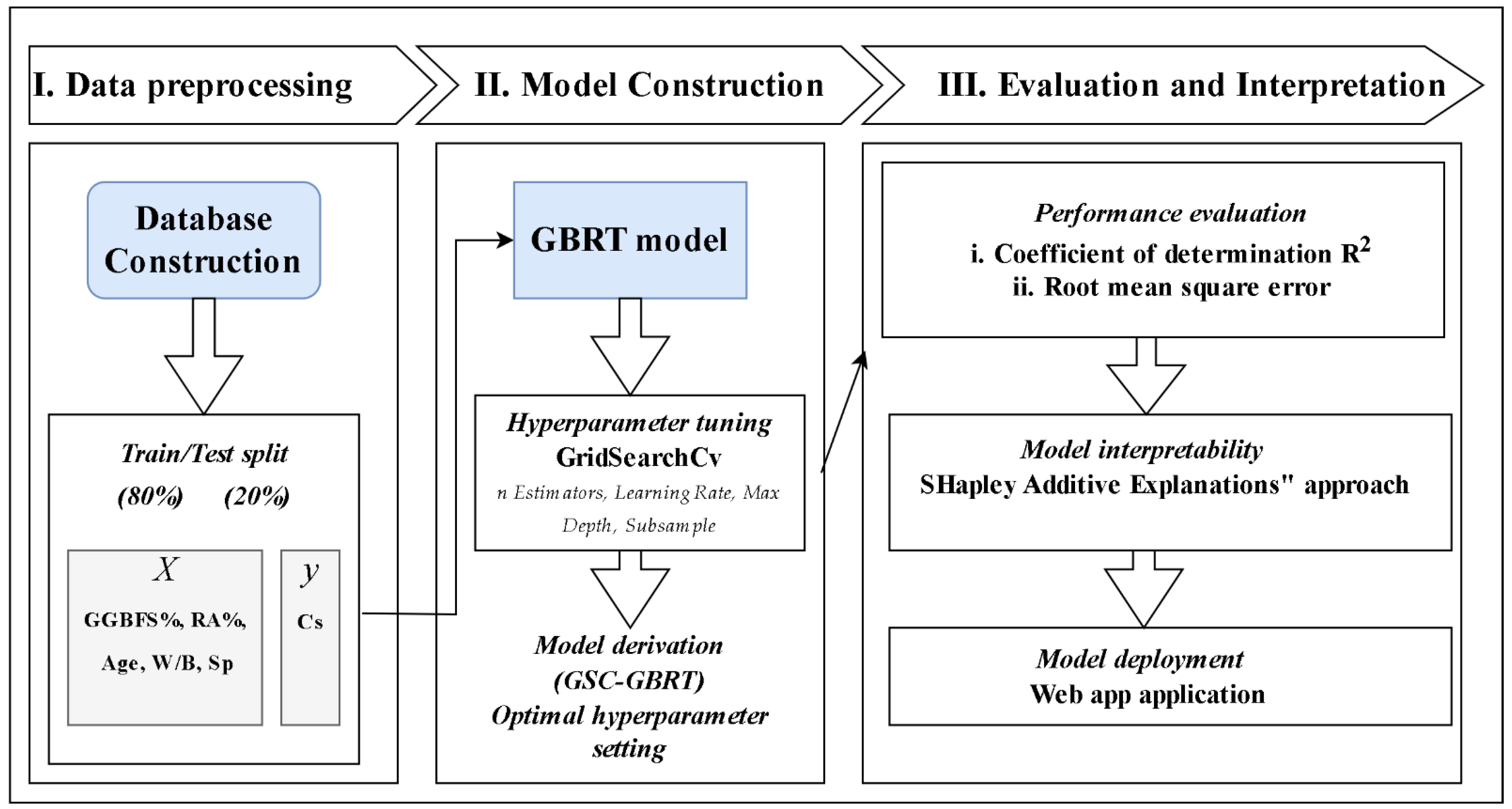
1. Introduction
In recent years, the design and construction of sustainable buildings has become a major goal. One of the most important factors influencing this criterion is the use of Portland cement substitutes. For instance, cement production consumes vast energy and significantly contributes to greenhouse gas emissions and environmental degradation. Therefore, a reduction in cement incorporated in concrete mixes is necessary to protect the environment. In addition, to avoid the negative impacts of burying hazardous industrial wastes, using recycled concrete aggregate (RCA) and ground granulated blast-furnace slag (GGBFS) as waste materials in concrete mixes would also allow us to reduce greenhouse gas emissions, since less cement and natural aggregate (NA) will be produced [
1].
Some researchers investigated the behavior of RCA in terms of durability and mechanical performance. They found that RCA has lower properties than natural concrete aggregate (NCA) [
2,
3,
4,
5,
6,
7].
Hence, concrete scientists must increase the qualities of RCA in order to improve the products produced with it due to the numerous environmental advantages of using RCA in the construction sector. Additionally, improving RCA makes it possible to utilize it to prepare concrete for a structure incorporating load-bearing structural members. However, old connected mortar, crushing techniques, and a poor interfacial transition zone (ITZ) are the critical causes for RCA’s inferior quality. Previous studies have shown that whereas RCA has five phases—NA, old ITZ, old cement paste, new ITZ, and new cement paste—NCA has three phases, which are NA, ITZ, and cement mixture. As a result, the rheological, mechanical, and durability characteristics of RCA are gradually decreased because of the higher significant porosity and water absorption capacity caused by higher number of phases. Various approaches have been reported in the literature to reduce the lower properties of RCA and make it similar to NCA. Incorporating supplemental cement-based materials such as ground granulated blast-furnace slag (GGBFS) was one of the solutions to improve the RCA properties and eliminate its lower properties [
8].
Slag cement, commonly known as GGBFS, is a by-product of the iron production sector. A hydraulic cementitious substance with pozzolanic properties is a slag cement. Any reactive aluminosilicate substance is referred to as pozzolan. Pozzolans interact with the cement hydration process by-products to generate concrete. Pozzolans do not often provide enough strength when combined with water alone; thus, cement must be added to the mixture. Because of this, it is widely believed in the concrete industry that cement, at the very least in a reasonable proportion, is necessary to provide the necessary strength. When combined with water, slag cement, which has cementitious qualities similar to cement, will hydrate and provide strength.
Studies on the impact of GGBFS on several RCA properties have been performed. When comparing with NCA, Çakır [
9] reported that concrete with 30% GGBFS and 50% RCA shows good mechanical properties. Similarly, according to Majhi and Nayak [
10], concrete containing 40% GGBFS and 50% RCA has good mechanical and physical properties. It was also found that this concrete is as durable as NCA. Rashad [
11] looked into how GGBFS content affects the compressive strength (Cs) and found that a mix with 50% GGBFS can have similar characteristics as concrete mix with ordinary Portland cement (OPC) content. In their study on the effects of 65% GGBFS on the properties of RCA, Ann et al. [
12] discovered that GGBFS enhances the resistance of RCA to permeability and corrosion when used with 100% RCA. Afroughsabet et al. [
13] studied the impact of adding 30% GGBFS to RCA. They found that substituting 30% OPC with GGBFS increased both the concrete splitting tensile and flexural strength while maintaining its Cs. Slag was shown to reduce both the water absorption and workability of concrete. RC beams using recycled aggregate from electric arc furnaces (EAF) were the subject of a study to determine how they would behave [
14]. According to the experimental results, EAF concrete beams have enhanced material qualities, resulting in higher ultimate flexural and shear capacities and smaller crack widths than equivalent standard RC beams. Another study [
15] concluded that utilizing ternary cements, which have the right proportions of blast-furnace slag and limestone filler, can minimize gaseous emissions without sacrificing the cement mechanical qualities and promote the effective use of by-products and natural resources.
One of the most crucial aspects to consider while building and engineering structures is testing the concrete Cs. Typically, the compression test for the specimens at the specified curing age is used in the lab to determine the Cs. However, in addition to time and money, a significant amount of material is needed to carry out this test. As a result, some researchers have developed a technique to estimate the Cs of eco-friendly concrete utilizing RAC as a replacement material for natural aggregate or GGBFS as a replacement material for ordinary cement.
2. Related Works
In civil engineering, supervised machine learning models have acquired a lot of momentum, especially for predicting eco-friendly concrete properties, because they can forecast the results with high accuracy. Researchers have presented many machine learning (ML)-based prediction models for forecasting the mechanical and physical properties of RCA. The suggested approaches have been validated as a reliable alternative to expensive and time-consuming testing in laboratory usually used to assess concrete qualities. For example, Han at al. [
16] presented an ensemble ML model for concrete derived from RCA to estimate the concrete modulus of elasticity. It is demonstrated that when compared to stand-alone models, the ensemble ML model consistently generates more precise predictions. Additionally, prediction models for the Cs of concrete incorporating recycled materials were suggested using random forest, linear regression, and nonlinear regression techniques [
17]. The models based on random forest and nonlinear regression were found to be more accurate than linear regression. Furthermore, Liu et al. [
18] used ML algorithms to predict the carbonation depth in RCA. According to the results, the random forest model outperforms the stand-alone artificial neural network (ANN) model and Gaussian progress regression model. Last but not least, 10 ML algorithms were tested using a dataset containing 962 experimental Cs of NCA and RCA [
19]. As they outperform existing methods, the ML models established for this work can be suggested as a valuable tool for the prediction of the Cs. In term of GGBFS, numerous studies established an ML model to forecast the mechanical characteristics of eco-friendly concrete that includes GGBFS material as a substitute for regular cement. The NN and ANFIS models for predicting chloride permeability in concrete were introduced by Boğa et al. [
20]. Their study used concrete specimens containing solely calcium nitrite-based corrosion inhibitor (CNI), GGBFS, and a mixture of these ingredients in various ratios. The evaluation of the results demonstrated that both models estimate the permeability of chloride with good precision. In addition, random forest was used by Mai et al. [
21] to forecast the Cs of GGBFS-containing concrete. RF performances in terms of R
2, RMSE, and MAE were 0.9729, 4.9585, and 3.9423, respectively. Han et al. [
22] created an innovative hybrid model for calculating the Cs of GGBFS concrete and validated the synergistic benefits of the hybrid algorithm over a single algorithm. The new PSO-BP hybrid neural network model outperformed basic ANNs trained by a single method and was shown to be suited for estimating the Cs of GGBFS concrete.
Table 1 provides a comprehensive summary of relevant prior work related to predicting the Cs of eco-friendly concrete.
5. Dataset Used
Various studies have investigated the Cs of environmentally friendly concrete. As a result, an extensive dataset with 164 experiments on the Cs of eco-friendly concrete incorporating both RA and GGBFS material was recently assembled in reference [
50]. The ML model for predicting the concrete Cs was trained and tested using this dataset. Details can be consulted in [
50]. According to [
39], the data collected from the collected experimental studies consider the effect of both GGBFS and RCA on the Cs of concrete. To unify their results, when collecting the data, specimens with only cube shapes of either 100 mm or 150 mm in length were considered. The authors used Rashid and Mansur’s equation to transform the Cs from a 100 mm cube specimen to the equivalent Cs from a 150 mm cube specimen. In addition, five of the data records had no RA and/or GGBFS in their combination proportions, indicating standard concrete blends.
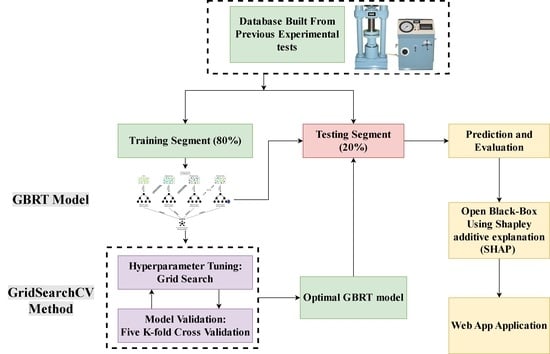
After being randomly sorted for the aim of constructing models, the gathered data records were divided into two fragments. First, the data records were split into training and testing data with 80% and 20%, respectively. Some relevant key parameters of the dataset utilized in this work is shown in
Table 2. The primary input factors that have a significant impact on the concrete Cs were the following ones: water/binder ratio (W/B), curing time (Age), the recycled aggregate percentage from total aggregate in the mixture (RA%), GGBFS material percentage from total binder used in the mixture (GGBFS%), and superplasticizer content (kg).
Table 2 presents the lowest, average, median, standard deviation, and maximum values of the input variables for the training and testing sets.
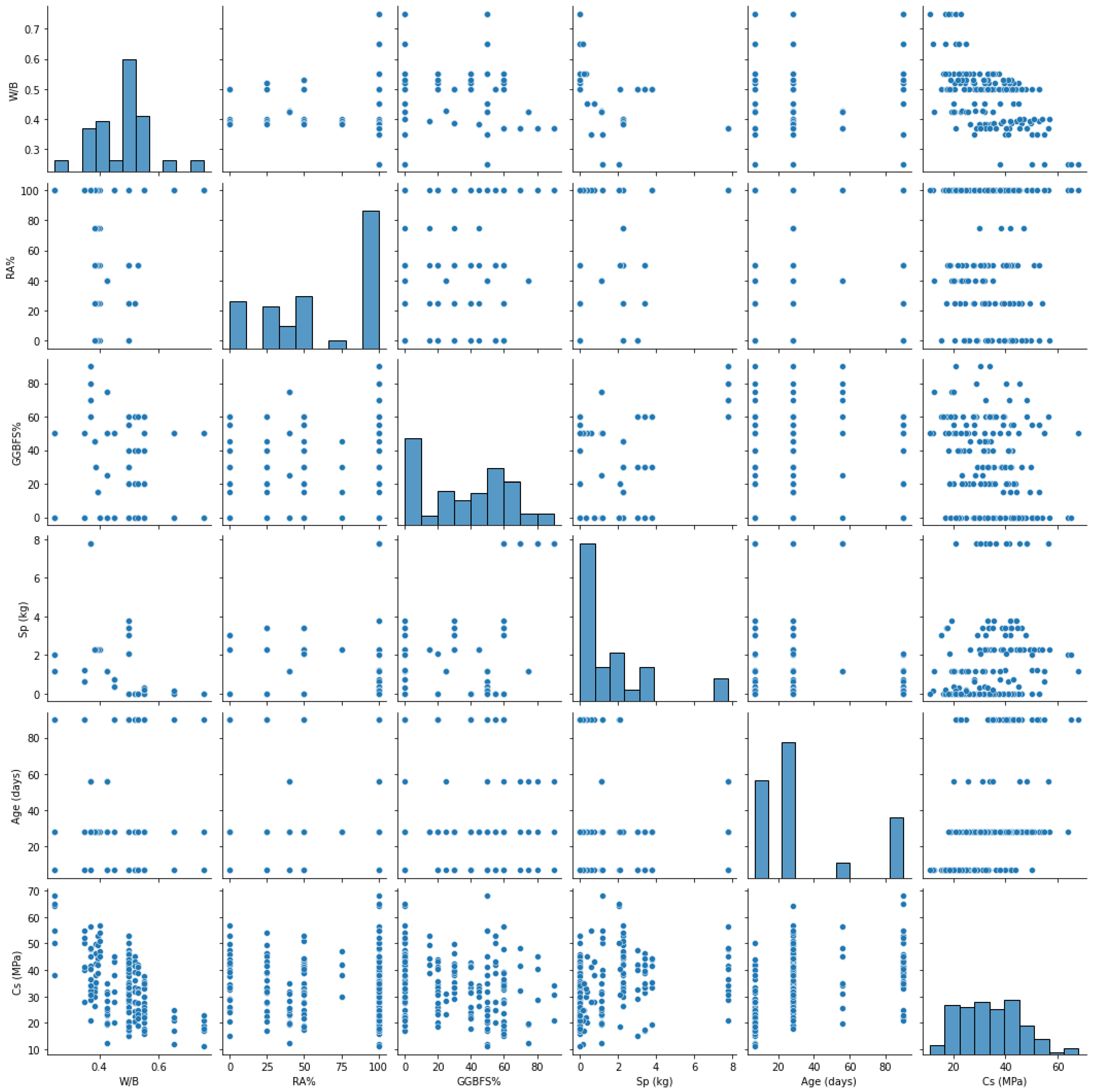
Figure 3 displays the relationships and statistical distributions of the Cs and the concrete components. Notably, none of the components are correlated, meaning that all the variables considered to forecast the concrete Cs are independent. Additionally, it can be seen that there is only a weak correlation between the W/B ratio and the Cs.
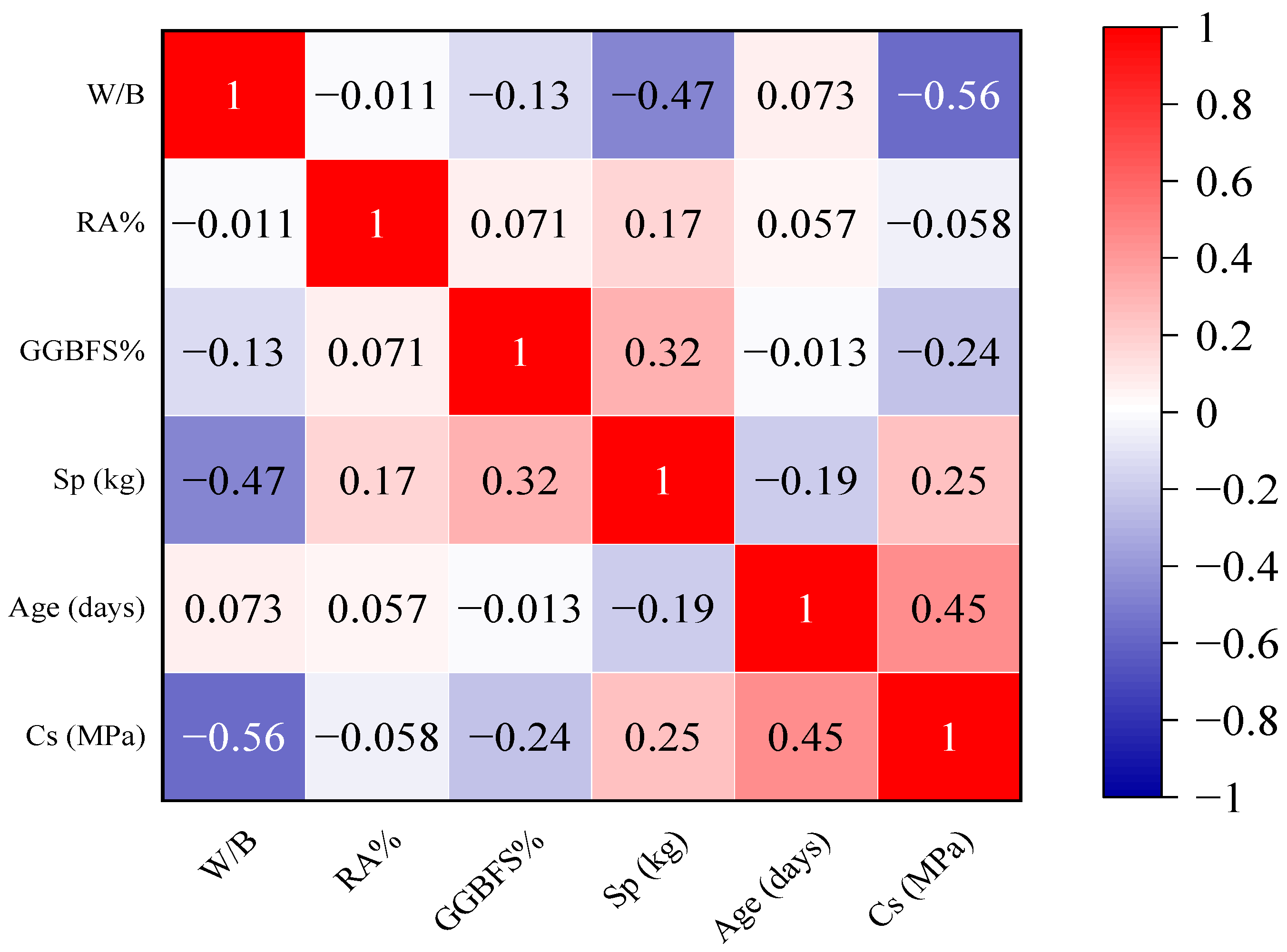
A heatmap, as shown in
Figure 4, clearly summarizes the association of the entire dataset (containing all of the ratios, weight, percentages, age, and Cs of concrete). It is possible to plot the heatmap in Python by using the Seaborn library. A correlation index near 1 indicates that the features are highly connected. A negative correlation value close to −1 indicates a perfect correlation of two features but moving in opposing directions. In contrast, two uncorrelated features have a correlation index near 0. As it can be noticed in the heatmap, W/B, RA%, and GGBFS% have a negative correlation with the output, while Age and Sp have a positive correlation.
The parameters in
Table 2 are utilized to produce environmentally friendly concrete. For completeness, a brief description of each variable is provided below to justify why they were considered concrete components in this study.
The W/B ratio has a significant influence on the concrete strength. Researchers noted that reducing the W/B ratio enhanced the Cs, splitting tensile strength, net flexural strength, and elastic modulus of self-compacting concretes fabricated using RA [
51]. Moreover, the 28-day Cs of RCA concretes with a W/B ratio of 0.40 could be increased to be higher than the 28-day Cs of NA concrete with a W/B ratio of 0.50 and be closer to the 28-day Cs of NA concrete with a W/B ratio of 0.45 through the use of fly ash at replacement rates of 15 and 25% by weight of binder in RCA concretes [
52]. In addition, the test findings demonstrated that the fly ash contributed more for the Cs at lower W/B ratios than it did in mixes made at higher W/B ratios.
The use of demolition waste as RA to create RAC has been investigated by several researchers [
53,
54]. However, RAC characteristics are inferior to NCA when porous mortar binds the RA [
15]. Furthermore, comparing RCA to NCA, a 30–40% reduction in Cs was noticed [
16]. Regardless, Aliabdo et al. [
55] found that while replacing coarse aggregate with RA results in a negligible drop in concrete strength, substituting fine recycled aggregate results in a considerable reduction. Therefore, RA% was added as a necessary concrete element in the dataset used in this study.
With the incorporation of RA, Cs tends to drop; however, adding superplasticizers (Sp) can improve the mix compactness, recovering up most of the strength loss [
56]. Cs increased when Sp dose was raised, and it was even more significant for Sp with higher water reduction capacities. With the proportion of added Sp, the mix density followed a similar pattern to Cs and slightly decreased towards a higher dosage [
56].
Some researchers discovered that the Cs of all self-compacting concrete (SCC) mixes dropped with an increase in RCA for SCC incorporating GGBFS and RCA [
57]. GGBFS as a cement replacement reduced the Cs at an early age compared to reference concrete, but at later ages (56 and 90 days), the Cs was equal or higher. The maximum Cs was achieved for SCC mixtures containing 15% GGBFS [
57].
The development of durable concrete is determined by its age. When both RCA and GGBFS content are increased, the short-term and long-term Cs of concrete fall [
10]. However, the strength growth rate with age increases when both RCA and GGBFS rise. This increase in strength growth rate results from GGBFS latent hydraulic activity and increased hydration of the unhydrated cement particles in RCA [
10].
7. Interpretation of the GBRT Model
In the absence of supporting theories, mathematical computations, or operational processes, the output findings or predictions of ML modeling can be challenging to explain [
61]. However, the contributions of input variables can be analyzed using feature importance, sensitivity analysis, or partial dependency analysis in order to evaluate those outputs and comprehend the trained models. Here, the multicollinearity problem and potential synergistic effects of the variables were effectively treated using the SHAP approach. In this section, the “SHapley Additive Explanations” approach [
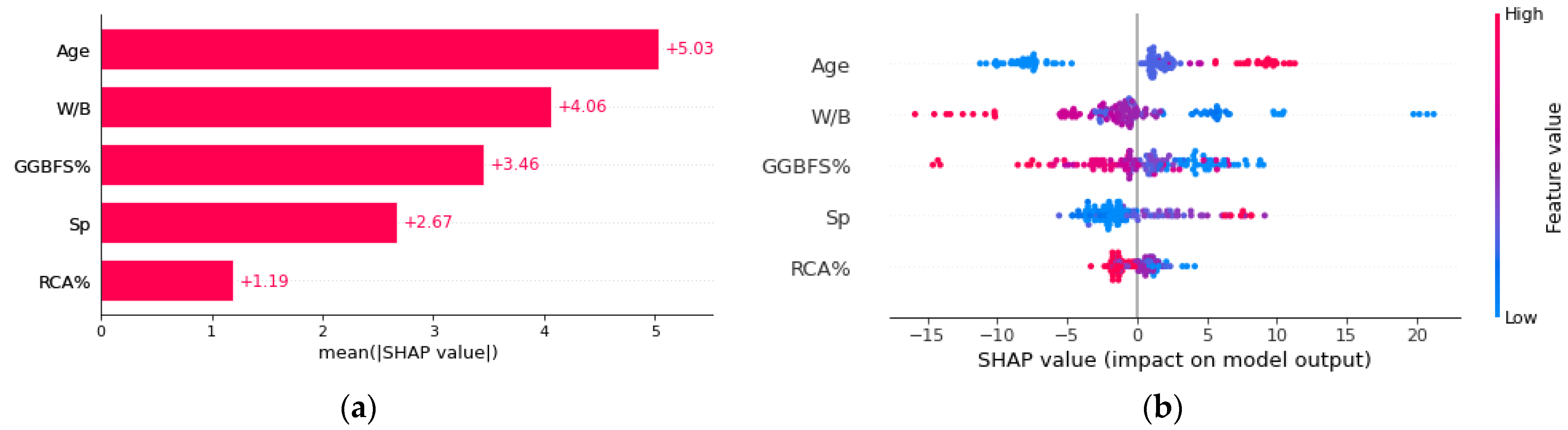
62], combined with the GSC-GBRT model, explains and clarifies the contribution of each input variable to the concrete Cs prediction. According to
Figure 9a, which displays the mean absolute SHAP values for each feature in the Cs modeling, the age in the concrete mixture has the highest mean SHAP value among the five input features. The descending order of input variable impact on GSC-GBRT model prediction accuracy is: AGE > W/B > GGBFS% > SP > RCA%.
The input features SHAP values are shown in
Figure 9b, with red denoting a high feature value and blue denoting a low feature value. The corresponding feature will benefit the output goal if the feature SHAP value is positive. When the SHAP value is more significant, the influence has a greater impact. For example, the age (red points) in
Figure 9b exhibited noticeably high SHAP values, which showed that the higher curing age had a detrimental effect on the prediction of the Cs. It is widely established from
Figure 9b that the W/B content, RCA%, and GGBFS% have a negative association with Cs. This is in line with earlier research [
8,
63].
A web application was developed using the suggested GSC-GBRT model to forecast the Cs of eco-friendly concrete at the Streamlit library. The user can theoretically forecast the Cs of eco-friendly concrete using the trained ML model based on the compiled dataset. W/B, RA%, GGBFS%, superplasticizer (kg), and age (days) are the first parameters the user enters using the online application sliders and radio buttons. In the next step, the concrete Cs in MPa is computed. The parameter ranges provided in the application match the feature ranges in the datasets used for ML training. The Streamlit web application can be accessed at the link given in [
64].
8. Conclusions
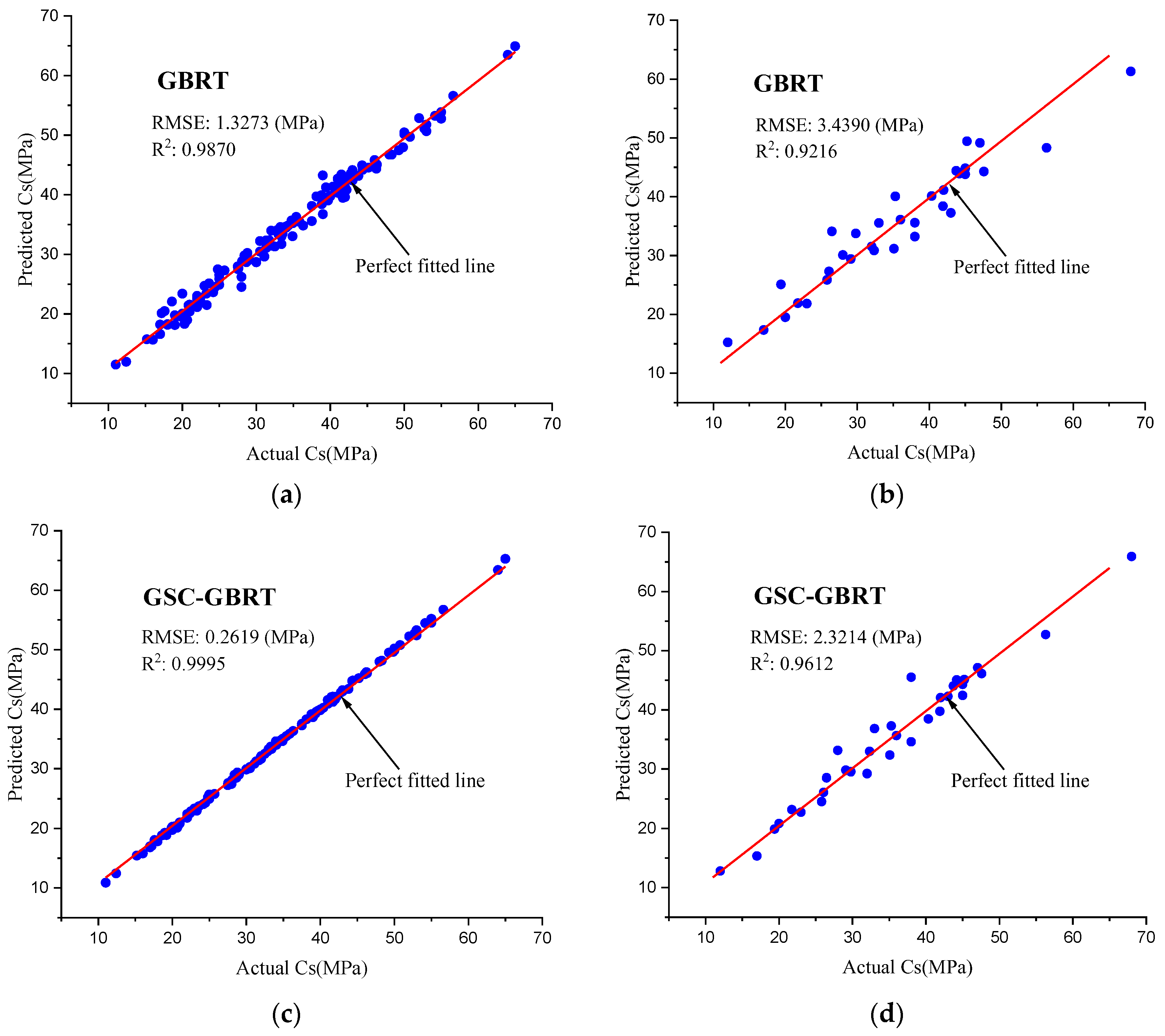
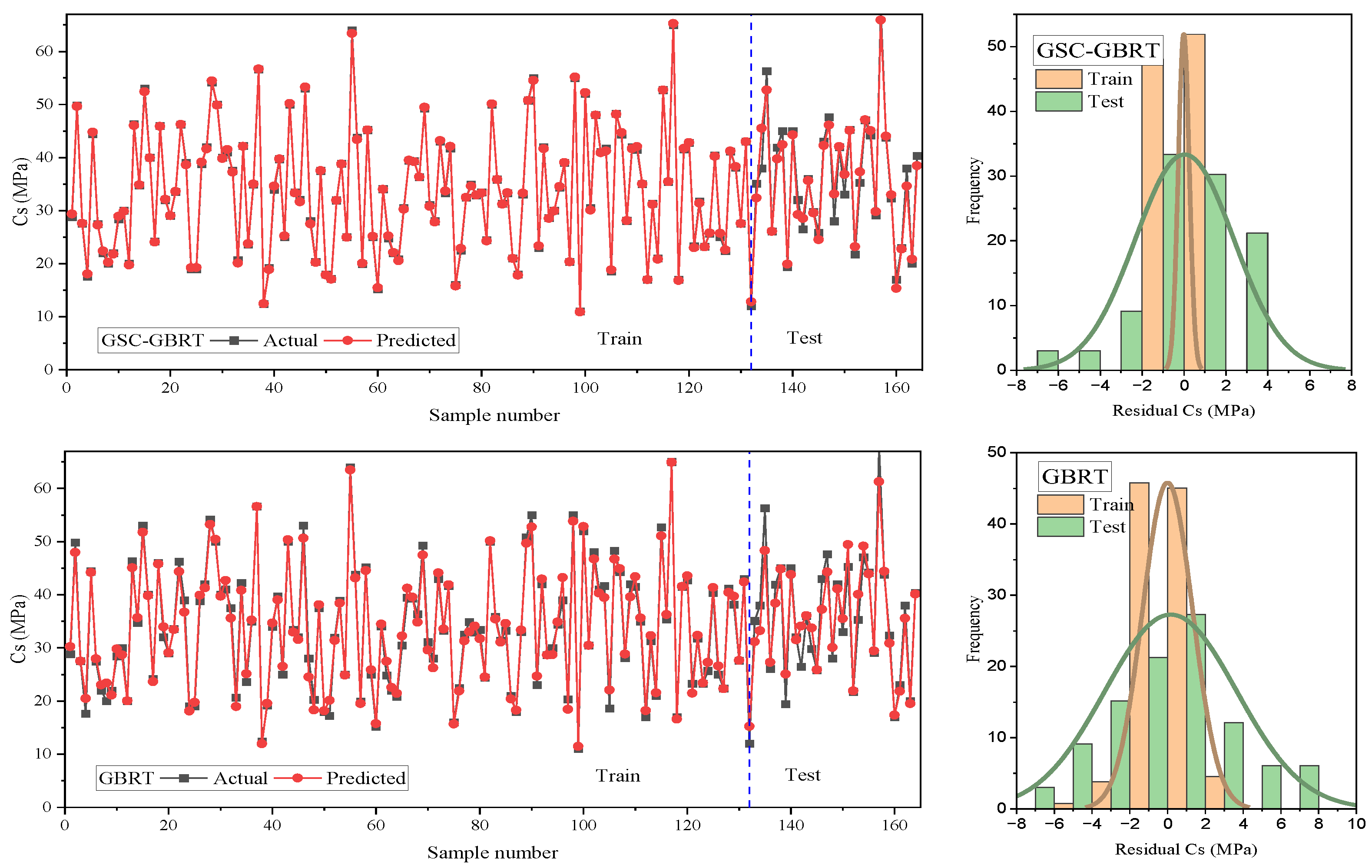
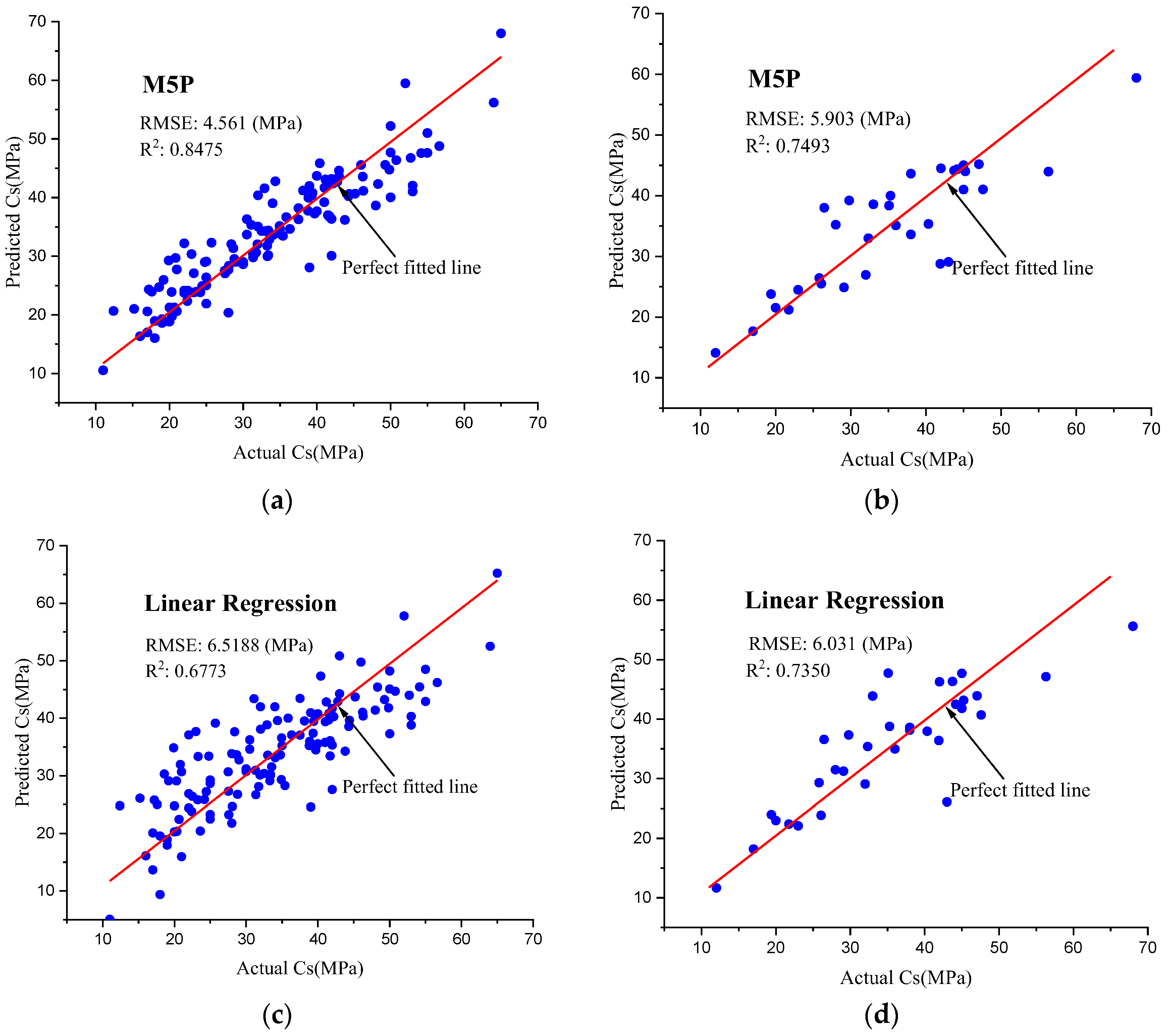
This research proposed a hybrid GSC-GBRT model for the prediction of the Cs of sustainable concrete. The GridSearchCV approach was firstly used to find the optimum parameters, and the optimized model was then used to forecast the Cs. The hybrid GSC-GBRT model obtained higher prediction accuracy and reduced error with R2 = 0.9612 and RMSE = 2.3214 when compared to the evaluation metrics of the original GBRT model with R2 = 0.9216 and RMSE = 3.4390 for the test set. The suggested GSC-GBRT model surpasses the initial GBRT model in assessment metrics, and it is suggested to be used as a tool for pre-estimating the Cs of concrete using the mix ratio prior to design and mixing.
According to the SHAP-based research, W/B and age are the two input factors that most significantly impact the concrete Cs among the five considered. Age and superplasticizer positively impact the output, and the Cs rises as a result. On the other hand, a rise in W/B, GGBFS%, and RA% causes the Cs to fall. Therefore, designers and engineers can use the significance and contribution of these factors to the output outcomes as a guide. Finally, in Streamlit, a web application for predicting Cs of eco-friendly concrete, was developed. The cloud has been used to deliver the application light version. Any web browser, including mobile ones, can be used to access and use it.
The GSC-GBRT model has several limitations while being competent and acceptable for estimating the Cs of eco-friendly concrete. Firstly, 164 experiments from the literature were used to construct the eco-friendly concrete dataset. The accuracy of the prediction models is significantly influenced by the completeness of the data, quantity, quality, and distribution of the input parameters. As new experimental data become available, the dataset may benefit from being updated. Secondly, like any ML method, the SHAP explanations and GSC-GBRT findings may only apply to the tested input data ranges.