Status and Challenges in Homogenization Methods for Lattice Materials
Abstract
:1. Introduction
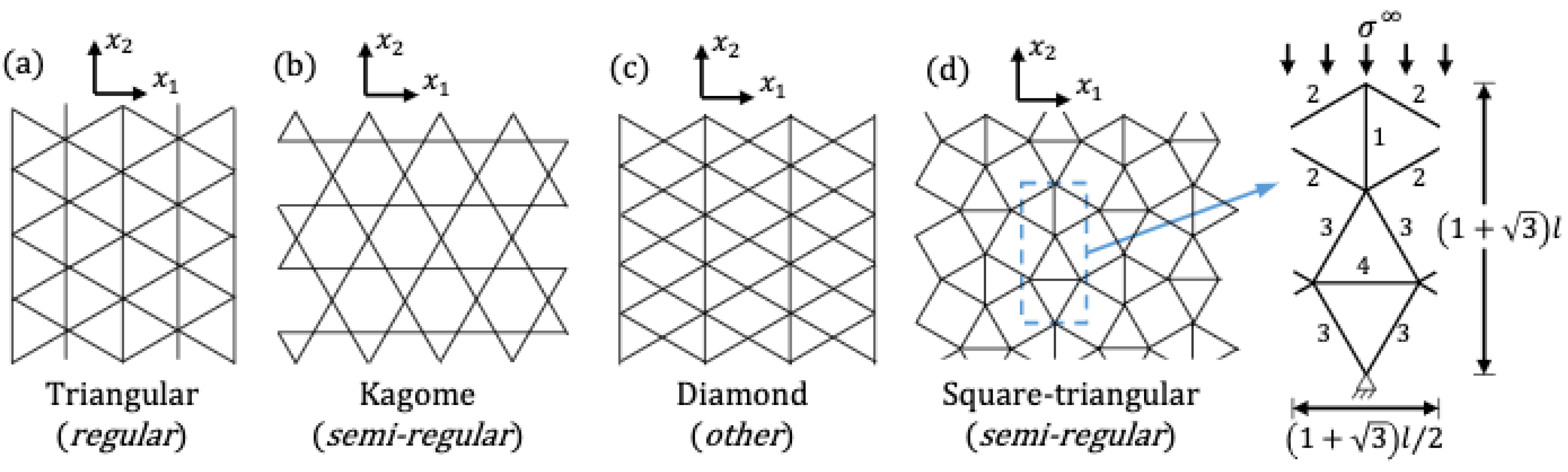
2. Background
3. Homogenization Methods
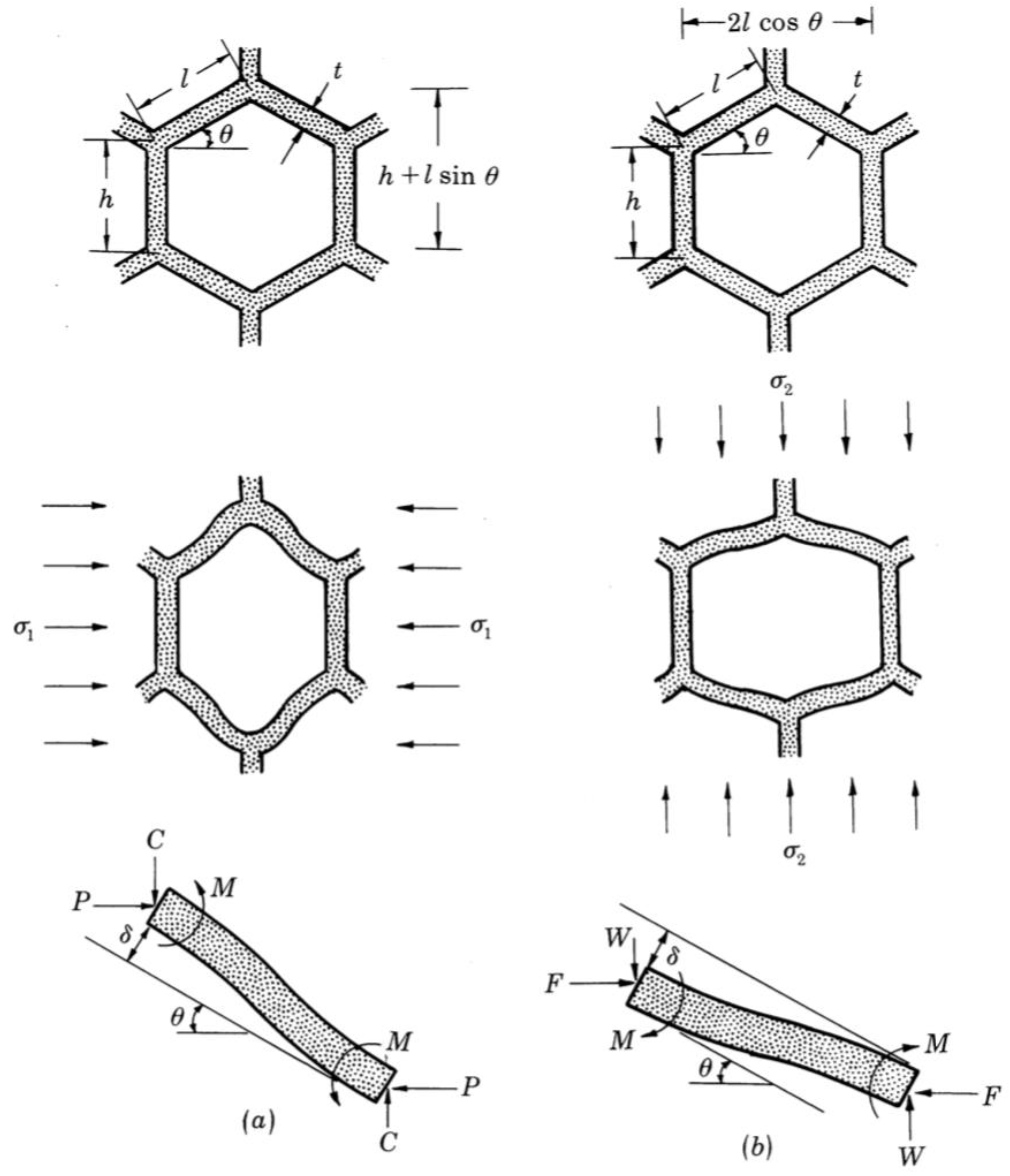
3.1. Beam Theory Approach
3.2. Strain Energy Equivalence: Surface Average Approach and Volume Average Approach
3.3. Micropolar Theory
3.4. Solid-State Physics Approach: Bloch’s Theorem and Cauchy Born Hypothesis
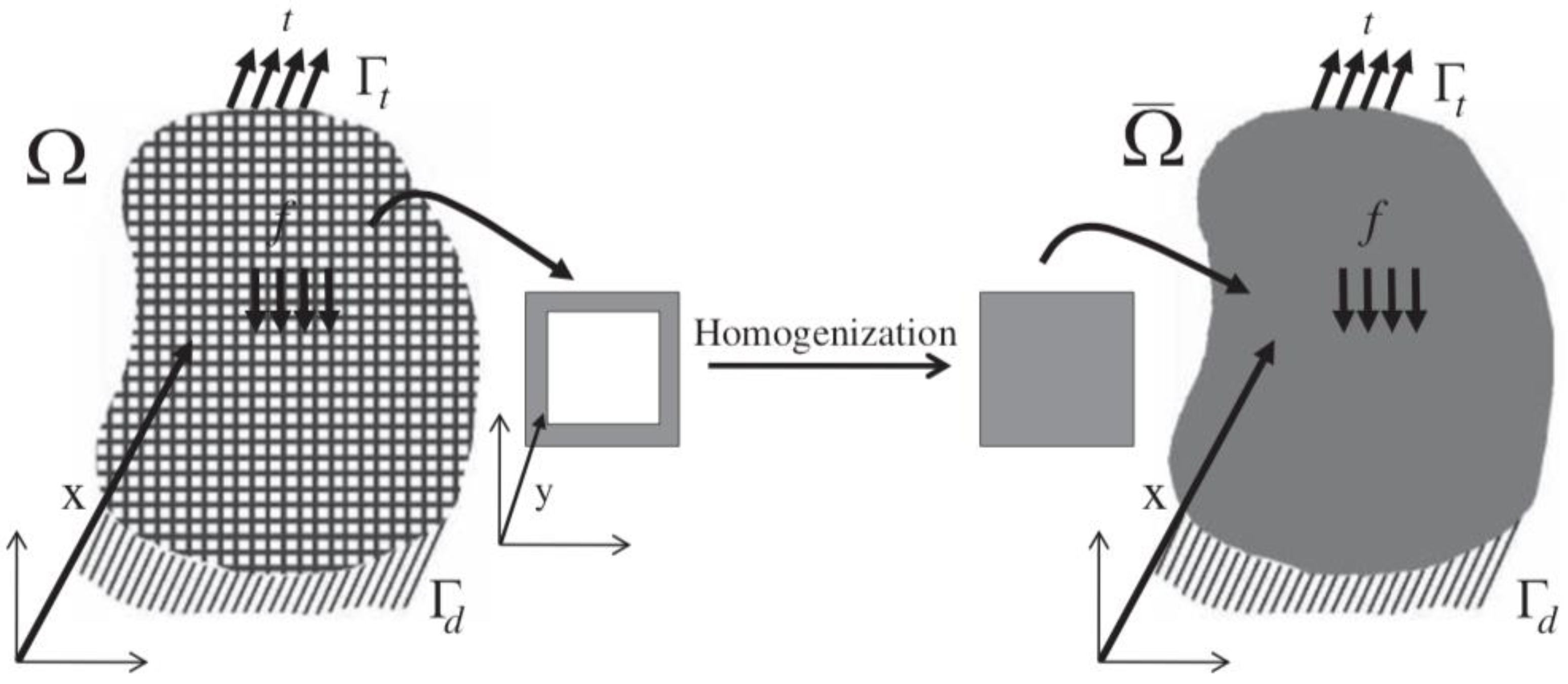
3.5. Asymptotic Homogenization Approach
3.6. Multi-Scale Homogenization Method for Lattice Materials
3.7. Machine Learning Approach: Data-Driven Model
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schroeder, V.; Savagatrup, S.; He, M.; Lin, S.; Swager, T.M. Carbon nanotube chemical sensors. Chem. Rev. 2019, 119, 599–663. [Google Scholar] [CrossRef] [PubMed]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Rashed, M.G.; Ashraf, M.; Mines, R.A.W.; Hazell, P.J. Metallic microlattice materials: A current state of the art on manufacturing, mechanical properties and applications. Mater. Des. 2016, 95, 518–533. [Google Scholar] [CrossRef]
- Bici, M.; Brischetto, S.; Campana, F.; Ferro, C.G.; Seclì, C.; Varetti, S.; Maggiore, P.; Mazza, A. Development of a multifunctional panel for aerospace use through SLM additive manufacturing. Procedia CIRP 2018, 67, 215–220. [Google Scholar] [CrossRef]
- Han, Y.; Wang, P.; Fan, H.; Sun, F.; Chen, L.; Fang, D. Free vibration of CFRC lattice-core sandwich cylinder with attached mass. Compos. Sci. Technol. 2015, 118, 226–235. [Google Scholar] [CrossRef]
- Jenett, B.E.; Calisch, S.E.; Cellucci, D.; Cramer, N.; Gershenfeld, N.A.; Swei, S.; Cheung, K.C. Digital Morphing Wing: Active Wing Shaping Concept Using Composite Lattice-Based Cellular Structures. Soft Robot. 2017, 4, 33–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.; Sun, F.; Wang, P.; Fan, H.; Fang, D. A novel carbon fiber reinforced lattice truss sandwich cylinder: Fabrication and experiments. Compos. Part A Appl. Sci. Manuf. 2016, 81, 313–322. [Google Scholar] [CrossRef]
- Wei, K.; Peng, Y.; Qu, Z.; Zhou, H.; Pei, Y.; Fang, D. Lightweight composite lattice cylindrical shells with novel character of tailorable thermal expansion. Int. J. Mech. Sci. 2018, 137, 77–85. [Google Scholar] [CrossRef]
- Cundy, H.M. Mathematical Models; Oxford University Press: Oxford, UK, 1956. [Google Scholar]
- Their, T.; St-Pierre, L. Stiffness and strength of a semi-regular lattice. Raken. Mek. 2017, 50, 137–140. [Google Scholar] [CrossRef]
- Arabnejad, S.; Pasini, D. Mechanical properties of lattice materials via asymptotic homogenization and comparison with alternative homogenization methods. Int. J. Mech. Sci. 2013, 77, 249–262. [Google Scholar] [CrossRef] [Green Version]
- Phani, A.S.; Hussein, M.I. Dynamics of Lattice Materials; Wiley Online Library: Hoboken, NJ, USA, 2017. [Google Scholar]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. London. A Math. Phys. Sci. 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Wang, A.-J.; McDowell, D.L. In-Plane Stiffness and Yield Strength of Periodic Metal Honeycombs. J. Eng. Mater. Technol. 2004, 126, 137–156. [Google Scholar] [CrossRef]
- Kelsey, S.; Gellatly, R.; Clark, B. The Shear Modulus of Foil Honeycomb Cores. Aircr. Eng. Aerosp. Technol. 1958, 30, 294–302. [Google Scholar] [CrossRef]
- Masters, I.; Evans, K. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Wang, X.L.; Stronge, W.J. Micropolar theory for two–dimensional stresses in elastic honeycomb. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 2091–2116. [Google Scholar] [CrossRef]
- Elsayed, M.S.; Pasini, D. Analysis of the elastostatic specific stiffness of 2D stretching-dominated lattice materials. Mech. Mater. 2010, 42, 709–725. [Google Scholar] [CrossRef] [Green Version]
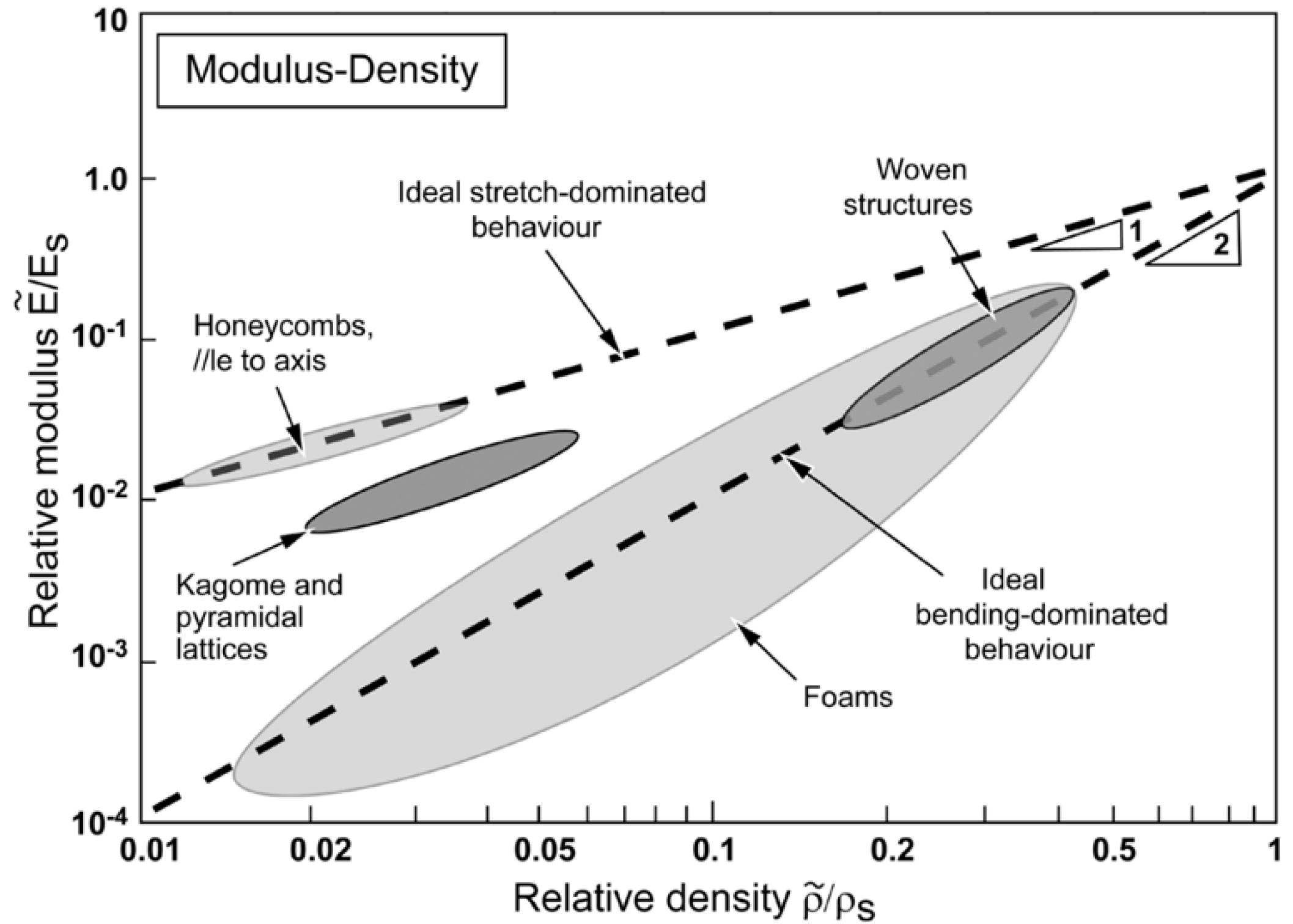
- Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Gonella, S.; Ruzzene, M. Homogenization and equivalent in-plane properties of two-dimensional periodic lattices. Int. J. Solids Struct. 2008, 45, 2897–2915. [Google Scholar] [CrossRef] [Green Version]
- Rezakhani, R.; Cusatis, G. Generalized mathematical homogenization of the lattice discrete particle model. In Proceedings of the 8th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Toledo, Spain, 10–14 March 2013; pp. 261–271. [Google Scholar]
- Tollenaere, H.; Cailleire, D. Continuous Modelling of Lattice Structures by Homogenization. Dev. Comput. Aided Des. Model. Civ. Eng. 2009, 29, 699–705. [Google Scholar] [CrossRef]
- Vigliotti, A.; Deshpande, V.S.; Pasini, D. Non linear constitutive models for lattice materials. J. Mech. Phys. Solids 2014, 64, 44–60. [Google Scholar] [CrossRef] [Green Version]
- Wang, A.-J.; McDowell, D. Yield surfaces of various periodic metal honeycombs at intermediate relative density. Int. J. Plast. 2005, 21, 285–320. [Google Scholar] [CrossRef]
- Park, S.-I.; Rosen, D.W.; Choi, S.-K.; Duty, C.E. Effective Mechanical Properties of Lattice Material Fabricated by Material Extrusion Additive Manufacturing. Addit. Manuf. 2014, 1, 12–23. [Google Scholar] [CrossRef]
- Salehian, A.; Inman, D.J. Dynamic analysis of a lattice structure by homogenization: Experimental validation. J. Sound Vib. 2008, 316, 180–197. [Google Scholar] [CrossRef]
- Du, Y.; Gu, D.; Xi, L.; Dai, D.; Gao, T.; Zhu, J.; Ma, C. Laser additive manufacturing of bio-inspired lattice structure: Forming quality, microstructure and energy absorption behavior. Mater. Sci. Eng. A 2020, 773, 138857. [Google Scholar] [CrossRef]
- Rehme, O.; Emmelmann, C. Rapid manufacturing of lattice structures with selective laser melting. In Laser-Based Micropackaging; International Society for Optics and Photonics: San Jose, CA, USA, 2006; Volume 6107, p. 61070K. [Google Scholar]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 325–332. [Google Scholar]
- Tran, H.T.; Chen, Q.; Mohan, J.; To, A.C. A new method for predicting cracking at the interface between solid and lattice support during laser powder bed fusion additive manufacturing. Addit. Manuf. 2020, 32, 101050. [Google Scholar] [CrossRef]
- Cheng, L.; Liang, X.; Belski, E.; Wang, X.; Sietins, J.M.; Ludwick, S.; To, A.C. Natural Frequency Optimization of Variable-Density Additive Manufactured Lattice Structure: Theory and Experimental Validation. J. Manuf. Sci. Eng. 2018, 140. [Google Scholar] [CrossRef]
- Christensen, R. Mechanics of cellular and other low-density materials. Int. J. Solids Struct. 2000, 37, 93–104. [Google Scholar] [CrossRef]
- Barchiesi, E.; Khakalo, S. Variational asymptotic homogenization of beam-like square lattice structures. Math. Mech. Solids 2019, 24, 3295–3318. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology optimization I—homogenization theory for media with periodic structure. Comput. Struct. 1998, 69, 707–717. [Google Scholar] [CrossRef]
- Koeppe, A.; Padilla, C.A.H.; Voshage, M.; Schleifenbaum, J.H.; Markert, B. Efficient numerical modeling of 3D-printed lattice-cell structures using neural networks. Manuf. Lett. 2018, 15, 147–150. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Linear multiscale analysis and finite element validation of stretching and bending dominated lattice materials. Mech. Mater. 2012, 46, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Askar, A.; Cakmak, A. A structural model of a micropolar continuum. Int. J. Eng. Sci. 1968, 6, 583–589. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.N.; Hu, G.K.; Sun, Q.; Zheng, Q.S. Micropolar continuum modelling of bi-dimensional tetrachiral lattices. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20130734. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.S.; McDowell, D.L. Generalized continuum modeling of 2-D periodic cellular solids. Int. J. Solids Struct. 2004, 41, 7399–7422. [Google Scholar] [CrossRef]
- Chiras, S.; Mumm, D.; Evans, A.; Wicks, N.; Hutchinson, J.; Dharmasena, K.; Wadley, H.; Fichter, S. The structural performance of near-optimized truss core panels. Int. J. Solids Struct. 2002, 39, 4093–4115. [Google Scholar] [CrossRef] [Green Version]
- Alwattar, T.A.; Mian, A. Development of an Elastic Material Model for BCC Lattice Cell Structures Using Finite Element Analysis and Neural Networks Approaches. J. Compos. Sci. 2019, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Arbabi, H.; Bunder, J.E.; Samaey, G.; Roberts, A.J.; Kevrekidis, I.G. Linking Machine Learning with Multiscale Numerics: Data-Driven Discovery of Homogenized Equations. JOM 2020, 72, 4444–4457. [Google Scholar] [CrossRef]
- Kollmann, H.T.; Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Deep learning for topology optimization of 2D metamaterials. Mater. Des. 2020, 196, 109098. [Google Scholar] [CrossRef]
- Settgast, C.; Hütter, G.; Kuna, M.; Abendroth, M. A hybrid approach to simulate the homogenized irreversible elastic–plastic deformations and damage of foams by neural networks. Int. J. Plast. 2020, 126, 102624. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Cheng, G.; Liu, S.; Liu, L. Comparison of prediction on effective elastic property and shape optimization of truss material with periodic microstructure. Int. J. Mech. Sci. 2006, 48, 400–413. [Google Scholar] [CrossRef]
- Xia, Z.; Zhou, C.; Yong, Q.; Wang, X. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites. Int. J. Solids Struct. 2006, 43, 266–278. [Google Scholar] [CrossRef] [Green Version]
- Hohe, J.R.; Becker, W. Effective stress-strain relations for two-dimensional cellular sandwich cores: Homogenization, material models, and properties. Appl. Mech. Rev. 2002, 55, 61–87. [Google Scholar] [CrossRef]
- Buannic, N.; Cartraud, P.; Quesnel, T. Homogenization of corrugated core sandwich panels. Compos. Struct. 2003, 59, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Hohe, J.; Becker, W. Determination of the elasticity tensor of non-orthotropic cellular sandwich cores. Tech. Mech.-Eur. J. Eng. Mech. 1999, 19, 259–268. [Google Scholar]
- Castaneda, P.P.; Suquet, P. On the effective mechanical behavior of weakly inhomogeneous nonlinear materials. Eur. J. Mech A Solids 1995, 14, 205–236. [Google Scholar]
- Staszak, N.; Garbowski, T.; Szymczak-Graczyk, A. Solid Truss to Shell Numerical Homogenization of Prefabricated Composite Slabs. Materials 2021, 14, 4120. [Google Scholar] [CrossRef] [PubMed]
- Cosserat, E.; Cosserat, F. Théorie des Corps Déformables; A. Hermann et fils: Strasbourg, France, 1909. [Google Scholar]
- Eringen, A.C. Linear theory of micropolar elasticity. Theory Micropolar Elast. 1965, 15, 909–923. [Google Scholar] [CrossRef]
- Phani, S.; Woodhouse, J.; Fleck, N.A. Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef] [Green Version]
- Bloch, F. Über die Quantenmechanik der Elektronen in Kristallgittern. Eur. Phys. J. A 1929, 52, 555–600. [Google Scholar] [CrossRef]
- Langley, R. A Note On The Force Boundary Conditions For Two-Dimensional Periodic Structures With Corner Freedoms. J. Sound Vib. 1993, 167, 377–381. [Google Scholar] [CrossRef]
- Langley, R.; Bardell, N.; Ruivo, H. The response of two-dimensional periodic structures to harmonic point loading: A theoretical and experimental study of a beam grillage. J. Sound Vib. 1997, 207, 521–535. [Google Scholar] [CrossRef]
- Born, M.; Huang, K.; Lax, M. Dynamical Theory of Crystal Lattices. Am. J. Phys. 1955, 23, 474. [Google Scholar] [CrossRef]
- Gurtin, M. Phase Transformations and Material Instabilities in Solids; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hutchinson, R.G. Mechanics of Lattice Materials; University of Cambridge: Cambridge, UK, 2005. [Google Scholar]
- Takano, N.; Ohnishi, Y.; Zako, M.; Nishiyabu, K. Microstructure-based deep-drawing simulation of knitted fabric reinforced thermoplastics by homogenization theory. Int. J. Solids Struct. 2001, 38, 6333–6356. [Google Scholar] [CrossRef]
- Hollister, S.J.; Kikuchi, N. A comparison of homogenization and standard mechanics analyses for periodic porous composites. Comput. Mech. 1992, 10, 73–95. [Google Scholar] [CrossRef] [Green Version]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Al-Haik, M.; Hussaini, M.; Garmestani, H. Prediction of nonlinear viscoelastic behavior of polymeric composites using an artificial neural network. Int. J. Plast. 2006, 22, 1367–1392. [Google Scholar] [CrossRef]
- Fritzen, F.; Fernández, M.; Larsson, F. On-the-Fly Adaptivity for Nonlinear Twoscale Simulations Using Artificial Neural Networks and Reduced Order Modeling. Front. Mater. 2019, 6, 75. [Google Scholar] [CrossRef]
- Le, B.A.; Yvonnet, J.; He, Q. Computational homogenization of nonlinear elastic materials using neural networks. Int. J. Numer. Methods Eng. 2015, 104, 1061–1084. [Google Scholar] [CrossRef]
- Zopf, C.; Kaliske, M. Numerical characterisation of uncured elastomers by a neural network based approach. Comput. Struct. 2017, 182, 504–525. [Google Scholar] [CrossRef]
- Wojciechowski, M. Application of artificial neural network in soil parameter identification for deep excavation numerical model. Comput. Assist. Methods Eng. Sci. 2017, 18, 303–311. [Google Scholar]
- Fan, Z.; Yan, J.; Wallin, M.; Ristinmaa, M.; Niu, B.; Zhao, G. Multiscale eigenfrequency optimization of multimaterial lattice structures based on the asymptotic homogenization method. Struct. Multidiscip. Optim. 2019, 61, 983–998. [Google Scholar] [CrossRef]
- Vlădulescu, F.; Constantinescu, D.M. Lattice structure optimization and homogenization through finite element analyses. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1490–1502. [Google Scholar] [CrossRef]
- Xu, L.; Qian, Z. Topology optimization and de-homogenization of graded lattice structures based on asymptotic homogenization. Compos. Struct. 2021, 277, 114633. [Google Scholar] [CrossRef]
- Zhang, J.; Sato, Y.; Yanagimoto, J. Homogenization-based topology optimization integrated with elastically isotropic lattices for additive manufacturing of ultralight and ultrastiff structures. CIRP Ann. 2021, 70, 111–114. [Google Scholar] [CrossRef]


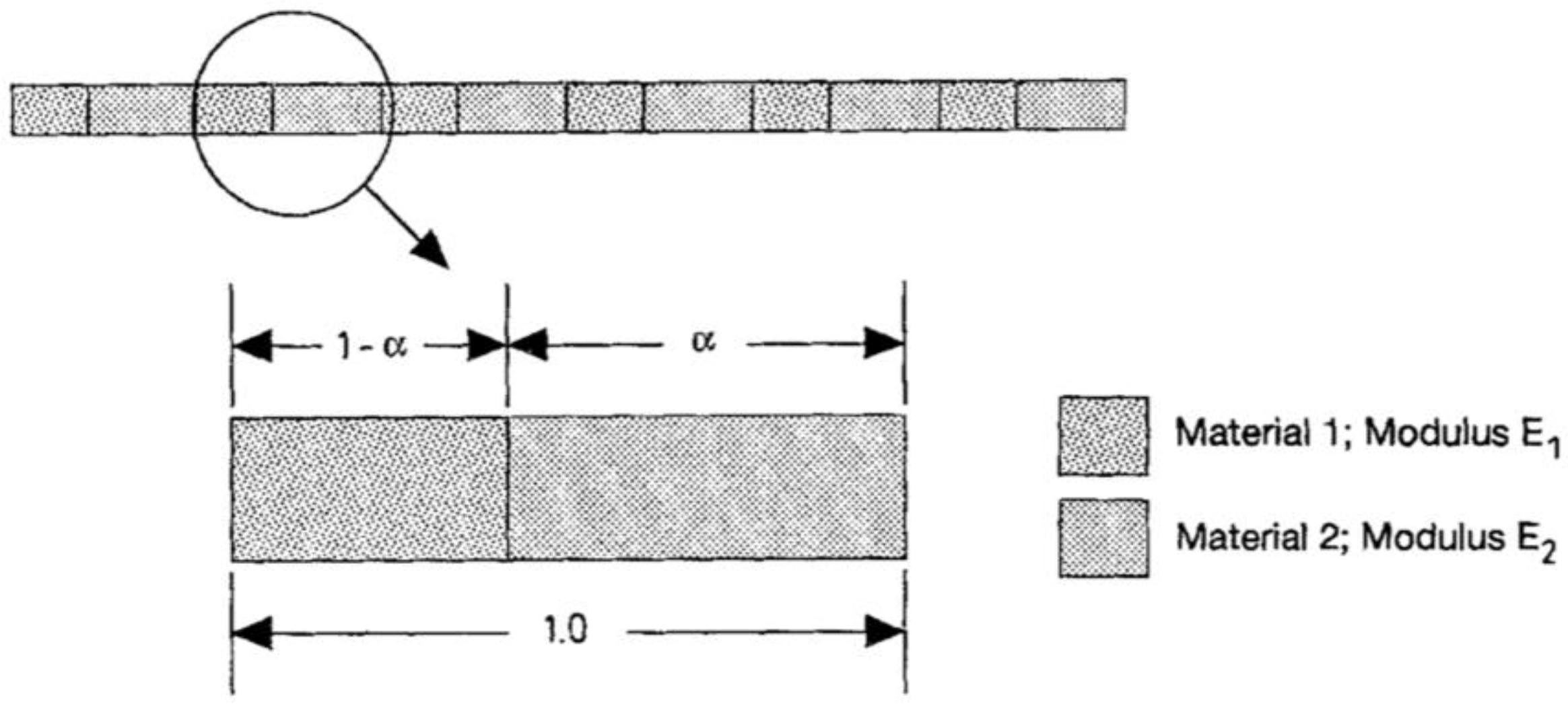
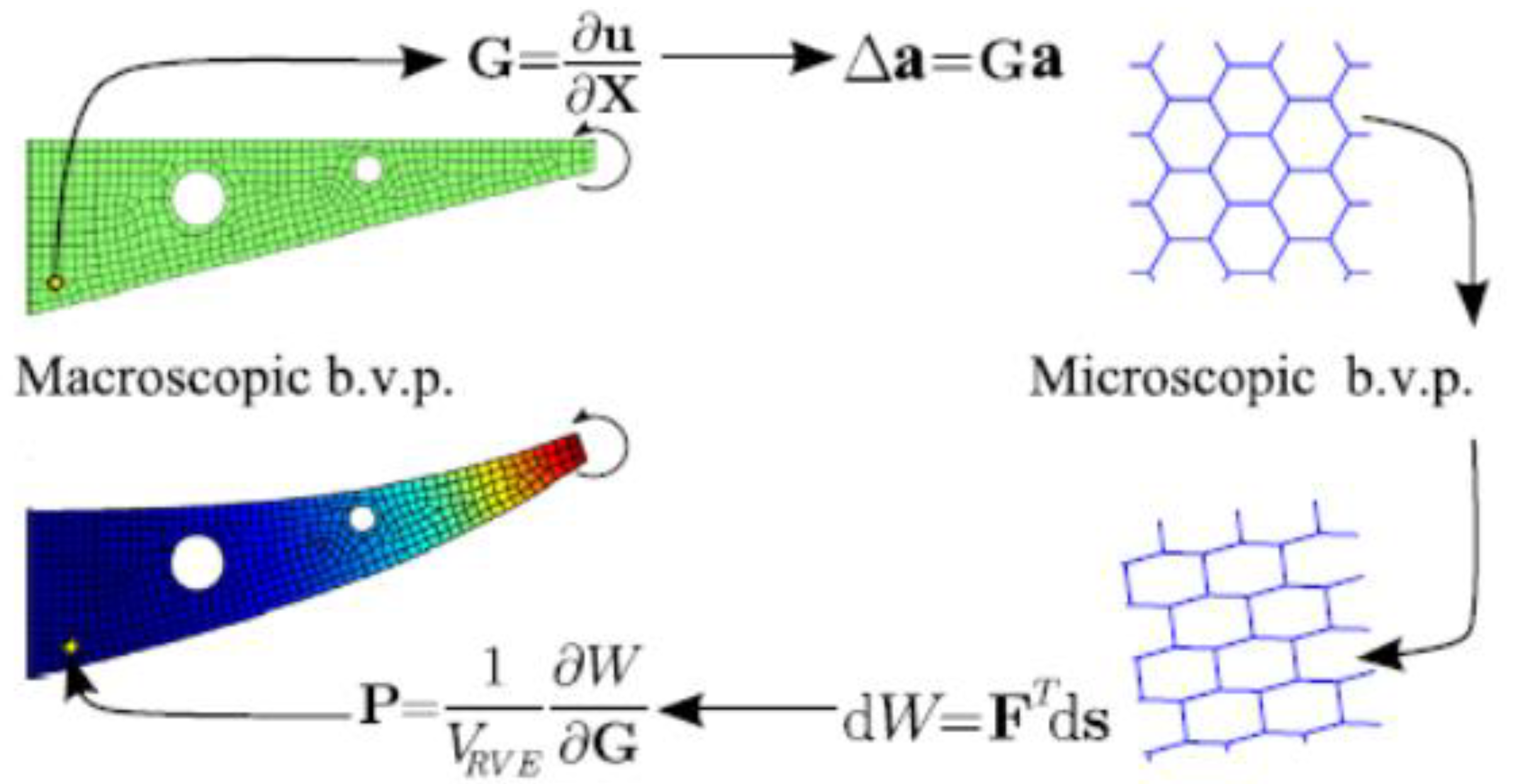

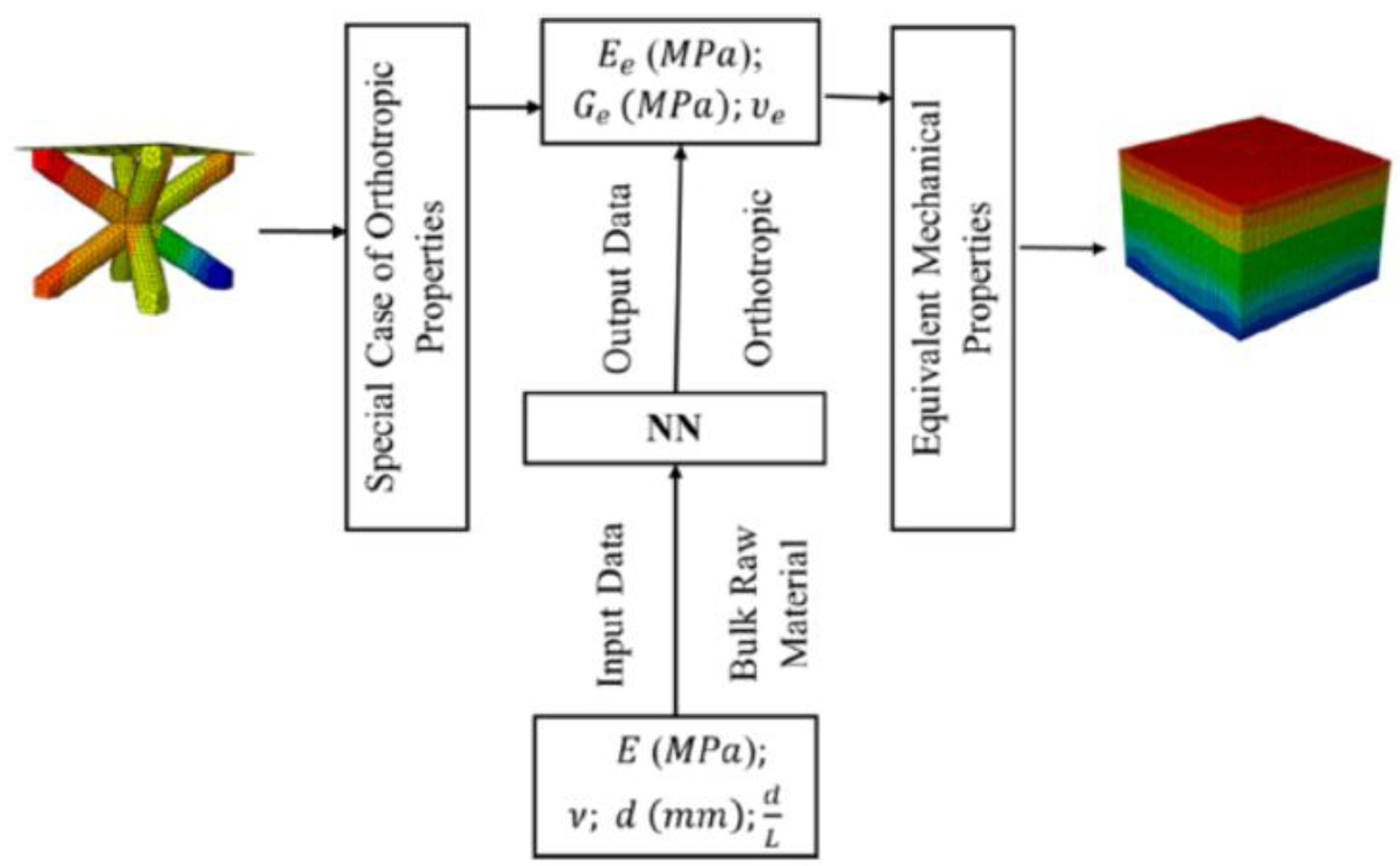
| Method | Underlying Theory | Highlights | Limitation |
|---|---|---|---|
| Beam Theory Approach [13,14,16,33] | Apply beam theory analysis on a single cell and assume uniform over the RVE |
|
|
| Strain Energy Equivalence [48,49,50,51,52] | The averages of particular mechanical properties with respect to either the surface of the volume have to be equal in order to obtain the equivalence condition of effective medium and its RVE |
|
|
| Micropolar Theory [17,38,39,40] | Introduce a new variable, microscopic rotation, in addition to translational deformations and assume that both displacement and rotations of a point are independent kinematic quantities |
|
|
| Bloch’s Theorem and Cauchy–Born Hypothesis [18,55] |
|
|
|
| Asymptotic Homogenization (AH) [11,35,62] |
|
|
|
| Multi-Scale Homogenization Method [24,37,64] | This method utilizes a two-scale approach
|
|
|
| Machine Learning Approach [36,42,43,44,45] | Use neural networks to do constitutive modeling based on either experiments or homogenization results as training data |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somnic, J.; Jo, B.W. Status and Challenges in Homogenization Methods for Lattice Materials. Materials 2022, 15, 605. https://doi.org/10.3390/ma15020605
Somnic J, Jo BW. Status and Challenges in Homogenization Methods for Lattice Materials. Materials. 2022; 15(2):605. https://doi.org/10.3390/ma15020605
Chicago/Turabian StyleSomnic, Jacobs, and Bruce W. Jo. 2022. "Status and Challenges in Homogenization Methods for Lattice Materials" Materials 15, no. 2: 605. https://doi.org/10.3390/ma15020605
APA StyleSomnic, J., & Jo, B. W. (2022). Status and Challenges in Homogenization Methods for Lattice Materials. Materials, 15(2), 605. https://doi.org/10.3390/ma15020605







