Modeling of Bimodular Bone Specimen under Four-Point Bending Fatigue Loading
Abstract
:1. Introduction
2. Materials and Methods
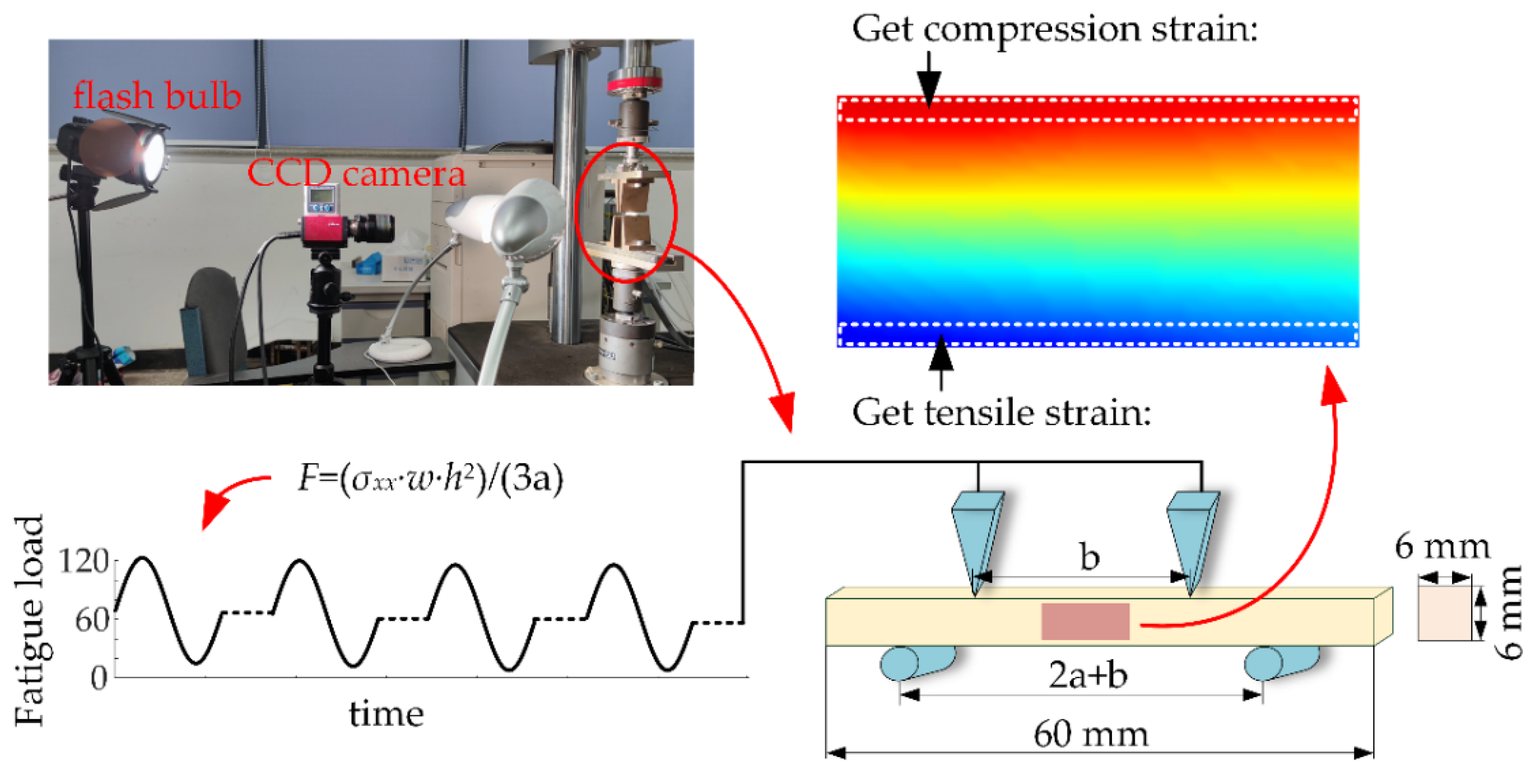
2.1. Fatigue Experiment
2.2. Digital Image Correlation
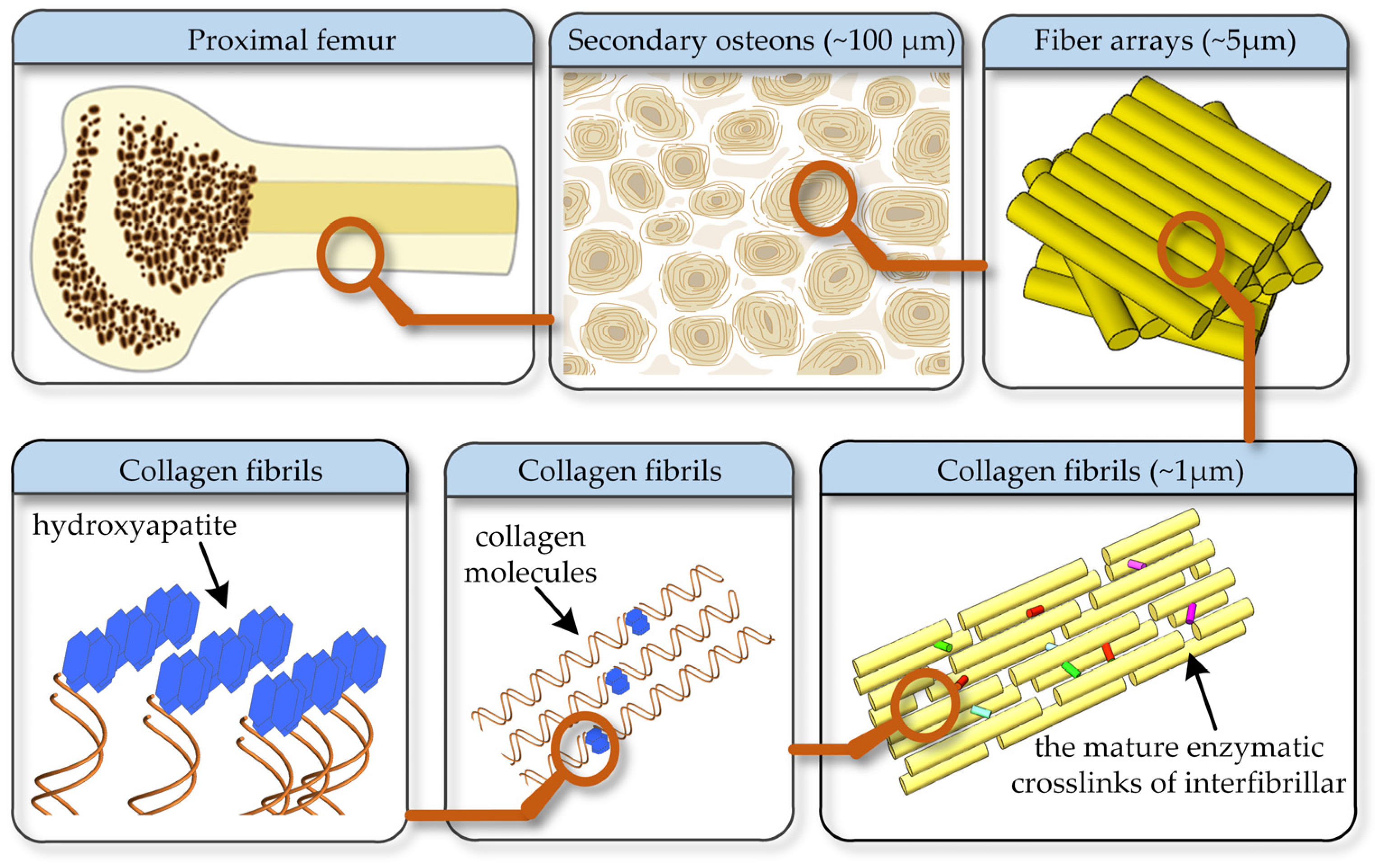
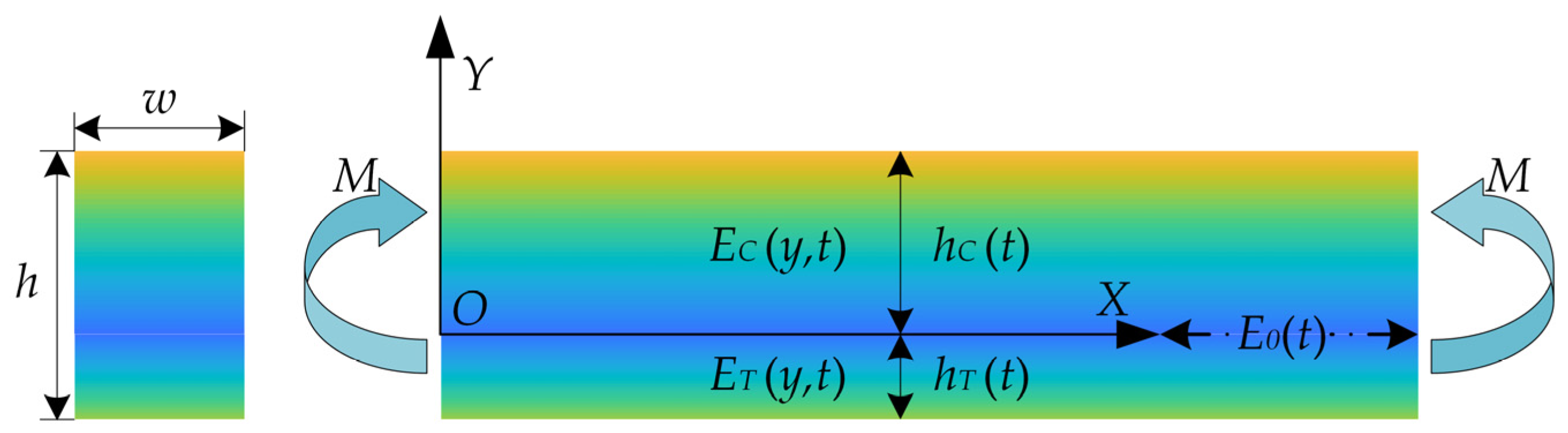
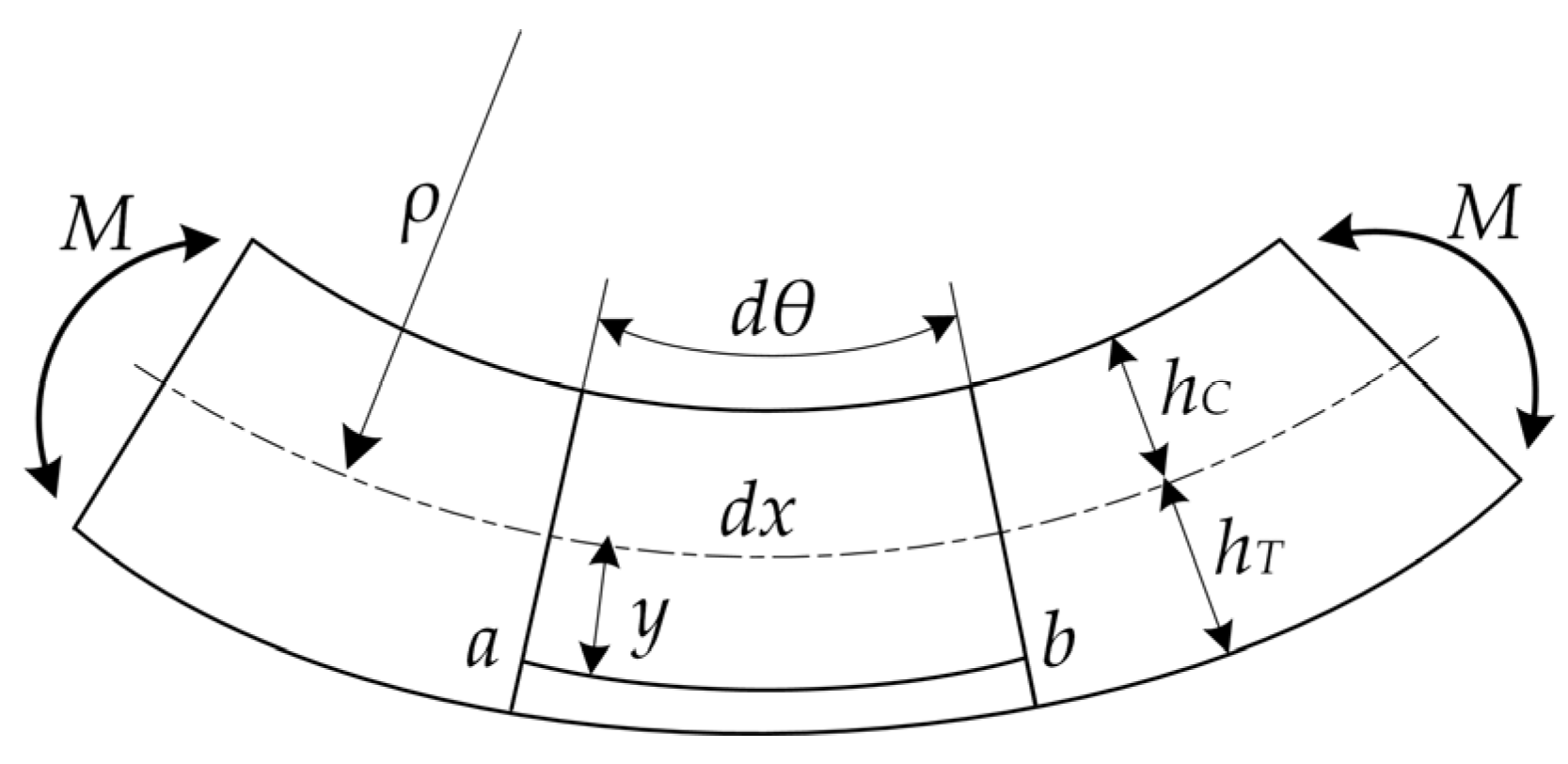
2.3. The Bimodular Structure of Cortical Bone under Pure Bending Fatigue
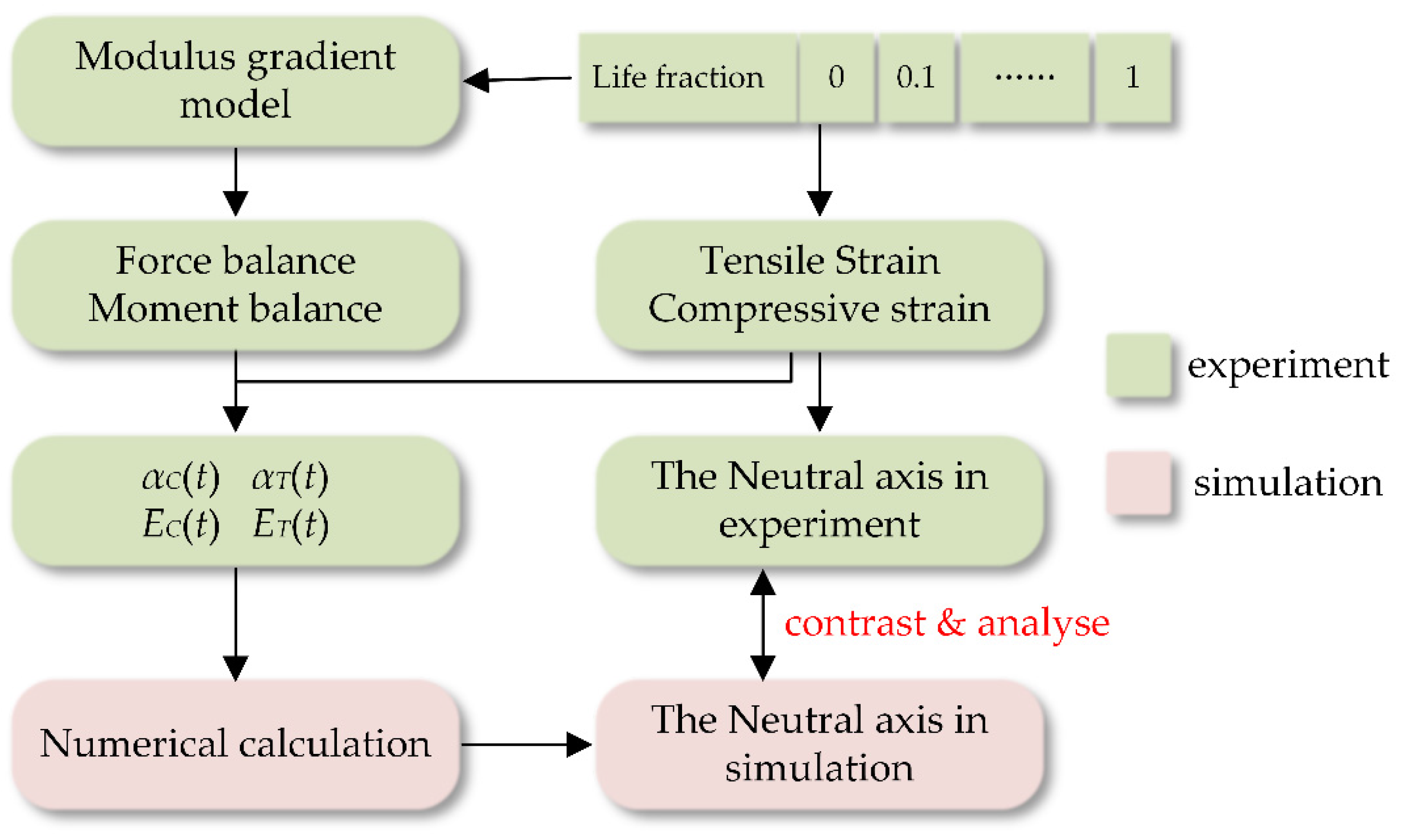
2.4. Finite Element Method Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Bone Source Statement
References
- Fujibayashi, S.; Kim, H.-M.; Neo, M.; Uchida, M.; Kokubo, T.; Nakamura, T. Repair of segmental long bone defect in rabbit femur using bioactive titanium cylindrical mesh cage. Biomaterials 2003, 24, 3445–3451. [Google Scholar] [CrossRef]
- Jager, I.; Fratzl, P. Mineralized collagen fibrils: A mechanical model with a staggered arrangement of mineral particles. Biophys. J. 2000, 79, 1737–1746. [Google Scholar] [CrossRef] [Green Version]
- Yoshikawa, H.; Myoui, A. Bone tissue engineering with porous hydroxyapatite ceramics. J. Artif. Organs 2005, 8, 131–136. [Google Scholar] [CrossRef]
- Qin, Q.H.; Qu, C.Y.; Ye, Q.J. Thermoelectroelastic solutions for surface bone remodeling under axial and transverse loads. Biomaterials 2005, 26, 6798–6810. [Google Scholar] [CrossRef]
- Qu, C.Y.; Qin, Q.H.; Kang, Y.L. A hypothetical mechanism of bone remodeling and modeling under electromagnetic loads. Biomaterials 2006, 27, 4050–4057. [Google Scholar] [CrossRef] [PubMed]
- Rho, J.-Y.; Kuhn-Spearing, L.; Zioupos, P. Mechanical properties and the hierarchical structure of bone. Med. Eng. Phys. 1998, 20, 92–102. [Google Scholar] [CrossRef]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Zimmermann, E.A.; Ritchie, R.O. Bone as a Structural Material. Adv. Healthc. Mater. 2015, 4, 1287–1304. [Google Scholar] [CrossRef]
- Diab, T.; Vashishth, D. Effects of damage morphology on cortical bone fragility. Bone 2005, 37, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Abdel-Wahab, A.; Silberschmidt, V.V. Analysis of fracture processes in cortical bone tissue. Eng. Fract. Mech. 2013, 110, 448–458. [Google Scholar] [CrossRef] [Green Version]
- Nalla, R.K.; StoLken, J.S.; Kinney, J.H.; Ritchie, R.O. Fracture in human cortical bone: Local fracture criteria and toughening mechanisms. J. Biomech. 2005, 38, 1517–1525. [Google Scholar] [CrossRef] [PubMed]
- Tai, K.; Dao, M.; Suresh, S.; Palazoglu, A.; Ortiz, C. Nanoscale heterogeneity promotes energy dissipation in bone. Nat. Mater. 2007, 6, 454–462. [Google Scholar] [CrossRef] [PubMed]
- Barak, M.M.; Currey, J.D.; Weiner, S.; Shahar, R. Are tensile and compressive Young’s moduli of compact bone different? J. Mech. Behav. Biomed. Mater. 2009, 2, 51–60. [Google Scholar] [CrossRef]
- Currey, J. Measurement of the Mechanical Properties of Bone: A Recent History. Clin. Orthop. Relat. Res. 2009, 467, 1948–1954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, M.; Au, C.L.; Lai, P.K.; Bonfield, W. Tensile and Compressive Behaviours and Properties of a Bone Analogue Biomaterial. Key Engineering Materials. Key Eng. Mater. 2005, 284–286, 693–696. [Google Scholar] [CrossRef]
- Yeni, Y.N.; Dong, X.N.; Fyhrie, D.P.; Les, C.M. The dependence between the strength and stiffness of cancellous and cortical bone tissue for tension and compression: Extension of a unifying principle. Bio-Med. Mater. Eng. 2004, 14, 303–310. [Google Scholar]
- Benecke, G.; Kerschnitzki, M.; Fratzl, P.; Gupta, H.S. Digital image correlation shows localized deformation bands in inelastic loading of fibrolamellar bone. J. Mater. Res. 2009, 24, 421–429. [Google Scholar] [CrossRef]
- Reilly, G.C.; Currey, J.D. The development of microcracking and failure in bone depends on the loading mode to which it is adapted. J. Exp. Biol. 1999, 202, 543–552. [Google Scholar] [CrossRef]
- Boyce, T.M.; Fyhrie, D.P.; Glotkowski, M.C.; Radin, E.L.; Schaffler, M.B. Damage type and strain mode associations in human compact bone bending fatigue. J. Orthop. Res. 1998, 16, 322–329. [Google Scholar] [CrossRef] [PubMed]
- Diab, T.; Condon, K.W.; Burr, D.B.; Vashishth, D. Age-related change in the damage morphology of human cortical bone and its role in bone fragility. Bone 2006, 38, 427–431. [Google Scholar] [CrossRef]
- Pidaparti, R.M.; Vogt, A. Experimental investigation of Poisson’s ratio as a damage parameter for bone fatigue. J. Biomed. Mater. Res. 2001, 59, 282–287. [Google Scholar] [CrossRef]
- Pattin, C.A.; Caler, W.E.; Carter, D.R. Cyclic mechanical property degradation during fatigue loading of cortical bone. J. Biomech. 1996, 29, 69–79. [Google Scholar] [CrossRef]
- Tran, A.D.; Bert, C.W. Bending of thick beams of bimodulus materials. Compos. Struct. 1982, 15, 627–642. [Google Scholar] [CrossRef]
- Ambartsumyan, S.A. Basic equations and relations in the theory of anisotropic bodies with different moduli in tension and compression. Inzh. Zhur. MTT (Proc. Acad. Sci. USSR Eng. J. Mech. Solids) 1969, 3, 51–61. [Google Scholar]
- Jones, R.M. Stress-strain relations for materials with different moduli in tension and compression. AIAA J. 1977, 15, 16–23. [Google Scholar] [CrossRef]
- Draper, E.; Goodship, A.E. A novel technique for four-point bending of small bone samples with semi-automatic analysis. J. Biomech. 2003, 36, 1497–1502. [Google Scholar] [CrossRef]
- Chen, Y.X.; Yang, D.S.; Ma, Y.S.; Tan, X.J.; Shi, Z.; Li, T.; Si, H.P. Experimental Investigation on the Mechanical Behavior of Bovine Bone Using Digital Image Correlation Technique. Appl. Bionics Biomech. 2015, 2015, 609132. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Lu, Z.X.; Xie, H.M. Mean intensity gradient: An effective global parameter for quality assessment of the speckle patterns used in digital image correlation. Opt. Lasers Eng. 2010, 48, 469–477. [Google Scholar] [CrossRef]
- Thompson, M.S.; Schell, H.; Lienau, J.; Duda, G.N. Digital image correlation: A technique for determining local mechanical conditions within early bone callus. Med. Eng. Phys. 2007, 29, 820–823. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.; Song, H.; Kang, Y. Experimental investigation of deformation and failure mechanisms in rock under indentation by digital image correlation. Eng. Fract. Mech. 2012, 96, 667–675. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.Y.; Dong, J.; He, X.T. One-Dimensional and Two-Dimensional Analytical Solutions for Functionally Graded Beams with Different Moduli in Tension and Compression. Materials 2018, 11, 830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, X.T.; Yang, Z.X.; Jing, H.X.; Sun, J.Y. One-Dimensional Theoretical Solution and Two-Dimensional Numerical Simulation for Functionally-Graded Piezoelectric Cantilever Beams with Different Properties in Tension and Compression. Polymers 2019, 11, 1728. [Google Scholar]
- Vashishth, D.; Koontz, J.; Qiu, S.J.; Lundin-Cannon, D.; Fyhrie, D.P. In vivo diffuse damage in human vertebral trabecular bone. Bone 2000, 26, 147–152. [Google Scholar] [CrossRef]
- Dominguez, V.M.; Agnew, A.M. Microdamage as a bone quality component: Practical guidelines for the two-dimensional analysis of linear microcracks in human cortical bone. JBMR Plus 2019, 3, e10203. [Google Scholar] [CrossRef] [Green Version]
- Ota, M.; Ishihara, S.; Fleck, C.; Goshima, T.; Eifler, D. Effect of stress ratio on the fatigue behaviour of compact bone. Proc. Inst. Mech. Eng. Part H 2005, 219, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, P.; Moore, T.; Gibson, L.J. A phenomenological model for predicting fatigue life in bovine trabecular bone. J. Biomech. Eng. 2004, 126, 330–339. [Google Scholar] [CrossRef] [PubMed]
- He, X.T.; Sun, J.Y.; Wang, Z.X.; Qiang, C.; Zheng, Z.L. General perturbation solution of large-deflection circular plate with different moduli in tension and compression under various edge conditions. Int. J. Non-Linear Mech. 2013, 55, 110–119. [Google Scholar] [CrossRef]
- He, X.T.; Pei, X.X.; Sun, J.Y.; Zheng, Z.L. Simplified theory and analytical solution for functionally graded thin plates with different moduli in tension and compression. Mech. Res. Commun. 2016, 74, 72–80. [Google Scholar] [CrossRef]



| Specimen | a (mm) | b (mm) | εC (με) | εT (με) | σxx (MPa) | Ne | N |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 34 | 3157 | 2953 | 120 | 200 | 8117 |
| 2 | 4 | 34 | 2749 | 2731 | 120 | 200 | 10,962 |
| 3 | 4 | 34 | 2726 | 2604 | 120 | 200 | 9279 |
| 4 | 4 | 34 | 2644 | 2544 | 120 | 200 | 12,665 |
| Average | 4 | 34 | 2819 | 2807 | 120 | 200 | 10,270 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Meng, X.; Qu, C. Modeling of Bimodular Bone Specimen under Four-Point Bending Fatigue Loading. Materials 2022, 15, 474. https://doi.org/10.3390/ma15020474
Yan Y, Meng X, Qu C. Modeling of Bimodular Bone Specimen under Four-Point Bending Fatigue Loading. Materials. 2022; 15(2):474. https://doi.org/10.3390/ma15020474
Chicago/Turabian StyleYan, Yufan, Xianjia Meng, and Chuanyong Qu. 2022. "Modeling of Bimodular Bone Specimen under Four-Point Bending Fatigue Loading" Materials 15, no. 2: 474. https://doi.org/10.3390/ma15020474
APA StyleYan, Y., Meng, X., & Qu, C. (2022). Modeling of Bimodular Bone Specimen under Four-Point Bending Fatigue Loading. Materials, 15(2), 474. https://doi.org/10.3390/ma15020474







