Evaluation of Laminated Composite Beam Theory Accuracy
Abstract
1. Introduction
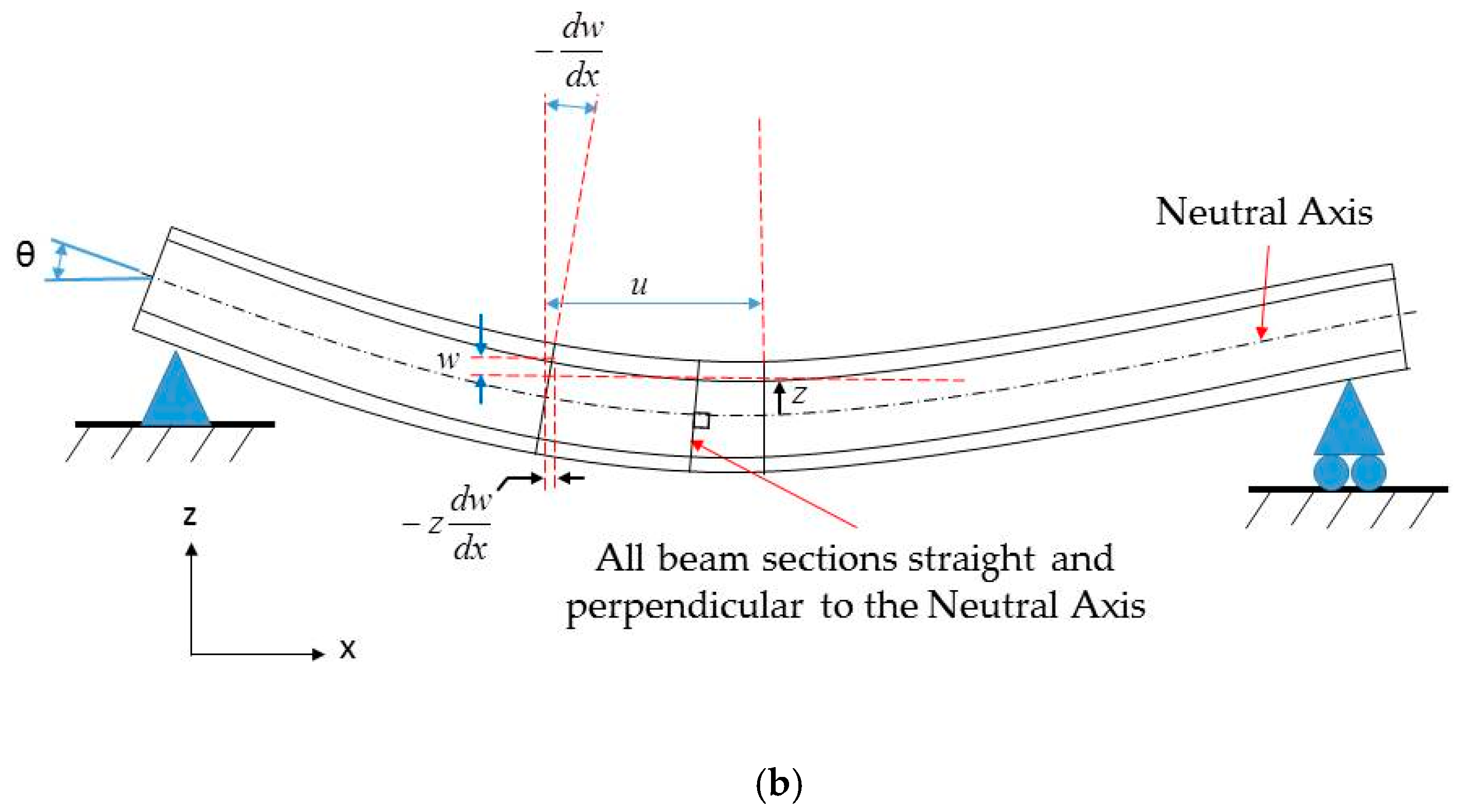
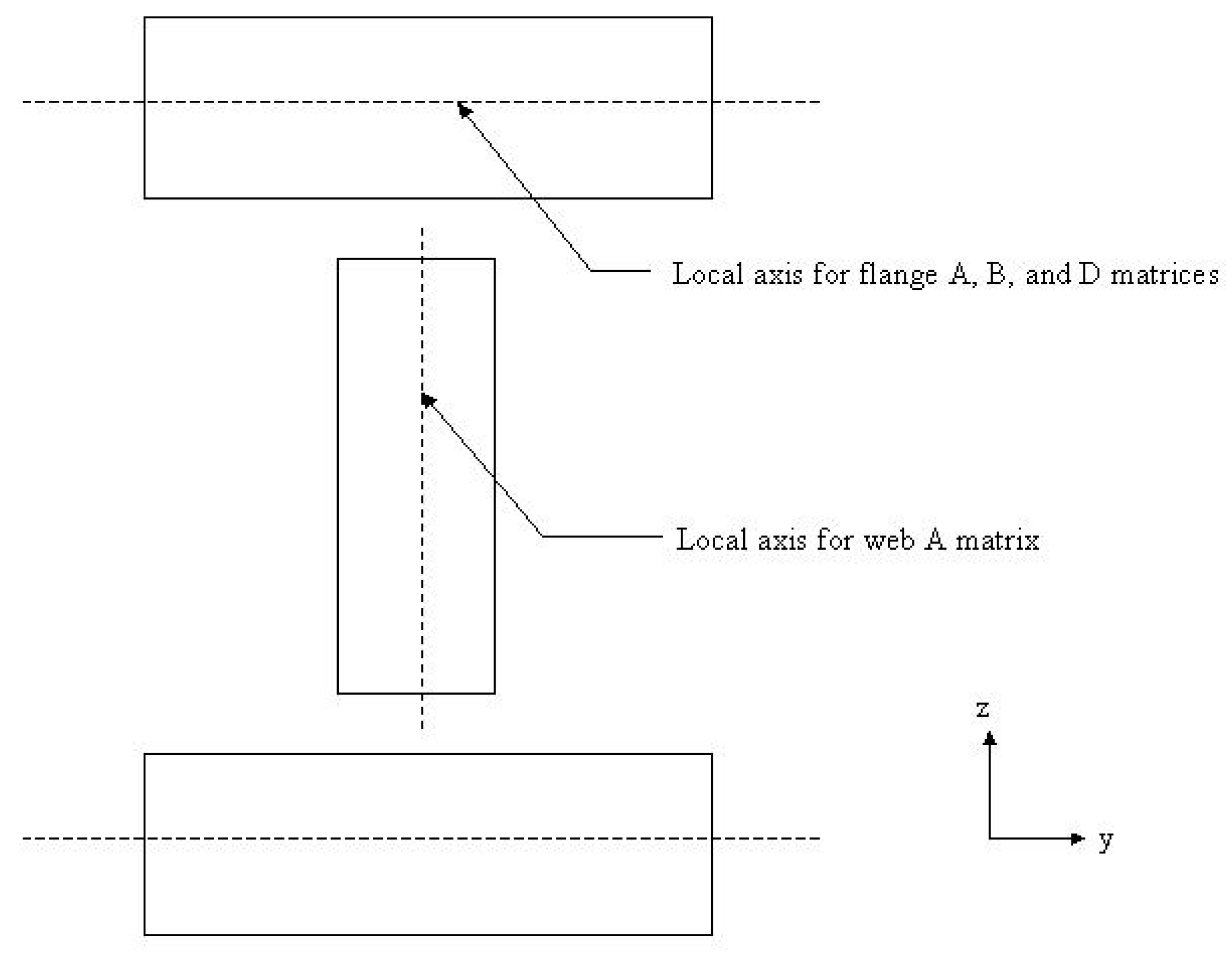
2. Theory of Composite Beams
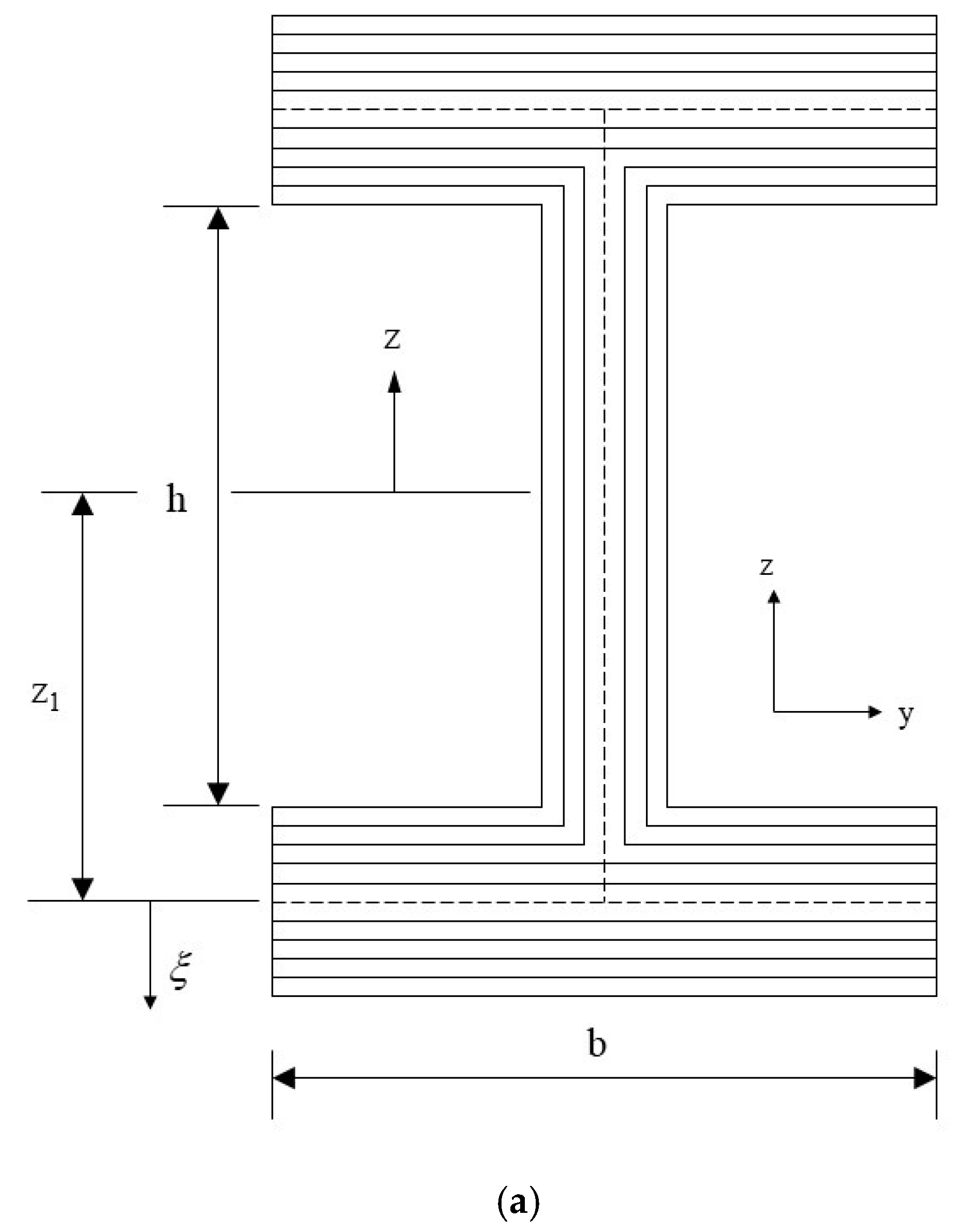
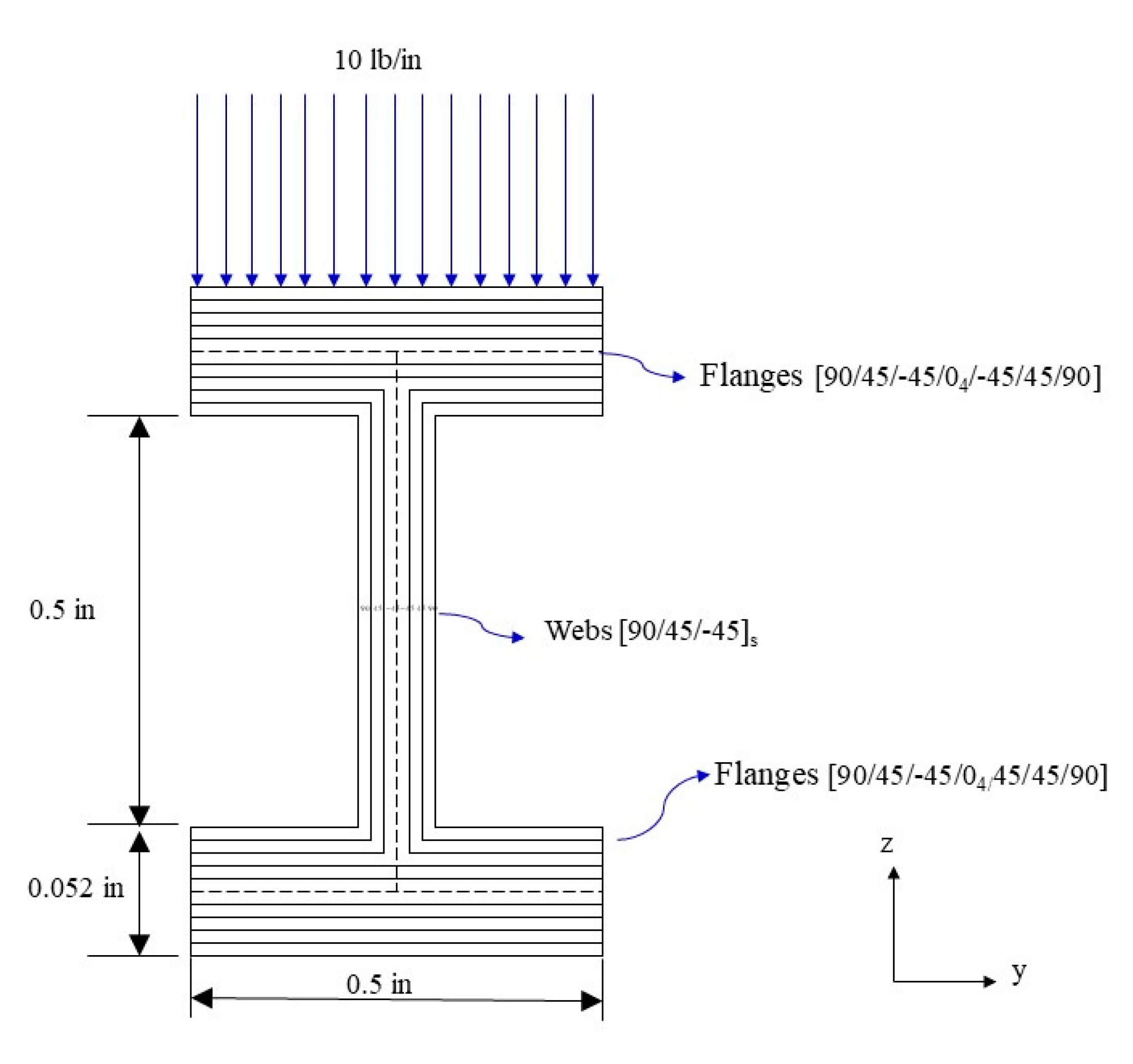
2.1. Symmetrical Laminated Composite I-Beam
- Narrow flange
- Wide flange
2.2. Nonsymmetrical Laminated Composite I-Beam
- Narrow flange
- Wide flange
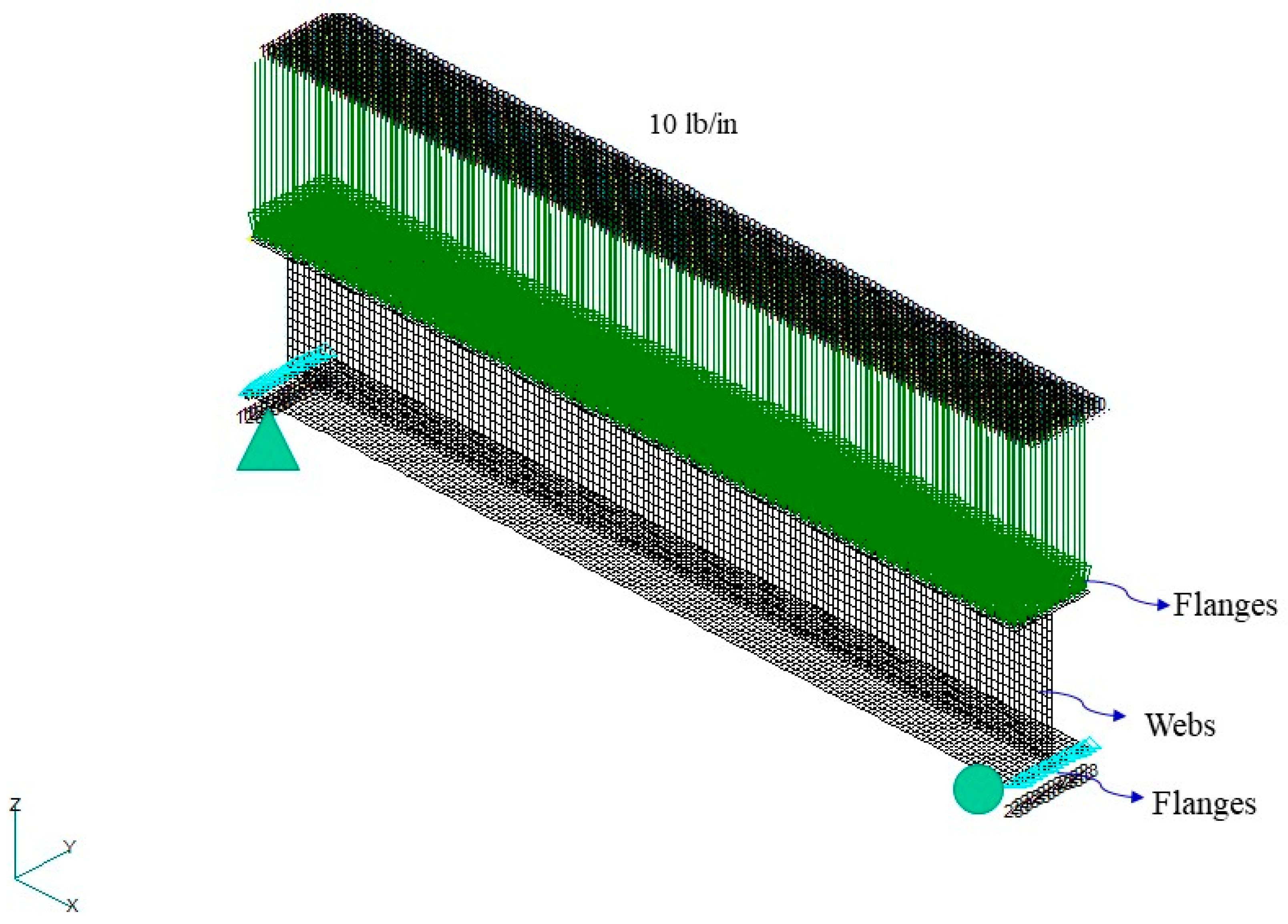
3. Finite Element Analysis Model
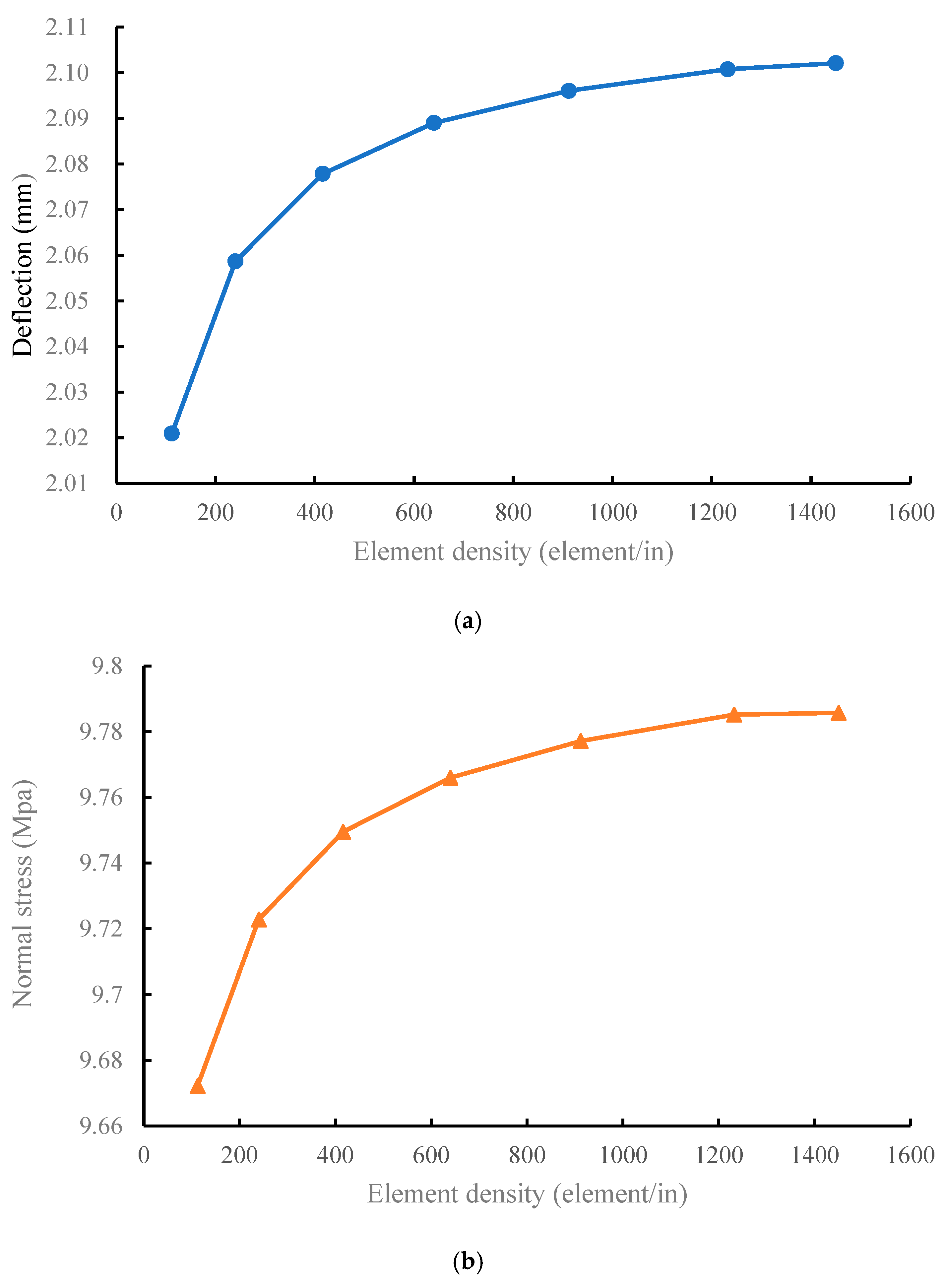
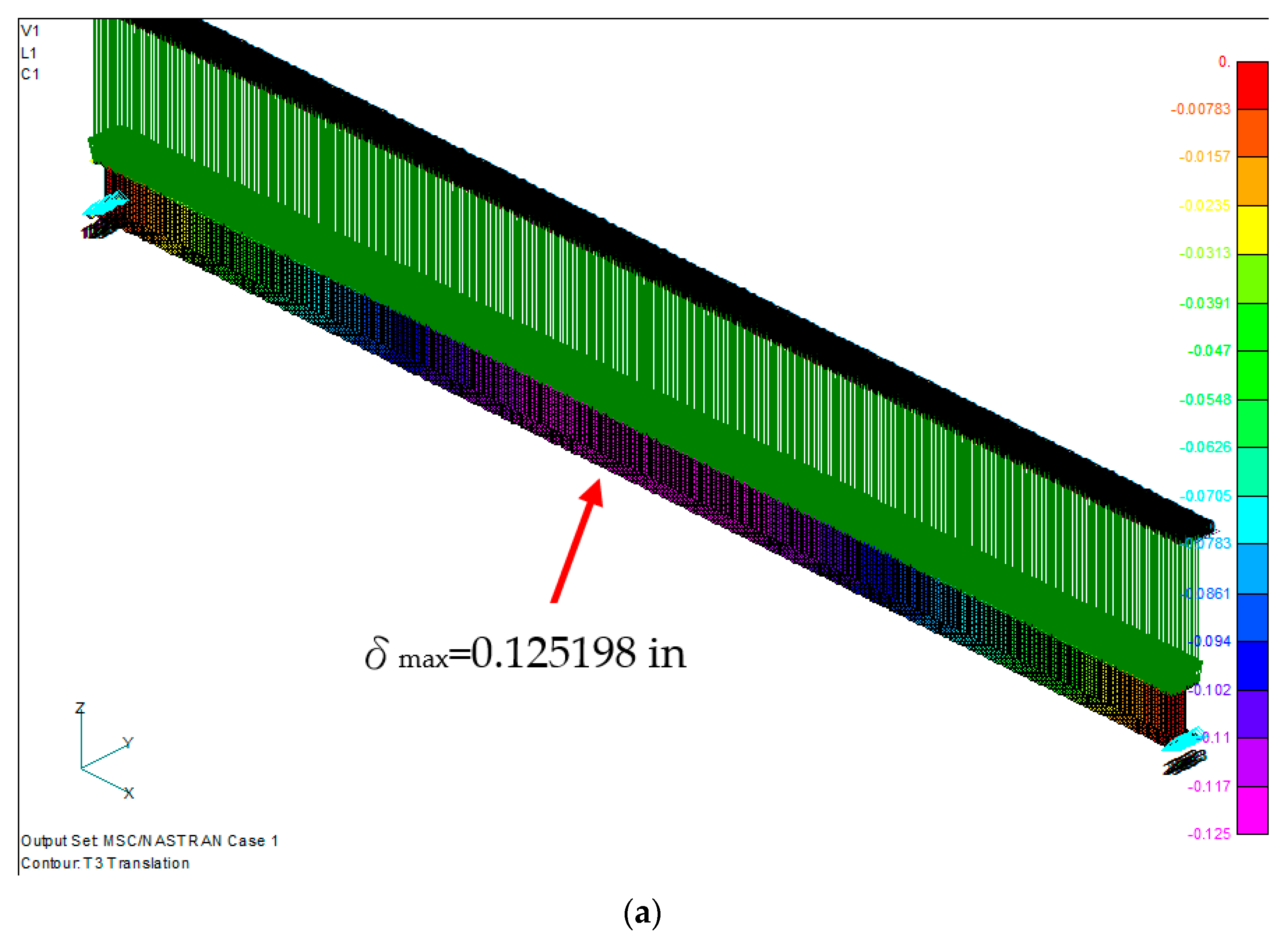
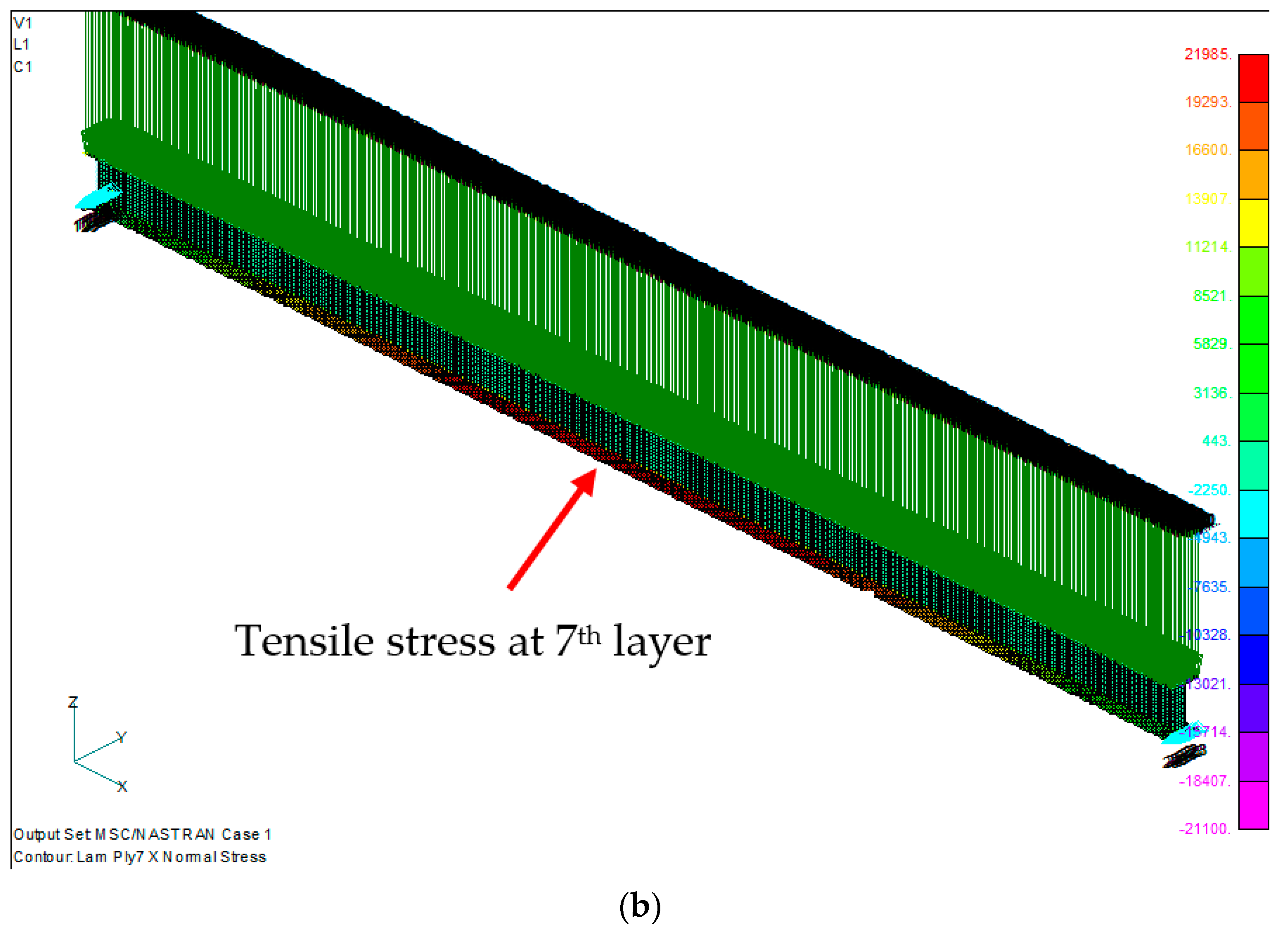
4. Results and Discussion
5. Conclusions
- (1)
- Analytical solutions provide a broad and rough assessment of composite beam structures. The scope of applicability of the formula was defined in detail by evaluating it in this study. Thus, the structural analysis of the composite beams can accurately obtain analysis data.
- (2)
- The composite beam theory only considers plane strain, and there is a significant error in the strain and stress analyses of the short beam structure. When the aspect ratio of the beam was >15, the error in the analytical solution was <5%. Analytical solutions exhibited the best reliability for the normal force assessment of symmetric or nonsymmetric laminated beams. Therefore, the derived formula is suitable for thin and long beams.
- (3)
- The change in the fiber angle of the laminate will improve the rigidity of the structure without changing the material. When the lamination sequence was changed and 0° ply was placed on the outermost layer of the flange, the effective stiffness of the nonsymmetric beam increased by 4–5% compared with that of the symmetric beam.
Author Contributions
Funding
Conflicts of Interest
References
- Elsheikh, A. Bistable Morphing Composites for Energy-Harvesting Applications. Polymers 2022, 14, 1893. [Google Scholar] [CrossRef]
- Chillara, V.S.C.; Dapino, M.J. Bistable Morphing Composites with Selectively-Prestressed Laminae. In Behavior and Mechanics of Multifunctional Materials and Composites 2017, Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, OR, USA, 25–29 March 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10165, p. 10165. [Google Scholar] [CrossRef]
- Sunil, B.R.; Reddy, G.P.K.; Patle, H.; Dumpala, R. Magnesium based surface metal matrix composites by friction stir processing. J. Magnes. Alloy. 2016, 4, 52–61. [Google Scholar] [CrossRef]
- Krishnan, R.; Pandiaraj, S.; Muthusamy, S.; Panchal, H.; Alsoufi, M.S.; Ibrahim, A.M.M.; Elsheikh, A. Biodegradable magnesium metal matrix composites for biomedical implants: Synthesis, mechanical performance, and corrosion behavior—A review. J. Mater. Res. Technol. 2022, 20, 650–670. [Google Scholar] [CrossRef]
- AElsheikh, A.H.; Abd Elaziz, M.; Ramesh, B.; Egiza, M.; Al-qaness, M.A. Modeling of drilling process of GFRP composite using a hybrid random vector functional link network/parasitism-predation algorithm. J. Mater. Res. Technol. 2021, 14, 298–311. [Google Scholar] [CrossRef]
- Najjar, I.M.R.; Sadoun, A.M.; Abd Elaziz, M.; Abdallah, A.W.; Fathy, A.; Elsheikh, A.H. Predicting kerf quality characteristics in laser cutting of basalt fibers reinforced polymer composites using neural network and chimp optimization. Alex. Eng. J. 2022, 61, 11005–11018. [Google Scholar] [CrossRef]
- Showaib, E.A.; Elsheikh, A.H. Effect of surface preparation on the strength of vibration welded butt joint made from PBT composite. Polym. Test. 2020, 83, 106319. [Google Scholar] [CrossRef]
- Alvarez-Montoya, J.; Carvajal-Castrillón, A.; Sierra-Pérez, J. In-flight and wireless damage detection in a UAV composite wing using fiber optic sensors and strain field pattern recognition. Mech. Syst. Signal Process. 2020, 136, 106526. [Google Scholar] [CrossRef]
- Gadomski, J.; Hernik, B.; Goraj, Z. Analysis and optimisation of a MALE UAV loaded structure. Aircr. Eng. Aerosp. Technol. Int. J. 2006, 78, 120–131. [Google Scholar] [CrossRef]
- Alsahlani, A.; Rahulan, T.; Abdulhassan, N. Composite Structural Analysis of a High Altitude, Solar Powered Unmanned Aerial Vehicle. Int. J. Mech. Eng. Robot. Res. 2017, 6, 71–76. [Google Scholar] [CrossRef][Green Version]
- Galatas, A.; Hassanin, H.; Zweiri, Y.; Seneviratne, L. Additive Manufactured Sandwich Composite/ABS Parts for Unmanned Aerial Vehicle Applications. Polymers 2018, 10, 1262. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, D.; Yang, M.; Xia, X.; Yao, Y. Optimization and analysis of composite sandwich box beam for solar drones. Chin. J. Aeronaut. 2021, 34, 148–165. [Google Scholar] [CrossRef]
- Abdulhameed, A.A.; Said, A.I. CFRP Laminates Reinforcing Performance of Short-Span Wedge-Blocks Segmental Beams. Fibers 2020, 8, 6. [Google Scholar] [CrossRef]
- Abdulhameed, A.A.; Said, A.I. Said, Systematic Design of Short-Span Segmental Beams Reinforced by CFRP Plates. Key Eng. Mater. 2020, 857, 130–137. [Google Scholar] [CrossRef]
- Abdulhameed, A.A.; Said, A.I. Experimental Investigation of the Behavior of Self-Form Segmental Concrete Masonry Arches. Fibers 2019, 7, 58. [Google Scholar] [CrossRef]
- Bank, L.C. Modifications to beam theory for bending and twisting of open-section composite beams. Compos. Struct. 1990, 15, 93–114. [Google Scholar] [CrossRef]
- Bank, L.C. Shear coefficients for thin-walled composite beams. Compos. Struct. 1987, 8, 47–61. [Google Scholar] [CrossRef]
- Bank, L.C.; Bednarczyk, P.J. A Beam Theory for Thin-walled Composite Beams. Compos. Struct. Technol. 1988, 32, 265–277. [Google Scholar] [CrossRef]
- Cowper, G.R. The Shear Coefficient in Timoshenko’s Beam Theory. J. Appl. Mech. 1996, 33, 335–340. [Google Scholar] [CrossRef]
- Yang, P.; Norris, C.H.; Stavsky, Y. Elastic wave propagation in heterogeneous plates. Int. J. Solids Struct. 1966, 2, 665–684. [Google Scholar] [CrossRef]
- Chandra, R.; Chopra, I. Experimental and Theoretical Analysis of Composite I-Beams with Elastic Couplings. In Proceedings of the 32th AIAA/ASME/ASCE/ASC Structures, Structural Dynamics and Materials Conference, Baltimore, MD, USA, 8–10 April 1991; AIAA: Washington, DC, USA, 1991. [Google Scholar]
- Bauld, N.R., Jr.; Tzeng, L.S. A Vlasov Theory for Fiber Reinforced Beams with Thin-Walled Open Cross-Sections. Int. J. Solids Struct. 1984, 20, 277–297. [Google Scholar] [CrossRef]
- Rehfield, L.W.; Atilgan, A.R. Shear Center and Elastic Axis and Their Usefulness for Composite Thin-Walled Beams. In Proceeding of the American Society for Composites, Fourth Technical Conference, Blacksburg, VA, USA, 2–5 October 1989; pp. 179–188. [Google Scholar]
- Chandra, R.; Stemple, A.D.; Chopra, I. Thin-Walled Composite Beam Under Bending, Torsional, and Extensional Loads. J. Aircr. 1990, 27, 619–626. [Google Scholar] [CrossRef]
- Gordaninejad, F. Bending of Thick Angle-Ply Bimodular Composite Plates. AIAA J. 1990, 28, 2005–2009. [Google Scholar] [CrossRef]
- Madenci, E.; Gülcü, Ş. Optimization of flexure stiffness of FGM beams via artificial neural networks by mixed FEM. Struct. Eng. Mech. 2020, 75, 633–642. [Google Scholar]
- Özütok, A.; Madenci, E. Static analysis of laminated composite beams based on higher-order shear deformation theory by using mixed-type finite element method. Int. J. Mech. Sci. 2017, 130, 234–243. [Google Scholar] [CrossRef]
- Reddy, J. An evaluation of equivalent-single-layer and layerwise theories of composite laminates. Compos. Struct. 1993, 25, 21–35. [Google Scholar] [CrossRef]
- Swanson, S.R. Advanced Composite Material; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Ugural, A.C. Mechanics of Materials; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
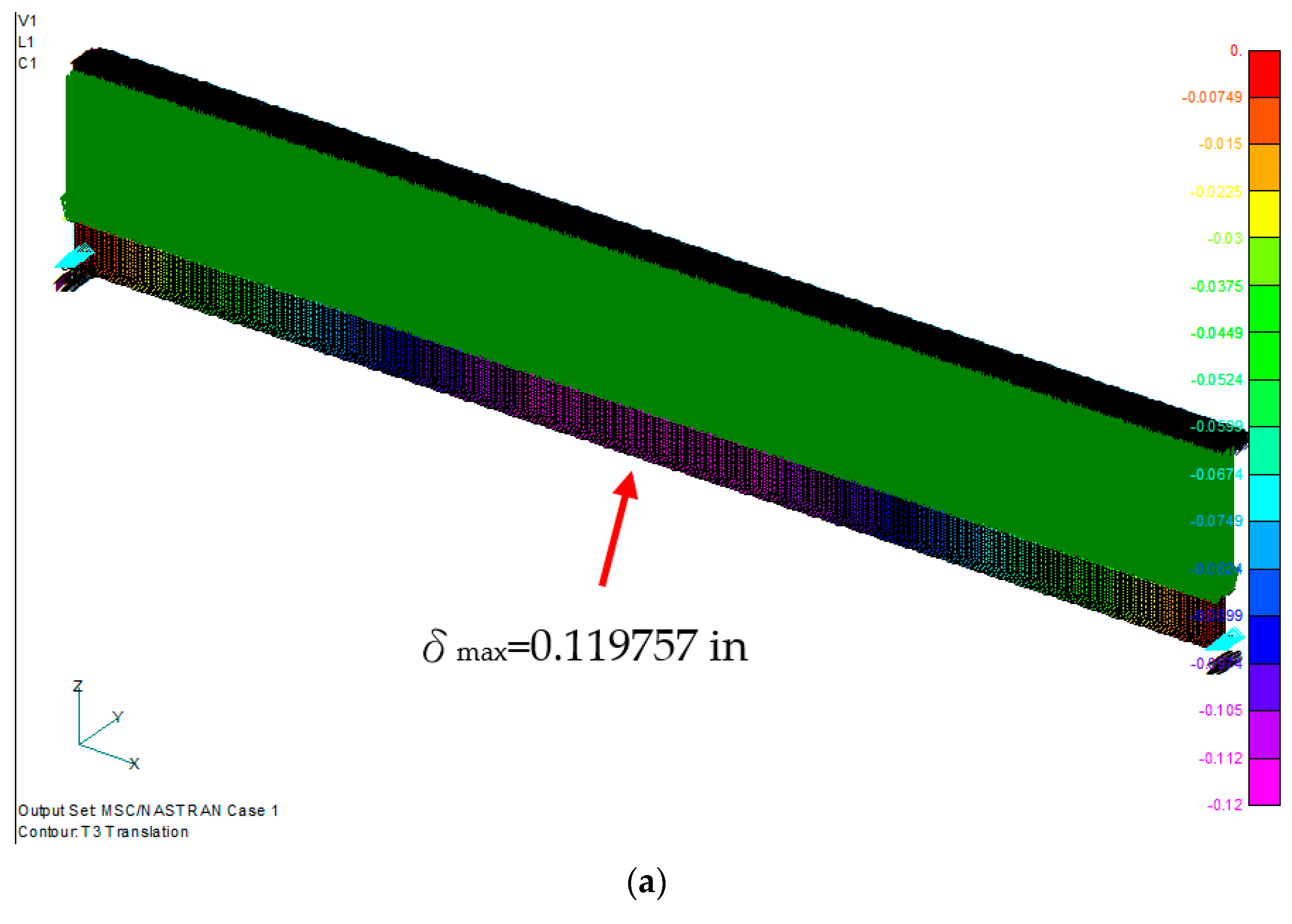
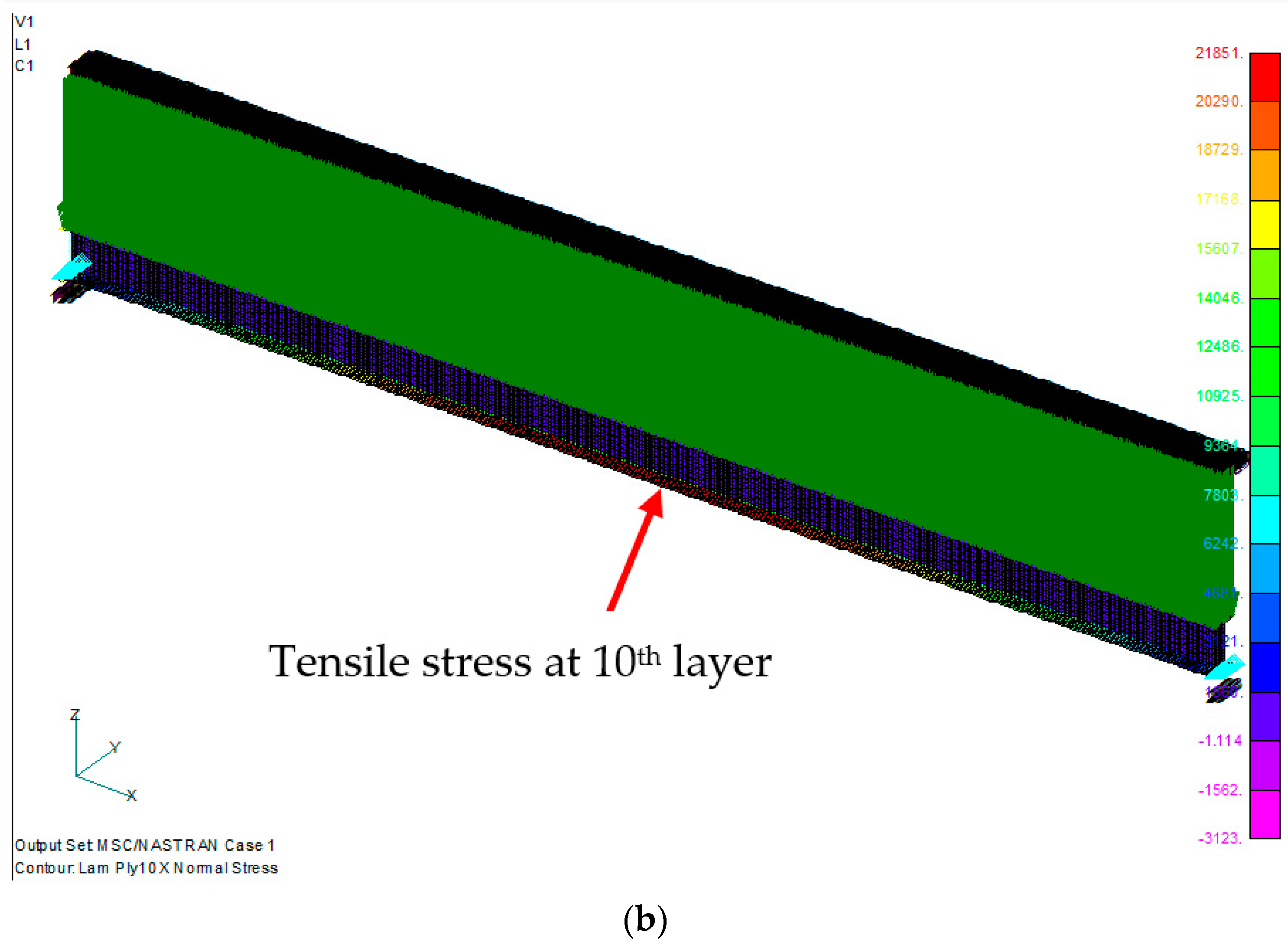
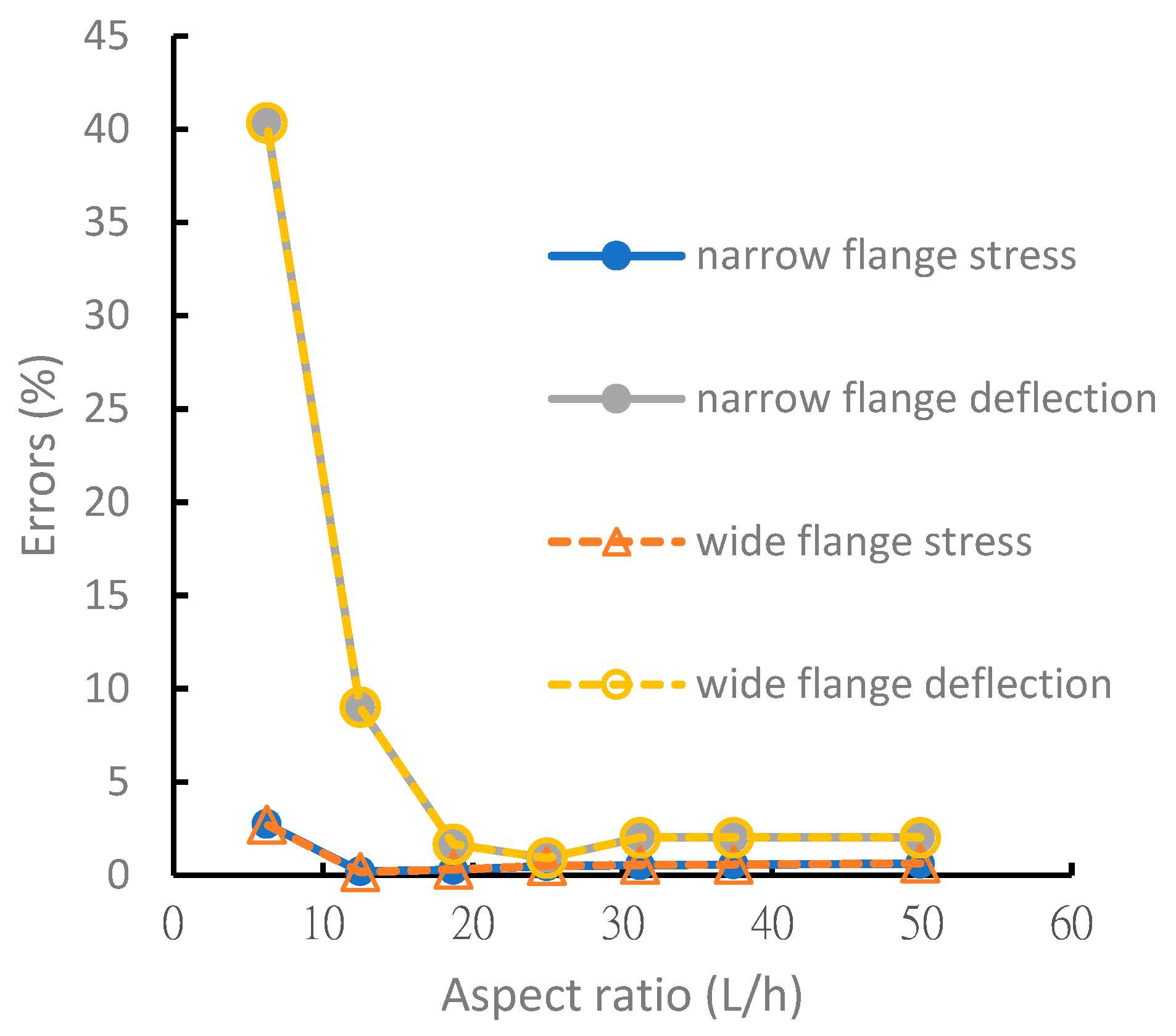
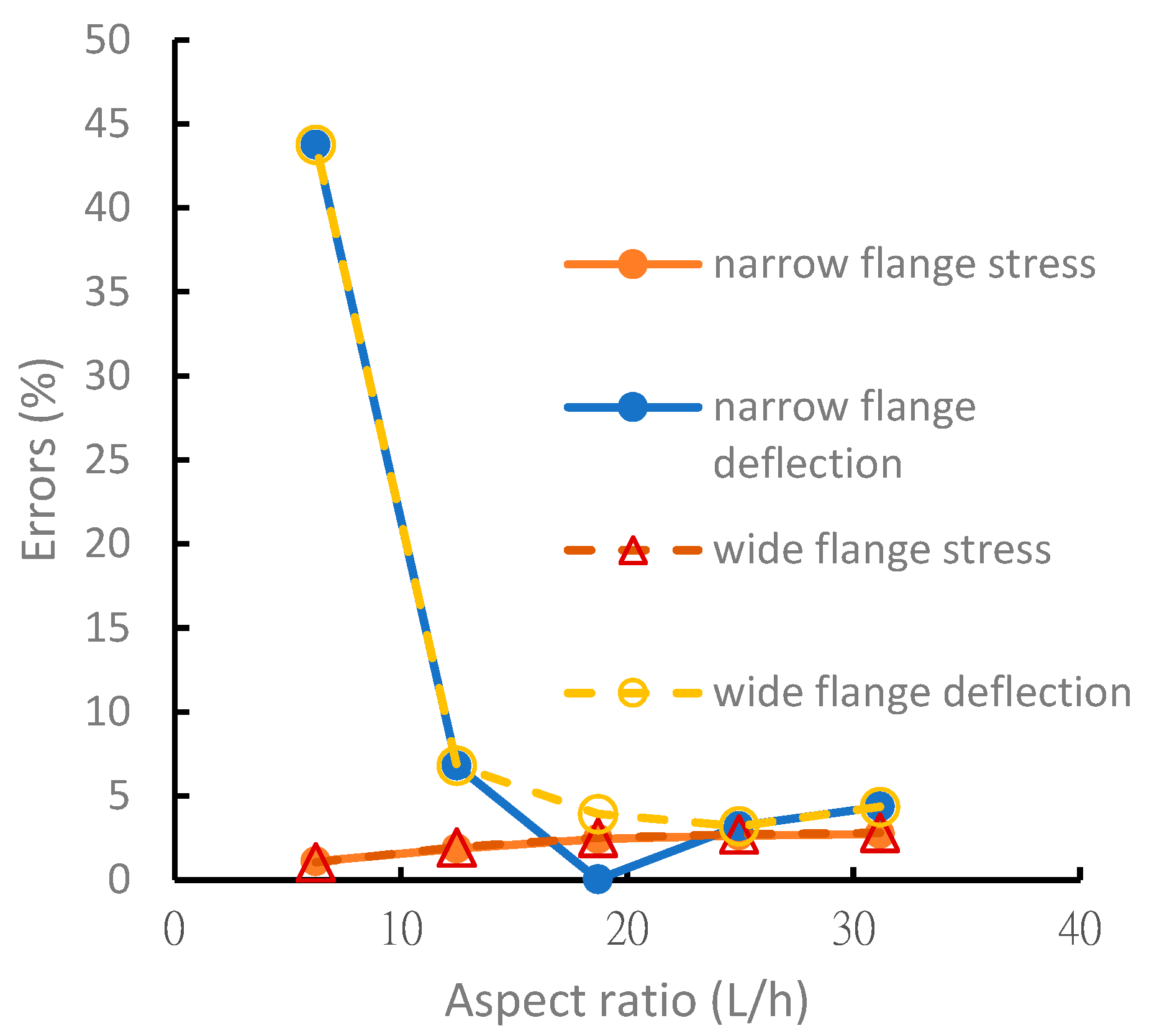
| Max. Normal Stress (psi) | Max. Deflection (in) | |||||
|---|---|---|---|---|---|---|
| Length (in) | Theoretical Analysis Solution | FEM Solution | Theoretical Analysis Solution | FEM Solution | ||
| Narrow Flange | Wide Flange | Narrow Flange | Wide Flange | |||
| 25 | 34,506.087 | 34,514.798 | 34,310.910 | 0.308363 | 0.308342 | 0.302105 |
| 20 | 22,083.896 | 22,089.471 | 21,978.570 | 0.126306 | 0.126297 | 0.125149 |
| 15 | 12,422.191 | 12,425.327 | 12,384.600 | 0.039964 | 0.039961 | 0.040620 |
| 10 | 5,520.974 | 5,522.368 | 5,531.170 | 0.007894 | 0.007894 | 0.008671 |
| 7.5 | 3,105.548 | 3,106.332 | 3,133.002 | 0.002500 | 0.002498 | 0.003072 |
| 5 | 1,380.243 | 1,380.592 | 1,419.221 | 0.000493 | 0.000493 | 0.000827 |
| Max. Normal Stress (psi) | Max. Deflection (in) | |||||
|---|---|---|---|---|---|---|
| Length (in) | Theoretical Analysis Solution | FEM Solution | Theoretical Analysis Solution | FEM Solution | ||
| Narrow Flange | Wide Flange | Narrow Flange | Wide Flange | |||
| 25 | 35,044.783 | 35,070.324 | 34,096.23 | 0.301742 | 0.30172 | 0.289010 |
| 20 | 22,428.661 | 22,445.007 | 21,843.75 | 0.123593 | 0.12359 | 0.119714 |
| 15 | 12,616.122 | 12,625.317 | 12,311.94 | 0.039106 | 0.03910 | 0.0388464 |
| 10 | 5,607.165 | 5,611.252 | 5,502.920 | 0.007725 | 0.00772 | 0.0082852 |
| 7.5 | 3,154.031 | 3,156.329 | 3,120.298 | 0.002444 | 0.00244 | 0.0029312 |
| 5 | 1,401.791 | 1,402.813 | 1,417.687 | 0.000483 | 0.00048 | 0.0008585 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Y.-T.; Hung, T.-P.; Ay, H.-C.; Tsai, H.-A.; Chiang, Y.-C. Evaluation of Laminated Composite Beam Theory Accuracy. Materials 2022, 15, 6941. https://doi.org/10.3390/ma15196941
Lyu Y-T, Hung T-P, Ay H-C, Tsai H-A, Chiang Y-C. Evaluation of Laminated Composite Beam Theory Accuracy. Materials. 2022; 15(19):6941. https://doi.org/10.3390/ma15196941
Chicago/Turabian StyleLyu, Yu-Ting, Tsung-Pin Hung, Her-Chang Ay, Hsiu-An Tsai, and Yih-Cherng Chiang. 2022. "Evaluation of Laminated Composite Beam Theory Accuracy" Materials 15, no. 19: 6941. https://doi.org/10.3390/ma15196941
APA StyleLyu, Y.-T., Hung, T.-P., Ay, H.-C., Tsai, H.-A., & Chiang, Y.-C. (2022). Evaluation of Laminated Composite Beam Theory Accuracy. Materials, 15(19), 6941. https://doi.org/10.3390/ma15196941






