Modeling Tracer Diffusion Coefficients of Any Type of Solutes in Polar and Non-Polar Dense Solvents
Abstract
1. Introduction
2. Model Development and Database
2.1. Rice and Gray Correlation
2.2. Parameters Optimization and Model Assessment
2.3. Database and Compounds Properties
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taylor, R.; Krishna, R. Multicomponent Mass Transfer; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Zêzere, B.; Portugal, I.; Gomes, J.R.B.; Silva, C.M. Revisiting Tracer Liu-Silva-Macedo Model for Binary Diffusion Coefficient Using the Largest Database of Liquid and Supercritical Systems. J. Supercrit. Fluids 2021, 168, 105073. [Google Scholar] [CrossRef]
- Wilke, C.R.; Chang, P. Correlation of Diffusion Coefficients in Dilute Solutions. AIChE J. 1955, 1, 264–270. [Google Scholar] [CrossRef]
- Liu, H.; Silva, C.M.; Macedo, E.A. New Equations for Tracer Diffusion Coefficients of Solutes in Supercritical and Liquid Solvents Based on the Lennard-Jones Fluid Model. Ind. Eng. Chem. Res. 1997, 36, 246–252. [Google Scholar] [CrossRef]
- Magalhães, A.L.; Cardoso, S.P.; Figueiredo, B.R.; Da Silva, F.A.; Silva, C.M. Revisiting the Liu-Silva-Macedo Model for Tracer Diffusion Coefficients of Supercritical, Liquid, and Gaseous Systems. Ind. Eng. Chem. Res. 2010, 49, 7697–7700. [Google Scholar] [CrossRef]
- Dymond, J.H. Corrected Enskog Theory and the Transport Coefficients of Liquids. J. Chem. Phys. 1974, 60, 969–973. [Google Scholar] [CrossRef]
- Silva, C.M.; Liu, H. Modelling of Transport Properties of Hard Sphere Fluids and Related Systems, and Its Applications. In Theory and Simulation of Hard-Sphere Fluids and Related Systems; Springer: Berlin, Germany, 2008; pp. 383–492. [Google Scholar]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids, 4th ed.; McGraw-Hill Book Company, Ed.; McGraw-Hill International Editions: New York, NY, USA, 1987. [Google Scholar]
- Millat, J.; Dymond, J.H.; Nieto de Castro, C.A. Transport Properties of Fluids-Their Correlation, Prediction and Estimation; Cambridge University Press: London, UK, 1996. [Google Scholar]
- Tyn, M.T.; Calus, W.F. Diffusion Coefficients in Dilute Binary Liquid Mixtures. J. Chem. Eng. Data 1975, 20, 106–109. [Google Scholar] [CrossRef]
- Magalhães, A.L.; Da Silva, F.A.; Silva, C.M. Tracer Diffusion Coefficients of Polar Systems. Chem. Eng. Sci. 2012, 73, 151–168. [Google Scholar] [CrossRef]
- Aniceto, J.P.S.; Zêzere, B.; Silva, C.M. Predictive Models for the Binary Diffusion Coefficient at Infinite Dilution in Polar and Nonpolar Fluids. Materials 2021, 14, 542. [Google Scholar] [CrossRef]
- Magalhães, A.L.; Lito, P.F.; Da Silva, F.A.; Silva, C.M. Simple and Accurate Correlations for Diffusion Coefficients of Solutes in Liquids and Supercritical Fluids over Wide Ranges of Temperature and Density. J. Supercrit. Fluids 2013, 76, 94–114. [Google Scholar] [CrossRef]
- Kong, C.Y.; Yakumaru, Y.; Funazukuri, T. Measurement and Correlation of Binary Diffusion Coefficients of Lithium Acetylacetonate in Supercritical Carbon Dioxide and in Liquid Ethanol. J. Supercrit. Fluids 2015, 104, 265–271. [Google Scholar] [CrossRef]
- Kong, C.Y.; Watanabe, K.; Funazukuri, T. Determination and Correlation of Infinite Dilution Binary Diffusion Coefficients for Aluminum Acetylacetonate in Supercritical and Liquid Fluids. Fluid Phase Equilib. 2015, 420, 83–88. [Google Scholar] [CrossRef]
- Funazukuri, T.; Yamasaki, T.; Taguchi, M.; Kong, C.Y. Measurement of Binary Diffusion Coefficient and Solubility Estimation for Dyes in Supercritical Carbon Dioxide by CIR Method. Fluid Phase Equilib. 2015, 420, 7–13. [Google Scholar] [CrossRef]
- Kong, C.Y.; Watanabe, K.; Funazukuri, T. Measurement and Correlation of the Diffusion Coefficients of Chromium(III) Acetylacetonate at Infinite Dilution in Supercritical Carbon Dioxide and in Liquid Ethanol. J. Chem. Thermodyn. 2017, 105, 86–93. [Google Scholar] [CrossRef]
- Kong, C.Y.; Sugiura, K.; Natsume, S.; Sakabe, J.; Funazukuri, T.; Miyake, K.; Okajima, I.; Badhulika, S.; Sako, T. Measurements and Correlation of Diffusion Coefficients of Ibuprofen in Both Liquid and Supercritical Fluids. J. Supercrit. Fluids 2020, 159, 104776. [Google Scholar] [CrossRef]
- Einstein, A. Über Die von Der Molekularkinetischen Theorie Der Wärme Geforderte Bewegung von in Ruhenden Flüssigkeiten Suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Rice, S.A.; Gray, P. The Statistical Mechanics of Simple Liquids: An Introduction to the Theory of Equilibrium and Non-Equilibrium Phenomena; Interscience Publication: Hoboken, NJ, USA, 1995. [Google Scholar]
- Helfand, E. Theory of the Molecular Friction Constant. Phys. Fluids 1961, 4, 681. [Google Scholar] [CrossRef]
- O’Toole, J.T.; Dahler, J.S. Molecular Friction in Dilute Gases. J. Chem. Phys. 1960, 33, 1496–1504. [Google Scholar] [CrossRef]
- Ruckenstein, E.; Liu, H. Self-Diffusion in Gases and Liquids. Ind. Eng. Chem. Res. 1997, 36, 3927–3936. [Google Scholar] [CrossRef]
- Brokaw, R.S. Predicting Transport Properties of Dilute Gases. Ind. Eng. Chem. Process Des. Dev. 1969, 8, 240–253. [Google Scholar] [CrossRef]
- Zêzere, B.; Iglésias, J.; Portugal, I.; Gomes, J.R.B.; Silva, C.M. Diffusion of Quercetin in Compressed Liquid Ethyl Acetate and Ethanol. J. Mol. Liq. 2020, 324, 114714. [Google Scholar] [CrossRef]
- Zêzere, B.; Silva, J.M.; Portugal, I.; Gomes, J.R.B.; Silva, C.M. Measurement of Astaxanthin and Squalene Diffusivities in Compressed Liquid Ethyl Acetate by Taylor-Aris Dispersion Method. Sep. Purif. Technol. 2020, 234, 116046. [Google Scholar] [CrossRef]
- Brovarets’, O.O.; Hovorun, D.M. Conformational Diversity of the Quercetin Molecule: A Quantum-Chemical View. J. Biomol. Struct. Dyn. 2020, 38, 2817–2836. [Google Scholar] [CrossRef] [PubMed]
- Ben-Amotz, D.; Herschbach, D.R. Estimation of Effective Diameters for Molecular Fluids. J. Phys. Chem. 1990, 94, 1038–1047. [Google Scholar] [CrossRef]
- Mansoori, G.A.; Carnahan, N.F.; Starling, K.E.; Leland, T.W. Equilibrium Thermodynamic Properties of the Mixture of Hard Spheres. J. Chem. Phys. 1971, 54, 1523–1525. [Google Scholar] [CrossRef]
- Magalhães, A.L.; Da Silva, F.A.; Silva, C.M. New Models for Tracer Diffusion Coefficients of Hard Sphere and Real Systems: Application to Gases, Liquids and Supercritical Fluids. J. Supercrit. Fluids 2011, 55, 898–923. [Google Scholar] [CrossRef]
- Lagarias, J.; Reeds, J.; Wright, M.; Wright, P. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Matlab 2017b; The MathWorks Inc.: Natick, MA, USA, 2017.
- Wong, C.-F. Diffusion Coefficients of Dissolved Gases in Liquids; University of Ottawa: Ottawa, ON, Canada, 1989. [Google Scholar]
- Funazukuri, T.; Hachisu, S.; Wakao, N. Measurement of Diffusion Coefficients of C18 Unsaturated Fatty Acid Methyl Esters, Naphthalene, and Benzene in Supercritical Carbon Dioxide by a Tracer Response Technique. Anal. Chem. 1989, 61, 118–122. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Reid, R.C. Diffusion and Mass Transfer in Supercritical Fluids. AIChE J. 1986, 32, 2034–2046. [Google Scholar] [CrossRef]
- Wells, T.; Foster, N.R.; Chaplin, R.P. Diffusion of Phenylacetic Acid and Vanillin in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 1992, 31, 927–934. [Google Scholar] [CrossRef]
- Pizarro, C.; Suárez-Iglesias, O.; Medina, I.; Bueno, J.L. Molecular Diffusion Coefficients of Phenylmethanol, 1-Phenylethanol, 2-Phenylethanol, 2-Phenyl-1-Propanol, and 3-Phenyl-1-Propanol in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2008, 43, 469–476. [Google Scholar] [CrossRef]
- Silva, C.M.; Filho, C.A.; Quadri, M.B.; Macedo, E.A. Binary Diffusion Coefficients of α-Pinene and β-Pinene in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2004, 32, 167–175. [Google Scholar] [CrossRef]
- Vaz, R.V.; Magalhães, A.L.; Valente, A.A.; Silva, C.M. Measurement and Modeling of Tracer Diffusivities of α-Pinene in Supercritical CO2, and Analysis of Their Hydrodynamic and Free-Volume Behaviors. J. Supercrit. Fluids 2016, 107, 690–698. [Google Scholar] [CrossRef]
- Suárez, J.J.; Bueno, J.L.; Medina, I.; Dizy, J. Applications of supercritical chromatography-Determination of molecular diffusivity. Afinidad 1992, 49, 101–113. [Google Scholar]
- Kong, C.Y.; Withanage, N.R.W.; Funazukuri, T.; Kagei, S. Binary Diffusion Coefficients and Retention Factors for Long-Chain Triglycerides in Supercritical Carbon Dioxide by the Chromatographic Impulse Response Method. J. Chem. Eng. Data 2005, 50, 1635–1640. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Infinite-Dilution Binary Diffusion Coefficient, Partition Ratio, and Partial Molar Volume for Ubiquinone CoQ10 in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 2002, 41, 2812–2818. [Google Scholar] [CrossRef]
- Xu, B.; Nagashima, K.; DeSimone, J.M.; Johnson, C.S., Jr. Diffusion of Water in Liquid and Supercritical Carbon Dioxide: An NMR Study. J. Phys. Chem. A 2003, 107, 1–3. [Google Scholar] [CrossRef]
- Kopner, A.; Hamm, A.; Ellert, J.; Feist, R.; Schneider, G.M. Determination of Binary Diffusion Coefficients in Supercritical Chlorotrifluoromethane and Sulfurhexafluoride with Supercritical Fluid Chromatography (SFC). Chem. Eng. Sci. 1987, 42, 2213–2218. [Google Scholar] [CrossRef]
- Wong, C.-L.; Soriano, A.N.; Li, M.-H. Infinite Dilution Diffusion Coefficients of [Bmim]-Based Ionic Liquids in Water and Its Molar Conductivities. J. Taiwan Inst. Chem. Eng. 2009, 40, 77–83. [Google Scholar] [CrossRef]
- Wong, C.-L.; Soriano, A.N.; Li, M.-H. Diffusion Coefficients and Molar Conductivities in Aqueous Solutions of 1-Ethyl-3-Methylimidazolium-Based Ionic Liquids. Fluid Phase Equilib. 2008, 271, 43–52. [Google Scholar] [CrossRef]
- Heintz, A.; Lehmann, J.K.; Schmidt, E.; Wandschneider, A. Diffusion Coefficients of Imidazolium Based Ionic Liquids in Aqueous Solutions. J. Solution Chem. 2009, 38, 1079–1083. [Google Scholar] [CrossRef]
- Gary-Bobo, C.; Weber, H.W. Diffusion of Alcohols and Amides in Water from 4 to 37. Deg. J. Phys. Chem. 1969, 73, 1155–1156. [Google Scholar] [CrossRef]
- Umecky, T.; Kuga, T.; Funazukuri, T. Infinite Dilution Binary Diffusion Coefficients of Several α-Amino Acids in Water over a Temperature Range from (293.2 to 333.2) K with the Taylor Dispersion Technique. J. Chem. Eng. Data 2006, 51, 1705–1710. [Google Scholar] [CrossRef]
- Umecky, T.; Omori, S.; Kuga, T.; Funazukuri, T. Effects of Hydroxyl Groups on Binary Diffusion Coefficients of α-Amino Acids in Dilute Aqueous Solutions. Fluid Phase Equilib. 2008, 264, 18–22. [Google Scholar] [CrossRef]
- Frank, M.J.W.; Kuipers, J.A.M.; van Swaaij, W.P.M. Diffusion Coefficients and Viscosities of CO2 + H2O, CO2 + CH3OH, NH3 + H2O, and NH3 + CH3OH Liquid Mixtures. J. Chem. Eng. Data 1996, 41, 297–302. [Google Scholar] [CrossRef]
- Mogi, N.; Sugai, E.; Fuse, Y.; Funazukuri, T. Infinite Dilution Binary Diffusion Coefficients for Six Sugars at 0.1 MPa and Temperatures from (273.2 to 353.2) K. J. Chem. Eng. Data 2007, 52, 40–43. [Google Scholar] [CrossRef]
- Maharajh, D. Solubility and Diffusion of Gases in Water; Simon Fraser University: Burnaby, BC, Canada, 1975. [Google Scholar]
- Witherspoon, P.A.; Bonoli, L. Correlation of Diffusion Coefficients for Paraffin, Aromatic, and Cycloparaffin Hydrocarbons in Water. Ind. Eng. Chem. Fundam. 1969, 8, 589–591. [Google Scholar] [CrossRef]
- Han, P.; Bartels, D.M. Temperature Dependence of Oxygen Diffusion in H2O and D2O. J. Phys. Chem. 1996, 100, 5597–5602. [Google Scholar] [CrossRef]
- Bonoli, L.; Witherspoon, P.A. Diffusion of Aromatic and Cycloparaffin Hydrocarbons in Water from 2 to 60.Deg. J. Phys. Chem. 1968, 72, 2532–2534. [Google Scholar] [CrossRef]
- Tominaga, T.; Yamamoto, S.; Takanaka, J.-I. Limiting Interdiffusion Coefficients of Benzene, Toluene, Ethylbenzene and Hexafluorobenzene in Water from 298 to 368 K. J. Chem. Soc. Faraday Trans. Phys. Chem. Condens. Phases 1984, 80, 941. [Google Scholar] [CrossRef]
- Tominaga, T.; Matsumoto, S.; Ishii, T. Limiting Interdiffusion of Some Aromatic Hydrocarbons in Water from 265 to 433 K. J. Phys. Chem. 1986, 90, 139–143. [Google Scholar] [CrossRef]
- Delgado, J.M.P.Q. Molecular Diffusion Coefficients of Organic Compounds in Water at Different Temperatures. J. Phase Equilibria Diffus. 2007, 28, 427–432. [Google Scholar] [CrossRef]
- Mutoru, J.W.; Leahy-Dios, A.; Firoozabadi, A. Modeling Infinite Dilution and Fickian Diffusion Coefficients of Carbon Dioxide in Water. AIChE J. 2011, 57, 1617–1627. [Google Scholar] [CrossRef]
- Jähne, B.; Heinz, G.; Dietrich, W. Measurement of the Diffusion Coefficients of Sparingly Soluble Gases in Water. J. Geophys. Res. 1987, 92, 10767–10776. [Google Scholar] [CrossRef]
- Riele, M.J.M.T.; Snijder, E.D.; van Swaaij, W.P.M. Diffusion Coefficients at Infinite Dilution in Water and in N-Methylpyrrolidone. J. Chem. Eng. Data 1995, 40, 34–36. [Google Scholar] [CrossRef][Green Version]
- Li, S.F.Y.; Ong, H.M. Infinite Dilution Diffusion Coefficients of Several Alcohols in Water. J. Chem. Eng. Data 1990, 35, 136–137. [Google Scholar] [CrossRef]
- Tominaga, T.; Matsumoto, S. Limiting Interdiffusion Coefficients of Some Hydroxylic Compounds in Water from 265 to 433 K. J. Chem. Eng. Data 1990, 35, 45–47. [Google Scholar] [CrossRef]
- Funazukuri, T.; Nishio, M. Infinite Dilution Binary Diffusion Coefficients of C5-Monoalcohols in Water in the Temperature Range from 273.2 K to 353.2 K at 0.1 MPa. J. Chem. Eng. Data 1999, 44, 73–76. [Google Scholar] [CrossRef]
- Okubo, Y.; Kong, C.Y.; Sakabe, J.; Funazukuri, T. Measurements of Infinite Dilution Binary Diffusion Coefficients of Acetylferrocene and 1,1′-Diacetylferrocene in Supercritical Carbon Dioxide and in Liquid Organic Solvents. J. Supercrit. Fluids 2021, 177, 105321. [Google Scholar] [CrossRef]
- Price, W.E.; Trickett, K.A.; Harris, K.R. Association of Caffeine in Aqueous Solution. Effects on Caffeine Intradiffusion. J. Chem. Soc. Faraday Trans. 1989, 85, 3281–3288. [Google Scholar] [CrossRef]
- Price, W.E. Tracer Caffeine Diffusion in Aqueous Solutions at 298 K. The Effect of Caffeine Self-Association. J. Chem. Soc. Faraday Trans. 1989, 85, 415–419. [Google Scholar] [CrossRef]
- Niesner, R.; Heintz, A. Diffusion Coefficients of Aromatics in Aqueous Solution. J. Chem. Eng. Data 2000, 45, 1121–1124. [Google Scholar] [CrossRef]
- Vivian, J.E.; King, C.J. Diffusivities of Slightly Soluble Gases in Water. AIChE J. 1964, 10, 220–221. [Google Scholar] [CrossRef]
- Ng, W.Y.; Walkley, J. Diffusion of Gases in Liquids: The Constant Size Bubble Method. Can. J. Chem. 1969, 47, 1075–1077. [Google Scholar] [CrossRef]
- Maharajh, D.M.; Walkley, D.J. The Temperature Dependence of the Diffusion Coefficients of Ar, CO2, CH4, CH3Cl, CH3Br, and CHCl2F in Water. Can. J. Chem. 1973, 51, 944–952. [Google Scholar] [CrossRef]
- Pratt, K.C.; Slater, D.H.; Wakeham, W.A. A Rapid Method for the Determination of Diffusion Coefficients of Gases in Liquids. Chem. Eng. Sci. 1973, 28, 1901–1903. [Google Scholar] [CrossRef]
- Bodnar, L.H.; Himmelblau, D.M. Continuous Measurement of Diffusion Coefficients of Gases in Liquids Using Glass Scintillators. Int. J. Appl. Radiat. Isot. 1962, 13, 1–6. [Google Scholar] [CrossRef]
- Woods, D.R. Mass Transfer Between a Liquid Jet and a Countercurrent Gas Stream; University of Wisconsin-Madison: Madison, WI, USA, 1961. [Google Scholar]
- Ferrell, R.T.; Himmelblau, D.M. Diffusion Coefficients of Nitrogen and Oxygen in Water. J. Chem. Eng. Data 1967, 12, 111–115. [Google Scholar] [CrossRef]
- Sun, C.K.J.; Chen, S.H. Tracer Diffusion in Dense Ethanol: A Generalized Correlation for Nonpolar and Hydrogen-Bonded Solvents. AIChE J. 1986, 32, 1367–1371. [Google Scholar] [CrossRef]
- Thomas, W.J.; Adams, M.J. Measurement of the Diffusion Coefficients of Carbon Dioxide and Nitrous Oxide in Water and Aqueous Solutions of Glycerol. Trans. Faraday Soc. 1965, 61, 668–673. [Google Scholar] [CrossRef]
- Tham, M.J.; Bhatia, K.K.; Gubbins, K.F. Steady-State Method for Studying Diffusion of Gases in Liquids. Chem. Eng. Sci. 1967, 22, 309–311. [Google Scholar] [CrossRef]
- Sovová, H.; Procházka, J. A New Method of Measurement of Diffusivities of Gases in Liquids. Chem. Eng. Sci. 1976, 31, 1091–1097. [Google Scholar] [CrossRef]
- Himmelblau, D.M. Diffusion of Dissolved Gases in Liquids. Chem. Rev. 1964, 64, 527–550. [Google Scholar] [CrossRef]
- Peaceman, D.W. Liquid-Side Resistance in Gas Absorption with and without Chemical Reaction; Massachusetts Institute of Technology: Cambridge, MA, USA, 1952. [Google Scholar]
- Ringbom, A. Über Die Bestimmung Der Diffusionskoeffizienten von Gasen in Flüssigkeiten. Zeitschrift Für Anorg. Und Allg. Chem. 1938, 238, 94–102. [Google Scholar] [CrossRef]
- Norman, W.S.; Sammak, F.Y.Y. Gas Absorption in a Packed Column-Part I: The Effect of Liquid Viscosity on the Mass Transfer Coefficient. Trans. Inst. Chem. Eng. 1963, 41, 109–116. [Google Scholar]
- Onda, K.; Okamoto, T.; Yamaji, Y. Measurement of the Diffusivities of CO2 in Liquids by Liquid Jets. Kagaku Kogaku 1960, 24, 918–925. [Google Scholar] [CrossRef]
- Nijsing, R.A.T.O.; Hendriksz, R.H.; Kramers, H. Absorption of CO2 in Jets and Falling Films of Electrolyte Solutions, with and without Chemical Reaction. Chem. Eng. Sci. 1959, 10, 88–104. [Google Scholar] [CrossRef]
- Hüfner, G. Ueber Die Bestimmung der Diffusions Coefficienten Einiger Gase Für Wasser. Ann. Phys. 1896, 296, 134–168. [Google Scholar] [CrossRef]
- Tominaga, T.; Matsumoto, S. Diffusion of Polar and Nonpolar Molecules in Water and Ethanol. Bull. Chem. Soc. Jpn. 1990, 63, 533–537. [Google Scholar] [CrossRef]
- Stefan, J. Über Die Diffusion Der Kohlensäure Durch Wasser Und Alkohol. Sitzungsberichte Kais. Akad. Wiss. Math. Klasse II Abtheilung 1878, 77, 371–409. [Google Scholar]
- Tammann, G.; Jessen, V. Über Die Diffusionskoeffizienten von Gasen in Wasser Und Ihre Temperaturabhängigkeit. Zeitschrift Für Anorg. Und Allg. Chem. 1929, 179, 125–144. [Google Scholar] [CrossRef]
- Tamimi, A.; Rinker, E.B.; Sandall, O.C. Diffusion Coefficients for Hydrogen Sulfide, Carbon Dioxide, and Nitrous Oxide in Water over the Temperature Range 293–368 K. J. Chem. Eng. Data 1994, 39, 330–332. [Google Scholar] [CrossRef]
- Versteeg, G.F.; Van Swaaij, W.P.M. Solubility and Diffusivity of Acid Gases (Carbon Dioxide, Nitrous Oxide) in Aqueous Alkanolamine Solutions. J. Chem. Eng. Data 1988, 33, 29–34. [Google Scholar] [CrossRef]
- Cadogan, S.P.; Maitland, G.C.; Trusler, J.P.M. Diffusion Coefficients of CO2 and N2 in Water at Temperatures between 298.15 K and 423.15 K at Pressures up to 45 MPa. J. Chem. Eng. Data 2014, 59, 519–525. [Google Scholar] [CrossRef]
- Mazarei, A.F.; Sandall, O.C. Diffusion Coefficients for Helium, Hydrogen, and Carbon Dioxide in Water at 25 °C. AIChE J. 1980, 26, 154–157. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Valente, A.J.M.; Santos, C.I.A.V.; Prazeres, P.M.R.A.; Lobo, V.M.M.; Burrows, H.D.; Esteso, M.A.; Cabral, A.M.T.D.P.V.; Veiga, F.J.B. Binary Mutual Diffusion Coefficients of Aqueous Solutions of α-Cyclodextrin, 2-Hydroxypropyl-α-Cyclodextrin, and 2-Hydroxypropyl-β-Cyclodextrin at Temperatures from (298.15 to 312.15) K. J. Chem. Eng. Data 2007, 52, 586–590. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Leaist, D.G.; Esteso, M.A.; Lobo, V.M.M.; Valente, A.J.M.; Santos, C.I.A.V.; Cabral, A.M.T.D.P.V.; Veiga, F.J.B. Binary Mutual Diffusion Coefficients of Aqueous Solutions of β-Cyclodextrin at Temperatures from 298.15 to 312.15 K. J. Chem. Eng. Data 2006, 51, 1368–1371. [Google Scholar] [CrossRef]
- Snijder, E.D.; te Riele, M.J.M.; Versteeg, G.F.; van Swaaij, W.P.M. Diffusion Coefficients of Several Aqueous Alkanolamine Solutions. J. Chem. Eng. Data 1993, 38, 475–480. [Google Scholar] [CrossRef]
- Wang, M.H.; Soriano, A.N.; Caparanga, A.R.; Li, M.-H. Mutual Diffusion Coefficients of Aqueous Solutions of Some Glycols. Fluid Phase Equilib. 2009, 285, 44–49. [Google Scholar] [CrossRef]
- Lin, I.-H.; Tan, C.-S. Diffusion of Benzonitrile in CO2-Expanded Ethanol. J. Chem. Eng. Data 2008, 53, 1886–1891. [Google Scholar] [CrossRef]
- Secuianu, C.; Maitland, G.C.; Trusler, J.P.M.; Wakeham, W.A. Mutual Diffusion Coefficients of Aqueous KCl at High Pressures Measured by the Taylor Dispersion Method. J. Chem. Eng. Data 2011, 56, 4840–4848. [Google Scholar] [CrossRef]
- Kuo, C.-C.; Li, M.-H. Measurements of Mutual Diffusion Coefficients of Binary Systems: Aquous N,N-Diethylethanolamine, N,N-Dimethylethanolamine, Monoisopropanolamine, Piperazine, and Sulfolane Solutions. Master’s Thesis, Chung Yuan Christian University, Jhongli, Taiwan, 2005. [Google Scholar]
- Chang, L.-C.; Lin, T.-I.; Li, M.-H. Mutual Diffusion Coefficients of Some Aqueous Alkanolamines Solutions. J. Chem. Eng. Data 2005, 50, 77–84. [Google Scholar] [CrossRef]
- Wang, M.H.; Soriano, A.N.; Caparanga, A.R.; Li, M.-H. Binary Mutual Diffusion Coefficient of Aqueous Solutions of Propylene Glycol and Dipropylene Glycol. J. Taiwan Inst. Chem. Eng. 2010, 41, 279–285. [Google Scholar] [CrossRef]
- Kuo, C.-C.; Li, M.H. Diffusion Coefficients of Aqueous N,N-Diethylethanolamine, N,N-Dimethylethanolamine, Monoisopropanolamine, Piperazine, and Sulfolane Solutions. J. Chin. Inst. Chem. Eng. 2006, 37, 341–353. [Google Scholar]
- Witherspoon, P.A.; Saraf, D.N. Diffusion of Methane, Ethane, Propane and n-Butane in Water from 25 to 43°. J. Phys. Chem. 1965, 69, 3752–3755. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Ortona, O.; Simões, S.M.N.; Santos, C.I.A.V.; Prazeres, P.M.R.A.; Valente, A.J.M.; Lobo, V.M.M.; Burrows, H.D. Binary Mutual Diffusion Coefficients of Aqueous Solutions of Sucrose, Lactose, Glucose, and Fructose in the Temperature Range from (298.15 to 328.15) K. J. Chem. Eng. Data 2006, 51, 1836–1840. [Google Scholar] [CrossRef]
- Yui, K.; Yamazaki, N.; Funazukuri, T. Infinite Dilution Binary Diffusion Coefficients for Compounds Derived from Biomass in Water at 0.1 MPa and Temperatures from (298.2 to 353.2) K. J. Chem. Eng. Data 2013, 58, 183–186. [Google Scholar] [CrossRef]
- Boerboom, A.J.; Kleyn, G. Diffusion Coefficients of Noble Gases in Water. J. Chem. Phys. 1969, 50, 1086–1088. [Google Scholar] [CrossRef]
- Haimour, N.; Sandall, O.C. Molecular Diffusivity of Hydrogen Sulfide in Water. J. Chem. Eng. Data 1984, 29, 20–22. [Google Scholar] [CrossRef]
- Suárez-Iglesias, O.; Medina, I.; Pizarro, C.; Bueno, J.L. Diffusion of Benzyl Acetate, 2-Phenylethyl Acetate, 3-Phenylpropyl Acetate, and Dibenzyl Ether in Mixtures of Carbon Dioxide and Ethanol. Ind. Eng. Chem. Res. 2007, 46, 3810–3819. [Google Scholar] [CrossRef]
- Derlacki, Z.J.; Easteal, A.J.; Edge, A.V.J.; Woolf, L.A.; Roksandic, Z. Diffusion Coefficients of Methanol and Water and the Mutual Diffusion Coefficient in Methanol-Water Solutions at 278 and 298 K. J. Phys. Chem. 1985, 89, 5318–5322. [Google Scholar] [CrossRef]
- Matthews, M.A.; Akgerman, A. Infinite Dilution Diffusion Coefficients of Methanol and 2-Propanol in Water. J. Chem. Eng. Data 1988, 33, 122–123. [Google Scholar] [CrossRef]
- Derks, P.W.J.; Hamborg, E.S.; Hogendoorn, J.A.; Niederer, J.P.M.; Versteeg, G.F. Densities, Viscosities, and Liquid Diffusivities in Aqueous Piperazine and Aqueous (Piperazine + N-Methyldiethanolamine) Solutions. J. Chem. Eng. Data 2008, 53, 1179–1185. [Google Scholar] [CrossRef]
- Hamborg, E.S.; Derks, P.W.J.; Kersten, S.R.A.; Niederer, J.P.M.; Versteeg, G.F. Diffusion Coefficients of N2O in Aqueous Piperazine Solutions Using the Taylor Dispersion Technique from (293 to 333) K and (0.3 to 1.4) Mol·dm −3. J. Chem. Eng. Data 2008, 53, 1462–1466. [Google Scholar] [CrossRef][Green Version]
- Wise, D.L.; Houghton, G. The Diffusion Coefficients of Ten Slightly Soluble Gases in Water at 10–60 °C. Chem. Eng. Sci. 1966, 21, 999–1010. [Google Scholar] [CrossRef]
- Plugatyr, A.; Svishchev, I.M. Molecular Diffusivity of Phenol in Sub- and Supercritical Water: Application of the Split-Flow Taylor Dispersion Technique. Jounal Phys. Chem. B 2011, 115, 2555–2562. [Google Scholar] [CrossRef] [PubMed]
- Castillo, R.; Garza, C. Temperature Dependence of the Mutual Diffusion Coefficients in Aqueous Solutions of Alkali Metal Chlorides. Int. J. Thermophys. 1993, 14, 1145–1152. [Google Scholar] [CrossRef]
- Funazukuri, T.; Nishimoton; Wakao, N. Binary Diffusion Coefficients of Organic Compounds in Hexane, Dodecane, and Cyclohexane at 303.2–333.2 K and 16.0 MPa. J. Chem. Eng. Data 1994, 39, 911–915. [Google Scholar] [CrossRef]
- Chen, S.H.; Davis, H.T.; Evans, D.F. Tracer Diffusion in Polyatomic Liquids. II. J. Chem. Phys. 1981, 75, 2540–2544. [Google Scholar] [CrossRef]
- Sun, C.K.J.; Chen, S.H. Tracer Diffusion of Aromatic Hydrocarbons in Liquid Cyclohexane up to Its Critical Temperature. AIChE J. 1985, 31, 1510–1515. [Google Scholar] [CrossRef]
- Zêzere, B.; Cordeiro, J.; Leite, J.; Magalhães, A.L.; Portugal, I.; Silva, C.M. Diffusivities of Metal Acetylacetonates in Liquid Ethanol and Comparison with the Transport Behavior in Supercritical Systems. J. Supercrit. Fluids 2019, 143, 259–267. [Google Scholar] [CrossRef]
- Toriurmi, M.; Katooka, R.; Yui, K.; Funazukuri, T.; Kong, C.Y.; Kagei, S. Measurements of Binary Diffusion Coefficients for Metal Complexes in Organic Solvents by the Taylor Dispersion Method. Fluid Phase Equilib. 2010, 297, 62–66. [Google Scholar] [CrossRef]
- Chen, B.H.C.; Sun, C.K.J.; Chen, S.H. Hard Sphere Treatment of Binary Diffusion in Liquid at High Dilution up to the Critical Temperature. J. Chem. Phys. 1985, 82, 2052–2055. [Google Scholar] [CrossRef]
- Sun, C.K.J.; Chen, S.H. Tracer Diffusion of Aromatic Hydrocarbons in N-Hexane up to the Supercritical Region. Chem. Eng. Sci. 1985, 40, 2217–2224. [Google Scholar]
- Chen, S.H.; Davis, H.T.; Evans, D.F. Tracer Diffusion in Polyatomic Liquids. III. J. Chem. Phys. 1982, 77, 2540–2544. [Google Scholar] [CrossRef]
- Chen, H.C.; Chen, S.H. Tracer Diffusion of Crown Ethers in N-Decane and n-Tetradecane: An Improved Correlation for Binary Systems Involving Normal Alkanes. Ind. Eng. Chem. Fundam. 1985, 24, 187–192. [Google Scholar] [CrossRef]
- Pollack, G.L.; Kennan, R.P.; Himm, J.F.; Stump, D.R. Diffusion of Xenon in Liquid Alkanes: Temperature Dependence Measurements with a New Method. Stokes--Einstein and Hard Sphere Theories. J. Chem. Phys. 1990, 92, 625–630. [Google Scholar] [CrossRef]
- Sun, C.K.J.; Chen, S.H. Diffusion of Benzene, Toluene, Naphthalene, and Phenanthrene in Supercritical Dense 2,3-Dimethylbutane. AIChE J. 1985, 31, 1904–1910. [Google Scholar] [CrossRef]
- Matthews, M.A.; Rodden, J.B.; Akgerman, A. High-Temperature Diffusion of Hydrogen, Carbon Monoxide, and Carbon Dioxide in Liquid n-Heptane, n-Dodecane, and n-Hexadecane. J. Chem. Eng. Data 1987, 32, 319–322. [Google Scholar] [CrossRef]
- Matthews, M.A.; Akgerman, A. Diffusion Coefficients for Binary Alkane Mixtures to 573 K and 3.5 MPa. AIChE J. 1987, 33, 881–885. [Google Scholar] [CrossRef]
- Rodden, J.B.; Erkey, C.; Akgerman, A. High-Temperature Diffusion, Viscosity, and Density Measurements in n-Eicosane. J. Chem. Eng. Data 1988, 33, 344–347. [Google Scholar] [CrossRef]
- Zêzere, B.; Magalhães, A.L.; Portugal, I.; Silva, C.M. Diffusion Coefficients of Eucalyptol at Infinite Dilution in Compressed Liquid Ethanol and in Supercritical CO2/Ethanol Mixtures. J. Supercrit. Fluids 2018, 133, 297–308. [Google Scholar] [CrossRef]
- Noel, J.M.; Erkey, C.; Bukur, D.B.; Akgerman, A. Infinite Dilution Mutual Diffusion Coefficients of 1-Octene and 1-Tetradecene in near-Critical Ethane and Propane. J. Chem. Eng. Data 1994, 39, 920–921. [Google Scholar] [CrossRef]
- Grushka, E.; Kikta, E.J. Diffusion in Liquids. II. Dependence of Diffusion Coefficients on Molecular Weight and on Temperature. J. Am. Chem. Soc. 1976, 98, 643–648. [Google Scholar] [CrossRef]
- Qian, R.Y.; Fan, Y.Q.; Shi, M.R.; Shi, J. Predictive Equation of Tracer Liquid Diffusion Coefficient from Viscosity. Chin. J. Chem. Eng. 1996, 4, 203–208. [Google Scholar]
- Lo, H.Y. Diffusion Coefficients in Binary Liquid N-Alkane Systems. J. Chem. Eng. Data 1974, 19, 236–241. [Google Scholar] [CrossRef]
- Bidlack, D.L.; Anderson, D.K. Mutual Diffusion in Nonideal Nonassociating Liquid Systems. J. Phys. Chem. 1964, 68, 3790–3794. [Google Scholar] [CrossRef]
- Alizadeh, A.A.; Wakeham, W.A. Mutual Diffusion Coefficients for Binary Mixtures of Normal Alkanes. Int. J. Thermophys. 1982, 3, 307–323. [Google Scholar] [CrossRef]
- Padrel de Oliveira, C.M.; Fareleira, J.M.N.A.; Nieto de Castro, C.A. Mutual Diffusivity in Binary Mixtures of N-Heptane with n-Hexane Isomers. Int. J. Thermophys. 1989, 10, 973–982. [Google Scholar] [CrossRef]
- Li, S.F.Y.; Yue, L.S. Composition Dependence of Binary Diffusion Coefficients in Alkane Mixtures. Int. J. Thermophys. 1990, 11, 537–554. [Google Scholar] [CrossRef]
- Li, S.F.Y.; Wakeham, W.A. Mutual Diffusion Coefficients for Two N-Octane Isomers in n-Heptane. Int. J. Thermophys. 1989, 10, 995–1003. [Google Scholar] [CrossRef]
- Matthews, M.A.; Rodden, J.B.; Akgerman, A. High-Temperature Diffusion, Viscosity, and Density Measurements in n-Hexadecane. J. Chem. Eng. Data 1987, 32, 317–319. [Google Scholar] [CrossRef]
- Leite, J.; Magalhães, A.L.; Valente, A.A.; Silva, C.M. Measurement and Modelling of Tracer Diffusivities of Gallic Acid in Liquid Ethanol and in Supercritical CO2 Modified with Ethanol. J. Supercrit. Fluids 2018, 131, 130–139. [Google Scholar] [CrossRef]
- Dymond, J.H.; Woolf, L.A. Tracer Diffusion of Organic Solutes in N-Hexane at Pressures up to 400 MPa. J. Chem. Soc. Faraday Trans. 1982, 78, 991–1000. [Google Scholar] [CrossRef]
- Safi, A.; Nicolas, C.; Neau, E.; Chevalier, J.L. Measurement and Correlation of Diffusion Coefficients of Aromatic Compounds at Infinite Dilution in Alkane and Cycloalkane Solvents. J. Chem. Eng. Data 2007, 52, 977–981. [Google Scholar] [CrossRef]
- Leffler, J.; Cullinan, H.T. Variation of Liquid Diffusion Coefficients with Composition. Dilute Ternary Systems. Ind. Eng. Chem. Fundam. 1970, 9, 88–93. [Google Scholar] [CrossRef]
- Harris, K.R.; Pua, C.K.N.; Dunlop, P.J. Mutual and Tracer Diffusion Coefficients and Frictional Coefficients for Systems Benzene-Chlorobenzene, Benzene-n-Hexane, and Benzene-n-Heptane at 25 °C. J. Phys. Chem. 1970, 74, 3518–3529. [Google Scholar] [CrossRef]
- Awan, M.A.; Dymond, J.H. Transport Properties of Nonelectrolyte Liquid Mixtures. X. Limiting Mutual Diffusion Coefficients of Fluorinated Benzenes in n-Hexane. Int. J. Thermophys. 1996, 17, 759–769. [Google Scholar] [CrossRef]
- Okamoto, M. Diffusion Coefficients Estimated by Dynamic Fluorescence Quenching at High Pressure: Pyrene, 9,10-Dimethylanthracene, and Oxygen in n-Hexane. Int. J. Thermophys. 2002, 23, 421–435. [Google Scholar] [CrossRef]
- Bidlack, D.L.; Kett, T.K.; Kelly, C.M.; Anderson, D.K. Diffusion in the Solvents Hexane and Carbon Tetrachloride. J. Chem. Eng. Data 1969, 14, 342–343. [Google Scholar] [CrossRef]
- Grushka, E.; Kikta, E.J. Extension of the Chromatographic Broadening Method of Measuring Diffusion Coefficients to Liquid Systems. I. Diffusion Coefficients of Some Alkylbenzenes in Chloroform. J. Phys. Chem. 1974, 78, 2297–2301. [Google Scholar] [CrossRef]
- Holmes, J.T.; Olander, D.R.; Wilke, C.R. Diffusion in Mixed Solvents. AIChE J. 1962, 8, 646–649. [Google Scholar] [CrossRef]
- Fan, Y.Q.; Qian, R.Y.; Shi, M.R.; Shi, J. Infinite Dilution Diffusion Coefficients of Several Aromatic Hydrocarbons in Octane and 2,2,4-Trimethylpentane. J. Chem. Eng. Data 1995, 40, 1053–1055. [Google Scholar] [CrossRef]
- Snijder, E.D.; te Riele, M.J.M.; Versteeg, G.F.; van Swaaij, W.P.M. Diffusion Coefficients of CO, CO2, N2O, and N2 in Ethanol and Toluene. J. Chem. Eng. Data 1995, 40, 37–39. [Google Scholar] [CrossRef]
- Moore, J.W.; Wellek, R.M. Diffusion Coefficients of N-Heptane and n-Decane in n-Alkanes and n-Alcohols at Several Temperatures. J. Chem. Eng. Data 1974, 19, 136–140. [Google Scholar] [CrossRef]
- Márquez, N.; Kreutzer, M.T.; Makkee, M.; Moulijn, J.A. Infinite Dilution Binary Diffusion Coefficients of Hydrotreating Compounds in Tetradecane in the Temperature Range from (310 to 475) K. J. Chem. Eng. Data 2008, 53, 439–443. [Google Scholar] [CrossRef]
- Kong, C.Y.; Watanabe, K.; Funazukuri, T. Diffusion Coefficients of Phenylbutazone in Supercritical CO2 and in Ethanol. J. Chromatogr. A 2013, 1279, 92–97. [Google Scholar] [CrossRef]
- Pratt, K.C.; Wakeham, W.A. The Mutual Diffusion Coefficient of Ethanol-Water Mixtures: Determination by a Rapid, New Method. Proc. R. Soc. London A 1974, 336, 393–406. [Google Scholar]
- Heintz, A.; Ludwig, R.; Schmidt, E. Limiting Diffusion Coefficients of Ionic Liquids in Water and Methanol: A Combined Experimental and Molecular Dynamics Study. Phys. Chem. Chem. Phys. 2011, 13, 3268–3273. [Google Scholar] [CrossRef]
- Sarraute, S.; Gomes, M.F.C.; Pádua, A.A.H. Diffusion Coefficients of 1-Alkyl-3-Methylimidazolium Ionic Liquids in Water, Methanol, and Acetonitrile at Infinite Dilution. J. Chem. Eng. Data 2009, 54, 2389–2394. [Google Scholar] [CrossRef]
- Hurle, R.L.; Woolf, L.A. Tracer Diffusion in Methanol and Acetonitrile under Pressure. J. Chem. Soc. Faraday Trans. 1982, 78, 2921–2928. [Google Scholar] [CrossRef]
- Sun, C.K.J.; Chen, S.H. Tracer Diffusion in Dense Methanol and 2-Propanol up to Supercritical Region: Understanding of Solvent Molecular Association and Development of an Empirical Correlation. Ind. Eng. Chem. Res. 1987, 26, 815–819. [Google Scholar] [CrossRef]
- Liu, Q.; Takemura, F.; Yabe, A. Solubility and Diffusivity of Carbon Monoxide in Liquid Methanol. J. Chem. Eng. Data 1996, 41, 589–592. [Google Scholar] [CrossRef]
- Lin, I.-H.; Tan, C.-S. Measurement of Diffusion Coefficients of P-Chloronitrobenzene in CO2-Expanded Methanol. J. Supercrit. Fluids 2008, 46, 112–117. [Google Scholar] [CrossRef]
- Funazukuri, T.; Sugihara, T.; Yui, K.; Ishii, T.; Taguchi, M. Measurement of Infinite Dilution Diffusion Coefficients of Vitamin K3 in CO2 Expanded Methanol. J. Supercrit. Fluids 2016, 108, 19–25. [Google Scholar] [CrossRef]
- Lee, Y.E.; Li, F.Y. Binary Diffusion Coefficients of the Methanol Water System in the Temperature Range 30–40 °C. J. Chem. Eng. Data 1991, 36, 240–243. [Google Scholar] [CrossRef]
- Pratt, K.C.; Wakeham, W.A. The Mutual Diffusion Coefficient for Binary Mixtures of Water and the Isomers of Propanol. Proc. R. Soc. Lond. A 1975, 342, 401–419. [Google Scholar]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Binary Diffusion Coefficients of Acetone in Carbon Dioxide at 308.2 and 313.2 K in the Pressure Range from 7.9 to 40 MPa. Int. J. Thermophys. 2000, 21, 651–669. [Google Scholar] [CrossRef]
- Sassiat, P.R.; Mourier, P.; Caude, M.H.; Rosset, R.H. Measurement of Diffusion Coefficients in Supercritical Carbon Dioxide and Correlation with the Equation of Wilke and Chang. Anal. Chem. 1987, 59, 1164–1170. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Infinite-Dilution Binary Diffusion Coefficients of 2-Propanone, 2-Butanone, 2-Pentanone, and 3-Pentanone in CO2. Int. J. Thermophys. 2000, 21, 1279–1290. [Google Scholar] [CrossRef]
- Kong, C.Y.; Funazukuri, T.; Kagei, S. Chromatographic Impulse Response Technique with Curve Fitting to Measure Binary Diffusion Coefficients and Retention Factors Using Polymer-Coated Capillary Columns. J. Chromatogr. A 2004, 1035, 177–193. [Google Scholar] [CrossRef]
- Nishiumi, H.; Fujita, M.; Agou, K. Diffusion of Acetone in Supercritical Carbon Dioxide. Fluid Phase Equilib. 1996, 117, 356–363. [Google Scholar] [CrossRef]
- Shenai, V.M.; Hamilton, B.L.; Matthews, M.A. Diffusion in Liquid and Supercritical Fluid Mixtures. In Supercritical Fluid Engineering Science-Fundamentals and Applications; Kiran, E., Brennecke, J.F., Eds.; American Chemical Society: Washington, WA, USA, 1992; pp. 92–103. [Google Scholar]
- Dahmen, N.; Kordikowski, A.; Schneider, G.M. Determination of Binary Diffusion Coefficients of Organic Compounds in Supercritical Carbon Dioxide by Supercritical Fluid Chromatography. J. Chromatogr. A 1990, 505, 169–178. [Google Scholar] [CrossRef]
- Suárez-Iglesias, O.; Medina, I.; Pizarro, C.; Bueno, J.L. Diffusion Coefficients of 2-Fluoroanisole, 2-Bromoanisole, Allylbenzene and 1,3-Divinylbenzene at Infinite Dilution in Supercritical Carbon Dioxide. Fluid Phase Equilib. 2007, 260, 279–286. [Google Scholar] [CrossRef]
- González, L.M.; Suárez-Iglesias, O.; Bueno, J.L.; Pizarro, C.; Medina, I. Limiting Binary Diffusivities of Aniline, Styrene, and Mesitylene in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2007, 52, 1286–1290. [Google Scholar] [CrossRef]
- González, L.M.; Bueno, J.L.; Medina, I. Determination of Binary Diffusion Coefficients of Anisole, 2,4-Dimethylphenol, and Nitrobenzene in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 2001, 40, 3711–3716. [Google Scholar] [CrossRef]
- Abaroudi, K. Limpieza de Matrices Sólidas Porosas de Interés Medioambiental Con Fluidos Supercríticos; Universidad Politécnica de Catalunã: Barcelona, Spain, 2001. [Google Scholar]
- Funazukuri, T.; Kong, C.Y.; Kikuchi, T.; Kagei, S. Measurements of Binary Diffusion Coefficient and Partition Ratio at Infinite Dilution for Linoleic Acid and Arachidonic Acid in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2003, 48, 684–688. [Google Scholar] [CrossRef]
- Han, Y.S.; Yang, Y.W.; Wu, P.D. Binary Diffusion Coefficients of Arachidonic Acid Ethyl Ester, Cis-5,8,11,14,17-Eicosapentaenoic Acid Ethyl Ester, and Cis-4,7,10,13,16,19-Docosahexanenoic Acid Ethyl Ester in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2007, 52, 555–559. [Google Scholar] [CrossRef]
- Liong, K.K.; Wells, P.A.; Foster, N.R. Diffusion Coefficients of Long-Chain Esters in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 1991, 30, 1329–1335. [Google Scholar] [CrossRef]
- Filho, C.A.; Silva, C.M.; Quadri, M.B.; Macedo, E.A. Infinite Dilution Diffusion Coefficients of Linalool and Benzene in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2002, 47, 1351–1354. [Google Scholar] [CrossRef]
- Swaid, I.; Schneider, G.M. Determination of Binary Diffusion Coefficients of Benzene and Some Alkylbenzenes in Supercritical CO2 between 308 and 328 K in the Pressure Range 80 to 160 Bar with Supercritical Fluid Chromatography (SFC). Ber. Bunsenges. Phys. Chem. Chem. 1979, 83, 969–974. [Google Scholar] [CrossRef]
- Suárez, J.J.; Bueno, J.L.; Medina, I. Determination of Binary Diffusion Coefficients of Benzene and Derivatives in Supercritical Carbon Dioxide. Chem. Eng. Sci. 1993, 48, 2419–2427. [Google Scholar] [CrossRef]
- Funazukuri, T.; Nishimoto, N. Tracer Diffusion Coefficients of Benzene in Dense CO2 at 313.2 K and 8.5–30 MPa. Fluid Phase Equilib. 1996, 125, 235–243. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Infinite Dilution Binary Diffusion Coefficients of Benzene in Carbon Dioxide by the Taylor Dispersion Technique at Temperatures from 308.15 to 328.15 K and Pressures from 6 to 30 MPa. Int. J. Thermophys. 2001, 22, 1643–1660. [Google Scholar] [CrossRef]
- Sengers, J.M.H.L.; Deiters, U.K.; Klask, U.; Swidersky, P.; Schneider, G.M. Application of the Taylor Dispersion Method in Supercritical Fluids. Int. J. Thermophys. 1993, 14, 893–922. [Google Scholar] [CrossRef]
- Ago, K.; Nishiumi, H. Mutual Diffusion Coefficients of Benzene in Supercritical Carbon Dioxide. J. Chem. Eng. Jpn. 1999, 32, 563–568. [Google Scholar] [CrossRef]
- Bueno, J.L.; Suárez, J.J.; Dizy, J.; Medina, I. Infinite Dilution Diffusion Coefficients: Benzene Derivatives as Solutes in Supercritical Carbon Dioxide. J. Chem. Eng. Data 1993, 38, 344–349. [Google Scholar] [CrossRef]
- Kong, C.Y.; Funazukuri, T.; Kagei, S. Binary Diffusion Coefficients and Retention Factors for Polar Compounds in Supercritical Carbon Dioxide by Chromatographic Impulse Response Method. J. Supercrit. Fluids 2006, 37, 359–366. [Google Scholar] [CrossRef]
- Catchpole, O.J.; King, M.B. Measurement and Correlation of Binary Diffusion Coefficients in near Critical Fluids. Ind. Eng. Chem. Res. 1994, 33, 1828–1837. [Google Scholar] [CrossRef]
- Fu, H.; Coelho, L.A.F.; Matthews, M.A. Diffusion Coefficients of Model Contaminants in Dense CO2. J. Supercrit. Fluids 2000, 18, 141–155. [Google Scholar] [CrossRef]
- Suárez-Iglesias, O.; Medina, I.; Pizarro, C.; Bueno, J.L. Limiting Diffusion Coefficients of Ethyl Benzoate, Benzylacetone, and Eugenol in Carbon Dioxide at Supercritical Conditions. J. Chem. Eng. Data 2008, 53, 779–784. [Google Scholar] [CrossRef]
- González, L.M.; Suárez-Iglesias, O.; Bueno, J.L.; Pizarro, C.; Medina, I. Application of the Corresponding States Principle to the Diffusion in CO2. AIChE J. 2007, 53, 3054–3061. [Google Scholar] [CrossRef]
- Man, C.W. Limiting Mutual Diffusion of Nonassociated Aromatic Solutes; The Hong Kong Polytechnic University: Hong Kong, 2001. [Google Scholar]
- Suárez, J.J.; Medina, I.; Bueno, J.L. Diffusion Coefficients in Supercritical Fluids: Available Data and Graphical Correlations. Fluid Phase Equilib. 1998, 153, 167–212. [Google Scholar] [CrossRef]
- Funazukuri, T. Measurements of Binary Diffusion Coefficients of 20 Organic Compounds in CO2 at 313.2 K and 16.0 MPa. J. Chem. Eng. Jpn. 1996, 29, 191–192. [Google Scholar] [CrossRef]
- Pizarro, C.; Suárez-Iglesias, O.; Medina, I.; Bueno, J.L. Diffusion Coefficients of N-Butylbenzene, n-Pentylbenzene, 1-Phenylhexane, 1-Phenyloctane, and 1-Phenyldodecane in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 2008, 47, 6783–6789. [Google Scholar] [CrossRef]
- Pizarro, C.; Suárez-Iglesias, O.; Medina, I.; Bueno, J.L. Diffusion Coefficients of Isobutylbenzene, Sec-Butylbenzene, and 3-Methylbutylbenzene in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2013, 58, 2001–2007. [Google Scholar] [CrossRef]
- González, L.M.; Bueno, J.L.; Medina, I. Measurement of Diffusion Coefficients for 2-Nitroanisole, 1,2-Dichlorobenzene and Tert-Butylbenzene in Carbon Dioxide Containing Modifiers. J. Supercrit. Fluids 2002, 24, 219–229. [Google Scholar] [CrossRef]
- Liong, K.K.; Wells, P.A.; Foster, N.R. Diffusion of Fatty Acid Esters in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 1992, 31, 390–399. [Google Scholar] [CrossRef]
- Wells, P.A. Diffusion in Supercritical Fluids; The University of New South Wales: Kensington, Australia, 1991. [Google Scholar]
- Lai, C.-C.; Tan, C.-S. Measurement of Molecular Diffusion Coefficient in Supercritical Carbon Dioxide Using a Coated Capillary Column. Ind. Eng. Chem. Res. 1995, 34, 674–680. [Google Scholar] [CrossRef]
- Knaff, G.; Schlünder, E.U. Diffusion Coefficients of Naphthalene and Caffeine in Supercritical Carbon Dioxide. Chem. Eng. Process. 1987, 21, 101–105. [Google Scholar] [CrossRef]
- Lauer, H.H.; McManigill, D.; Board, R.D. Mobile-Phase Transport Properties of Liquefied Gases in near Critical and Supercritical Fluid Chromatography. Anal. Chem. 1983, 55, 1370–1375. [Google Scholar] [CrossRef]
- Tyn, M.T.; Calus, W.F. Temperature and Concentration Dependence of Mutual Diffusion Coefficients of Some Binary Liquid Systems. J. Chem. Eng. Data 1975, 20, 310–316. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Binary Diffusion Coefficients, Partition Ratios and Partial Molar Volumes at Infinite Dilution for β-Carotene and α-Tocopherol in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2003, 27, 85–96. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Murooka, N.; Kagei, S. Measurements of Binary Diffusion Coefficients and Partition Ratios for Acetone, Phenol, α-Tocopherol, and β-Carotene in Supercritical Carbon Dioxide with a Poly(Ethylene Glycol)-Coated Capillary Column. Ind. Eng. Chem. Res. 2000, 39, 4462–4469. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Measurements of Binary Diffusion Coefficients for Some Low Volatile Compounds in Supercritical Carbon Dioxide by Input–Output Response Technique with Two Diffusion Columns Connected in Series. Fluid Phase Equilib. 2002, 194, 1169–1178. [Google Scholar] [CrossRef]
- Dong, X.; Su, B.; Xing, H.; Bao, Z.; Yang, Y.; Ren, Q. Cosolvent Effects on the Diffusions of 1,3-Dichlorobenzene, L-Carvone, Geraniol and 3-Fluorophenol in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2011, 58, 216–225. [Google Scholar] [CrossRef]
- Dong, X.; Su, B.; Xing, H.; Yang, Y.; Ren, Q. Diffusion Coefficients of L-Menthone and L-Carvone in Mixtures of Carbon Dioxide and Ethanol. J. Supercrit. Fluids 2010, 55, 86–95. [Google Scholar] [CrossRef]
- Cordeiro, J.; Magalhães, A.L.; Valente, A.A.; Silva, C.M. Experimental and Theoretical Analysis of the Diffusion Behavior of Chromium(III) Acetylacetonate in Supercritical CO2. J. Supercrit. Fluids 2016, 118, 153–162. [Google Scholar] [CrossRef]
- Filho, C.A.; Silva, C.M.; Quadri, M.B.; Macedo, E.A. Tracer Diffusion Coefficients of Citral and D-Limonene in Supercritical Carbon Dioxide. Fluid Phase Equilib. 2003, 204, 65–73. [Google Scholar] [CrossRef]
- Kong, C.Y.; Gu, Y.Y.; Nakamura, M.; Funazukuri, T.; Kagei, S. Diffusion Coefficients of Metal Acetylacetonates in Supercritical Carbon Dioxide. Fluid Phase Equilib. 2010, 297, 162–167. [Google Scholar] [CrossRef]
- Yang, Y.N.; Matthews, M.A. Diffusion of Chelating Agents in Supercritical CO2 and a Predictive Approach for Diffusion Coefficients. J. Chem. Eng. Data 2001, 46, 588–595. [Google Scholar] [CrossRef]
- Kong, C.Y.; Takahashi, N.; Funazukuri, T.; Kagei, S. Measurements of Binary Diffusion Coefficients and Retention Factors for Dibenzo-24-Crown-8 and 15-Crown-5 in Supercritical Carbon Dioxide by Chromatographic Impulse Response Technique. Fluid Phase Equilib. 2007, 257, 223–227. [Google Scholar] [CrossRef]
- Cooper, E. Diffusion Coefficients at Infinite Dilution in Alcohol Solvents at Temperatures to 348 K and Pressures to 17 MPa; University of Ottawa: Ottawa, ON, Canada, 1992. [Google Scholar]
- Dahmen, N.; Dulberg, A.; Schneider, G.M.M. Determination of Binary Diffusion Coefficients in Supercritical Carbon Dioxide with Supercritical Fluid Chromatography (SFC). Ber. Bunsenges. Phys. Chem. 1990, 94, 384–386. [Google Scholar] [CrossRef]
- Umezawa, S.; Nagashima, A. Measurement of the Diffusion Coefficients of Acetone, Benzene, and Alkane in Supercritical CO2 by the Taylor Dispersion Method. J. Supercrit. Fluids 1992, 5, 242–250. [Google Scholar] [CrossRef]
- Silva, C.M.; Macedo, E.A. Diffusion Coefficients of Ethers in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 1998, 37, 1490–1498. [Google Scholar] [CrossRef]
- Pizarro, C.; Suárez-Iglesias, O.; Medina, I.; Bueno, J.L. Using Supercritical Fluid Chromatography to Determine Diffusion Coefficients of 1,2-Diethylbenzene, 1,4-Diethylbenzene, 5-Tert-Butyl-m-Xylene and Phenylacetylene in Supercritical Carbon Dioxide. J. Chromatogr. A 2007, 1167, 202–209. [Google Scholar] [CrossRef]
- Pizarro, C.; Suárez-Iglesias, O.; Medina, I.; Bueno, J.L. Binary Diffusion Coefficients for 2,3-Dimethylaniline, 2,6-Dimethylaniline, 2-Methylanisole, 4-Methylanisole and 3-Nitrotoluene in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2009, 48, 1–8. [Google Scholar] [CrossRef]
- Kong, C.Y.; Nakamura, M.; Sone, K.; Funazukuri, T.; Kagei, S. Measurements of Binary Diffusion Coefficients for Ferrocene and 1,1′-Dimethylferrocene in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2010, 55, 3095–3100. [Google Scholar] [CrossRef]
- Higashi, H.; Iwai, Y.; Nakamura, Y.; Yamamoto, S.; Arai, Y. Correlation of Diffusion Coefficients for Naphthalene and Dimethylnaphthalene Isomers in Supercritical Carbon Dioxide. Fluid Phase Equilib. 1999, 166, 101–110. [Google Scholar] [CrossRef]
- Higashi, H.; Iwai, Y.; Takahashi, Y.; Uchida, H.; Arai, Y. Diffusion Coefficients of Naphthalene and Dimethylnaphthalene in Supercritical Carbon Dioxide. Fluid Phase Equilib. 1998, 144, 269–278. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Effects of Molecular Weight and Degree of Unsaturation on Binary Diffusion Coefficients for Lipids in Supercritical Carbon Dioxide. Fluid Phase Equilib. 2004, 219, 67–73. [Google Scholar] [CrossRef]
- Funazukuri, T.; Kong, C.Y.; Kagei, S. Binary Diffusion Coefficient, Partition Ratio, and Partial Molar Volume for Docosahexaenoic Acid, Eicosapentaenoic Acid and α-Linolenic Acid at Infinite Dilution in Supercritical Carbon Dioxide. Fluid Phase Equilib. 2003, 206, 163–178. [Google Scholar] [CrossRef]
- Wong, C.-F.; Hayduk, W. Molecular Diffusivities for Propene in 1-Butanol, Chlorobenzene, Ethylene Glycol, and n-Octane at Elevated Pressures. J. Chem. Eng. Data 1990, 35, 323–328. [Google Scholar] [CrossRef]
- Pizarro, C.; Suárez-Iglesias, O.; Medina, I.; Bueno, J.L. Binary Diffusion Coefficients of 2-Ethyltoluene, 3-Ethyltoluene, and 4-Ethyltoluene in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2009, 54, 1467–1471. [Google Scholar] [CrossRef]
- Kong, C.Y.; Sone, K.; Sako, T.; Funazukuri, T.; Kagei, S. Solubility Determination of Organometallic Complexes in Supercritical Carbon Dioxide by Chromatographic Impulse Response Method. Fluid Phase Equilib. 2011, 302, 347–353. [Google Scholar] [CrossRef]
- Akgerman, A.; Erkey, C.; Orejuela, M. Limiting Diffusion Coefficients of Heavy Molecular Weight Organic Contaminants in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 1996, 35, 911–917. [Google Scholar] [CrossRef]
- Lin, R.; Tavlarides, L.L. Diffusion Coefficients of Diesel Fuel and Surrogate Compounds in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2010, 52, 47–55. [Google Scholar] [CrossRef]
- Funazukuri, T.; Hachisu, S.; Wakao, N. Measurements of Binary Diffusion Coefficients of C16-C24 Unsaturated Fatty Acid Methyl Esters in Supercritical Carbon Dioxide. Ind. Eng. Chem. Res. 1991, 30, 1323–1329. [Google Scholar] [CrossRef]
- Funazukuri, T.; Ishiwata, Y. Diffusion Coefficients of Linoleic Acid Methyl Ester, Vitamin K3 and Indole in Mixtures of Carbon Dioxide and n-Hexane at 313.2 K, and 16.0 MPa and 25.0 MPa. Fluid Phase Equilib. 1999, 164, 117–129. [Google Scholar] [CrossRef]
- Kong, C.Y.; Withanage, N.R.W.; Funazukuri, T.; Kagei, S. Binary Diffusion Coefficients and Retention Factors for γ-Linolenic Acid and Its Methyl and Ethyl Esters in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2006, 37, 63–71. [Google Scholar] [CrossRef]
- Kong, C.Y.; Mori, M.; Funazukuri, T.; Kagei, S. Measurements of Binary Diffusion Coefficients, Retention Factors and Partial Molar Volumes for Myristoleic Acid and Its Methyl Ester in Supercritical Carbon Dioxide. Anal. Sci. 2006, 22, 1431–1436. [Google Scholar] [CrossRef]
- Funazukuri, T.; Ishiwata, Y.; Wakao, N. Predictive Correlation for Binary Diffusion Coefficients in Dense Carbon Dioxide. AIChE J. 1992, 38, 1761–1768. [Google Scholar] [CrossRef]
- Lamb, D.M.; Adamy, S.T.; Woo, K.W.; Jonas, J. Transport and Relaxation of Naphthalene in Supercritical Fluids. J. Phys. Chem. 1989, 93, 5002–5005. [Google Scholar] [CrossRef]
- U.S. Department of Commerce National Institute of Standards and Technology (NIST). Available online: https://www.nist.gov/ (accessed on 22 August 2020).
- Yaws, C.L. Chemical Properties Handbook: Physical, Thermodynamic, Environmental, Transport, Safety, and Health Related Properties for Organic and Inorganic Chemicals; McGraw-Hill Professional: New York, NY, USA, 1998. [Google Scholar]
- Cibulka, I.; Ziková, M. Liquid Densities at Elevated Pressures of 1-Alkanols from C1 to C10: A Critical Evaluation of Experimental Data. J. Chem. Eng. Data 1994, 39, 876–886. [Google Scholar] [CrossRef]
- Cibulka, I.; Hnědkovský, L.; Takagi, T. P−ρ−T Data of Liquids: Summarization and Evaluation. 4. Higher 1-Alkanols (C11, C12, C14, C16), Secondary, Tertiary, and Branched Alkanols, Cycloalkanols, Alkanediols, Alkanetriols, Ether Alkanols, and Aromatic Hydroxy Derivatives. J. Chem. Eng. Data 1997, 42, 415–433. [Google Scholar] [CrossRef]
- Cibulka, I.; Takagi, T.; Růžička, K. P−ρ−T Data of Liquids: Summarization and Evaluation. 7. Selected Halogenated Hydrocarbons. J. Chem. Eng. Data 2000, 46, 2–28. [Google Scholar] [CrossRef]
- Cibulka, I.; Takagi, T. P−ρ−T Data of Liquids: Summarization and Evaluation. 8. Miscellaneous Compounds. J. Chem. Eng. Data 2002, 47, 1037–1070. [Google Scholar] [CrossRef]
- Viswanath, D.S.; Ghosh, T.K.; Prasad, D.H.; Dutt, N.V.K.; Rani, K.Y. Viscosity of Liquids: Theory, Estimation, Experiment, and Data; Springer: Dordrecht, The Netherlands, 2007; ISBN 978-1-4020-5482-2. [Google Scholar]
- Lucas, K. Ein Einfaches Verfahren zur Berechnung der Viskosität von Gasen und Gasgemischen. Chem. Ing. Tech. 1974, 46, 157. [Google Scholar] [CrossRef]
- Assael, M.J.; Dymond, J.H.; Polimatidou, S.K. Correlation and Prediction of Dense Fluid Transport Coefficients. Fluid Phase Equilib. 1994, 15, 189–201. [Google Scholar] [CrossRef]
- Cano-Gómez, J.J.; Iglesias-Silva, G.A.; Rico-Ramírez, V.; Ramos-Estrada, M.; Hall, K.R. A New Correlation for the Prediction of Refractive Index and Liquid Densities of 1-Alcohols. Fluid Phase Equilib. 2015, 387, 117–120. [Google Scholar] [CrossRef]
- Pádua, A.A.H.; Fareleira, J.M.N.A.; Calado, J.C.G.; Wakeham, W.A. Density and Viscosity Measurements of 2,2,4-Trimethylpentane (Isooctane) from 198 K to 348 K and up to 100 MPa. J. Chem. Eng. Data 1996, 41, 1488–1494. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Schreiber, D.R. Improving Equation-of-State Accuracy in the Critical Region; Equations for Carbon Dioxide and Neopentane as Examples. Fluid Phase Equilib. 1988, 41, 1–17. [Google Scholar] [CrossRef]
- Altunin, V.V.; Skhabetinov, M. Viscosity of Liquid and Gaseous Carbon Dioxide at Temperatures 220−1300 K and Pressure up to 1200 Bar. Teploenergetika 1972, 8, 85–89. [Google Scholar]
- IAPWS. Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam. In International Steam Tables; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2008; pp. 7–150. [Google Scholar]


| Solvent | Polar | Water | Non-Polar | SC-CO2 | Global |
|---|---|---|---|---|---|
| Nsys | 89 | 133 | 154 | 177 | 553 |
| NDP | 1405 | 1266 | 1113 | 5028 | 8812 |
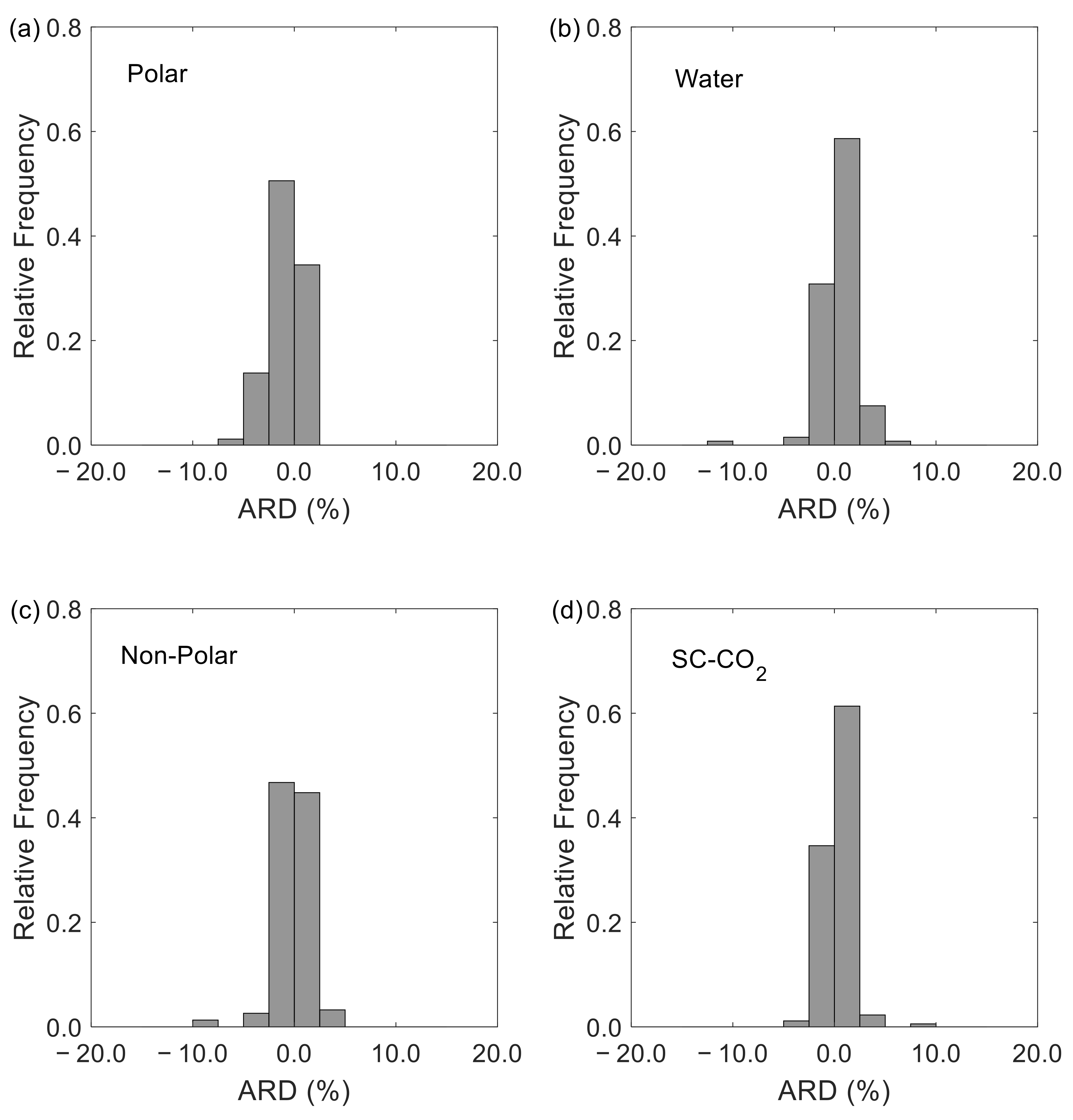
| AARD (%) | 3.77 | 3.96 | 3.29 | 3.23 | 3.43 |
| ARD (%) | −0.36 | 0.16 | −0.31 | 0.35 | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zêzere, B.; Portugal, I.; Gomes, J.R.B.; Silva, C.M. Modeling Tracer Diffusion Coefficients of Any Type of Solutes in Polar and Non-Polar Dense Solvents. Materials 2022, 15, 6416. https://doi.org/10.3390/ma15186416
Zêzere B, Portugal I, Gomes JRB, Silva CM. Modeling Tracer Diffusion Coefficients of Any Type of Solutes in Polar and Non-Polar Dense Solvents. Materials. 2022; 15(18):6416. https://doi.org/10.3390/ma15186416
Chicago/Turabian StyleZêzere, Bruno, Inês Portugal, José R. B. Gomes, and Carlos M. Silva. 2022. "Modeling Tracer Diffusion Coefficients of Any Type of Solutes in Polar and Non-Polar Dense Solvents" Materials 15, no. 18: 6416. https://doi.org/10.3390/ma15186416
APA StyleZêzere, B., Portugal, I., Gomes, J. R. B., & Silva, C. M. (2022). Modeling Tracer Diffusion Coefficients of Any Type of Solutes in Polar and Non-Polar Dense Solvents. Materials, 15(18), 6416. https://doi.org/10.3390/ma15186416








