Design, Manufacture, and Characterization of Auxetic Yarns with Multiple Core/Wrap Structure by Braiding Method
Abstract
:1. Introduction
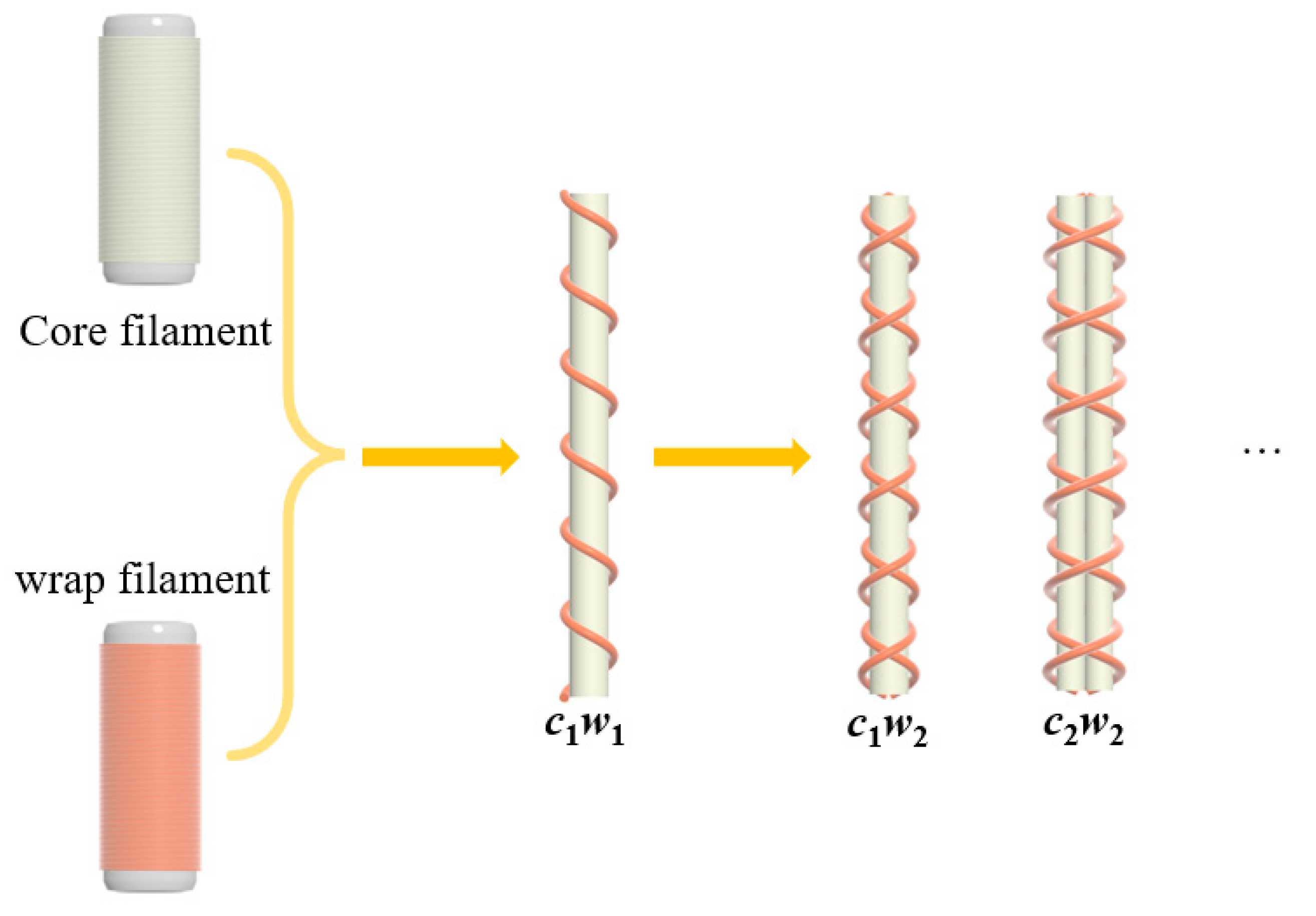
2. Materials and Methods
3. Results
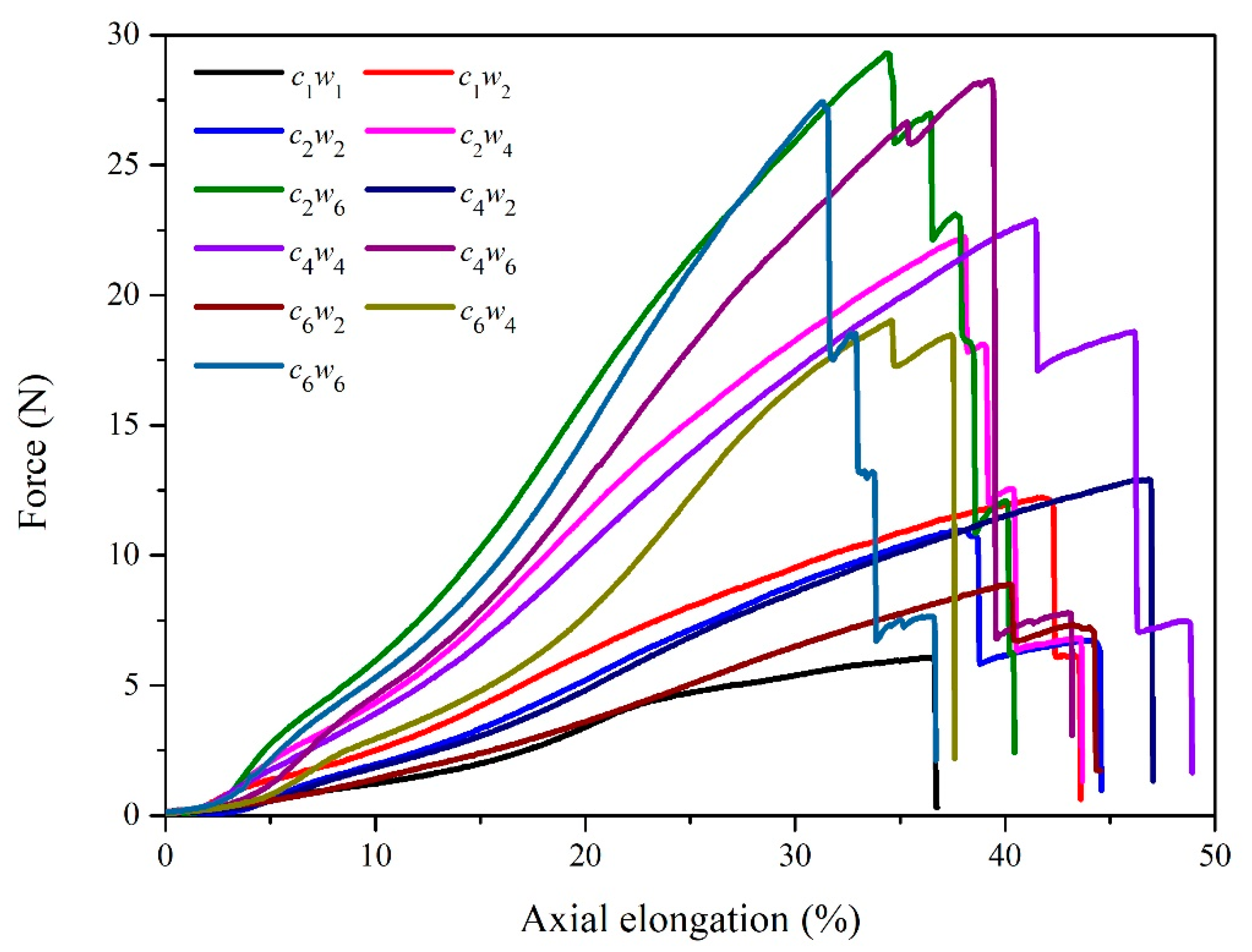
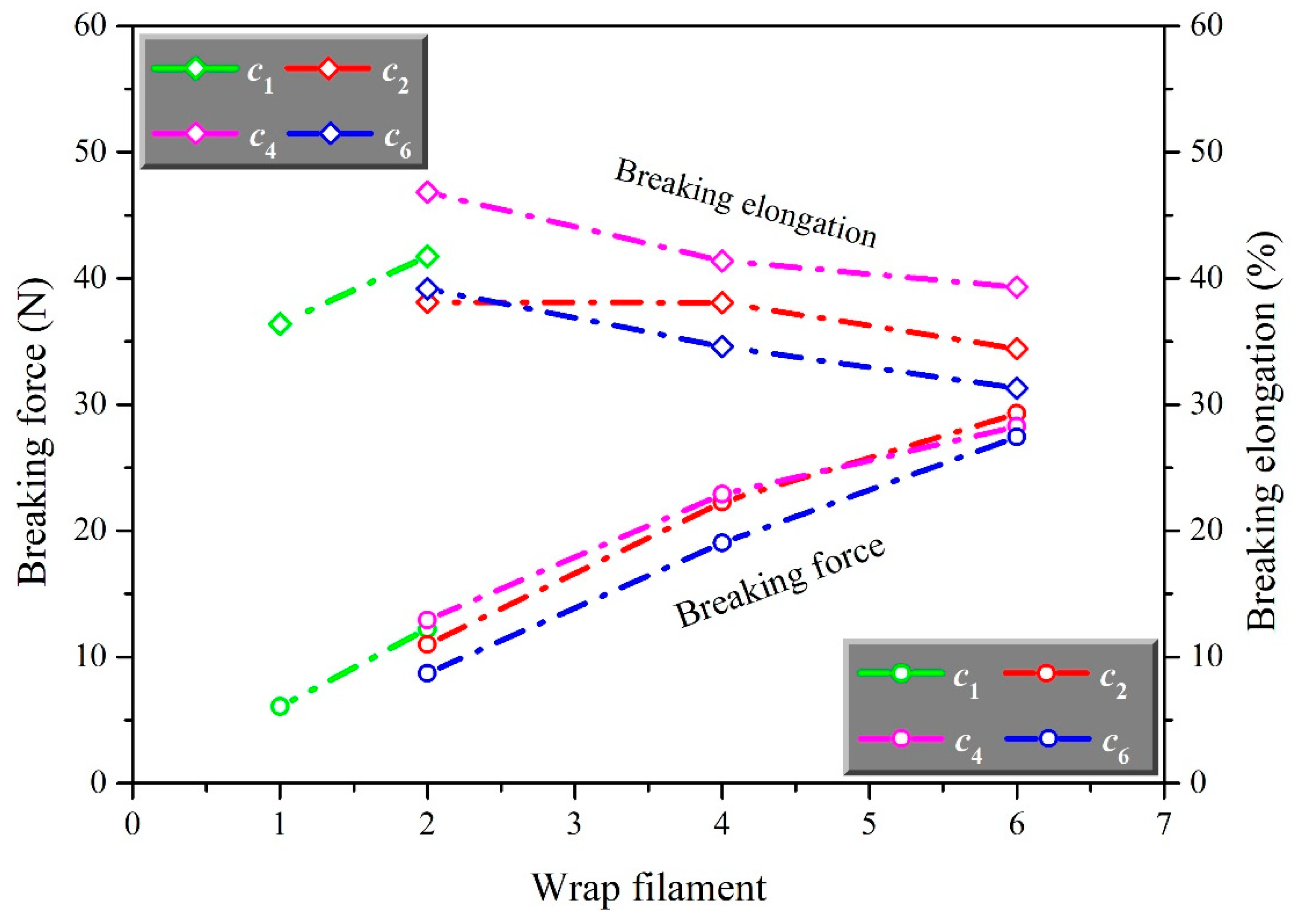
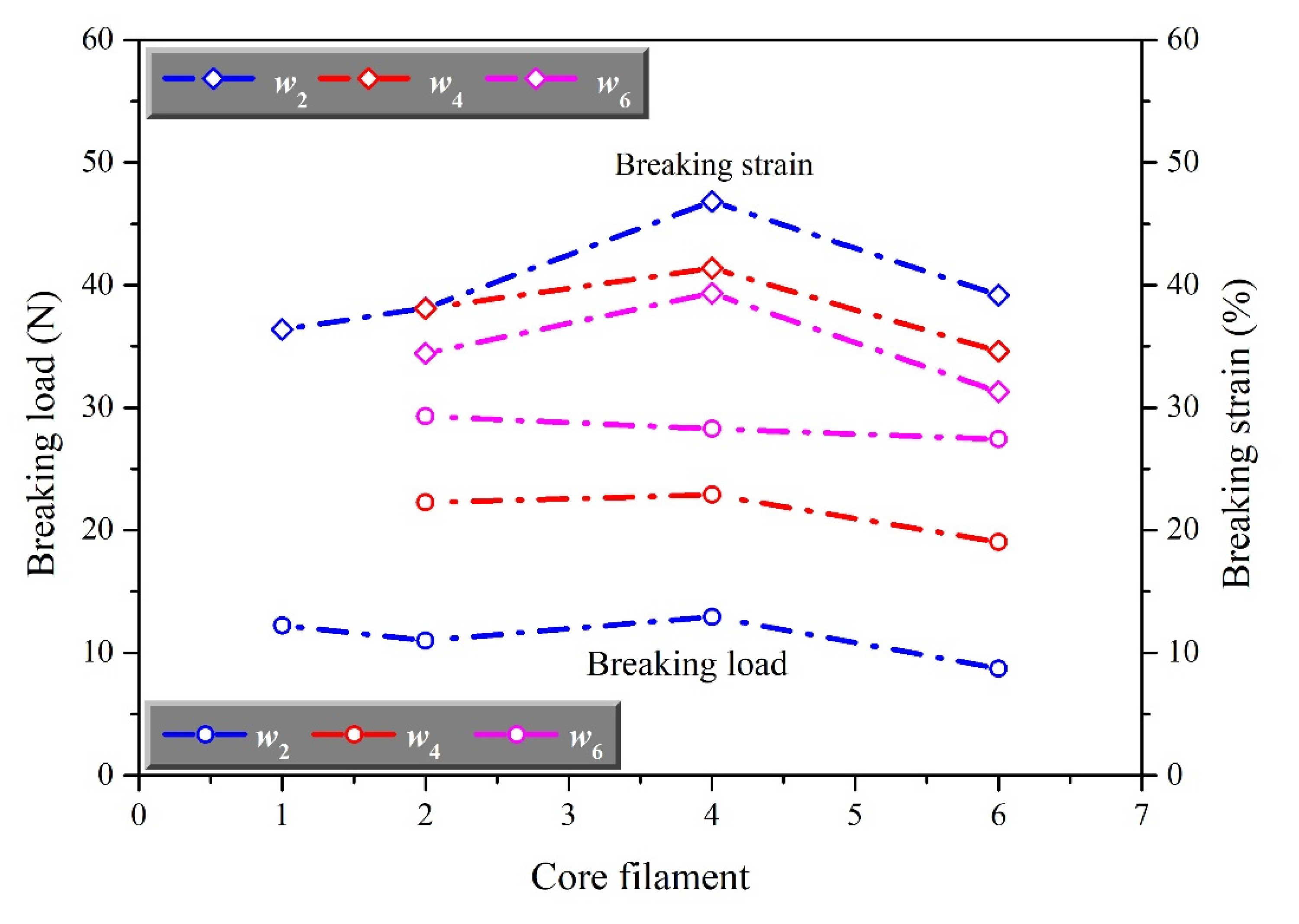
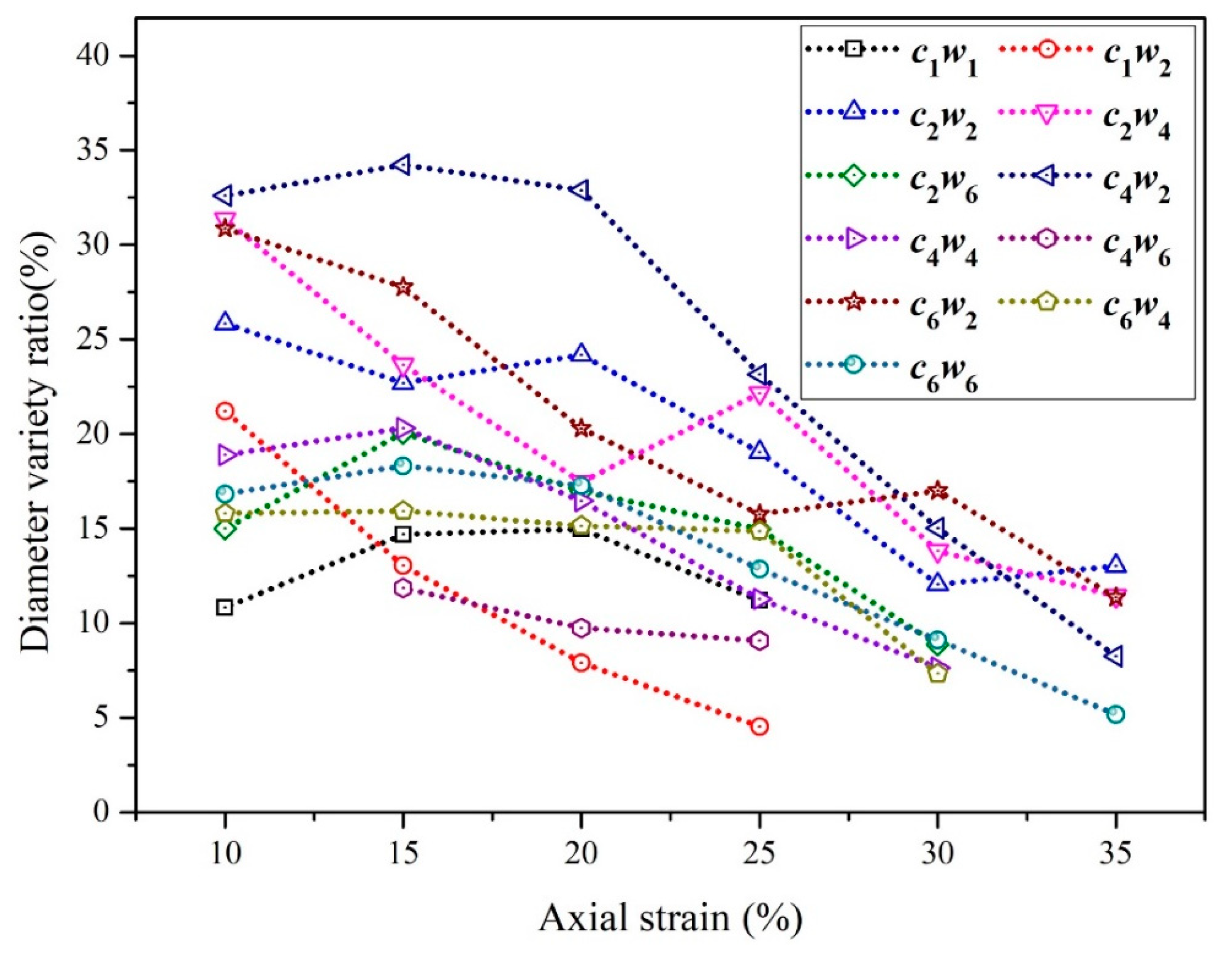
3.1. The Effect of Structure on Mechanical Property
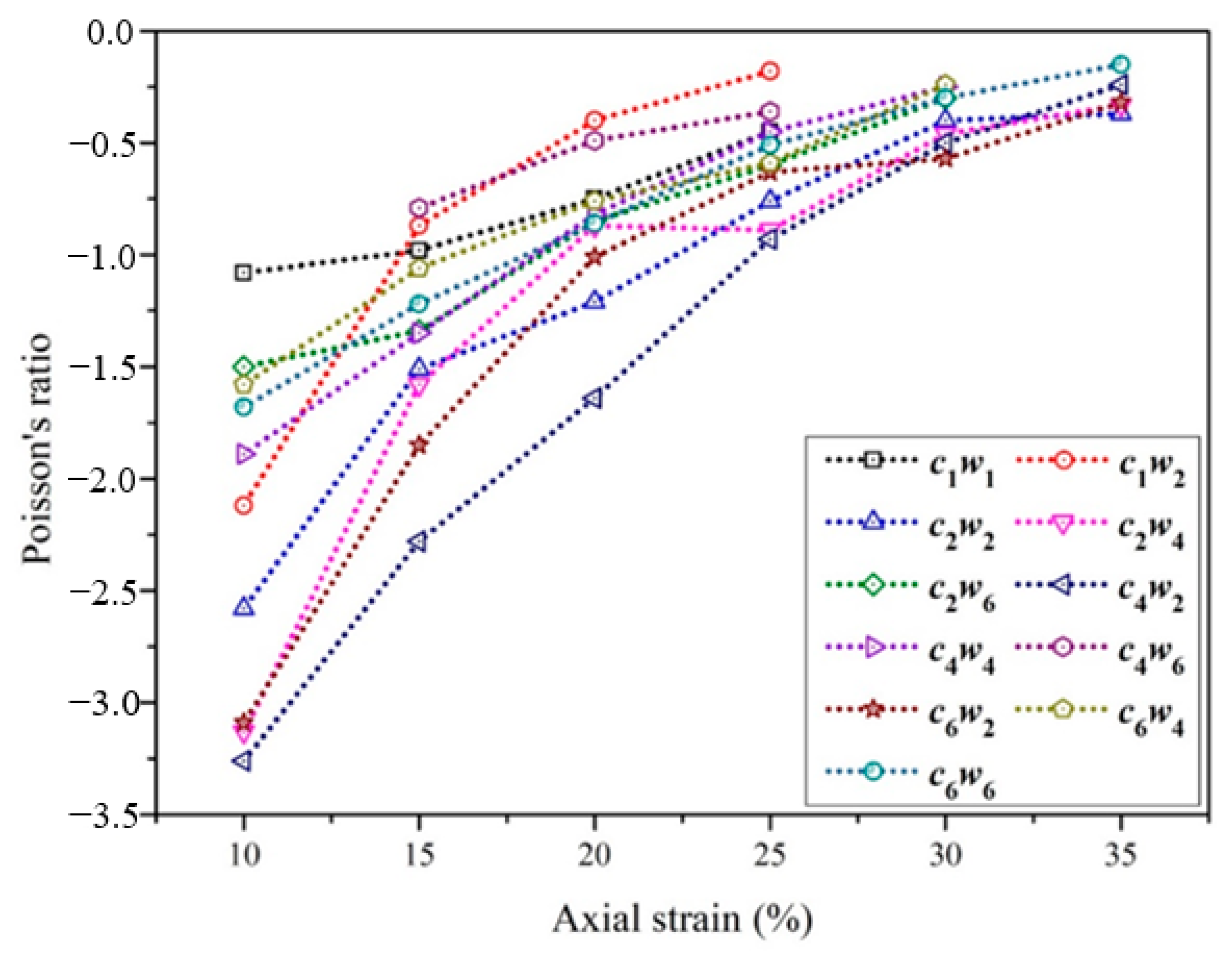
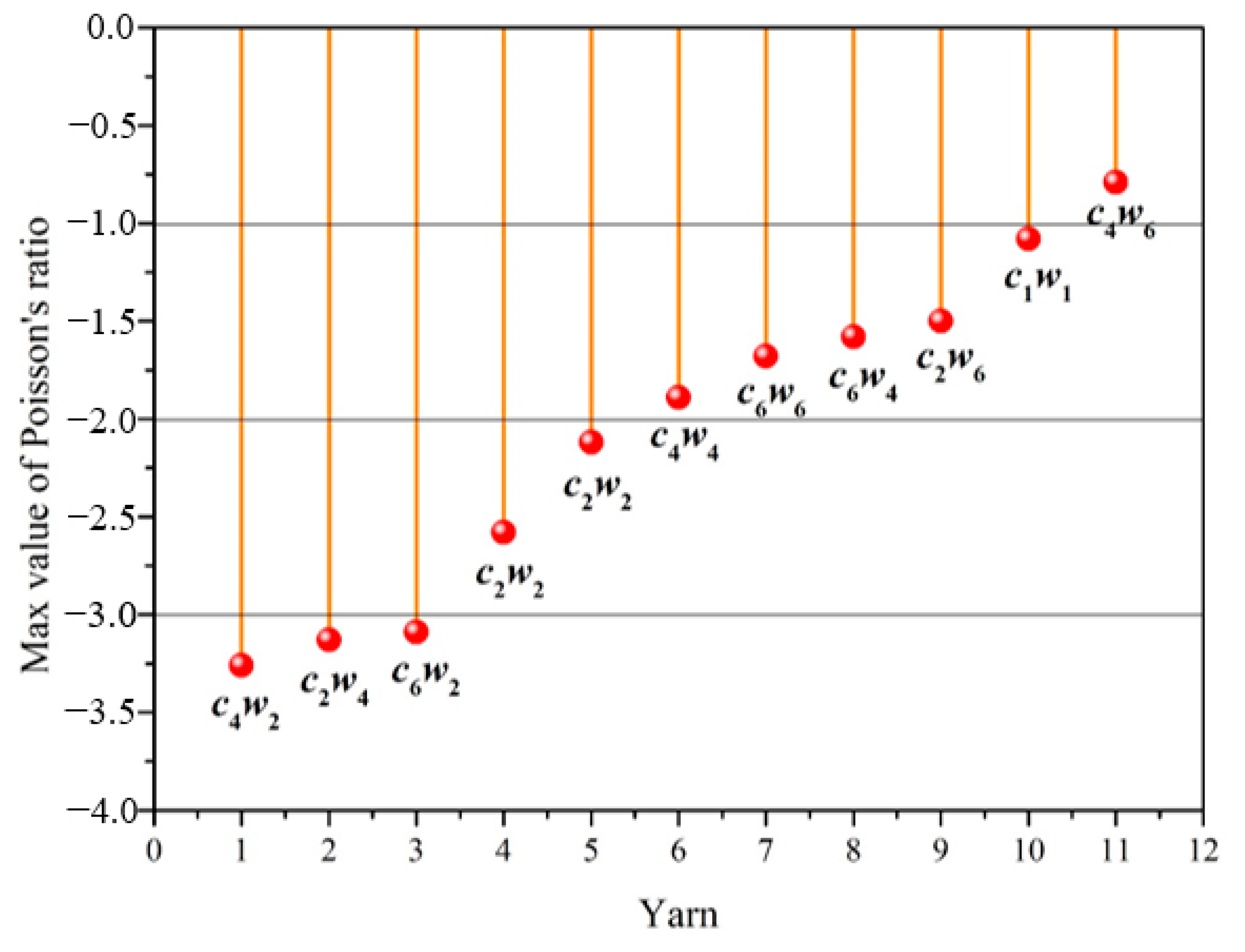
3.2. The Effect of Structure on Poisson’s Ratio
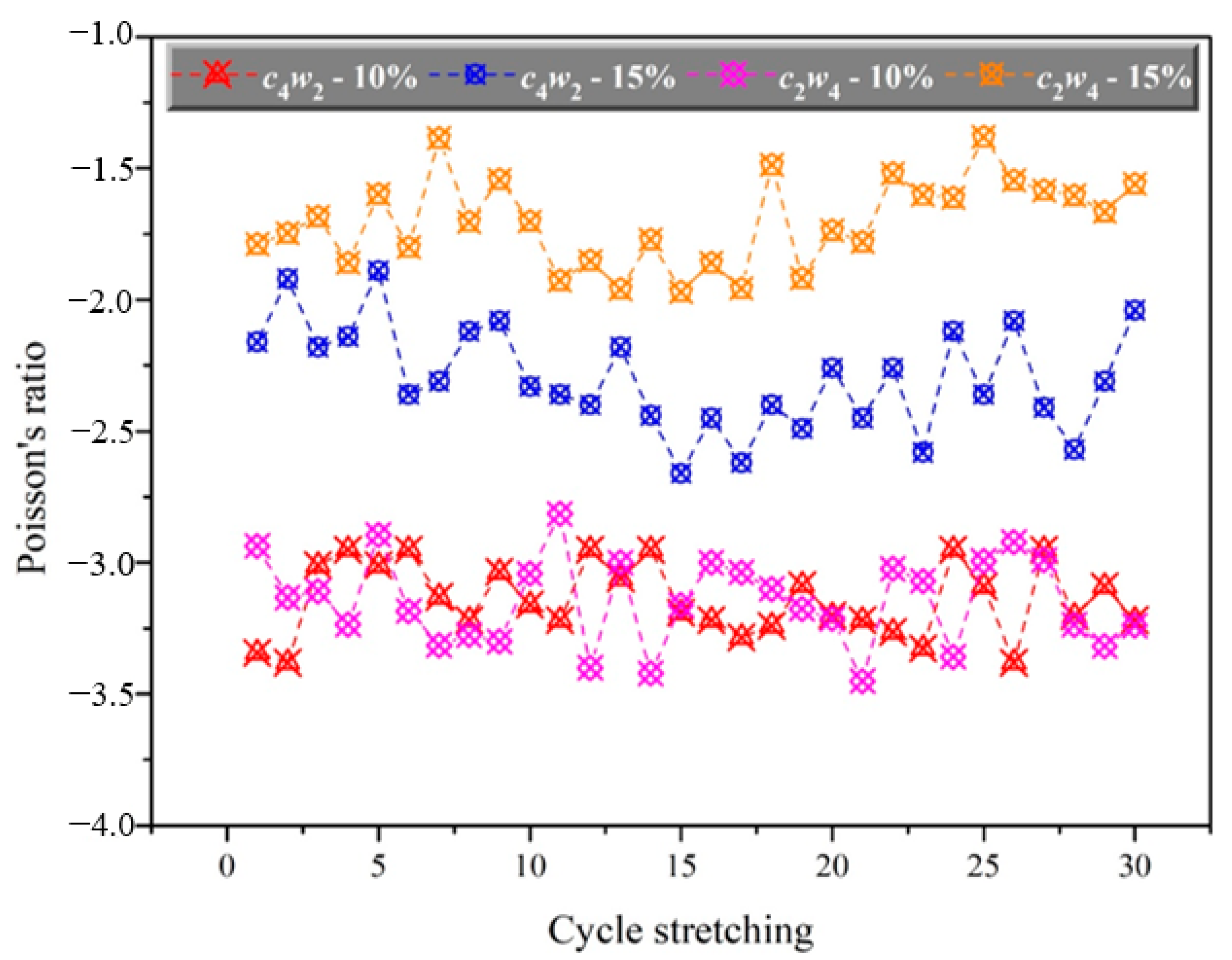
3.3. Auxetic Effect under Cycle Stretching
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart. Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Saxena, K.K.; Das, R.; Calius, E.P. Three decades of auxetics research-materials with negative Poisson′s ratio: A review. Adv. Eng. Mater. 2016, 18, 1847–1870. [Google Scholar] [CrossRef]
- Steffens, F.; Oliveira, F.R.; Fangueiro, R. Energy absorption from composite reinforced with high performance auxetic textile structure. J. Compos. Mater. 2021, 55, 1003–1013. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K. Expanding materials and applications: Exploiting auxetic textiles. Tech. Text. Intl. 2005, 777, 29–34. [Google Scholar]
- Jiang, N.; Hu, H. Auxetic yarn made with circular braiding technology. Phys. Status. Solidi. B 2019, 256, 1800168. [Google Scholar] [CrossRef]
- Cao, H.J.; Zulifqar, A.; Hua, T.; Hu, H. Bi-stretch auxetic woven fabrics based on foldable geometry. Text. Res. J. 2019, 89, 2694–2712. [Google Scholar] [CrossRef]
- Wang, X.T.; Wang, B.; Wen, Z.H.; Ma, L. Fabrication and mechanical properties of CFRP composite three-dimensional double-arrow-head auxetic structures. Compos. Sci. Technol. 2018, 164, 92–102. [Google Scholar] [CrossRef]
- Ge, Z.Y.; Hu, H.; Liu, S.R. A novel plied yarn structure with negative Poisson′s ratio. J. Text. Inst. 2016, 107, 578–588. [Google Scholar] [CrossRef]
- McAfee, J.; Faisal, N.H. Parametric sensitivity analysis to maximise auxetic effect of polymeric fibre based helical yarn. Compos. Struct. 2017, 162, 1–12. [Google Scholar] [CrossRef]
- Zeng, J.F.; Hu, H. A theoretical analysis of deformation behavior of auxetic plied yarn structure. Smart. Mater. Struct. 2018, 27, 075003. [Google Scholar] [CrossRef]
- Miller, W.; Hook, P.; Smith, C.W.; Wang, X.; Evans, K.E. The manufacture and characterisation of a novel, low modulus, negative Poisson’s ratio composite. Compos. Sci. Technol. 2009, 69, 651–655. [Google Scholar] [CrossRef]
- Zhou, M.; Du, Z.Q. Effects of structural parameters and performance on Poisson’s ratio of auxetic yarn. Adv. Mater. Res. 2013, 821–822, 252–258. [Google Scholar] [CrossRef]
- Du, Z.Q.; Zhou, M.; He, L.E.; Liu, H.L. Study on negative Poisson’s ratio of auxetic yarn under tension: Part2—Experimental verification. Text. Res. J. 2015, 85, 768–774. [Google Scholar] [CrossRef]
- Sloan, M.R.; Wright, J.R.; Evans, K.E. The helical auxetic yarn—A novel structure for composites and textiles; geometry, manufacture and mechanical properties. Mech. Mater. 2011, 43, 476–486. [Google Scholar] [CrossRef]
- Zhang, G.H.; Ghita, O.R.; LIN, C.P.; Evans, K.E. Large-scale manufacturing of helical auxetic yarns using a novel semi-coextrusion process. Text. Res. J. 2017, 88, 2590–2601. [Google Scholar] [CrossRef]
- Jiang, N.; Hu, H. A study of tubular braided structure with negative Poisson’s ratio behavior. Text. Res. J. 2017, 88, 2810–2824. [Google Scholar] [CrossRef]
- Ma, P.B.; Chang, Y.P.; Boakye, A.; Jiang, G.M. Review on the knitted structures with auxetic effect. J. Text. Inst. 2017, 108, 947–961. [Google Scholar] [CrossRef]

| Preparation Method | Materials | Structure | Parameters | Maximum of Negative Poisson’s Ratio |
|---|---|---|---|---|
| Ring-spinning | Core: rubber filament Wrap: nylon filament | Helical Wrapping structure | Initial helical angle: 25°~35° | >−2 |
| Hollow spindle | Core: polyurethane Wrap: nylon filament | Helical Wrapping structure | Initial helical angle: 13°~25° | >−2 |
| Braiding | Stiff yarn: polyester Core/Elastic yarn: polyester and rubber | Tubular braided structure | Initial Braiding angle: 12°~36° | >−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Chen, H.; Li, Y.; Du, Z. Design, Manufacture, and Characterization of Auxetic Yarns with Multiple Core/Wrap Structure by Braiding Method. Materials 2022, 15, 6300. https://doi.org/10.3390/ma15186300
Liu S, Chen H, Li Y, Du Z. Design, Manufacture, and Characterization of Auxetic Yarns with Multiple Core/Wrap Structure by Braiding Method. Materials. 2022; 15(18):6300. https://doi.org/10.3390/ma15186300
Chicago/Turabian StyleLiu, Sai, Haoyu Chen, Yizhu Li, and Zhaoqun Du. 2022. "Design, Manufacture, and Characterization of Auxetic Yarns with Multiple Core/Wrap Structure by Braiding Method" Materials 15, no. 18: 6300. https://doi.org/10.3390/ma15186300
APA StyleLiu, S., Chen, H., Li, Y., & Du, Z. (2022). Design, Manufacture, and Characterization of Auxetic Yarns with Multiple Core/Wrap Structure by Braiding Method. Materials, 15(18), 6300. https://doi.org/10.3390/ma15186300






