Finite Element Analysis of Elastoplastic Elements in the Iwan Model of Bolted Joints
Abstract
:1. Introduction
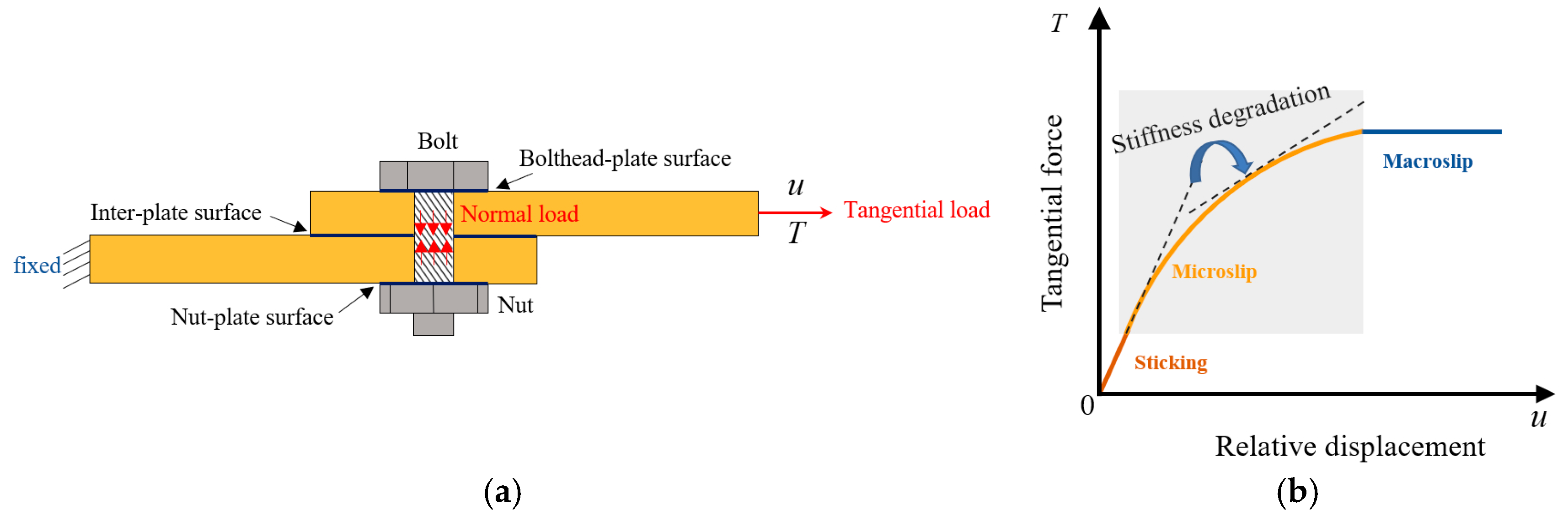
2. The Iwan Model and the Microslip Friction Modeling Approach
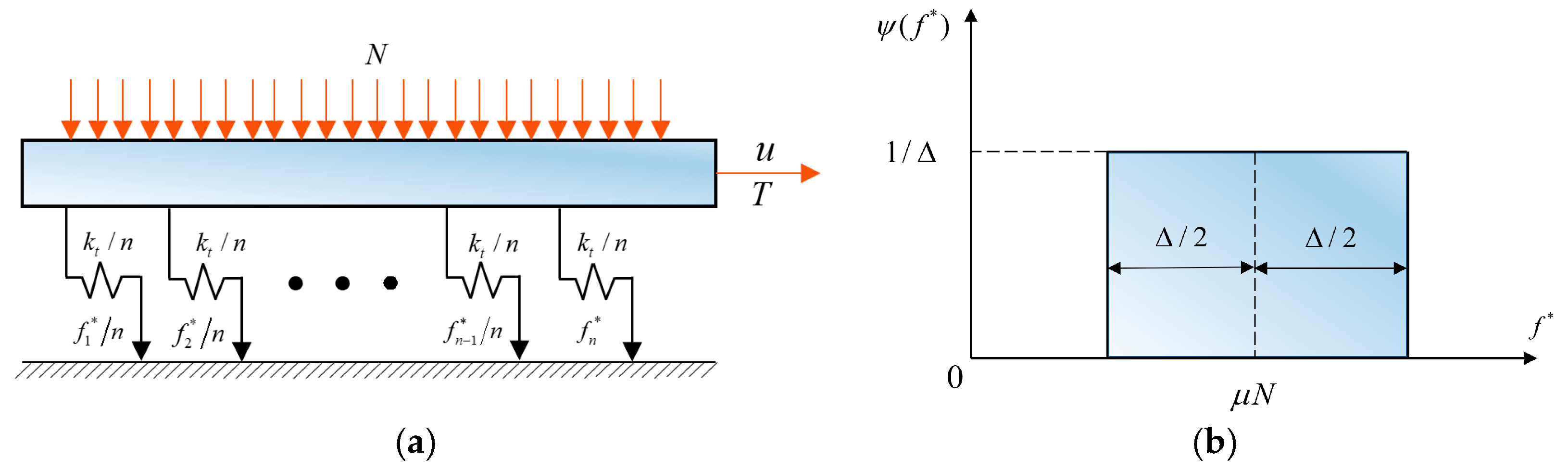
2.1. The Iwan Model
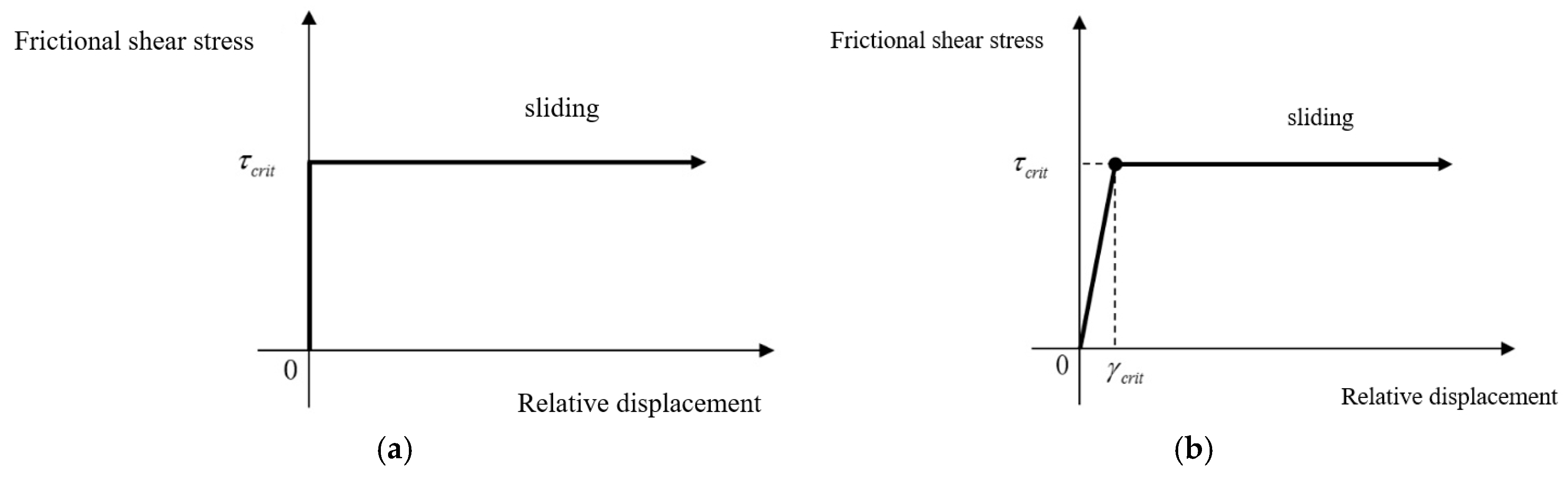
2.2. The Microslip Friction Modeling Approach
3. Calculation and Analysis
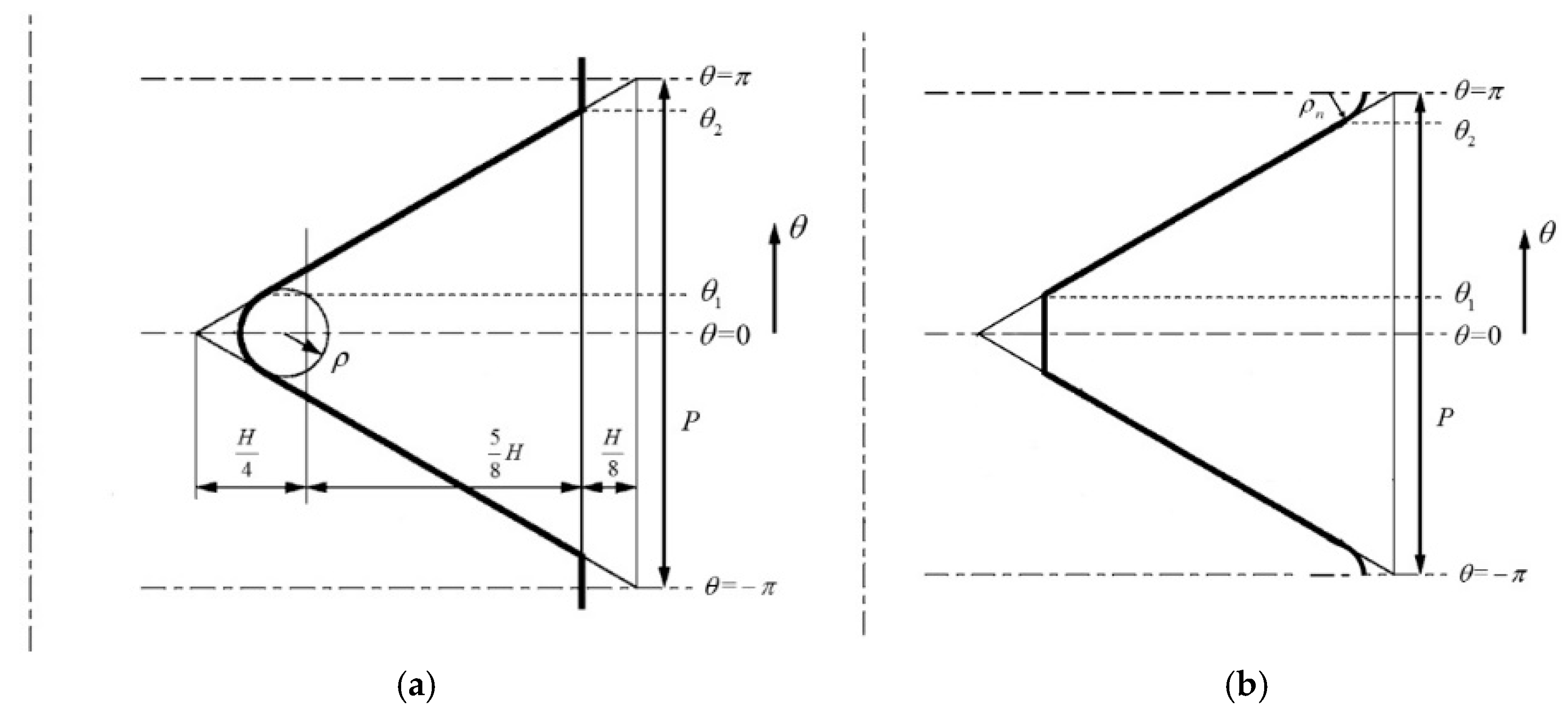
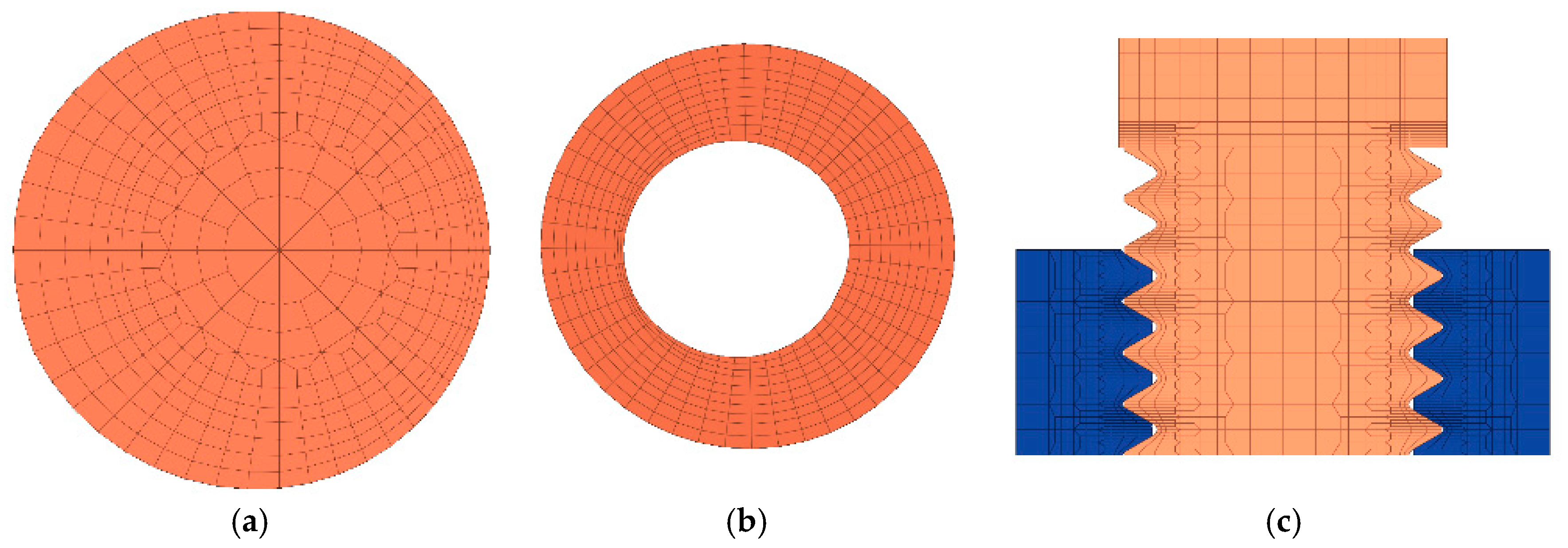
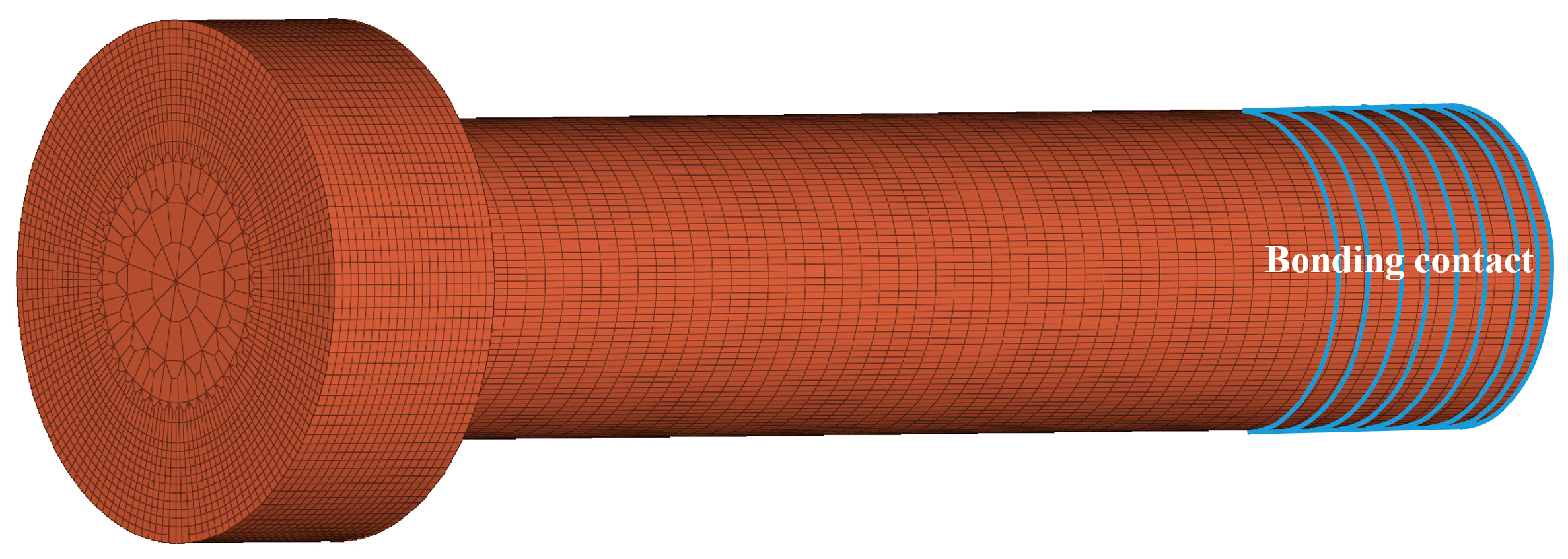
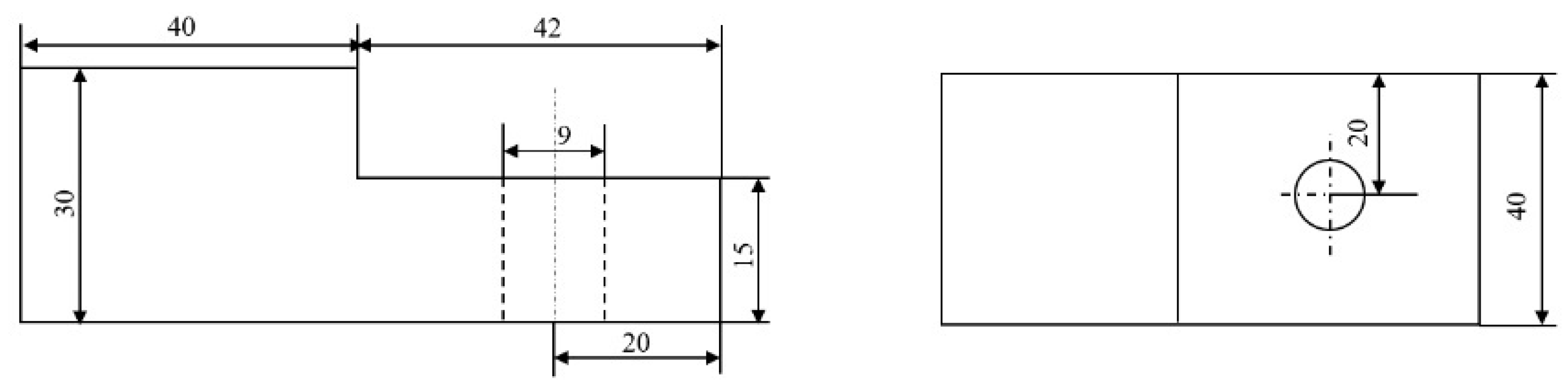
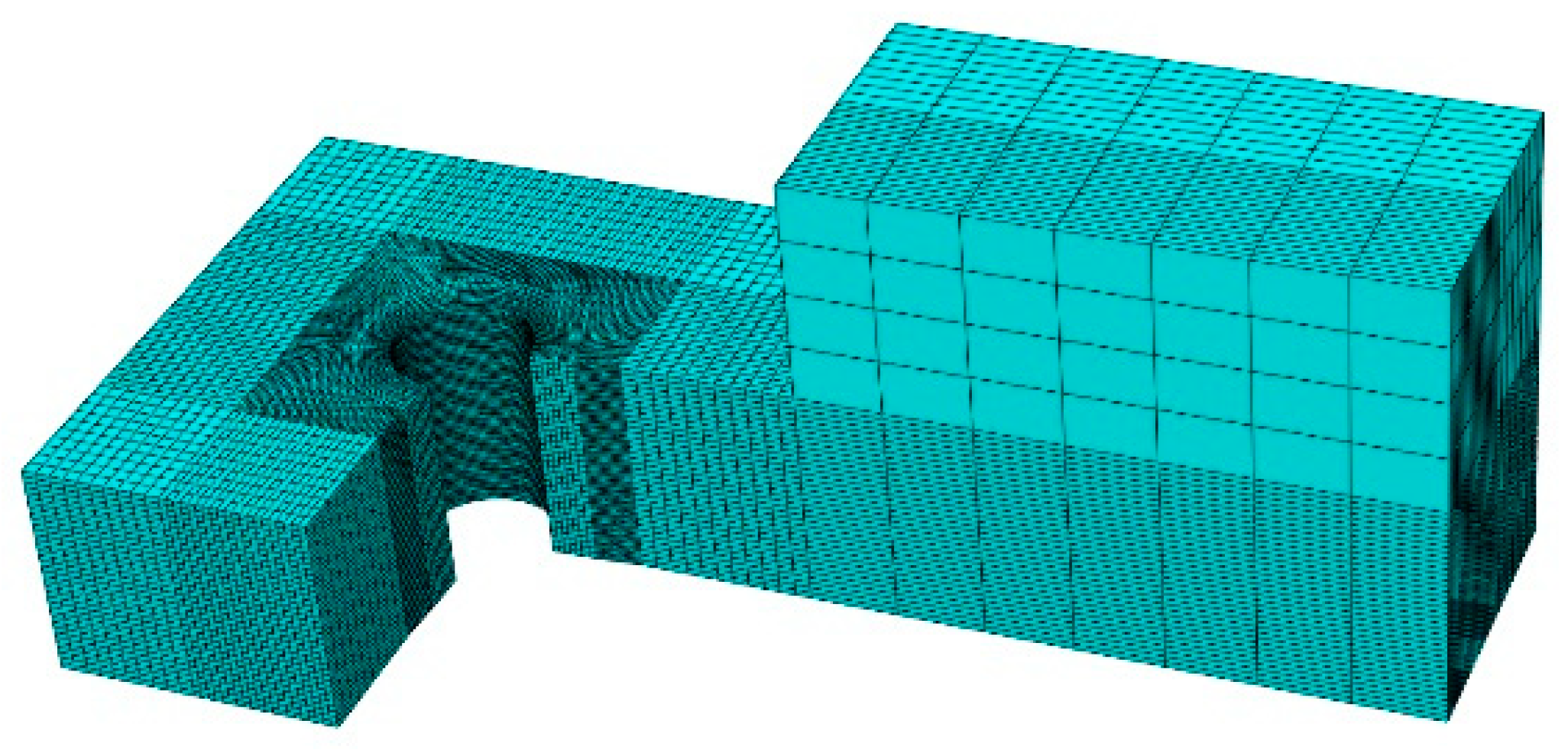
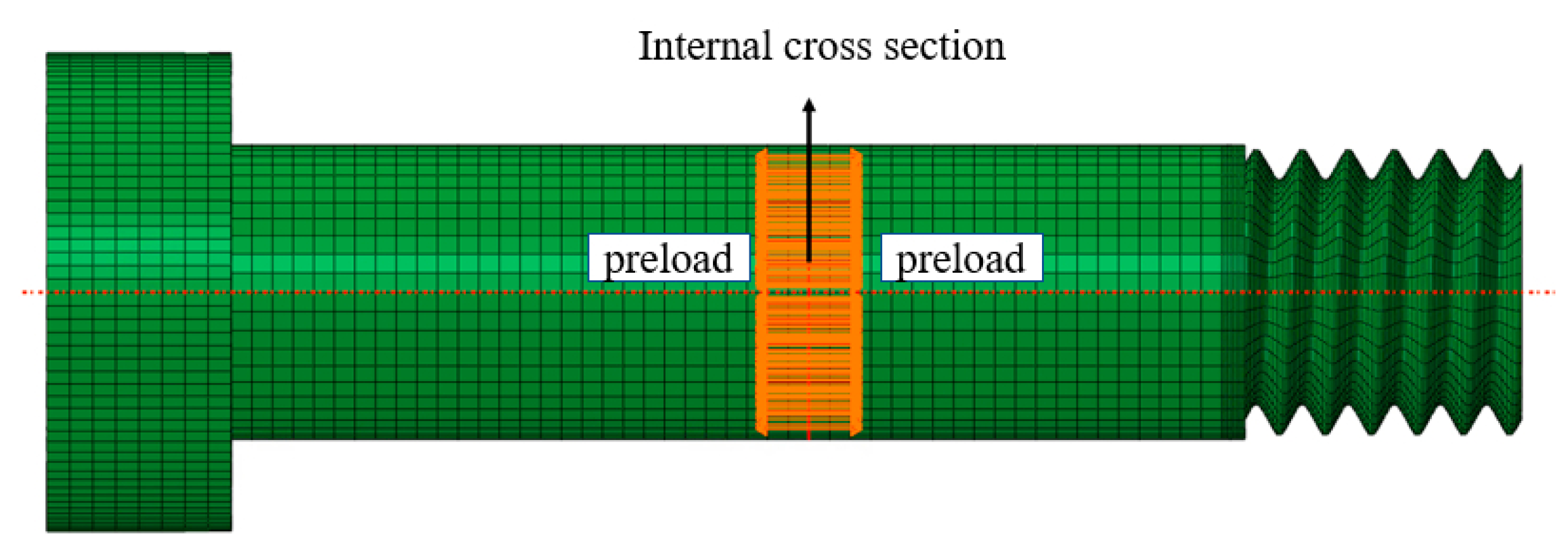
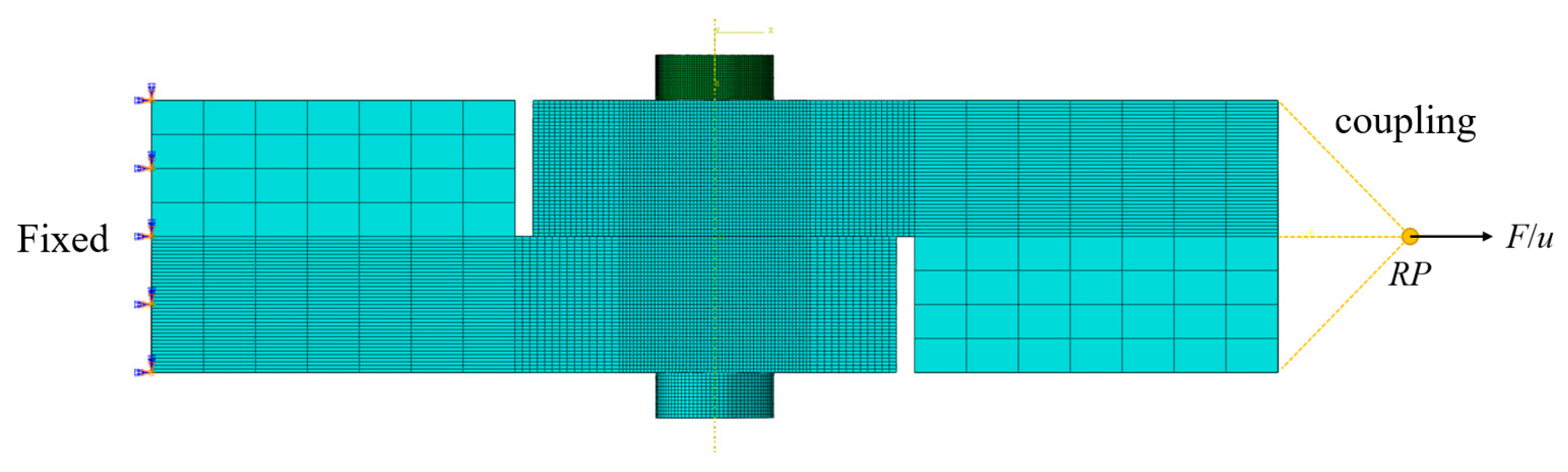
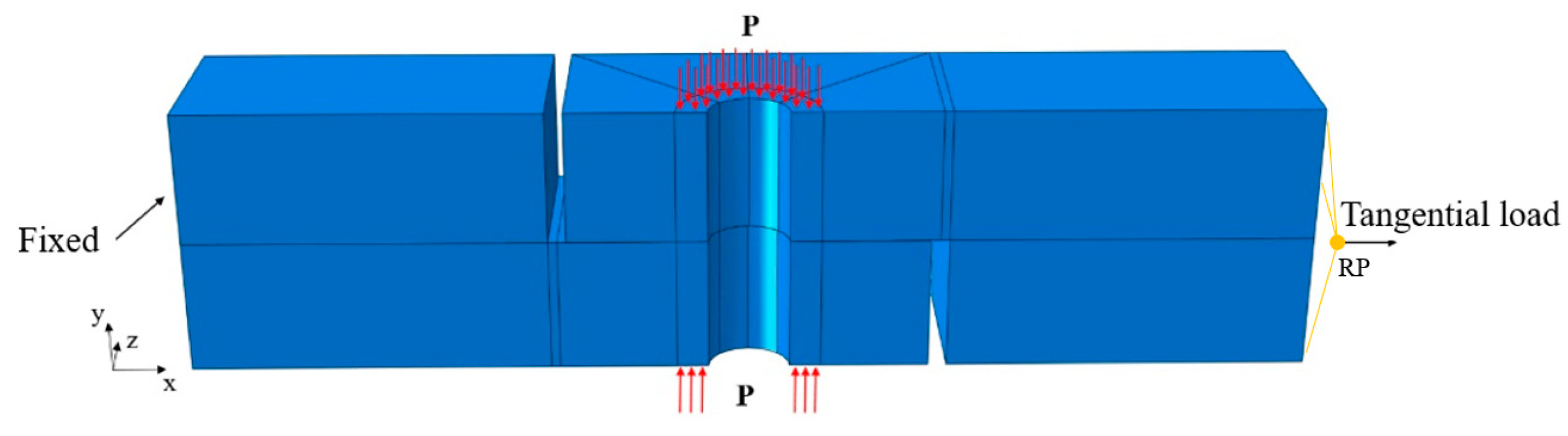
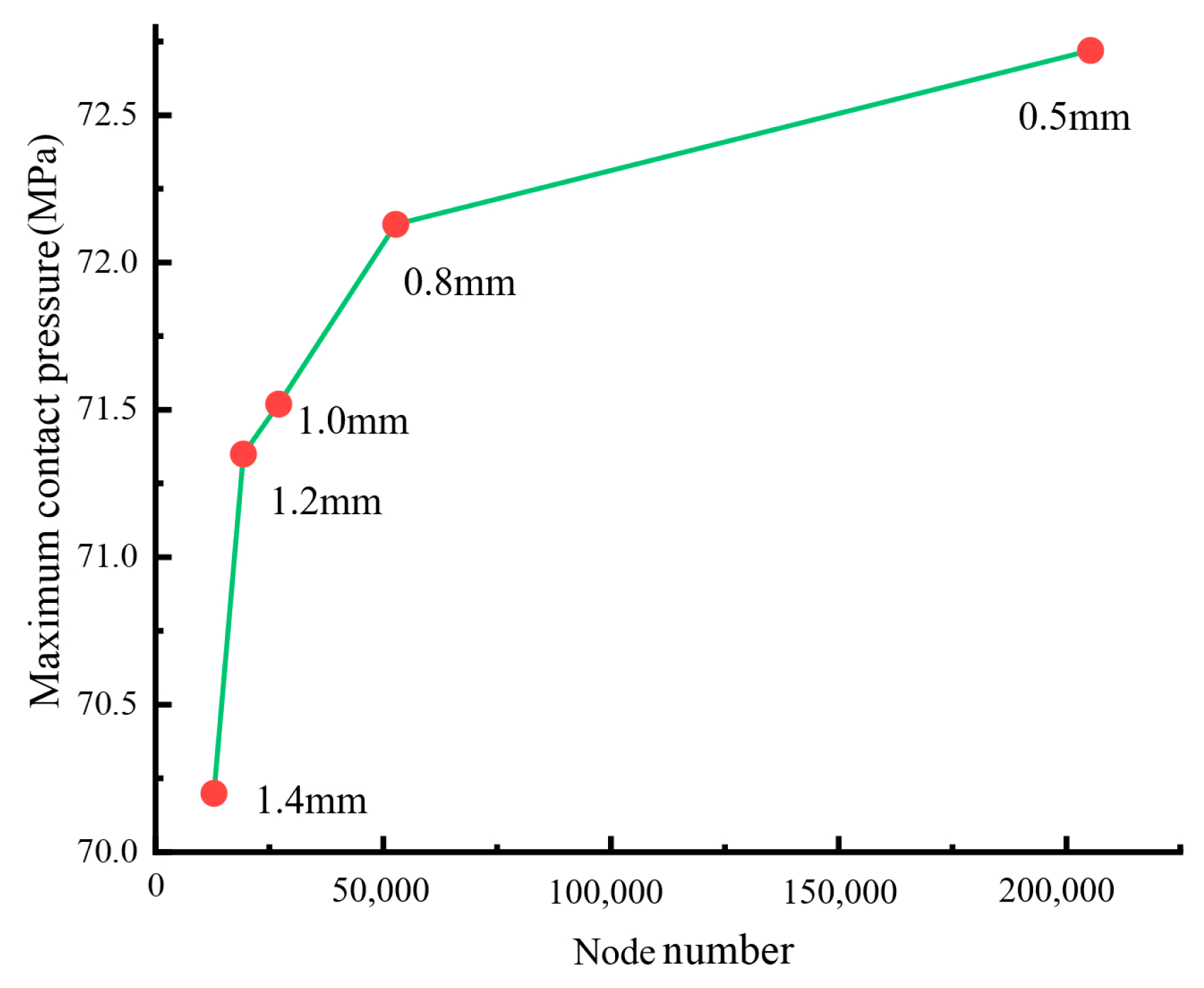
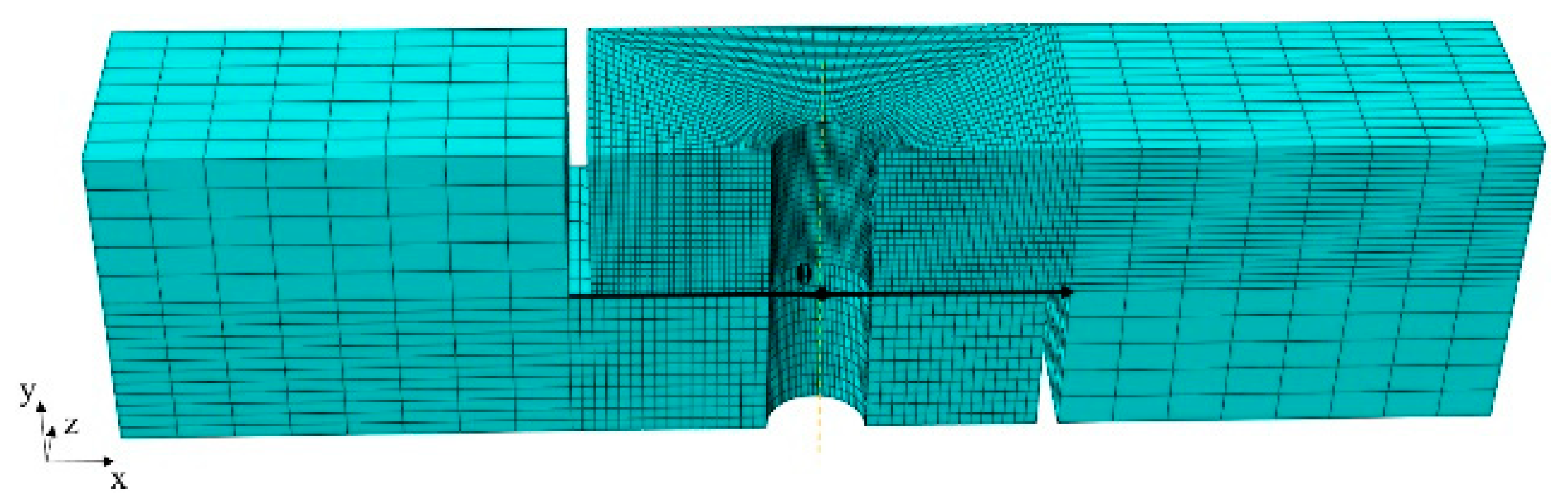
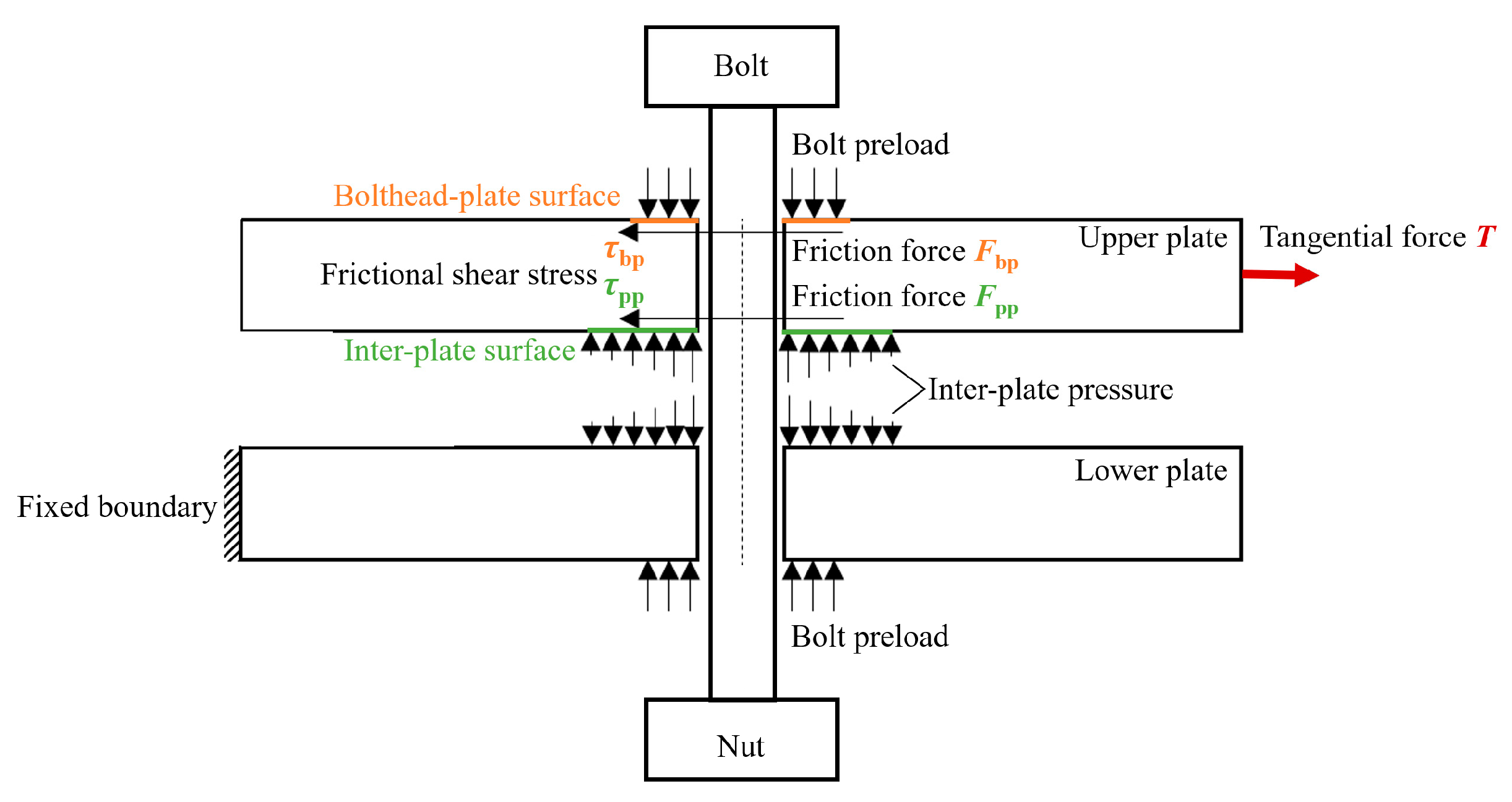
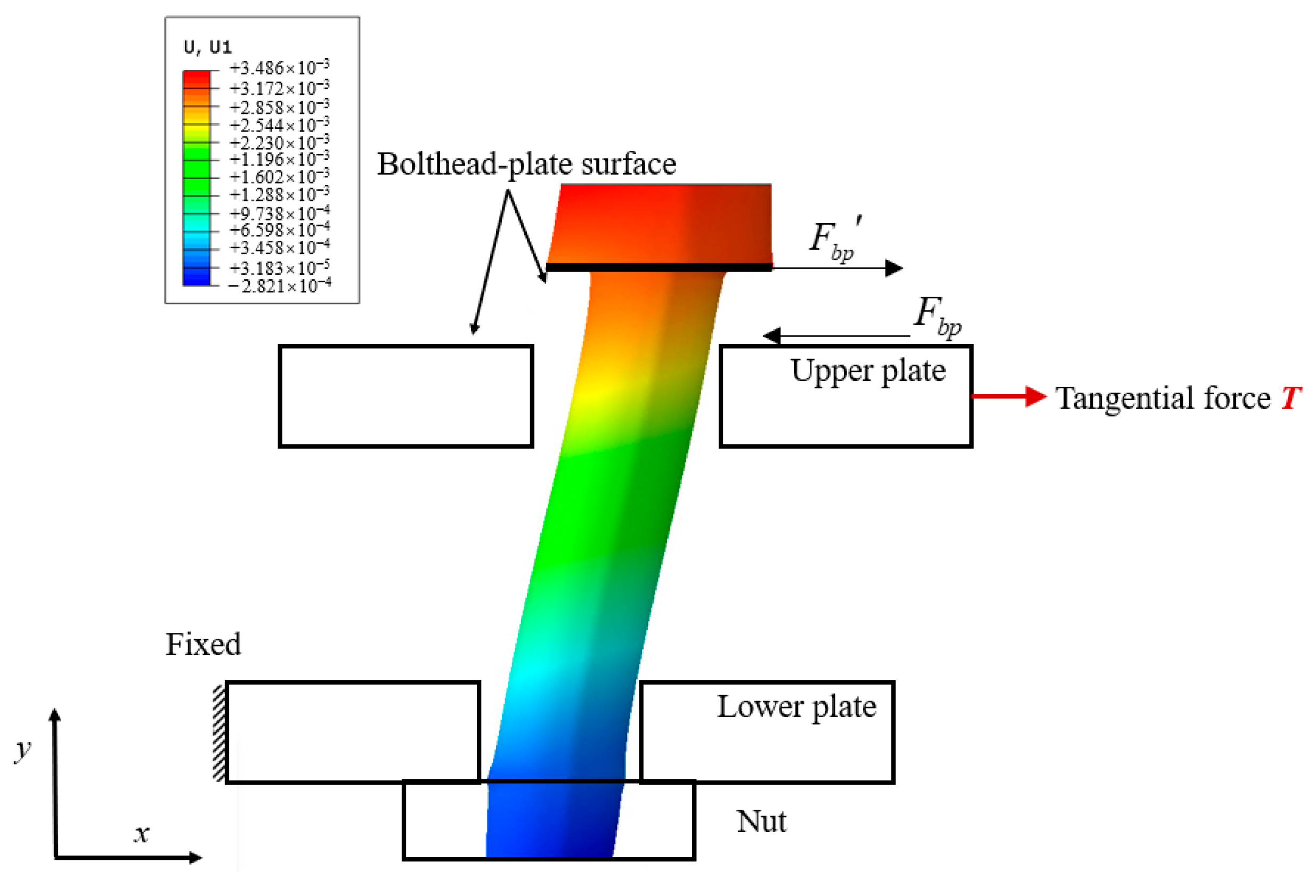
3.1. Finite Element Modeling
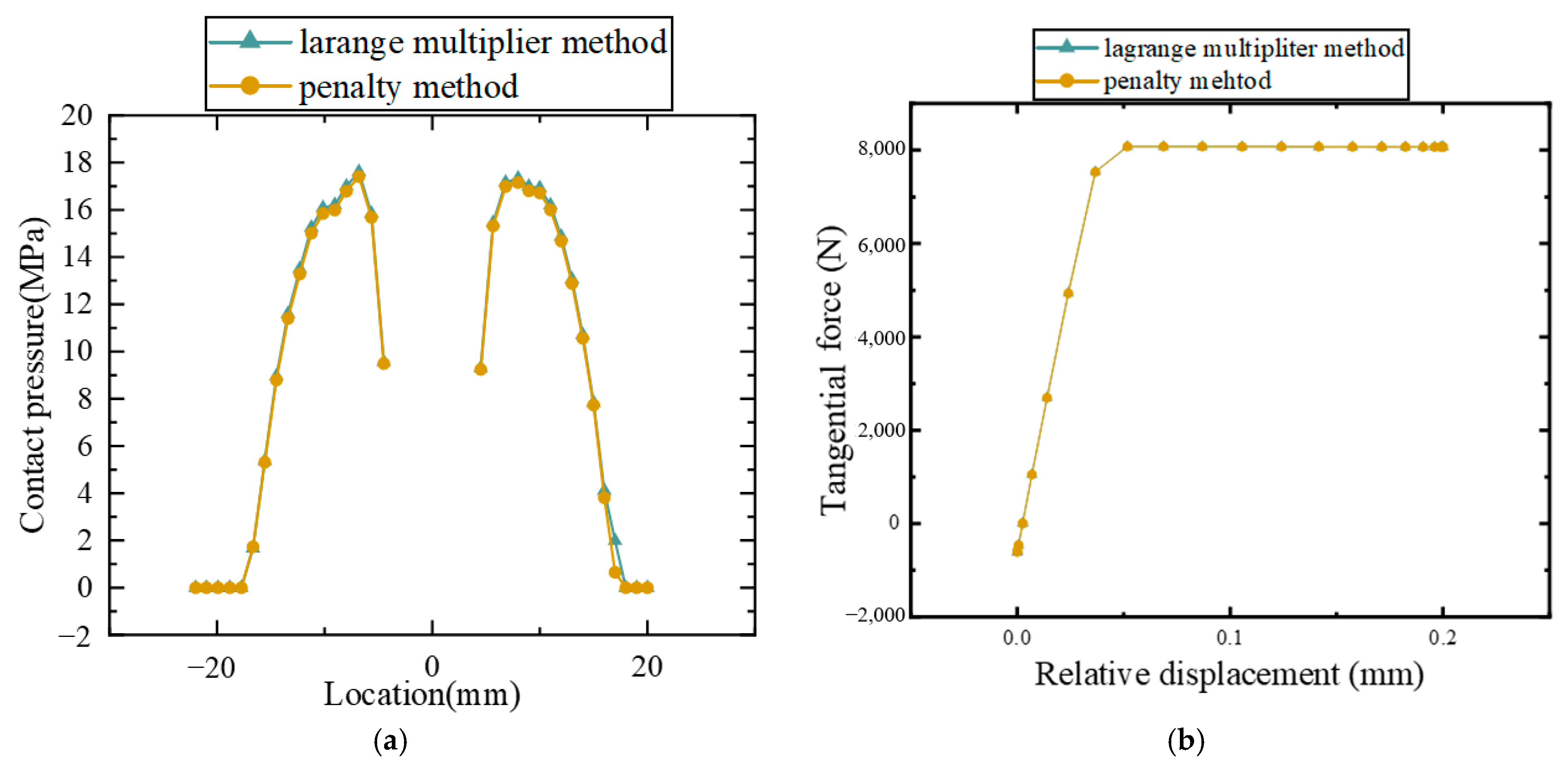
3.2. Analysis of the Lagrange Multiplier and Penalty Method
3.3. Analysis of the Thread Model and the Simplified Model
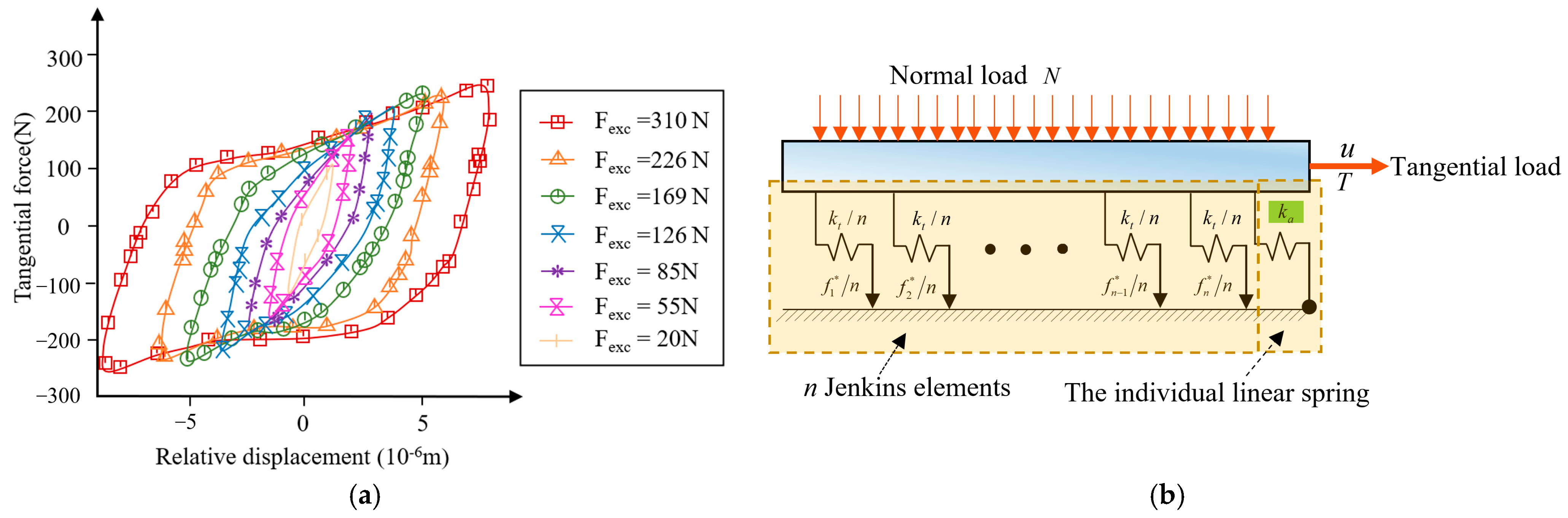
3.4. Analysis of Elastoplastic Elements under Mixed-Mode Loading
4. Discussion
- (1)
- The penalty method sacrifices accuracy for convergence, but it is closer to the real situation than the Lagrange multiplier method. Through analysis, the calculation results of both methods are the same for lapped plates, and the penalty method is more suitable for the contact analysis of bolted plates.
- (2)
- A threaded connection reduces the normal and tangential stiffness of the joints compared to bonding contact, but the reduction is negligible. Therefore, in finite element analysis, it is feasible to use bonding contact to replace the threaded connection.
- (3)
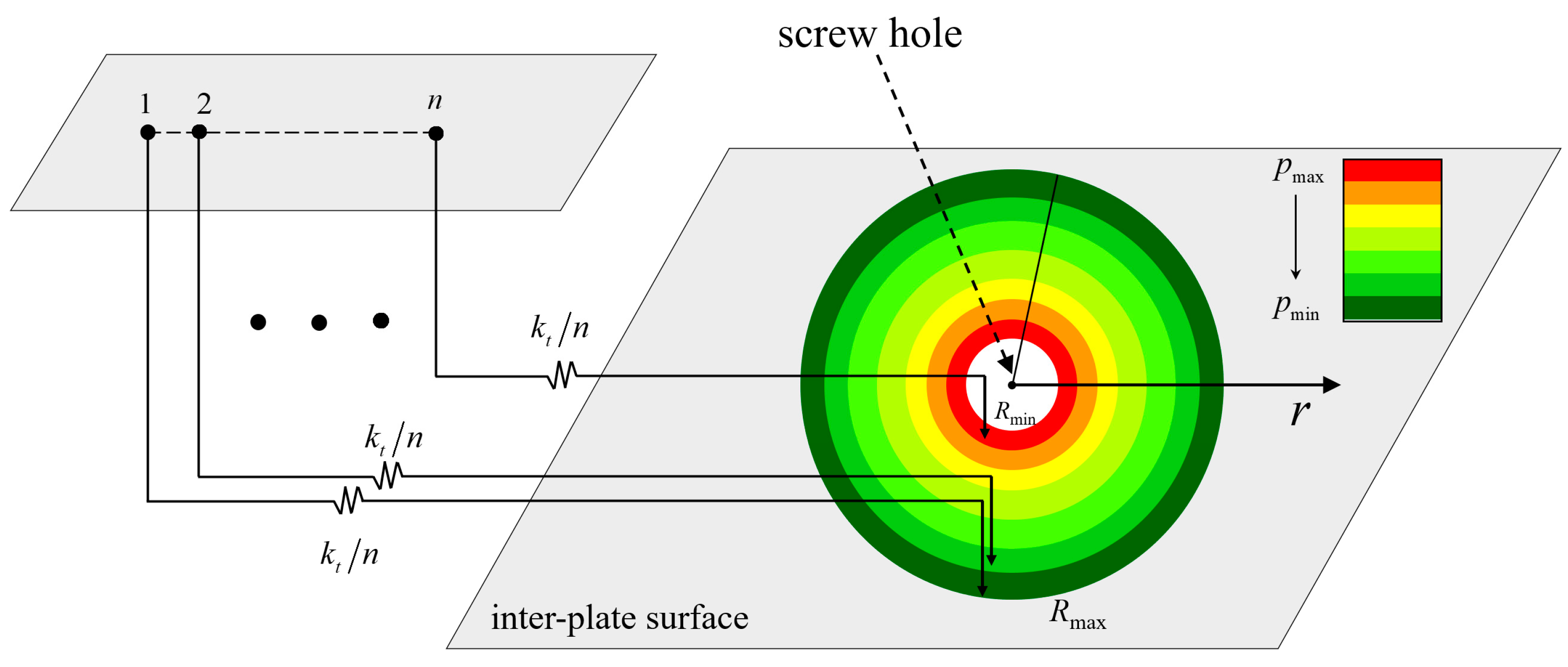
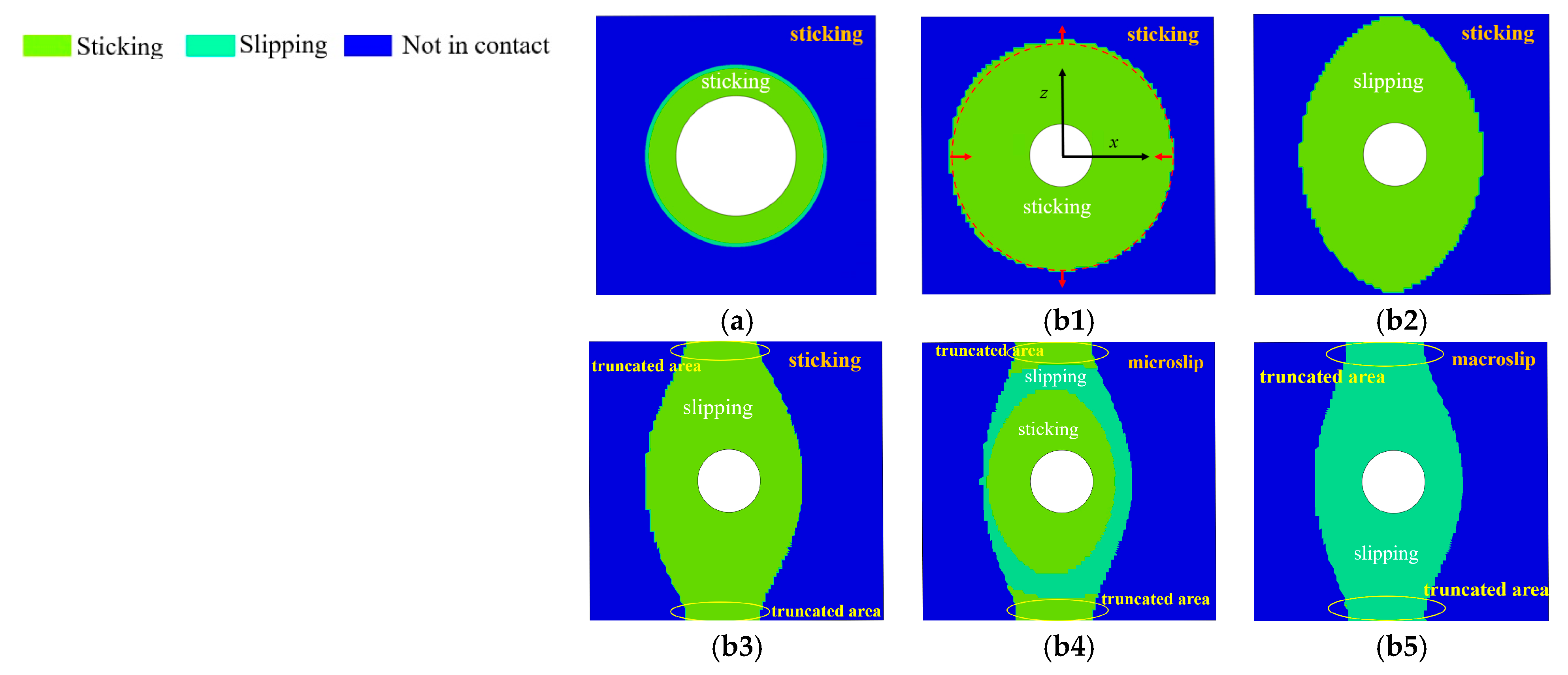
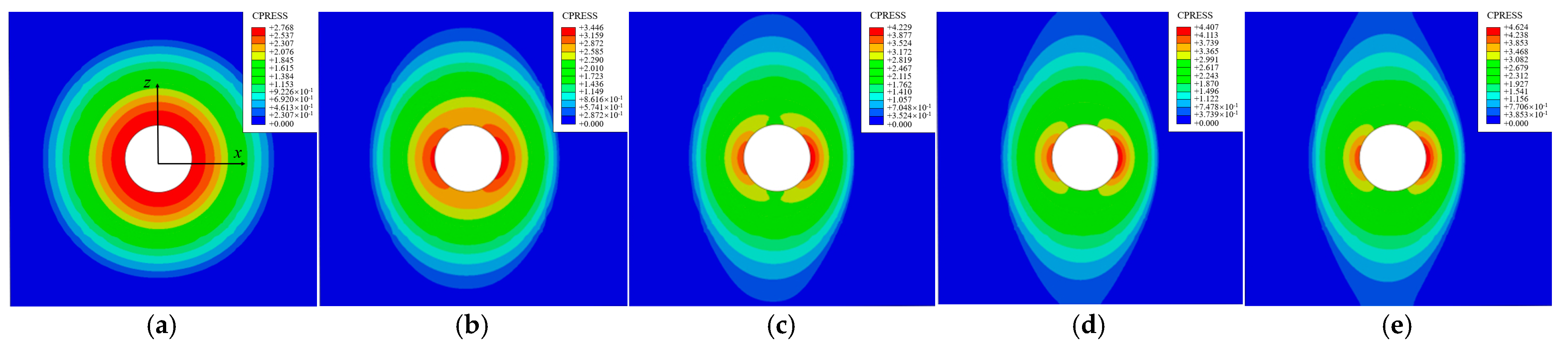
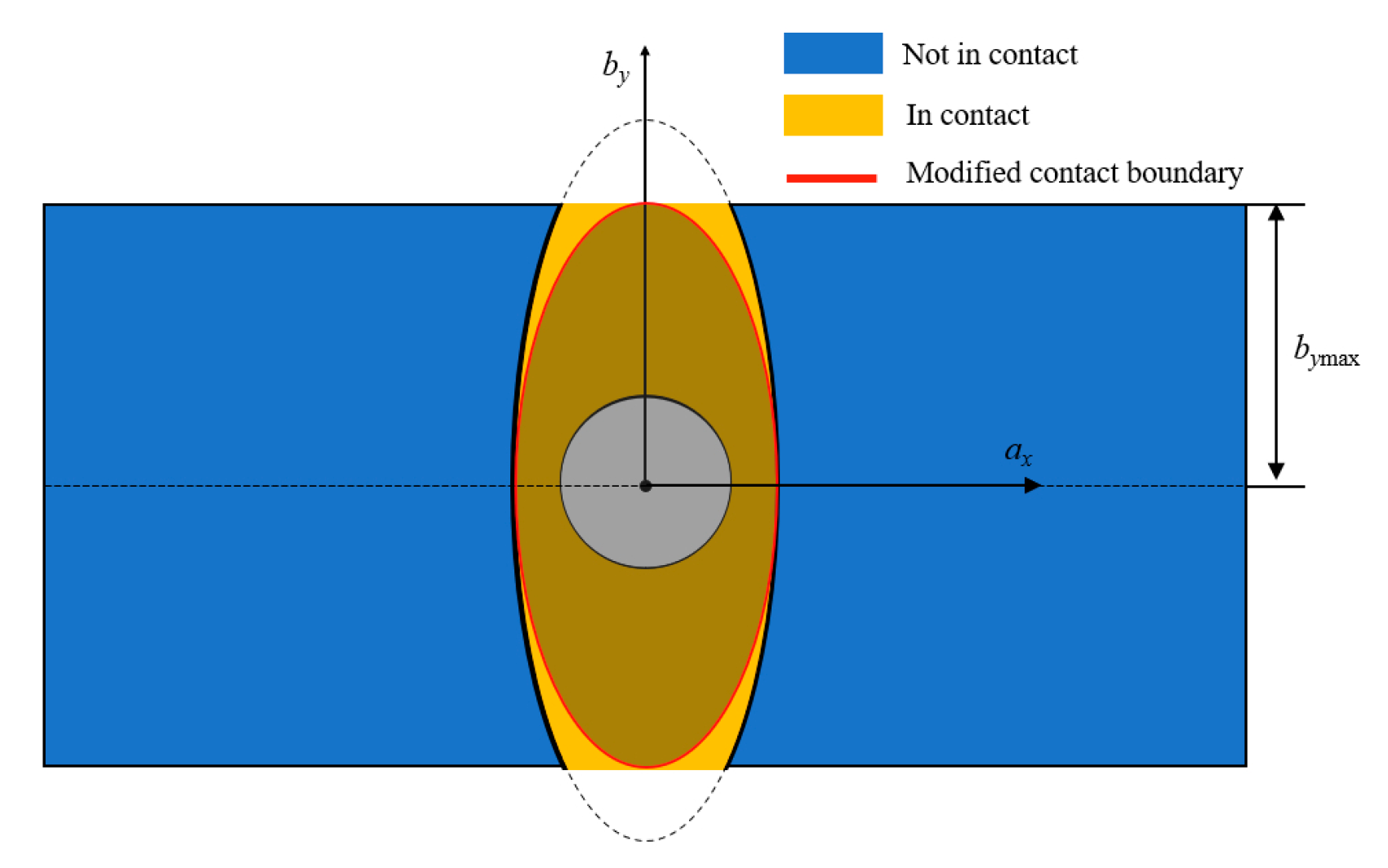
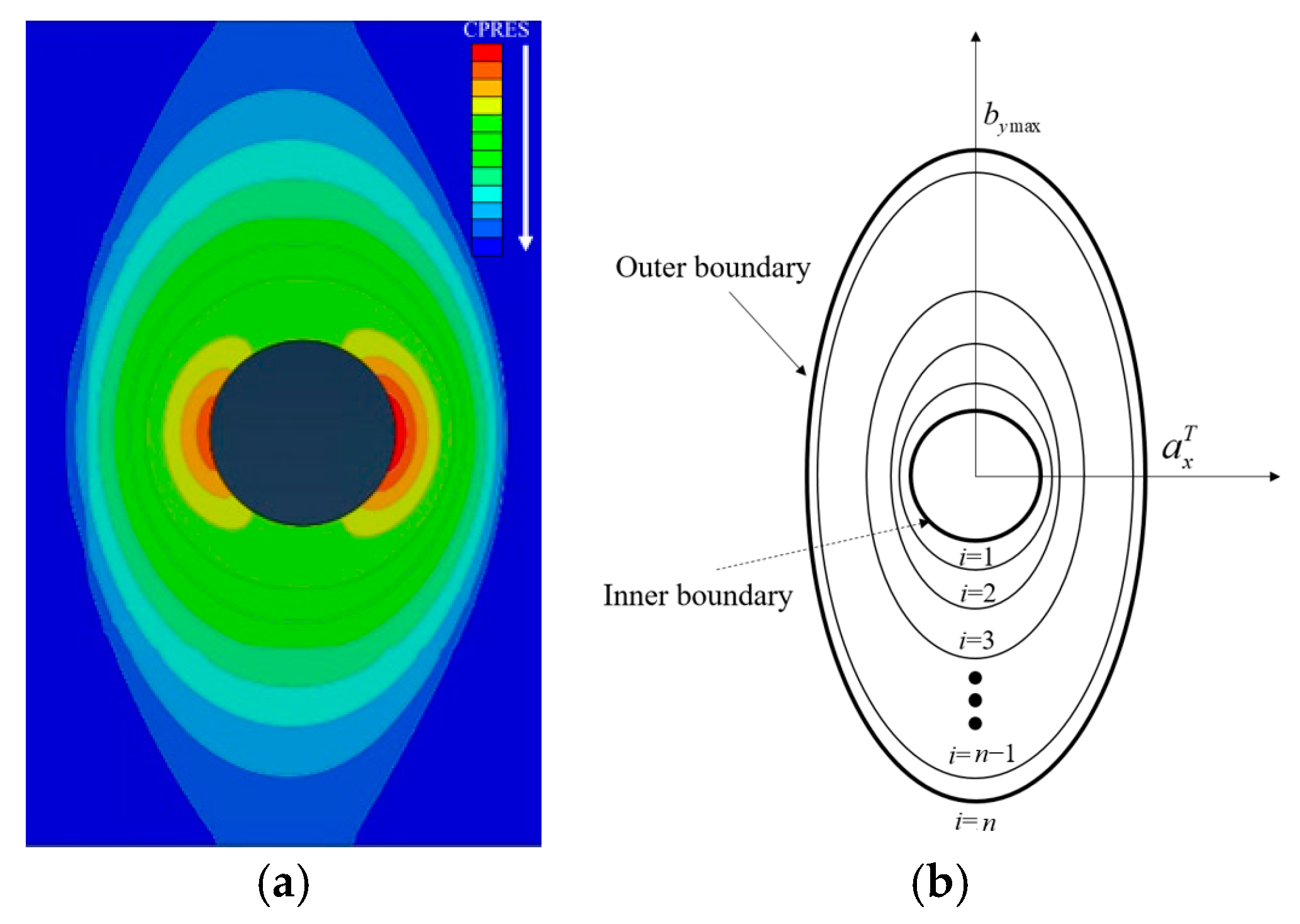
- The contact area of the inter-plate surface changes with the tangential load under mixed-mode loading, and the contact boundary can be represented by an ellipse function. In microslip, the semi-major axis remains unchanged and the semi-minor axis is a function of the tangential force T.
- (4)
- On the premise of the known dynamic pressure distribution, the contact area can be discretized by the different ellipticity. The discrete method can be applied to dynamic elliptical boundaries, and the DFs of friction shear stress and critical sliding force can be solved.
- (5)
- The residual stiffness of the Iwan model is derivative of static friction to relative displacement, and the static friction force causes the bending of the screw.
- (1)
- The pressure distribution law under mixed-mode loading needs to be studied, and a function needs to be constructed to characterize the pressure distribution in the non-circular area.
- (2)
- Experiments are indispensable to verify the theory. Designing equivalent bolted plates to overcome the shortcomings of ultrasonic methods to measure pressure distribution across multiple interfaces may be a feasible technique.
- (3)
- The mapping of the parameter in the constitutive model is still not clear, and the mapping parameter also needs to be studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| tangential force | Relative displacement | ||
| normal load | friction coefficient | ||
| amplitude of excitation force | Residual stiffness | ||
| number of Jenkins elements | maximum radius of contact area | ||
| radius of the hole | friction shear stress on the bolthead-plate surface | ||
| Contact pressure | friction shear stress on the inter-plate surface | ||
| tangential contact stiffness | friction force on the bolthead-plate surface | ||
| corrected pressure | friction force on the inter-plate surface | ||
| sliding area | amplitude of the cyclic load | ||
| critical sliding force | semi-minor axis of the contact boundary | ||
| range of critical sliding force | semi-minor axis of the ith ellipse | ||
| semi-major axis of the contact boundary | semi-major of the ith ellipse | ||
| thread height | ellipticity of the ith ellipse | ||
| DF | density function | ratio of the sliding area to the contact area | |
| contact pressure under mixed-mode loading | corrected contact pressure under mixed-mode loading |
References
- Wu, Z.; Wang, B.; Ma, X. On-orbit spacecraft connection structure dynamics and parameter identification. Chin. J. Astronaut. 1998, 104–110. [Google Scholar]
- Ungar, E.E. Energy Dissipation at Structural Joints: Mechanisms and Magnitudes; US Air Force Flight Dynamics Laboratory: Wright-Patterson Air Force Base, OH, USA, 1964. [Google Scholar]
- Segalman, D.J.; Gregory, D.L.; Starr, M.J.; Resor, B.R.; Jew, M.D.; Lauffer, J.P.; Ames, N.M. Handbook on Dynamics of Jointed Structure; Sandia National Laboratories: Albuquerque, NM, USA, 2009.
- Ito, Y. A Contribution to the Effective Range of the Preload on a Bolted Joint. In Proceedings of the Fourteenth International Machine Tool Design and Research Conference; Koenigsberger, F., Tobias, S.A., Eds.; Macmillan Education: London, UK, 1974; pp. 503–507. [Google Scholar]
- Mantelli, M.B.; Milanez, F.H.; Pereira, E.N.; Fletcher, L.S. Statistical Model for Pressure Distribution of Bolted Joints. J. Thermophys. Heat Transf. 2010, 24, 432–437. [Google Scholar] [CrossRef]
- Iwan, W.D. A Distributed-Element Model for Hysteresis and Its Steady-State Dynamic Response. J. Appl. Mech. 1966, 33, 893–900. [Google Scholar] [CrossRef]
- Gaul, L.; Mayer, M. Modeling of contact interfaces in built-up structures by zero-thickness elements. In Proceedings of the IMAC-XXXVI Conference & Exposition on Structural Dynamics, Orlando, FL, USA, 12–15 December 2008. [Google Scholar]
- Ferri, A.A. Friction Damping and Isolation Systems. J. Vib. Acoust. 1995, 117, 196–206. [Google Scholar] [CrossRef]
- Kou, J.; Xu, F.; Xie, W.; Zhang, X.; Feng, W. A theoretical 4-stage shear model for single-lap torqued bolted-joint with clearances. Compos. Struct. 2018, 186, 1–16. [Google Scholar] [CrossRef]
- Lu, S.; Hua, D.; Li, Y.; Li, P. Establishment and Verification of Nonlinear Bolt Head Connection Stiffness Theoretical Model Based on Levenberg-Marquardt Method. IEEE Access 2020, 8, 189354–189364. [Google Scholar] [CrossRef]
- Song, Y.; Hartwigsen, C.J.; McFarland, D.M.; Vakakis, A.F.; Bergman, L.A. Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements. J. Sound Vib. 2004, 273, 249–276. [Google Scholar] [CrossRef]
- Segalman, D.J. An Initial Overview of Iwan Modeling for Mechanical Joints; Sandia National Laboratories: Albuquerque, NM, USA, 2001.
- Segalman, D.J. Modelling joint friction in structural dynamics. Struct. Control. Health Monit. 2006, 13, 430–453. [Google Scholar] [CrossRef]
- Li, Y.; Hao, Z. A six-parameter Iwan model and its application. Mech. Syst. Signal Processing 2016, 68–69, 354–365. [Google Scholar] [CrossRef]
- Li, D.; Botto, D.; Xu, C.; Liu, T.; Gola, M. A micro-slip friction modeling approach and its application in underplatform damper kinematics. Int. J. Mech. Sci. 2019, 161–162, 105029. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, F.; Sun, K.; Mu, X.; Zhang, Y.; Sun, Q. Study on tangential stiffness nonlinear softening of bolted joint in friction-sliding process. Tribol. Int. 2021, 156, 106856. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Vivio, F. Analysis of multi-bolt composite joints with a user-defined finite element for the evaluation of load distribution and secondary bending. Compos. Part B Eng. 2021, 227, 109378. [Google Scholar] [CrossRef]
- Chen, D.; Ma, Y.; Hou, B.; Liu, R.; Zhang, W. Tightening behavior of bolted joint with non-parallel bearing surface. Int. J. Mech. Sci. 2019, 153–154, 240–253. [Google Scholar] [CrossRef]
- Liu, F.; Yao, W.; Zhao, L.; Wu, H.; Zhang, X.; Zhang, J. An improved 2D finite element model for bolt load distribution analysis of composite multi-bolt single-lap joints. Compos. Struct. 2020, 253, 112770. [Google Scholar] [CrossRef]
- Sun, Q.; Lin, Q.; Yang, B.; Zhang, X.; Wang, L. Mechanism and quantitative evaluation model of slip-induced loosening for bolted joints. Assem. Autom. 2020, 40, 577–588. [Google Scholar] [CrossRef]
- Abad, J.; Medel, F.J.; Franco, J.M. Determination of Valanis model parameters in a bolted lap joint: Experimental and numerical analyses of frictional dissipation. Int. J. Mech. Sci. 2014, 89, 289–298. [Google Scholar] [CrossRef] [Green Version]
- de Benedetti, M.; Garofalo, G.; Zumpano, M.; Barboni, R. On the damping effect due to bolted junctions in space structures subjected to pyro-shock. Acta Astronaut. 2007, 60, 947–956. [Google Scholar] [CrossRef]
- Khajeh Salehani, M.; Irani, N.; Nicola, L. Modeling adhesive contacts under mixed-mode loading. J. Mech. Phys. Solids 2019, 130, 320–329. [Google Scholar] [CrossRef]
- Mangalekar, R.; Ramdas, C.; Dawari, B. Study of Interfacial Pressure Distribution for Preloaded Bolted Connection. In Proceedings of the 2nd International Conference on Communication and Signal Processing (ICCASP 2016), Lonere, India, 26–27 December 2016; pp. 265–270. [Google Scholar]
- Tirovic, M.; Voller, G.P. Interface pressure distributions and thermal contact resistance of a bolted joint. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2339–2354. [Google Scholar] [CrossRef]
- Li, D.; Botto, D.; Xu, C.; Gola, M. A new approach for the determination of the Iwan density function in modeling friction contact. Int. J. Mech. Sci. 2020, 180, 105671. [Google Scholar] [CrossRef]
- Gaul, L.; Lenz, J. Nonlinear dynamics of structures assembled by bolted joints. Acta Mech. 1997, 125, 169–181. [Google Scholar] [CrossRef]
- Li, D.; Xu, C.; Botto, D.; Zhang, Z.; Gola, M. A fretting test apparatus for measuring friction hysteresis of bolted joints. Tribol. Int. 2020, 151, 106431. [Google Scholar] [CrossRef]
- Lobitz, D.; Gregory, D.; Smallwood, D. Comparison of Finite Element Predictions to Measurements from the Sandia Microslip Experiment. In Proceedings of the IMAC-XIX: A Conference on Structural Dynamics, Kissimmee, FL, USA, 5–8 February 2001; Volume 2. [Google Scholar]
- Simulia. Abaqus 6.10—Abaqus/CAE User’s Manual; Simulia: Johnston, RI, USA, 2010. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-A.; Zhu, M.; Xie, X.; Li, B.; Liang, T.-X.; Shao, Z.-Q.; Liu, Y.-L. Finite Element Analysis of Elastoplastic Elements in the Iwan Model of Bolted Joints. Materials 2022, 15, 5817. https://doi.org/10.3390/ma15175817
Wang S-A, Zhu M, Xie X, Li B, Liang T-X, Shao Z-Q, Liu Y-L. Finite Element Analysis of Elastoplastic Elements in the Iwan Model of Bolted Joints. Materials. 2022; 15(17):5817. https://doi.org/10.3390/ma15175817
Chicago/Turabian StyleWang, Sheng-Ao, Min Zhu, Xin Xie, Biao Li, Tian-Xi Liang, Zhao-Qun Shao, and Yi-Long Liu. 2022. "Finite Element Analysis of Elastoplastic Elements in the Iwan Model of Bolted Joints" Materials 15, no. 17: 5817. https://doi.org/10.3390/ma15175817
APA StyleWang, S.-A., Zhu, M., Xie, X., Li, B., Liang, T.-X., Shao, Z.-Q., & Liu, Y.-L. (2022). Finite Element Analysis of Elastoplastic Elements in the Iwan Model of Bolted Joints. Materials, 15(17), 5817. https://doi.org/10.3390/ma15175817




