Effect of Mn Doping on the Optical and Electrical Properties of Double Perovskite Sr2TiCoO6
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Preparation
2.2. Material Characterization
3. Results and Discussion
3.1. Structural Analysis
3.2. SEM Analysis
3.3. FTIR Analysis
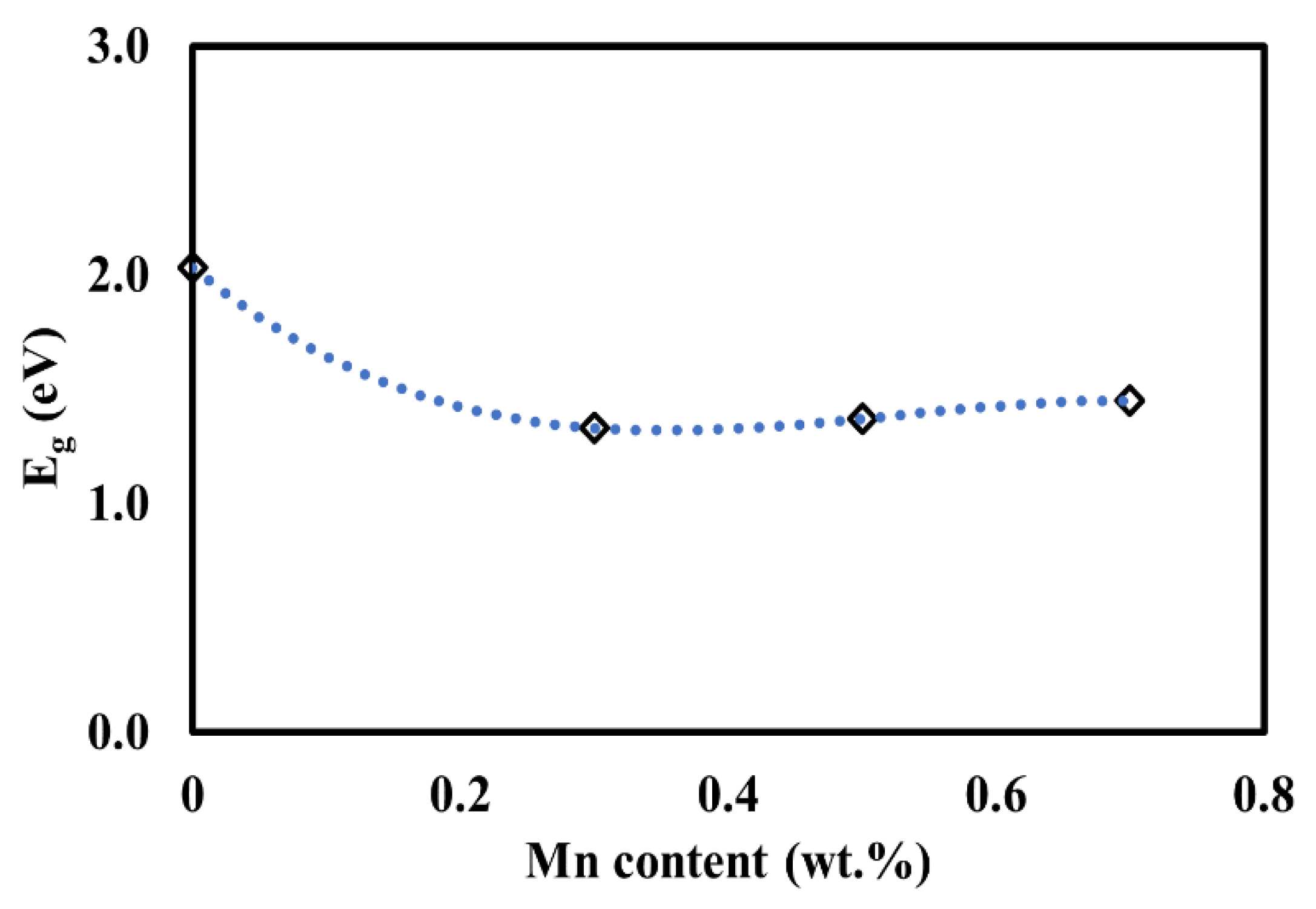
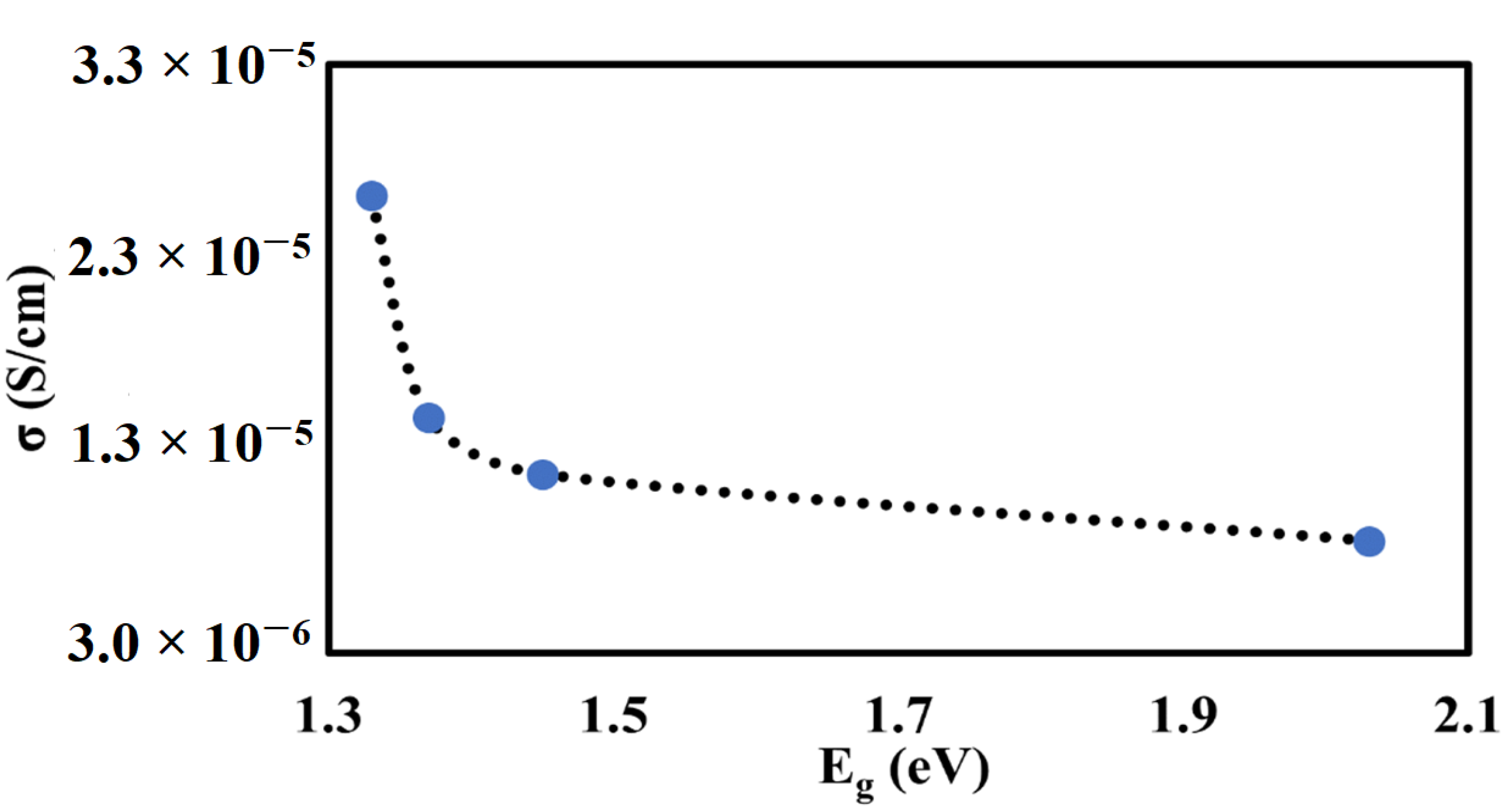
3.4. UV–Vis Analysis
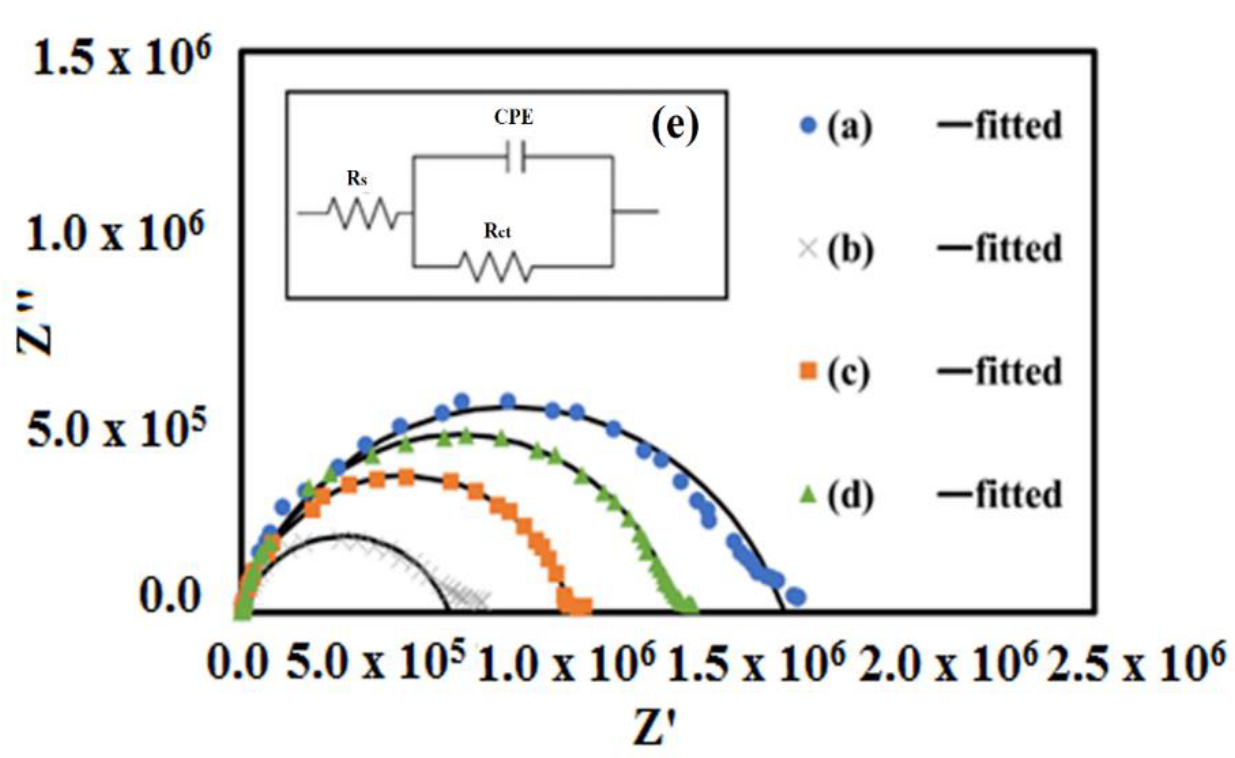
3.5. AC Impedance Analysis
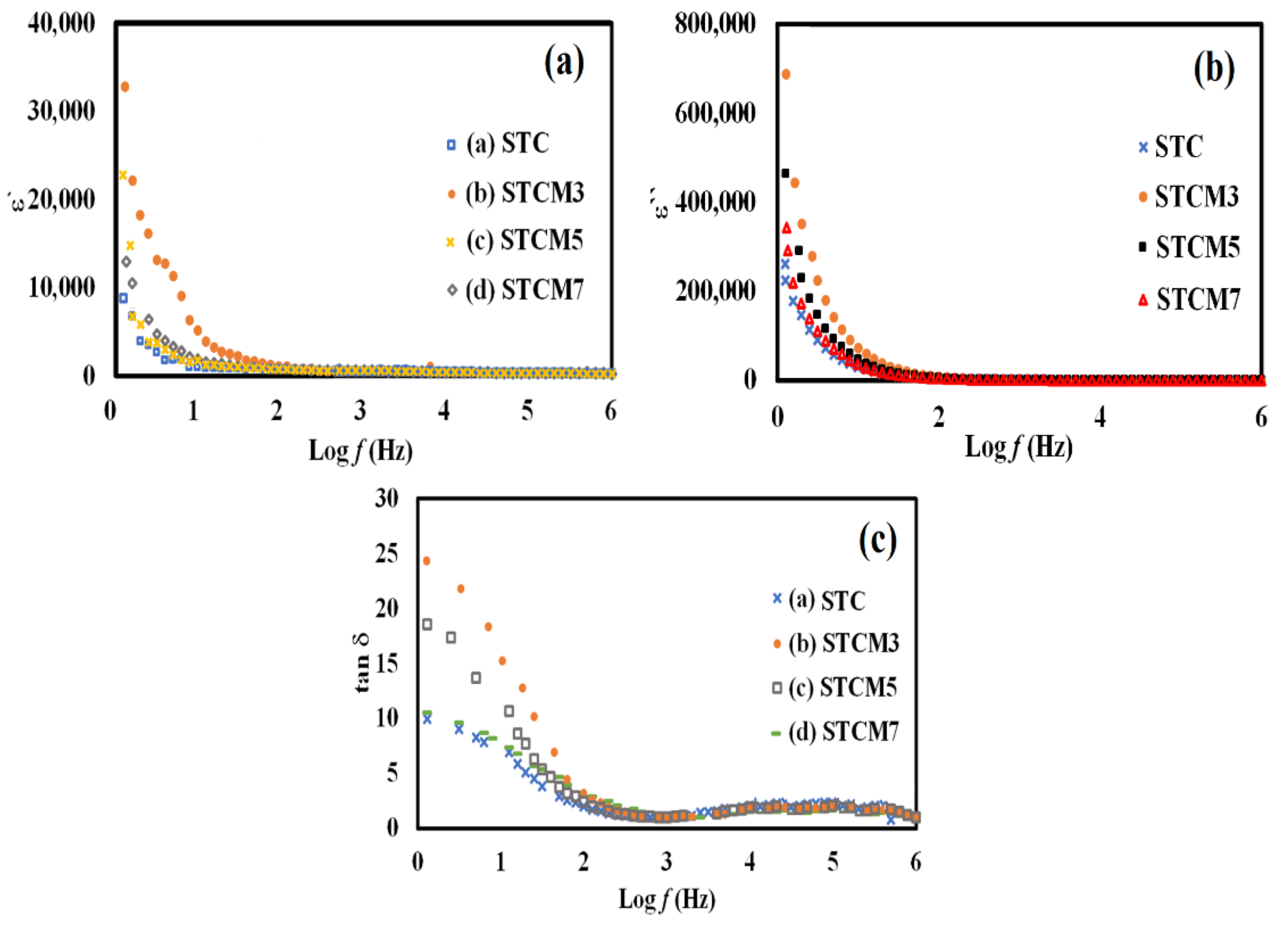
3.6. Dielectric Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Y.-H.; Liang, G.; Croft, M.; Lehtimäki, M.; Karppinen, M.; Goodenough, J.B. Double-perovskite anode materials Sr2MMoO6 (M = Co, Ni) for solid oxide fuel cells. Chem. Mater. 2009, 21, 2319–2326. [Google Scholar] [CrossRef]
- Sengodan, S.; Choi, S.; Jun, A.; Shin, T.H.; Ju, Y.-W.; Jeong, H.Y.; Shin, J.; Irvine, J.; Kim, G. Layered oxygen-deficient double perovskite as an efficient and stable anode for direct hydrocarbon solid oxide fuel cells. Nat. Mater. 2004, 14, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Pi, J.; Liu, Q.; Liang, Q.; Qiu, J.; Guo, J.; Long, Z.; Zhou, D.; Wang, Q. All-inorganic lead free double perovskite li-battery anode material hosting high Li+ ion concentrations. J. Phys. Chem. Lett. 2021, 12, 4125–4129. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Su, L.; Yang, M.; Hu, M.; Bao, J.; Wei, J.; Zhou, Z. A composite of Co nanoparticles highly dispersed on N-rich carbon substrates: An efficient electrocatalyst for Li–O2 battery cathodes. Chem. Commun. 2014, 50, 776–778. [Google Scholar] [CrossRef]
- Shi, C.-Y.; Hao, Y.-M.; Hu, Z.-B. Microstructure and colossal dielectric behavior of Ca2TiMnO6 ceramics. Scr. Mater. 2011, 64, 272–275. [Google Scholar] [CrossRef]
- Roy, P.; Bose, I.; Maiti, T. Synthesis and characterization of Sr2TiMO6(M = Fe, Co) double perovskites for high temperature thermoelectric applications. Integr. Ferroelectr. 2016, 174, 34–42. [Google Scholar] [CrossRef]
- Saxena, M.; Roy, P.; Acharya, M.; Bose, I.; Tanwar, K.; Maiti, T. Enhanced thermoelectric figure-of-merit in environmentally benign BaxSr2-xTiCoO6 double perovskites. Appl. Phys. Lett. 2016, 109, 263903. [Google Scholar] [CrossRef]
- Ortega-San Martin, L.; Chapman, J.P.; Lezama, L.; Sánchez-Marcos, J.; Rodríguez-Fernández, J.; Arriortua, M.I.; Rojo, T. Factors determining the effect of Co(II) in the ordered double perovskite structure: Sr2CoTeO6. J. Mater. Chem. 2005, 15, 183–193. [Google Scholar] [CrossRef]
- Augsburger, M.S.; Viola, M.C.; Pedregosa, J.C.; Muñoz, A.; Alonso, J.A.; Carbonio, R.E. Preparation, crystal and magnetic structures of two new double perovskites: Ca2CoTeO6 and Sr2CoTeO6. J. Mater. Chem. 2005, 15, 993–1001. [Google Scholar] [CrossRef]
- Muta, H.; Kurosaki, K.; Yamanaka, S. Thermoelectric properties of rare earth doped SrTiO3. J. Alloy. Compd. 2003, 350, 292–295. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.L.; Li, Y.; Su, W.B.; Zhu, Y.H.; Li, J.C.; Mei, L.M. Influence of rare earth doping on thermoelectric properties of SrTiO3 ceramics. J. Appl. Phys. 2013, 114, 223714. [Google Scholar] [CrossRef]
- Ateia, E.E.; Mohamed, A.T.; Elshimy, H. The impact of antisite disorder on the physical properties of La2FeB”O6 (B” = Fe, Ni and Co) double perovskites. Appl. Nanosci. 2020, 10, 1489–1499. [Google Scholar] [CrossRef]
- Manoun, B.; Igartua, J.M.; Lazor, P.; Ezzahi, A. High temperature induced phase transitions in Sr2ZnWO6 and Sr2CoWO6 double perovskite oxides: Raman spectroscopy as a tool. J. Mol. Struct. 2012, 1029, 81–85. [Google Scholar] [CrossRef]
- Nomura, S.; Kawakubo, T. Phase transition in Sr(NiW)0.5O3-Ba(NiW)0.5O3 System. J. Phys. Soc. Jpn. 1962, 17, 1771–1776. [Google Scholar] [CrossRef]
- Fresia, E.J.; Katz, L.; Ward, R. Cation substitution in perovskite-like phases. J. Am. Chem. Soc. 1959, 81, 4783–4785. [Google Scholar] [CrossRef]
- Kato, H.; Okuda, T.; Okimoto, Y.; Tomioka, Y.; Oikawa, K.; Kamiyama, T.; Tokura, Y. Structural and electronic properties of the ordered double perovskites A2MReO6 (A=Sr,Ca; M=Mg,Sc,Cr,Mn,Fe,Co,Ni,Zn). Phys. Rev. B 2004, 69, 184412. [Google Scholar] [CrossRef]
- Borchani, S.M.; Koubaa, W.C.-R.; Megdiche, M. Structural, magnetic and electrical properties of a new double-perovskite LaNaMnMoO6 material. R. Soc. Open Sci. 2017, 4, 170920. [Google Scholar] [CrossRef] [Green Version]
- Radaelli, P.G.; Iannone, G.; Marezio, M.; Hwang, H.Y.; Cheong, S.-W.; Jorgensen, J.D.; Argyriou, D.N. Structural effects on the magnetic and transport properties of perovskite A1-xA′xMnO3 (x = 0.25, 0.30). Phys. Rev. B 1997, 56, 8265–8276. [Google Scholar] [CrossRef]
- Das, R.; Choudhary, R. Structural and electrical properties of double perovskite: (BaSr)FeMoO6. Phys. B Phys. Condens. Matter 2021, 603, 412522. [Google Scholar] [CrossRef]
- Harrell, Z.; Enriquez, E.; Chen, A.; Dowden, P.; Mace, B.; Lü, X.; Jia, Q.; Chen;, C. Oxygen content tailored magnetic and electronic properties in cobaltite double perovskite thin films. Appl. Phys. Lett. 2017, 110, 093102. [Google Scholar] [CrossRef]
- La Mattina, F.; Bednorz, J.G.; Alvarado, S.F.; Shengelaya, A.; Müller, K.A.; Keller, H. Controlled oxygen vacancies and space correlation with Cr3+ in SrTiO3. Phys. Rev. B 2009, 80, 075122. [Google Scholar] [CrossRef] [Green Version]
- David, W.I.F.; Shankland, K.; McCusker, L.B.; Baerlocher, C. Structure Determination from Powder Diffraction Data; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Zenkins, R.; Snyder, R.L. Introduction to X-Ray Powder Diffractometry; John Wiley and Sons Inc.: New York, NY, USA, 1996. [Google Scholar]
- Pecharsky, V.K.; Zavalij, P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Saxena, M.; Maiti, T. Compositional modification of Sr2TiCoO6 double perovskites by Mo and La for high temperature thermoelectric applications. Ceram. Int. 2018, 44, 2732–2737. [Google Scholar] [CrossRef]
- Sudha; Saxena, M.; Balani, K.; Maiti, T. Structure and thermoelectric properties of calcium doped Sr2TiCoO6 double perovskites. Mater. Sci. Eng. B 2019, 244, 65–71. [Google Scholar] [CrossRef]
- Jaganyi, D.; Altaf, M.; Wekesa, I. Synthesis and characterization of whisker-shaped MnO2 nanostructure at room temperature. Appl. Nanosci. 2013, 3, 329–333. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Hai, Z.; Diwu, J.; Zhang, Q.; Gao, L.; Cui, D.; Zang, J.; Liu, J.; Xue, C. Synthesis and microwave absorption properties of core-shell structured Co3O4-PANI nanocomposites. J. Nanomater. 2015, 2015, 845983. [Google Scholar] [CrossRef] [Green Version]
- Kamarulzaman, N.; Kasim, M.F.; Chayed, N.F. Elucidation of the highest valence band and lowest conduction band shifts using XPS for ZnO and Zn0.99Cu0.01O band gap changes. Results Phys. 2016, 6, 217–230. [Google Scholar] [CrossRef] [Green Version]
- Kamarulzaman, N.; Yusoff, R.; Kamarudin, N.; Shaari, N.; Aziz, N.A.; Bustam, M.; Blagojevic, N.; Elcombe, M.; Blackford, M.; Avdeev, M.; et al. Investigation of cell parameters, microstructures and electrochemical behaviour of LiMn2O4 normal and nano powders. J. Power Sources 2009, 188, 274–280. [Google Scholar] [CrossRef]
- Sangiorgi, N.; Aversa, L.; Tatti, R.; Verucchi, R.; Sanson, A. Spectrophotometric method for optical band gap and electronic transitions determination of semiconductor materials. Opt. Mater. 2017, 64, 18–25. [Google Scholar] [CrossRef]
- Saadon, N.A.F.M.; Ali, N.M.; Ibrahim, N.; Mohamed, Z. Structural, optical and dielectric properties of Sr2Ni1−xMgxWO6 (x = 0.00, 0.02, 0.04, and 0.06) double perovskite. J. Mater. Chem. C 2021, 9, 13439–13446. [Google Scholar] [CrossRef]
- Mohamed, Z.; Shahron, I.S.; Ibrahim, N.; Maulud, M.F. Influence of ruthenium doping on the crystal structure and magnetic properties of Pr0.67Ba0.33Mn1–xRuxO3 manganites. Crystals 2020, 10, 295. [Google Scholar] [CrossRef] [Green Version]
- Halizan, M.Z.M.; Mohamed, Z.; Yahya, A.K. Structural properties of tellurium based double perovskite with small doped of manganese. AIP Conf. Proc. 2021, 2368, 030005. [Google Scholar]
- Prasanna, R.; Gold-Parker, A.; Leijtens, T.; Conings, B.; Babayigit, A.; Boyen, H.-G.; Toney, M.F.; McGehee, M.D. Band gap tuning via lattice contraction and octahedral tilting in perovskite materials for photovoltaics. J. Am. Chem. Soc. 2017, 139, 11117–11124. [Google Scholar] [CrossRef] [PubMed]
- Karim, M.M.S.; Ganose, A.M.; Pieters, L.; Leung, W.W.W.; Wade, J.; Zhang, L.; Scanlon, D.O.; Palgrave, R.G. Anion distribution, structural distortion and symmetry-driven optical band gap bowing in mixed halide Cs2SnX6 vacancy ordered double perovskites. Chem. Mater. 2019, 31, 9430–9444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dakshinamurthy, A.C.; Sudakar, C. Bandgap engineering and sublattice distortion driven bandgap bowing in Cs2Ag1-xNaxBiCl6 double perovskites. Appl. Phys. Lett. 2021, 118, 131902. [Google Scholar] [CrossRef]
- Das, R.; Choudhary, R.N.P. Dielectric relaxation and magneto-electric characteristics of lead-free double perovskite: Sm2NiMnO6. J. Adv. Ceram. 2019, 8, 174–185. [Google Scholar] [CrossRef] [Green Version]
- Macdonald, J.R. Impedance spectroscopy and its use in analyzing the steady-state AC response of solid and liquid electrolytes. J. Electroanal. Chem. Interfacial Electrochem. 1987, 223, 25–50. [Google Scholar] [CrossRef]
- Mahato, D.K.; Dutta, A.; Sinha, T. Dielectric relaxation and ac conductivity of double perovskite oxide Ho2ZnZrO6. Phys. B Condens. Matter 2011, 406, 2703–2708. [Google Scholar] [CrossRef]
- Achary, P.G.R.; Dehury, S.K.; Choudhary, R.N.P. Structural, electrical and dielectric properties of double perovskites: BiHoZnZrO6 and BiHoCuTiO6. J. Mater. Sci. Mater. Electron. 2018, 29, 6805–6816. [Google Scholar] [CrossRef]
- Kamarulzaman, N.; Aziz, N.D.A.; Kasim, M.F.; Chayed, N.F.; Subban, R.H.Y.; Badar, N. Anomalies in wide band gap SnO2 nanostructures. J. Solid State Chem. 2019, 277, 271–280. [Google Scholar] [CrossRef]
- Žužić, A.; Ressler, A.; Šantić, A.; Macan, J.; Gajović, A. The effect of synthesis method on oxygen nonstoichiometry and electrical conductivity of Sr-doped lanthanum manganites. J. Alloys Compd. 2022, 907, 164465. [Google Scholar] [CrossRef]
- Montenegro-Hernández, A.; Dager, P.; Caneiro, A.; Mogni, L. Structural properties and electrical conductivity of perovskite-type oxides in SOFCs. J. Phys. Conf. Ser. 2019, 1219, 012001. [Google Scholar] [CrossRef]
- Debbebi, I.S.; Megdiche-Borchani, S.; Cheikhrouhou-Koubaa, W.; Cheikhrouhou, A. Study of complex impedance spectroscopic properties of La0.7-xDyxSr0.3MnO3 perovskite oxides. R. Soc. Open Sci. 2018, 5, 172201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiglusz, R.; Gaki, A.; Kakali, G.; Chuchmała, A.; Stręk, W. Conductivity and electrical properties of La1-xSrxMnO3-δ nanopowders. J. Rare Earths 2009, 24, 651–654. [Google Scholar] [CrossRef]
- Singh, D.N.; Sinha, T.; Mahato, D. Electric modulus, scaling and ac conductivity of La2CuMnO6 double perovskite. J. Alloys Compd. 2017, 729, 1226–1233. [Google Scholar] [CrossRef]
- Gaikwad, V.M.; Acharya, S.A. Acharya, perovskite-spinel composite approach to modify room temperature structural, magnetic and dielectric behaviour of BiFeO3. J. Alloys Compd. 2017, 695, 3689–3703. [Google Scholar] [CrossRef]
- Alias, F.I.H.; Rajmi, R.; Maulud, M.F.; Mohamed, Z. Structural, optical and dielectric properties of tellurium-based double perovskite Sr2Ni1−xZnxTeO6. RSC Adv. 2021, 11, 31631–31640. [Google Scholar] [CrossRef]
- Halizan, M.Z.M.; Mohamed, Z.; Yahya, A.K. Understanding the structural, optical, and dielectric characteristics of SrLaLiTe1−xMnxO6 perovskites. Sci. Rep. 2021, 11, 9744. [Google Scholar] [CrossRef]
- Shinde, K.P.; Thorat, N.D.; Pawar, S.S.; Pawar, S.H. Combustion synthesis and characterization of perovskite La0.9Sr0.1MnO3. J. Mater. Chem. Phys. 2012, 134, 881–885. [Google Scholar] [CrossRef]
- Husain, S.; Bhat, I.; Khan, W.; Al-Khataby, L. Structural and dielectric properties of La0.8Te0.2MnO3. J. Solid State Commun. 2013, 157, 29–33. [Google Scholar] [CrossRef]
- Lazarević, Z.; Jovalekić, Č.; Sekulić, D.L.; Milutinović, A.; Baloš, S.; Slankamenac, M.; Romčević, N. Structural, electrical and dielectric properties of spinel nickel ferrite prepared by of mechanochemical synthesis. J. Mater. Res. Bull. 2013, 48, 4368–4378. [Google Scholar] [CrossRef]
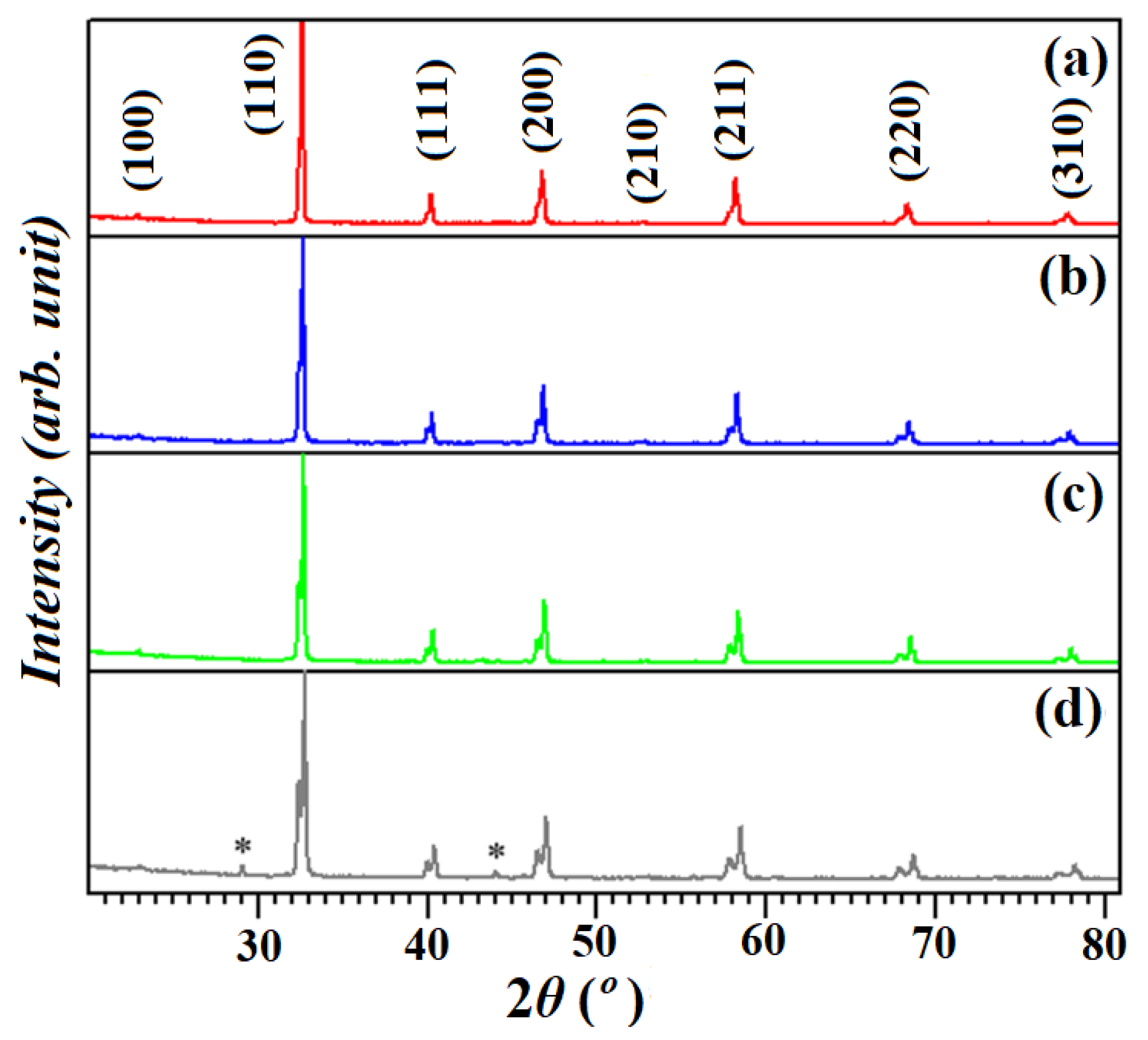
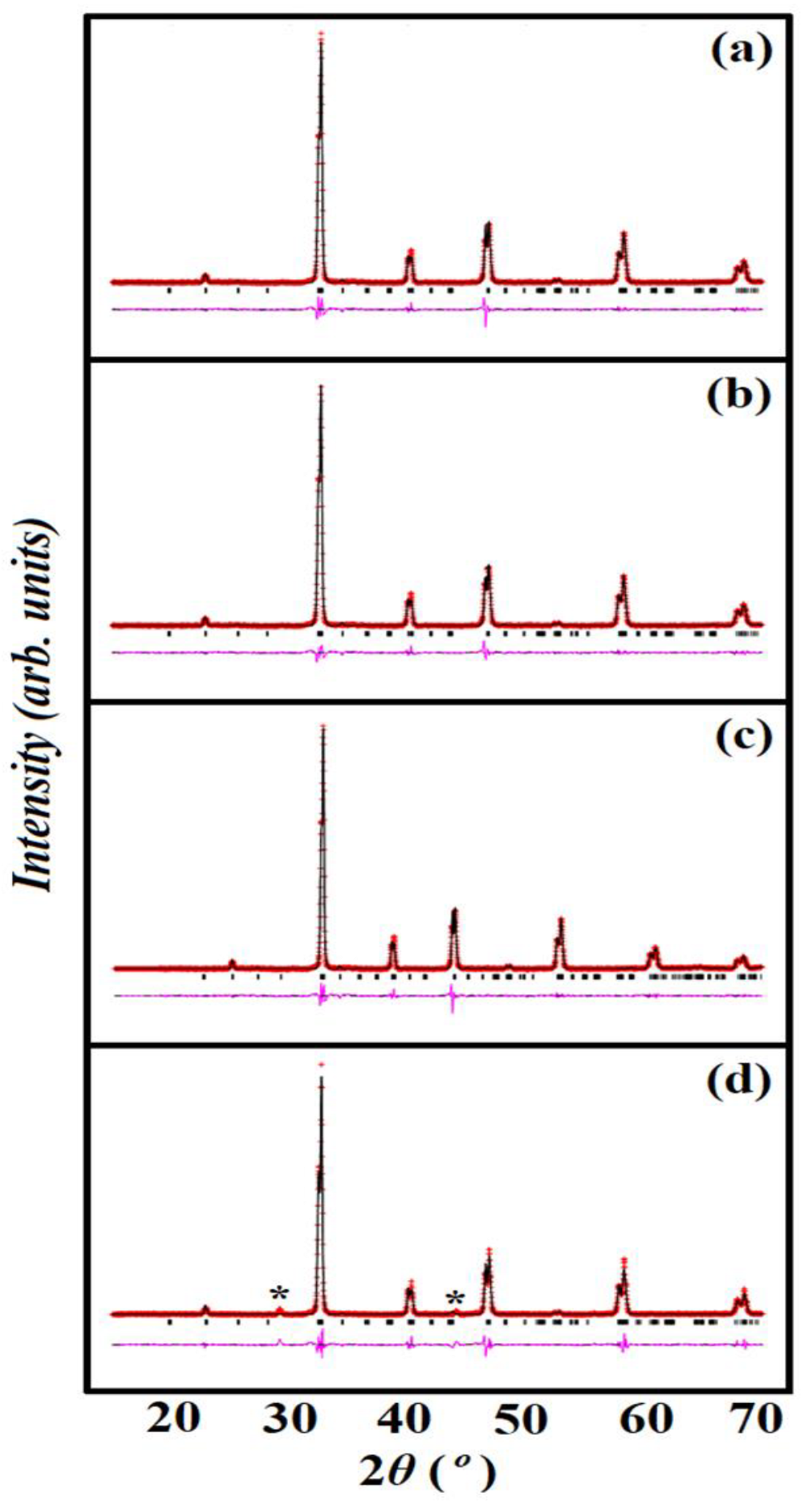


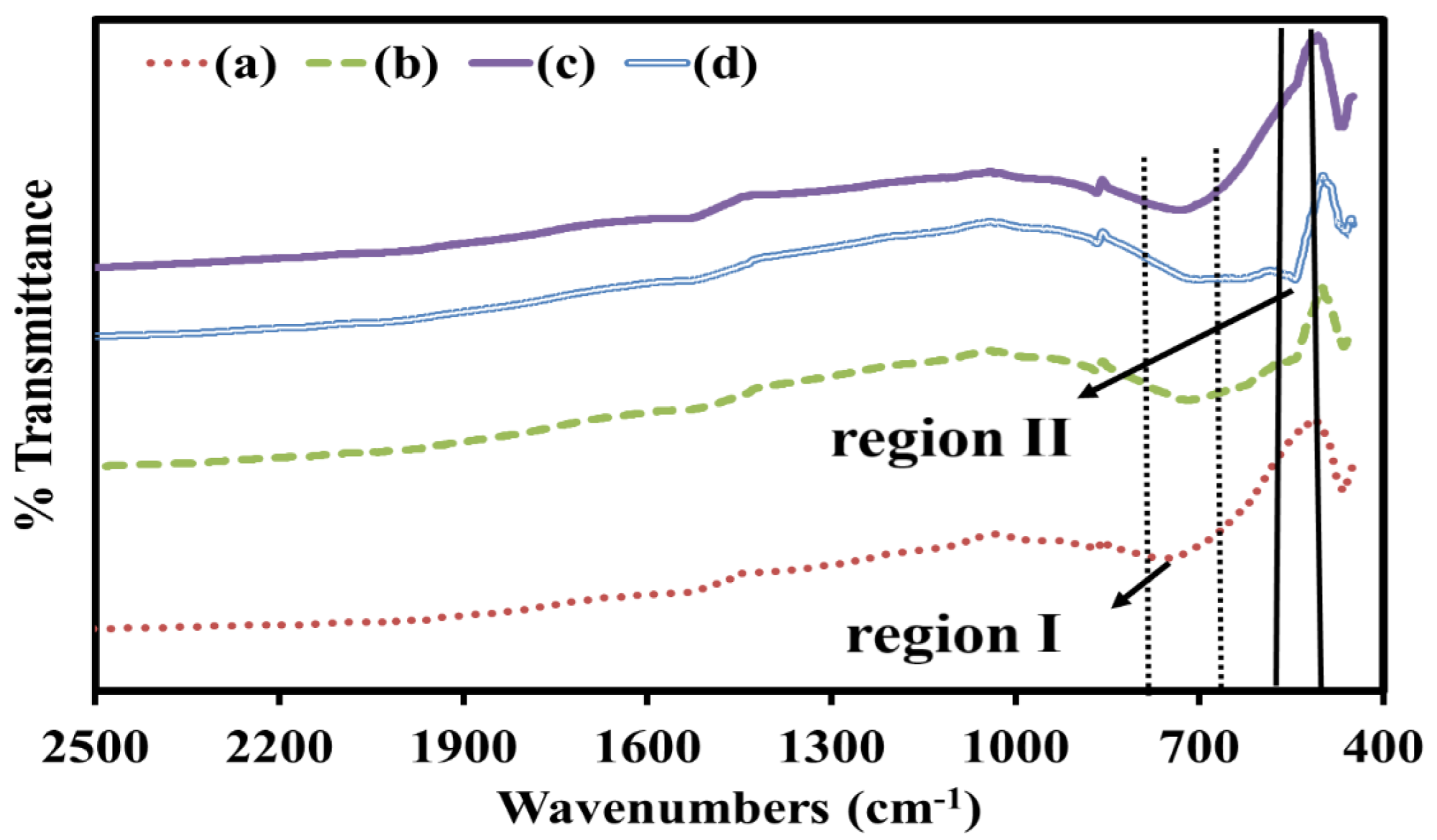
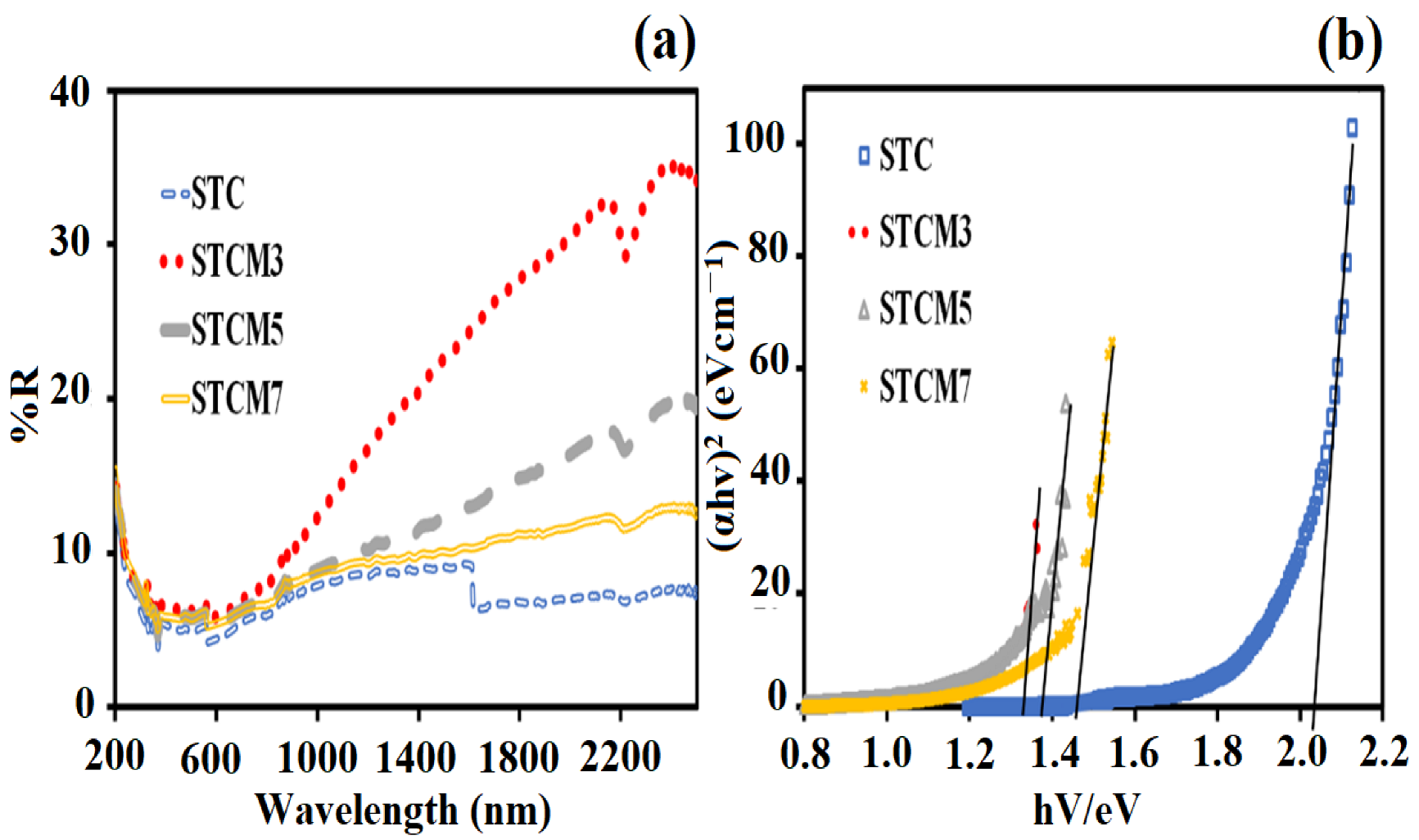
| Doping Content (x) | STC (x = 0.0) | STCM3 (x = 0.3) | STCM5 (x = 0.5) | STCM7 (x = 0.7) |
|---|---|---|---|---|
| Lattice parameter | ||||
| Space group | P21/n | P21/n | P21/n | P21/n |
| Symmetry | monoclinic | monoclinic | monoclinic | monoclinic |
| a (Å) | 5.4861 | 5.4873 | 5.5001 | 5.5039 |
| b (Å) | 5.5292 | 5.5315 | 5.5253 | 5.5200 |
| c (Å) | 7.7474 | 7.7441 | 7.7434 | 7.7539 |
| a = β = γ | 90 | 90 | 90 | 90 |
| Unit cell volume (Å)3 | ||||
| Unit cell volume | 235.034 | 235.055 | 235.342 | 235.569 |
| Goodness of fit | ||||
| λ2 | 1.467 | 2.012 | 1.451 | 3.041 |
| Rp | 0.0230 | 0.0345 | 0.0471 | 0.1504 |
| RWP | 0.0358 | 0.0506 | 0.0858 | 0.2587 |
| Samples | Band Gap Values (eV) |
|---|---|
| STC | 2.03 |
| STCM3 | 1.33 |
| STCM5 | 1.37 |
| STCM7 | 1.45 |
| Samples | Average Rb (Ω) | Conductivity, (S/cm) at 25 °C |
|---|---|---|
| STC | 1.67 × 106 | 8.69 × 10−6 |
| STCM3 | 5.59 × 105 | 2.63 × 10−5 |
| STCM5 | 9.69 × 105 | 1.50 × 10−5 |
| STCM7 | 1.18 × 106 | 1.21 × 10−5 |
| Samples ID | Dielectric Constant, ε′ at 0.1 Hz | Dielectric Loss, ε″ at 0.1 Hz | Loss Tangent, tan δ at 0.1 Hz |
|---|---|---|---|
| STC | 88.0 × 102 | 46.3 × 104 | 9.0 |
| STCM3 | 33.2 × 103 | 68.9 × 104 | 24.2 |
| STCM5 | 23.1 × 103 | 34.4 × 104 | 17.3 |
| STCM7 | 13.1 × 103 | 26.1 × 104 | 12.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aziz, N.D.A.; Kamarulzaman, A.S.; Ibrahim, N.; Mohamed, Z. Effect of Mn Doping on the Optical and Electrical Properties of Double Perovskite Sr2TiCoO6. Materials 2022, 15, 5123. https://doi.org/10.3390/ma15155123
Aziz NDA, Kamarulzaman AS, Ibrahim N, Mohamed Z. Effect of Mn Doping on the Optical and Electrical Properties of Double Perovskite Sr2TiCoO6. Materials. 2022; 15(15):5123. https://doi.org/10.3390/ma15155123
Chicago/Turabian StyleAziz, Nor Diyana Abdul, Alyea Sofea Kamarulzaman, Norazila Ibrahim, and Zakiah Mohamed. 2022. "Effect of Mn Doping on the Optical and Electrical Properties of Double Perovskite Sr2TiCoO6" Materials 15, no. 15: 5123. https://doi.org/10.3390/ma15155123
APA StyleAziz, N. D. A., Kamarulzaman, A. S., Ibrahim, N., & Mohamed, Z. (2022). Effect of Mn Doping on the Optical and Electrical Properties of Double Perovskite Sr2TiCoO6. Materials, 15(15), 5123. https://doi.org/10.3390/ma15155123






