Denouement of the Energy-Amplitude and Size-Amplitude Enigma for Acoustic-Emission Investigations of Materials
Abstract
:1. Introduction
2. Expressions for the Exponents of Scaling Relations
3. Analysis and Discussion of Experimental Data on Scaling Exponents
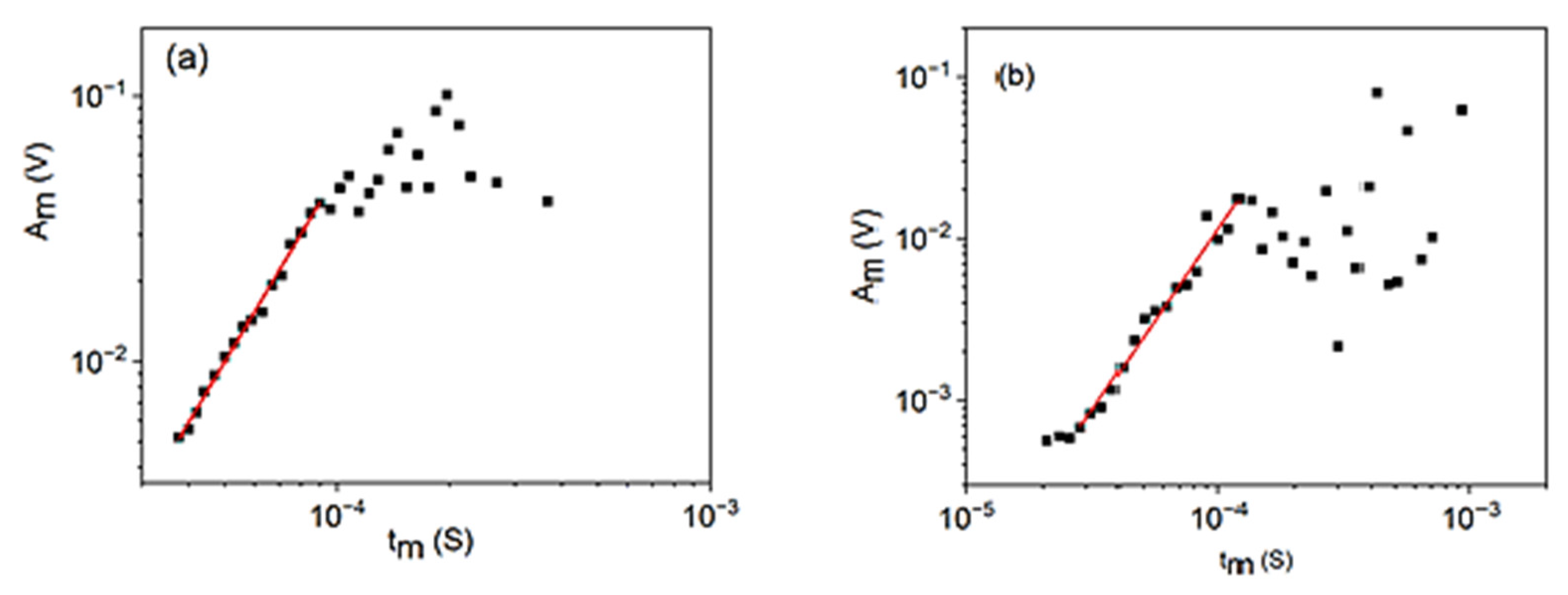
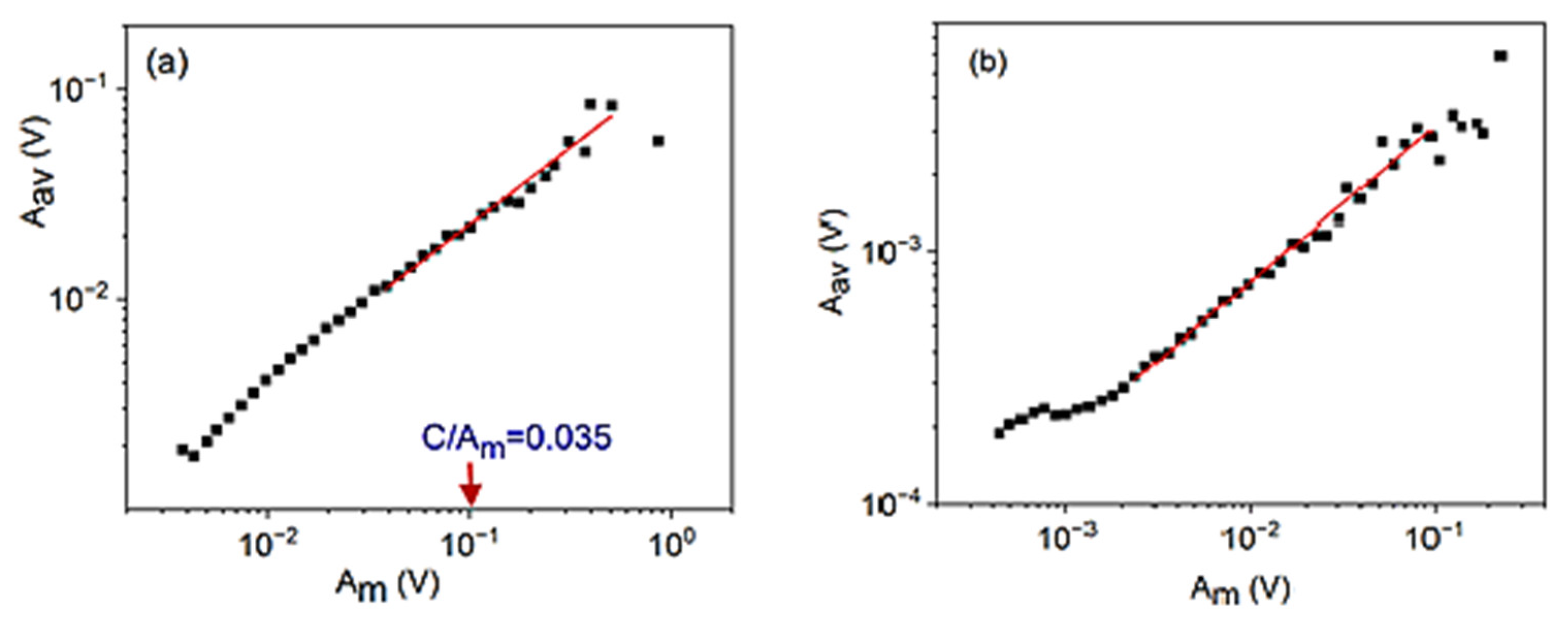
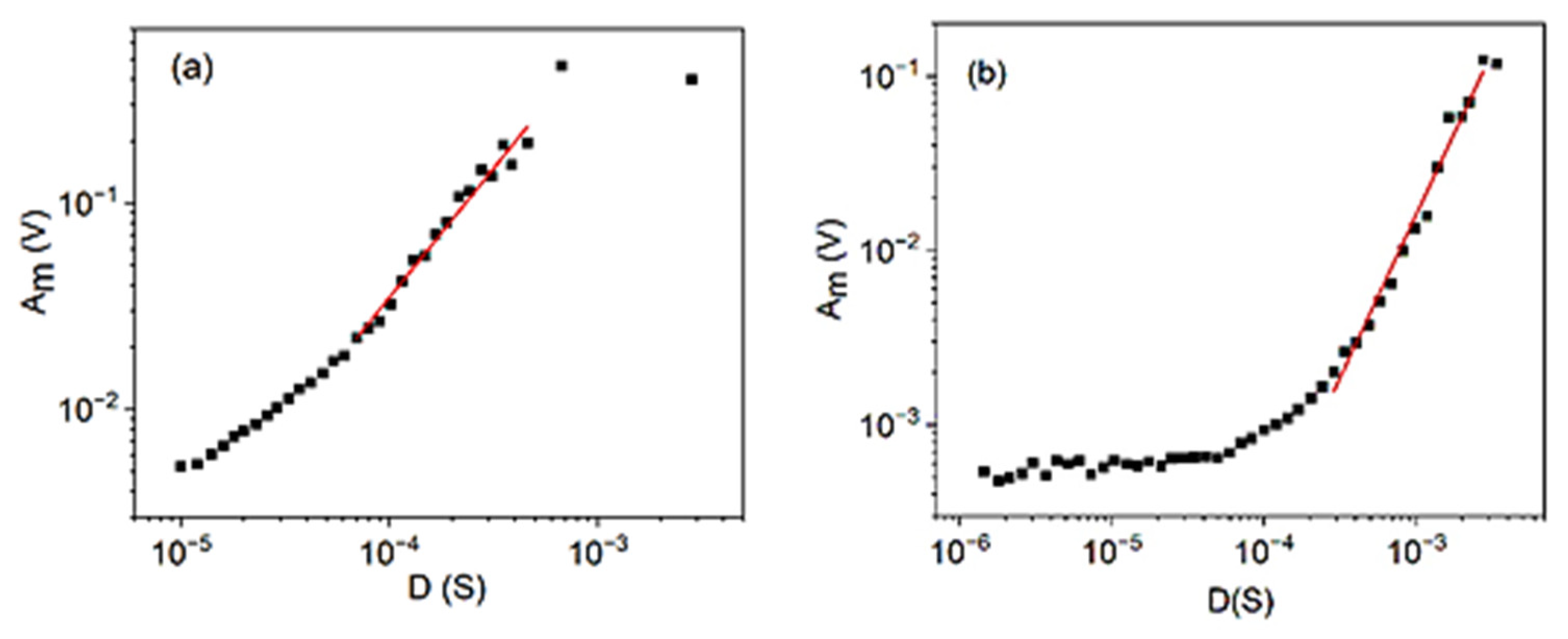
3.1. Relations between Am and Aav, Am and tm, and Am and D
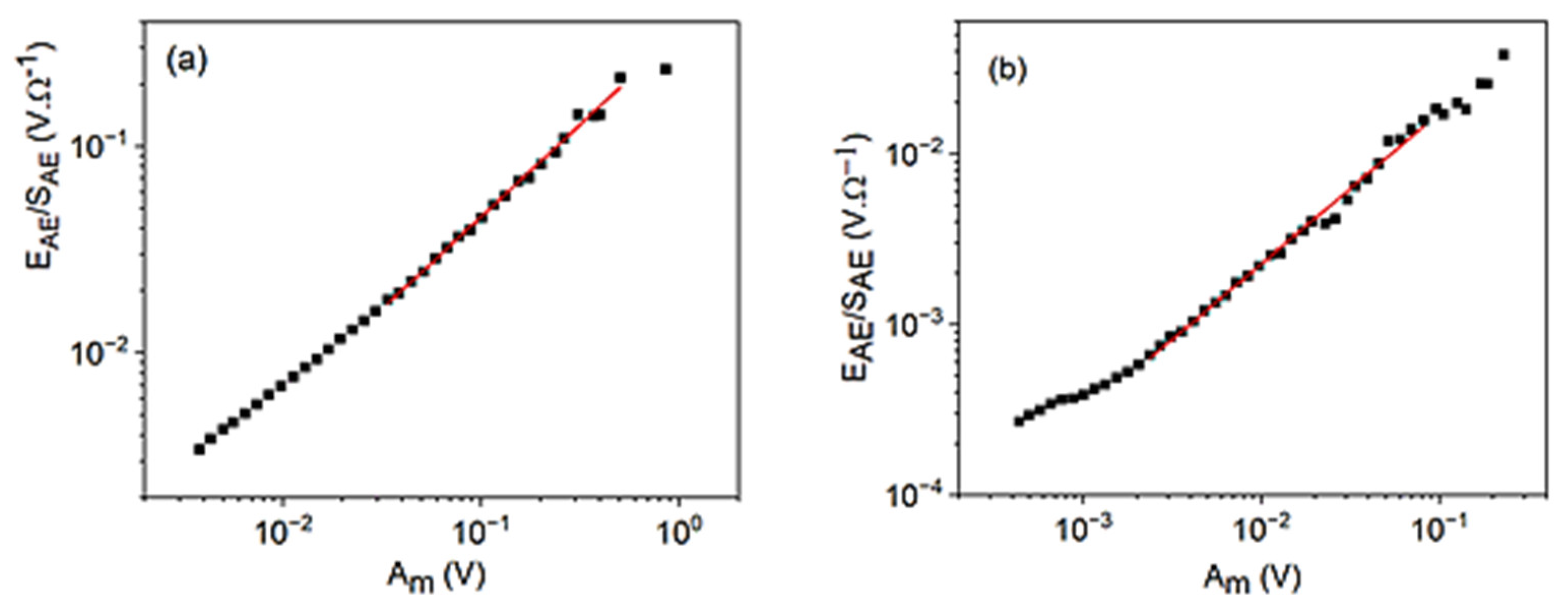
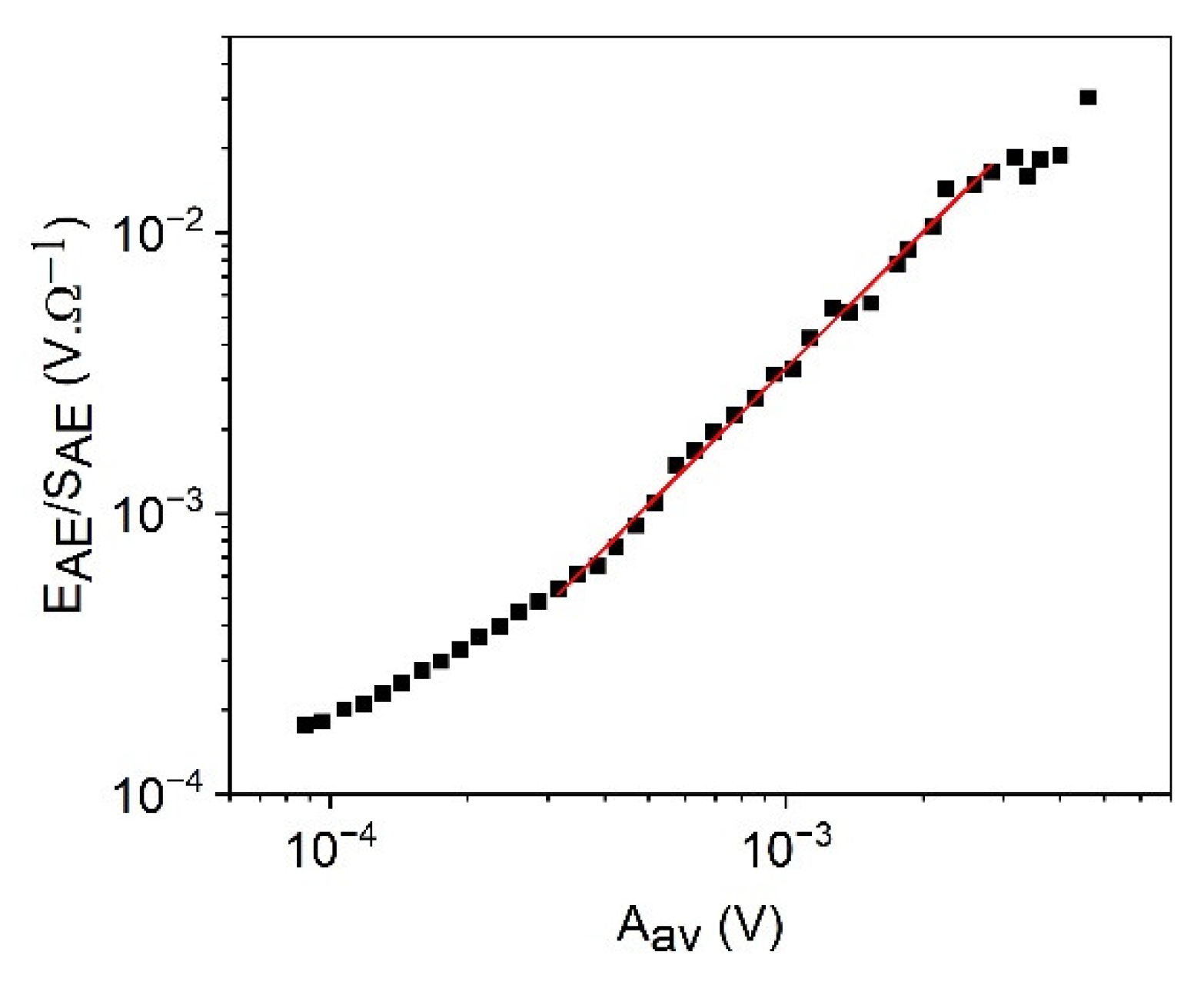
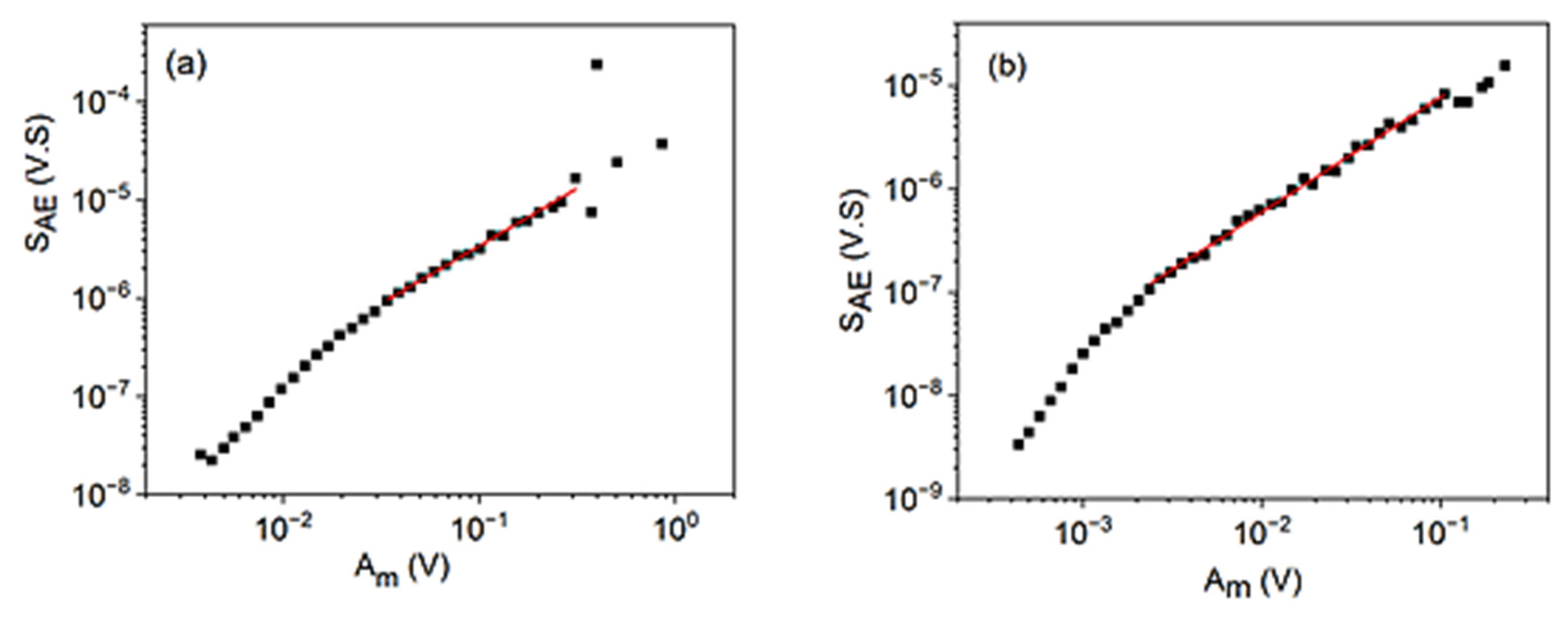
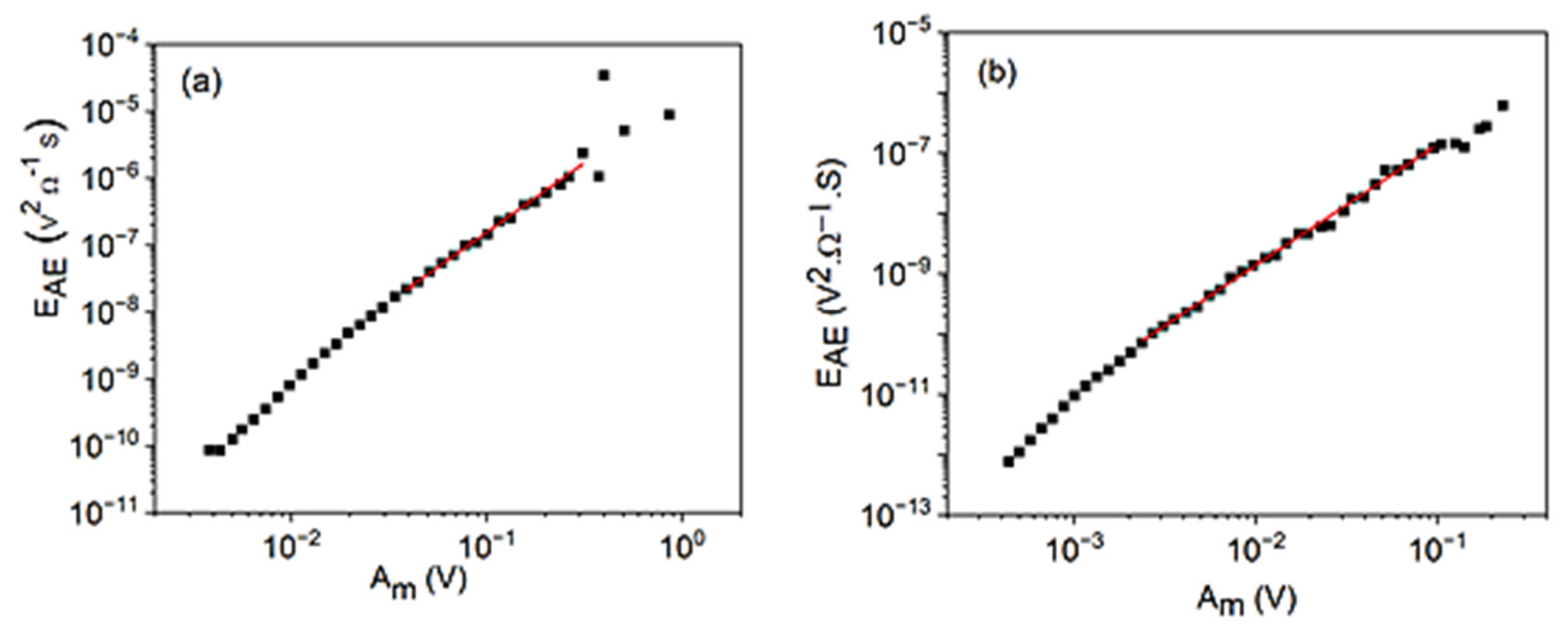
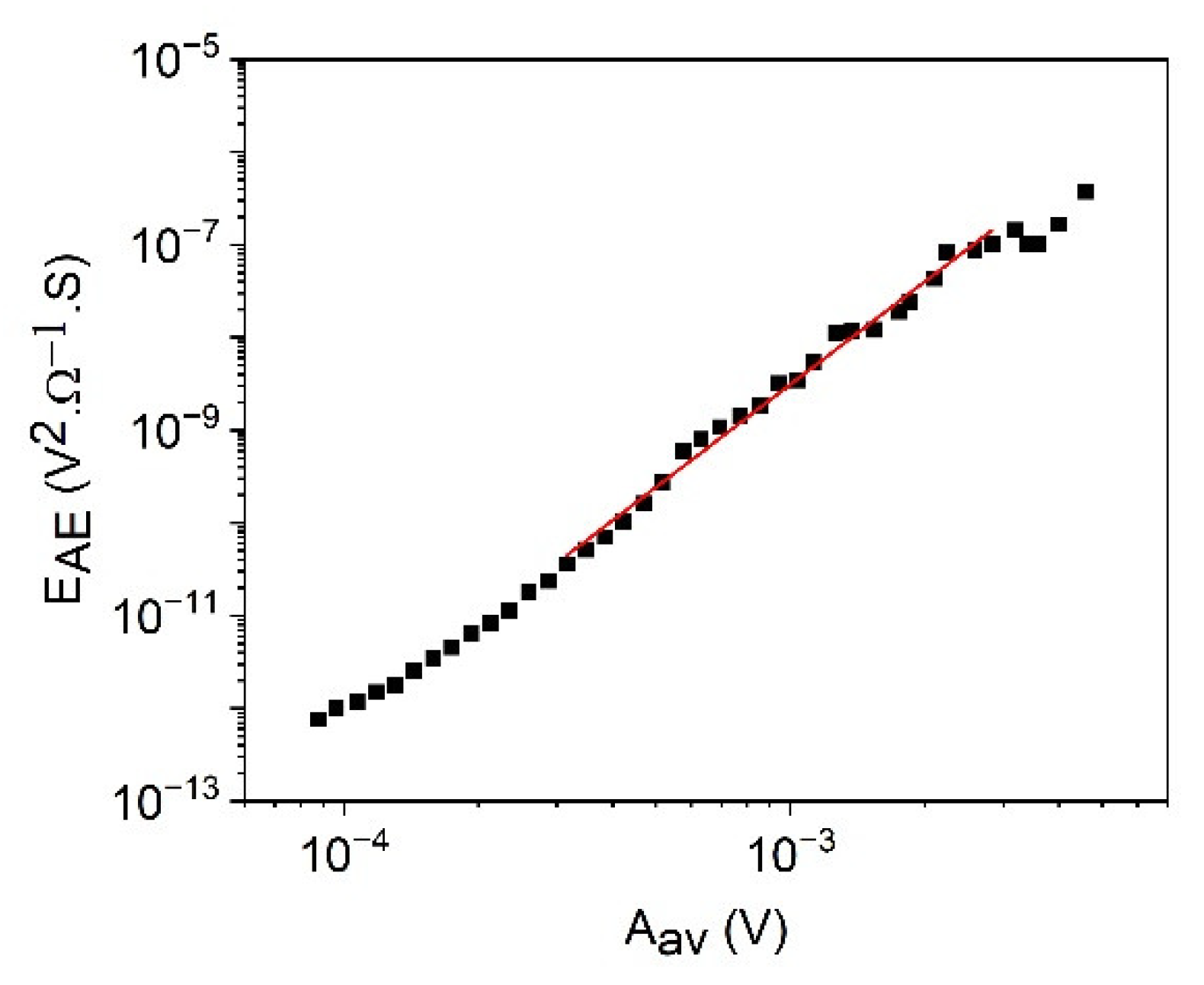
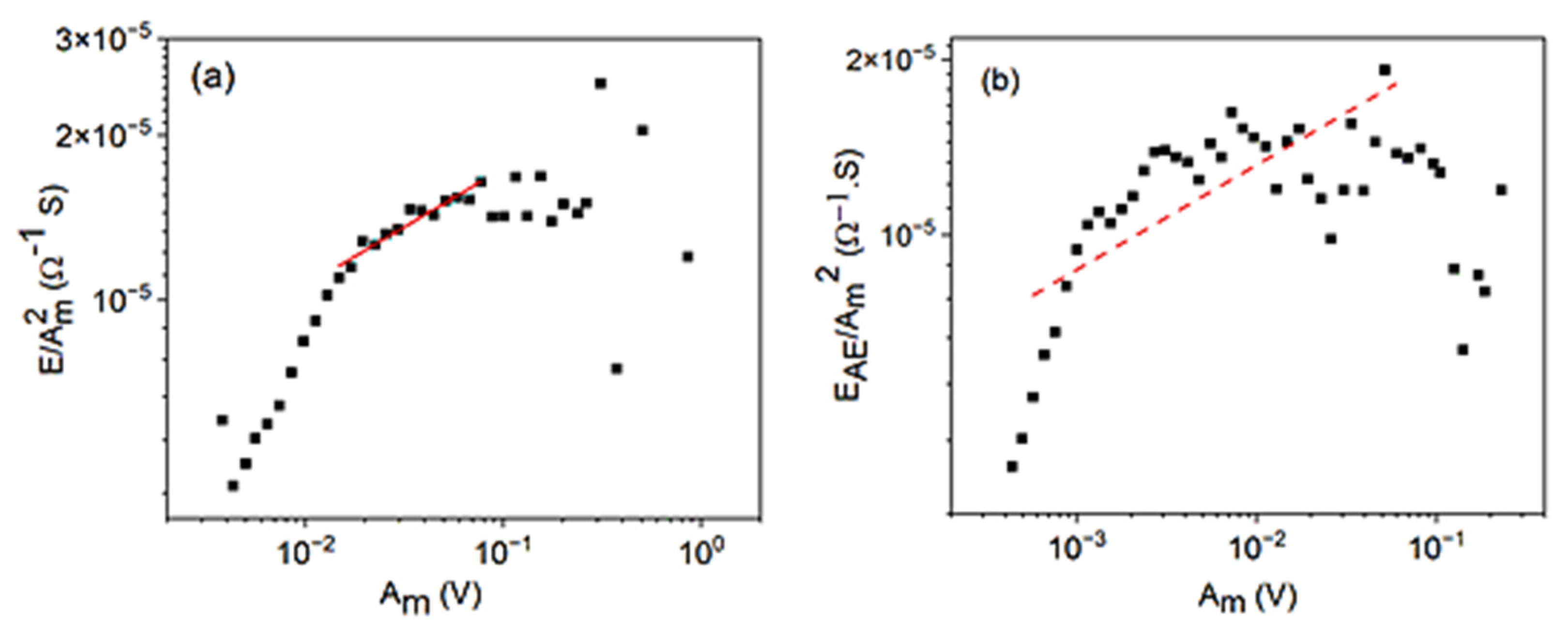
3.2. Scaling Relations between EAE, SAE, , and the Amplitude, Am
3.3. Scaling Relation between and the Amplitude as Well as between and the Duration Time, D
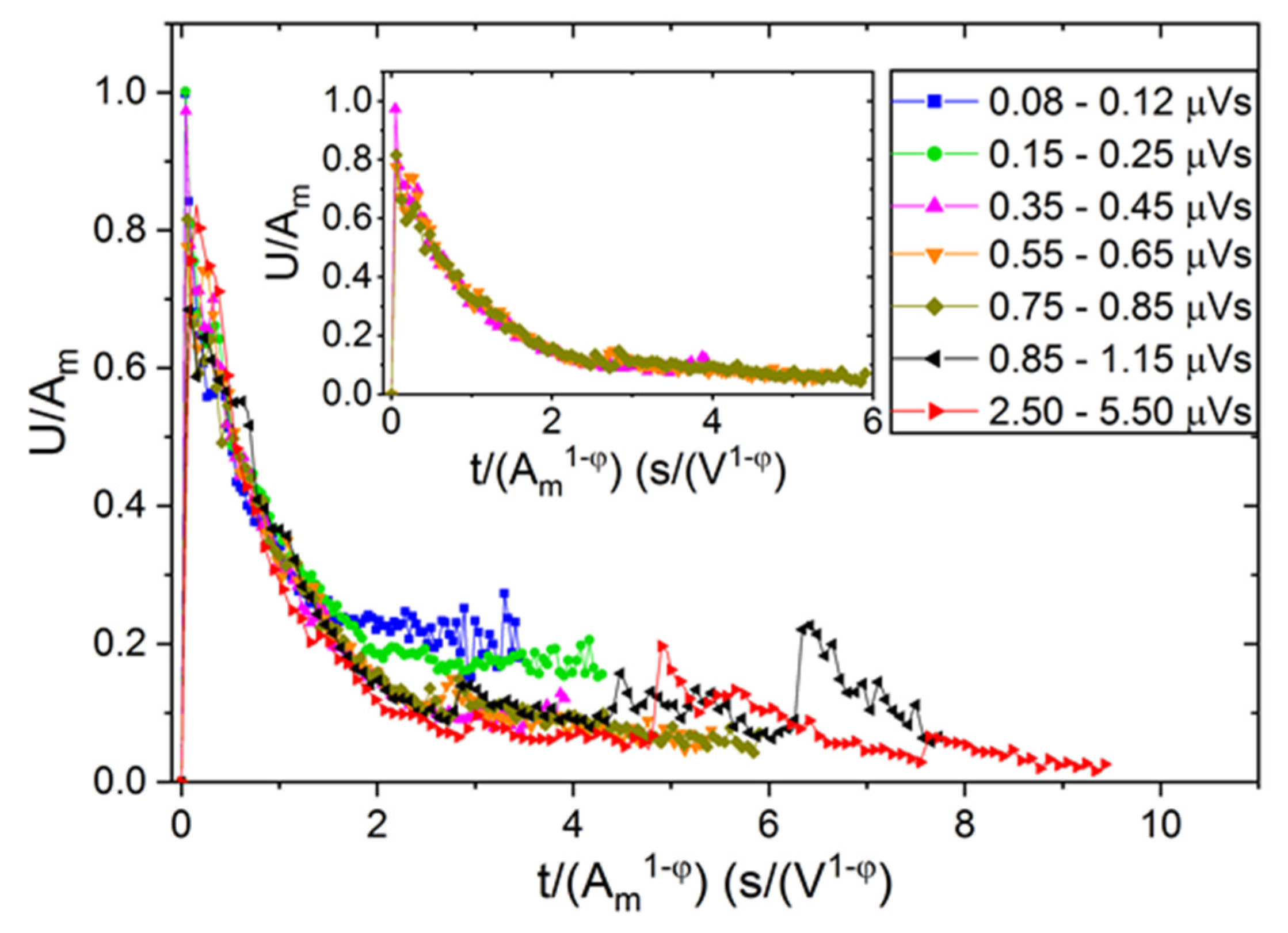
4. Temporal Shape of Avalanches
- (i)
- assume that B is constant in (14), and both the voltage and time scales will be normalized by Am;
- (ii)
- assume that the scaling parameters are not proportional to each other, but the relation holds (see Equations (14), (23) and (24)), i.e., the voltage scale will be reduced by Am and the time scale by .
5. Relation between the Energy and Amplitude for Analysis of Multi-Avalanche Processes
6. Conclusions
- (i)
- from the relation between measured maximum amplitude (Am ~ Um) and tm, the value of φ could be determined, and was obtained (the same values in both alloys);
- (ii)
- the φ parameter appears in the expression of the power exponents for the relation between the energy and Am as well as between the area and Am; these are and , respectively, which provide a denouement of the enigma;
- (iii)
- experimental values of exponents of different scaling relations between the measured AE parameters (energy, area, amplitudes, duration time) are consistent with the above relations;
- (iv)
- using Am and parameters for reducing the voltage and time scales, respectively, nice, common temporal-avalanche shapes were obtained for different bins of area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kuntz, M.C.; Setna, J.P. Noise in disordered systems: The power spectrum and dynamic exponents in avalanche models. Phys. Rev. B 2000, 62, 11699. [Google Scholar] [CrossRef] [Green Version]
- Setna, J.P.; Dahmen, K.A.; Myers, C.R. Crackling noise. Nature 2001, 410, 242–250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salje, E.K.; Dahmen, K. Crackling noise in disordered materials. Annu. Rev. Condens. Matter Phys. 2014, 5, 233–254. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Bohn, F.; Sommer, R.L.; Durin, G.; Zapperi, S.S.; Setna, J.P. Universality beyond power laws and the average avalanche shape. Nat. Phys. 2011, 7, 316–320. [Google Scholar] [CrossRef] [Green Version]
- Laurson, L.; Illa, X.; Santucci, S.; Tallakstad, K.T.; Maloy, K.J.; Alava, M.J. Evolution of the average avalanche shape with the universality class. Nat. Commun. 2013, 4, 2927. [Google Scholar] [CrossRef] [Green Version]
- LeBlanc, M.; Angheluta, L.; Dahmen, K.; Goldenfeld, N. Universal fluctuations and extreme statistics of avalanches near the depinning transition. Phys. Rev. E 2013, 87, 022126. [Google Scholar] [CrossRef] [Green Version]
- Dobrinevski, A.; Le Doussal, P.; Weise, K.J. Avalanche shape and exponents beyond mean-field theory. EPL 2015, 108, 66002. [Google Scholar] [CrossRef] [Green Version]
- Chi-Cong, V.; Weiss, J. Asymmetric Damage Avalanche Shape in Quasibrittle Materials and Subavalanche (Aftershock) Clusters. Phys. Rev. Lett. 2020, 125, 105502. [Google Scholar] [CrossRef]
- Spark, G.; Maas, R. Shapes and velocity relaxation of dislocation avalanches in Au and Nb microcrystals. Acta Mater. 2018, 152, 86–95. [Google Scholar] [CrossRef] [Green Version]
- Bohn, F.; Correa, M.A.; Carara, M.; Papanikolau, S.; Durin, G.; Sommer, R.L. Statistical properties of Barkhausen noise in amorphous ferromagnetic films. Phys. Rev. E 2014, 90, 032821. [Google Scholar] [CrossRef] [Green Version]
- Durin, G.; Zapperi, S. Scaling Exponents for Barkhausen Avalanches in Polycrystalline and Amorphous Ferromagnets. Phys. Rev. Lett. 2000, 84, 4705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rafols, I.; Vives, E. Statistics of avalanches in martensitic transformations. II. Modeling. Phys. Rev. B 1995, 52, 12651. [Google Scholar] [CrossRef] [Green Version]
- Carrillo, L.; Mañosa, L.; Ortin, J.; Planes, A.; Vives, E. Experimental Evidence for Universality of Acoustic Emission Avalanche Distributions during Structural Transitions. Phys. Rev. B 1998, 81, 1889. [Google Scholar] [CrossRef] [Green Version]
- Planes, A.; Mañosa, L.; Vives, E. Acoustic emission in martensitic transformations. J. Alloys Compd. 2013, 577, S699–S704. [Google Scholar] [CrossRef]
- Durin, G.; Bohn, F.; Correa, A.; Sommer, R.L.; Le Doussal, P.; Wiesse, K.J. Quantitative Scaling of Magnetic Avalanches. Phys. Rev. Lett. 2016, 117, 087201. [Google Scholar] [CrossRef] [Green Version]
- Rosinberg, M.L.; Vives, E. Metastability, Hysteresis, Avalanches, and Acoustic Emission: Martensitic Transitions in Functional Materials. In Disorder and Strain Induced Complexity in Functional Materials; Kakeshita, T., Fukuda, T., Saxena, A., Planes, A., Eds.; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 148, pp. 249–272. ISBN 978-3-642-20943-7. [Google Scholar]
- Vives, E.; Baro, J.; Planes, A. From labquakes in porous materials to earthquakes. In Avalanches in Functional Materials and Geophysics; Salje, E.K.H., Setna, A., Planes, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 31–58. [Google Scholar]
- Baro, J.; Dahmen, K.A.; Davidsen, J.; Planes, A.; Castillo, P.O.; Nataf, G.F.; Salje, E.K.H.; Vives, E. Experimental Evidence of Accelerated Seismic Release without Critical Failure in Acoustic Emissions of Compressed Nanoporous Materials. Phys. Rev. Lett. 2018, 120, 245501. [Google Scholar] [CrossRef] [Green Version]
- Baro, J. Avalanches in Out of Equilibrium Systems: Statistical Analysis of Experiments and Simulations. Ph.D. Thesis, University of Barcelona, Barcelona, Spain, 2018. [Google Scholar]
- Beke, D.L.; Daróczi, L.; Tóth, L.Z.; Bolgár, M.K.; Samy, N.M.; Hudák, A. Acoustic Emissions during Structural Changes in Shape Memory Alloys. Metals 2019, 9, 58. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Go, B.; Ding, X.; Sun, J.; Salje, E.K.H. Real-time monitoring dislocations, martensitic transformations and detwinning in stainless steel: Statistical analysis and machine learning. J. Mater. Sci. Technol. 2021, 92, 31. [Google Scholar] [CrossRef]
- Chen, Y.; Gou, B.; Chen, C.; Ding, X.; Sun, J.; Salje, E.K.H. Fine structures of acoustic emission spectra: How to separate dislocation movements and entanglements in 316L stainless steel. Appl. Phys. Let. 2020, 117, 262901. [Google Scholar] [CrossRef]
- Antonaglia, J.; Wright, W.J.; Gu, X.; Byer, R.R.; Hufnagel, T.C.; LeBlanc, M.; Uhl, J.T.; Dahmen, K.A. Bulk metallic glasses deform via avalanches. Phys. Rev. Lett. 2014, 112, 1555501. [Google Scholar] [CrossRef]
- Makinen, T.; Karppinen, P.; Ovaska, M.; Laurson, L.; Alava, M.J. Propagating bands of plastic deformation in a metal alloy as critical avalanches. Sci. Adv. 2020, 6, eabc7350. [Google Scholar] [CrossRef] [PubMed]
- Casals, B.; Dahmen, K.A.; Gou, B.; Rooke, S.; Salje, E.K.H. The duration-energy-size enigma for acoustic emission. Sci. Rep. 2021, 11, 5590. [Google Scholar] [CrossRef] [PubMed]
- Samy, N.M.; Bolgár, N.M.; Barta, N.; Daróczi, L.; Tóth, L.Z.; Chumlyakov, Y.I.; Karaman, I.; Beke, D.L. Thermal, acoustic and magnetic noises emitted during martensitic transformation in single crystalline Ni45Co5Mn36.6In13.4 meta-magnetic shape memory alloy. J. Alloys Compd. 2019, 778, 669–680. [Google Scholar] [CrossRef]
- Kamel, S.M.; Daróczi, L.; Tóth, L.Z.; Samy, N.M.; Panchenko, E.; Chumlyakov, Y.I.; Beke, D.L. Acoustic and DSC investigations of burst like shape recovery of Ni49Fe18Ga27Co6 shape memory single crystal. 2022; to be published. [Google Scholar]
- Daróczi, L.; Elrasasi, T.Y.; Arjmandbasi, T.; Tóth, L.Z.; Veres, B.; Beke, D.L. Change of Acoustic Emission Characteristics during Temperature Induced Transition fromTwinning to Dislocation Slip under Compression in Polycrystalline Sn. Materials 2021, 15, 224. [Google Scholar] [CrossRef]
- Chen, Y.; Gou, B.; Yuan, B.; Ding, X.; Sun, J.; Salje, E.K.H. Multiple Avalanche Processes in Acoustic Emission Spectroscopy: Multibranching of the Energy-Amplitude Scaling. Phys. Status Solidi B 2021, 259, 2100465. [Google Scholar] [CrossRef]
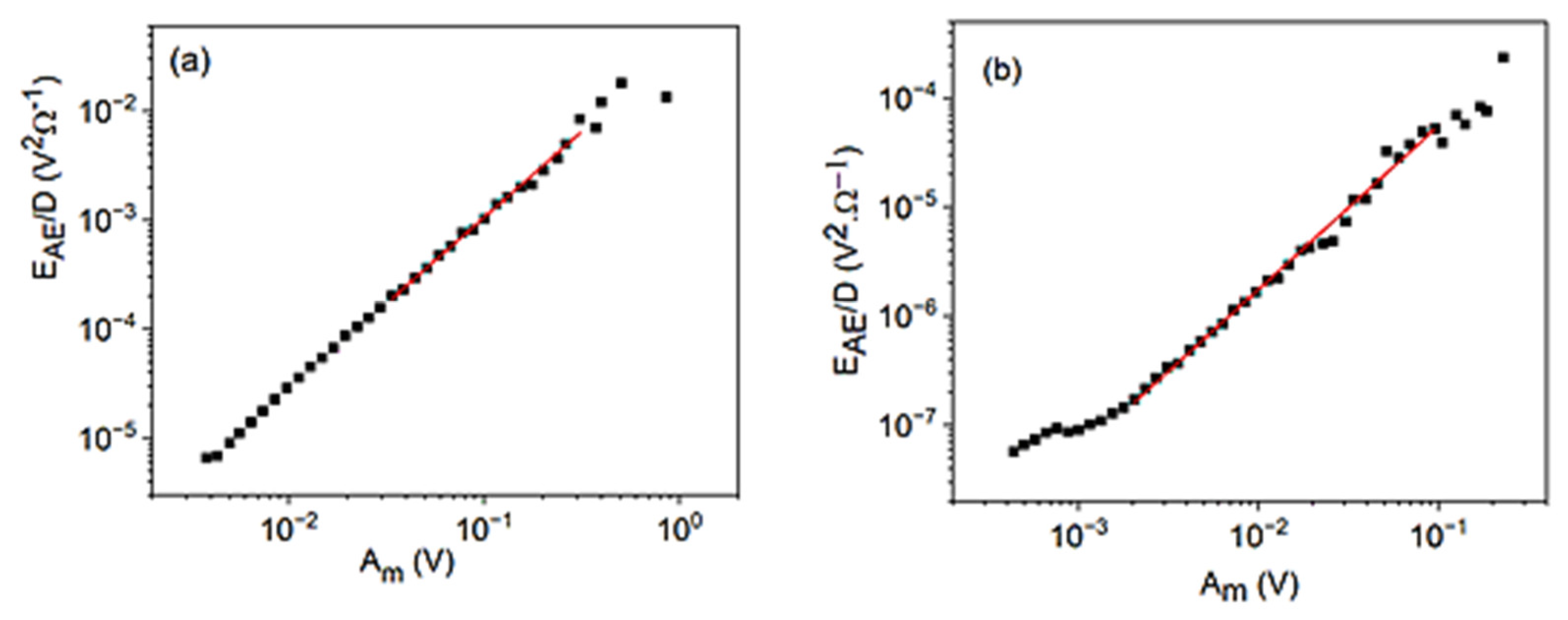
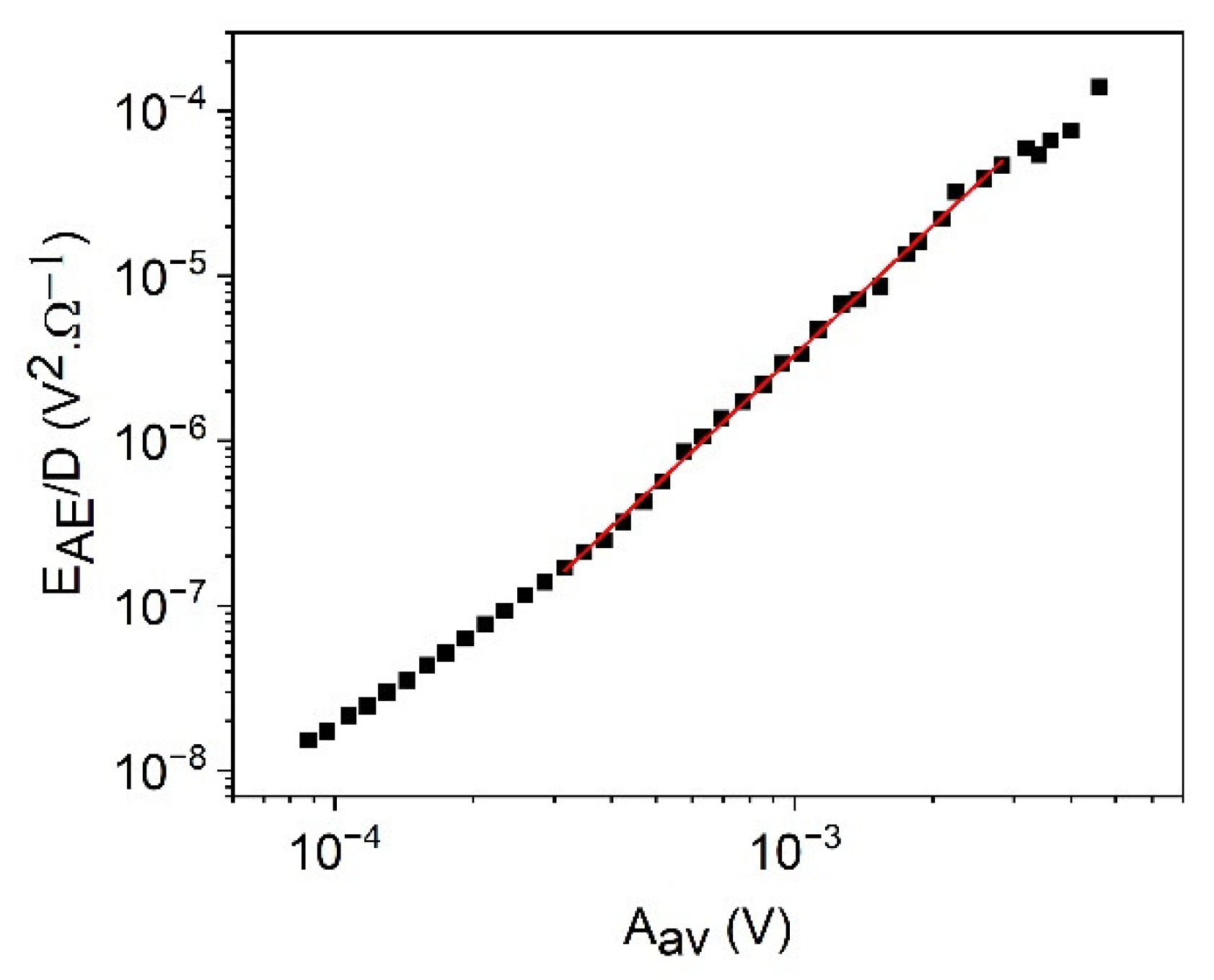
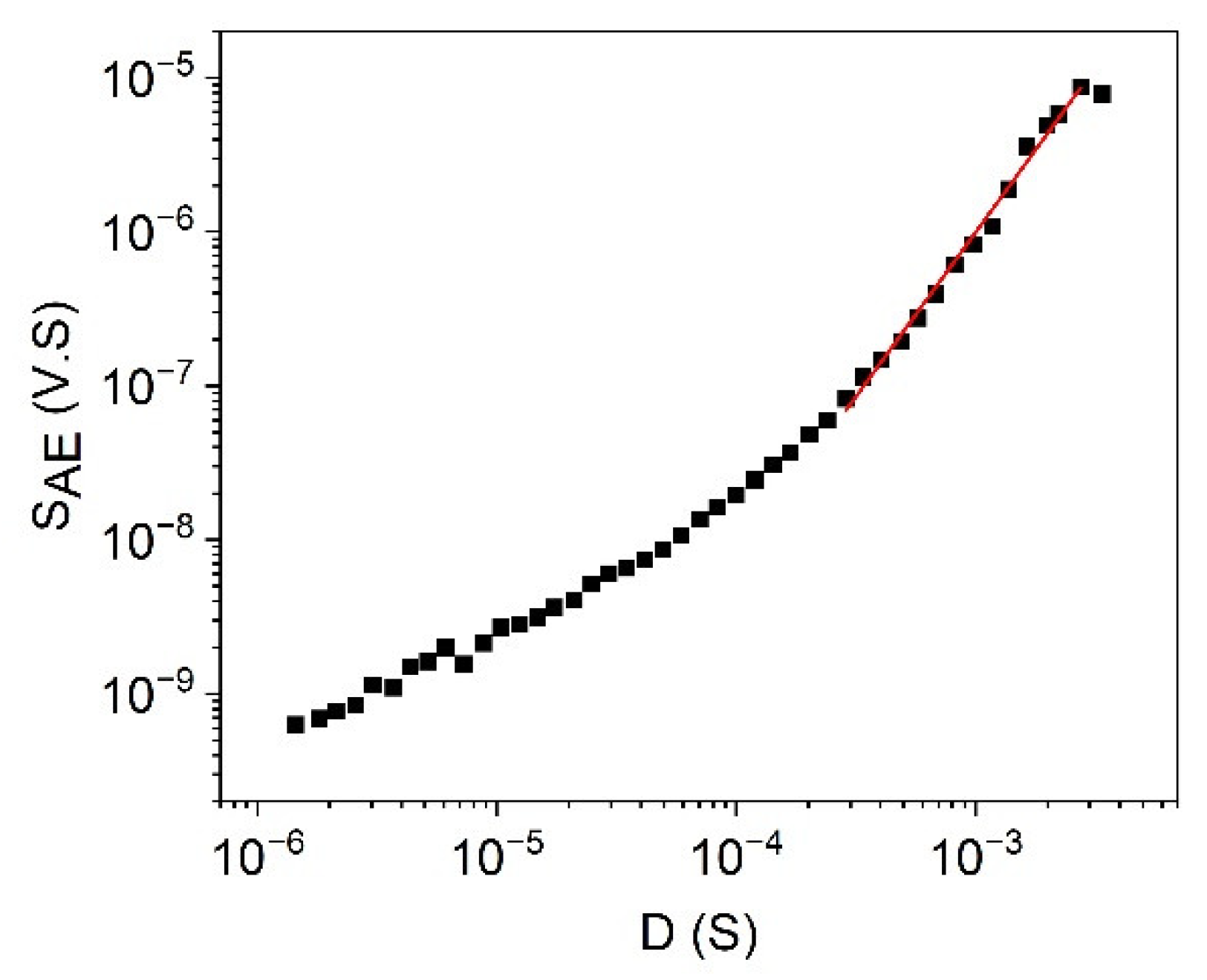
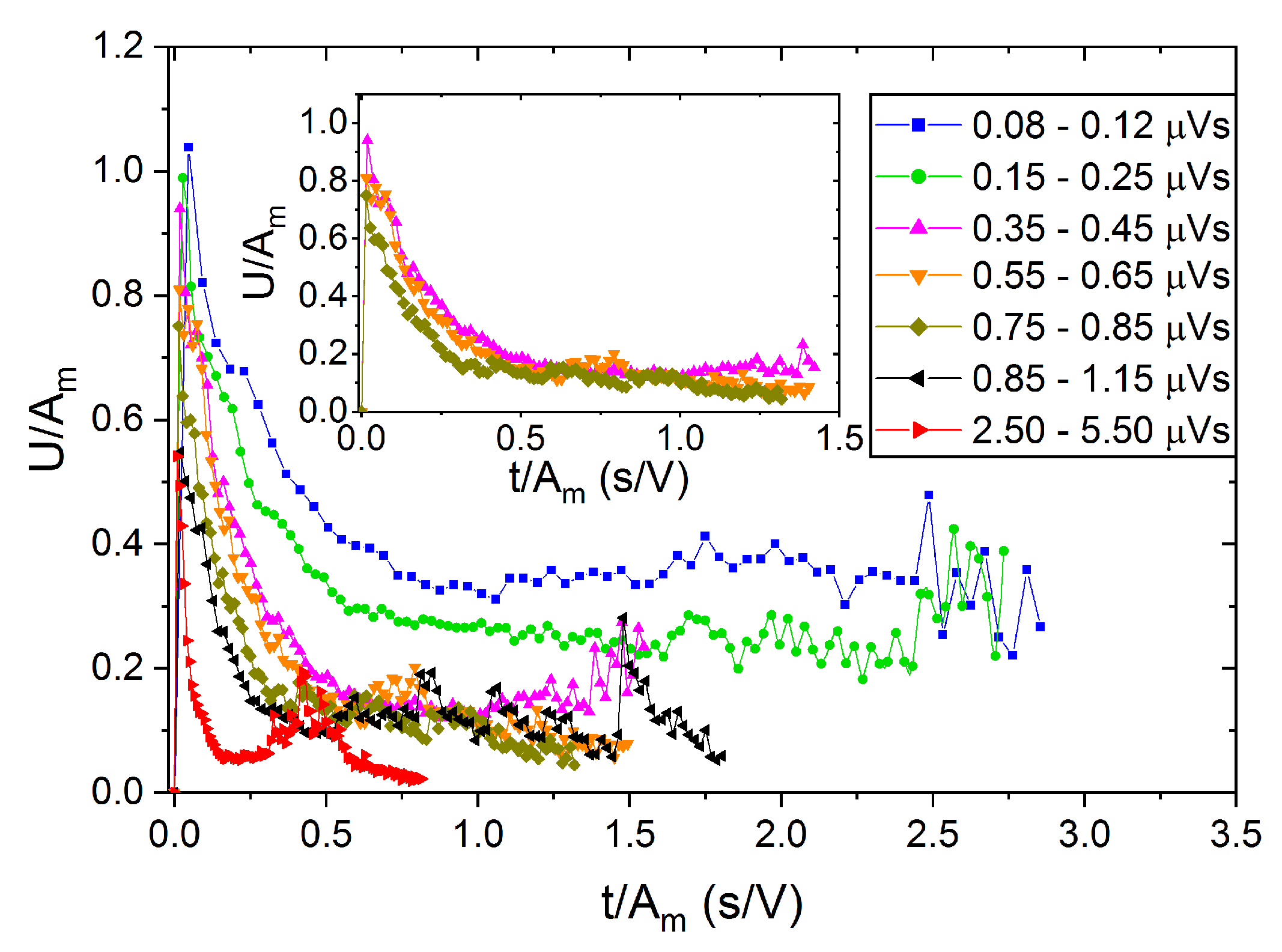
| Equation | Value of φ | |
|---|---|---|
| Alloy A | Alloy B | |
| (25) | 0.6 ± 0.1 | 0.6 ± 0.1 |
| (32) | 0.8 ± 0.1 | 0.90 ± 0.08 |
| (37) | 0.9 ± 0.1 | 1.0 ± 0.1 |
| Average | 0.77 ± 0.11 | 0.83 ± 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamel, S.M.; Samy, N.M.; Tóth, L.Z.; Daróczi, L.; Beke, D.L. Denouement of the Energy-Amplitude and Size-Amplitude Enigma for Acoustic-Emission Investigations of Materials. Materials 2022, 15, 4556. https://doi.org/10.3390/ma15134556
Kamel SM, Samy NM, Tóth LZ, Daróczi L, Beke DL. Denouement of the Energy-Amplitude and Size-Amplitude Enigma for Acoustic-Emission Investigations of Materials. Materials. 2022; 15(13):4556. https://doi.org/10.3390/ma15134556
Chicago/Turabian StyleKamel, Sarah M., Nora M. Samy, László Z. Tóth, Lajos Daróczi, and Dezső L. Beke. 2022. "Denouement of the Energy-Amplitude and Size-Amplitude Enigma for Acoustic-Emission Investigations of Materials" Materials 15, no. 13: 4556. https://doi.org/10.3390/ma15134556
APA StyleKamel, S. M., Samy, N. M., Tóth, L. Z., Daróczi, L., & Beke, D. L. (2022). Denouement of the Energy-Amplitude and Size-Amplitude Enigma for Acoustic-Emission Investigations of Materials. Materials, 15(13), 4556. https://doi.org/10.3390/ma15134556







