Research and Statistical Analysis on Impact Resistance of Steel Fiber Expanded Polystyrene Concrete and Expanded Polystyrene Concrete
Abstract
:1. Introduction
2. Experimental
2.1. Materials and Mix Proportions
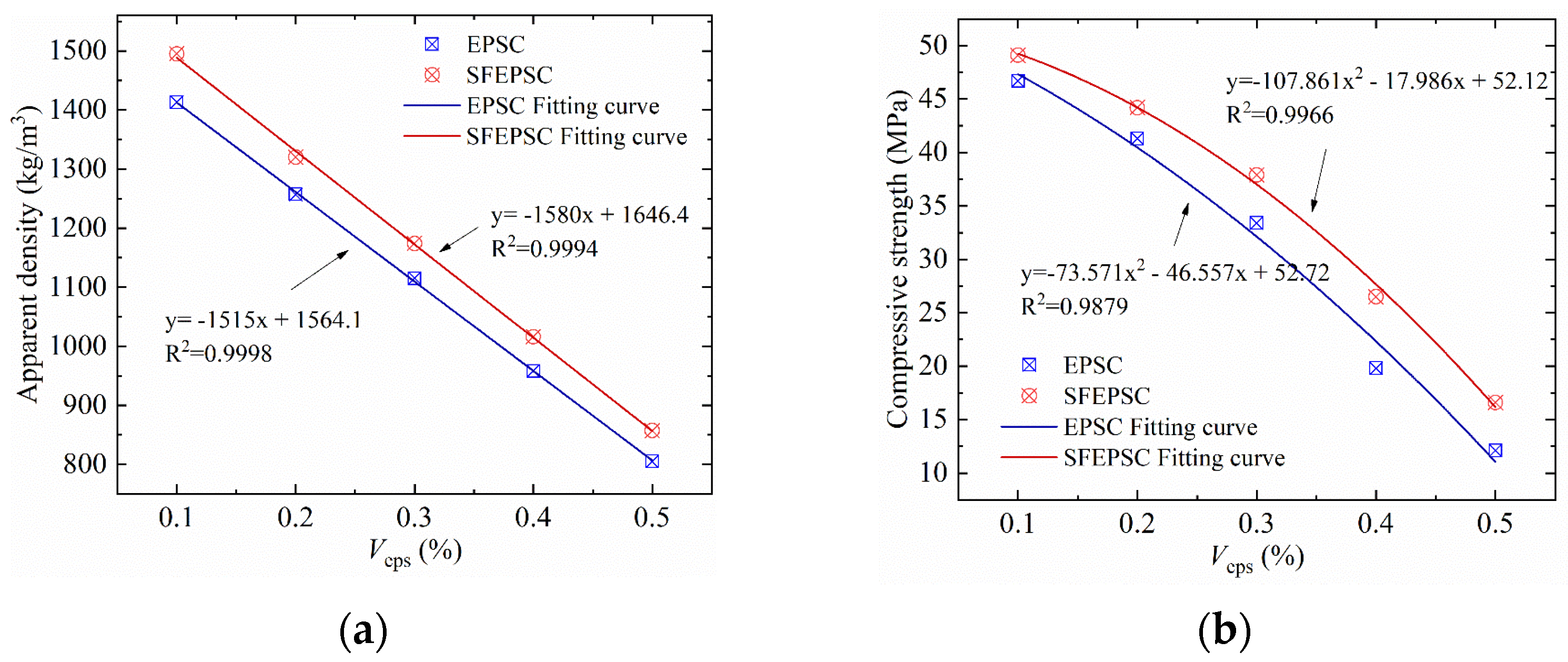
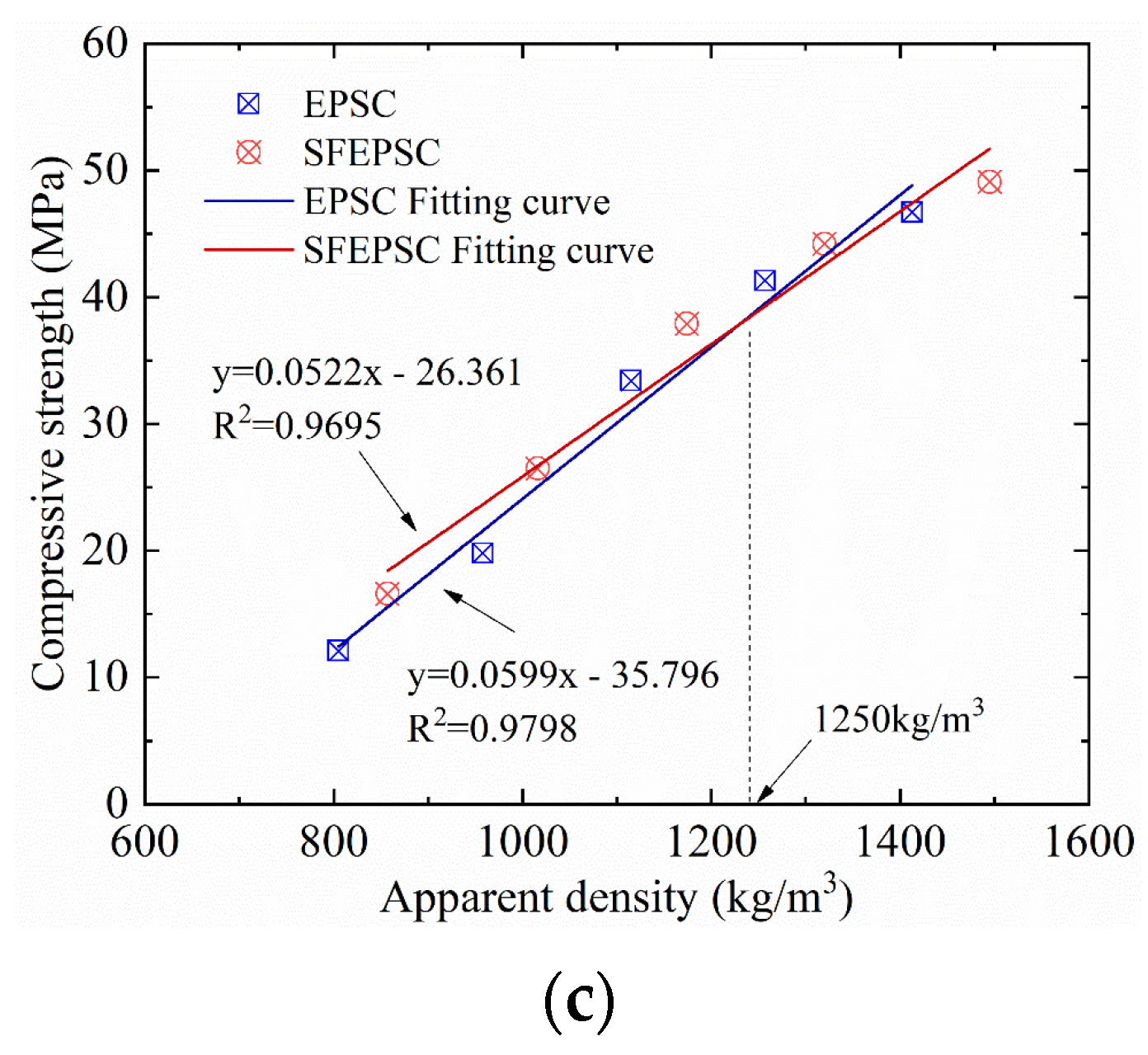
2.2. The Influence of Veps and Apparent Density on Compressive Strength
2.3. Drop-Weight Test Device and Test Method
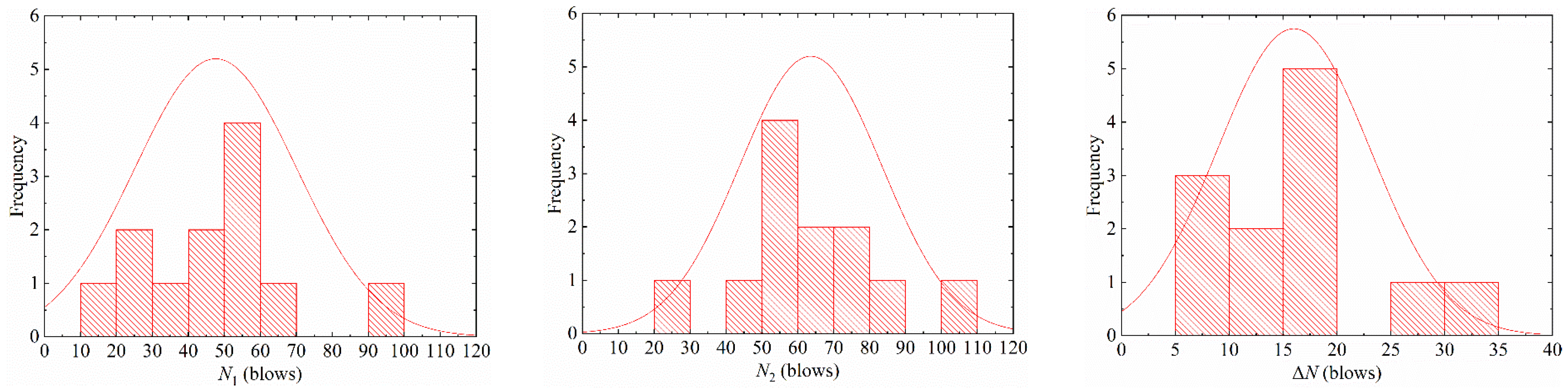
2.4. Test Results and Statistical Analysis
3. Probability Distribution Characteristics
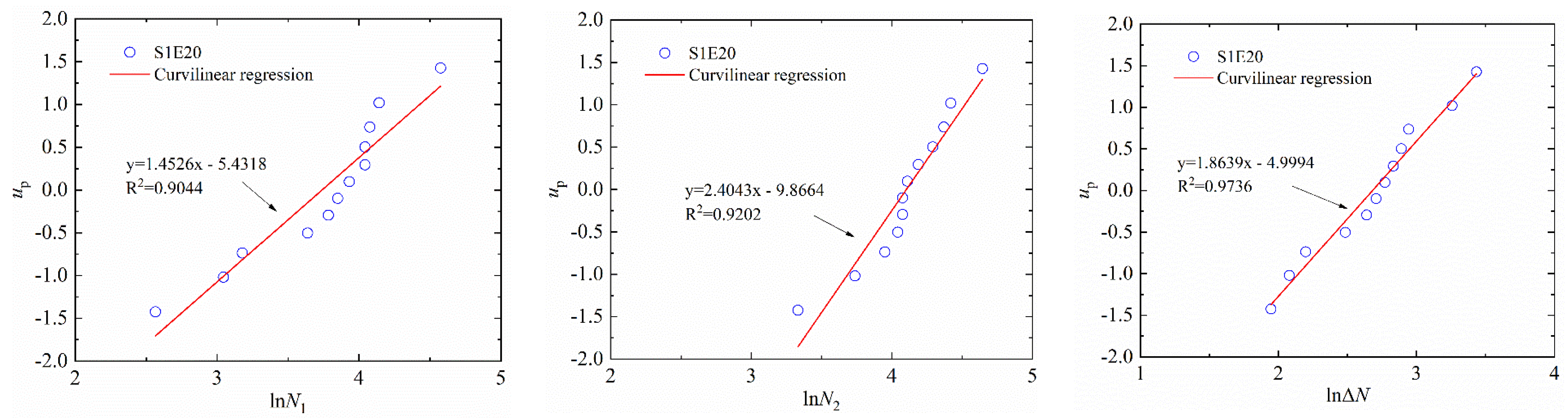
3.1. Log-Normal Distribution
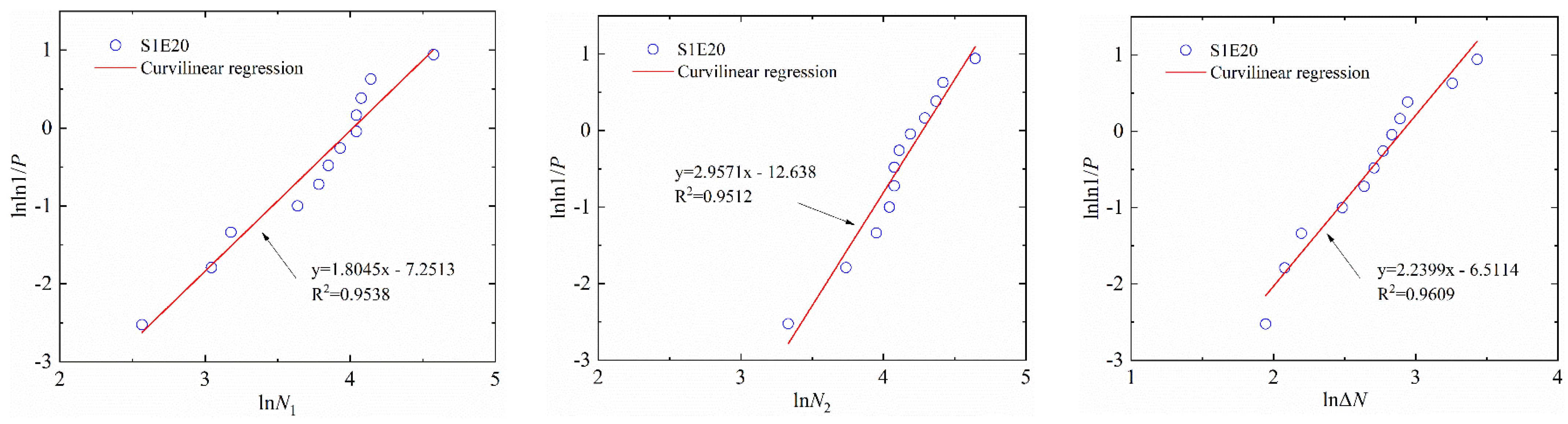
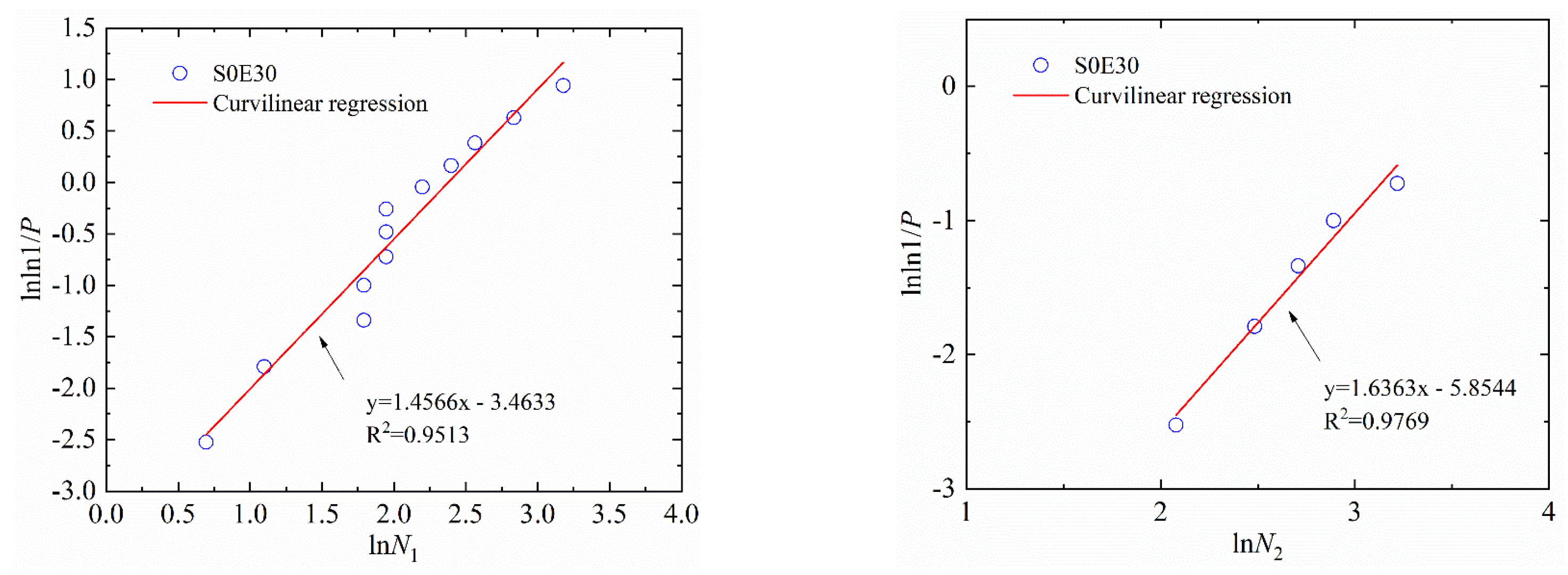
3.2. Weibull Distribution
3.3. Curve of SFEPSC and EPSC Impact Resistance
4. Destruction Mode and Energy Consumption Mechanism
4.1. Destruction Mode
4.2. Energy Consumption Mechanism
5. Conclusions
- The apparent density of the two types of concrete specimens had a linear relationship with Veps and compressive strength. The compressive strength had a quadratic relationship with Veps. The apparent density and compressive strength of SFEPSC were higher than EPSC at the same volume of EPS;
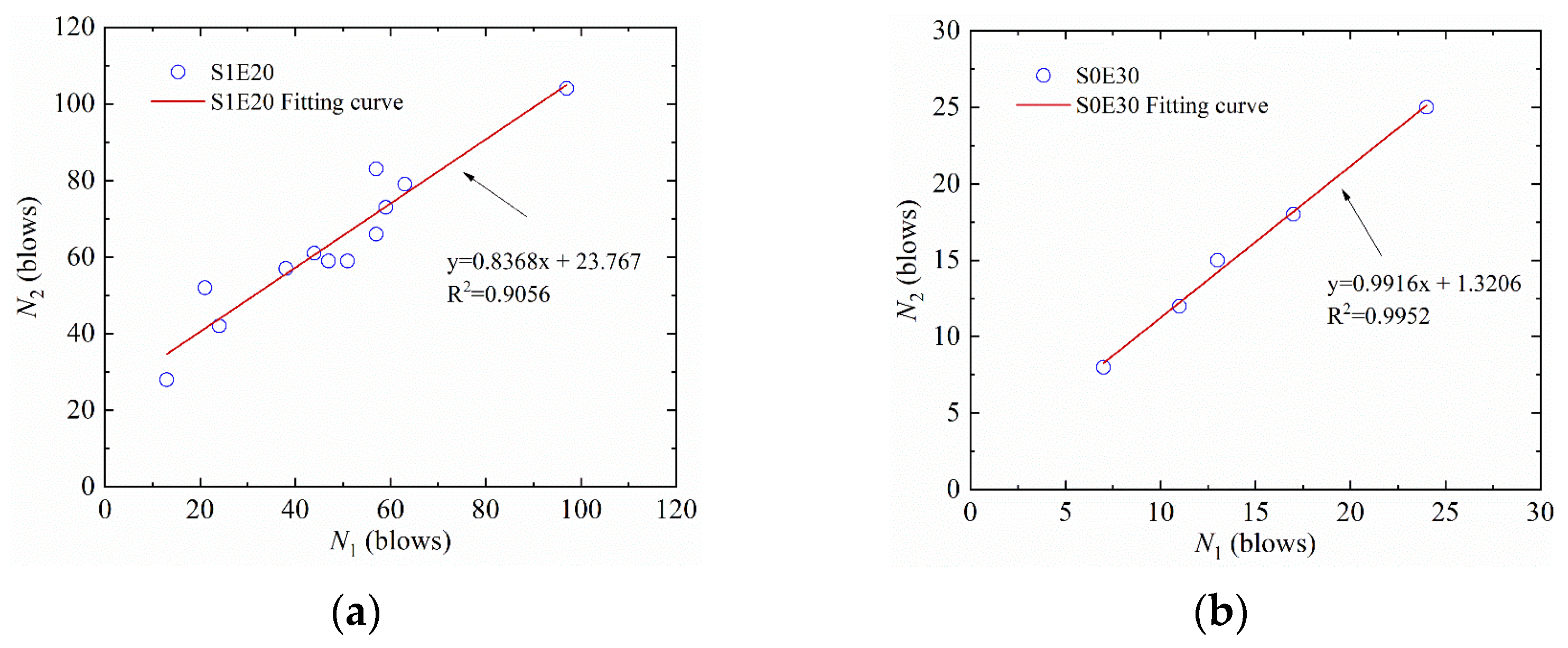
- By adding SF to EPSC, the impact resistance of SFEPSC was higher than EPSC. It had a highly linear relationship between the first visible crack, N1, and the ultimate failure, N2, and S1E20 had the best impact resistance;
- The log-normal distribution and the two-parameter Weibull distribution could better describe the impact resistance of the first visible crack and the ultimate failure of SFEPSC and the EPSC at the first visible crack;
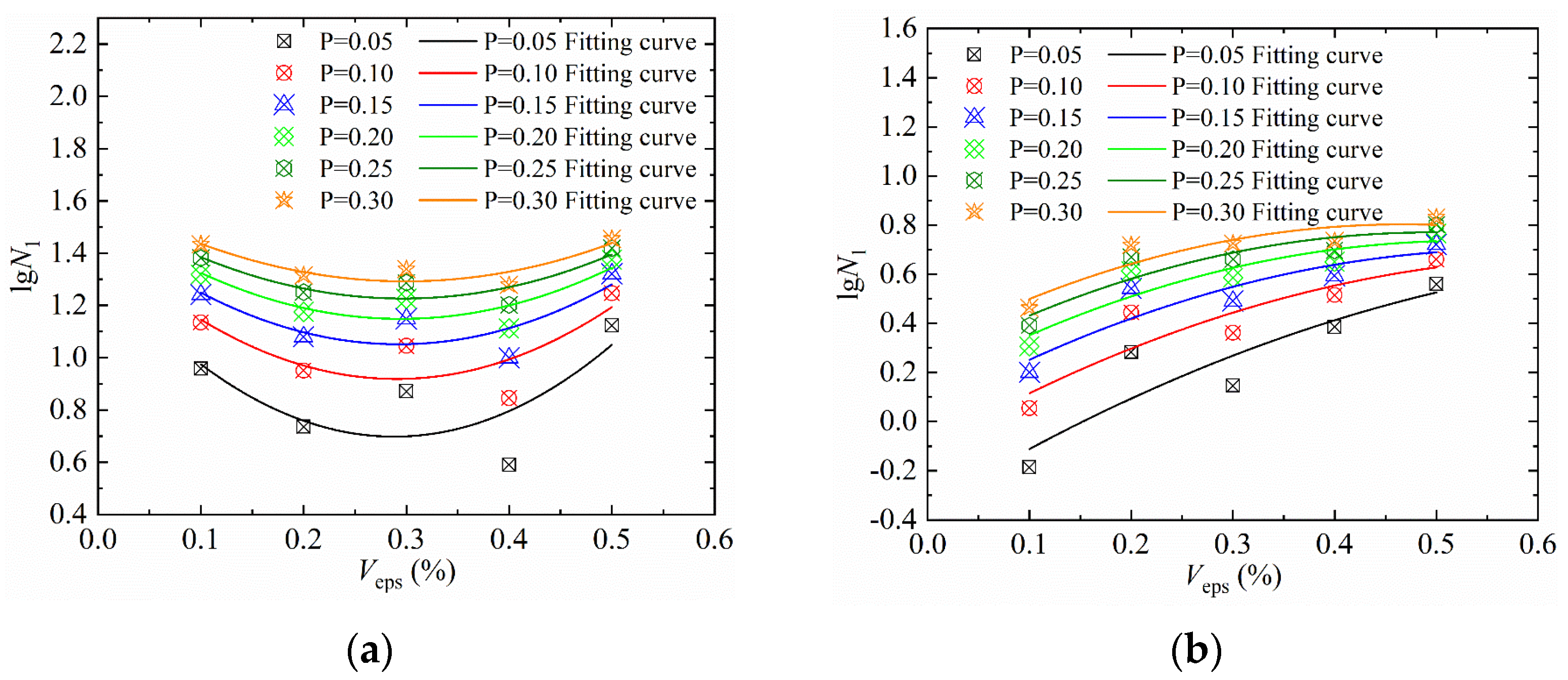
- Under different failure probabilities, the impact resistance of SFEPSC had a concave quadratic relationship with Veps, while EPSC had a convex quadratic relationship. The impact resistance of both types could be tested and predicted by the P − Veps − lgN curve;
- The failure modes of the two types of concrete specimens were different. By adding SF, the pits of EPSC specimens became deepened before splitting. The pit depth of both specimens increased with the increase in Veps, and the fractures were relatively rough;
- The energy consumption mechanism of both types of concrete specimens was different. EPSC dissipated shock loads by the EPS particles. By adding SF to EPSC, especially after the first cracking of the specimen, the SF energy absorption and friction energy dissipation characteristics were more obvious.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, P.; Zhang, S.; Wang, X.; Wang, C. Derivation of the True Strain Rate Effect of Roller Compacted Concrete (RCC) from Impact-Induced Fragmentation. J. Adv. Concr. Technol. 2021, 19, 1040–1051. [Google Scholar] [CrossRef]
- Rahmani, T.; Kiani, B.; Shekarchi, M.; Safari, A. Statistical and experimental analysis on thebehavior of fiber reinforced concrete subjected to drop weight test. Constr. Build. Mater. 2012, 37, 360–369. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, P.; Wang, C.; Wang, G.; Lu, W.; Cao, K. Failure criteria calibration based on the triaxial compression behavior of roller compacted concrete (RCC). Mater. Struct. 2021, 54, 7. [Google Scholar] [CrossRef]
- Wang, C.; Wei, P.; Wang, X.; Wang, G.; Lu, W.; Cao, K. Blast-Resistance and Damage Evaluation of Concrete Gravity Dam Exposed to Underwater Explosion: Considering the Initial Stress Field. KSCE J. Civ. Eng. 2021, 25, 2922–2935. [Google Scholar] [CrossRef]
- Li, Q.; Wang, G.; Lu, W.; Niu, X.; Chen, M.; Yan, P. Failure modes and effect analysis of concrete gravity dams subjected to underwater contact explosion considering the hydrostatic pressure. Eng. Fail. Anal. 2018, 85, 62–76. [Google Scholar] [CrossRef]
- Lu, L.; Zhu, Y.; Zou, D.G.; Fan, Q.; Dong, S. Evaluation of anti-explosion performance of Shuibuya concrete-faced rockfill dam slabs subjected to strong shock waves caused by an underwater explosion. Adv. Mech. Eng. 2019, 11, 168781401882220. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Wang, P. Element Analysis of Tunnel Structure with EPS Granule Layers Subjected to Blast Load. J. Highw. Transp. Res. Dev. 2016, 10, 53–58. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Fan, J.; Fang, Q.; Long, Y. Mesoscopic investigation of layered graded metallic foams under dynamic compaction. Adv. Struct. Eng. 2018, 21, 2081–2098. [Google Scholar] [CrossRef]
- Yan, L.; Su, P.; Han, Y.; Han, B. Effects of Aluminum Foam Filling on Compressive Strength and Energy Absorption of Metallic Y-Shape Cored Sandwich Panel. Metals 2020, 10, 1670. [Google Scholar] [CrossRef]
- Xin, Y.; Yan, H.; Cheng, S.; Li, H. Drop weight impact tests on composite sandwich panel of aluminum foam and epoxy resin. Mech. Adv. Mater. Struct. 2021, 28, 343–356. [Google Scholar] [CrossRef]
- Jones, M.R.; McCarthy, A. Preliminary views on the potential of foamed concrete as a structural material. Mag. Concr. Res. 2005, 57, 21–31. [Google Scholar] [CrossRef]
- Park, S.B.; Yoon, E.S.; Lee, B.I. Effects of processing and materials variations on mechanical properties of lightweight cement composites. Cem. Concr. Res. 1999, 29, 193–200. [Google Scholar] [CrossRef]
- Roslan, A.F.; Awang, H.; Mydin, M.A.O. Effects of various additives on drying shrinkage, compressive and flexural strength of lightweight foamed concrete (LFC). In Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; Volume 626, pp. 594–604. [Google Scholar]
- Deng, Z.; Cheng, H.; Wang, Z.; Zhu, G.; Zhong, H. Compressive behavior of the cellular concrete utilizing millimeter-size spherical saturated SAP under high strain-rate loading. Constr. Build. Mater. 2016, 119, 96–106. [Google Scholar] [CrossRef]
- Serrano, R.; Cobo, A.; Prieto, M.I.; de las NievesGonzález, M. Analysis of fire resistance of concrete with polypropylene or steel fibers. Constr. Build. Mater. 2016, 122, 302–309. [Google Scholar] [CrossRef] [Green Version]
- Eidan, J.; Rasoolan, I.; Rezaeian, A.; Poorveis, D. Residual mechanical properties of polypropylene fiber-reinforced concrete after heating. Constr. Build. Mater. 2019, 198, 195–206. [Google Scholar] [CrossRef]
- Yuan, Z.; Wen, H.; Liu, Y.; Wang, Q. Synergistic effect between piperazine pyrophosphate and melamine polyphosphate in flame retarded glass fiber reinforced polypropylene. Polym. Degrad. Stab. 2021, 184, 109477. [Google Scholar] [CrossRef]
- Smarzewski, P.; Barnat-Hunek, D. Property assessment of hybrid fiber-reinforced ultra-high-performance concrete. Int. J. Civ. Eng. 2018, 16, 593–606. [Google Scholar] [CrossRef] [Green Version]
- Abd, S.M.; Ismail, D.K.; Ghalib, D. Mechanical properties of the light weight foamed concrete with steel fiber of different aspect ratio. In Proceedings of the 2018 1st International Scientific Conference of Engineering Sciences-3rd Scientific Conference of Engineering Science (ISCES), IEEE, Diyala, Iraq, 10–11 January 2018; pp. 305–310. [Google Scholar]
- Wang, S.; Le HT, N.; Poh, L.H.; Quek, S.T.; Zhang, M. Effect of high strain rate on compressive behavior of strain-hardening cement composite in comparison to that of ordinary fiber-reinforced concrete. Constr. Build. Mater. 2017, 136, 31–43. [Google Scholar] [CrossRef]
- Li, Y.; Pimienta, P.; Pinoteau, N.; Tan, K.H. Effect of aggregate size and inclusion of polypropylene and steel fibers on explosive spalling and pore pressure in ultra-high-performance concrete (UHPC) at elevated temperature. Cem. Concr. Compos. 2019, 99, 62–71. [Google Scholar] [CrossRef]
- Hou, L.; Li, J.; Lu, Z.; Niu, Y. Influence of foaming agent on cement and foam concrete. Constr. Build. Mater. 2021, 280, 122399. [Google Scholar] [CrossRef]
- Kearsley, E.P.; Wainwright, P.J. The effect of porosity on the strength of foamed concrete. Cem. Concr. Res. 2002, 32, 233–239. [Google Scholar] [CrossRef]
- Neramitkornburi, A.; Horpibulsuk, S.; Shen, S.L.; Chinkulkijniwat, A.; Arulrajah, A.; Disfani, M.M. Durability against wetting–drying cycles of sustainable Lightweight Cellular Cemented construction material comprising clay and fly ash wastes. Constr. Build. Mater. 2015, 77, 41–49. [Google Scholar] [CrossRef]
- Sayadi, A.A.; Tapia, J.V.; Neitzert, T.R.; Clifton, G.C. Effects of expanded polystyrene (EPS) particles on fire resistance, thermal conductivity and compressive strength of foamed concrete. Constr. Build. Mater. 2016, 112, 716–724. [Google Scholar] [CrossRef]
- Ayse, K.; Filiz KA, R. Properties of concrete containing waste expanded polystyrene and natural resin. Constr. Build. Mater. 2016, 105, 572–578. [Google Scholar]
- GB/T 17671–1999; Method of Testing Cements–Determination of Strength. China Standards Press: Beijing, China, 1999.
- Ahmad, S.H.; Arockiasamy, M.; Balaguru, P.N.; Ball, C.G.; Ball, H.P., Jr.; Batson, G.B.; Daniel, J.I. Measurement of Properties of Fiber Reinforced Concrete; American Concrete Institute: Farmington Hills, MI, USA, 1988. [Google Scholar]
- Song, P.S.; Hwang, S.; Sheu, B.C. Statistical evaluation for impact resistance of steel-fibre-reinforced concretes. Mag. Concr. Res. 2004, 56, 437–442. [Google Scholar] [CrossRef]
- Kilinc, K.; Celik, A.O.; Tuncan, M.; Tuncan, A.; Arslan, G.; Arioz, O. Statistical distributions of in situ microcore concrete strength. Constr. Build. Mater. 2012, 26, 393–403. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H.; Myers, S.L.; Ye, K. Probability and Statistics for Engineers and Scientists; Macmillan: New York, NY, USA, 1993. [Google Scholar]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal distributions across the sciences: Keys and clues: On the charms of statistics, and how mechanical models resembling gambling machines offer a link to a handy way to characterize log-normal distributions, which can provide deeper insight into variability and probability—Normal or log-normal: That is the question. BioScience 2001, 51, 341–352. [Google Scholar]
- Bajaj, V.; Singh, S.P.; Singh, A.P.; Kaushik, S.K. Flexural fatigue analysis of hybrid fibre-reinforced concrete. Mag. Concr. Res. 2012, 64, 361–373. [Google Scholar] [CrossRef]
- Singh, S.P.; Kaushik, S.K. Flexural fatigue life distributions and failure probability of steel fibrous concrete. Mater. J. 2000, 97, 658–667. [Google Scholar]
- The Britannica Guide to Statistics and Probability; Britannica Educational Publishing: Chicago, IL, USA, 2010.
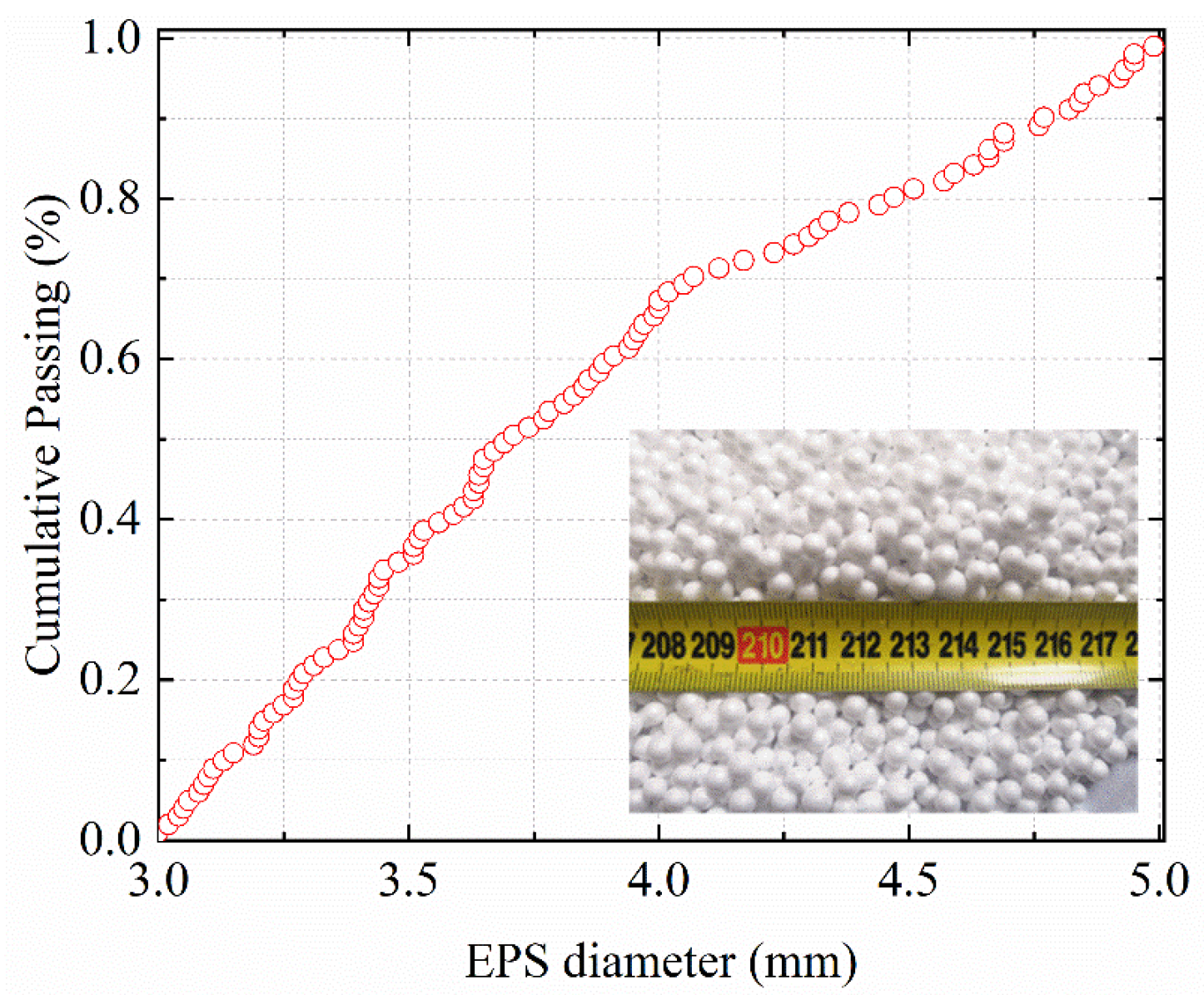










| Oxide | SiO2 | Al2O3 | Fe2O3 | CaO | MgO | Na2O | K2O | SO3 | NaO | Loss |
|---|---|---|---|---|---|---|---|---|---|---|
| PC (%) | 21.60 | 4.13 | 4.72 | 64.44 | 2.06 | 0.11 | 0.56 | 0.74 | - | 1.64 |
| Ms (%) | 94.43 | 0.93 | 0.97 | 0.28 | 0.77 | - | - | - | 1.39 | 1.23 |
| Particle Size/mm | Apparent Density | Bulk Density | Mud Content | Crush Index/% |
|---|---|---|---|---|
| <10 | 2490 | 1370 | 0.57 | 7.9 |
| Type | W/B | W (kg) | Binders (kg) | FA (kg) | CA (kg) | PS (kg) | SF (%) | EPS (kg) | Slump (mm) | ρd (kg/m3) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PC | Ms | ||||||||||
| S0E0 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | - | - | 115 | 1568 |
| S1E10 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | 78.5 | 2.8 | 71 | 1495 |
| S1E20 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | 78.5 | 3.1 | 84 | 1320 |
| S1E30 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | 78.5 | 10.7 | 98 | 1174 |
| S1E40 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | 78.5 | 16.7 | 117 | 1016 |
| S1E50 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | 78.5 | 25 | 124 | 857 |
| S0E10 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | - | 2.8 | 110 | 1413 |
| S0E20 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | - | 3.1 | 116 | 1257 |
| S0E30 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | - | 10.7 | 123 | 1115 |
| S0E40 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | - | 16.7 | 129 | 958 |
| S0E50 | 0.44 | 238.2 | 487.2 | 54.1 | 230 | 536 | 2.8 | - | 25 | 135 | 805 |
| Number | N1/N2 | ΔN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1E10 | S1E20 | S1E30 | S1E40 | S1E50 | S1E10 | S1E20 | S1E30 | S1E40 | S1E50 | |
| 1 | 36/52 | 24/42 | 57/66 | 62/69 | 61/75 | 16 | 18 | 9 | 7 | 14 |
| 2 | 20/22 | 38/57 | 21/28 | 75/83 | 34/43 | 2 | 19 | 7 | 8 | 9 |
| 3 | 49/78 | 13/28 | 39/48 | 10/19 | 33/41 | 29 | 15 | 9 | 9 | 8 |
| 4 | 28/59 | 21/52 | 60/68 | 54/59 | 80/91 | 31 | 31 | 8 | 5 | 11 |
| 5 | 101/109 | 59/73 | 23/34 | 41/48 | 37/42 | 8 | 14 | 11 | 7 | 5 |
| 6 | 34/40 | 97/104 | 41/50 | 89/98 | 51/60 | 6 | 7 | 9 | 9 | 9 |
| 7 | 69/79 | 57/83 | 33/45 | 66/69 | 62/73 | 10 | 26 | 12 | 3 | 11 |
| 8 | 60/84 | 44/61 | 25/33 | 50/61 | 47/55 | 24 | 17 | 8 | 11 | 8 |
| 9 | 39/54 | 47/59 | 69/77 | 58/64 | 31/43 | 15 | 12 | 8 | 6 | 12 |
| 10 | 69/84 | 63/79 | 27/33 | 43/55 | 36/44 | 15 | 16 | 6 | 12 | 8 |
| 11 | 82/97 | 57/66 | 87/96 | 17/24 | 34/42 | 15 | 9 | 20 | 7 | 8 |
| 12 | 57/69 | 51/59 | 32/41 | 43/52 | 34/41 | 12 | 8 | 9 | 9 | 7 |
| Number | S0E10 | S0E20 | S0E30 | S0E40 | S0E50 | S0E10 | S0E20 | S0E30 | S0E40 | S0E50 |
| 1 | 21/22 | 16/17 | 3 | 3 | 9/12 | 1 | 1 | 0 | 0 | 3 |
| 2 | 2 | 3 | 6 | 5 | 12/15 | 0 | 0 | 0 | 0 | 3 |
| 3 | 3 | 4 | 6 | 5 | 7 | 0 | 0 | 0 | 0 | 0 |
| 4 | 2 | 6 | 7/8 | 6 | 7 | 0 | 0 | 1 | 0 | 0 |
| 5 | 4 | 7/8 | 7 | 15/17 | 9 | 0 | 1 | 0 | 2 | 0 |
| 6 | 6 | 7/8 | 17/18 | 7 | 13/15 | 0 | 1 | 1 | 0 | 2 |
| 7 | 6 | 7/9 | 9 | 8 | 11/12 | 0 | 2 | 0 | 0 | 1 |
| 8 | 11/12 | 10/11 | 11/12 | 8 | 8/9 | 1 | 1 | 1 | 0 | 1 |
| 9 | 3 | 9 | 13/15 | 10/12 | 8 | 0 | 0 | 2 | 2 | 0 |
| 10 | 4 | 6/7 | 7 | 7 | 7 | 0 | 1 | 0 | 0 | 0 |
| 11 | 2 | 4 | 2 | 5 | 4 | 0 | 0 | 0 | 0 | 0 |
| 12 | 5 | 6 | 24/25 | 9/10 | 6 | 0 | 0 | 1 | 1 | 0 |
| Specimen Type | Rank | a | b | R2 |
|---|---|---|---|---|
| S1E10 | 12 | 0.9619 | 17.297 | 0.8717 |
| S1E20 | 12 | 0.8368 | 23.767 | 0.9056 |
| S1E30 | 12 | 0.9993 | 8.7812 | 0.9941 |
| S1E40 | 12 | 0.9796 | 8.7839 | 0.9876 |
| S1E50 | 12 | 1.085 | 5.3405 | 0.9854 |
| S0E10 | 2 | / | / | / |
| S0E20 | 6 | 0.5589 | 4.3181 | 0.4356 * |
| S0E30 | 5 | 0.9916 | 1.3206 | 0.9952 |
| S0E40 | 3 | / | / | / |
| S0E50 | 5 | 1.1163 | 0.7674 | 0.8505 |
| Statistical Parameters | N1/N2 | ΔN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1E10 | S1E20 | S1E30 | S1E40 | S1E5`0 | S1E10 | S1E20 | S1E30 | S1E40 | S1E50 | |
| Rank | 12/12 | 12/12 | 12/12 | 12/12 | 12/12 | 12 | 12 | 12 | 12 | 12 |
| 54/69 | 48/64 | 43/53 | 51/58 | 45/54 | 15 | 16 | 10 | 7 | 9 | |
| σ | 24/25 | 22/20 | 21/21 | 22/22 | 16/17 | 9 | 7 | 4 | 3 | 2 |
| COV% | 44/36 | 45/31 | 49/39 | 43/38 | 35/31 | 60 | 44 | 40 | 43 | 22 |
| S0E10 | S0E20 | S0E30 | S0E40 | S0E50 | S0E10 | S0E20 | S0E30 | S0E40 | S0E50 | |
| Rank | 12/2 | 12/6 | 12/5 | 12/3 | 12/5 | 2 | 6 | 5 | 3 | 5 |
| 6/17 | 8/10 | 9/20 | 7/13 | 8/13 | 3 | 3 | 2 | 4 | 3 | |
| σ | 5/7 | 4/4 | 6/6 | 3/4 | 3/3 | 0.4 ┌ | 0.7 ┌ | 0.7 ┌ | 0.8 ┌ | 1.2 ┌ |
| COV% | 83/41 | 50/40 | 66/30 | 43/31 | 38/23 | 13 | 23 | 35 | 20 | 40 |
| Blows | Specimen Type | Rank | α1 | β1 | R2 |
|---|---|---|---|---|---|
| N1 | S1E10 | 12 | 1.7699 | 6.8763 | 0.981 |
| S1E20 | 12 | 1.4526 | 5.4318 | 0.9044 | |
| S1E30 | 12 | 1.8015 | 6.5863 | 0.9672 | |
| S1E40 | 12 | 1.2228 | 4.6319 | 0.8114 | |
| S1E50 | 12 | 2.536 | 9.5326 | 0.8723 | |
| N2 | S1E10 | 12 | 1.8087 | 7.5191 | 0.8802 |
| S1E20 | 12 | 2.4043 | 9.8664 | 0.9202 | |
| S1E30 | 12 | 2.1558 | 8.3488 | 0.9657 | |
| S1E40 | 12 | 1.6411 | 6.5333 | 0.8409 | |
| S1E50 | 12 | 2.711 | 10.715 | 0.8253 | |
| ΔN | S1E10 | 12 | 1.0574 | 2.6636 | 0.8838 |
| S1E20 | 12 | 1.8639 | 4.9994 | 0.9736 | |
| S1E30 | 12 | 2.5355 | 5.6296 | 0.8299 | |
| S1E40 | 12 | 2.1484 | 4.2773 | 0.8922 | |
| S1E50 | 12 | 2.9983 | 6.5431 | 0.9297 |
| Blows | Specimen Type | Rank | α1 | β1 | R2 |
|---|---|---|---|---|---|
| N1 | S0E10 | 12 | 1.1292 | 1.6642 | 0.9114 |
| S0E20 | 12 | 1.631 | 3.1423 | 0.9615 | |
| S0E30 | 12 | 1.2035 | 2.4456 | 0.9503 | |
| S0E40 | 12 | 2.0013 | 3.832 | 0.9480 | |
| S0E50 | 12 | 2.5494 | 5.3148 | 0.9392 | |
| N2 | S0E10 | 2 | / | / | / |
| S0E20 | 6 | 1.3246 | 3.6669 | 0.7554 * | |
| S0E30 | 5 | 1.0304 | 3.5533 | 0.9871 | |
| S0E40 | 3 | / | / | / | |
| S0E50 | 5 | 2.0239 | 5.8892 | 0.9199 | |
| ΔN | S0E10 | 2 | / | / | / |
| S0E20 | 6 | 1.2931 | 0.5297 | 0.5594 * | |
| S0E30 | 5 | 1.1369 | 0.638 | 0.6292 * | |
| S0E40 | 3 | / | / | / | |
| S0E50 | 5 | 0.734 | 0.3714 | 0.8348 * |
| Blows | Specimen Type | Rank | α2 | β2 | R2 |
|---|---|---|---|---|---|
| N1 | S1E10 | 12 | 2.1463 | 8.8421 | 0.9895 |
| S1E20 | 12 | 1.8045 | 7.2513 | 0.9538 | |
| S1E30 | 12 | 2.1105 | 8.2194 | 0.9071 | |
| S1E40 | 12 | 1.5533 | 6.3873 | 0.8947 | |
| S1E50 | 12 | 2.8833 | 11.341 | 0.7705 | |
| N2 | S1E10 | 12 | 2.2727 | 9.9512 | 0.9497 |
| S1E20 | 12 | 2.9517 | 12.638 | 0.9512 | |
| S1E30 | 12 | 2.5281 | 10.294 | 0.9075 | |
| S1E40 | 12 | 2.0628 | 8.7153 | 0.9078 | |
| S1E50 | 12 | 3.0452 | 12.54 | 0.7116 | |
| ΔN | S1E10 | 12 | 1.3215 | 3.8322 | 0.9432 |
| S1E20 | 12 | 2.2399 | 6.5114 | 0.9609 | |
| S1E30 | 12 | 2.9144 | 6.9744 | 0.7493 | |
| S1E40 | 12 | 2.677 | 5.8332 | 0.9467 | |
| S1E50 | 12 | 3.6184 | 8.3999 | 0.9254 |
| Blows | Specimen Type | Rank | α2 | β2 | R2 |
|---|---|---|---|---|---|
| N1 | S0E10 | 12 | 1.297 | 2.4149 | 0.8217 |
| S0E20 | 12 | 1.9356 | 4.2325 | 0.9254 | |
| S0E30 | 12 | 1.4566 | 3.4633 | 0.9513 | |
| S0E40 | 12 | 2.4008 | 5.1005 | 0.9323 | |
| S0E50 | 12 | 3.1015 | 6.9694 | 0.9499 | |
| N2 | S0E10 | 2 | / | / | / |
| S0E20 | 6 | 1.9619 | 5.7343 | 0.6989 * | |
| S0E30 | 5 | 1.6363 | 5.8544 | 0.9769 | |
| S0E40 | 3 | / | / | / | |
| S0E50 | 5 | 3.2481 | 9.6494 | 0.9298 | |
| ΔN | S0E10 | 2 | / | / | / |
| S0E20 | 6 | 2.1052 | 1.066 | 0.6252 * | |
| S0E30 | 5 | 1.8973 | 1.2126 | 0.6851 * | |
| S0E40 | 3 | / | / | / | |
| S0E50 | 5 | 1.1474 | 0.8118 | 0.8007 * |
| Blows | Failure Probability | Log-Normal Distribution | Weibull Distribution | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1E10 | S1E20 | S1E30 | S1E40 | S1E50 | S1E10 | S1E20 | S1E30 | S1E40 | S1E50 | ||
| N1 | 0.05 | 19 | 14 | 16 | 12 | 22 | 9 | 5 | 7 | 4 | 13 |
| 0.10 | 24 | 17 | 19 | 15 | 26 | 14 | 9 | 11 | 7 | 18 | |
| 0.15 | 27 | 20 | 22 | 19 | 29 | 17 | 12 | 14 | 10 | 21 | |
| 0.20 | 30 | 24 | 24 | 22 | 31 | 21 | 15 | 17 | 13 | 24 | |
| 0.25 | 33 | 26 | 27 | 25 | 33 | 24 | 18 | 19 | 16 | 26 | |
| 0.30 | 36 | 29 | 29 | 29 | 35 | 27 | 21 | 22 | 19 | 29 | |
| N2 | 0.05 | 26 | 31 | 22 | 20 | 28 | 12 | 17 | 12 | 9 | 17 |
| 0.10 | 31 | 36 | 27 | 25 | 32 | 18 | 24 | 17 | 14 | 23 | |
| 0.15 | 36 | 39 | 30 | 28 | 36 | 23 | 28 | 21 | 18 | 27 | |
| 0.20 | 40 | 43 | 33 | 32 | 38 | 28 | 32 | 24 | 21 | 30 | |
| 0.25 | 44 | 46 | 35 | 36 | 41 | 32 | 36 | 27 | 25 | 33 | |
| 0.30 | 48 | 49 | 38 | 39 | 43 | 36 | 39 | 30 | 29 | 36 | |
| S0E10 | S0E20 | S0E30 | S0E40 | S0E50 | S0E10 | S0E20 | S0E30 | S0E40 | S0E50 | ||
| N1 | 0.05 | 1.8 | 3.8 | 3.5 | 4.2 | 5.6 | 0.7 | 1.9 | 1.4 | 2.4 | 3.6 |
| 0.10 | 2.4 | 4.6 | 4.5 | 4.9 | 6.3 | 1.1 | 2.8 | 2.3 | 3.3 | 4.6 | |
| 0.15 | 2.9 | 5.2 | 5.3 | 5.4 | 6.8 | 1.6 | 3.5 | 3.1 | 3.9 | 5.3 | |
| 0.20 | 3.4 | 5.8 | 6.0 | 5.9 | 7.2 | 2.0 | 4.1 | 3.8 | 4.5 | 5.8 | |
| 0.25 | 3.8 | 6.3 | 6.8 | 6.3 | 7.6 | 2.5 | 4.7 | 4.6 | 5.0 | 6.3 | |
| 0.30 | 4.3 | 6.8 | 7.5 | 6.7 | 8 | 2.9 | 5.2 | 5.3 | 5.4 | 6.8 | |
| Concrete Type | P | Log-Normal Distribution | Weibull Distribution | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| m | n | l | R2 | m | n | l | R2 | |||
| SFEPSC | 0.05 | 4.9524 | 2.9085 | 1.5316 | 0.7469 | 7.8211 | 4.5077 | 1.3480 | 0.6315 | |
| 0.10 | 4.1660 | 2.4702 | 1.5819 | 0.8143 | 6.2630 | 3.6392 | 1.4477 | 0.6781 | ||
| 0.15 | 3.6355 | 2.1744 | 1.6158 | 0.8785 | 5.3249 | 3.1162 | 1.5077 | 0.7231 | ||
| 0.20 | 3.2138 | 1.9393 | 1.6428 | 0.8943 | 4.6387 | 2.7337 | 1.5516 | 0.7706 | ||
| 0.25 | 2.8520 | 1.7377 | 1.6659 | 0.9259 | 4.0889 | 2.4271 | 1.5868 | 0.8226 | ||
| 0.30 | 2.5272 | 1.5566 | 1.6867 | 0.9789 | 3.6236 | 2.1678 | 1.6116 | 0.9001 | ||
| EPSC | 0.05 | −2.0230 | −2.2338 | 0.1027 | 0.8428 | −1.5322 | −2.5134 | −0.3475 | 0.8159 | |
| 0.10 | −2.1575 | −2.1571 | 0.2261 | 0.8940 | −1.7988 | −2.3615 | −0.1030 | 0.8801 | ||
| 0.15 | −2.2482 | −2.1054 | 0.3093 | 0.9179 | −1.9592 | −2.2701 | 0.0442 | 0.9194 | ||
| 0.20 | −2.3204 | −2.0643 | 0.3755 | 0.9436 | −2.0766 | −2.2032 | 0.1519 | 0.9453 | ||
| 0.25 | −2.3822 | −2.0290 | 0.4323 | 0.9348 | −2.1707 | −2.1496 | 0.2382 | 0.9482 | ||
| 0.30 | −2.4378 | −1.9974 | 0.4833 | 0.9208 | −2.2503 | −2.1042 | 0.3112 | 0.9479 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, W.; Zhang, S. Research and Statistical Analysis on Impact Resistance of Steel Fiber Expanded Polystyrene Concrete and Expanded Polystyrene Concrete. Materials 2022, 15, 4216. https://doi.org/10.3390/ma15124216
Huo W, Zhang S. Research and Statistical Analysis on Impact Resistance of Steel Fiber Expanded Polystyrene Concrete and Expanded Polystyrene Concrete. Materials. 2022; 15(12):4216. https://doi.org/10.3390/ma15124216
Chicago/Turabian StyleHuo, Wenlong, and Sherong Zhang. 2022. "Research and Statistical Analysis on Impact Resistance of Steel Fiber Expanded Polystyrene Concrete and Expanded Polystyrene Concrete" Materials 15, no. 12: 4216. https://doi.org/10.3390/ma15124216
APA StyleHuo, W., & Zhang, S. (2022). Research and Statistical Analysis on Impact Resistance of Steel Fiber Expanded Polystyrene Concrete and Expanded Polystyrene Concrete. Materials, 15(12), 4216. https://doi.org/10.3390/ma15124216





