The Application of a Hybrid Method for the Identification of Elastic–Plastic Material Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods of Identifying Material Parameters
- P-A: In situ hardness testers with the appropriate research software used for determining indentation curves. These curves are transferred to the computer, and parameter identification is performed based on this.
- P-B: The P-A procedure is supplemented with a laser profiler, which provides data on the imprinted shape. The imprint profile and indentation profile are both applied in the identification process.
- P-C: The third procedure is based on reading the coordinates of the imprint profile obtained by using a manual hardness tester. These data are input for inverse analysis.
2.2. The Application of NN to Analyze Regression and Identification Problems
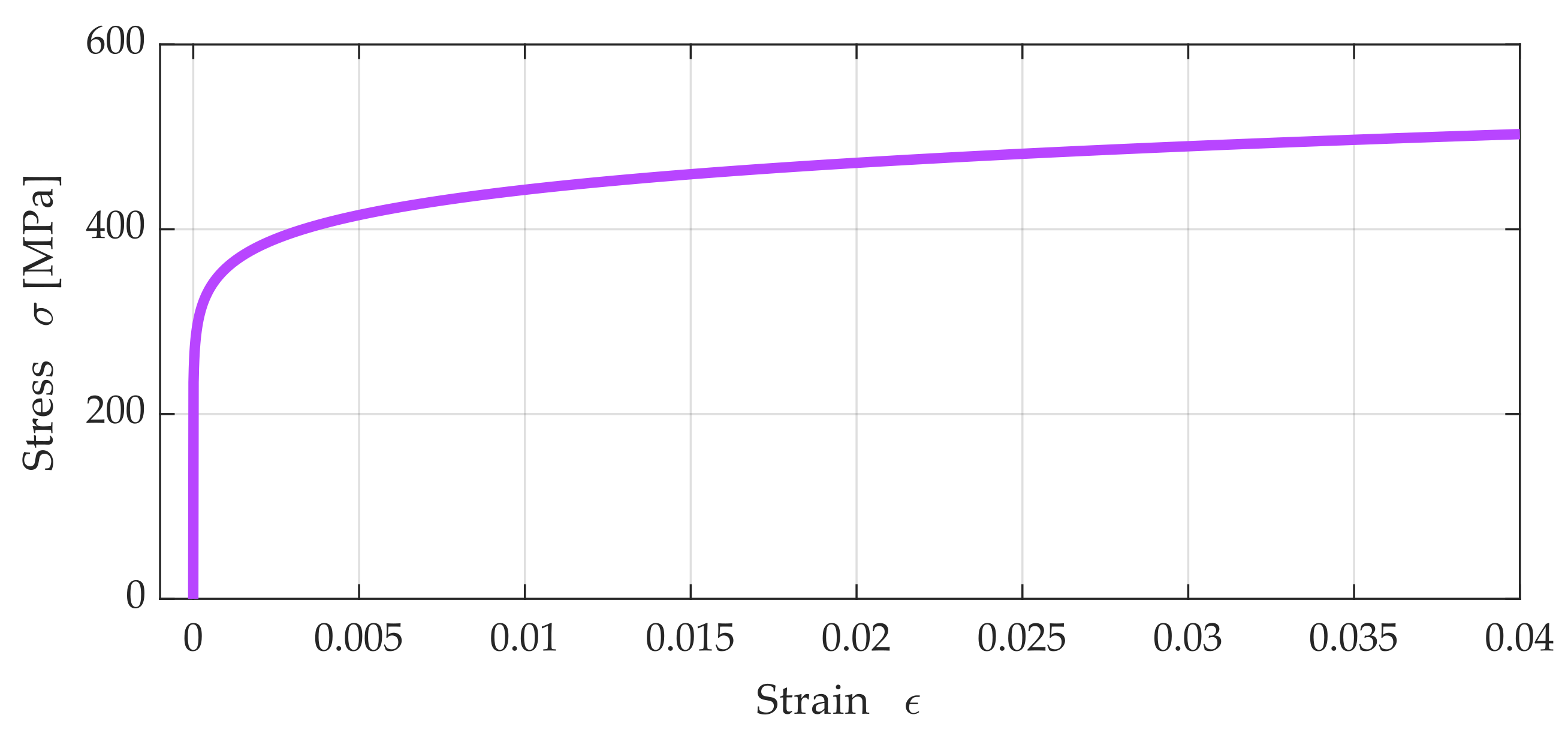
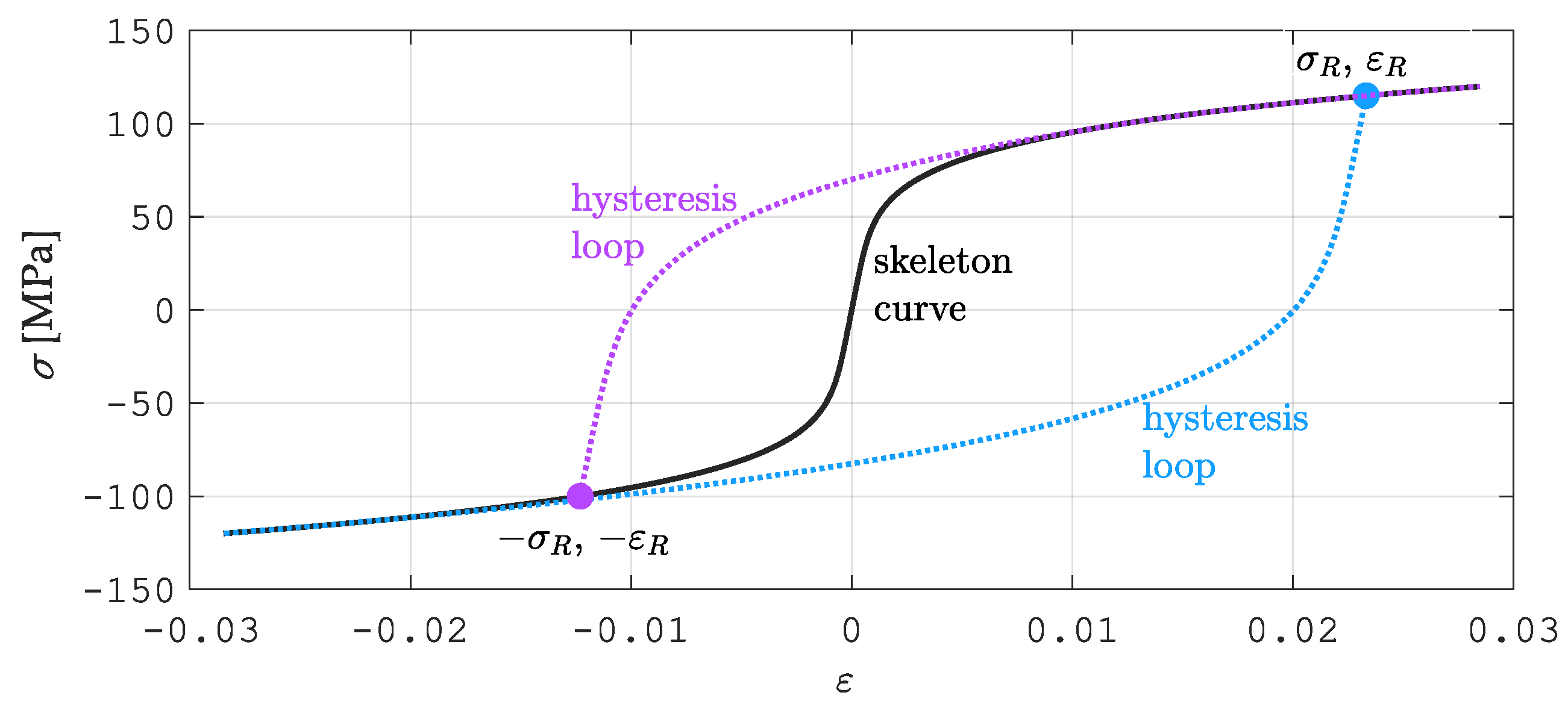
2.3. Ramberg–Osgood Material Model
- If the analysis is conducted within the elastic range (for ), then the stress corresponding to the permanent strain 0.1% can be assumed as a second reference point.
- If the analysis is conducted within the plastic range (for ), then the tensile strength corresponding to the highest point of the curve can be assumed as a second reference point.
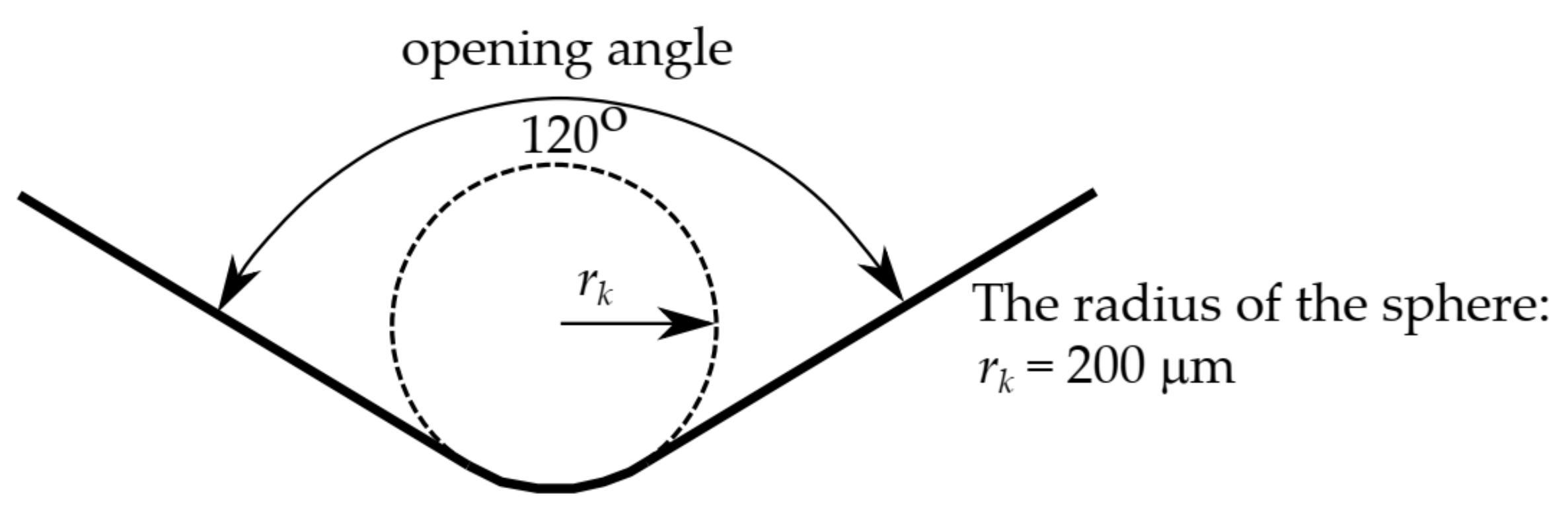
2.4. Samples Generation by FEM
- Young’s Modulus 170 GPa ≤ E ≤ 220 GPa 9 parts;
- Yield stress 330 MPa ≤ ≤ 460 MPa 13 parts;
- Exponent 0 ≤ n ≤ 0.2 40 parts.
3. Case Study
- Mean squared error (MSE):where
- —pairs of data;
- —reference data;
- —computed values.
- Average absolute relative error (avr epi):
- Linear regression coefficient (ri):where
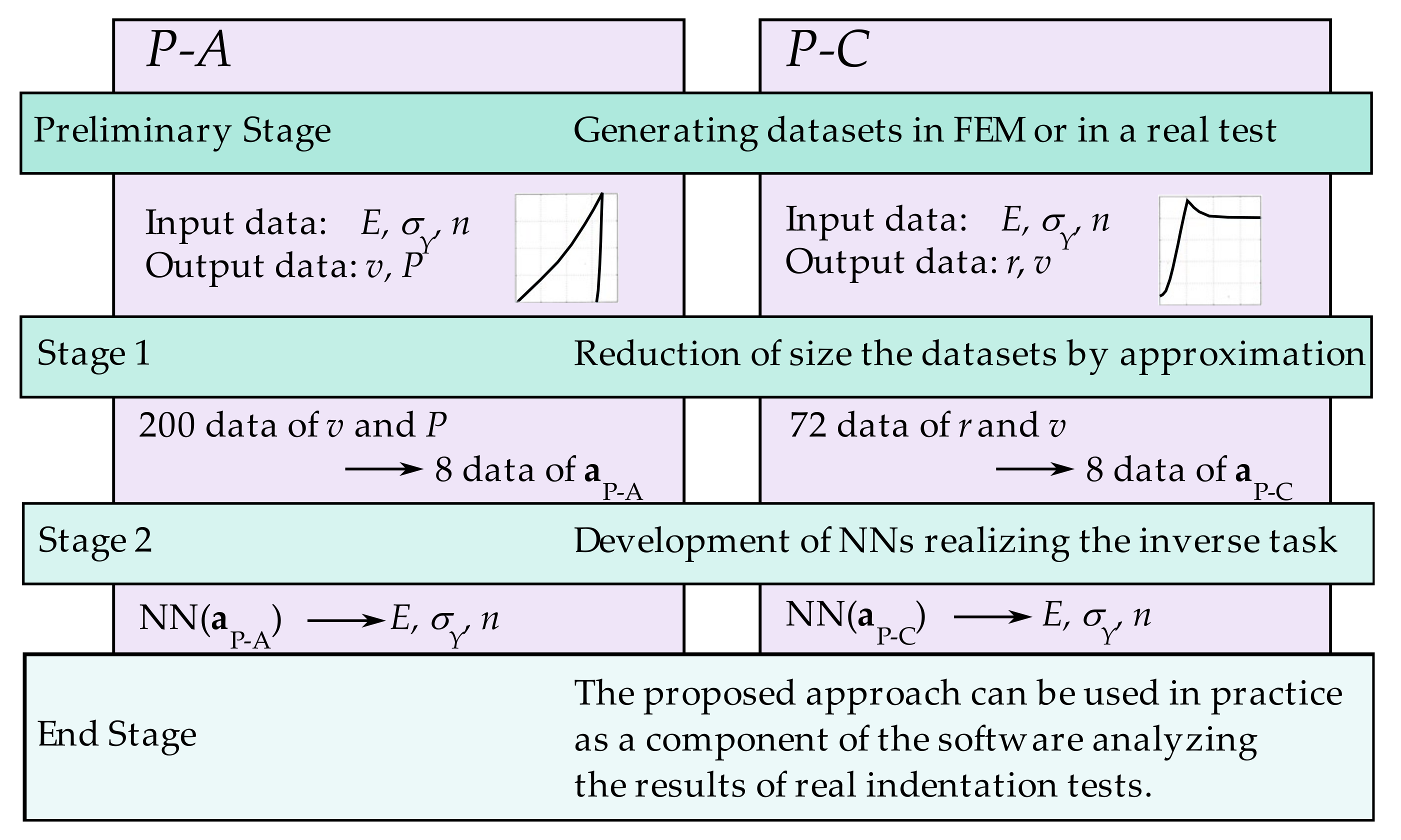
3.1. Stage 1 for P-A Procedure
3.2. Stage 1 for P-C Procedure
3.3. Stage 2 for Procedures: P-A and P-C
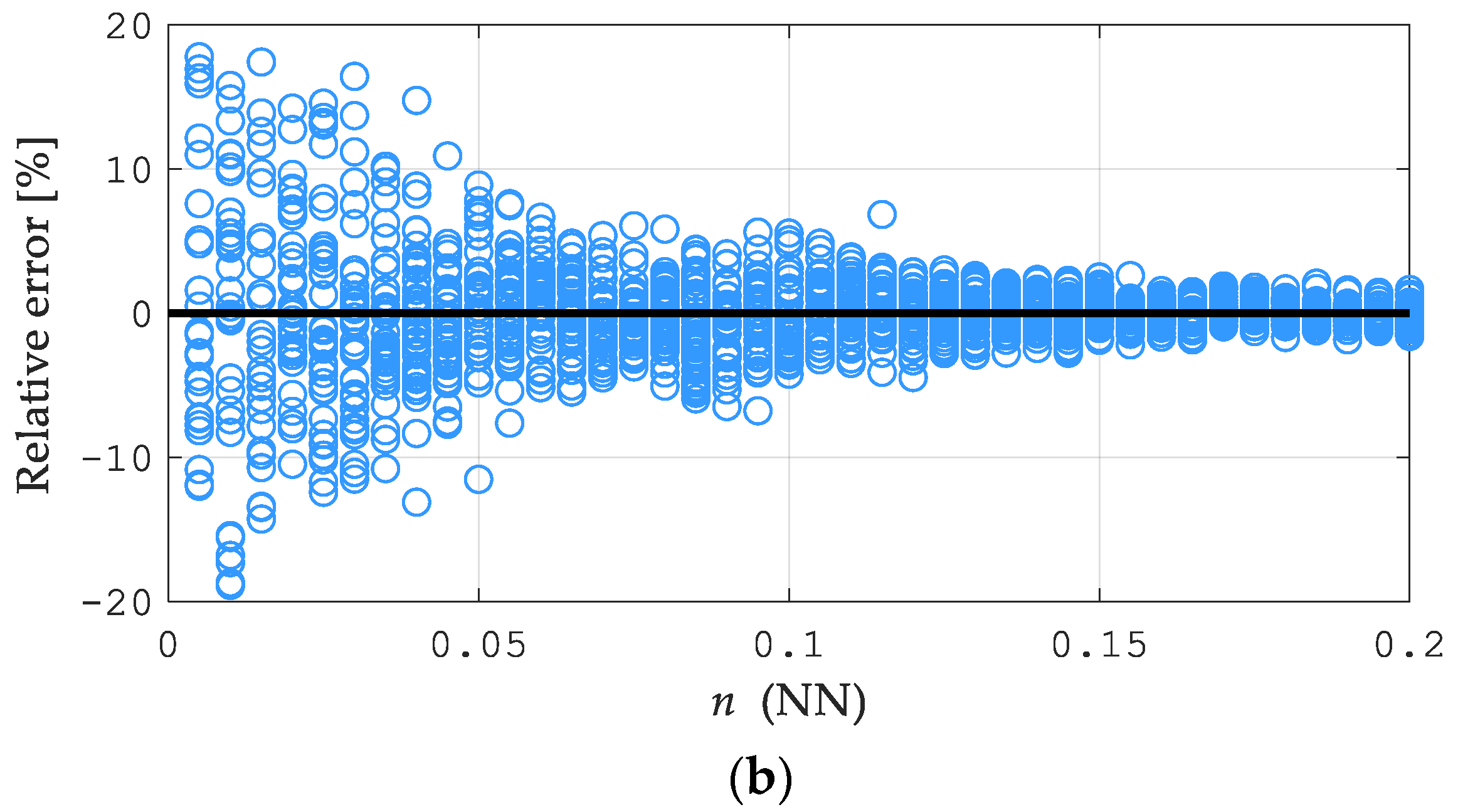
4. Results and Discussion
5. Conclusions
- A neural network with back-propagation (PBNN) can be effectively used for identifying material parameters described by Ramberg–Osgood’s law, i.e., Young’s modulus yield point and the material hardening exponent ;
- A correctly performed approximation process is an effective way to reduce the multidimensionality of the input space of a neural network and allows for achieving a satisfactory accuracy in the estimation of material parameters;
- In the suggested approach of the two-stage hybrid identification of elastic–plastic parameters, the accuracy and parameter estimation errors of the P-A and P-C procedures are similar.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | artificial neural network |
| CPU | central processor unit |
| FEA | finite element analysis |
| FEM | finite element method |
| FLNN | feedforward layered neural network |
| HC | hard computing |
| KLT | Karhunen–Loève transform |
| MLP | multilayer perceptron |
| MSE | mean square error |
| MSEL | mean square errors of learning |
| MSET | mean square errors of testing |
| NN | neural network |
| PBNN | neural network with back-propagation |
| PCA | principal component analysis |
| POD | proper orthogonal decomposition |
| R–O | Ramberg–Osgood |
| SC | soft computing |
| initial Young’s modulus | |
| activation function | |
| output function | |
| computed values set | |
| reference data set | |
| known strain | |
| permanent strain | |
| strain points during unloading | |
| yield offset | |
| stress points during unloading | |
| yield stress | |
| plastic strain for the adopted elastic limit | |
| determined stress | |
| vector of approximation base functions | |
| vector of coordinates of approximating functions | |
| NN parameter vector (weights and biases) | |
| NN input vector | |
| NN output vector | |
| parameter characterizing material strengthening degree | |
| radial indenter coordinates | |
| vertical displacement of indenter | |
| Poisson’s ratio |
References
- Miller, B. Neurocomputing in Selected Problems of Structural Identification and Damage Detection; Oficyna Wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 2013. [Google Scholar]
- Padgurskas, J.; Rukuiža, R.; Žunda, A. Evaluation of Tribological and Mechanical Properties of Carbon Steel with Fluoroligomeric Film at Piezoelectric Actuator Contact. Coatings 2022, 12, 463. [Google Scholar] [CrossRef]
- Yin, H.; Bai, X.; Fu, H. Prediction of Work Hardening in Bearing Steels Undergoing Rolling Contact Loading with a Dislocation-Based Model. Metals 2022, 12, 555. [Google Scholar] [CrossRef]
- Xue, H.; He, J.; Jia, W.; Zhang, J.; Wang, S.; Zhang, S.; Yang, H.; Wang, Z. An approach for obtaining mechanical property of austenitic stainless steel by using continuous indentation test analysis. Structures 2020, 28, 2752–2759. [Google Scholar] [CrossRef]
- Bolzon, G.; Zvirko, O. An indentation based investigation on the characteristics of artificially aged pipeline steels. Procedia Struct. Integr. 2017, 3, 172–175. [Google Scholar] [CrossRef]
- Prato, A.; Longana, M.L.; Hussain, A.; Wisnom, M.R. Post-Impact Behaviour of Pseudo-Ductile Thin-Ply Angle-Ply Hybrid Composites. Materials 2019, 12, 579. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Xie, W.-Q.; Liu, Q.-S.; Yang, X.-M.; Tang, S.-H.; Wu, J. Development and application of an in-situ indentation testing system for the prediction of tunnel boring machine performance. Int. J. Rock Mech. Min. Sci. 2021, 147, 104899. [Google Scholar] [CrossRef]
- Xia, J.; Won, C.; Kim, H.; Lee, W.; Yoon, J. Artificial Neural Networks for Predicting Plastic Anisotropy of Sheet Metals Based on Indentation Test. Materials 2022, 15, 1714. [Google Scholar] [CrossRef]
- Jeong, K.; Lee, H.; Kwon, O.M.; Jung, J.; Kwon, D.; Han, H.N. Prediction of uniaxial tensile flow using finite element-based indentation and optimized artificial neural networks. Mater. Des. 2020, 196, 109104. [Google Scholar] [CrossRef]
- Katarzyński, S.; Kocańda, S.; Zakrzewski, M. Examining Mechanical Properties of Metals; WNT: Warsaw, Poland, 1969. (In Polish) [Google Scholar]
- Low, S. Rockwell Hardness Measurement of Metallic Materials; U.S. Government Printing Office: Washington, DC, USA, 2001. [Google Scholar]
- Herrman, K. Hardness Testing: Principles and Applications; ASM International: Materials Park, OH, USA, 2011; ISBN 978-1-61503-832-9. [Google Scholar]
- Noor, A.K. Computational structures technology: Leap frogging into the twenty-first century. Comput. Struct. 1999, 73, 1–31. [Google Scholar] [CrossRef]
- Noor, A.; Andersen, C. Hybrid analytical technique for the nonlinear analysis of curved beams. Comput. Struct. 1992, 43, 823–830. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Logic, Neural Networks and Soft Computing. Commun. ACM 1994, 37, 77–84. [Google Scholar] [CrossRef]
- Zadeh, L. Soft computing and fuzzy logic. IEEE Softw. 1994, 11, 48–56. [Google Scholar] [CrossRef]
- Pabisek, E. Hybrid Systems Integrating FEM and ANN for the Analysis of Selected Problems of Structural and Materials Mechanics; Monograph, 369, Series Civil Engineering; Cracow University of Technology: Kraków, Poland, 2008. (In Polish) [Google Scholar]
- Waszczyszyn, Z.; Pabisek, E.; Kaliszuk, J. Hybrid Computational Systems in Structural Mechanics. Tech. J. Crac. Univ. Technol. 2010, 20, 135–146. [Google Scholar]
- Rauch, Ł.; Kuziak, R.; Gierulski, B.; Pietrzyk, M. Hybrid Support Systems for Designing Metal Processing Technology; Iron Metallurgy Institute: Gliwice, Poland, 2010; Volume 1, pp. 142–148. (In Polish) [Google Scholar]
- Muliana, A.; Haj-Ali, R.M.; Steward, R.; Saxena, A. Artificial neural network and finite element modeling of nanoindentation tests. Met. Mater. Trans. A 2002, 33, 1939–1947. [Google Scholar] [CrossRef]
- Krasiński, M.; Lefik, M. Two Scales, Hybrid Model for Soils, Involving Artificial Neural Network and Finite Element Procedure. Stud. Geotech. Mech. 2014, 36, 29–36. [Google Scholar] [CrossRef]
- Javadi, A.A.; Tan, T.P.; Zhang, M. Neural Network for Constitutive Modelling in Finite Element Analysis. Comput. Assist. Mech. Eng. Sci. 2003, 10, 523–529. [Google Scholar]
- Widłaszewski, J.; Nowak, Z.; Kurp, P. Effect of Pre-Stress on Laser-Induced Thermoplastic Deformation of Inconel 718 Beams. Materials 2021, 14, 1847. [Google Scholar] [CrossRef]
- Anysz, H.; Zbiciak, A.; Ibadov, N. The Influence of Input Data Standardization Method on Prediction Accuracy of Artificial Neural Networks. Procedia Eng. 2016, 153, 66–70. [Google Scholar] [CrossRef]
- Anysz, H.; Narloch, P. Designing the Composition of Cement Stabilized Rammed Earth Using Artificial Neural Networks. Materials 2019, 12, 1396. [Google Scholar] [CrossRef]
- Beskopylny, A.; Lyapin, A.; Anysz, H.; Meskhi, B.; Veremeenko, A.; Mozgovoy, A. Artificial Neural Networks in Classification of Steel Grades Based on Non-Destructive Tests. Materials 2020, 13, 2445. [Google Scholar] [CrossRef]
- Bolzon, G.; Buljak, V.; Maier, G.; Miller, B. Assessment of elastic–plastic material parameters comparatively by three procedures based on indentation test and inverse analysis. Inverse Probl. Sci. Eng. 2011, 19, 815–837. [Google Scholar] [CrossRef]
- Phadikar, J.; Bogetti, T.; Karlsson, A. On the uniqueness and sensitivity of indentation testing of isotropic materials. Int. J. Solids Struct. 2013, 50, 3242–3253. [Google Scholar] [CrossRef]
- Alkorta, J.; Martinez-Esnaola, J.M.; Sevillano Gil, J. Absence of one-to-one correspondence between elastoplastic properties and sharp-indentation load–penetration data. J. Mater. Res. 2005, 20, 432–437. [Google Scholar] [CrossRef]
- PN-EN ISO 6508-1:2007; Metallic Materials—Rockwell Hardness Test—Part 1: Test Method (Scales A, B, C, D, E, F, G, H, K, N, T). Polish Committee for Standardization: Warsaw, Poland, 2007.
- PN-EN ISO 6508-2:2007; Metallic Materials—Vickers Hardness Test—Part 2: Verification and Calibration of Testing Machines (Scales A, B, C, D, E, F, G, H, K, N, T). Polish Committee for Standardization: Warsaw, Poland, 2007.
- PN-EN ISO 6508-3:2007; Metallic Materials—Rockwell Hardness Test—Part 3: Calibration of Reference Blocks (Scales A, B, C, D, E, F, G, H, K, N, T). Polish Committee for Standardization: Warsaw, Poland, 2007.
- Garret, J. Where and Why Artificial Neural Networks Are Applicable in Civil Engineering. J. Eng. ASCE 1994, 8, 129–130. [Google Scholar]
- Waszczyszyn, Z. Artificial Neural Networks in Civil Engineering: Another Five Years of Research in Poland. Comput. Assist. Methods Eng. Sci. 2017, 18, 131–146. [Google Scholar]
- Adeli, H. Neural Networks in Civil Engineering: 1989–2000. Comput. Aided Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Dudzik, A.; Potrzeszcz-Sut, B. Hybrid Approach to the First Order Reliability Method in the Reliability Analysis of a Spatial Structure. Appl. Sci. 2021, 11, 648. [Google Scholar] [CrossRef]
- Dudzik, A.; Potrzeszcz-Sut, B. The structural reliability analysis using explicit neural state functions. MATEC Web Conf. 2019, 262, 10002. [Google Scholar] [CrossRef][Green Version]
- Stepien, A.; Potrzeszcz-Sut, B.; Prentice, D.P.; Oey, T.J.; Balonis, M. The Role of Glass Compounds in Autoclaved Bricks. Buildings 2020, 10, 41. [Google Scholar] [CrossRef]
- Paez, T.L. Neural Networks in Mechanical System Simulation, Identification, and Assessment. Shock. Vib. 1993, 1, 243060. [Google Scholar] [CrossRef][Green Version]
- PN-EN 1993-1-4: 2007; Design of Steel Structures—Part 1–4: General Rules—Supplementary Rules for Stainless Steel Structures. Polish Committee for Standardization: Warsaw, Poland, 2007.
- PN-EN 1999-1-1:2011; Design of Aluminum Structures. Part 1-1: General Rules. Polish Committee for Standardization: Warsaw, Poland, 2011.
- Ramberg, W.; Osgood, W. Description of Stress-Strain Curves by Three Parameters; Technical Note No 902; National Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- AS/NZS 4673:2001; Cold Formed Stainless Steel Structures. Standards Australia: Sydney, NSW, Australia, 2001.
- SEI/ASCE 8-02; Specification for the Design of Cold-Formed Stainless Steel Structural Members. American Society of Civil Engineers: Reston, VA, USA, 2002.
- Ma, D.; Ong, C.W.; Zhang, T. An Instrumented Indentation Method for Young’s Modulus Measurement with Accuracy Estimation. Exp. Mech. 2009, 49, 719–729. [Google Scholar] [CrossRef]
- Hibbitt, Karlsson & Sorensen, Inc. ABAQUS/Standard, Theory and User’s Manuals; Hibbitt, Karlsson & Sorensen, Inc.: Pawtucket, RI, USA, 2005. [Google Scholar]
- Ghaboussi, J.; Pecknold, D.; Zhang, M.; Haj-Ali, R. Autoprogressive Training of Neural Network Constitutive Models. Int. J. Numer. Methods Eng. 1998, 42, 105–126. [Google Scholar] [CrossRef]
- Potrzeszcz-Sut, B.; Pabisek, E. ANN Constitutive Material Model in the Shakedown Analysis of an Aluminum Structure. Comput. Assist. Methods Eng. Sci. 2014, 21, 49–58. [Google Scholar]
- Akazawa, T.; Nakashima, M.; Sakaguchi, O. Simple Model for Simulating Hysteretic Behavior Involving Significant Strain Hardening. In Proceedings of the Eleventh World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Karamizadeh, S.; Abdullah, S.M.; Manaf, A.A.; Zamani, M.; Hooman, A. An Overview of Principal Component Analysis. J. Signal Inf. Process. 2013, 4, 173–175. [Google Scholar] [CrossRef]
- Bolzon, G.; Maier, G.; Panico, M. Material model calibration by indentation, imprint mapping and inverse analysis. Int. J. Solids Struct. 2004, 41, 2957–2975. [Google Scholar] [CrossRef]
- Hudson Beale, M.; Hagan, M.; Demuth, H. Neural Network Toolbox for Use with MATLAB. User’s Guide; The MathWorks Inc.: Natick, MA, USA, 2011. [Google Scholar]
- MathWorks. MATLAB® Primer; The MathWorks. Inc.: Natick, MA, USA, 1984. [Google Scholar]
- Galushkin, A.I. Neural Networks Theory; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]

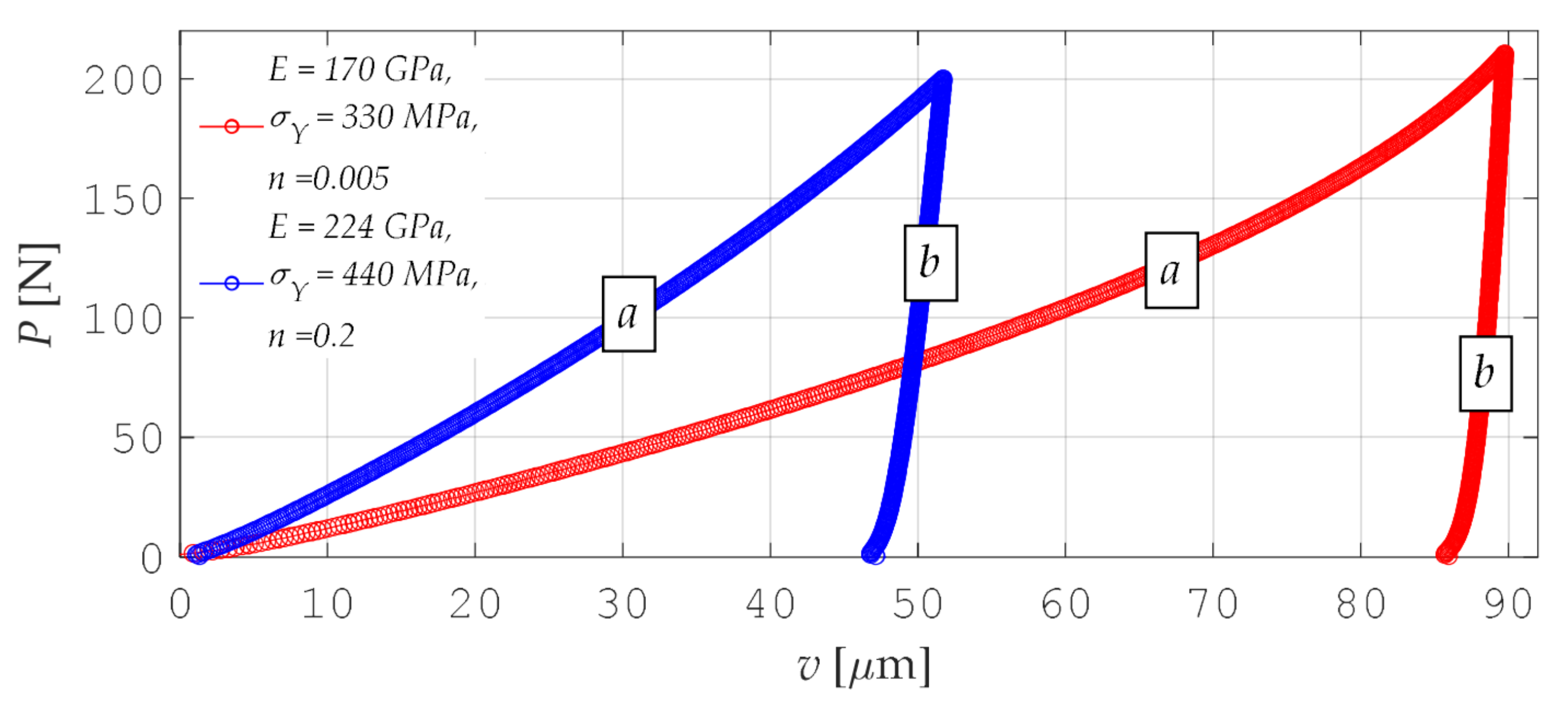
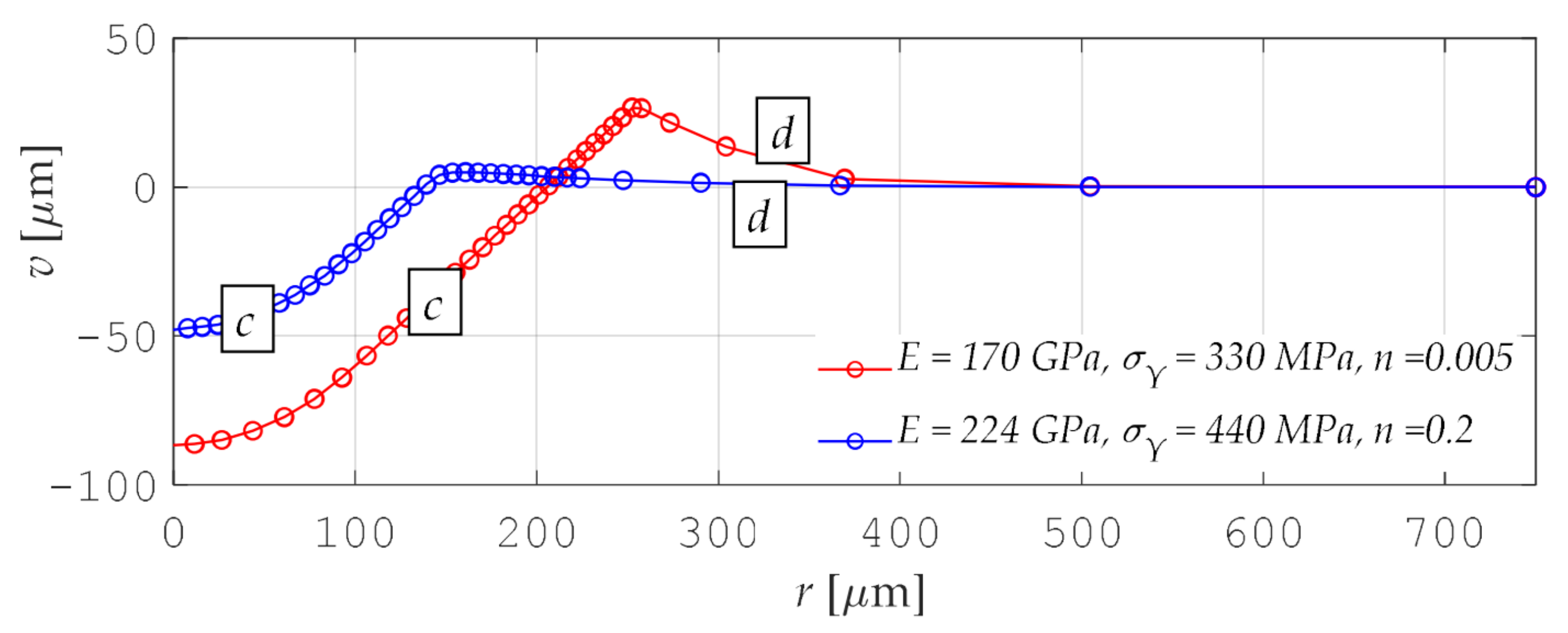

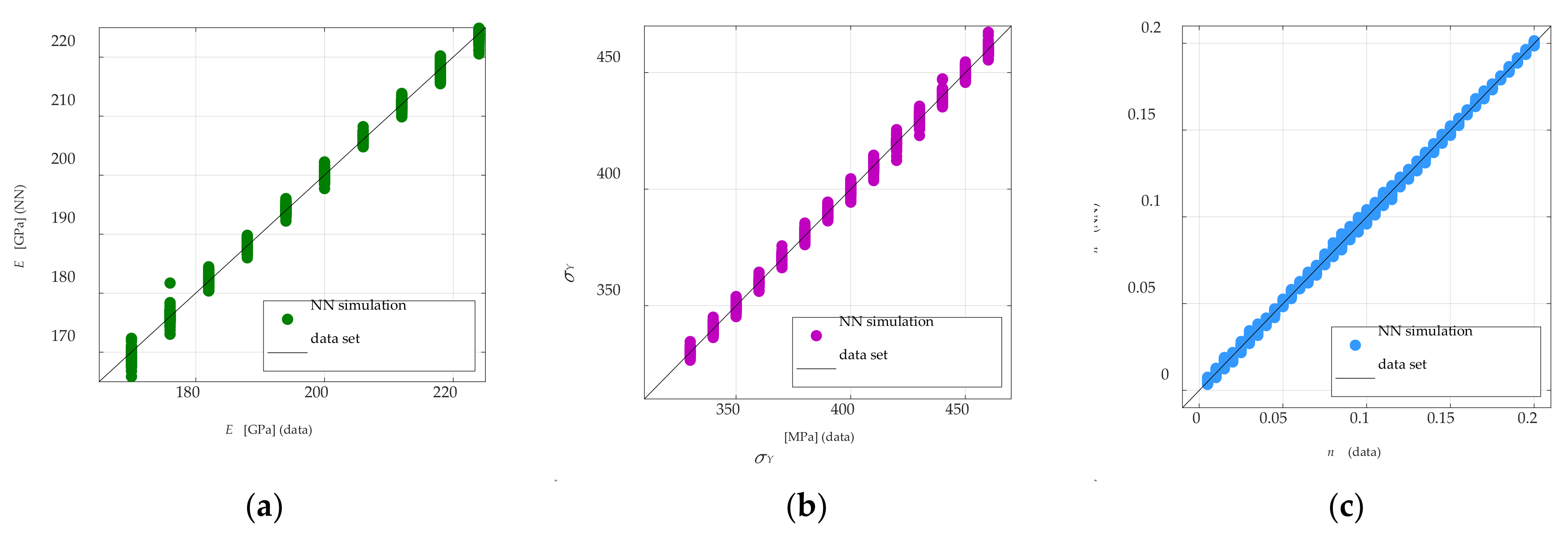

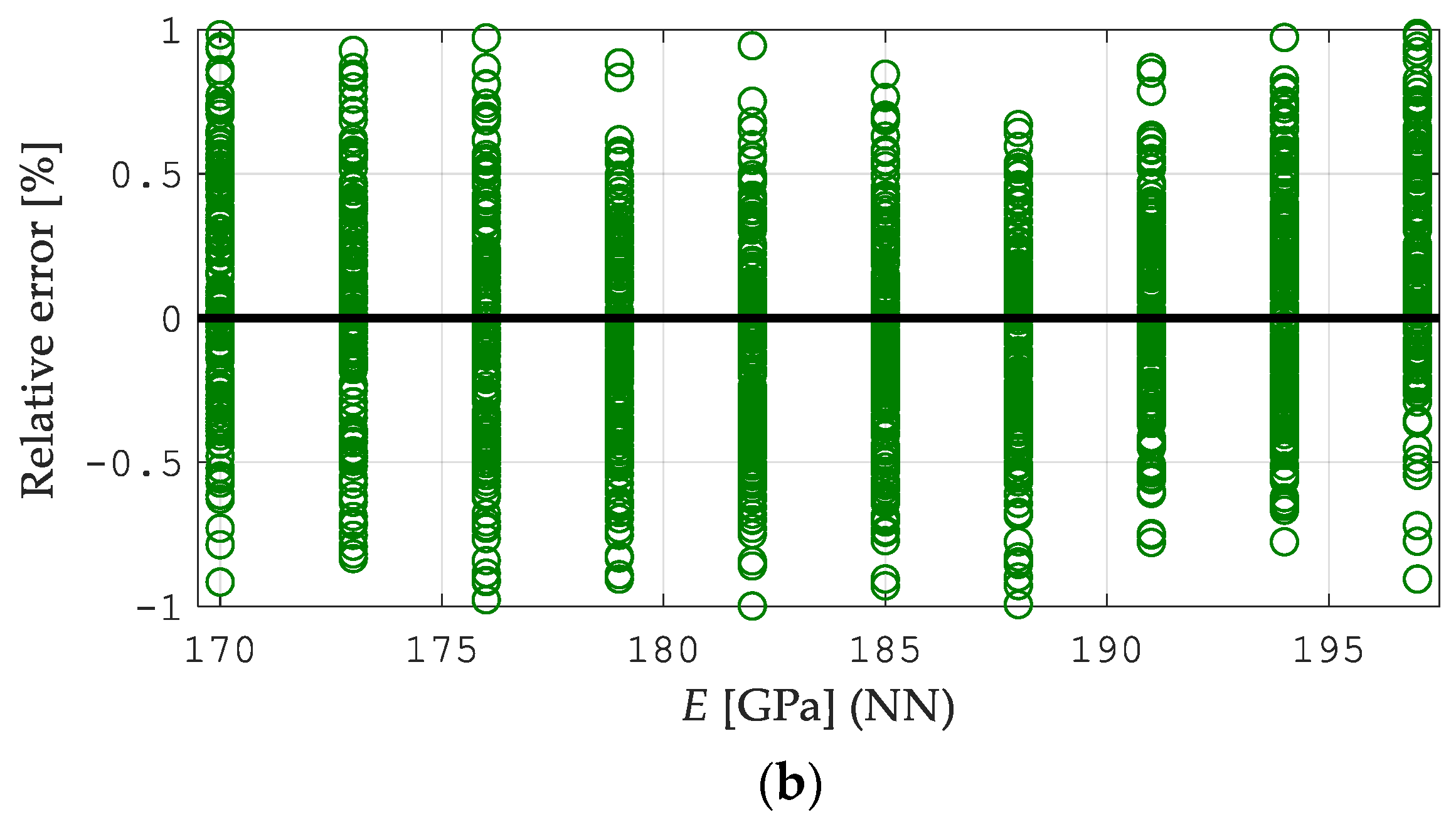


| Procedure | Curve | avr ep (%) | MSE | r |
|---|---|---|---|---|
| P-A | a | 1.601 | 0.4751 | 0.9996 |
| b | 0.229 | 0.1003 | 0.9982 | |
| P-C | c | 2.227 | 0.7693 | 0.9989 |
| d | 0.980 | 0.3874 | 0.9975 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Potrzeszcz-Sut, B.; Dudzik, A. The Application of a Hybrid Method for the Identification of Elastic–Plastic Material Parameters. Materials 2022, 15, 4139. https://doi.org/10.3390/ma15124139
Potrzeszcz-Sut B, Dudzik A. The Application of a Hybrid Method for the Identification of Elastic–Plastic Material Parameters. Materials. 2022; 15(12):4139. https://doi.org/10.3390/ma15124139
Chicago/Turabian StylePotrzeszcz-Sut, Beata, and Agnieszka Dudzik. 2022. "The Application of a Hybrid Method for the Identification of Elastic–Plastic Material Parameters" Materials 15, no. 12: 4139. https://doi.org/10.3390/ma15124139
APA StylePotrzeszcz-Sut, B., & Dudzik, A. (2022). The Application of a Hybrid Method for the Identification of Elastic–Plastic Material Parameters. Materials, 15(12), 4139. https://doi.org/10.3390/ma15124139







