Effects of Freeze–Thaw Cycles on the Internal Voids Structure of Asphalt Mixtures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Asphalt Mixtures Design
2.3. Freeze–Thaw Cycle Test
2.4. Image Processing
2.4.1. CT Scan
2.4.2. Image Processing
3. Results and Discussion
3.1. Void Distribution Law
3.1.1. Void Feature
3.1.2. Changes in Void Characteristics
3.1.3. Void Variation Distribution
3.2. Distribution Quantification
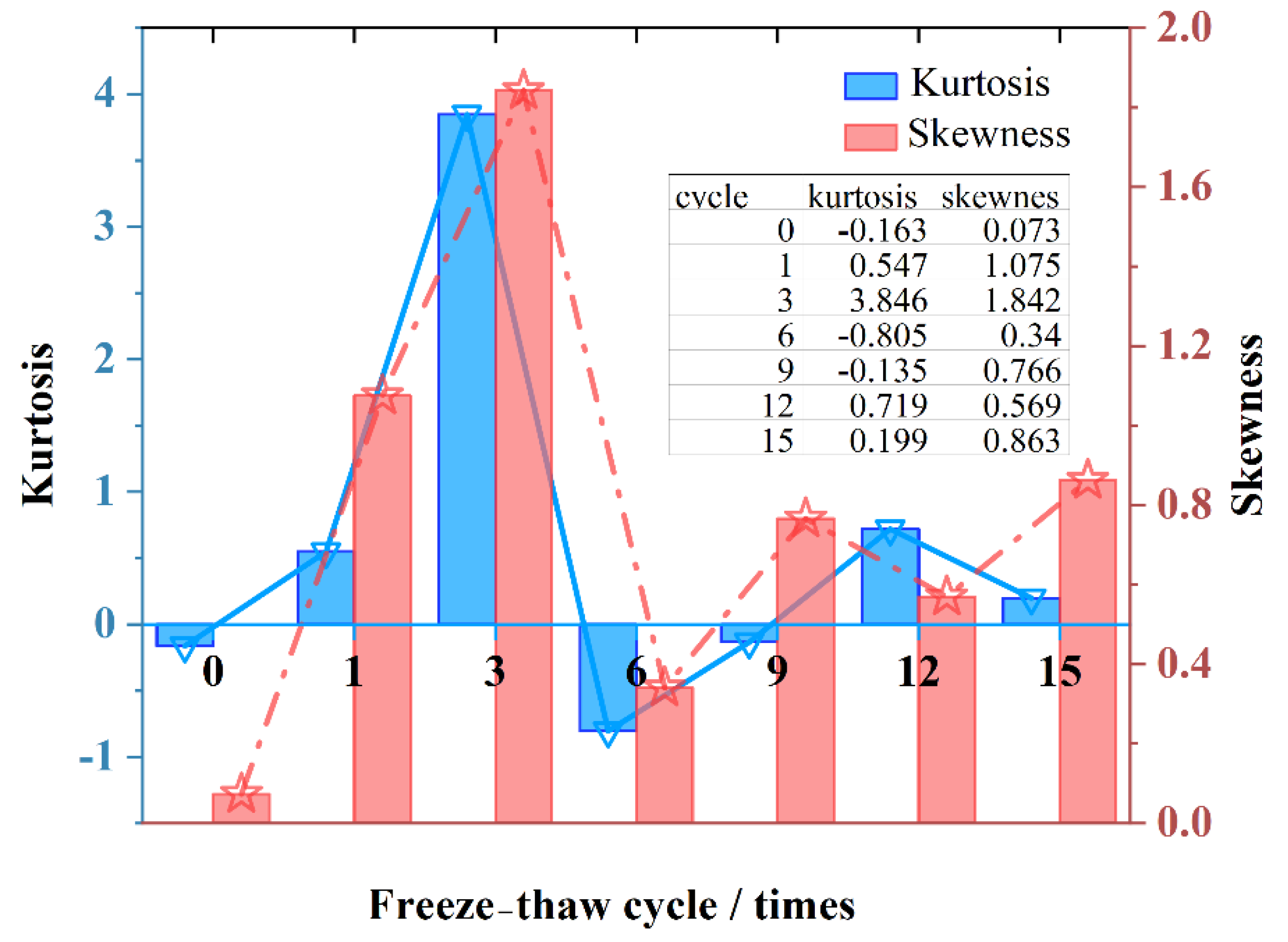
3.2.1. Kurtosis and Skewness
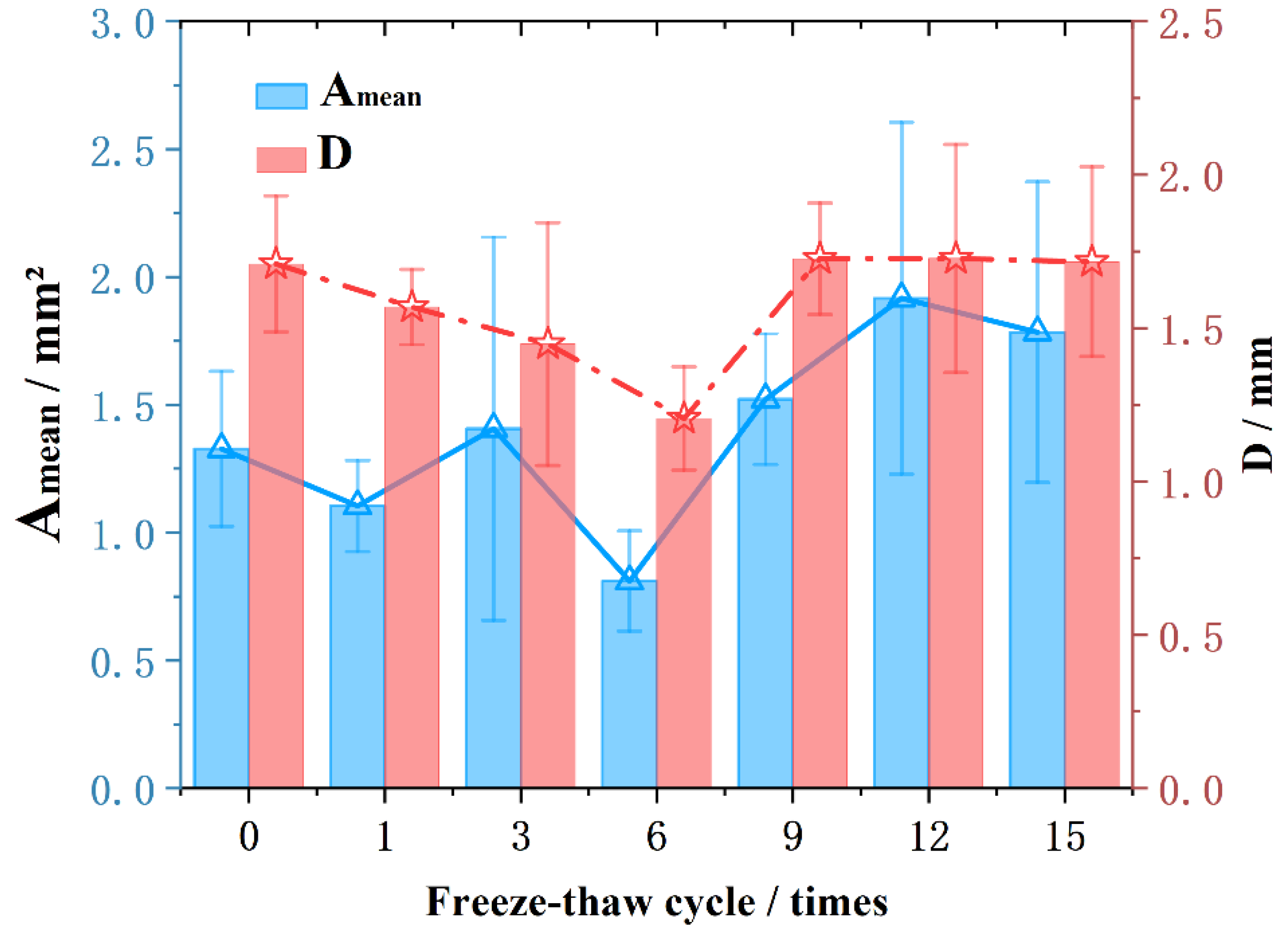
3.2.2. Freeze–Thaw Void Shape
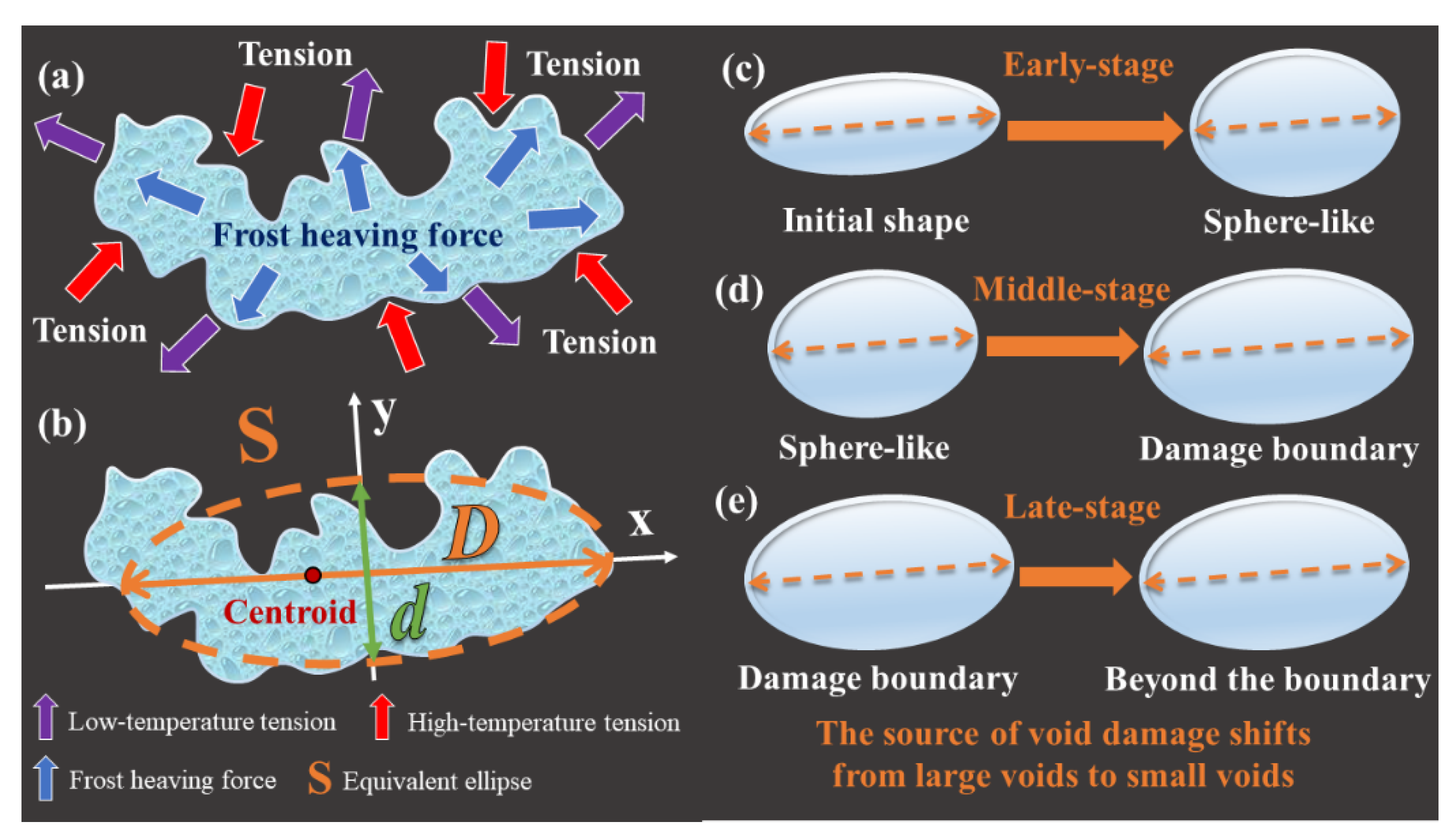
3.3. Freeze–Thaw Void Morphology Theory
4. Conclusions
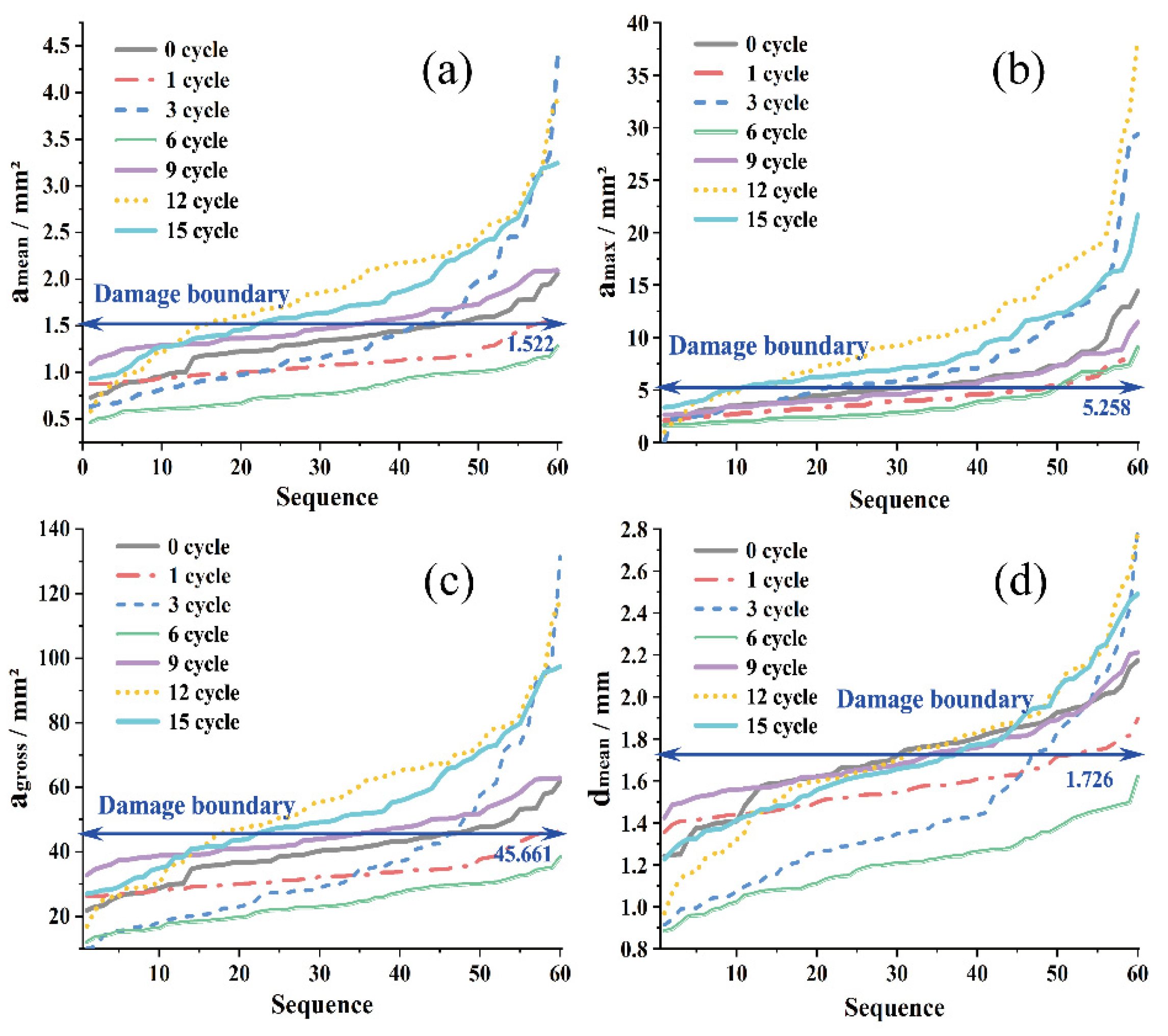
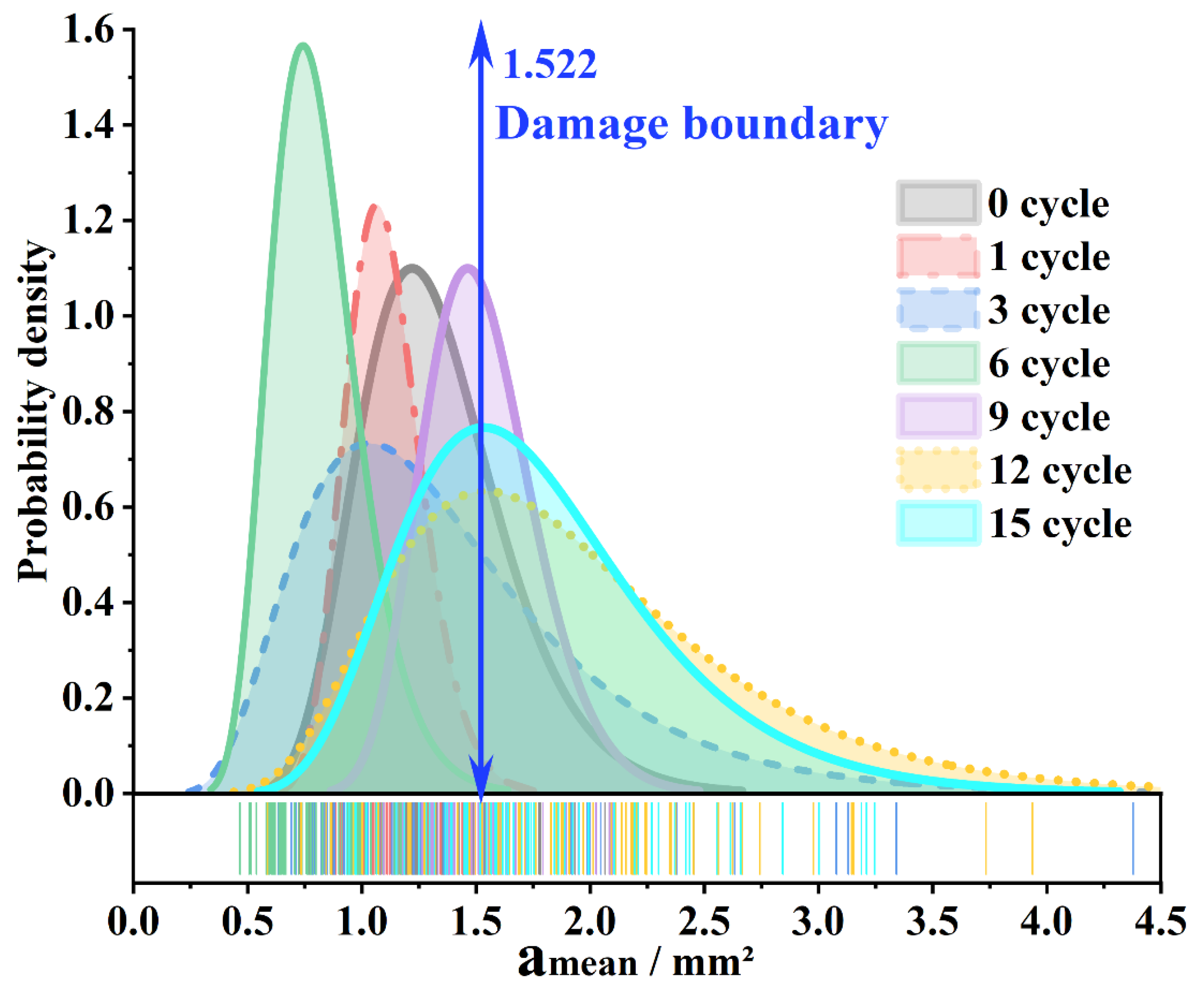
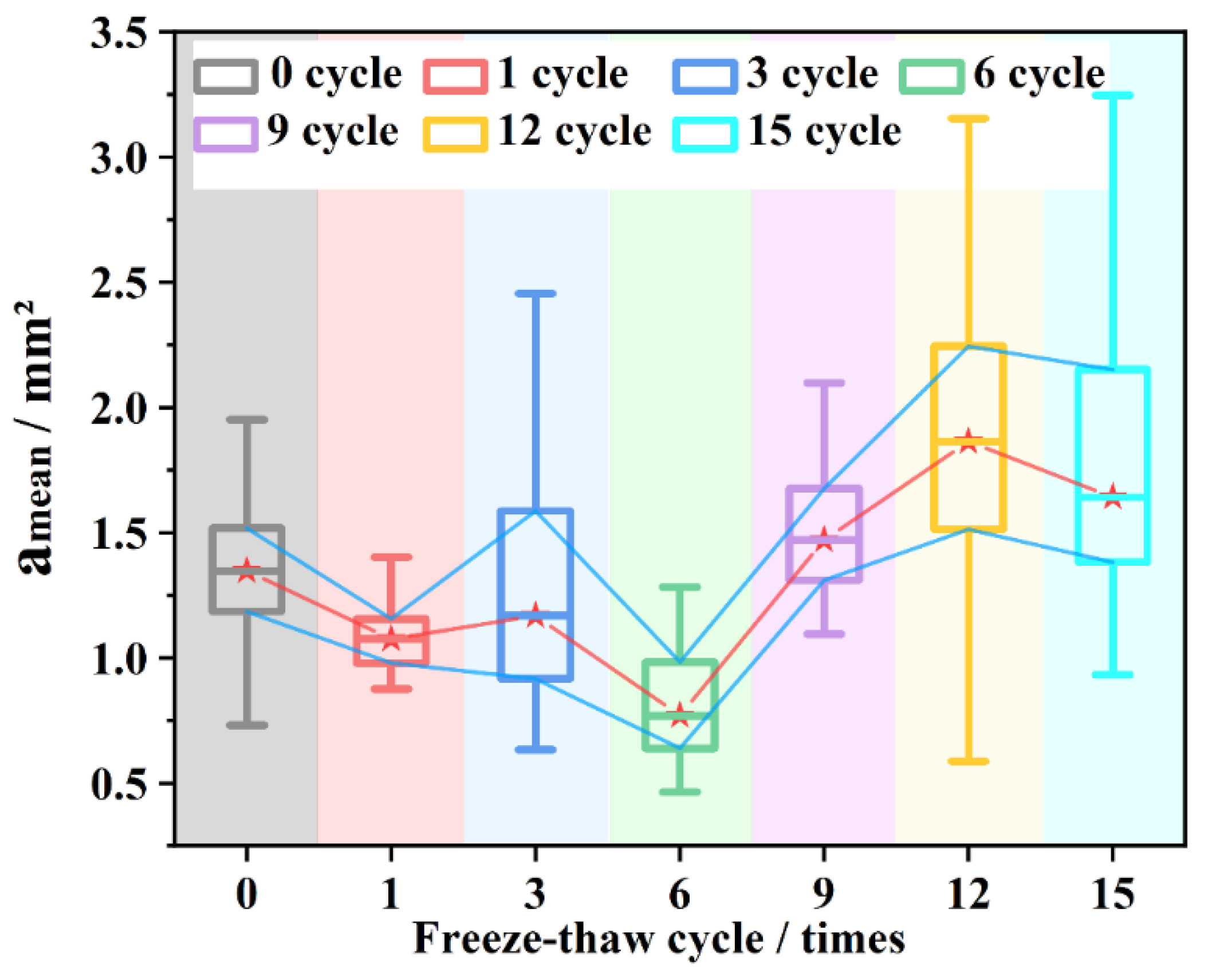
- The voids were irreversibly damaged after the ninth freeze–thaw cycle. The average values of the indicators of the ninth cycle are used as the damage boundary. After the damage boundary is exceeded, the degree of irreversible damage caused by freezing and thawing increases, the rebound of large voids decreases significantly, and the small voids continue to fluctuate. The accumulation of freeze–thaw damage is reflected in the springback failure of large voids;
- From the statistical value of , it can be seen that middle-stage (6~9 cycles) is the critical stage of freeze–thaw damage. The large void area tends to stabilize in the late-stage (12~15 cycles). The frost resistance of the asphalt mixture is the strongest in the early stage (0~3 cycles). The source of void damage shifts from large voids to small voids;
- The fluctuation of void growth mainly comes from the contraction and expansion in the short axis direction. The main reason for the irreversible damage is the springback failure in the long axis direction, which leads to the collective increase of the small void area in 6~9 cycles. In the late-stage of freeze–thaw damage (12~15 cycles), the remained stable, the source of damage shifted to small voids, and the fluctuations of damage and deepened short-axis fluctuations came from smaller voids.
- According to the change trend of , the morphological evolution of freeze–thaw voids is divided into three stages. In the early-stage, shrinks, the shape of the void tends to be round, and the freeze–thaw resistance is strong. In the middle-stage, grows, the void area grows steadily, and the durability decreases as a whole. In the late-stage, remained stable, the void area fluctuated slightly but tended to be stable, and the freeze–thaw damage was irreversible and further deepened.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fakhri, M.; Siyadati, S.A.; Aliha, M.R.M. Impact of Freeze-Thaw Cycles on Low Temperature Mixed Mode I/II Cracking Properties of Water Saturated Hot Mix Asphalt: An Experimental Study. Constr. Build. Mater. 2020, 261, 119939. [Google Scholar] [CrossRef]
- You, L.; You, Z.; Dai, Q.; Xie, X.; Washko, S.; Gao, J. Investigation of Adhesion and Interface Bond Strength for Pavements Underlying Chip-Seal: Effect of Asphalt-Aggregate Combinations and Freeze-Thaw Cycles on Chip-Seal. Constr. Build. Mater. 2019, 203, 322–330. [Google Scholar] [CrossRef]
- Wang, W.; Wang, L.; Xiong, H.; Luo, R. A Review and Perspective for Research on Moisture Damage in Asphalt Pavement Induced by Dynamic Pore Water Pressure. Constr. Build. Mater. 2019, 204, 631–642. [Google Scholar] [CrossRef]
- Sanfilippo, D.; Ghiassi, B.; Alexiadis, A.; Hernandez, A.G. Combined Peridynamics and Discrete Multiphysics to Study the Effects of Air Voids and Freeze-Thaw on the Mechanical Properties of Asphalt. Materials 2021, 14, 1579. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Qin, X.; Pang, W.; Wang, W. Performance Deterioration of Asphalt Mixture under Chloride Salt Erosion. Materials 2021, 14, 3339. [Google Scholar] [CrossRef]
- Li, F.; Zhou, S.; Chen, S.; Yang, Z.; Yang, J.; Zhu, X.; Du, Y.; Zhou, P.; Cheng, Z. Preparation of Low-Temperature Phase Change Materials Microcapsules and Its Application to Asphalt Pavement. J. Mater. Civ. Eng. 2018, 30, 04018303. [Google Scholar] [CrossRef]
- Alsaif, A.; Bernal, S.A.; Guadagnini, M.; Pilakoutas, K. Freeze-Thaw Resistance of Steel Fibre Reinforced Rubberised Concrete. Constr. Build. Mater. 2019, 195, 450–458. [Google Scholar] [CrossRef]
- Hong, B.; Lu, G.; Gao, J.; Wang, D. Evaluation of Polyurethane Dense Graded Concrete Prepared Using the Vacuum Assisted Resin Transfer Molding Technology. Constr. Build. Mater. 2021, 269, 121340. [Google Scholar] [CrossRef]
- Wang, M.; Xing, C. Evaluation of Microstructural Features of Buton Rock Asphalt Components and Rheological Properties of Pure Natural Asphalt Modified Asphalt. Constr. Build. Mater. 2021, 267, 121132. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, Y.; Ma, G.; Tan, G.; Sun, X.; Yang, S. Further Investigation on Damage Model of Eco-Friendly Basalt Fiber Modified Asphalt Mixture under Freeze-Thaw Cycles. Appl. Sci. 2018, 9, 60. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Wang, W.; Gong, Y.; Wang, S.; Yang, S.; Sun, X. Comparative Study on the Damage Characteristics of Asphalt Mixtures Reinforced with an Eco-Friendly Basalt Fiber under Freeze-Thaw Cycles. Materials 2018, 11, 2488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, C.; Wu, C.; Liu, K.; Jiang, K. Study on the Durability of Bamboo Fiber Asphalt Mixture. Materials 2021, 14, 1667. [Google Scholar] [CrossRef]
- Luo, D.; Khater, A.; Yue, Y.; Abdelsalam, M.; Zhang, Z.; Li, Y.; Li, J.; Iseley, D.T. The Performance of Asphalt Mixtures Modified with Lignin Fiber and Glass Fiber: A Review Dong. Constr. Build. Mater. 2019, 209, 377–387. [Google Scholar] [CrossRef]
- Cheng, Y.; Yu, D.; Gong, Y.; Zhu, C.; Tao, J.; Wang, W. Laboratory Evaluation on Performance of Eco-Friendly Basalt Fiber and Diatomite Compound Modified Asphalt Mixture. Materials 2018, 11, 2400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Badeli, S.; Carter, A.; Dore, G.; Saliani, S. Evaluation of the Durability and the Performance of an Asphalt Mix Involving Aramid Pulp Fiber (APF): Complex Modulus before and after Freeze-Thaw Cycles, Fatigue, and TSRST Tests. Constr. Build. Mater. 2018, 174, 60–71. [Google Scholar] [CrossRef]
- Gao, J.; Sha, A.; Wang, Z.; Tong, Z.; Liu, Z. Utilization of Steel Slag as Aggregate in Asphalt Mixtures for Microwave Deicing. J. Clean. Prod. 2017, 152, 429–442. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Guo, H.; Yan, F. Thermal Transfer Characteristics of Asphalt Mixtures Containing Hot Poured Steel Slag through Microwave Heating. J. Clean Prod. 2021, 308, 127225. [Google Scholar] [CrossRef]
- Lou, B.; Sha, A.; Barbieri, D.M.; Liu, Z.; Zhang, F.; Jiang, W.; Hoff, I. Characterization and Microwave Healing Properties of Different Asphalt Mixtures Suffered Freeze-Thaw Damage. J. Clean. Prod. 2021, 320, 128823. [Google Scholar] [CrossRef]
- Yu, H.; He, Z.; Qian, G.; Gong, X.; Qu, X. Research on the Anti-Icing Properties of Silicone Modified Polyurea Coatings (SMPC) for Asphalt Pavement. Constr. Build. Mater. 2020, 242, 117793. [Google Scholar] [CrossRef]
- Yao, T.; Han, S.; Men, C.; Zhang, J.; Luo, J.; Li, Y. Performance Evaluation of Asphalt Pavement Groove-Filled with Polyurethane-Rubber Particle Elastomer. Constr. Build. Mater. 2021, 292, 123434. [Google Scholar] [CrossRef]
- Tarefder, R.; Faisal, H.; Barlas, G. Freeze-Thaw Effects on Fatigue LIFE of Hot Mix Asphalt and Creep Stiffness of Asphalt Binder. Cold Reg. Sci. Technol. 2018, 153, 197–204. [Google Scholar] [CrossRef]
- Badeli, S.; Carter, A.; Dore, G. Complex Modulus and Fatigue Analysis of Asphalt Mix after Daily Rapid Freeze-Thaw Cycles. J. Mater. Civ. Eng. 2018, 30, 04018056. [Google Scholar] [CrossRef]
- Das, B.P.; Das, S.; Siddagangaiah, A.K. Probabilistic Modeling of Fatigue Damage in Asphalt Mixture. Constr. Build. Mater. 2021, 269, 121300. [Google Scholar] [CrossRef]
- Boz, I.; Habbouche, J.; Diefenderfer, S. The Use of the Indirect Tensile Test to Evaluate the Resistance of Asphalt Mixtures to Cracking and Moisture-Induced Damage. In Airfield and Highway Pavements 2021: Pavement Materials and Sustainability; Ozer, H., Rushing, J.F., Leng, Z., Eds.; Amer Soc Civil Engineers: New York, NY, USA, 2021; pp. 104–114. [Google Scholar]
- Karimi, M.M.; Dehaghi, E.A.; Behnood, A. A Fracture-Based Approach to Characterize Long-Term Performance of Asphalt Mixes under Moisture and Freeze-Thaw Conditions. Eng. Fract. Mech. 2021, 241, 107418. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, C. Random Generation of Asphalt Mixture Mesostructure and Thermal–Mechanical Coupling Analysis at Low Temperature. Constr. Build. Mater. 2021, 280, 122537. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wu, Q.; Xu, H.; Liu, P.; Oeser, M. Damage Evolution of Asphalt Mixture under Freeze-Thaw Cyclic Loading from a Mechanical Perspective. Int. J. Fatigue 2021, 142, 105923. [Google Scholar] [CrossRef]
- Zarei, M.; Kordani, A.A.; Ghamarimajd, Z.; Khajehzadeh, M.; Khanjari, M.; Zahedi, M. Evaluation of Fracture Resistance of Asphalt Concrete Involving Calcium Lignosulfonate and Polyester Fiber under Freeze-Thaw Damage. Theor. Appl. Fract. Mech. 2022, 117, 103168. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Zhao, X.; Yu, C.; Zhou, X. Quantitative Evaluations on Influences of Aggregate Surface Texture on Interfacial Adhesion Using 3D Printing Aggregate. Constr. Build. Mater. 2022, 328, 127022. [Google Scholar] [CrossRef]
- Wu, H.; Li, P.; Nian, T.; Zhang, G.; He, T.; Wei, X. Evaluation of Asphalt and Asphalt Mixtures’ Water Stability Method under Multiple Freeze-Thaw Cycles. Constr. Build. Mater. 2019, 228, 117089. [Google Scholar] [CrossRef]
- Guo, Q.; Li, G.; Gao, Y.; Wang, K.; Dong, Z.; Liu, F.; Zhu, H. Experimental Investigation on Bonding Property of Asphalt-Aggregate Interface under the Actions of Salt Immersion and Freeze-Thaw Cycles. Constr. Build. Mater. 2019, 206, 590–599. [Google Scholar] [CrossRef]
- Xu, H.; Chen, F.; Yao, X.; Tan, Y. Micro-Scale Moisture Distribution and Hydrologically Active Pores in Partially Saturated Asphalt Mixtures by X-ray Computed Tomography. Constr. Build. Mater. 2018, 160, 653–667. [Google Scholar] [CrossRef]
- Wu, S.; Yang, J.; Yang, R.; Zhu, J.; Liu, S.; Wang, C. Investigation of Microscopic Air Void Structure of Anti-Freezing Asphalt Pavement with X-ray CT and MIP. Constr. Build. Mater. 2018, 178, 473–483. [Google Scholar] [CrossRef]
- Xu, G.; Yu, Y.; Cai, D.; Xie, G.; Chen, X.; Yang, J. Multi-Scale Damage Characterization of Asphalt Mixture Subject to Freeze-Thaw Cycles. Constr. Build. Mater. 2020, 240, 117947. [Google Scholar] [CrossRef]
- Xu, G.; Chen, X.; Cai, X.; Yu, Y.; Yang, J. Characterization of Three-Dimensional Internal Structure Evolution in Asphalt Mixtures during Freeze-Thaw Cycles. Appl. Sci. 2021, 11, 4316. [Google Scholar] [CrossRef]
- Li, Z.; Hao, P.; Liu, H.; Xu, J. Effect of Cement on the Strength and Microcosmic Characteristics of Cold Recycled Mixtures Using Foamed Asphalt. J. Clean Prod. 2019, 230, 956–965. [Google Scholar] [CrossRef]
- Hengzhen, L.; Huining, X.; Xusheng, Y.; Yiqiu, T. Investigation of Water Phases on Freeze-Thaw Damage on Asphalt Mixture by Using Information Entropy. Road Mater. Pavement Des. 2021. [Google Scholar] [CrossRef]
- Xu, H.; Li, H.; Tan, Y.; Wang, L.; Hou, Y. A Micro-Scale Investigation on the Behaviors of Asphalt Mixtures under Freeze-Thaw Cycles Using Entropy Theory and a Computerized Tomography Scanning Technique. Entropy 2018, 20, 68. [Google Scholar] [CrossRef] [Green Version]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2011.
- JTG E42-2005; Test Methods of Aggregate for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2005.
- Liu, J.; Zhang, T.; Guo, H.; Wang, Z.; Wang, X. Evaluation of Self-Healing Properties of Asphalt Mixture Containing Steel Slag under Microwave Heating: Mechanical, Thermal Transfer and Voids Microstructural Characteristics. J. Clean. Prod. 2022, 342, 130932. [Google Scholar] [CrossRef]
- Rezanezhad, M.; Lajevardi, S.A.; Karimpouli, S. Application of Equivalent Circle and Ellipse for Pore Shape Modeling in Crack Growth Problem: A Numerical Investigation in Microscale. Eng. Fract. Mech. 2021, 253, 107882. [Google Scholar] [CrossRef]
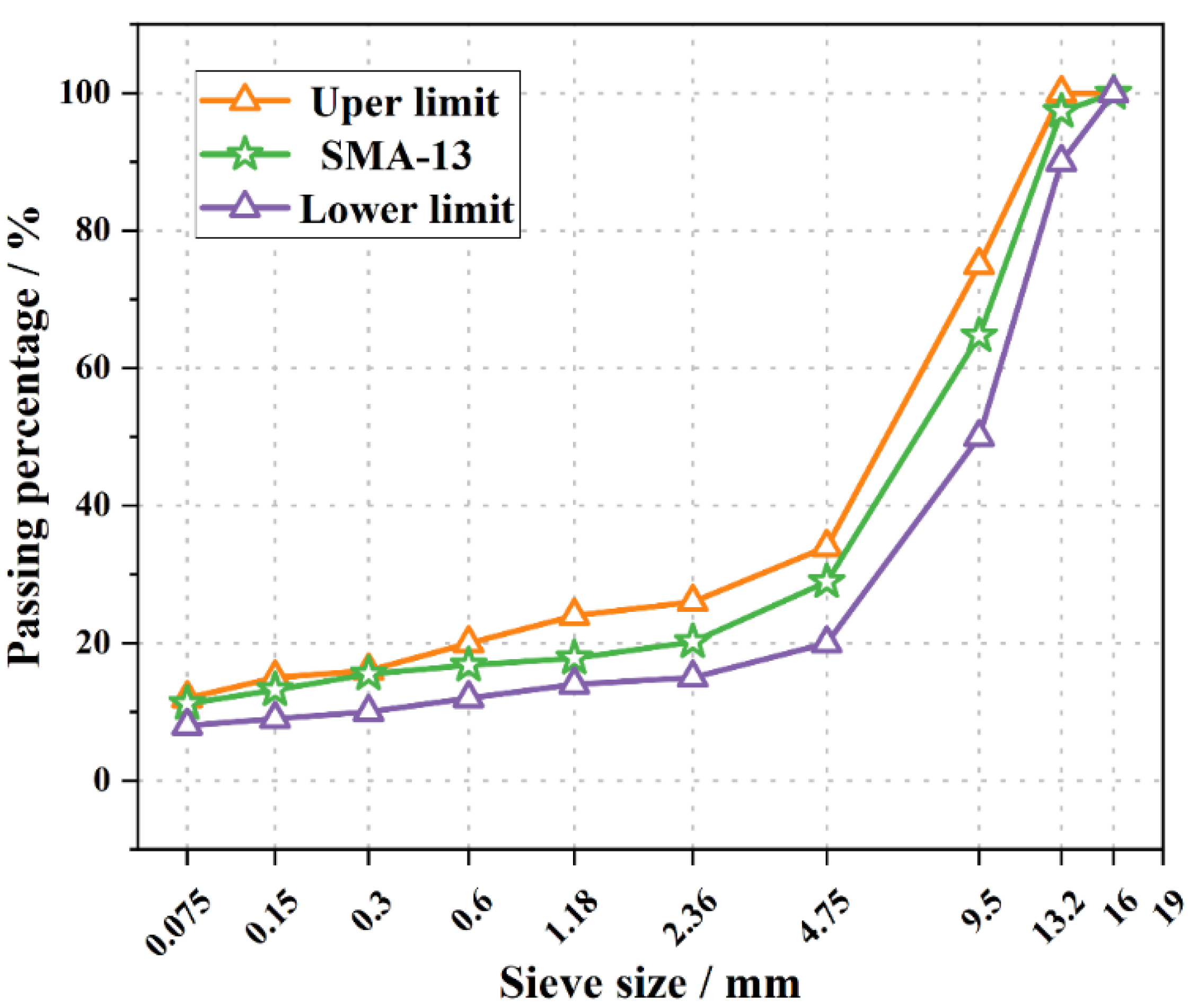


| Properties | Test Results | Test Methods (JTG E20-2011) |
|---|---|---|
| Penetration (25 °C, 100 g, 5 s; 0.1 mm) | 65 | T0604 |
| Ductility (5 °C, 5 cm/min; cm) | 43 | T0605 |
| Softening point (°C) | 64 | T0606 |
| Sieve (mm) | Apparent Specific Gravity (g/cm3) | Crushing Value (%) | Los Angeles Abrasion (%) | Water Absorption (%) |
|---|---|---|---|---|
| 13.2~16 | 2.806 | 15.3 | 21.3 | 0.62 |
| 9.5~13.2 | 2.805 | 13.6 | 19 | 0.60 |
| 4.75~9.5 | 2.805 | 13.9 | 19 | 0.28 |
| 2.36~4.75 | 2.726 | 16.7 | 15.8 | 0.70 |
| 1.18~2.36 | 2.783 | - | - | 0.65 |
| 0.6~1.18 | 2.785 | - | - | |
| 0.3~0.6 | 2.765 | - | - | |
| 0.15~0.3 | 2.759 | - | - | |
| 0.075~0.15 | 2.716 | - | - |
| Cycle/Times | Mean Value | Range | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|
| 0~3 | 0.302 | 2.304 | 0.396 | 1.312 |
| 6~9 | 0.712 | 0.309 | 0.075 | 0.105 |
| 12~15 | 0.177 | 0.683 | 0.122 | 0.690 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Jing, H.; Liu, J. Effects of Freeze–Thaw Cycles on the Internal Voids Structure of Asphalt Mixtures. Materials 2022, 15, 3560. https://doi.org/10.3390/ma15103560
Yu D, Jing H, Liu J. Effects of Freeze–Thaw Cycles on the Internal Voids Structure of Asphalt Mixtures. Materials. 2022; 15(10):3560. https://doi.org/10.3390/ma15103560
Chicago/Turabian StyleYu, Di, Haosen Jing, and Jianan Liu. 2022. "Effects of Freeze–Thaw Cycles on the Internal Voids Structure of Asphalt Mixtures" Materials 15, no. 10: 3560. https://doi.org/10.3390/ma15103560
APA StyleYu, D., Jing, H., & Liu, J. (2022). Effects of Freeze–Thaw Cycles on the Internal Voids Structure of Asphalt Mixtures. Materials, 15(10), 3560. https://doi.org/10.3390/ma15103560







