Modelling the Relations of Rheological Characteristics with Composition of Plaster Mortar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characteristics of Materials and Design of Experiment
- x—vector of normalized factors,
- xi = (Xi − X0i)/ΔXi, X0i = (Xi.min + Xi.max)/2, ΔXi = (Xi.max − Xi.min)/2
- Xi = xi · ΔXi + X0i.
- Predesign of the experiment, i.e., selection of the factors to be varied, limits of varying them, properties, the level of which should be determined, considering physico-chemical, technological, and other a priori knowledge.
- Design of the experiment, with regard to the rational form of the polynomial model and possible existence of present experimental points and “forbidden” areas in the factor domain.
- Building the regression model adequate for experimental data, with insignificant estimates eliminated.
- Solving a variety of scientific and industrial problems, making decisions on the basis of individual ES-model (for separate criteria) and their complexity, extracting as much as possible scientific and industrial information from the models.
2.2. Testing Method
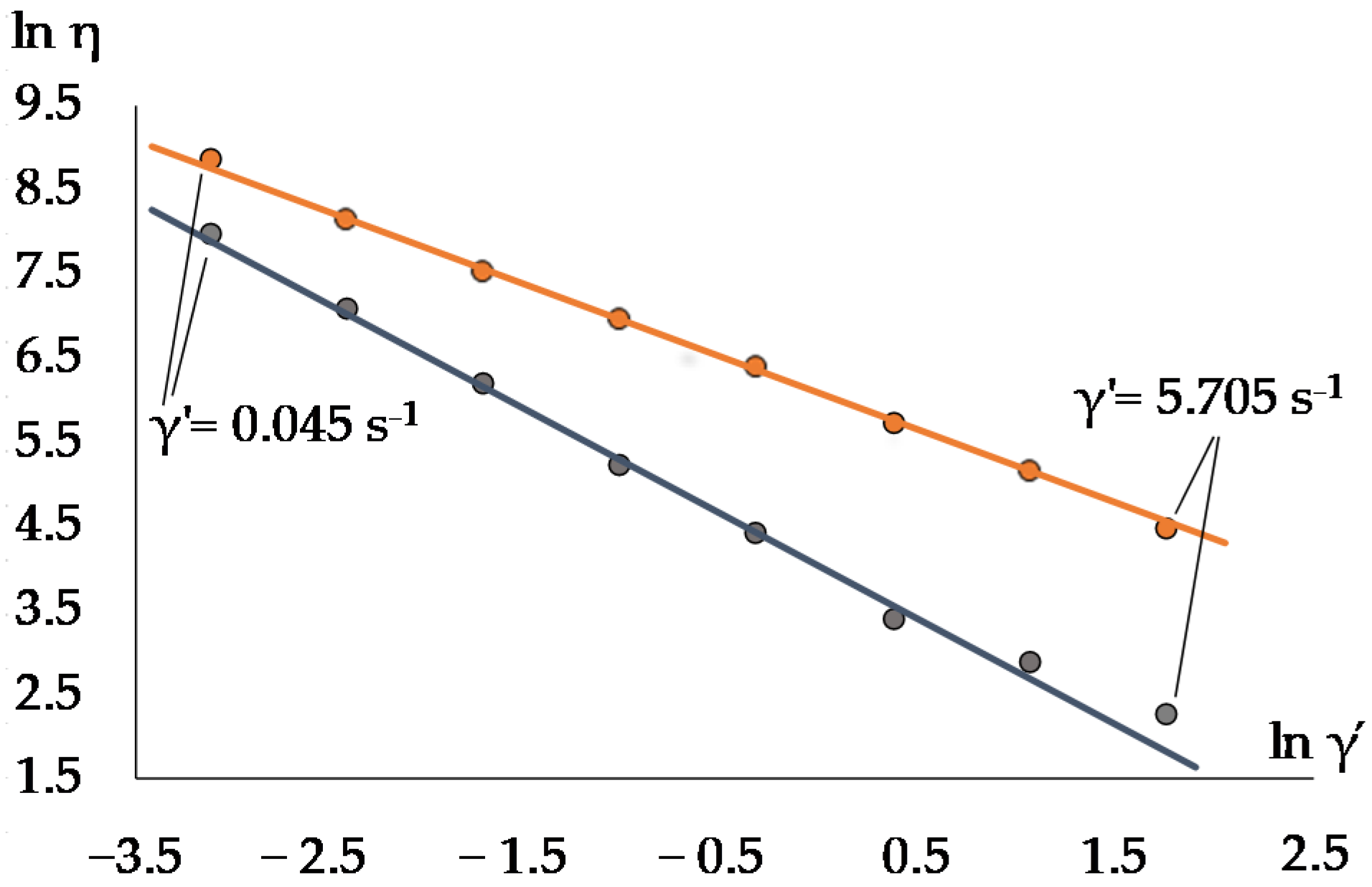
2.3. Method of Measuring Theological Parameters
3. Results
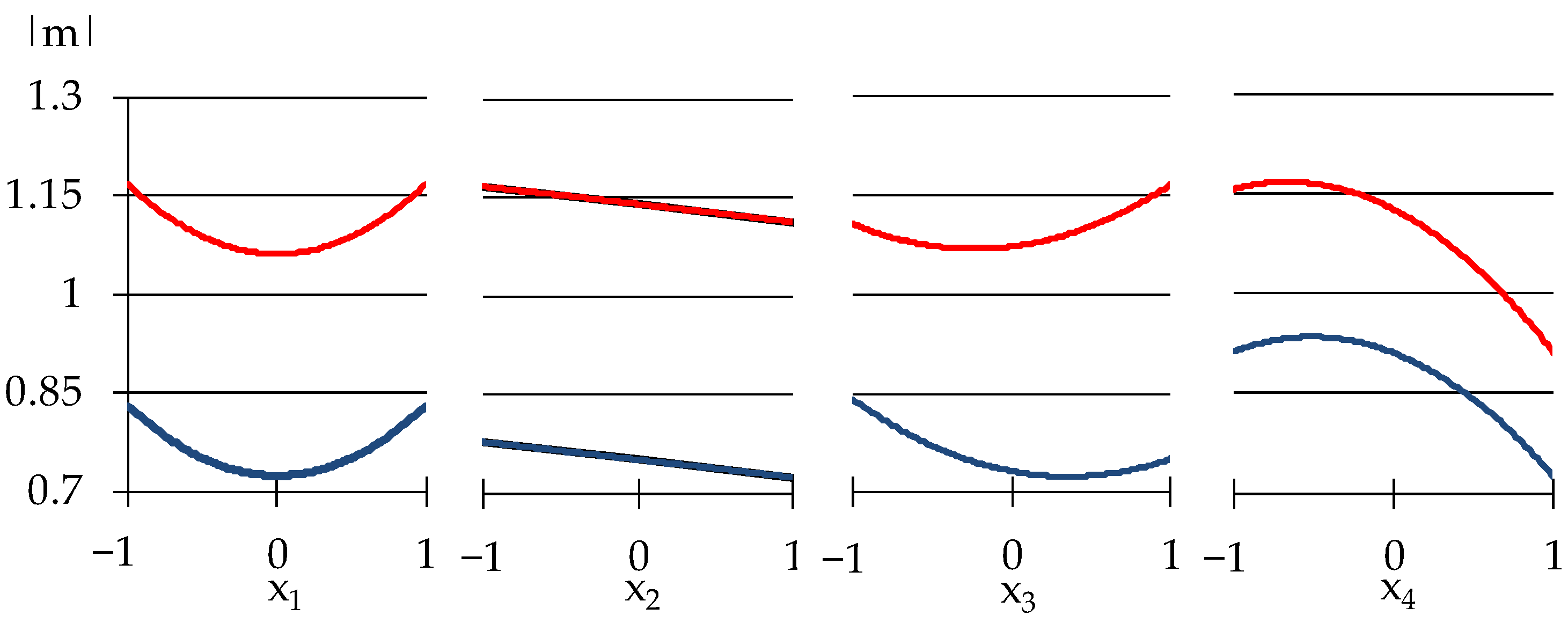
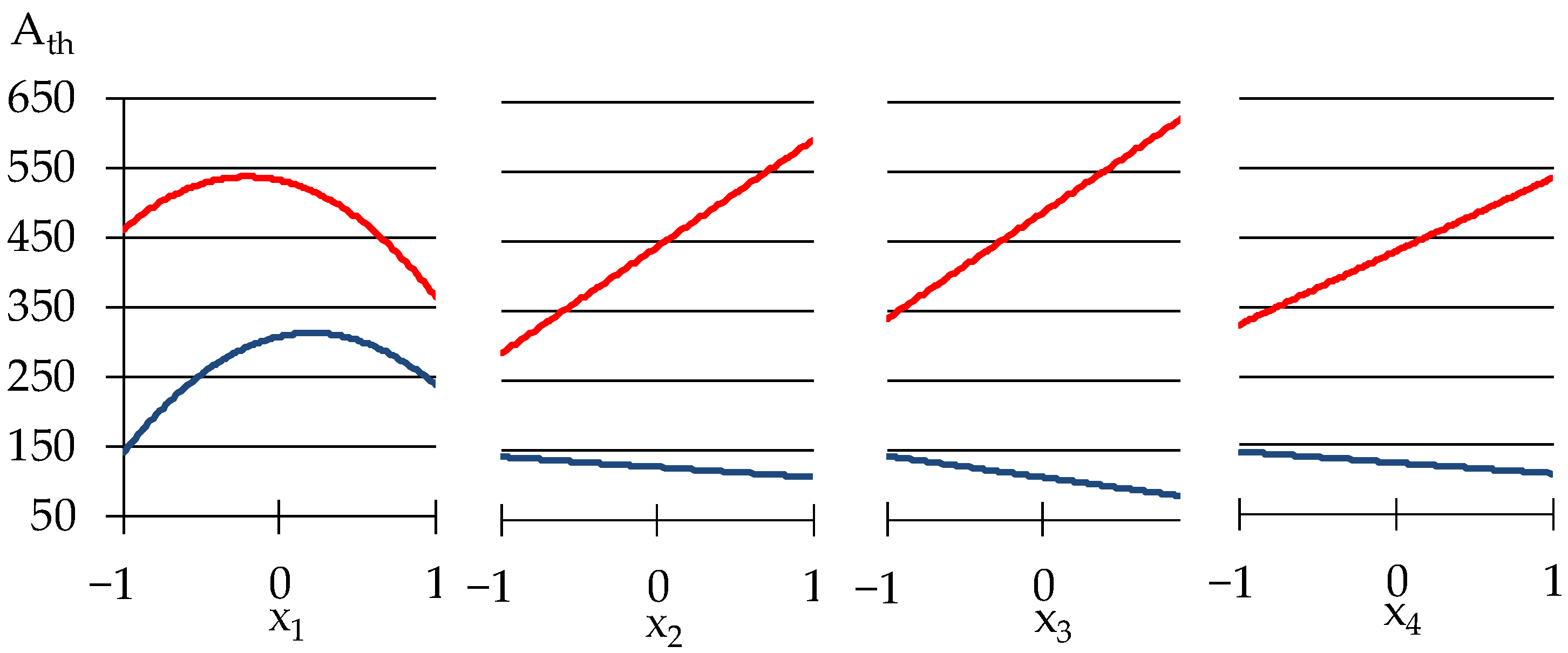
3.1. Effects of Varied Components on Rheological Properties
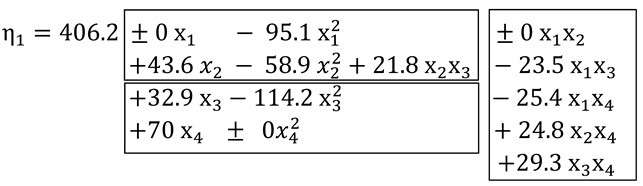
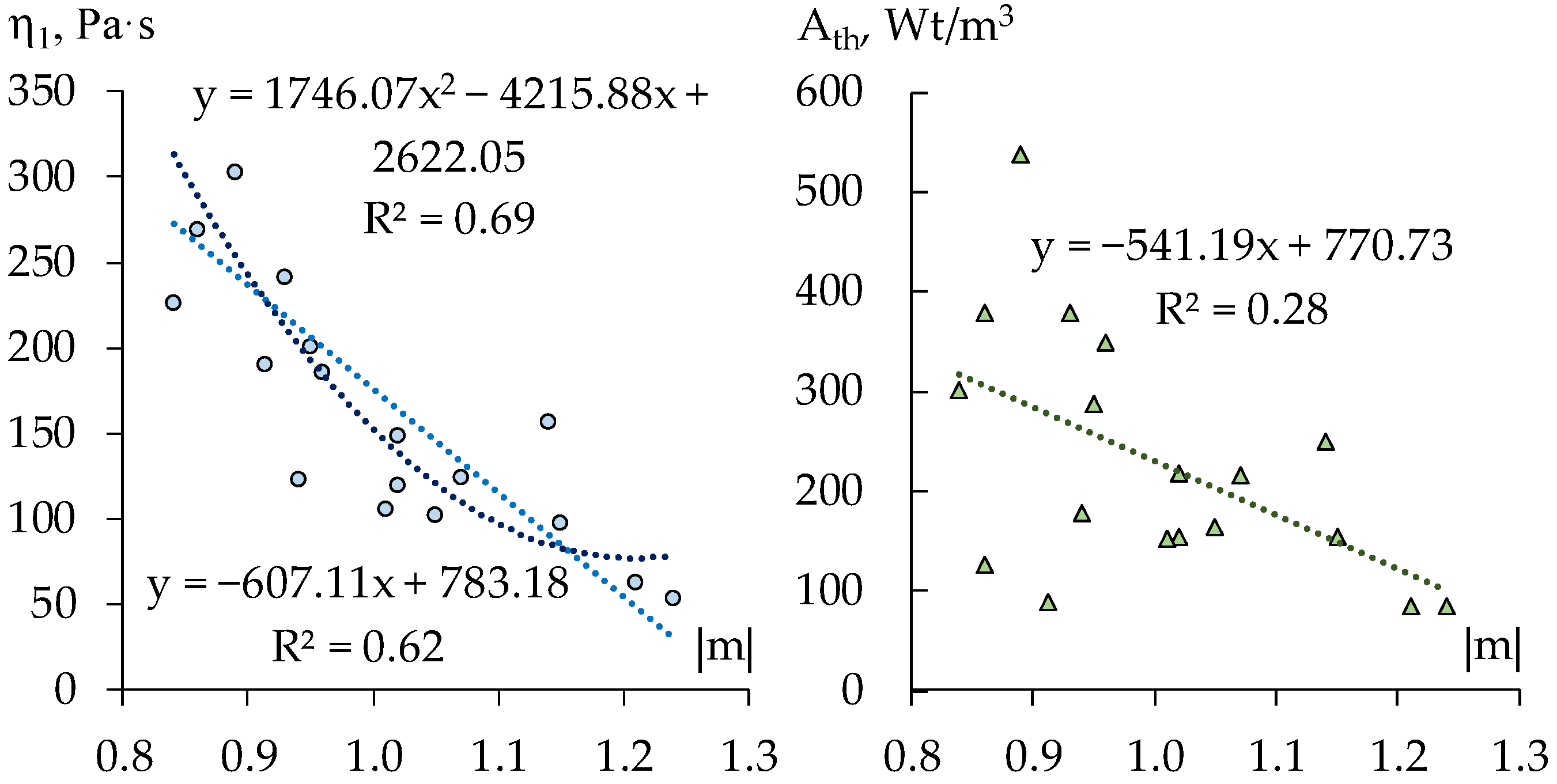
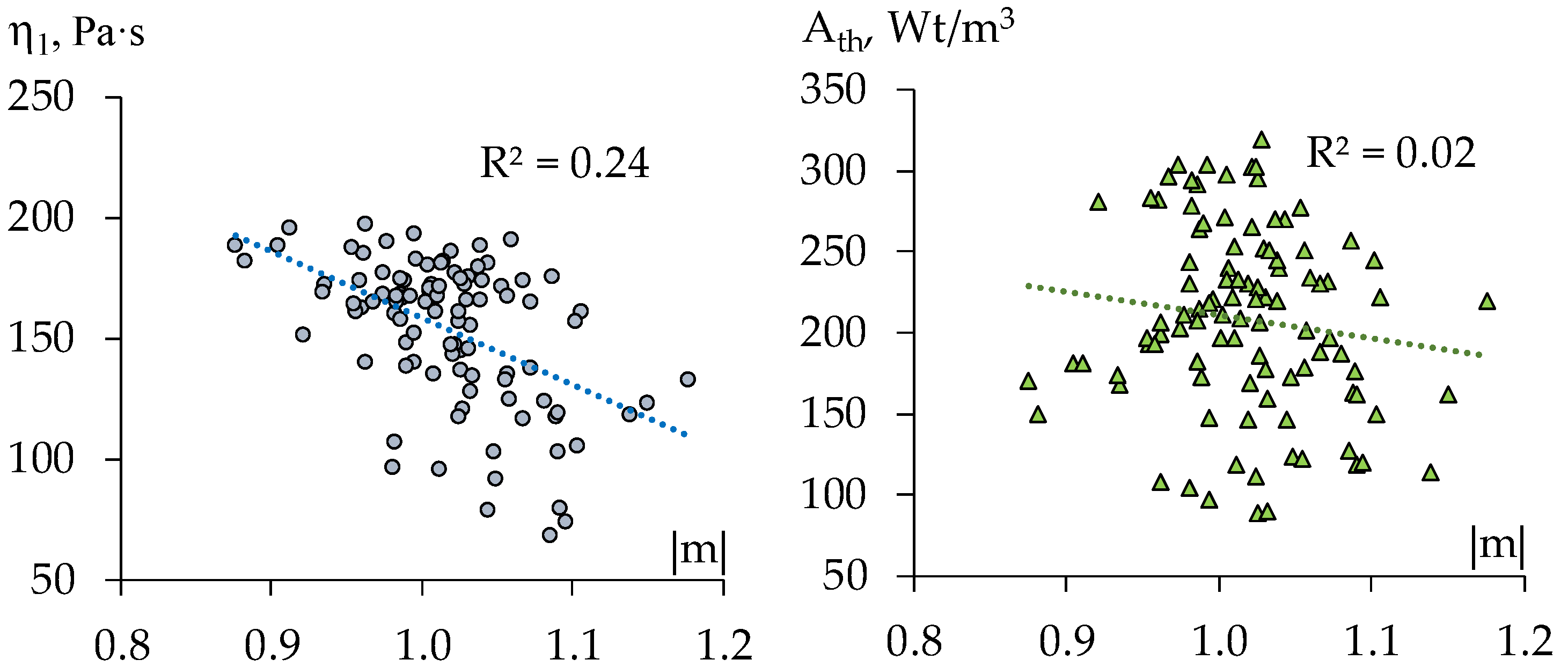
3.2. Correlation between Rheological Characteristics
4. Conclusions
- -
- Estimating the viscosity of technological mix of any composition at any shear rate in the studied region;
- -
- Inverse problems, of determining the shear rate that would provide the necessary viscosity of the mix, or of finding acceptable, optimal, and compromise compositions by rheological criteria together with operational properties of hardened composites.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Tattersall, G.H.; Banfill, P.F.G. The Rheology of Fresh Concrete; Pitman Books Limited: London, UK, 1983; p. 356. [Google Scholar]
- Ferraris, C.F.; Obla, K.H.; Hill, R. The influence of mineral admixtures on the rheology of cement paste and concrete. Cem. Concr. Res. 2001, 31, 245–255. [Google Scholar] [CrossRef]
- Han, S.; Yan, P.Y.; Kong, X.M. Study on the compatibility of cement-superplasticizer system based on the amount of free solution. Sci. China. Tech. Sci. 2011, 54, 183–189. [Google Scholar] [CrossRef]
- Rubio-Hernández, F.J.; Velázquez-Navarro, J.F.; Ordonez-Belloc, L.M. Rheology of concrete: A study case based upon the use of the concrete equivalent mortar. Mater. Struct. 2013, 46, 587–605. [Google Scholar] [CrossRef]
- Sheinn, A.M.; Ho, D.W.; Tam, C.T. Rheological model for self-compacting concrete-paste rheology. In Proceedings of the 27th Conference on Our World in Concrete and Structures, Singapore, 29–30 August 2002; pp. 517–523. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.464.2926&rep=rep1&type=pdf (accessed on 17 November 2021).
- Wallevik, J.E. Rheological properties of cement paste: Thixotropic behavior and structural breakdown. Cem. Concr. Res. 2009, 39, 14–29. [Google Scholar] [CrossRef]
- Haiqiang, J.; Mamadou, F.; Erol, Y.; Yanhui, L.; Lei, Y. Effect of mineral admixtures on flow properties of fresh cemented paste backfill: Assessment of time dependency and thixotropy. Powder Technol. 2020, 372, 258–266. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, J.; Lu, C.-X.; Cui, X.-Y.; Li, S.-Y.; Wang, X. Rheological behavior of fresh cement pastes with a graphene oxide additive. New Carbon Mater. 2016, 31, 574–584. [Google Scholar] [CrossRef]
- Rostami, M.R.; Abbassi-Sourki, F.; Bouhendi, H. Synergistic effect of branched polymer/nano silica on the microstructures of cement paste and their rheological behaviors. Constr. Build. Mater. 2019, 201, 159–170. [Google Scholar] [CrossRef]
- Jiang, S.; Shan, B.; Ouyang, J.; Zhang, W.; Yu, X.; Li, P.; Han, B. Rheological properties of cementitious composites with nano/fiber fillers. Constr. Build. Mater. 2018, 158, 786–800. [Google Scholar] [CrossRef]
- Ma, S.; Qian, Y.; Kawashima, S. Performance-based study on the rheological and hardened properties of blended cement mortars incorporating palygorskite clays and carbon nanotubes. Constr. Build. Mater. 2018, 171, 663–671. [Google Scholar] [CrossRef]
- Suárez, J.D.P.; Guarin, G.N.H.; Lizarazo-Marriaga, J. Effect of nanosilica particles on the rheological and mechanical properties of cement pastes using polyhydroxyl and polycarboxylate-based superplasticizers. Eur. J. Environ. Civ. Eng. 2020, 24, 2230–2254. [Google Scholar] [CrossRef]
- Colangelo, F.; Farina, I.; Travaglioni, M.; Salzano, C.; Cioffi, R.; Petrillo, A. Innovative Materials in Italy for Eco-Friendly and Sustainable Buildings. Materials 2021, 14, 2048. [Google Scholar] [CrossRef]
- Mikanovic, N.; Jolicoeur, C. Influence of superplasticizers on the rheology and stability of limestone and cement pastes. Cem. Concr. Res. 2008, 38, 907–919. [Google Scholar] [CrossRef]
- Brumaud, C.; Baumann, R.; Schmitz, M.; Radler, M.; Roussel, N. Cellulose ethers and yield stress of cement pastes. Cem. Con. Res. 2014, 55, 14–21. [Google Scholar] [CrossRef]
- Sonebi, M.; Lachemi, M.; Hossain, K.M.A. Optimisation of rheological parameters and mechanical properties of superplasticised cement grouts containing metakaolin and viscosity modifying admixture. Constr. Build. Mater. 2013, 38, 126–138. [Google Scholar] [CrossRef]
- Spychał, E.; Czapik, P. The Influence of HEMC on Cement and Cement-Lime Composites Setting Processes. Materials 2020, 13, 5814. [Google Scholar] [CrossRef]
- Chen, N.; Wang, P.; Zhao, L.; Zhang, G. Water retention mechanism of HPMC in cement mortar. Materials 2020, 13, 2918. [Google Scholar] [CrossRef] [PubMed]
- Vyšvařil, M.; Hegrová, M.; Žižlavský, T. Influence of cellulose ethers on fresh state properties of lime mortars. Solid State Phenom. 2018, 276, 69–74. [Google Scholar] [CrossRef]
- Paiva, H.; Esteves, L.; Cachim, P.; Ferreira, V. Rheology and hardened properties of single-coat render mortars with different types of water retaining agents. Constr. Build. Mater. 2009, 23, 1141–1146. [Google Scholar] [CrossRef]
- Lyashenko, T.; Kryukovskaya, S. Modelling the influence of composition on rheological parameters and mechanical properties of fibre reinforced polymer-cement mortars. In Proceedings of International Symposium Brittle matrix composites 10, Warsaw, Poland, 15–17 October 2012; Brandt, A.M., Olek, J., Glinicki, M.A., Leung, C.K.Y., Eds.; Woodhead Publ. Ltd.: Cambridge, UK, 2013; pp. 177–186. [Google Scholar] [CrossRef]
- Xu, W.; Tian, M.; Li, Q. Time-dependent rheological properties and mechanical performance of fresh cemented tailings backfill containing flocculants. Miner. Eng. 2020, 145, 106064. [Google Scholar] [CrossRef]
- Silva, B.A.; Ferreira Pinto, A.P.; Gomes, A.; Candeias, A. Impact of a viscosity-modifying admixture on the properties of lime mortars. J. Build. Eng. 2020, 31, 101132. [Google Scholar] [CrossRef]
- Wallevik, O.H.; Feys, D.; Wallevik, J.E.; Khayat, K.H. Avoiding inaccurate interpretations of rheological measurements for cement-based materials. Cem. Concr. Res. 2015, 78, 100–109. [Google Scholar] [CrossRef]
- Taylor, H.F. Cement Chemistry, 2nd ed.; Thomas Telford Ltd.: London, UK, 1997. [Google Scholar] [CrossRef]
- Uriev, N.B.; Ivanov, Y.P. Strukturoobrazovaniye i Reologiya Neorganicheskikh Dispersnykh Sistem i Materialov (Structure Formation and Rheology of Inorganic Disperse Systems and Materials); BAN: Sofia, Bulgaria, 1991. [Google Scholar]
- Rebinder, P.A. Fiziko-Khimicheskaya Mekhanika Novaya Oblast’ Nauki (Physicochemical Mechanics is a New Field of Science); Znaniye: Moscow, Russia, 1958. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013; p. 725. Available online: http://www.ru.ac.bd/stat/wp-content/uploads/sites/25/2019/03/502_06_Montgomery-Design-and-analysis-of-experiments-2012.pdf (accessed on 16 November 2021).
- Вознесенский, В.А.; Выровой, В.Н.; Керш, В.Я.; Ляшенко, Т.В.; Азарова, С.Я.; Гризан, Ю.М.; Коваль, С.В.; Можарова, Л.А.; Трофимова, Л.Е. Sovremennyye Metody Optimizatsii Kompozitsionnykh Materialov (Contemporary Methods of Optimization of Composite Materials); Budivelnik: Kiev, Ukraine, 1983; p. 144. Available online: http://mx.ogasa.org.ua/handle/123456789/7573 (accessed on 28 December 2021).
- Lyashenko, T.V.; Voznesensky, V.A. Composition-Process Fields Methodology in Computational Building Materials Science; Astroprint: Odessa, Ukraine, 2017; p. 168. Available online: http://mx.ogasa.org.ua/handle/123456789/3665 (accessed on 28 November 2021). (In Russian)
- Nizina, T.A.; Balukov, A.S. Eksperimentalno-statisticheskie modeli svoystv modificirovannyh dispersnoarmirovannyh melkozernistyh betonov (Experimental-statistical models of properties of modified fiber-reinforced fine-grained concretes). Mag. Civ. Eng. 2016, 62, 13–25. [Google Scholar] [CrossRef]
- Koval, S. Optimizatsiya reologicheskikh parametrov matritsy samouplotnyayushchegosya betona s ispolzovaniyem modeley «smes–tekhnologiya–svoystva» (Optimization of the rheological parameters of matrix of self-compacting concrete with the use of models «mixture–technology–properties»). Bull. Natl. Tech. Univ. «KhPI» 2011, 59, 86–92. Available online: http://library.kpi.kharkov.ua/files/Vestniki/2011_59.pdf (accessed on 25 November 2021).
- Voznesensky, V.A.; Lyashenko, T.V.; Ivanov, Y.P.; Nikolov, I.I. EVM i Optimizaciya Kompozicionnyh Materialov (Computers and Optimization of Composite Materials); Budivelnik: Kiev, Ukraine, 1989; p. 240. Available online: http://mx.ogasa.org.ua/handle/123456789/332 (accessed on 25 November 2021).
- Lyashenko, T.V.; Voznesensky, V.A. Experimental-statistical modeling in computational materials science. In Proceedings of 3rd International Applied Statistics in Industry Conference, Dallas, TX, USA, 5–7 June 1995; pp. 287–298. Available online: https://drive.google.com/file/d/0BzKYSjvwhyiecDl2enEta0dQc28/view (accessed on 17 November 2021).
- DIN 18555-7:2019-04. Testing of Mortars Containing Mineral Binders—Part 7: Determination of the Water Retention Value of Fresh Mortars by the Filter Plate Method; Beuth Verlag: Berlin, Germany, 2019; p. 8. [Google Scholar] [CrossRef]
- DIN 53019-1:2008-09. Viscometry—Measurement of Viscosities and Flow Curves by Means of Rotational Viscometers—Part 1: Principles and Measuring Geometry; Beuth Verlag: Berlin, Germany, 2008; p. 22. [Google Scholar] [CrossRef]
- Schramm, G. A Practical Approach to Rheology and Rheometry, 2rd ed.; Gebrueder Haake: Karlsruhe, Germany, 1994; p. 290. [Google Scholar]
- Derec, C.; Ducouret, G.; Ajdari, A.; Lequeux, F. Aging and nonlinear rheology in suspensions of polyethylene oxide-protected silica particles. Phys. Rev. 2003, 67, 61403. [Google Scholar] [CrossRef]
- Mason, T.G.; Bibette, J.; Weitz, D.A. Yielding and flow of monodisperse emulsions. J. Colloid Interface Sci. 1996, 179, 439–448. [Google Scholar] [CrossRef] [Green Version]
- Nachbaur, L.; Mutin, J.C.; Nonat, A.; Choplin, L. Dynamic mode rheology of cement and tricalcium silicate pastes from mixing to setting. Cem. Concr. Res. 2001, 31, 183–192. [Google Scholar] [CrossRef]
- Bouras, R.; Chaouche, M.; Kaci, S. Influence of viscosity-modifying admixtures on the thixotropic behaviour of cement pastes. Appl. Rheol. 2008, 18, 45604-1–45604-8. [Google Scholar] [CrossRef]
- Schwartzentruber, D.A.L.; Le Roy, R.; Cordin, J. Rheological behaviour of fresh cement pastes formulated from a Self Compacting Concrete (SCC). Cem. Concr. Res. 2006, 36, 1203–1213. [Google Scholar] [CrossRef]
- Ortiz-Álvarez, N.; Lizarazo-Marriaga, J.; Brando, P.; Santos-Panqueva, Y.; Carrillo, J. Rheological properties of cement-based materials using a biopolymer viscosity modifying admixture (BVMA) under different dispersion conditions. Cem. Concr. Comp. 2021, 124, 104224. [Google Scholar] [CrossRef]
- Benli, A.; Karatas, M.; Toprak, H.A. Mechanical characteristics of self-compacting mortars with raw and expanded vermiculite as partial cement replacement at elevated temperatures. Constr. Build. Mat. 2020, 239, 117895. [Google Scholar] [CrossRef]
- Kotwica, Ł.; Pichór, W.; Nocuń-Wczelik, W. Study of pozzolanic action of ground waste expanded perlite by means of thermal methods. J. Therm. Anal. Calorim. 2016, 123, 607–613. [Google Scholar] [CrossRef] [Green Version]
- Barnes, H.A.; Hutton, J.F.; Walters, K. An Introduction to Rheology, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1989; p. 200. Available online: http://150.254.87.41/SERP-Chem/C/books/rheology/An%20Introduction%20to%20Rheology.pdf (accessed on 25 November 2021).
- Baldino, N.; Gabriele, D.; Lupi, F.R.; Seta, L.; Zinno, R. Rheological behaviour of fresh cement pastes: Influence of synthetic zeolites, limestone and silica fume. Cem. Concr. Res. 2014, 63, 38–45. [Google Scholar] [CrossRef]
- Lowke, D. Thixotropy of SCC–A model describing the effect of particle packing and superplasticizer adsorption on thixotropic structural build-up of the mortar phase based on interparticle interactions. Cem. Concr. Res. 2018, 104, 94–104. [Google Scholar] [CrossRef]
- Lyashenko, T.; Voznesensky, V.; Ivanov, Y.; Pischeva, T. Ispolzovaniye metodov Monte-Karlo pri analize vzaimosvyazi mezhdu polyami reologicheskikh pokazateley kompozitsiy dlya otdelochnykh rabot (On the use of Monte Carlo methods for the analysis of the interrelation between rheological characteristics of finishing composites). Bull. Odessa State Acad. Civ. Eng. Archit. 2001, 3, 57–64. Available online: http://mx.ogasa.org.ua/handle/123456789/927 (accessed on 21 December 2021). (In Russian).
- Kroese, D.P.; Chan, J.C.C. Statistical Modeling and Computation, 1st ed.; Springer: New York, NY, USA, 2014; p. 400. [Google Scholar] [CrossRef]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today. WIREs Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Lyashenko, T.V. Does Abrasion resistance correlate to strength? Bull. Odessa State Acad. Civ. Eng. Archit. 2016, 64, 153–159. Available online: http://mx.ogasa.org.ua/bitstream/123456789/589/1/Does%20abrasion%20resistance%20correlate%20to%20strength.pdf (accessed on 17 November 2021).



| Mixture Components | Basic Characteristics |
|---|---|
| Portland cement | Additive-free cement produced by “Baltsem” M500 mark (PC I-500-N D0) (European quality certificate EN-197-1, CEM I 42.5 N). Specific surface is 300 m2/kg and fineness is 11.3% |
| Calcium hydroxide | Contention of CaO + MgO—73% by weight, water demand is 70%, bulk density is 0.5 kg/dm3 |
| Limestone shell rock | Shell rock, with specific surface Ss.d. = 400 m2/kg, sifted through a sieve of 0.63 mm. |
| Quartz sand | Quartz sand from the Volnogorsk Mining and Metallurgical Combine. Density of quartz is 2.04 g/cm3, the particle size modulus is 1.1, the content of dust and clay particles is 0.3%, the clay content in the lumps is 0%, and the moisture content is 3.6%. The work used sand sifted through a sieve of 0.63. |
| Perlite sand | Perlite sand from the Beregovsky quarry of the Transcarpathian region. Expanded perlite fraction 0.16–1.05, grade in terms of bulk density 100, bulk density is 80 kg/m3, heat conductance at 25 ± 5 °C no more 0.052 Wt/m °C |
| Tylose MH60010 | Water-retaining additive, methyl hydroxyethyl cellulose. Tylose is a water-soluble non-ionic cellulose ether, which is a derivative of the natural cellulose material. |
| Vinnapas RE5034 N | Adhesion improving additive, copolymer of vinyl chloride, ethylene, and vinyl laurate |
| Hostapur OSB | Air-entraining additive. Humidity—2%, sodium sulfate content of not more than 5.5%, potassium carbonate content of not more than 4%, bulk density—0.3 t/m3 |
| Vinnapas 8031H | Water repellent, a triple copolymer of ethylene, vinyl laurate, and vinyl chloride. Bulk weight–450 ± 50 g/L, preferred particle size 0.3–9 microns, minimum glass transition temperature about 0 °C. |
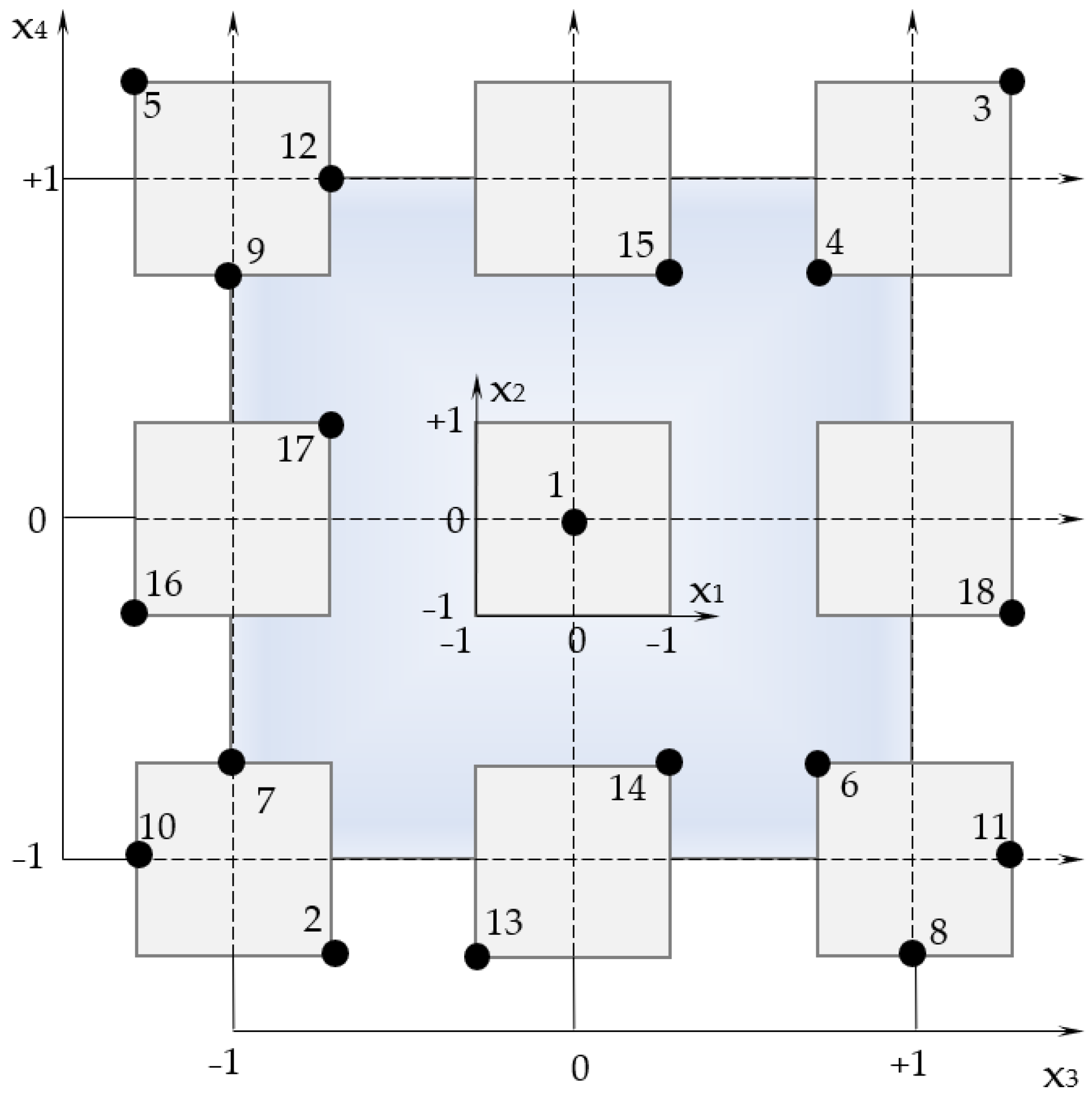
| Number of Composition | Normalised Levels | Dosages (w.p. in 1000 w.p. of Dry Mix) | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | Limestone | Perlite | Tylose | Vinnapas | |
| 1 | 0 | 0 | 0 | 0 | 80 | 40 | 1.15 | 1.5 |
| 2 | 1 | −1 | −1 | −1 | 100 | 30 | 1 | 1 |
| 3 | 1 | 1 | 1 | 1 | 100 | 50 | 1.3 | 2 |
| 4 | −1 | −1 | 1 | 1 | 60 | 30 | 1.3 | 2 |
| 5 | −1 | 1 | −1 | 1 | 60 | 50 | 1 | 2 |
| 6 | −1 | 1 | 1 | −1 | 60 | 50 | 1.3 | 1 |
| 7 | 0 | 1 | −1 | −1 | 80 | 50 | 1 | 1 |
| 8 | 0 | −1 | 1 | −1 | 80 | 30 | 1.3 | 1 |
| 9 | 0 | −1 | −1 | 1 | 80 | 30 | 1 | 2 |
| 10 | −1 | 0 | −1 | −1 | 60 | 40 | 1 | 1 |
| 11 | 1 | 0 | 1 | −1 | 100 | 40 | 1.3 | 1 |
| 12 | 1 | 0 | −1 | 1 | 100 | 40 | 1 | 2 |
| 13 | −1 | −1 | 0 | −1 | 60 | 30 | 1.15 | 1 |
| 14 | 1 | 1 | 0 | −1 | 100 | 50 | 1.15 | 1 |
| 15 | 1 | −1 | 0 | 1 | 100 | 30 | 1.15 | 2 |
| 16 | −1 | −1 | −1 | 0 | 60 | 30 | 1 | 1.5 |
| 17 | 1 | 1 | −1 | 0 | 100 | 50 | 1 | 1.5 |
| 18 | 1 | −1 | 1 | 0 | 100 | 30 | 1.15 | 1.5 |
| No | Viscosity η1 (Pa·s) | The Error of Ostwald–de–Waele Model | Destruction Rate |m| | Thixotropy Ath (Wt/m3) |
|---|---|---|---|---|
| 1 | 425 | 0.04 | 0.86 | 215 |
| 2 | 120 | 0.89 | 1.02 | 153 |
| 3 | 303 | 0.99 | 0.89 | 370 |
| 4 | 226 | 0.13 | 0.84 | 201 |
| 5 | 200.6 | 0.06 | 0.95 | 183 |
| 6 | 123.9 | 0.09 | 1.07 | 137 |
| 7 | 122.8 | 0.40 | 0.94 | 98 |
| 8 | 186.3 | 0.09 | 0.96 | 252 |
| 9 | 148.5 | 0.05 | 1.02 | 96 |
| 10 | 102.5 | 0.08 | 1.05 | 100 |
| 11 | 97.5 | 0.09 | 1.15 | 97 |
| 12 | 190.6 | 0.08 | 0.91 | 49 |
| 13 | 63.1 | 0.13 | 1.21 | 60 |
| 14 | 241.3 | 0.07 | 0.93 | 230 |
| 15 | 269.3 | 0.05 | 0.86 | 78 |
| 16 | 105.5 | 0.10 | 1.01 | 94 |
| 17 | 156.9 | 0.08 | 1.14 | 150 |
| 18 | 54.2 | 0.14 | 1.24 | 55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moskalova, K.; Lyashenko, T.; Aniskin, A. Modelling the Relations of Rheological Characteristics with Composition of Plaster Mortar. Materials 2022, 15, 371. https://doi.org/10.3390/ma15010371
Moskalova K, Lyashenko T, Aniskin A. Modelling the Relations of Rheological Characteristics with Composition of Plaster Mortar. Materials. 2022; 15(1):371. https://doi.org/10.3390/ma15010371
Chicago/Turabian StyleMoskalova, Khrystyna, Tatiana Lyashenko, and Aleksej Aniskin. 2022. "Modelling the Relations of Rheological Characteristics with Composition of Plaster Mortar" Materials 15, no. 1: 371. https://doi.org/10.3390/ma15010371
APA StyleMoskalova, K., Lyashenko, T., & Aniskin, A. (2022). Modelling the Relations of Rheological Characteristics with Composition of Plaster Mortar. Materials, 15(1), 371. https://doi.org/10.3390/ma15010371








