Bandstructure and Size-Scaling Effects in the Performance of Monolayer Black Phosphorus Nanodevices
Abstract
:1. Introduction
2. Methods
2.1. DFT-Based Tight-Binding Hamiltonian
2.2. Quantum Transport with NEGF

2.3. Top-of-the-Barrier Device Model
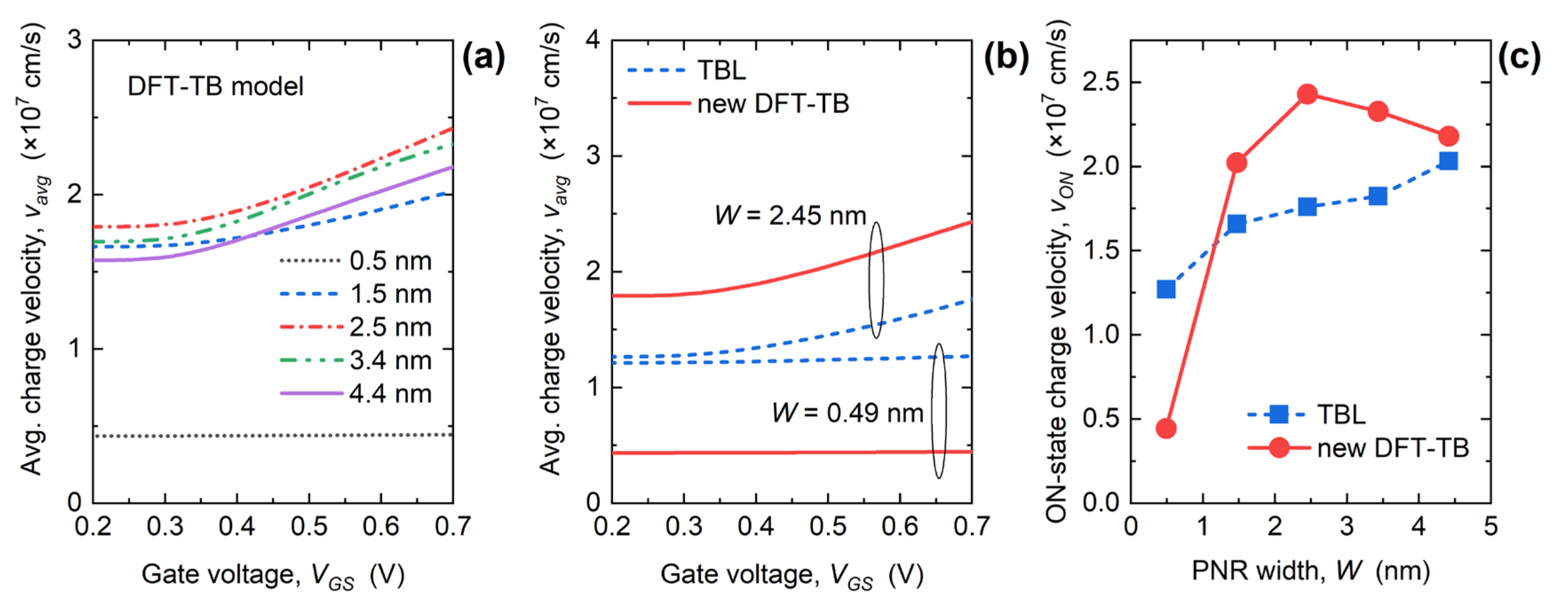
3. Results and Discussions
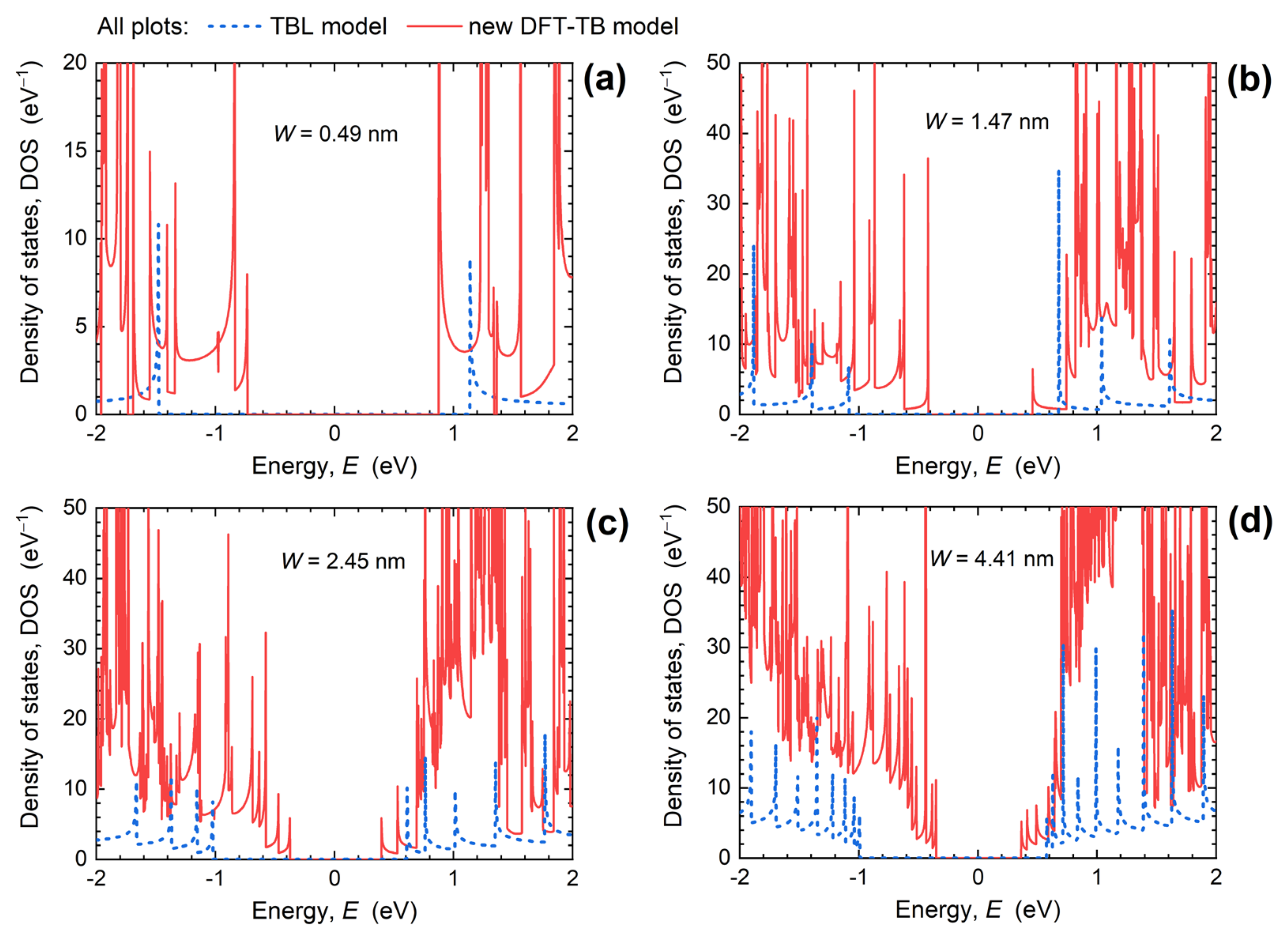
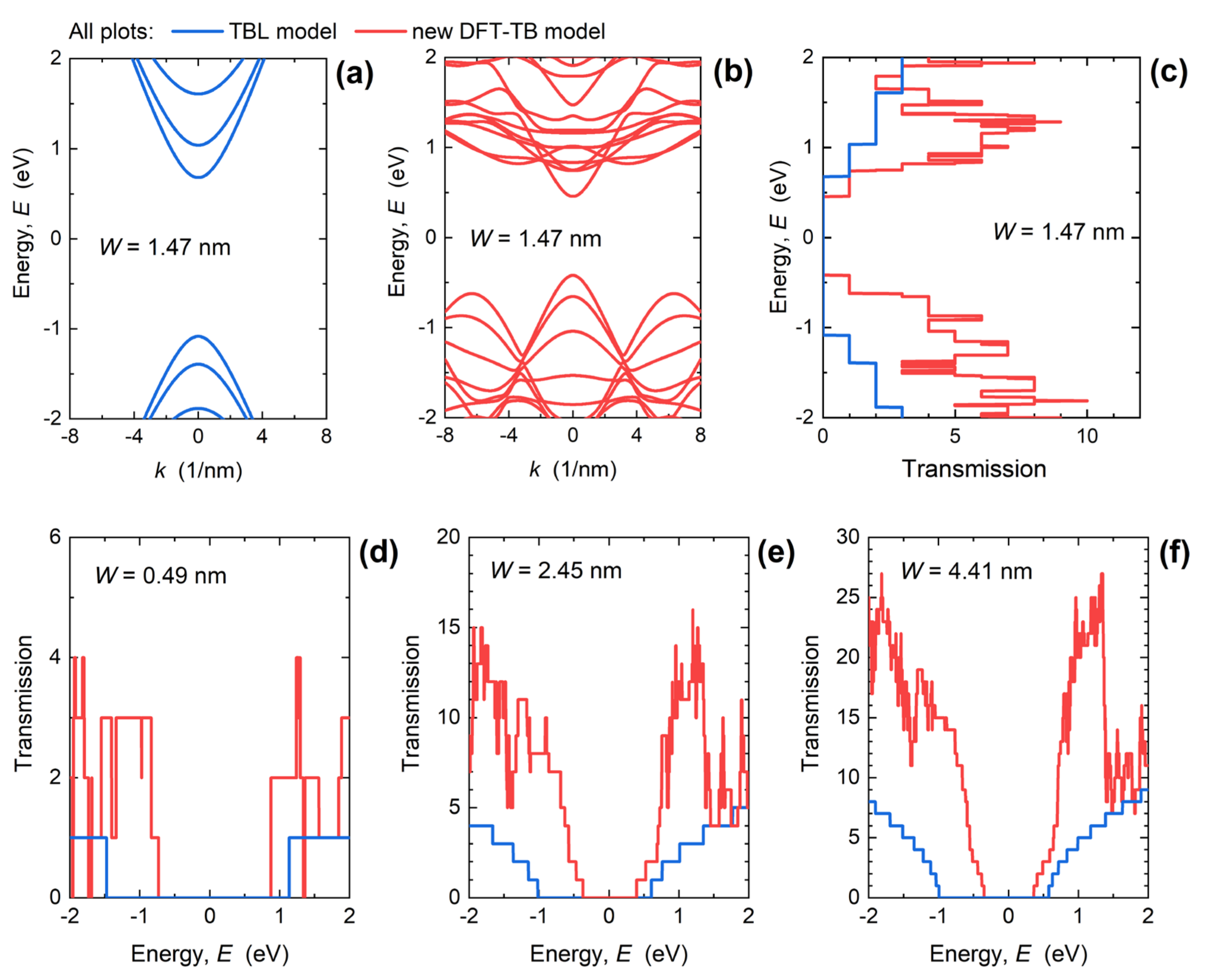
3.1. Electronic and Transport Properties of Ultra-Narrow PNRs
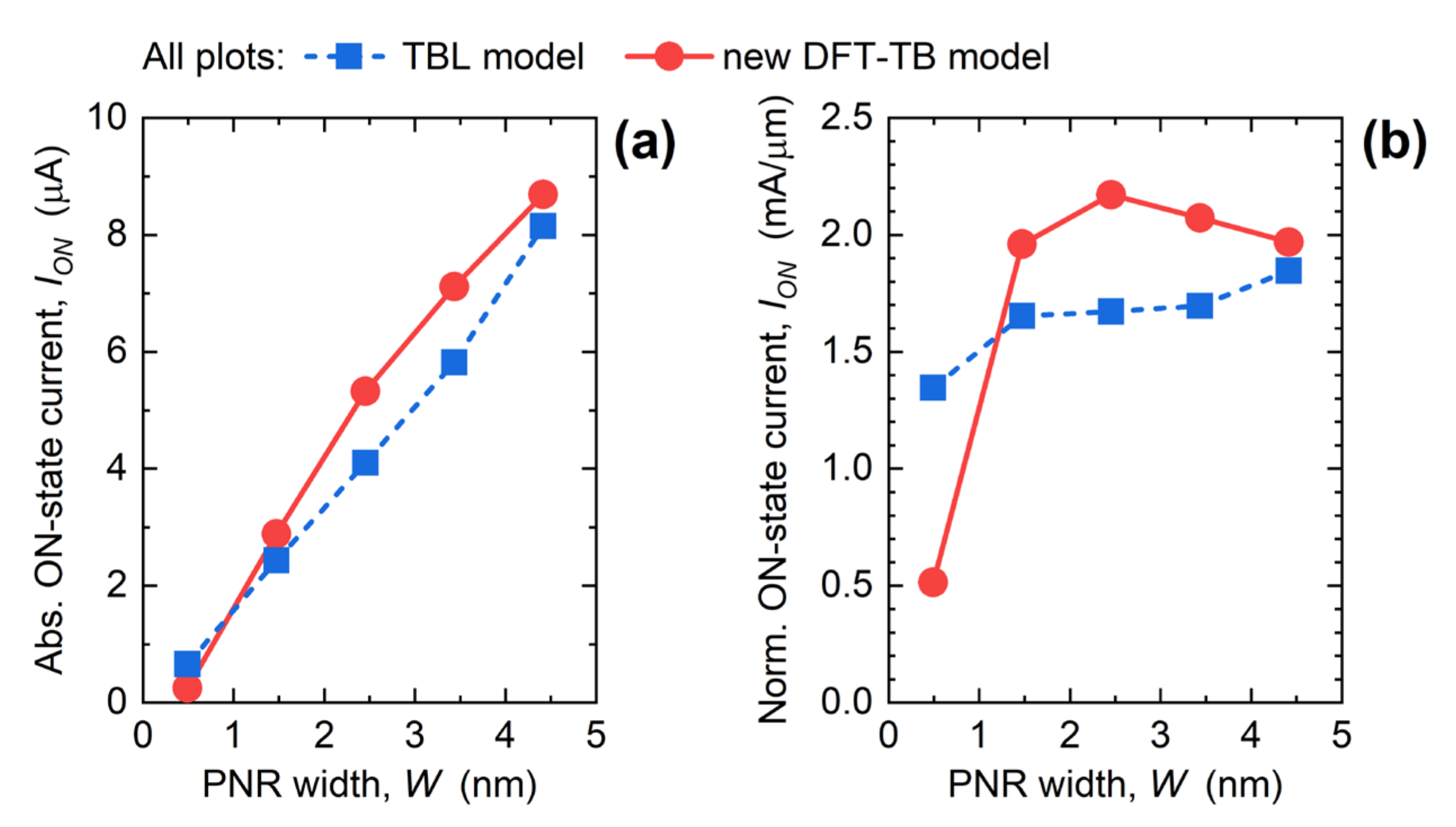
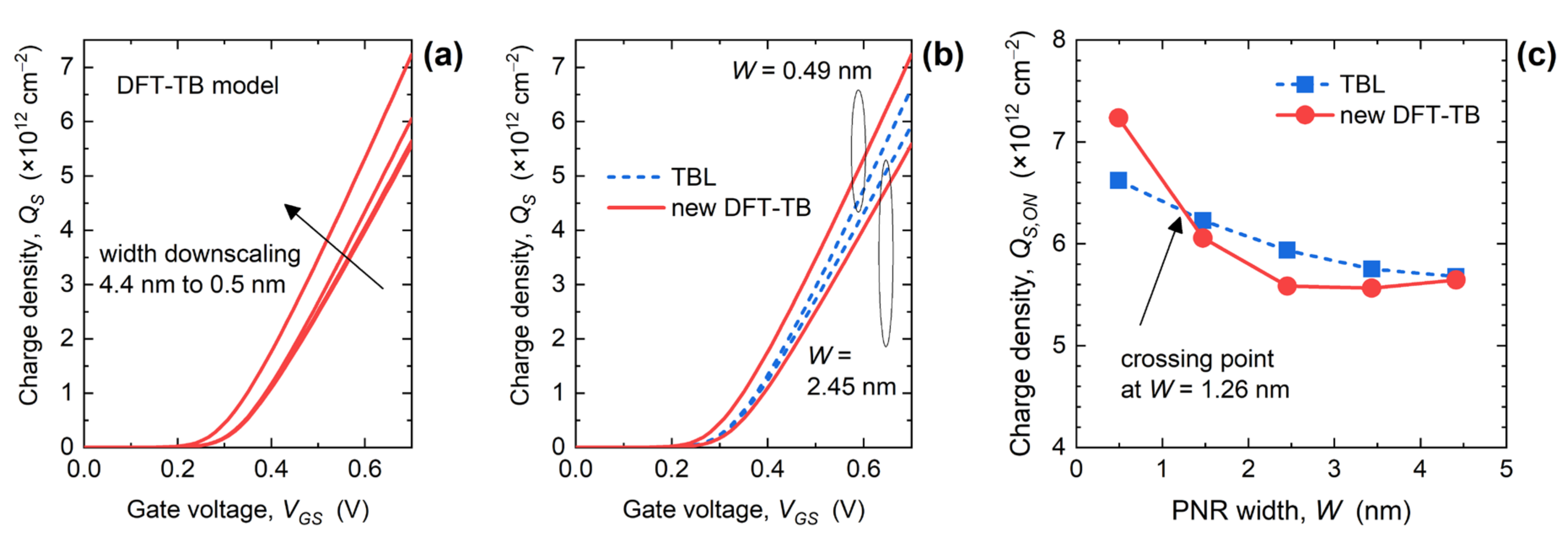
3.2. Performance of Ultra-Scaled PNR FETs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, S.; Demarteau, M.; Roelofs, A. Ambipolar Phosphorene Field Effect Transistor. ACS Nano 2014, 8, 11730–11738. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black Phosphorus Field-Effect Transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haratipour, N.; Robbins, M.C.; Koester, S.J. Black Phosphorus P-MOSFETs with 7-Nm HfO2 Gate Dielectric and Low Contact Resistance. IEEE Electron Device Lett. 2015, 36, 411–413. [Google Scholar] [CrossRef]
- Klinkert, C.; Szabó, Á.; Stieger, C.; Campi, D.; Marzari, N.; Luisier, M. 2-D Materials for Ultrascaled Field-Effect Transistors: One Hundred Candidates under the Ab Initio Microscope. ACS Nano 2020, 14, 8605–8615. [Google Scholar] [CrossRef]
- Cao, X.; Guo, J. Simulation of Phosphorene Field-Effect Transistor at the Scaling Limit. IEEE Trans. Electron Devices 2015, 62, 659–665. [Google Scholar] [CrossRef]
- Guo, H.; Lu, N.; Dai, J.; Wu, X.; Zeng, X.C. Phosphorene Nanoribbons, Phosphorus Nanotubes, and van Der Waals Multilayers. J. Phys. Chem. C 2014, 118, 14051–14059. [Google Scholar] [CrossRef] [Green Version]
- Taghizadeh Sisakht, E.; Zare, M.H.; Fazileh, F. Scaling Laws of Band Gaps of Phosphorene Nanoribbons: A Tight-Binding Calculation. Phys. Rev. B 2015, 91, 085409. [Google Scholar] [CrossRef] [Green Version]
- Poljak, M.; Suligoj, T. Immunity of Electronic and Transport Properties of Phosphorene Nanoribbons to Edge Defects. Nano Res. 2016, 9, 1723–1734. [Google Scholar] [CrossRef]
- Poljak, M.; Suligoj, T. The Potential of Phosphorene Nanoribbons as Channel Material for Ultrascaled Transistors. IEEE Trans. Electron Devices 2018, 65, 290–294. [Google Scholar] [CrossRef]
- Watts, M.C.; Picco, L.; Russell-Pavier, F.S.; Cullen, P.L.; Miller, T.S.; Bartuś, S.P.; Payton, O.D.; Skipper, N.T.; Tileli, V.; Howard, C.A. Production of Phosphorene Nanoribbons. Nature 2019, 568, 216–220. [Google Scholar] [CrossRef]
- Zhang, W.; Enriquez, H.; Tong, Y.; Mayne, A.J.; Bendounan, A.; Smogunov, A.; Dappe, Y.J.; Kara, A.; Dujardin, G.; Oughaddou, H. Flat Epitaxial Quasi-1D Phosphorene Chains. Nat. Commun. 2021, 12, 5160. [Google Scholar] [CrossRef]
- Luisier, M.; Klimeck, G. Atomistic Full-Band Simulations of Silicon Nanowire Transistors: Effects of Electron-Phonon Scattering. Phys. Rev. B 2009, 80, 155430. [Google Scholar] [CrossRef] [Green Version]
- Pizzi, G.; Gibertini, M.; Dib, E.; Marzari, N.; Iannaccone, G.; Fiori, G. Performance of Arsenene and Antimonene Double-Gate MOSFETs from First Principles. Nat. Commun. 2016, 7, 12585. [Google Scholar] [CrossRef] [Green Version]
- Afzalian, A.; Pourtois, G. ATOMOS: An ATomistic MOdelling Solver for Dissipative DFT Transport in Ultra-Scaled HfS2 and Black Phosphorus MOSFETs. In Proceedings of the 2019 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Udine, Italy, 4–6 September 2019; pp. 1–4. [Google Scholar]
- Marin, E.G.; Perucchini, M.; Marian, D.; Iannaccone, G.; Fiori, G. Modeling of Electron Devices Based on 2-D Materials. IEEE Trans. Electron Devices 2018, 65, 4167–4179. [Google Scholar] [CrossRef]
- Afzalian, A.; Akhoundi, E.; Gaddemane, G.; Duflou, R.; Houssa, M. Advanced DFT–NEGF Transport Techniques for Novel 2-D Material and Device Exploration Including HfS2/WSe2 van Der Waals Heterojunction TFET and WTe2/WS2 Metal/Semiconductor Contact. IEEE Trans. Electron Devices 2021, 68, 5372–5379. [Google Scholar] [CrossRef]
- Afzalian, A. Ab Initio Perspective of Ultra-Scaled CMOS from 2D-Material Fundamentals to Dynamically Doped Transistors. npj 2D Mater. Appl. 2021, 5, 5. [Google Scholar] [CrossRef]
- Rudenko, A.N.; Katsnelson, M.I. Quasiparticle Band Structure and Tight-Binding Model for Single- and Bilayer Black Phosphorus. Phys. Rev. B 2014, 89, 201408. [Google Scholar] [CrossRef] [Green Version]
- Poljak, M. Electron Mobility in Defective Nanoribbons of Monoelemental 2D Materials. IEEE Electron Dev. Lett. 2020, 41, 151–154. [Google Scholar] [CrossRef]
- Yin, D.; Yoon, Y. Design Strategy of Two-Dimensional Material Field-Effect Transistors: Engineering the Number of Layers in Phosphorene FETs. J. Appl. Phys. 2016, 119, 214312. [Google Scholar] [CrossRef]
- Poljak, M.; Matić, M.; Zeljko, A. Minimum Contact Resistance in Monoelemental 2D Material Nanodevices with Edge-Contacts. IEEE Electron Device Lett. 2021, 42, 1240–1243. [Google Scholar] [CrossRef]
- Liang, L.; Wang, J.; Lin, W.; Sumpter, B.G.; Meunier, V.; Pan, M. Electronic Bandgap and Edge Reconstruction in Phosphorene Materials. Nano Lett. 2014, 14, 6400–6406. [Google Scholar] [CrossRef]
- Poljak, M.; Matić, M. Bandstructure Effects in Phosphorene Nanoribbon MOSFETs from NEGF Simulations Using a New DFT-Based Tight-Binding Hamiltonian Model. In Proceedings of the 2021 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Dallas, TX, USA, 27–29 September 2021; pp. 180–183. [Google Scholar]
- Poljak, M.; Matić, M. DFT-Based Tight-Binding Model for Atomistic Simulations of Phosphorene Nanoribbons. In Proceedings of the 2021 44th International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 27 September–1 October 2021; pp. 80–84. [Google Scholar]
- Ozaki, T. Variationally Optimized Atomic Orbitals for Large-Scale Electronic Structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- OpenMX Website. Available online: http://www.openmx-square.org/ (accessed on 9 February 2021).
- Nakhaee, M.; Ketabi, S.A.; Peeters, F.M. Tight-Binding Studio: A Technical Software Package to Find the Parameters of Tight-Binding Hamiltonian. Comput. Phys. Commun. 2020, 254, 107379. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Poljak, M.; Song, E.B.; Wang, M.; Suligoj, T.; Wang, K.L. Influence of Edge Defects, Vacancies, and Potential Fluctuations on Transport Properties of Extremely Scaled Graphene Nanoribbons. IEEE Trans. Electron Devices 2012, 59, 3231–3238. [Google Scholar] [CrossRef]
- Poljak, M.; Glavan, M.; Kuzmić, S. Accelerating Simulation of Nanodevices Based on 2D Materials by Hybrid CPU-GPU Parallel Computing. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019; pp. 51–56. [Google Scholar]
- Sancho, M.P.L.; Sancho, J.M.L.; Sancho, J.M.L.; Rubio, J. Highly Convergent Schemes for the Calculation of Bulk and Surface Green Functions. J. Phys. F Met. Phys. 1985, 15, 851. [Google Scholar] [CrossRef]
- Poljak, M.; Matić, M. Metallization-Induced Quantum Limits of Contact Resistance in Graphene Nanoribbons with One-Dimensional Contacts. Materials 2021, 14, 3670. [Google Scholar] [CrossRef] [PubMed]
- Datta, S. Quantum Transport: Atom to Transistor, 2nd ed.; Cambridge University Press: New York, NY, USA, 2005; ISBN 0-521-63145-9. [Google Scholar]
- Poljak, M. Intrinsic Capabilities for Digital Switching of Silicene Nanoribbons with Edge Defects. IEEE Trans. Electron Devices 2020, 67, 354–359. [Google Scholar] [CrossRef]
- Rahman, A.; Guo, J.; Datta, S.; Lundstrom, M.S. Theory of Ballistic Nanotransistors. IEEE Trans. Electron Devices 2003, 50, 1853–1864. [Google Scholar] [CrossRef] [Green Version]
- Kaneko, S.; Tsuchiya, H.; Kamakura, Y.; Mori, N.; Ogawa, M. Theoretical Performance Estimation of Silicene, Germanene, and Graphene Nanoribbon Field-Effect Transistors under Ballistic Transport. Appl. Phys. Express 2014, 7, 035102. [Google Scholar] [CrossRef]
- Carvalho, A.; Rodin, A.S.; Neto, A.H.C. Phosphorene Nanoribbons. Europhys. Lett. 2014, 108, 47005. [Google Scholar] [CrossRef]
- IEEE International Roadmap for Devices and Systems (IRDS), 2021 Edition. Available online: https://irds.ieee.org/ (accessed on 1 October 2021).
- Gaddemane, G.; Vandenberghe, W.G.; Van de Put, M.L.; Chen, S.; Tiwari, S.; Chen, E.; Fischetti, M.V. Theoretical Studies of Electronic Transport in Monolayer and Bilayer Phosphorene: A Critical Overview. Phys. Rev. B 2018, 98, 115416. [Google Scholar] [CrossRef] [Green Version]
- Gaddemane, G.; Van de Put, M.L.; Vandenberghe, W.G.; Chen, E.; Fischetti, M.V. Monte Carlo Analysis of Phosphorene Nanotransistors. J. Comput. Electron. 2021, 20, 60–69. [Google Scholar] [CrossRef]
- Driussi, F.; Venica, S.; Gahoi, A.; Gambi, A.; Giannozzi, P.; Kataria, S.; Lemme, M.C.; Palestri, P.; Esseni, D. Improved Understanding of Metal–Graphene Contacts. Microelectron. Eng. 2019, 216, 111035. [Google Scholar] [CrossRef]
- Gahoi, A.; Kataria, S.; Driussi, F.; Venica, S.; Pandey, H.; Esseni, D.; Selmi, L.; Lemme, M.C. Dependable Contact Related Parameter Extraction in Graphene–Metal Junctions. Adv. Electron. Mater. 2020, 6, 2000386. [Google Scholar] [CrossRef]
- Du, Y.; Liu, H.; Deng, Y.; Ye, P.D. Device Perspective for Black Phosphorus Field-Effect Transistors: Contact Resistance, Ambipolar Behavior, and Scaling. ACS Nano 2014, 8, 10035–10042. [Google Scholar] [CrossRef] [Green Version]
- Telesio, F.; le Gal, G.; Serrano-Ruiz, M.; Prescimone, F.; Toffanin, S.; Peruzzini, M.; Heun, S. Ohmic Contact Engineering in Few–Layer Black Phosphorus: Approaching the Quantum Limit. Nanotechnology 2020, 31, 334002. [Google Scholar] [CrossRef]
- Poljak, M.; Matić, M. Quantum Transport Simulations of Phosphorene Nanoribbon MOSFETs: Effects of Metal Contacts, Ballisticity and Series Resistance. In Proceedings of the 2020 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Kobe, Japan, 23 September–6 October 2020; pp. 371–374. [Google Scholar]
- Poljak, M. Impact of Width Scaling and Parasitic Series Resistance on the Performance of Silicene Nanoribbon MOSFETs. IEEE Trans. Electron Devices 2020, 67, 4705–4708. [Google Scholar] [CrossRef]
- Szabo, A.; Rhyner, R.; Carrillo-Nunez, H.; Luisier, M. Phonon-Limited Performance of Single-Layer, Single-Gate Black Phosphorus n- and p-Type Field-Effect Transistors. In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 297–300. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poljak, M.; Matić, M. Bandstructure and Size-Scaling Effects in the Performance of Monolayer Black Phosphorus Nanodevices. Materials 2022, 15, 243. https://doi.org/10.3390/ma15010243
Poljak M, Matić M. Bandstructure and Size-Scaling Effects in the Performance of Monolayer Black Phosphorus Nanodevices. Materials. 2022; 15(1):243. https://doi.org/10.3390/ma15010243
Chicago/Turabian StylePoljak, Mirko, and Mislav Matić. 2022. "Bandstructure and Size-Scaling Effects in the Performance of Monolayer Black Phosphorus Nanodevices" Materials 15, no. 1: 243. https://doi.org/10.3390/ma15010243
APA StylePoljak, M., & Matić, M. (2022). Bandstructure and Size-Scaling Effects in the Performance of Monolayer Black Phosphorus Nanodevices. Materials, 15(1), 243. https://doi.org/10.3390/ma15010243





