Abstract
Structures located on the coast are subjected to the long-term influence of chloride ions, which cause the corrosion of steel reinforcements in concrete elements. This corrosion severely affects the performance of the elements and may shorten the lifespan of an entire structure. Even though experimental activities in laboratories might be a solution, they may also be problematic due to time and costs. Thus, the application of individual machine learning (ML) techniques has been investigated to predict surface chloride concentrations (Cc) in marine structures. For this purpose, the values of Cc in tidal, splash, and submerged zones were collected from an extensive literature survey and incorporated into the article. Gene expression programming (GEP), the decision tree (DT), and an artificial neural network (ANN) were used to predict the surface chloride concentrations, and the most accurate algorithm was then selected. The GEP model was the most accurate when compared to ANN and DT, which was confirmed by the high accuracy level of the K-fold cross-validation and linear correlation coefficient (R2), mean absolute error (MAE), mean square error (MSE), and root mean square error (RMSE) parameters. As is shown in the article, the proposed method is an effective and accurate way to predict the surface chloride concentration without the inconveniences of laboratory tests.
1. Introduction
Reinforced concrete (RC) structures are known for their longevity and resistance, which are very valuable in civil engineering practices [1]. This includes the construction of harbor docks, marine structures, and coastal roads. Concrete structures with both steel and composite reinforcement provide strong stability against corrosive action in an alkaline environment [2]. This is mainly due to the massive passive oxide film around reinforcing steel, which can be affected by the presence of chloride ions in sea and coastal structures [3]. These ions first accumulate on the surface of a RC structure and then slowly penetrate into the concrete element [4]. This ultimately demolishes the oxide film and provokes the corrosion of steel, which, in turn, leads to spalling and cracking of the concrete and the reduction of the load-carrying capacity of RC structures [5]. This process significantly reduces the serviceability of an RC structure, causing it to not last for the amount of time for which it was designed. The corrosion process of steel bars embedded in porous concrete is presented in Figure 1. Surface chloride concentrations affect the corrosion of steel and the performance of entire buildings and have a devastating effect in civil engineering [6,7,8]. The durability of a structure is an important parameter in RC buildings for maintaining an adequate service life of concrete structures [9]. Thus, predicting the design service life of concrete structures has become more popular in recent times. However, all prediction models are different and depend on influential factors and the destruction mechanisms of structures [10].
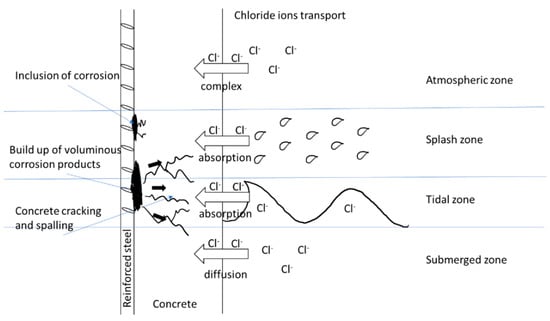
Figure 1.
Corrosion process caused by an aggressive chloride environment.
The appearance of chloride ions is a major issue in marine environments and has a very negative effect on RCC structures [11,12]. The possible transmission mechanism of chloride ions into concrete is dependent on the zone where the element is, i.e., the tidal, splash, submerged, and atmospheric zones [13]. The transport of chloride ions in concrete is mainly due to diffusion or the absorption mechanism [14]. The diffusion mechanism that occurs in the submerged zone is due to the saturation of the concrete. However, the absorption mechanism takes place in the tidal and splash zones. This allows the transport of chloride ions into RCC structures. However, the ingress of chloride ions in the atmospheric zone is quite complex when compared to the other zones [15]. This is because of factors associated with the zone, such as the direction and speed of the wind, the salinity level of the water reservoir, and the distance between the sea and the RCC structures. This study focuses on three zones, and omits the atmospheric zone due to its previously described limitations.
The ingress movement of chloride ions in RCC structures is calculated using Fick’s second law of diffusion, as shown in Equation (1). This is mostly used when designing the service life of structures located in a marine environment [16].
where
C(x,t)—chloride concentration at distance (x) from the surface after the time of exposure (t), mol/m3;
Co—concentration of chloride ions in concrete at the initial stage of their occurrence, mol/m3;
x—depth from the exposed concrete surface, mm;
D—coefficient of apparent chloride diffusion, mm2/s;
Cs—apparent surface chloride amount, mol/m3;
Erf—error function;
Co is constant and is not affected by any type of concrete. However, the movement of chloride ions in the marine environment is determined by Cs and D. The coefficient of apparent chloride diffusion is a material property that depends primarily on time. It can be determined based on information referring to the composition and microstructure of a material. Cs concentration in diffusion law has a complex nature, as it not only depends on a material’s properties, but also on the environmental conditions and time. This creates ambiguity when making an accurate prediction of chloride ingress in a marine environment. Therefore, studies are needed to build a strong model that uses machine learning approaches, which can accurately predict the amount of apparent surface chloride.
The aim of this study is to predict the surface chloride concentration in marine structures through the application of the gene expression programing algorithm. The levels of accuracy of GEP, DT and an ANN were evaluated and compared in order to choose the most accurate algorithm for the purpose of the study. The most effective algorithm was GEP when compared to DT and ANN. Statistical analyses and K-fold cross validation were used to check the accuracy and validity of all the models. The usability of the proposed algorithm was also compared with other algorithms in the literature, which was important for the purpose of this research.
2. Materials and Methods
2.1. Apparent Surface Chloride Content
The value of surface chloride concentration Cs is an important variable when describing the transmission of chloride into structures [17]. It is obtained on site, or during laboratory investigations, as depicted in Figure 2. It can be seen that a convention zone is present in the investigated concrete element of the marine structure; however, there is no such zone in the concrete element investigated during the laboratory tests. The value of Cs was obtained through the use of the bulk diffusion profile of chloride using a fitting curve. This variable is the most significant, as it describes the aggression of chloride, quantitative durability, and the prediction of service life of RCC structures.

Figure 2.
Schematic diagrams for determining Cs under different conditions.
It is worth mentioning that the Cs value used in the calculations is considered to be constant for the zone in which an element is located. This creates uncertainty due to the complex nature of chloride ion transmission, as it depends on many factors, such as material properties (cement composition, binder properties, and water-to-cement ratio), and environmental factors (zonation, chloride content, depth, relative humidity, and temperature). Many attempts have been made to predict apparent chloride concentrations using logarithmic and exponential functions, or by correlating a concentration with the binder-to-water ratio, material variables, and environmental effects. However, there is still no accurate prediction model that is based on only a small number of variables. In contrast, when using machine learning algorithms, prediction models are more accurate and might be successfully used [18]. In this article, 642 data samples obtained from the literature survey [19] were used to predict surface chloride concentrations through the use of machine learning algorithms.
2.2. Machine Learning (ML) and Ensemble Learning (EL) Approaches
Machine learning (ML) is used as an efficient way to predict the mechanical properties of concrete, and its exemplary use is illustrated in Table 1. ML algorithms are more effective than simple correlation models due to the fact that they use the values of more than one variable to predict surface chloride concentrations. Artificial neural networks (ANN), the decision tree (DT), support vector machines (SVM), random forests (RF), gene expression programming (GEP), and deep learning (DL) are the most common algorithms for analyzing the mechanical properties of concrete [20]. Behnood et al. [21] used an ANN with an optimizer as a multi-objective grey wolves (MOGW) model for predicting the mechanical response of silica fume concrete. Getahun et al. [22] used an ANN algorithm to very accurately predict the compressive strength and tensile strength of waste concrete. Ling et al. [23] predicted the compressive strength of concrete in marine environments using SVM and then compared the obtained results with ANN and DT models. It was proved that the SVM was the most accurate. Zaher et al. [24] predicted the compressive property of lightweight foamed concrete using various machine learning techniques. The authors concluded that the extreme learning machine (ELM) was the most accurate and it was successfully applied for predicting the compressive strength of concrete. Woubish et al. [25] used a machine learning approach for the assessment of the durability of reinforced concrete structures. The author revealed that machine learning techniques are useful and that they play a substantial role in predicting the durability of structures when compared to functional CO2 and Cl‒ ingress models. Suguru et al. [26] developed a model to automatically detect cracks in concrete structures with the use of machine learning. Photographs of concrete structures were used as learning data, and then deep learning was used to detect the cracks. Similarly, Wassim et al. [27] indicated that machine learning models have a high level of accuracy.

Table 1.
Prediction properties with different approaches.
2.3. Description of the Obtained Data
The data used to model the prediction of the surface chloride concentration are taken from published literature. These data were taken from articles describing the surface chloride concentrations in the tidal zone [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62], splash zone [49,50,54,55,60,63,64] and submerged zone [54,56,60,65,66,67,68]. The data consist of 12 inputs (cement, fine and coarse aggregate, silica fume, fly ash, blast furnace slag, superplasticizer, water, exposure time, annual mean temperature, chloride content, and exposure time) and one output (surface chloride concentration). Jupitar python was used to describe the distribution of each input parameter that was applied in the prediction model and is presented in Figure 3. It is well stated that the performance of a model is significantly affected by its variables [69]. The data variables that were used for modeling, with their ranges, are listed in Table 2 and Table 3.
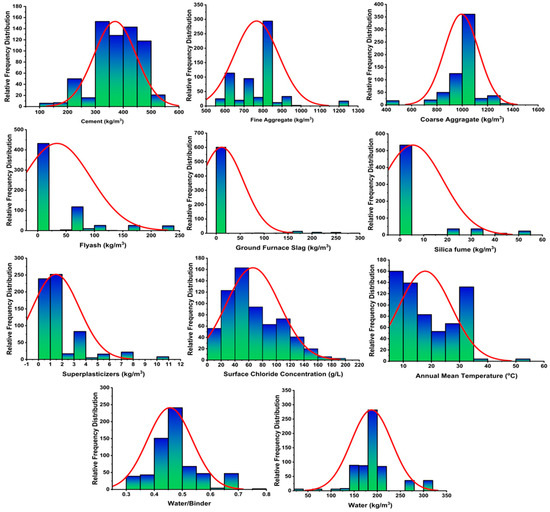
Figure 3.
The distribution of input parameters used in the prediction of models.

Table 2.
Range of input and output variables.

Table 3.
Descriptive analysis of parameters.
2.4. Machine Learning Algorithms
This section describes the algorithms used when modeling the prediction of surface chloride concentrations in the concrete elements of marine structures. The prediction of Cs was made using ANN, DT and GEP. A detailed flowchart of the used methodology is presented in Figure 4.
Figure 4.
Flowchart of the research approach.
The decision tree algorithm is based on a classification technique with supervised learning and is used to solve various computational problems with both a regression and classification nature. The tree-like structure of the decision tree can be used to solve the problem. In this algorithm, the nodes are divided into two consecutive sub-nodes up to the end nodes, which, in turn, determine the shape of the decision tree. The identification of the attributes from the root node at each level is considered to be a challenging task when using the decision tree algorithm. The whole procedure is called “the selection of attributes”. The division in the nodes is made on the basis of criteria. In the case of regression issues, the division is made by determining the point of separation, while in the case of classification issues, the criterion for division is the value of one of the classes. Different learning algorithms were used to split the nodes in order to obtain a convergence of the results. Moreover, a convergence of the results can also be obtained by using n number of trees in the algorithm.
ANN is considered to be one of the most popular machine learning algorithms. An ANN can be used for learning, predicting and making decisions based on input data. The basic datasets for ANN models include training, testing, and validation. During the training process, the ANN learns based on the patterns of the prediction model. The validation process evaluates the accuracy of the trained model. According to the literature survey, the feed forward and the feed forward back propagation (FFBP) neural networks are the most commonly used when solving engineering problems [70]. These types of ANN consist of input, hidden and output layers that contain neurons [71]. It is activated using the activation function, as can be seen in Figure 5.

Figure 5.
Scheme of the ANN.
GEP is a transformative algorithm that designs computer-based programs and models. These programs usually have a tree structure that is capable of modifying its size (size, shape and arrangement), like in the case of chromosomes. For this reason, GEP, being a genotype–phenotypic system, can be much more effective when compared to adaptive techniques. The programming language of GEP is known as Karva language and is the same as the LISP languages. The stages of GEP are shown in Figure 6. GEP has many advantages over other classical regression techniques, as, in other methods, some functions are initially defined and then analyzed. However, in GEP, no predefined function is taken into consideration.
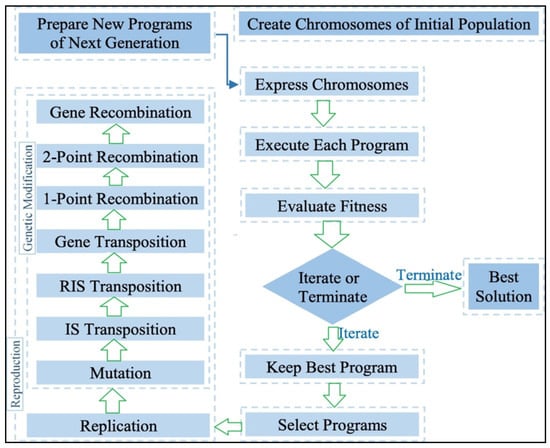
Figure 6.
Scheme of gene expression programming.
Machine learning algorithms, such as ANNs and ensemble models, are successfully used to predict the concentration of ions in various conditions. It is possible to predict the chloride concentration in columns at different heights above the water level. In such cases, the error of each individual estimation is less than 20% [72]. Moreover, the service life of a concrete element can be modeled based on the chloride concentration at different depths in a sample. Linear regression was used for this purpose. The accuracy obtained by the linear correlation coefficient varied from 0.83 to 1.0 and was dependent on the zone in which the element was located [73]. In turn, ensemble models were used to predict the surface chloride concentration of marine concrete elements with good accuracy. This accuracy was proved by obtaining a relatively high value of the linear coefficient of correlation R2—equal to 0.83 [74]. Even though algorithms were previously used to predict the chloride concentration in concrete elements, there are no records of using gene expression programming for predicting chloride concentrations on the surface of marine concrete elements.
3. Results and Their Analyses
3.1. Statistical Analysis
The results of the statistical analyses (presented as a relation between the measured value of Cs and the value identified by the machine learning algorithms) and the error distribution charts are presented in Figure 7. ANN gives a strong relation in the form of R2 = 0.84, as can be seen in Figure 7a—with its error distribution shown in Figure 7b. The error distribution in Figure 7b illustrates that the average error of the training set is equal to 0.108 MPa. Moreover, the maximum and minimum error values of the training set were noted as 0.801 MPa and 0.0035 MPa, respectively. In addition, 69.1 percent of the data showed an error of less than 0.10 MPa, however, 64.3 percent of the data showed an error between 0.01 MPa and 0.10 MPa, as illustrated in Figure 7b.
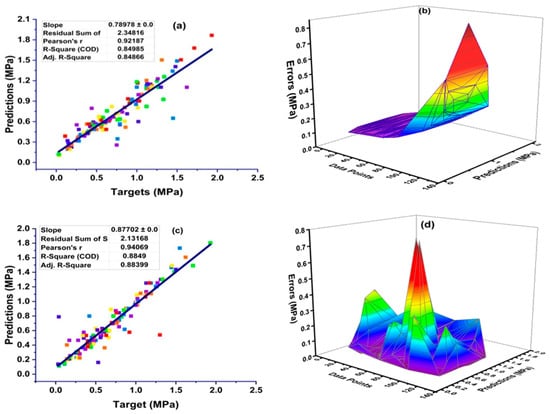
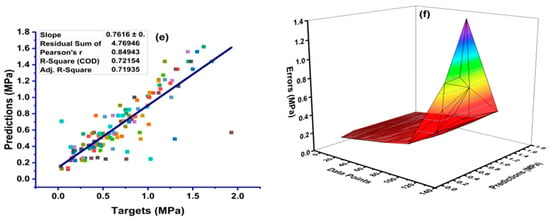
Figure 7.
The results of the numerical analyses, which present the relationship between the predicted variable and the experimentally determined variable, as well as the distribution of errors for the ANN (a,b); GEP (c,d); and DT (e,f).
The prediction of surface chloride concentration by employing the GEP algorithm yields a strong relationship between the targeted and output values of chloride concentrations, as shown in Figure 7c. It is also clear that this model gives a better response with less variance. GEP with an R2 value of 0.88 had a better accuracy when compared to the ANN (R2 equal to 0.84) and DT (R2 equal to 0.72), as depicted in Figure 7. In turn, Figure 7d indicates the error distribution of the linear regression model. It can be seen that 72.86 percent of the data showed an error between 0.01 MPa and 0.10 MPa, and that the average error of the training set was equal to 0.080 MPa. Moreover, the maximum and minimum errors were equal to 0.76 MPa and 0.004 MPa.
The influence of variables on the prediction of surface chloride concentrations using linear regression is illustrated in Figure 7e. The algorithm yields a decreased or poor correlation when predicting targets, which is indicated by the value of R2 being equal to 0.72, as shown in Figure 7e. In addition, Figure 7f presents the error distribution of the linear regression model and shows an average value of error equal to 0.12 MPa, with a maximum error value of 1.36 MPa. In turn, 82.1 percent of the model has an error between 0.005 MPa and 0.25 MPa.
3.2. K-Fold Cross Validation
The actual performance of the models was analyzed using the statistical cross-validation method. This method was used to evaluate the performance of the model. The K-fold validation test takes place in such a way that data are set randomly and split into k-groups. In this case, the data were divided into 10 groups, of which nine were used for training, and one was used for validation of the model. This was then repeated ten times in order to obtain the average value of these repetitions. When using the 10-fold cross-validation method, it is possible to obtain a relatively high performance of a model. Moreover, a statistical check was also applied to evaluate the model [72]. This statistical analysis is a check that shows the response of the model towards the prediction, as illustrated in the form of the equations listed below (Equations (2)–(5)).
where,
- —experimental value;
- —predicted value;
- —mean experimental value;
- —mean predicted value obtained by the model;
- n—number of samples.
Correlation coefficient (R2), mean absolute error (MAE), mean square error (MSE), and root mean square error (RMSE) were all used to evaluate the result of cross-validation, as can be seen in Figure 8. A comparison of all three individual model techniques indicated fluctuation in their outputs. The GEP model showed fewer errors with a much better R2 value when compared to the ANN and DT. The average R2 value of GEP modeling was equal to 0.79, with maximum and minimum values being 0.94 and 0.65, as illustrated in Figure 8a. The average value of R2 for the ANN model was equal to 0.71, with the maximum and minimum values being 0.89 and 0.62. Similarly, the DT model gave an average R2 value of 0.82, with maximum and minimum values being 0.93 and 0.68, as illustrated in Figure 8b,c. The values of the errors of all the models were relatively low in the case of the validation process. For GEP, they were: MAE = 7.03 MPa, MSE = 6.12 MPa, and RMSE = 2.46 MPa (Figure 8a). In the case of the ANN, they were: MAE = 7.56 MPa, MSE = 6.60 MPa, and RMSE = 2.54 MPa (Figure 8b); and in the case of the decision tree, they were: MAE = 7.66 MPa, MSE = 6.85 MPa, and RMSE = 2.61 MPa (Figure 8c). Moreover, the K-fold cross validation of all the applied models and statistical checks are listed in Table 4 and Table 5, respectively.
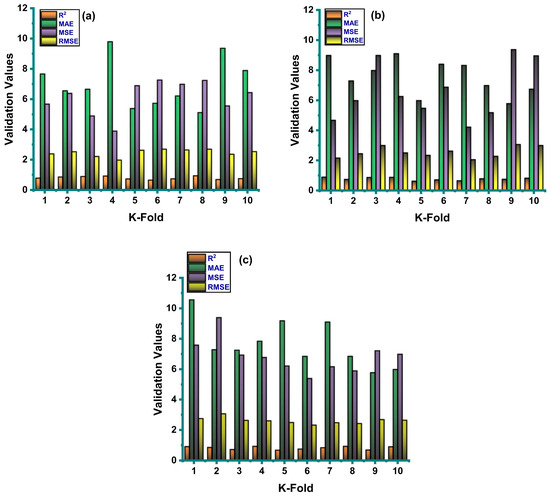
Figure 8.
Statistical indicator for k-fold cross-validation. (a) GEP model. (b) ANN model. (c) DT model.

Table 4.
Results of k-fold cross validation.

Table 5.
Statistical checks.
4. Discussion
This research describes the predictive performance of chloride concentrations on the surface of marine structures using individual supervised machine learning algorithms. The three machine learning algorithms used during the investigation were: artificial neural network, decision tree, and gene express programming. GEP, with an R2 value of 0.88, was the most accurate when compared to the ANN (R2 equal to 0.84) and DT (R2 equal to 0.72). This algorithm was also compared with those used in [18], and the results of the comparison accuracy are presented in Figure 9.

Figure 9.
Comparison of the accuracy of different machine learning algorithms.
It can be seen from Figure 9 that the proposed GEP algorithm accurately describes chloride surface concentrations when compared to other algorithms. This is confirmed by the very high value of linear correlation coefficient R2, which is on a comparable level to other algorithms used in the literature.
5. Conclusions
This research describes the predictive performance of chloride concentrations on the surface of marine structures using individual supervised machine learning algorithms. The three algorithms—the artificial neural network, the decision tree, and gene expression programming—were used for the investigations. The most accurate among these three was GEP, which was proved by the fact that it obtained the highest value of the linear correlation coefficient and the lowest values of the parameters describing the errors of prediction. The following conclusions can be drawn:
- ●
- The GEP algorithm is very effective for predicting chloride surface concentrations and can be successfully used for this purpose. This was also proved by comparing it with other algorithms used in the literature.
- ●
- The presented method does not depend on the zone in which it is used (except the atmospheric zone where the transport of chloride ions is more difficult to describe).
- ●
- The high performance of the GEP algorithm was also proved using k-fold validation.
The chloride surface concentration model, which uses gene expression programming, was proposed in this work. It can be successfully used without the need of investing significant time and money, as is the case with long term experiments. However, there is still room for improvement:
- ●
- The dataset can be expanded with laboratory tests, field tests, or numerical analyses using different upsizing methods (e.g., Monte Carlo).
- ●
- There is still the possibility of expanding the dataset with the results of surface chloride concentrations obtained for elements located in the atmospheric zone.
- ●
- Due to the fact that there is no model in the literature that is 100% accurate, there is still the possibility of using a different, more accurate, algorithm.
Author Contributions
A.A.—conceptualization, modeling, and writing the original draft; F.F.—visualization and review; K.A.O.—editing, review, and funding; K.Ś.-W.—data acquisition; S.C.—review, editing, and visualization. All authors have read and agreed to the published version of the manuscript.
Funding
The article processing charge (APC) was funded by the Faculty of Civil Engineering of Cracow University of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this article are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Notations | |
| ML | Machine learning |
| HPC | High performance concrete |
| GGBS | Ground granulated blast furnace slag |
| GEP | Genetic engineering programming |
| ANN | Artificial neural network |
| Dt | Decision tree |
| DL | Deep learning |
| DM | Deep machine |
| RF | Random forest |
| GB | Gradient boosting |
| FA | Fly ash |
| SF | Silica fume |
| POFA | Palm oil fuel ash |
| SCC | Self-compacting concrete |
| RHA | Rice husk ash |
| RKSA | Random kitchen sink algorithm |
| SVM | Support vector machine |
| ANFIS | Adaptive neuro fuzzy inference system |
| IREMSVM-FR | Intelligent rule-based enhanced multiclass support vector machine |
| RMS | Response surface method |
References
- Scott, R.H.; Chikermane, S.; Vidakovic, M.; McKinley, B.; Sun, T.; Banerji, P.; Grattan, K.T.V. Development of low cost packaged fibre optic sensors for use in reinforced concrete structures. Meas. J. Int. Meas. Confed. 2019, 135, 617–624. [Google Scholar] [CrossRef]
- Ryl, J.; Wysocka, J.; Cieslik, M.; Gerengi, H.; Ossowski, T.; Krakowiak, S.; Niedzialkowski, P. Understanding the origin of high corrosion inhibition efficiency of bee products towards aluminium alloys in alkaline environments. Electrochim. Acta 2019, 304, 263–274. [Google Scholar] [CrossRef]
- Moreno, J.D.; Bonilla, M.; Adam, J.M.; Borrachero, M.V.; Soriano, L. Determining corrosion levels in the reinforcement rebars of buildings in coastal areas. A case study in the Mediterranean coastline. Constr. Build. Mater. 2015, 100, 11–21. [Google Scholar] [CrossRef]
- Zhang, P.; Cong, Y.; Vogel, M.; Liu, Z.; Müller, H.S.; Zhu, Y.; Zhao, T. Steel reinforcement corrosion in concrete under combined actions: The role of freeze-thaw cycles, chloride ingress, and surface impregnation. Constr. Build. Mater. 2017, 148, 113–121. [Google Scholar] [CrossRef]
- Balafas, I.; Burgoyne, C.J. Environmental effects on cover cracking due to corrosion. Cem. Concr. Res. 2010, 40, 1429–1440. [Google Scholar] [CrossRef]
- Ann, K.Y.; Ahn, J.H.; Ryou, J.S. The importance of chloride content at the concrete surface in assessing the time to corrosion of steel in concrete structures. Constr. Build. Mater. 2009, 23, 239–245. [Google Scholar] [CrossRef]
- Nikoo, M.; Sadowski, Ł.; Nikoo, M. Prediction of the Corrosion Current Density in Reinforced Concrete Using a Self-Organizing Feature Map. Coatings 2017, 7, 160. [Google Scholar] [CrossRef]
- Sadowski, L. Non-destructive investigation of corrosion current density in steel reinforced concrete by artificial neural networks. Archiv. Civ. Mech. Eng. 2013, 13, 104–111. [Google Scholar] [CrossRef]
- Ali, B.; Qureshi, L.A.; Shah, S.H.A.; Rehman, S.U.; Hussain, I.; Iqbal, M. A step towards durable, ductile and sustainable concrete: Simultaneous incorporation of recycled aggregates, glass fiber and fly ash. Constr. Build. Mater. 2020, 251, 118980. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, Z.; Du, J.; Sui, L.; Xing, F. Bond behavior of FRP-to-concrete interface under sulfate attack: An experimental study and modeling of bond degradation. Constr. Build. Mater. 2015, 85, 9–21. [Google Scholar] [CrossRef]
- Akiyama, M.; Frangopol, D.M.; Suzuki, M. Integration of the effects of airborne chlorides into reliability-based durability design of reinforced concrete structures in a marine environment. Struct. Infrastruct. Eng. 2012, 8, 125–134. [Google Scholar] [CrossRef]
- Sadowski, L.; Nikoo, M. Corrosion current density prediction in reinforced concrete by imperialist competitive algorithm. Neural Comput. Appl. 2014, 25, 1627–1638. [Google Scholar] [CrossRef]
- Dai, J.G.; Akira, Y.; Wittmann, F.H.; Yokota, H.; Zhang, P. Water repellent surface impregnation for extension of service life of reinforced concrete structures in marine environments: The role of cracks. Cem. Concr. Compos. 2010, 32, 101–109. [Google Scholar] [CrossRef]
- Moradllo, M.K.; Shekarchi, M.; Hoseini, M. Time-dependent performance of concrete surface coatings in tidal zone of marine environment. Constr. Build. Mater. 2012, 30, 198–205. [Google Scholar] [CrossRef]
- Zuquan, J.; Xia, Z.; Tiejun, Z.; Jianqing, L. Chloride ions transportation behavior and binding capacity of concrete exposed to different marine corrosion zones. Constr. Build. Mater. 2018, 177, 170–183. [Google Scholar] [CrossRef]
- Liu, Q.-F.; Hu, Z.; Lu, X.-Y.; Yang, J.; Azim, I.; Sun, W. Prediction of Chloride Distribution for Offshore Concrete Based on Statistical Analysis. Materials 2020, 13, 174. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Chateauneuf, A.; Sánchez-Silva, M.; Bressolette, P.; Schoefs, F. A comprehensive probabilistic model of chloride ingress in unsaturated concrete. Eng. Struct. 2011, 33, 720–730. [Google Scholar] [CrossRef]
- Chen, W.B.; Zhou, W.H.; Sadowski, Ł.; Yin, Z.Y. Metaheuristic model for the interface shear strength between granular soil and structure considering surface morphology. Comput. Geotech. 2021, 135, 104141. [Google Scholar] [CrossRef]
- Cai, R.; Han, T.; Liao, W.; Huang, J.; Li, D.; Kumar, A.; Ma, H. Prediction of surface chloride concentration of marine concrete using ensemble machine learning. Cem. Concr. Res. 2020, 136, 106164. [Google Scholar] [CrossRef]
- Hoang, N.D.; Chen, C.T.; Liao, K.W. Prediction of chloride diffusion in cement mortar using Multi-Gene Genetic Programming and Multivariate Adaptive Regression Splines. Measurement 2017, 112, 141–149. [Google Scholar] [CrossRef]
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 202, 54–64. [Google Scholar] [CrossRef]
- Getahun, M.A.; Shitote, S.M.; Gariy, Z.C.A. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018, 190, 517–525. [Google Scholar] [CrossRef]
- Ling, H.; Qian, C.; Kang, W.; Liang, C.; Chen, H. Combination of Support Vector Machine and K-Fold cross validation to predict compressive strength of concrete in marine environment. Constr. Build. Mater. 2019, 206, 355–363. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Taffese, W.Z.; Sistonen, E. Machine learning for durability and service-life assessment of reinforced concrete structures: Recent advances and future directions. Autom. Constr. 2017, 77, 1–14. [Google Scholar] [CrossRef]
- Yokoyama, S.; Matsumoto, T. Development of an Automatic Detector of Cracks in Concrete Using Machine Learning. Procedia Eng. 2017, 1250–1255. [Google Scholar] [CrossRef]
- Chaabene, W.B.; Flah, M.; Nehdi, M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020, 260. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modelling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 126032. [Google Scholar] [CrossRef]
- Balf, F.R.; Kordkheili, H.M.; Kordkheili, A.M. A New Method for Predicting the Ingredients of Self-Compacting Concrete (SCC) Including Fly Ash (FA) Using Data Envelopment Analysis (DEA). Arab. J. Sci. Eng. 2020, 1–22. [Google Scholar] [CrossRef]
- Bušić, R.; Benšić, M.; Miličević, I.; Strukar, K. Prediction models for the mechanical properties of self-compacting concrete with recycled rubber and silica fume. Materials 2020, 13, 1821. [Google Scholar] [CrossRef]
- Azimi-Pour, M.; Eskandari-Naddaf, H.; Pakzad, A. Linear and non-linear SVM prediction for fresh properties and compressive strength of high volume fly ash self-compacting concrete. Constr. Build. Mater. 2020, 230, 117021. [Google Scholar] [CrossRef]
- Saha, P.; Debnath, P.; Thomas, P. Prediction of fresh and hardened properties of self-compacting concrete using support vector regression approach. Neural Comput. Appl. 2020, 32, 7995–8010. [Google Scholar] [CrossRef]
- Al-Mughanam, T.; Aldhyani, T.H.H.; Alsubari, B.; Al-Yaari, M. Modeling of compressive strength of sustainable self-compacting concrete incorporating treated palm oil fuel ash using artificial neural network. Sustainability 2020, 12, 9322. [Google Scholar] [CrossRef]
- Javed, M.F.; Farooq, F.; Memon, S.A.; Akbar, A.; Khan, M.A.; Aslam, F.; Alyousef, R.; Alabduljabbar, H.; Rehman, S.K.U. New prediction model for the ultimate axial capacity of concrete-filled steel tubes: An evolutionary approach. Crystals 2020, 10, 741. [Google Scholar] [CrossRef]
- Aslam, F.; Farooq, F.; Amin, M.N.; Khan, K.; Waheed, A.; Akbar, A.; Javed, M.F.; Alyousef, R.; Alabdulijabbar, H. Applications of Gene Expression Programming for Estimating Compressive Strength of High-Strength Concrete. Adv. Civ. Eng. 2020. [Google Scholar] [CrossRef]
- Farooq, F.; Amin, M.N.; Khan, K.; Sadiq, M.R.; Javed, M.F.; Aslam, F.; Alyousef, R. A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Asteris, P.G.; Kolovos, K.G. Self-compacting concrete strength prediction using surrogate models. Neural Comput. Appl. 2019, 31, 409–424. [Google Scholar] [CrossRef]
- Selvaraj, S.; Sivaraman, S. Prediction model for optimized self-compacting concrete with fly ash using response surface method based on fuzzy classification. Neural Comput. Appl. 2019, 31, 1365–1373. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, G.; Huang, Y.; Sun, J.; Aslani, F.; Nener, B. Modelling uniaxial compressive strength of lightweight self-compacting concrete using random forest regression. Constr. Build. Mater. 2019, 210, 713–719. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T.; Hamze-Ziabari, S.M. M5’ and mars based prediction models for properties of selfcompacting concrete containing fly ash. Period. Polytech. Civ. Eng. 2018, 62, 281–294. [Google Scholar] [CrossRef]
- Sathyan, D.; Anand, K.B.; Prakash, A.J.; Premjith, B. Modeling the Fresh and Hardened Stage Properties of Self-Compacting Concrete using Random Kitchen Sink Algorithm. Int. J. Concr. Struct. Mater. 2018, 12, 1–10. [Google Scholar] [CrossRef]
- Vakhshouri, B.; Nejadi, S. Prediction of compressive strength of self-compacting concrete by ANFIS models. Neurocomputing 2018, 280, 13–22. [Google Scholar] [CrossRef]
- Douma, O.B.; Boukhatem, B.; Ghrici, M.; Tagnit-Hamou, A. Prediction of properties of self-compacting concrete containing fly ash using artificial neural network. Neural Comput. Appl. 2017, 28, 707–718. [Google Scholar] [CrossRef]
- Yaman, M.A.; Abd Elaty, M.; Taman, M. Predicting the ingredients of self compacting concrete using artificial neural network. Alex. Eng. J. 2017, 56, 523–532. [Google Scholar] [CrossRef]
- Asteris, P.G.; Kolovos, K.G.; Douvika, M.G.; Roinos, K. Prediction of self-compacting concrete strength using artificial neural networks. Eur. J. Environ. Civ. Eng. 2016, 20, s102–s122. [Google Scholar] [CrossRef]
- Siddique, R.; Aggarwal, P.; Aggarwal, Y. Prediction of compressive strength of self-compacting concrete containing bottom ash using artificial neural networks. Adv. Eng. Softw. 2011, 42, 780–786. [Google Scholar] [CrossRef]
- Prasad, B.K.R.; Eskandari, H.; Reddy, B.V.V. Prediction of compressive strength of SCC and HPC with high volume fly ash using ANN. Constr. Build. Mater. 2009, 23, 117–128. [Google Scholar] [CrossRef]
- Chalee, W.; Jaturapitakkul, C.; Chindaprasirt, P. Predicting the chloride penetration of fly ash concrete in seawater. Mar. Struct. 2009, 22, 341–353. [Google Scholar] [CrossRef]
- Costa, A.; Appleton, J. Chloride penetration into concrete in marine environment-Part I: Main parameters affecting chloride penetration. Mater. Struct. Constr. 1999, 32, 252–259. [Google Scholar] [CrossRef]
- Huan, X.U.E.; Zuquan, J.I.N.; Xiaojie, W. Chloride ion penetration into concrete exposed to marine environment for a long period. Ocean Eng. 2015, 33, 60–65. [Google Scholar]
- Moradllo, M.K.; Sadati, S.; Shekarchi, M. Quantifying maximum phenomenon in chloride ion profiles and its influence on service-life prediction of concrete structures exposed to seawater tidal zone-A field oriented study. Constr. Build. Mater. 2018, 180, 109–116. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Wang, Y.; Li, Q.; Xiao, Z. Prediction model of long-term chloride diffusion into plain concrete considering the effect of the heterogeneity of materials exposed to marine tidal zone. Constr. Build. Mater. 2018, 159, 297–315. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Zhang, Y.; Huang, J.; Zhuang, H.X.; Zhang, J.Z. Time dependence and similarity analysis of peak value of chloride concentration of concrete under the simulated chloride environment. Constr. Build. Mater. 2018, 181, 609–617. [Google Scholar] [CrossRef]
- Safehian, M.; Ramezanianpour, A.A. Assessment of service life models for determination of chloride penetration into silica fume concrete in the severe marine environmental condition. Constr. Build. Mater. 2013, 48, 287–294. [Google Scholar] [CrossRef]
- Nanukuttan, S.V.; Basheer, L.; McCarter, W.J.; Robinson, D.J.; Basheer, P.M. Muhammed Basheer, Full-scale marine exposure tests on treated and untreated concretes-initial 7-year results. ACI Mater. J. 2008, 105, 81–87. [Google Scholar] [CrossRef]
- Markeset, G.; Skjølsvold, O. Time Dependent Chloride Diffusion Coefficient-Field Studies of Concrete Exposed to Marine Environment in Norway. In Proceedings of the 2nd International Symposium on Service Life Design for Infrastructure, Delft, The Netherlands, 4–6 October 2010; pp. 83–90. [Google Scholar]
- Safehian, M.; Ramezanianpour, A.A. Prediction of RC structure service life from field long term chloride diffusion. Comput. Concr. 2015, 15, 589–606. [Google Scholar] [CrossRef]
- Song, H.W.; Lee, C.H.; Ann, K.Y. Factors influencing chloride transport in concrete structures exposed to marine environments. Cem. Concr. Compos. 2008, 30, 113–121. [Google Scholar] [CrossRef]
- Pack, S.W.; Jung, M.S.; Song, H.W.; Kim, S.H.; Ann, K.Y. Prediction of time dependent chloride transport in concrete structures exposed to a marine environment. Cem. Concr. Res. 2010, 40, 302–312. [Google Scholar] [CrossRef]
- Ghods, P.; Chini, M.; Alizadeh, R.; Hoseini, M. The Effect of Different Exposure Conditions on the Chloride Diffusion into Concrete in the Persian Gulf Region. In Proceedings of the 3th ConMAT; University of British Columbia: Vancouver, BC, Canada, 2005. [Google Scholar]
- Farahani, A.; Taghaddos, H.; Shekarchi, M. Prediction of long-term chloride diffusion in silica fume concrete in a marine environment. Cem. Concr. Compos. 2015, 59, 10–17. [Google Scholar] [CrossRef]
- Gao, Y.H.; Zhang, J.Z.; Zhang, S.; Zhang, Y.R. Probability distribution of convection zone depth of chloride in concrete in a marine tidal environment. Constr. Build. Mater. 2017, 140, 485–495. [Google Scholar] [CrossRef]
- Pang, L.; Li, Q. Service life prediction of RC structures in marine environment using long term chloride ingress data: Comparison between exposure trials and real structure surveys. Constr. Build. Mater. 2016, 113, 979–987. [Google Scholar] [CrossRef]
- Valipour, M.; Pargar, F.; Shekarchi, M.; Khani, S.; Moradian, M. In situ study of chloride ingress in concretes containing natural zeolite, metakaolin and silica fume exposed to various exposure conditions in a harsh marine environment. Constr. Build. Mater. 2013, 46, 63–70. [Google Scholar] [CrossRef]
- Alizadeh, R.; Ghods, P.; Chini, M.; Hoseini, M.; Ghalibafian, M.; Shekarchi, M. Effect of Curing Conditions on the Service Life Design of RC Structures in the Persian Gulf Region. J. Mater. Civ. Eng. 2008, 20, 2–8. [Google Scholar] [CrossRef]
- Tang, L. Chloride Ingress in Concrete Exposed to Marine Environment—Field Data up to 10 Years Exposure; Swedish National Testing and Research Institute: Borås, Sweden, 2003; ISBN 91-7848-948-2. [Google Scholar]
- Lindvall, A. Chloride ingress data from field and laboratory exposure-Influence of salinity and temperature. Cem. Concr. Compos. 2007, 29, 88–93. [Google Scholar] [CrossRef]
- Dousti, A.; Rashetnia, R.; Ahmadi, B.; Shekarchi, M. Influence of exposure temperature on chloride diffusion in concretes incorporating silica fume or natural zeolite. Constr. Build. Mater. 2013, 49, 393–399. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Jahangir, H.; Eidgahee, D.R. A new and robust hybrid artificial bee colony algorithm-ANN model for FRP-concrete bond strength evaluation. Compos. Struct. 2021, 257, 113160. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Ju, X.; Wu, L.; Lin, C.; Yang, X.; Yang, C. Prediction of chloride concentration with elevation in concrete exposed to cyclic drying-wetting conditions in marine environments. Constr. Build. Mater. 2021, 278, 122370. [Google Scholar] [CrossRef]
- Oluwaseun Azeez, M.; Abd El Fattah, A. Service Life Modeling of Concrete with SCMs Using Effective Diffusion Coefficient and a New Binding Model. Crystals 2020, 10, 967. [Google Scholar] [CrossRef]
- Hadzima-Nyarko, M.; Nyarko, E.K.; Ademović, N.; Miličević, I.; Kalman Šipoš, T. Modelling the Influence of Waste Rubber on Compressive Strength of Concrete by Artificial Neural Networks. Materials 2019, 12, 561. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).