Some Inconsistencies in the Nonlinear Buckling Plate Theories—FSDT, S-FSDT, HSDT
Abstract
1. Introduction
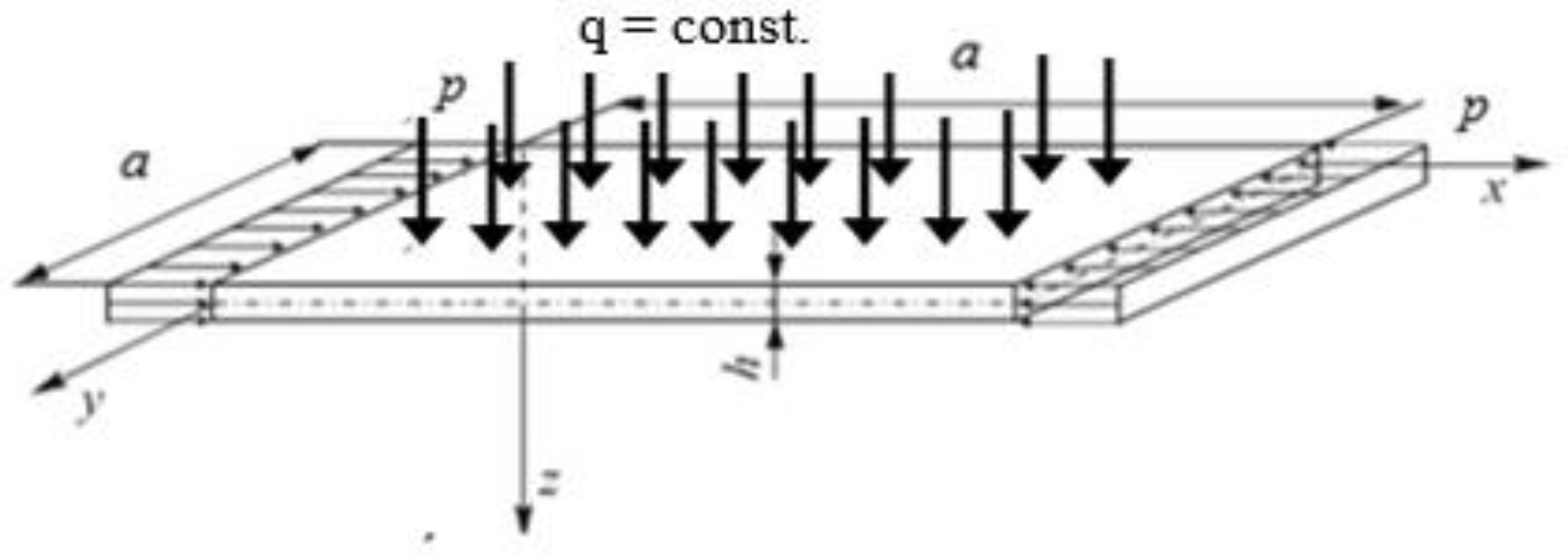
2. Formulation of the Problem
- FSDT
- S-FSDT
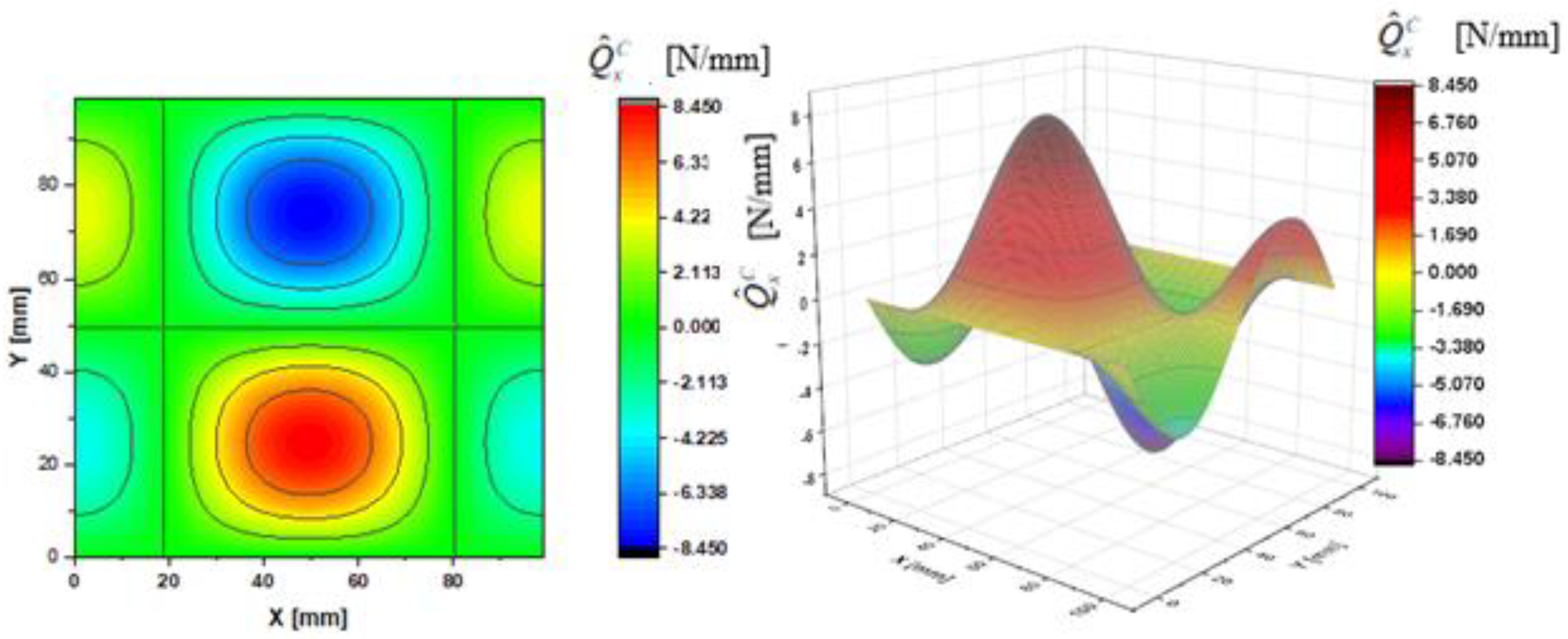
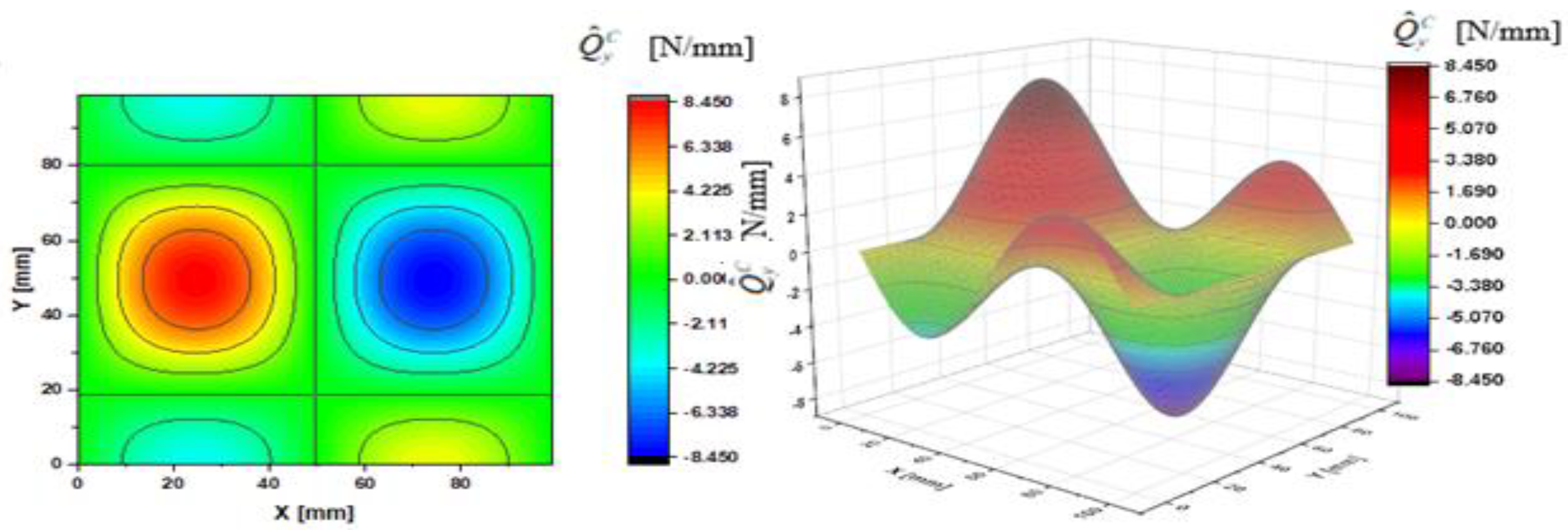
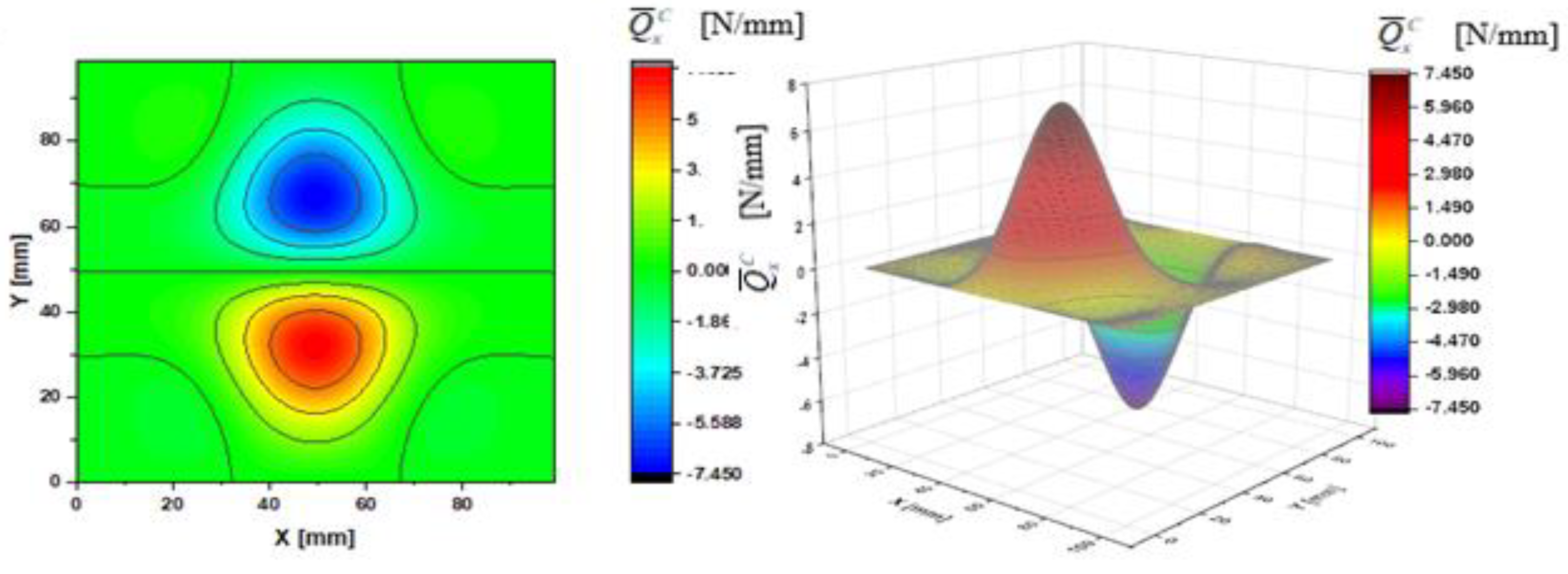
3. Results of the Calculations
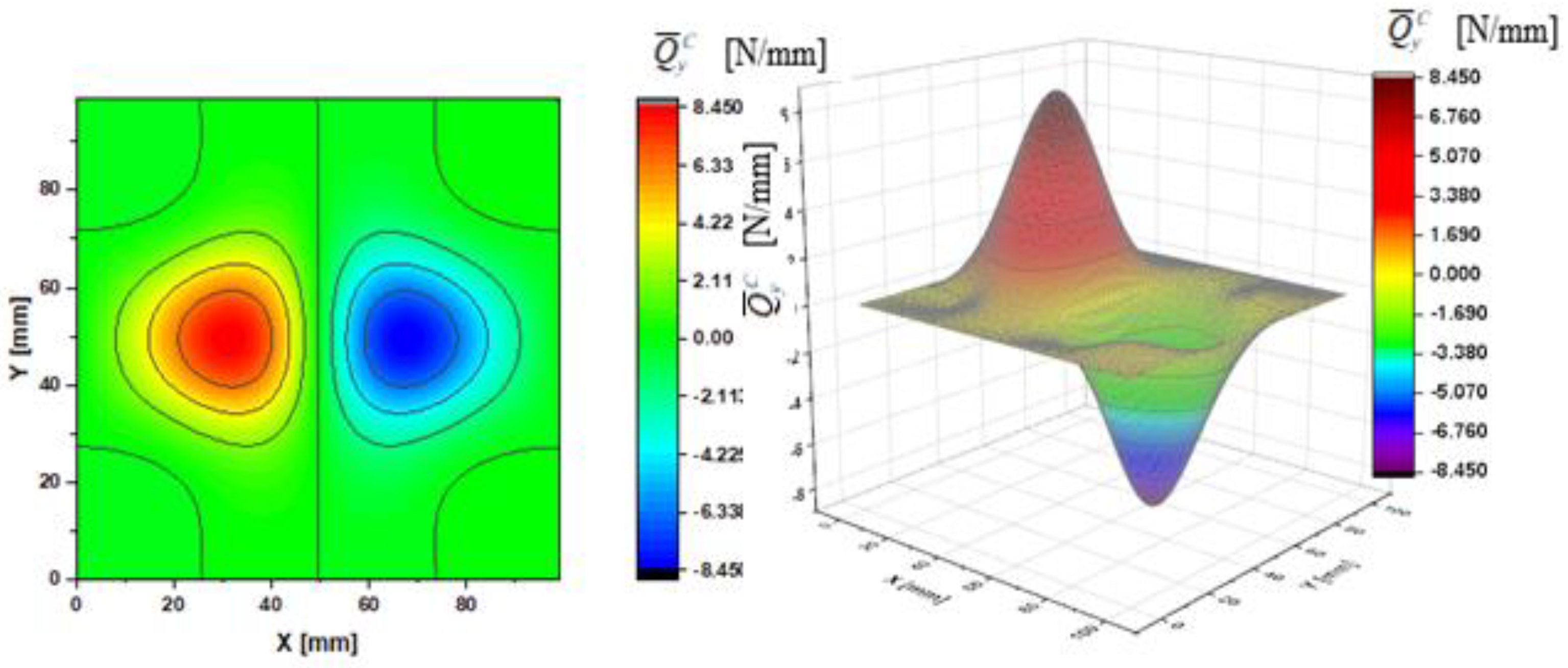
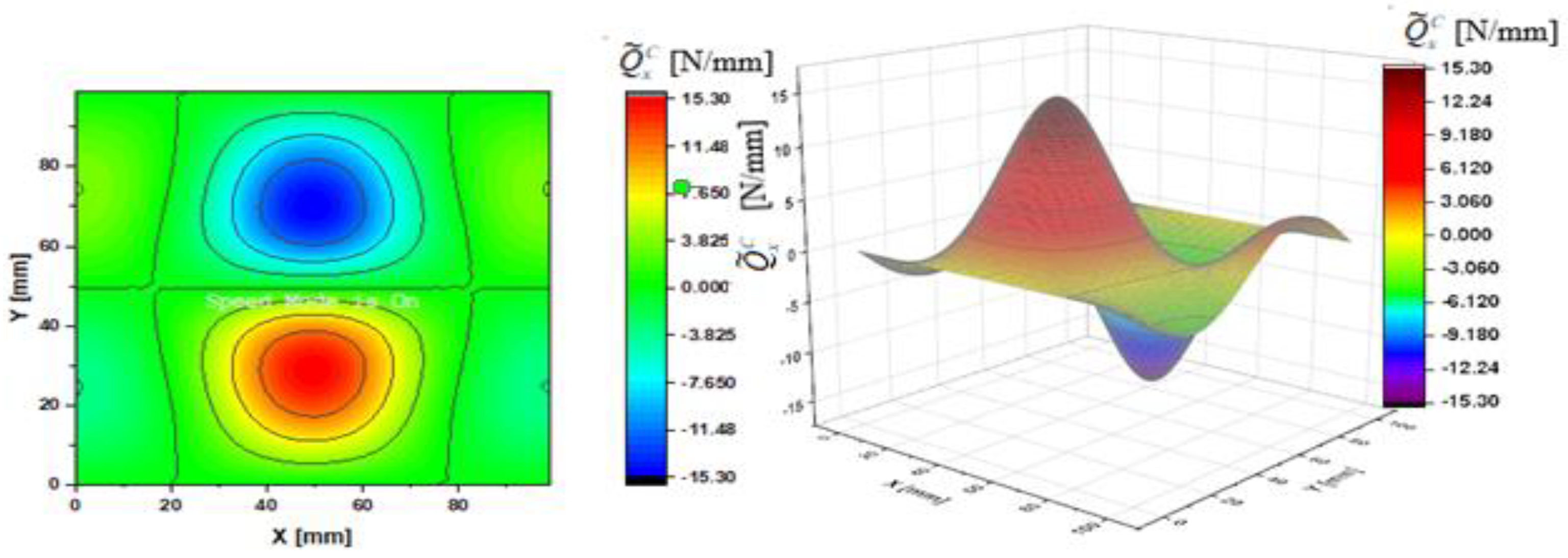
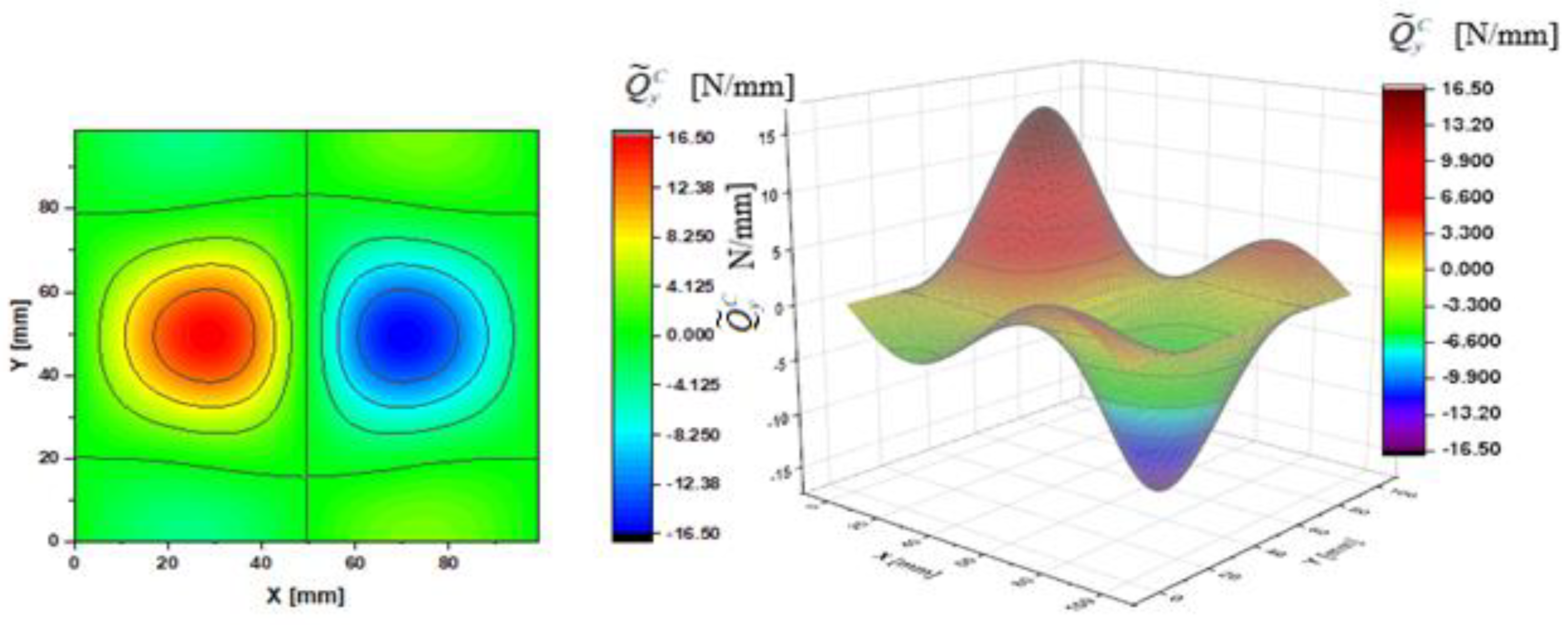
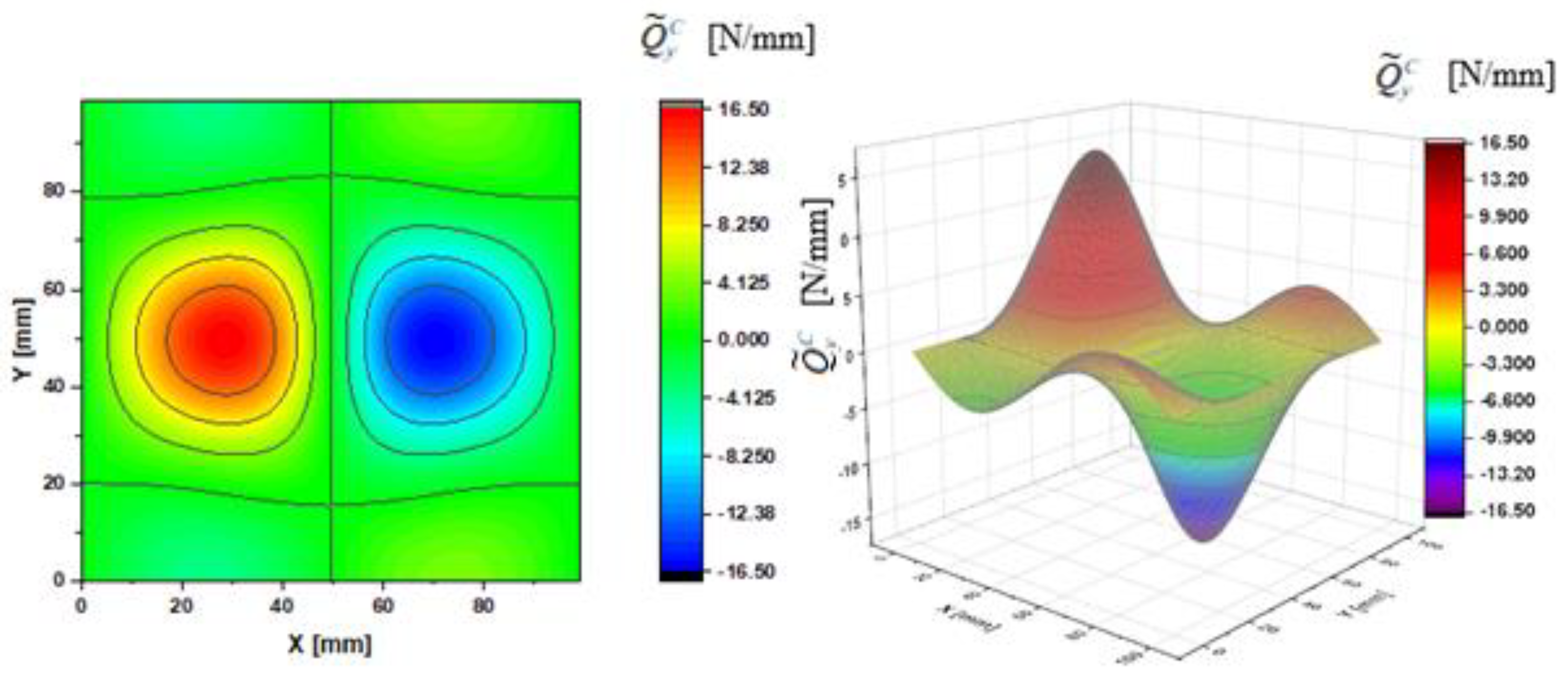
- Case A— and ;
- Case B— and .
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation
| a, h | geometrical dimensions of the plate |
| D | plate bending stiffness |
| E, G | Young’s and Kirchhoff’s modulus |
| F | function of Airy forces |
| inner in-plane sectional forces | |
| inner bending moment-sectional forces | |
| , | critical stress, dimensionless critical stress |
| , | transverse loading, dimensionless transverse loading |
| membrane components of transverse forces | |
| bending components of transverse forces | |
| total components of transverse forces | |
| u, v, w | components of the plate displacement along the axis x, y, z |
| shear deflection | |
| reduction factor | |
| angles of transverse shear | |
| membrane strains | |
| dimensionless amplitude deflection | |
| dimensionless coefficient | |
| upper index referring to the FSDT, the S-FSDT, the CPT | |
| bending strains | |
| Poisson’s ratio | |
| function of potential | |
| , | angles of rotation of the transverse normal due to bending |
Appendix A
Appendix A.1. FSDT, S-FSDT, and CPT-Fundamental Equations
Appendix A.1.1. FSDT
Appendix A.1.2. S-FSDT
Appendix A.1.3. CPT
Appendix A.2. Nonlinear Problem of Distributions of Transverse Shear Forces in the Square Plate Subject Simultaneously to Compression and Transverse Loading
Appendix A.2.1. Equation of Inseparability of Deformations
Appendix A.2.2. CPT-Solution to the Nonlinear Problem of Stability
- and (the plate subject to uniform compression, transverse loading neglected)
- and (the plate subject to uniform transverse loading, compression neglected)
Appendix A.2.3. S-FSDT-Solution to the Nonlinear Problem of Stability
- and(the plate subject to uniform compression, transverse loading neglected)
- and(the plate subject to uniform transverse loading, compression neglected)
Appendix A.2.4. FSDT-Solution to the Nonlinear Problem of Stability
- and(the plate subject to uniform compression, transverse loading neglected)
- and(the plate subject to uniform transverse loading, compression neglected)
References
- Reissner, E. On the theory of bending of elastic plates. J. Math. Phys. 1944, 23, 184–191. [Google Scholar] [CrossRef]
- Reissner, E. The effect of transverse shear deformation on the bending of elastic plates. ASME J. Appl. Mech. 1945, 12, A69–A77. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates. ASME J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Baptista, M. An elementary derivation of basic equations of the Reissner and Mindlin plate theories. Eng. Struct. 2010, 32, 906–909. [Google Scholar] [CrossRef]
- Baptista, M. Comparison of Reissner, Mindlin and Reddy plate models with exact three dimensional solution for simply supported isotropic and transverse inextensible rectangular plate. Meccanica 2012, 47, 257–268. [Google Scholar] [CrossRef]
- Chróścielewski, J.; Makowski, J.; Pietraszkiewicz, W. Statyka i Dynamika Powłok Wielopłatowych; IPPT PAN: Warsaw, Poland, 2004. (In Polish) [Google Scholar]
- Wu, S.R. Reissner-Mindlin plate theory for elastodynamics. J. Appl. Math. 2004, 3, 179–189. [Google Scholar] [CrossRef]
- Lo, K.H.; Christensen, R.M.; Wu, E.M. A high-order theory of plate deformation. Part 1: Homogeneous plates. ASME J. Appl. Mech. 1977, 44, 663–668. [Google Scholar] [CrossRef]
- Lo, K.H.; Christensen, R.M.; Wu, E.M. A high-order theory of plate deformation. Part 2: Laminated plates. ASME J. Appl. Mech. 1977, 44, 669–676. [Google Scholar] [CrossRef]
- Reddy, J.N. A general non-linear third-order theory of plates with moderate thickness. Int. J. Non-Linear Mech. 1990, 25, 677–686. [Google Scholar] [CrossRef]
- Reddy, J.N.; Phan, N.D. Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory. J. Sound Vib. 1985, 98, 157–170. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Reddy, J.N. A general nonlinear third-order theory of functionally graded plates. Int. J. Aerosp. Lightweight Struct. 2011, 1, 1–21. [Google Scholar] [CrossRef]
- Taylor, M.W.; Vasiliev, V.V.; Dillard, D.A. On the problem of shear-locking in finite elements based on shear deformable plate theory. Int. J. Solids Struct. 1997, 34, 859–875. [Google Scholar] [CrossRef]
- Vasiliev, V.V. Modern conceptions of plate theory. Compos. Struct. 2000, 48, 39–48. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Lure, S.A. On refined theories of beams, plates, and shells. J. Comput. Math. 1992, 26, 546–557. [Google Scholar] [CrossRef]
- Cai, L.; Rong, T.; Chen, D. Generalized mixed variational methods for Reissner plate and its applications. Comput. Mech. 2002, 30, 29–37. [Google Scholar] [CrossRef]
- Cen, S.; Shang, Y. Developments of Mindlin-Reissner plate elements. Math. Probl. Eng. 2015, 12, 456740. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 4th ed.; McGraw-Hill Book Co.: London, UK, 1991; Volume 2. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice-Hall International, Inc.: Watertown, MA, USA, 1996. [Google Scholar]
- Endo, M.; Kimura, N. An alternative formulation of the boundary value problem for the Timoshenko beam and Mindlin plate. J. Sound Vib. 2007, 301, 355–373. [Google Scholar] [CrossRef]
- Kim, S.E.; Thai, H.-T.; Lee, J. A two variable refined plate theory for laminated composite plates. Compos. Struct. 2009, 89, 197–205. [Google Scholar] [CrossRef]
- Kim, S.-E.; Thai, H.-T.; Lee, J. Buckling analysis of plates using the two variable refined plate theory. Thin-Walled Struct. 2009, 47, 455–462. [Google Scholar] [CrossRef]
- Park, M.; Choi, D.-H. A two-variable first-order shear deformation theory considering in-plane rotation for bending, buckling and free vibration analyses of isotropic plates. Appl. Math. Model. 2018, 61, 49–71. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Patel, H.G. A two variable refined plate theory for orthotropic plate analysis. Int. J. Solids Struct. 2006, 43, 6783–6799. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Patel, H.G. Free vibrations of plate using two variable refined plate theory. J. Sound Vib. 2006, 296, 979–999. [Google Scholar] [CrossRef]
- Shimpi, R.P. Refined plate theory and its variants. AIAA J. 2002, 40, 137–146. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Shetty, R.A.; Guha, A. A single variable refined theory for free vibrations of a plate using inertia related terms in displacements. Eur. J. Mech. A/Solids 2017, 65, 136–148. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Jankowski, J. Effect of membrane components of transverse forces on magnitudes of total transverse forces in the nonlinear stability of plate structures. Materials 2020, 13, 5262. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Krolak, M. Modal coupled instabilities of thin-walled composite plate and shell structures. Compos. Struct. 2006, 76, 303–313. [Google Scholar] [CrossRef]
- Ghugal, Y.M.; Shimpi, R.P. A review of refined shear deformation theories of isotropic and anisotropic laminated plates. J. Reinf. Plast. Compos. 2002, 21, 775–813. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials, 2nd ed.; Taylor and Francis, Inc.: Philadelphia, PA, USA, 1999. [Google Scholar]
- Adim, B.; Daouadji, T.H.; Rabahi, A. A simple higher order shear deformation theory for mechanical behavior of laminated composite plates. Int. J. Adv. Struct. Eng. 2016, 8, 103–117. [Google Scholar] [CrossRef]
- Daouadji, T.H.; Tounsi, A.; Adda Bedia, E.A. A new higher order shear deformation model for static behavior of functionally graded plates. Adv. Appl. Math. Mech. 2013, 5, 351–364. [Google Scholar] [CrossRef]
- Navale, K.U.; Pise, C.P. A review on high order shear deformation theory for orthotropic composite laminates. Int. J. Eng. Res. Technol. 2021, 10, 477–481. [Google Scholar]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Roque, C.M.C.; Jorge, R.M.N.; Soares, C.M.M. Buckling behaviour of cross-ply laminated plates by a higher-order shear deformation theory. Sci. Eng. Compos. Mater. 2012, 19, 119–125. [Google Scholar] [CrossRef]
- Reddy, J.N. Introduction to the Finite Element Method; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Shi, P.; Dong, C.; Sun, F.; Liu, W.; Hu, Q. A new higher order shear deformation theory for static, vibration and buckling responses of laminated plates with the isogeometric analysis. Compos. Struct. 2018, 204, 342–358. [Google Scholar] [CrossRef]
- Srividhya, S.; Kumar, B.; Gupta, R.K.; Rajagopal, A. Nonlinear analysis of FGM plates using generalised higher order shear deformation theory. Int. J. Mater. Struct. Integr. 2019, 13, 3–15. [Google Scholar] [CrossRef]
- Swain, P.R.; Adhikari, B.; Dash, P. A higher-order polynomial shear deformation theory for geometrically nonlinear free vibration response of laminated composite plate. Mech. Adv. Mater. Struct. 2019, 26, 129–138. [Google Scholar] [CrossRef]
- Thai, H.-T.; Choi, D.-H. A simple first-order shear deformation theory for laminated composite plates. Compos. Struct. 2013, 106, 754–763. [Google Scholar] [CrossRef]
- Yi, S.-C.; Yao, L.-Q.; Tang, B.-J. A novel higher-order shear and normal deformable plate theory for the static, free vibration and buckling analysis of functionally graded plates. Math. Probl. Eng. 2017, 6879508. [Google Scholar] [CrossRef]
- Volmir, A.S. Flexible Plates and Shells; State Publishing House of Technical-Theoretical Literature: Moscow, Russia, 1956. (In Russian) [Google Scholar]

| Symbole | Load | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Theory | Symbol | Unit | Case A | Case B | ||||||
| W/h | ||||||||||
| 0.5 | 1.0 | 1.5 | 2.0 | 0.5 | 1.0 | 1.5 | 2.0 | |||
| CPT | MPa | 192.8 | 0.0 | |||||||
| - | 203 | 236 | 291 | 368 | 0.0 | |||||
| MPa | 0.0 | 0.075 | 0.17 | 0.32 | 0.54 | |||||
| N/mm | 2.10 | 4.20 | 6.30 | 8.40 | 2.10 | 4.20 | 6.30 | 8.40 | ||
| N/mm | 2.10 | 4.20 | 6.30 | 8.40 | 2.10 | 4.20 | 6.30 | 8.40 | ||
| N/mm | 0.08 | 0.72 | 2.94 | 7.40 | 0.13 | 1.06 | 3.56 | 8.44 | ||
| N/mm | 0.13 | 1.06 | 3.56 | 8.44 | 0.13 | 1.06 | 3.56 | 8.44 | ||
| N/mm | 2.06 | 4.79 | 8.95 | 15.3 | 2.22 | 5.16 | 9.63 | 16.4 | ||
| N/mm | 2.22 | 5.16 | 9.63 | 16.4 | 2.22 | 5.16 | 9.63 | 16.4 | ||
| S-FSDT | MPa | 192.6 | 0.0 | |||||||
| - | 0.9989 | |||||||||
| N/mm | 2.05 | 4.79 | 8.95 | 15.3 | 2.22 | 5.16 | 9.62 | 16.4 | ||
| N/mm | 2.21 | 5.16 | 9.62 | 16.4 | 2.22 | 5.16 | 9.62 | 16.4 | ||
| - | 0.04 | 0.15 | 0.33 | 0.48 | 0.06 | 0.20 | 0.37 | 0.51 | ||
| - | 0.06 | 0.20 | 0.37 | 0.51 | 0.06 | 0.20 | 0.37 | 0.51 | ||
| FSDT | MPa | 192.6 | 0.0 | |||||||
| - | 0.9989 | |||||||||
| N/mm | 1.67 | 4.00 | 7.78 | 13.7 | 1.82 | 4.37 | 8.45 | 14.9 | ||
| N/mm | 1.81 | 4.37 | 8.45 | 14.9 | 1.82 | 4.37 | 8.45 | 14.9 | ||
| - | 0.05 | 0.18 | 0.38 | 0.51 | 0.07 | 0.24 | 0.42 | 0.57 | ||
| - | 0.07 | 0.24 | 0.42 | 0.57 | 0.07 | 0.24 | 0.42 | 0.57 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolakowski, Z.; Jankowski, J. Some Inconsistencies in the Nonlinear Buckling Plate Theories—FSDT, S-FSDT, HSDT. Materials 2021, 14, 2154. https://doi.org/10.3390/ma14092154
Kolakowski Z, Jankowski J. Some Inconsistencies in the Nonlinear Buckling Plate Theories—FSDT, S-FSDT, HSDT. Materials. 2021; 14(9):2154. https://doi.org/10.3390/ma14092154
Chicago/Turabian StyleKolakowski, Zbigniew, and Jacek Jankowski. 2021. "Some Inconsistencies in the Nonlinear Buckling Plate Theories—FSDT, S-FSDT, HSDT" Materials 14, no. 9: 2154. https://doi.org/10.3390/ma14092154
APA StyleKolakowski, Z., & Jankowski, J. (2021). Some Inconsistencies in the Nonlinear Buckling Plate Theories—FSDT, S-FSDT, HSDT. Materials, 14(9), 2154. https://doi.org/10.3390/ma14092154






