In Situ Computed Tomography—Analysis of a Single-Lap Shear Test with Clinch Points
Abstract
:1. Introduction
2. Materials and Methods
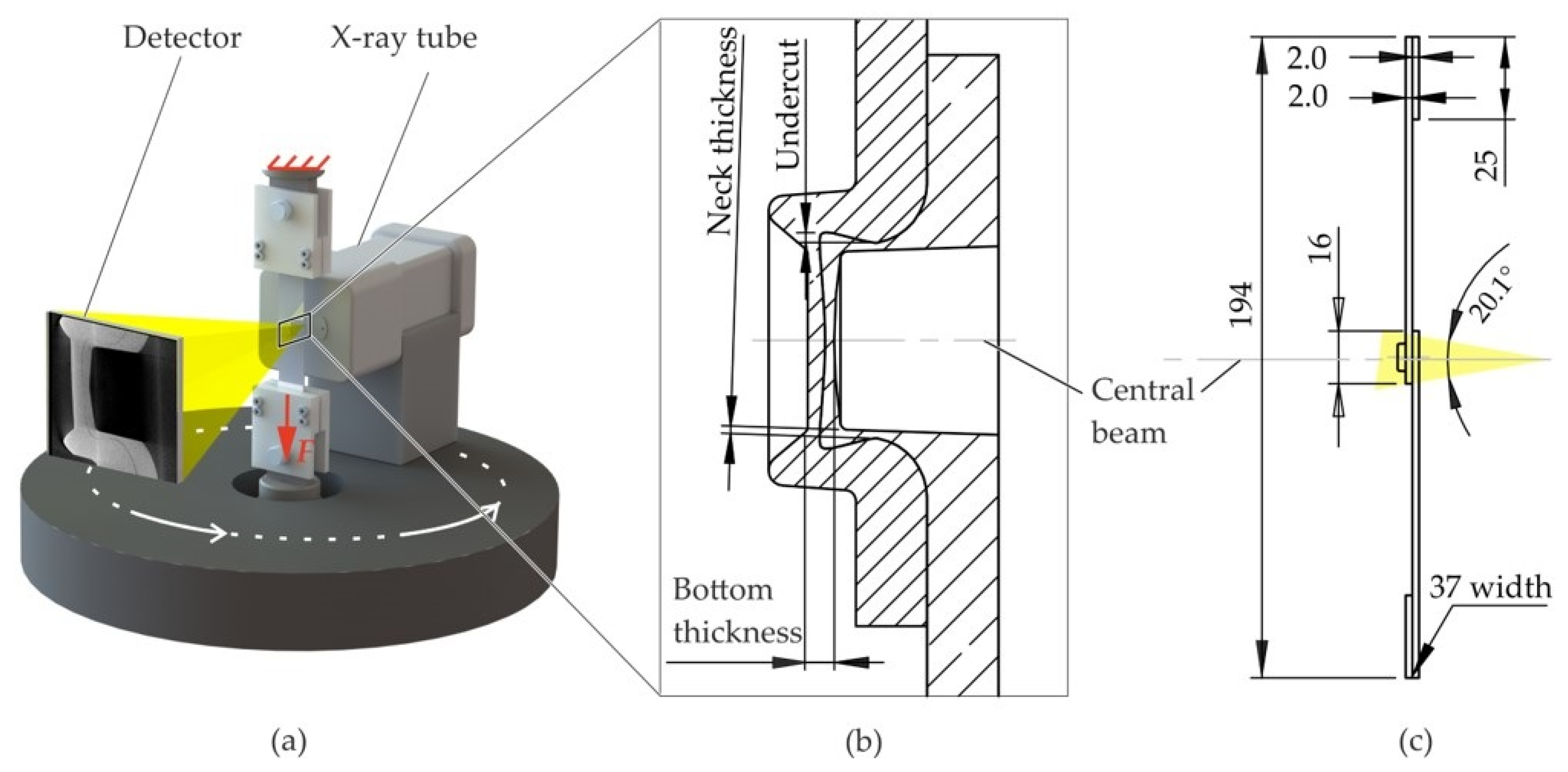
2.1. In Situ Lap Shear Test
2.2. Enhancing the Detectability of the Sheet–Sheet Interface Using Radiopaque Materials
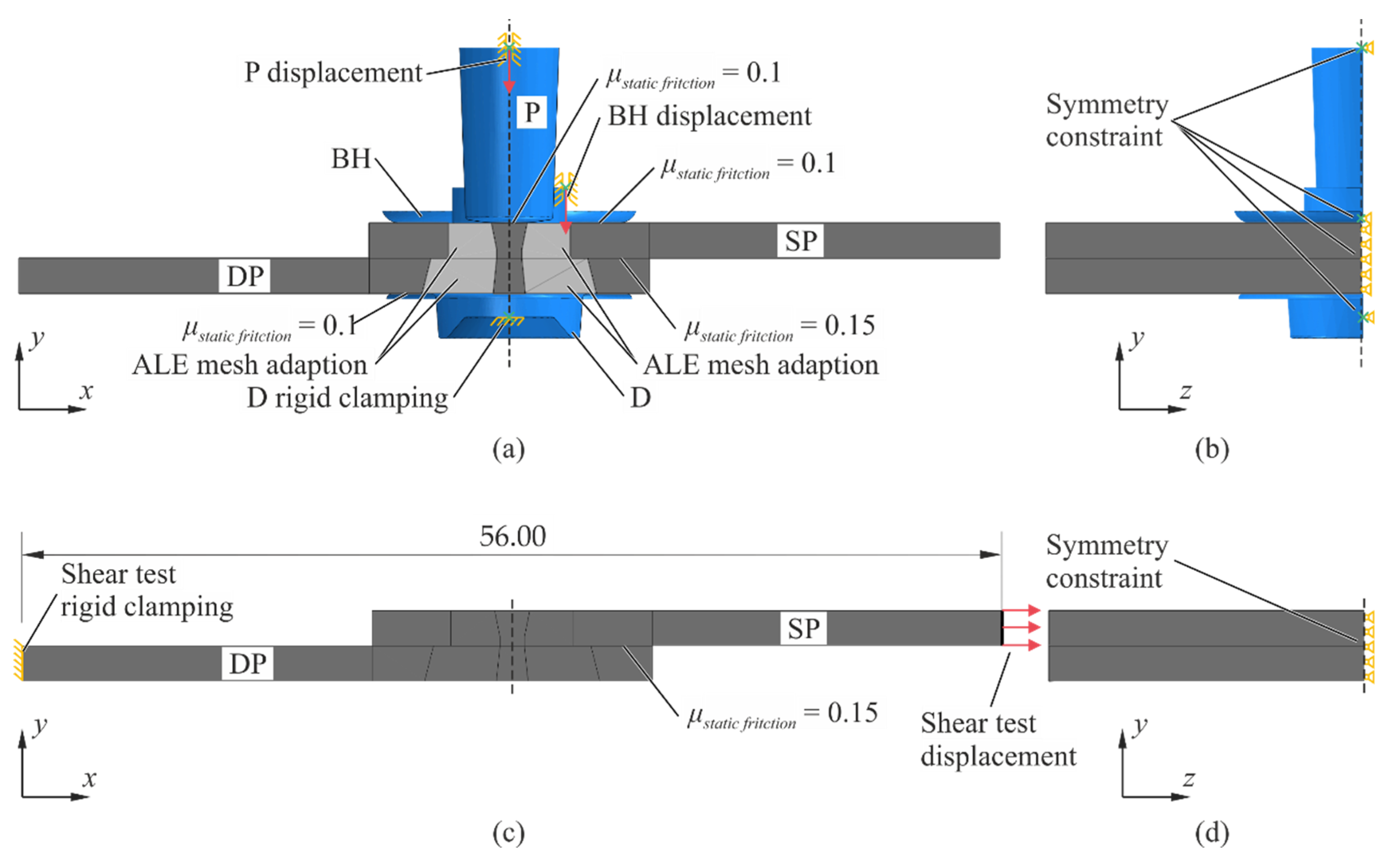
2.3. Numerical Model
3. Results
3.1. Numerical Model Validation
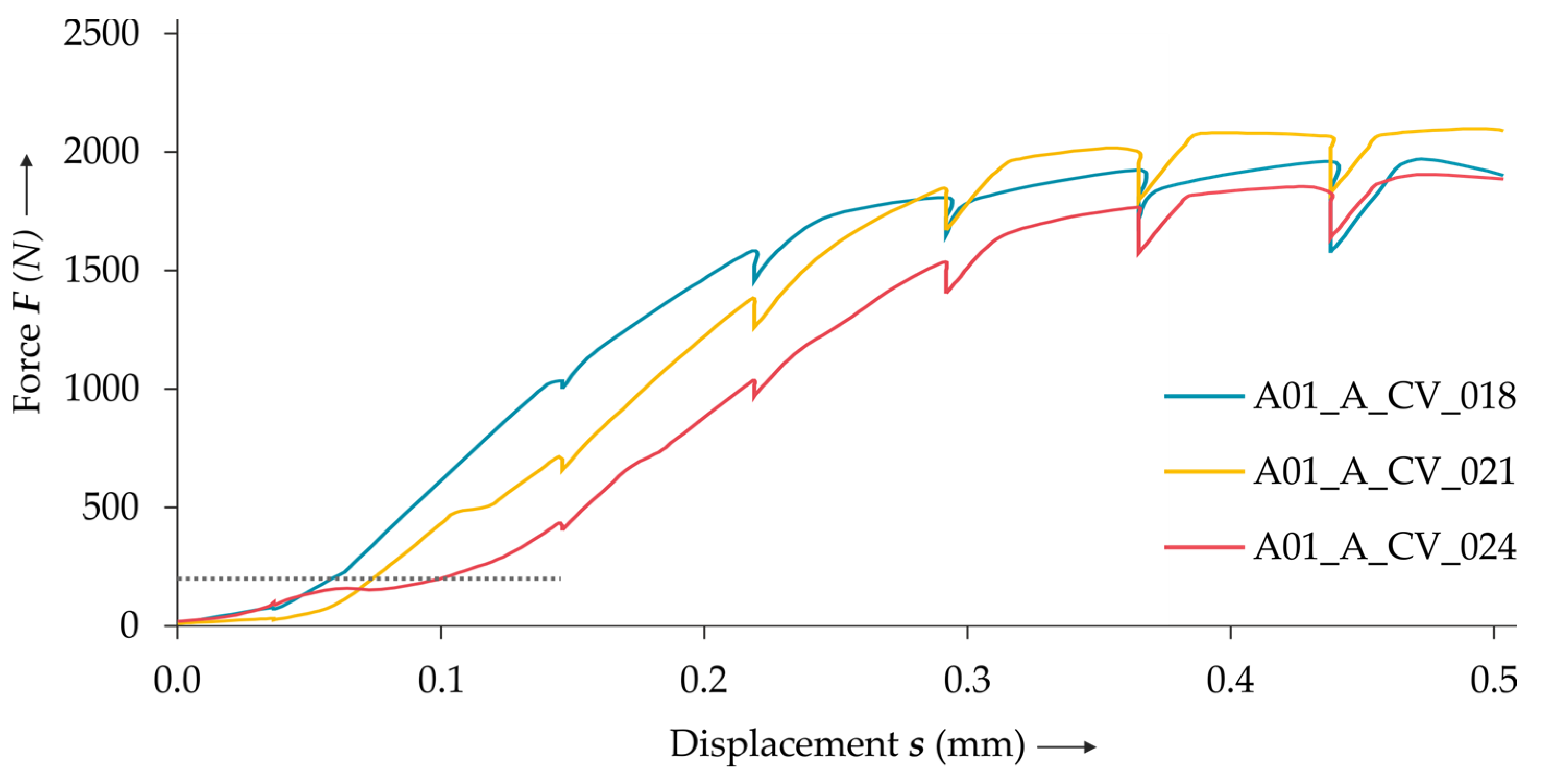
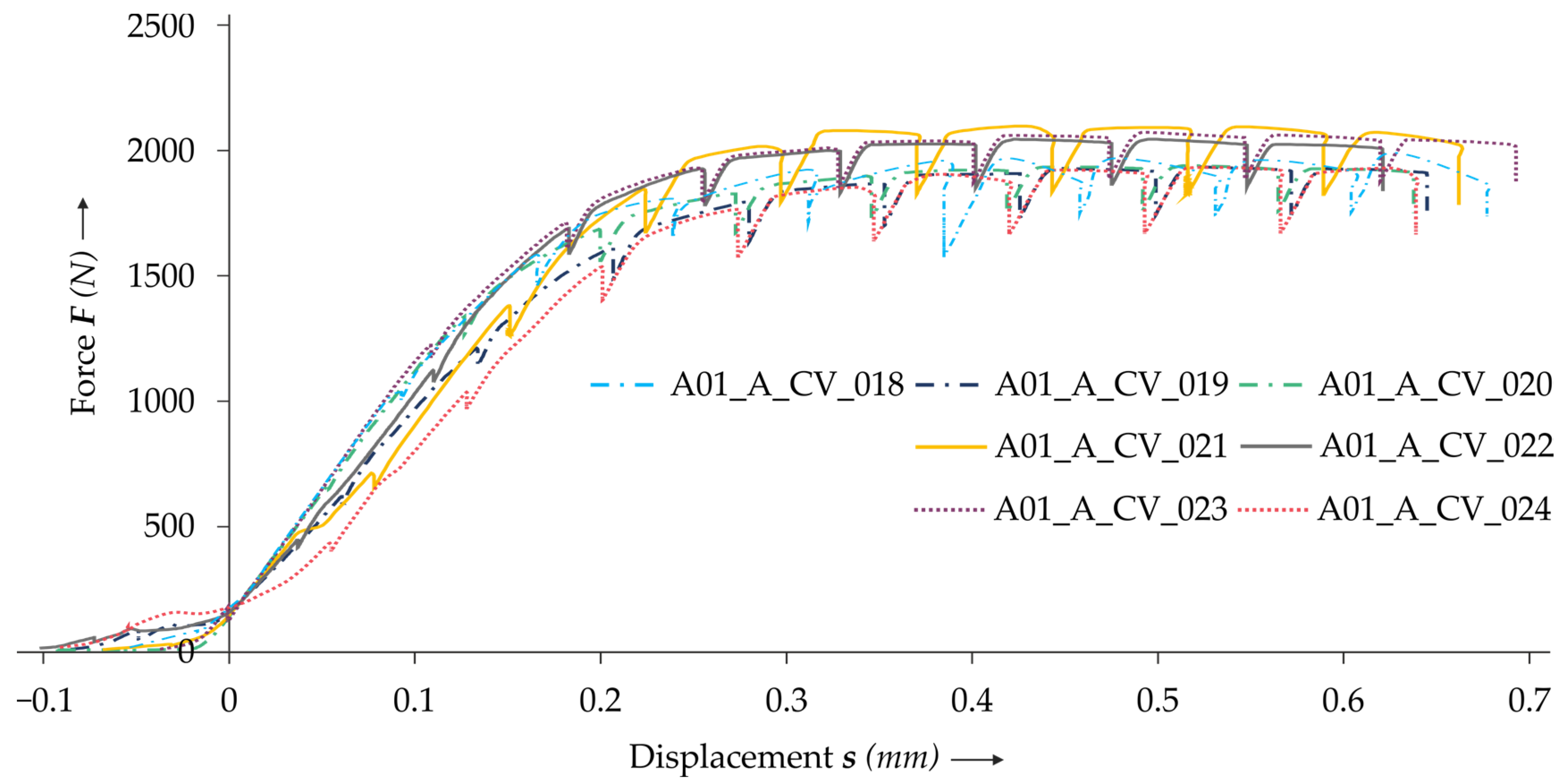
3.2. Influence of the Radiopaque Materials
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Organization for Standardization. ISO 12996:2013(en), Mechanical Joining—Destructive Testing of Joints—Specimen Dimensions and Test Procedure for Tensile Shear Testing of Single Joints; International Organization for Standardization: Geneva, Switzerland, 2013. [Google Scholar]
- Jiang, T.; Liu, Z.-X.; Wang, P.-C. Quality inspection of clinched joints of steel and aluminum. Int. J. Adv. Manuf. Technol. 2015, 76, 1393–1402. [Google Scholar] [CrossRef]
- Carmignato, S.; Dewulf, W.; Leach, R. Industrial X-ray Computed Tomography; Springer International Publishing: Cham, UK, 2018; ISBN 978-3-319-59571-9. [Google Scholar]
- Nicoletto, G.; Konečná, R.; Fintova, S. Characterization of microshrinkage casting defects of Al–Si alloys by X-ray computed tomography and metallography. Int. J. Fatigue 2012, 41, 39–46. [Google Scholar] [CrossRef]
- Du Plessis, A.; Olawuyi, B.J.; Boshoff, W.P.; Le Roux, S.G. Simple and fast porosity analysis of concrete using X-ray computed tomography. Mater. Struct. 2016, 49, 553–562. [Google Scholar] [CrossRef]
- Böhm, R.; Stiller, J.; Behnisch, T.; Zscheyge, M.; Protz, R.; Radloff, S.; Gude, M.; Hufenbach, W. A quantitative comparison of the capabilities of in situ computed tomography and conventional computed tomography for damage analysis of composites. Compos. Sci. Technol. 2015, 110, 62–68. [Google Scholar] [CrossRef]
- Jones, A.C.; Arns, C.H.; Sheppard, A.P.; Hutmacher, D.W.; Milthorpe, B.K.; Knackstedt, M.A. Assessment of bone ingrowth into porous biomaterials using MICRO-CT. Biomaterials 2007, 28, 2491–2504. [Google Scholar] [CrossRef] [PubMed]
- Holub, W.; Haßler, U. Detection and Evaluation of Ondulations in Glass-Fiber Reinforced Materials. In Proceedings of the 4th Conference on Industrial Computed Tomography (iCT), Wels, Austria, 19–21 September 2012. [Google Scholar]
- Drossel, W.G.; Mauermann, R.; Grützner, R.; Mattheß, D. Numerical and Experimental Analysis of Self Piercing Riveting Process with Carbon Fiber-Reinforced Plastic and Aluminium Sheets. KEM 2013, 554–557, 1045–1054. [Google Scholar] [CrossRef]
- Pejryd, L.; Beno, T.; Carmignato, S. Computed Tomography as a Tool for Examining Surface Integrity in Drilled Holes in CFRP Composites. Procedia CIRP 2014, 13, 43–48. [Google Scholar] [CrossRef]
- Füßel, R.; Gude, M.; Mertel, A. In-situ X-ray computed tomography analysis of adhesively bonded riveted lap joints. In Proceedings of the 17th European Conference on Composite Materials, Munich, Germany, 26–30 June 2016. [Google Scholar]
- Kunz, H.; Stammen, E.; Dilger, K. Local displacement measurements within adhesives using particle tracking and In Situ computed tomography. J. Adhes. 2017, 93, 531–549. [Google Scholar] [CrossRef]
- Pottmeyer, F.; Bittner, J.; Pinter, P.; Weidenmann, K.A. In-Situ CT Damage Analysis of Metal Inserts Embedded in Carbon Fiber-Reinforced Plastics. Exp. Mech. 2017, 57, 1411–1422. [Google Scholar] [CrossRef]
- Köhler, D.; Kupfer, R.; Troschitz, J.; Gude, M. Clinching in In-situ CT–Experimental Study on Suitable Tool Materials. In Proceedings of the 24th International Conference on Material Forming (ESAFORM 2021), online, 14–16 April 2021. [Google Scholar]
- Bielak, C.R.; Böhnke, M.; Beck, R.; Bobbert, M.; Meschut, G. Numerical analysis of the robustness of clinching process considering the pre-forming of the parts. J. Adv. Join. Process. 2021, 3, 100038. [Google Scholar] [CrossRef]
- Eshtayeh, M.M.; Hrairi, M. Recent and future development of the application of finite element analysis in clinching process. Int. J. Adv. Manuf. Technol. 2016, 84, 2589–2608. [Google Scholar] [CrossRef]
- Kaðèák, L.; Spiðák, E.; Kubík, R.; Mucha, J. Finite Element Calculation of Clinching with Rigid Die of Three Steel Sheets. Strength Mater. 2017, 49, 488–499. [Google Scholar] [CrossRef]
- Kaščák, L.; Mucha, J.; Spišák, E.; Kubík, R. Wear Study of Mechanical Clinching Dies During Joining of Advanced High-Strength Steel Sheets. Strength Mater. 2017, 49, 726–737. [Google Scholar] [CrossRef]
- Knörr, M. Auslegung von Massivumformwerkzeugen Gegen Versagen Durch Ermüdung; Springer: Berlin/Heidelberg, Germany, 1996; ISBN 9783540615354. [Google Scholar]
- Dassault Systémes Simulia Corp. Abaqus Users Manual 2017: Version 2017, Providence, RI. Available online: https://abaqus-docs.mit.edu/2017/English/SIMACAEITNRefMap/simaitn-c-friction.htm (accessed on 29 May 2020).
- Köhler, D.; Kupfer, R.; Gude, M. Clinching in in-situ CT—A numerical study on suitable tool materials. J. Adv. Join. Process. 2020, 2, 100034. [Google Scholar] [CrossRef]
- Cong, W.; Pfeiffer, F.; Bech, M.; Bunk, O.; David, C.; Wang, G. Dark-field Tomography: Modeling and Reconstruction. 2010. Available online: https://arxiv.org/pdf/1003.2155 (accessed on 24 March 2021).





| Test Division | Parameter | Unit | Value |
|---|---|---|---|
| Specimen | Punch penetration | mm | 4.7 |
| Joining speed | mm/s | 2 | |
| Heat treatment temperature (T6) | K | 458.15 | |
| Heat treatment duration (T6) | min | 20 | |
| CT system | Acceleration voltage | V | 1.50 × 105 |
| Tube current | A | 7.0 × 10−5 | |
| X-ray projections | - | 1440 (4 per 1°) | |
| Exposure time | s | 6.25 | |
| Resolution | mm | 7.58 × 10−3 | |
| Magnification | - | 16.8 | |
| In situ testing machine | In situ CT elongation steps | mm | 0.08; 0.15; 0.22; 0.30; 0.37; 0.44; 0.52; 0.59; 0.66 |
| Test speed | mm/min | 2 |
| Specimen | Copper Spray Treatment | Investigation Method |
|---|---|---|
| A01_A_CV_018 | One sheet treated | In situ CT lap shear test |
| A01_A_CV_019 | One sheet treated | Ex situ CT and lap shear test |
| A01_A_CV_020 | One sheet treated | Ex situ CT and lap shear test |
| A01_A_CV_021 | Both sheets treated | In situ CT lap shear test |
| A01_A_CV_022 | Both sheets treated | Ex situ CT and lap shear test |
| A01_A_CV_023 | No treatment | Ex situ CT and lap shear test |
| A01_A_CV_024 | No treatment | In situ CT lap shear test |
| Measurement Method | Max. Clinching Force (N) | Bottom Thickness (mm) | Undercut (mm) | Neck Thickness (mm) |
|---|---|---|---|---|
| Microsection measurement [12] | 3.25 × 104–3.35 × 104 | 0.67–0.72 | 0.25–0.31 | 0.45–0.52 |
| Reference model | 3.20 × 104 | 0.68 | 0.31 | 0.43 |
| Auxiliary model | 3.09 × 104 | 0.68 | 0.30 | 0.44 |
| 3D model | 3.12 × 104 | 0.68 | 0.28 | 0.45 |
| Copper Spray Treatment | Bottom Thickness (mm) | Undercut (mm) | Neck Thickness (mm) |
|---|---|---|---|
| Not treated | 0.65 | unidentifiable | unidentifiable |
| One sheet treated | 0.64 | 0.23–0.33 | 0.45–0.50 |
| Both sheet treated | 0.64 | 0.23–0.27 | 0.45–0.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Köhler, D.; Kupfer, R.; Troschitz, J.; Gude, M. In Situ Computed Tomography—Analysis of a Single-Lap Shear Test with Clinch Points. Materials 2021, 14, 1859. https://doi.org/10.3390/ma14081859
Köhler D, Kupfer R, Troschitz J, Gude M. In Situ Computed Tomography—Analysis of a Single-Lap Shear Test with Clinch Points. Materials. 2021; 14(8):1859. https://doi.org/10.3390/ma14081859
Chicago/Turabian StyleKöhler, Daniel, Robert Kupfer, Juliane Troschitz, and Maik Gude. 2021. "In Situ Computed Tomography—Analysis of a Single-Lap Shear Test with Clinch Points" Materials 14, no. 8: 1859. https://doi.org/10.3390/ma14081859
APA StyleKöhler, D., Kupfer, R., Troschitz, J., & Gude, M. (2021). In Situ Computed Tomography—Analysis of a Single-Lap Shear Test with Clinch Points. Materials, 14(8), 1859. https://doi.org/10.3390/ma14081859







