Vertex Displacement-Based Discontinuous Deformation Analysis Using Virtual Element Method
Abstract
1. Introduction
2. Basic Principles of DDA
3. Demerits Caused by the Original Degrees of Freedom and Previous Attempts to Construct a Vertex Displacement-Based DDA
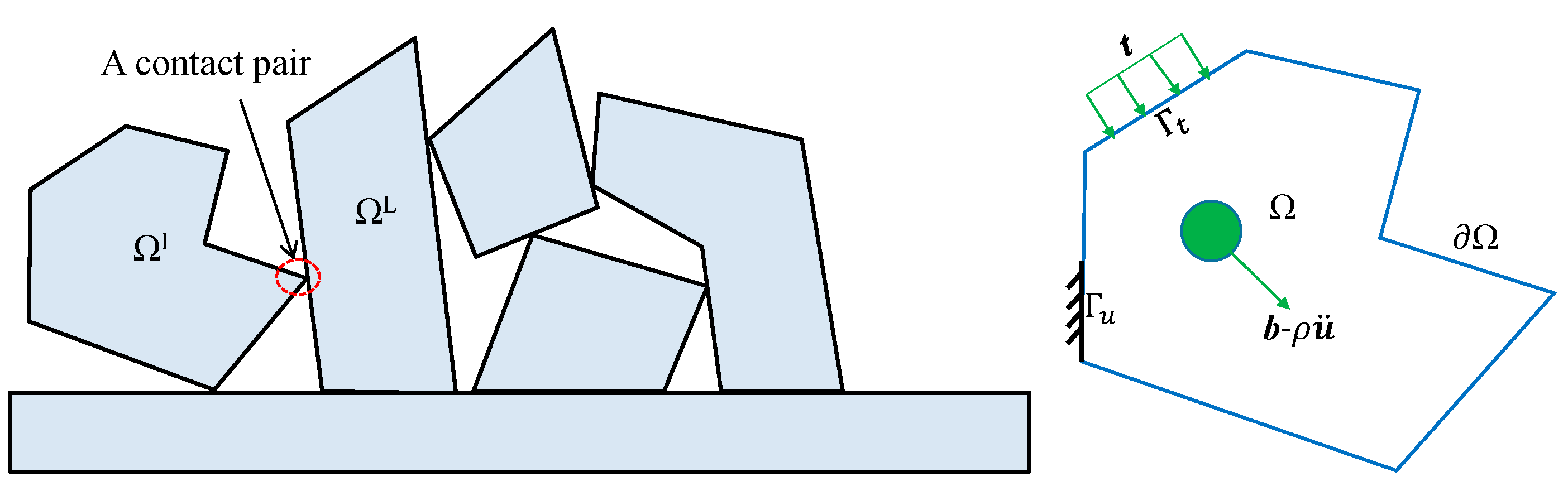
3.1. Demerits Caused by the Original Degrees of Freedom in DDA
3.2. Previous Attempts to Construct Vertex Displacement-Based DDA
4. Vertex Displacement-Based DDA Using VEM
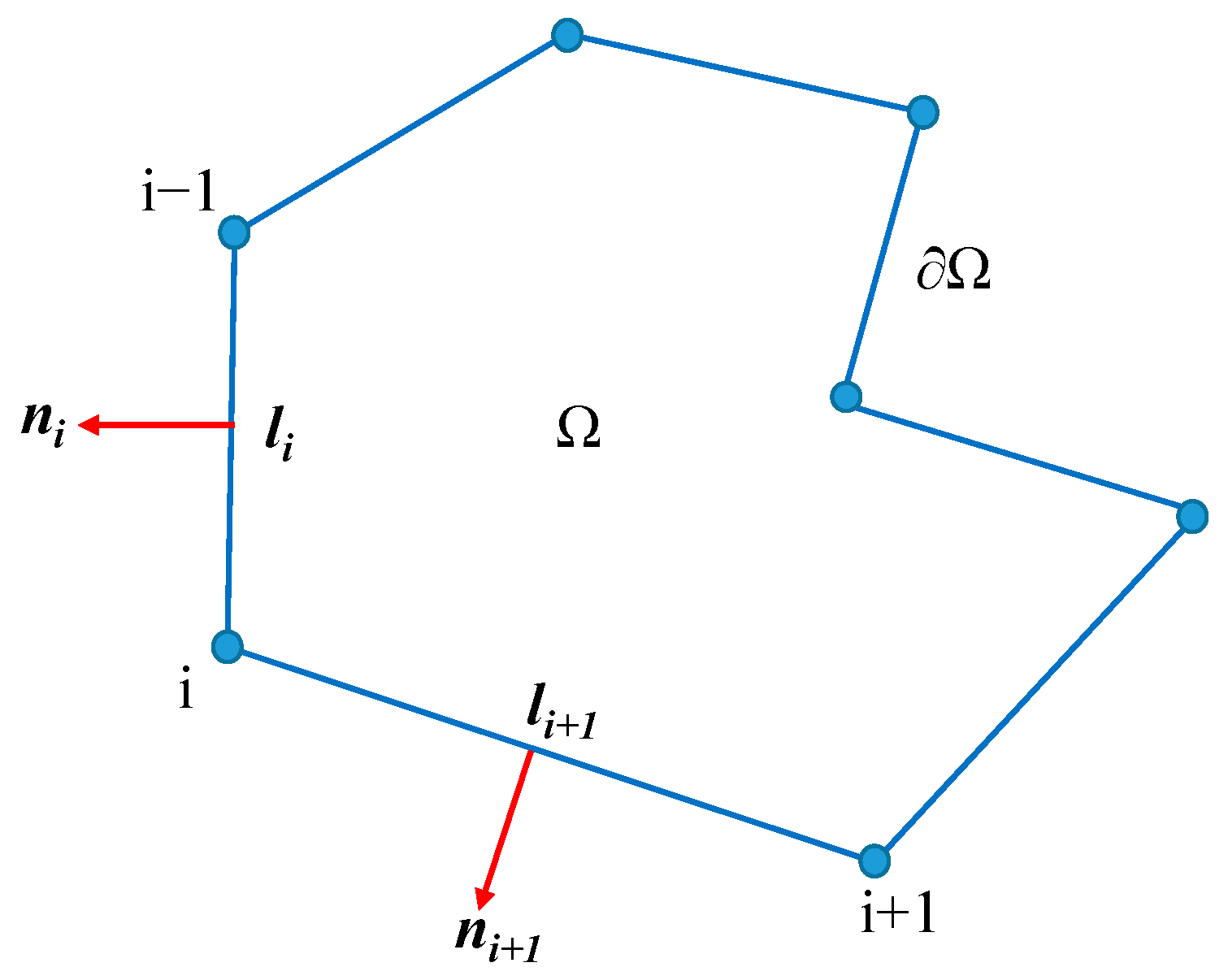
4.1. Virtual Element Spaces
4.2. The Projection Operator ΠPu: V1(Ω)→P1(Ω)
4.3. Computation of α(u, v) and f(v)
4.4. Computation of J’(v) Due to the Contact Constraints
5. Numerical Examples
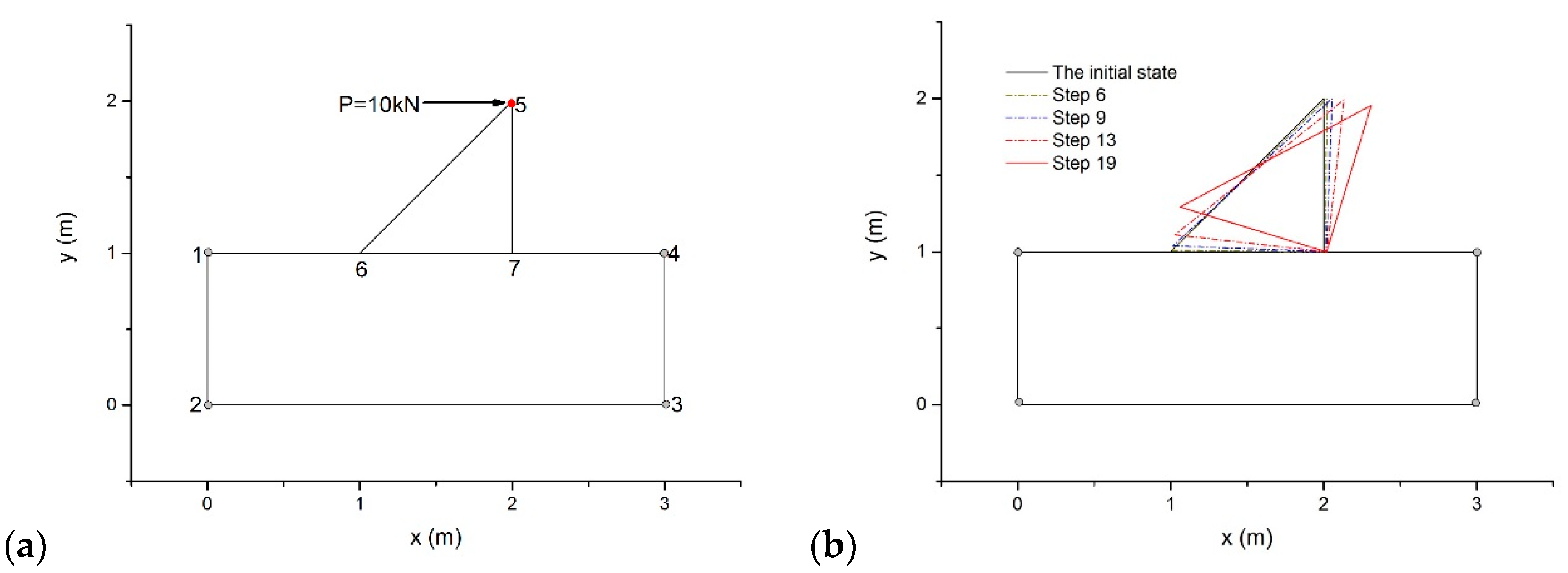
5.1. Rotating Triangular Block Problem
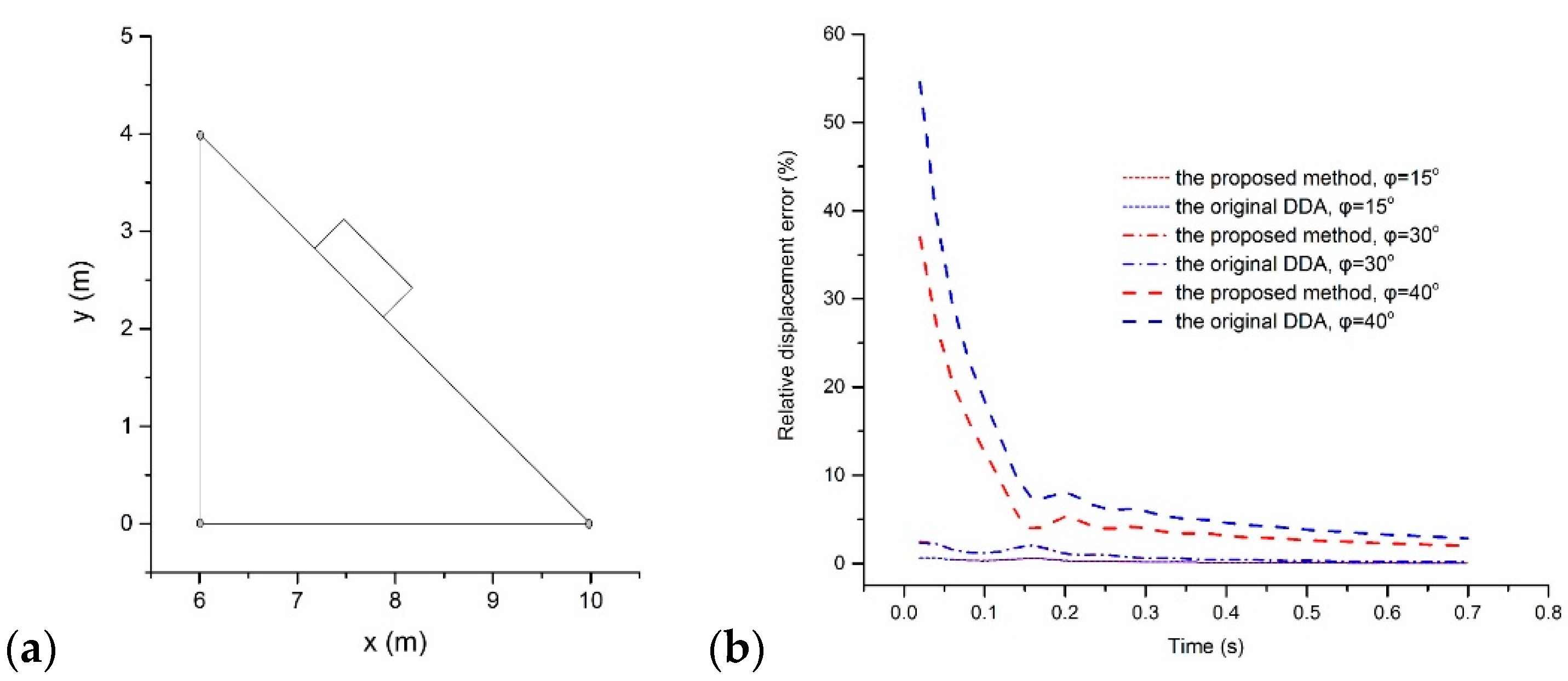
5.2. Sliding Problem
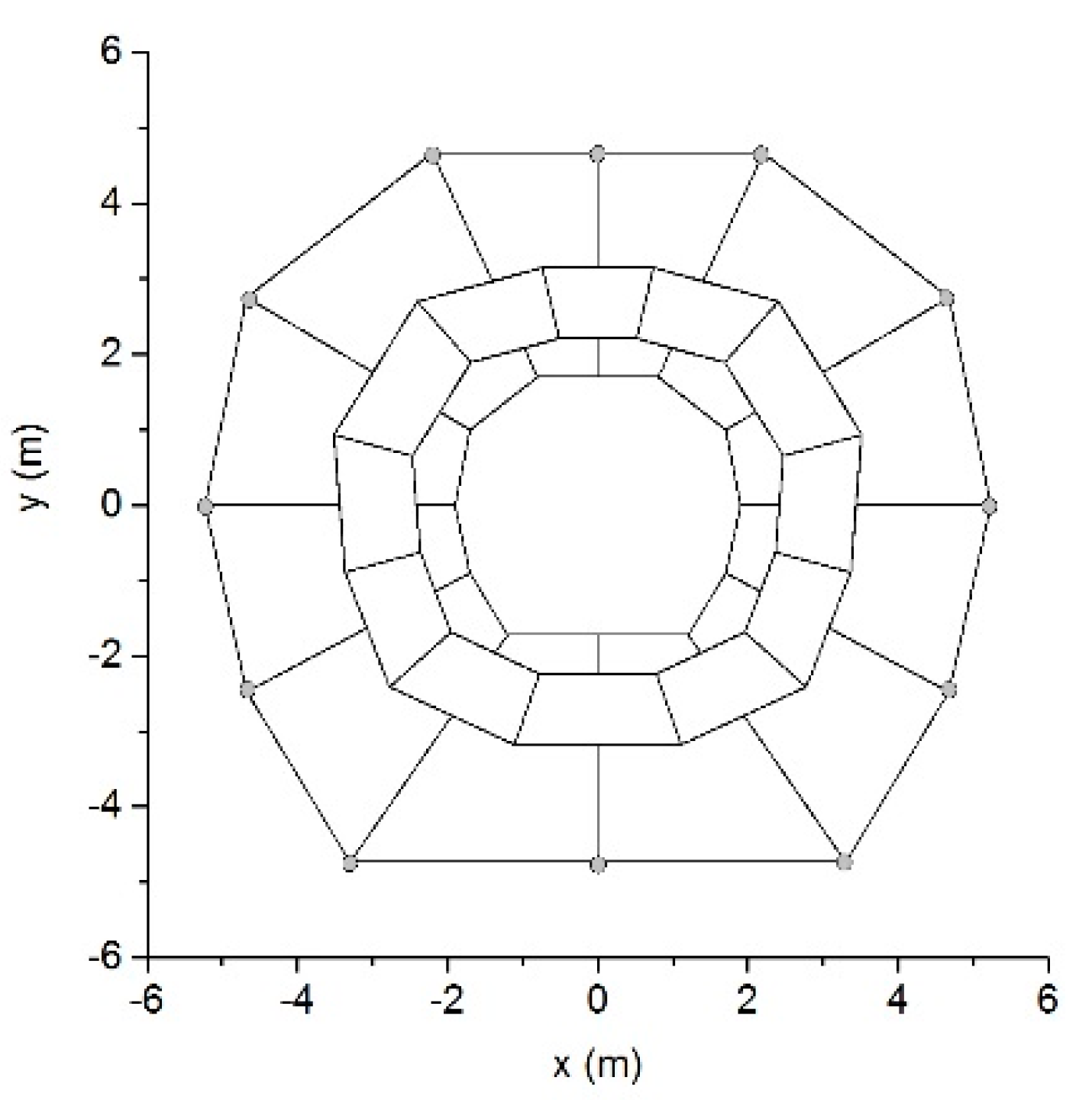
5.3. Surrounding Rock Problem
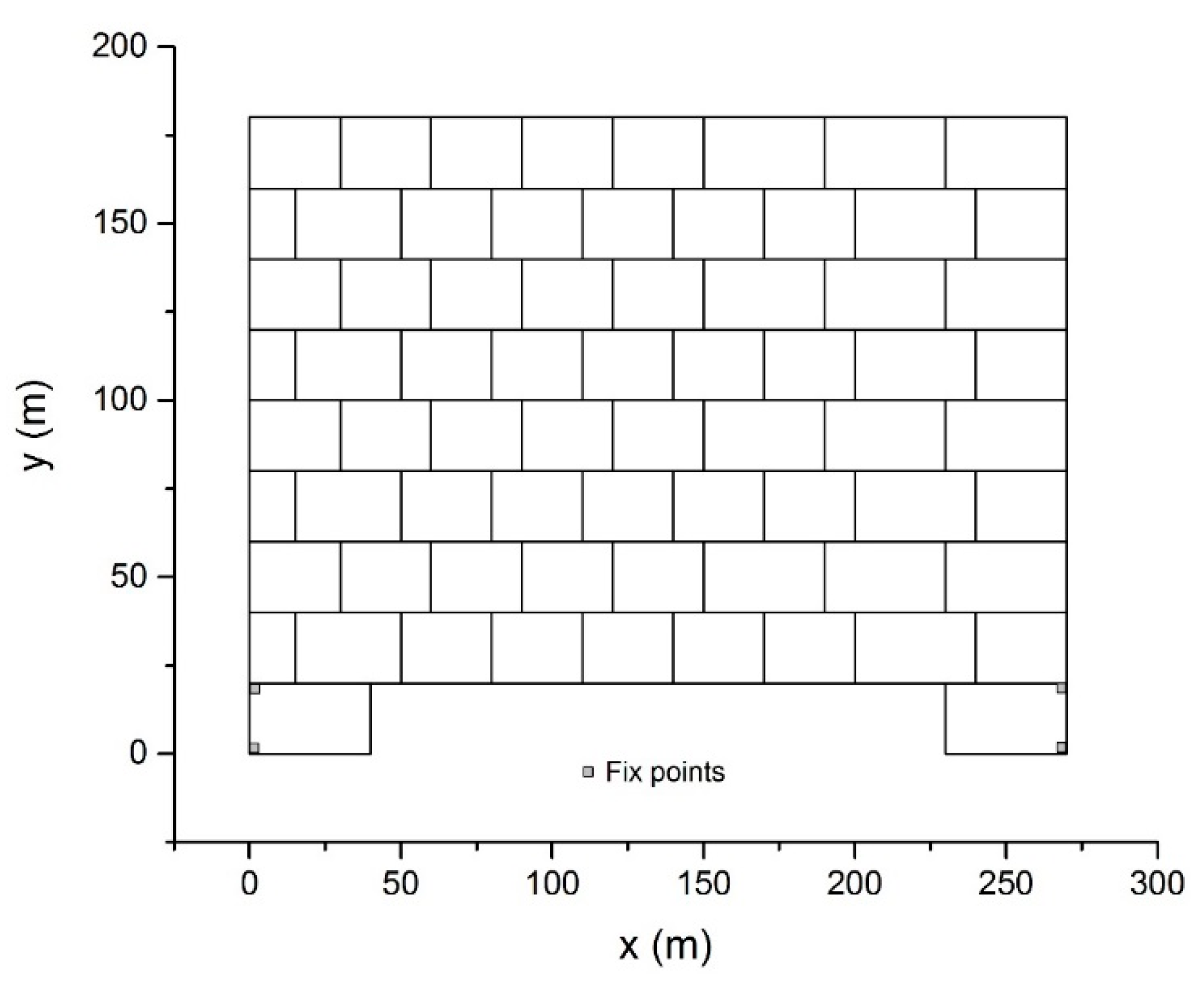
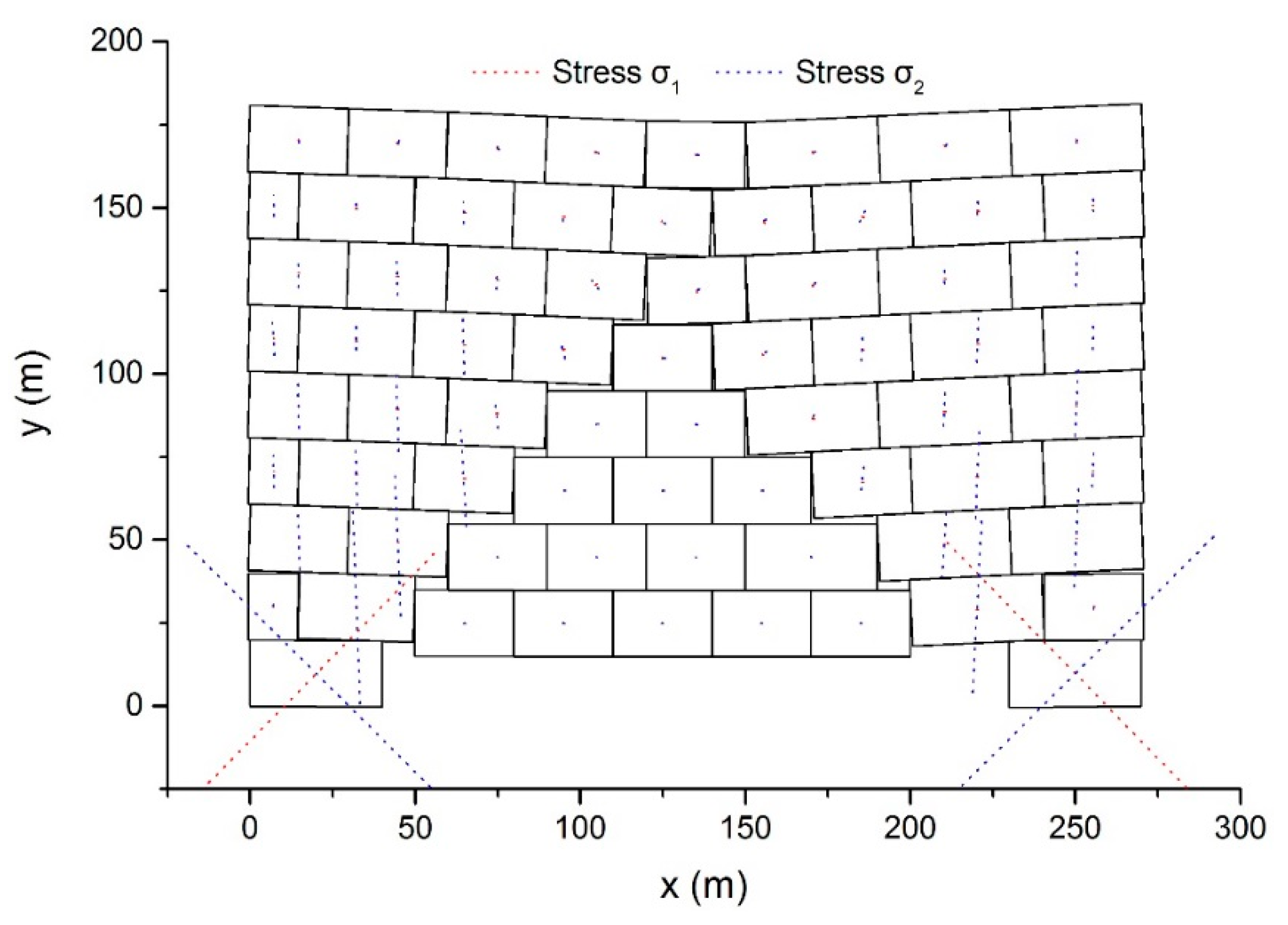
5.4. Block Wall Failure Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, G.H. Discontinuous Deformation Analysis—A New Numerical Model for the Statics and Dynamics of Block Systems. Ph.D. Thesis, Department of Civil Engineering University of California, Berkeley, CA, USA, 1988. [Google Scholar]
- MacLaughlin, M.M.; Doolin, D.M. Review of validation of the discontinuous deformation analysis (DDA) method. Int. J. Numer. Anal. Meth. Geomech. 2006, 30, 271–305. [Google Scholar] [CrossRef]
- Jing, L.R. Formulation of discontinuous deformation analysis (DDA)—an implicit discrete element model for block systems. Eng. Geol. 1998, 49, 371–381. [Google Scholar] [CrossRef]
- Yang, Y.T.; Xu, D.D.; Liu, F.; Zheng, H. Modeling the entire progressive failure process of rock slopes using a strength-based criterion. Comput. Geotech. 2020, 126, 103726. [Google Scholar] [CrossRef]
- Chen, K.T.; Wu, J.H. Simulating the failure process of the Xin Mo landslide using discontinuous deformation analysis. Eng. Geol. 2018, 239, 269–281. [Google Scholar] [CrossRef]
- Hatzor, Y.H.; Arzi, A.A.; Zaslavsky, Y.; Shapira, A. Dynamic stability analysis of jointed rock slopes using the DDA method: King Herod’s Palace, Masada, Israel. Int. J. Rock Mech. Min. Sci. 2004, 41, 813–832. [Google Scholar] [CrossRef]
- Fu, X.D.; Sheng, Q.; Zhang, Y.H.; Chen, J.; Zhang, S.K.; Zhang, Z.P. Computation of the safety factor for slope stability using discontinuous deformation analysis and the vector sum method. Comput. Geotech. 2017, 92, 68–76. [Google Scholar] [CrossRef]
- Ning, Y.J.; Yang, J.; An, X.M.; Ma, G.W. Modelling rock fracturing and blast-induced rock mass failure via advanced discretization within the discontinuous deformation analysis framework. Comput. Geotech. 2011, 38, 40–49. [Google Scholar] [CrossRef]
- Tang, C.A.; Tang, S.B.; Gong, B.; Bai, H.M. Discontinuous deformation and displacement analysis: From continuous to discontinuous. Sci. China Tech. Sci. 2015, 58, 1567–1574. [Google Scholar] [CrossRef]
- Chen, Y.J.; Zhang, X.; Zhu, W.S.; Wang, W. Modified discontinuous deformation analysis for rock failure: Crack propagation. Geomech. Eng. 2018, 14, 325–336. [Google Scholar]
- Liu, X.Y.; Zhao, Z.Y.; Ma, S.Q. Simulating stress wave with flat-top partition of unity based high-order discontinuous deformation analysis. Eng. Anal. Bound. Elem. 2018, 91, 110–123. [Google Scholar] [CrossRef]
- Chen, G.Q.; He, M.C.; Fan, F.S. Rock burst analysis using DDA numerical simulation. Int. J. Geomech. 2018, 18, 04018001. [Google Scholar] [CrossRef]
- Ning, Y.; Yang, Z.; Wei, B.; Gu, B. Advances in two-dimensional discontinuous deformation analysis for rock-mass dynamics. Int. J. Geomech. 2016, 17, E6016001. [Google Scholar] [CrossRef]
- Cai, Y.; Liang, G.; Shi, G.H. Studying impact problem by LDDA method. In Discontinuous Deformation Analysis (DDA) and Simulations of Discontinuous Media; TSI Press: San Antonio, TX, USA, 1996. [Google Scholar]
- Bao, H.R.; Zhao, Z.Y.; Tian, Q. On the implementation of augmented Lagrangian method in the two-dimensional discontinuous deformation analysis. Int. J. Numer. Anal. Meth. Geomech. 2014, 38, 551–571. [Google Scholar] [CrossRef]
- Zheng, H.; Jiang, W. Discontinuous deformation analysis based on complementary theory. Sci. China Ser. E Technol. Sci. 2009, 52, 2547–2554. [Google Scholar] [CrossRef]
- Jiang, W.; Zheng, H. Discontinuous deformation analysis based on variational inequality theory. Int. J. Comput. Methods 2011, 8, 193–208. [Google Scholar] [CrossRef]
- Lin, S.; Xie, Z. Performance of DDA time integration. Sci. China Technol. Sci. 2015, 58, 1558–1566. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; Zhang, X.L.; Zhao, J.; Liu, Q.S. Viscous boundary of DDA for modeling stress wave propagation in jointed rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 1070–1076. [Google Scholar] [CrossRef]
- Jiang, Q.; Chen, Y.; Zhou, C.; Yeung, M.-C.R. Kinetic Energy Dissipation and Convergence Criterion of Discontinuous Deformations Analysis (DDA) for Geotechnical Engineering. Rock Mech. Rock Eng. 2012, 46, 1443–1460. [Google Scholar] [CrossRef]
- Beyabanaki, S.A.R.; Jafari, A.; Yeung, M.R. High-order three-dimensional discontinuous deformation analysis (3-D DDA). Int. J. Numer. Meth. Biomed. Eng. 2010, 26, 1522–1547. [Google Scholar] [CrossRef]
- Grayeli, R.; Hatami, K. Implementation of the finite element method in the three-dimensional discontinuous deformation analysis (3D-DDA). Int. J. Numer. Anal. Meth. Geomech. 2008, 32, 1883–1902. [Google Scholar] [CrossRef]
- Wang, J.Q.; Lin, G. Static and dynamic stability analysis using 3D-DDA with incision body scheme. Earthq. Eng. Eng. Vib. 2006, 5, 273–284. [Google Scholar] [CrossRef]
- Liu, J.; Geng, Q.D.; Kong, X.J. A fast common plane identification algorithm for 3D contact problems. Comput. Geotech. 2009, 36, 41–51. [Google Scholar] [CrossRef]
- Ali, R.K.; Ahmad, J.; Wu, J.H. A new algorithm to identify contact patterns between convex blocks for three-dimensional discontinuous deformation analysis. Comput. Geotech. 2008, 35, 746–759. [Google Scholar]
- Zhu, H.; Wu, W.; Chen, J.; Ma, G.; Liu, X.; Zhuang, X. Integration of three dimensional discontinuous deformation analysis (DDA) with binocular photogrammetry for stability analysis of tunnels in blocky rock mass. Tunn. Undergr. Space Technol. 2016, 51, 30–40. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; Huang, G.H.; Zhao, Z.Y.; Zheng, F.; Wang, L. An improved three-dimensional spherical DDA model for simulating rock failure. Sci. China Tech. Sci. 2015, 58, 1533–1541. [Google Scholar] [CrossRef]
- Shi, G.H. Contact theory. Sci. China Tech. Sci. 2015, 58, 1450–1496. [Google Scholar] [CrossRef]
- Song, X.Y.; Huang, D.; Zeng, B. GPU-based parallel computation for discontinuous deformation analysis (DDA) method and its application to modelling earthquake-induced landslide. Comput. Geotech. 2017, 86, 80–94. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Zheng, H. Explicit Discontinuous Deformation Analysis Method with Lumped Mass Matrix for Highly Discrete Block System. Int. J. Geomech. 2018, 18, 04018098. [Google Scholar] [CrossRef]
- MacLaughlin, M.M.; Sitar, N. Rigid body rotations in DDA. In Proceedings of the First International Forum on Discontinuous Deformation Analysis (DDA) and Simulations of Discontinuous Media, Berkeley, CA, USA, 12–14 June 1996; TSI Press: San Antonio, TX, USA, 1996; pp. 620–635. [Google Scholar]
- Cheng, Y.M.; Zhang, Y.H. Rigid body rotation and block internal discretization in DDA analysis. Int. J. Numer. Anal. Meth. Geomech. 2000, 24, 567–578. [Google Scholar] [CrossRef]
- Jiang, W.; Zheng, H. An efficient remedy for the false volume expansion of DDA when simulating large rotation. Comput. Geotech. 2015, 70, 18–23. [Google Scholar] [CrossRef]
- Koo, C.Y.; Chern, J.C. Modification of the DDA method for rigid block problems. Int. J. Rock Mech. Mining. Sci. 1998, 35, 683–693. [Google Scholar] [CrossRef]
- Ke, T.C. The Issue of Rigid-Body Rotation in DDA. In Proceedings of the First International Forum on Discontinuous Deformation Analysis (DDA) and Simulations of Discontinuous Media, Berkeley, CA, USA, 12–14 June 1996; TSI Press: San Antonio, TX, USA, 1996; pp. 318–326. [Google Scholar]
- Jiang, W.; Wang, Y.H.; Sun, G.H.; Song, P.C.; Mao, C. Discontinuous Deformation Analysis Based on Wachspress Interpolation Function for Detailed Stress Distribution. Math. Probl. Eng. 2018, 2018, 4079035. [Google Scholar] [CrossRef]
- Dasgupta, G. Interpolants within convex polygon: Wachspress′ shape functions. J. Aerosp. Eng. 2003, 16, 1–8. [Google Scholar] [CrossRef]
- Sukumar, N. Construction of polygonal interpolants: A maximum entropy interpolation. Int. J. Numer. Meth. Eng. 2004, 61, 2159–2181. [Google Scholar] [CrossRef]
- Jiang, W.; Xu, J.J.; Zheng, H.; Wang, Y.H.; Sun, G.H.; Yang, Y.T. Novel displacement function for discontinuous deformation analysis based on mean value coordinates. Int. J. Numer. Meth. Eng. 2020, 121, 4768–4792. [Google Scholar] [CrossRef]
- Joshi, P.; Meyer, M.; DeRose, T.; Green, B.; Sanocki, T. Harmonic coordinates for character articulation. ACM Trans. Graph. 2007, 26, 1–9. [Google Scholar] [CrossRef]
- Talischi, C.; Pereira, A.; Menezes, I.F.M.; Paulino, G.H. Gradient correction for polygonal and polyhedral finite elements. Int. J. Numer. Methods Eng. 2015, 102, 728–747. [Google Scholar] [CrossRef]
- Talischi, C.; Paulino, G.H. Addressing integration error for polygonal finite elements through polynomial projections: A patch test connection. Math. Models Methods Appl. Sci. 2014, 24, 1701–1727. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Brezzi, F.; Cangiani, A.; Manzini, G.; Marini, L.D.; Russo, A. Basic principles of virtual element methods. Math. Models Methods Appl. Sci. 2013, 23, 199–214. [Google Scholar] [CrossRef]
- Ahmad, B.; Alsaedi, A.; Brezzi, F.; Marini, L.D.; Russo, A. Equivalent projectors for virtual element methods. Comput. Math. Appl. 2013, 66, 376–391. [Google Scholar] [CrossRef]
- da Veiga LBo Brezzi, F.; Marini, L.D. Virtual Elements for Linear Elasticity Problems. SIAM J. Numer. Anal. 2013, 51, 794–812. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Brezzi, F.; Marini, L.D.; Russo, A. The hitchhiker′s guide to the virtual element method. Math. Models Methods Appl. Sci. 2014, 24, 1541–1573. [Google Scholar] [CrossRef]
- Park, K.; Chi, H.; Paulino, G.H. On nonconvex meshes for elastodynamics using virtual element methods with explicit time integration. Comput. Methods Appl. Mech. Eng. 2019, 356, 669–684. [Google Scholar] [CrossRef]
- Gain, A.L.; Talischi, C.; Paulino, G.H. On the Virtual Element Method for three-dimensional linear elasticity problems on arbitrary polyhedral meshes. Comput. Methods Appl. Mech. Eng. 2014, 282, 132–160. [Google Scholar] [CrossRef]
- Wriggers, P.; Rust, W.T.; Reddy, B.D. A virtual element method for contact. Comput. Mech. 2016, 58, 1039–1050. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Brezzi, F.; Dassi, F.; Marini, L.D.; Russo, A. Virtual Element approximation of 2D magnetostatic problems. Comput. Methods Appl. Mech. Eng. 2017, 327, 173–195. [Google Scholar] [CrossRef]
- Wriggers, P.; Reddy, B.D.; Rust, W.; Hudobivnik, B. Efficient virtual element formulations for compressible and incompressible finite deformations. Comput. Mech. 2017, 60, 253–268. [Google Scholar] [CrossRef]
- Chi, H.; da Veiga, L.B.; Paulino, G. Some basic formulations of the virtual element method (VEM) for finite deformations. Comput. Methods Appl. Mech. Eng. 2017, 318, 148–192. [Google Scholar] [CrossRef]






| Time Step | The Original DDA with the Post-Adjustment Strategy | The New Method | The Rotational Angle r0 | ||
|---|---|---|---|---|---|
| Penetrations in the Equilibrium Equations (m) | Penetrations in the Updated Configurations (m) | Penetrations in the Equilibrium Equations (m) | Penetrations in the Updated Configurations (m) | ||
| 1 | 8.3289 × 10−9 | 8.3288 × 10−9 | 8.32890 × 10−9 | 8.32890 × 10−9 | −0.000001 |
| 2 | 2.5026 × 10−8 | 2.5026 × 10−8 | 2.50260 × 10−8 | 2.50260 × 10−8 | −0.000000 |
| 3 | 7.4918 × 10−8 | 7.4918 × 10−8 | 7.49180 × 10−8 | 7.49180 × 10−8 | −0.000000 |
| 4 | 3.3772 × 10−7 | 1.4587 × 10−7 | 3.37720 × 10−7 | 3.37720 × 10−7 | −0.001073 |
| 5 | 1.0094 × 10−6 | −7.2045 × 10−7 | 1.00970 × 10−6 | 1.00970 × 10−6 | −0.003218 |
| 6 | 3.0067 × 10−6 | −1.8379 × 10−6 | 3.01240 × 10−6 | 3.01240 × 10−6 | −0.005375 |
| 7 | 8.9005 × 10−6 | −7.2391 × 10−7 | 8.92310 × 10−6 | 8.92310 × 10−6 | −0.007554 |
| 8 | 2.6114 × 10−5 | 9.8896 × 10−6 | 2.62290 × 10−5 | 2.62290 × 10−5 | −0.009768 |
| 9 | 7.5032 × 10−5 | 5.0108 × 10−5 | 7.54400 × 10−5 | 7.54400 × 10−5 | −0.012047 |
| 10 | 2.0631 × 10−4 | 1.7005 × 10−4 | 2.07880 × 10−4 | 2.07880 × 10−4 | −0.014444 |
| 11 | 4.9419 × 10−4 | 4.4322 × 10−4 | 4.97090 × 10−4 | 4.97090 × 10−4 | −0.017006 |
| 12 | 7.6165 × 10−4 | 6.9448 × 10−4 | 7.63320 × 10−4 | 7.63320 × 10−4 | −0.019372 |
| 13 | 6.5260 × 10−4 | 5.7022 × 10−4 | 6.50170 × 10−4 | 6.50170 × 10−4 | −0.021275 |
| 14 | 3.2463 × 10−4 | 2.2251 × 10−4 | 3.22710 × 10−4 | 3.22710 × 10−4 | −0.023478 |
| 15 | 2.6022 × 10−4 | 1.2772 × 10−4 | 2.68970 × 10−4 | 2.68970 × 10−4 | −0.026494 |
| 16 | 5.7111 × 10−4 | 3.9996 × 10−4 | 5.96770 × 10−4 | 5.96770 × 10−4 | −0.029810 |
| 17 | 9.6448 × 10−4 | 7.5227 × 10−4 | 9.91470 × 10−4 | 9.91470 × 10−4 | −0.032847 |
| 18 | 9.2970 × 10−4 | 6.7950 × 10−4 | 9.13440 × 10−4 | 9.13440 × 10−4 | −0.035286 |
| 19 | 3.3880 × 10−4 | 4.7618 × 10−5 | 2.94330 × 10−4 | 2.94330 × 10−4 | −0.037664 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Sun, G.; Liu, L.; Jiang, W. Vertex Displacement-Based Discontinuous Deformation Analysis Using Virtual Element Method. Materials 2021, 14, 1252. https://doi.org/10.3390/ma14051252
Luo H, Sun G, Liu L, Jiang W. Vertex Displacement-Based Discontinuous Deformation Analysis Using Virtual Element Method. Materials. 2021; 14(5):1252. https://doi.org/10.3390/ma14051252
Chicago/Turabian StyleLuo, Hongming, Guanhua Sun, Lipeng Liu, and Wei Jiang. 2021. "Vertex Displacement-Based Discontinuous Deformation Analysis Using Virtual Element Method" Materials 14, no. 5: 1252. https://doi.org/10.3390/ma14051252
APA StyleLuo, H., Sun, G., Liu, L., & Jiang, W. (2021). Vertex Displacement-Based Discontinuous Deformation Analysis Using Virtual Element Method. Materials, 14(5), 1252. https://doi.org/10.3390/ma14051252






