Investigation on the Thermodynamic Stability of Nanocrystalline W-Based Alloys: A Combined Theoretical and Experimental Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Identification of Thermodynamically Stable Nanocrystalline Alloys
2.2. Experimental Assessment of the Thermodynamic Stability of Nanocrystalline Alloys
2.2.1. Fabrication of Metal Nanoalloys
2.2.2. Thermal Treatment of Mechanically Alloyed Powders
2.2.3. Characterization
3. Results and Discussion
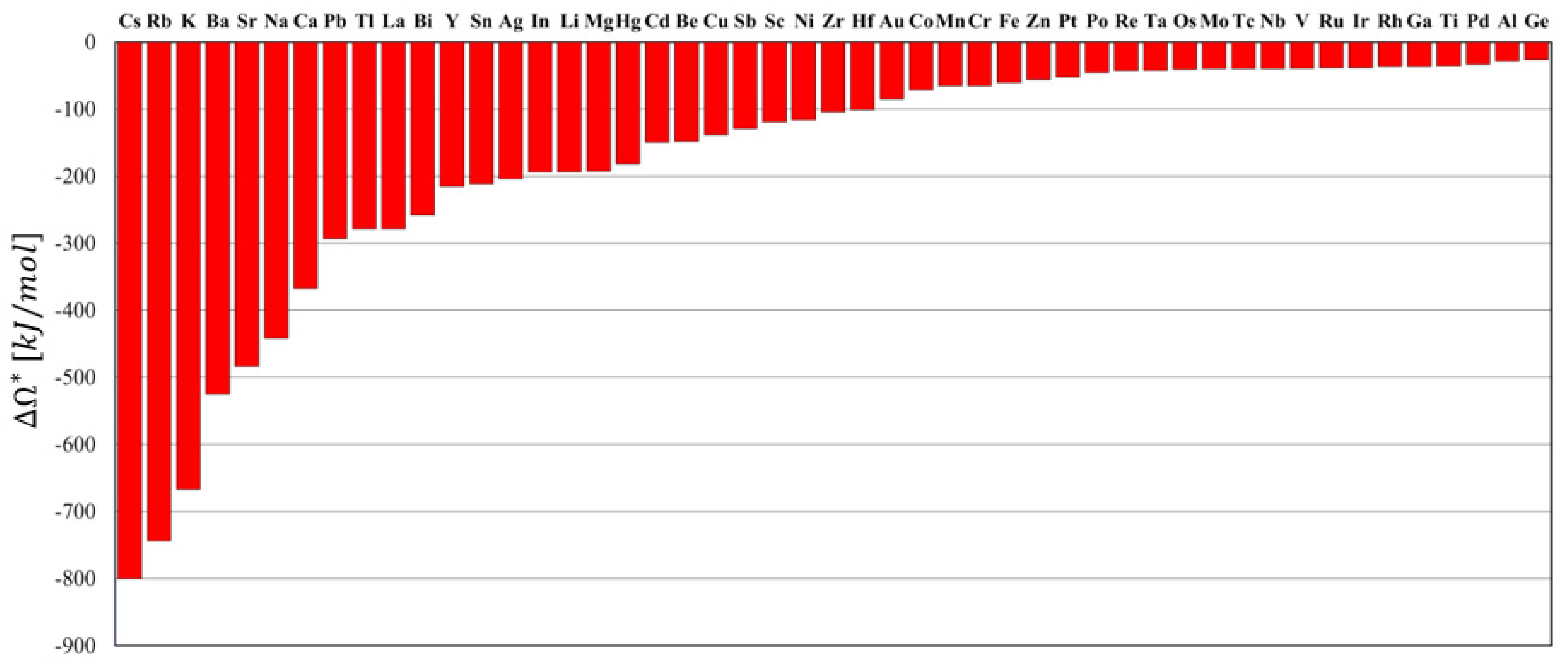
3.1. Identification of Thermodynamically Stable Nanocrystalline W-Based Alloys
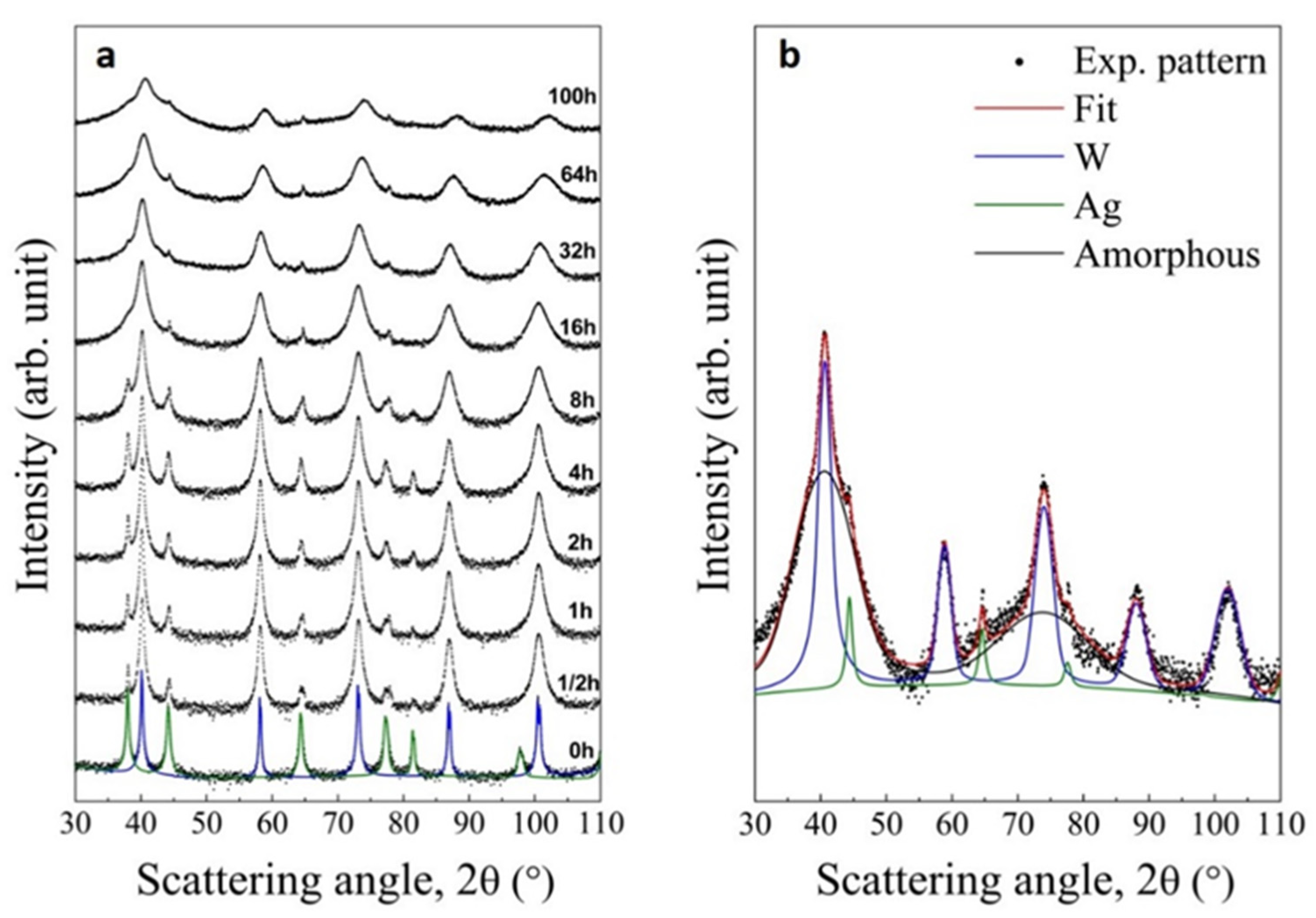
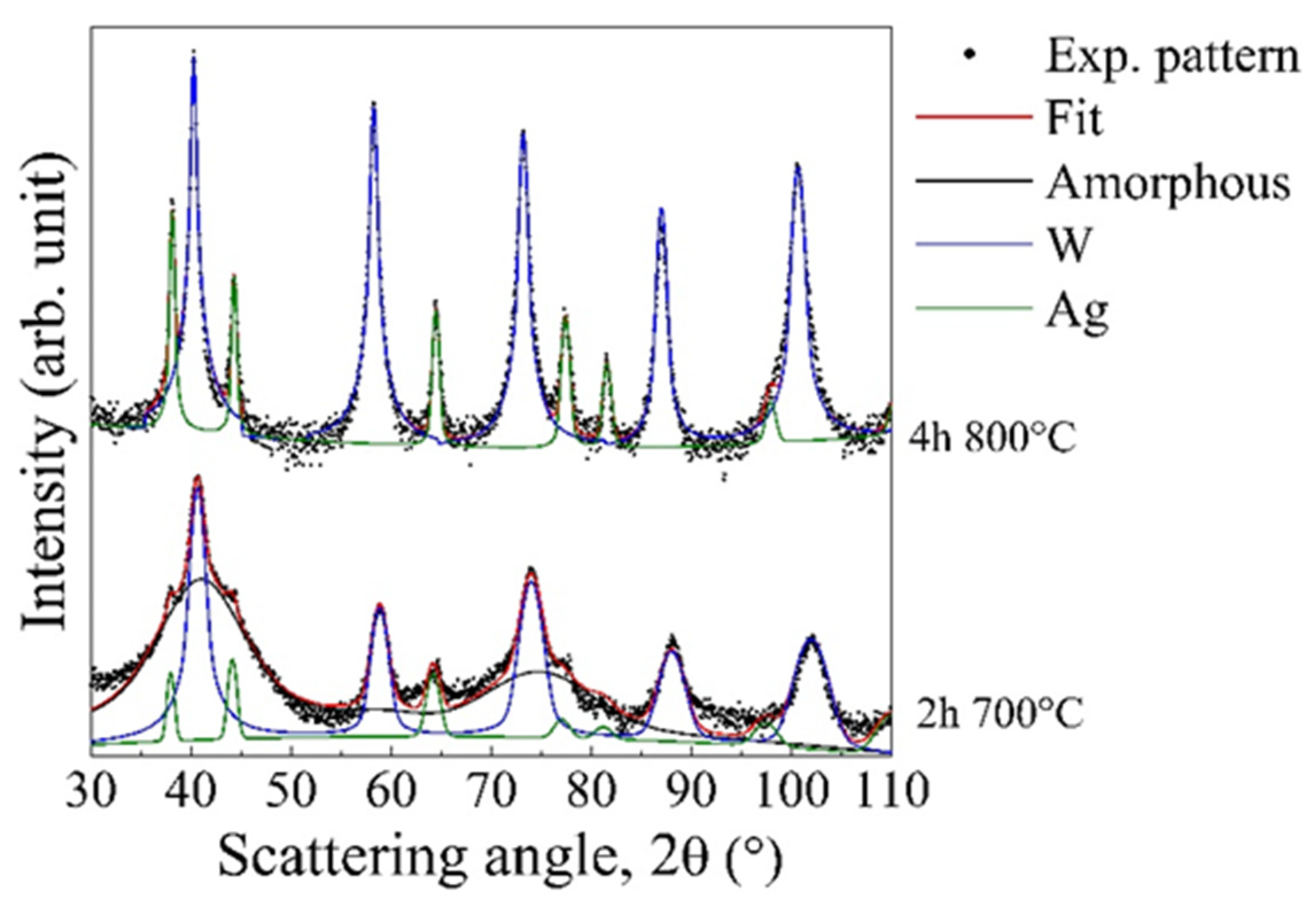
3.2. Experimental Validation of the Theoretical Approach
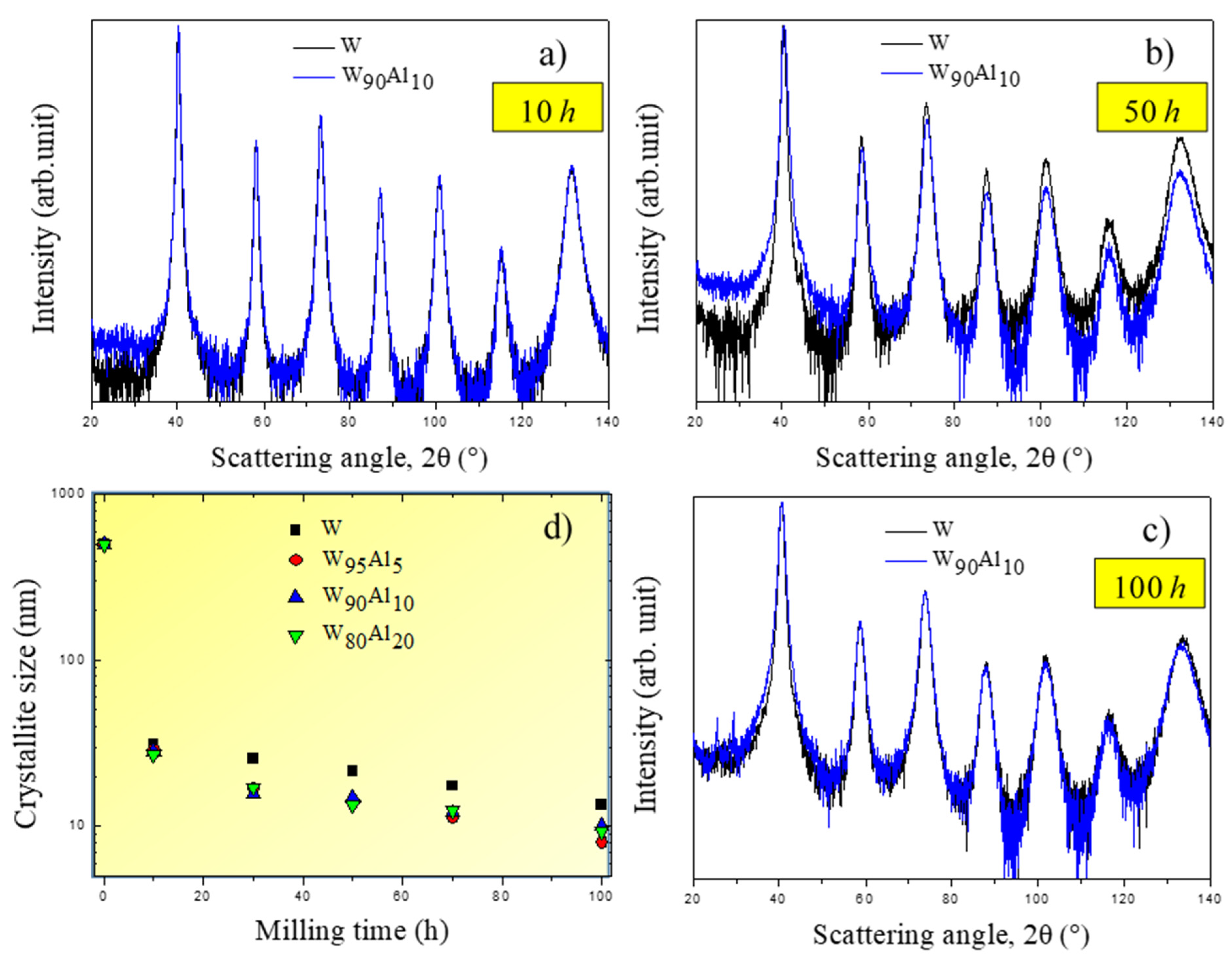
3.3. Comparison between Theoretical Predictions and Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gleiter, H. Nanocrystalline materials. Prog. Mater. Sci. 1989, 33, 223–315. [Google Scholar] [CrossRef] [Green Version]
- Suryanarayana, C.; Kock, C.C. Nanocrystalline materials—Current research and future directions. Hyperfine Interact. 2000, 130, 5–44. [Google Scholar] [CrossRef]
- Gusev, A.I.; Rempel, A. Nanocrystalline Materials; Cambridge International Science Publishing: Cambridge, UK, 2004. [Google Scholar]
- Lu, L.; Shen, Y.; Chen, X.; Qian, L.; Lu, K. Ultrahigh strength and high electrical conductivity in copper. Science 2004, 304, 422–427. [Google Scholar] [CrossRef] [Green Version]
- Whang, S.H. (Ed.) Nanostructured Metals and Alloys; Woodhead Publishing Limited: Cambridge, UK, 2011. [Google Scholar]
- Kumpmann, A.; Günther, B.; Kunze, H.D. Thermal stability of ultrafine-grained metals and alloys. Mater. Sci. Eng. A 1993, 168, 165–169. [Google Scholar] [CrossRef]
- Westerdal, M.; Rights, A.; Copyright, I. On the room-temperature grain growth in nanocrystalline copper. Scr. Metall. Mater. 1994, 30, 577–581. [Google Scholar]
- Haber, J.A.; Buhro, W.E. Kinetic instability of nanocrystalline aluminum prepared by chemical synthesis; facile room-temperature grain growth. J. Am. Chem. Soc. 1998, 120, 10847–10855. [Google Scholar] [CrossRef]
- Ames, M.; Markmann, J.; Karos, R.; Michels, A.; Tschöpe, A.; Birringer, R. Unraveling the nature of room temperature grain growth in nanocrystalline materials. Acta Mater. 2008, 56, 4255–4266. [Google Scholar] [CrossRef]
- Pantleon, K.; Somers, M.A.J. Interpretation of microstructure evolution during self-annealing and thermal annealing of nanocrystalline electrodeposits—A comparative study. Mater. Sci. Eng. A 2010, 528, 65–71. [Google Scholar] [CrossRef]
- Chookajorn, T.; Murdoch, H.A.; Schuh, C.A. Design of stable nanocrystalline alloys. Science 2012, 337, 951–954. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.C.; Sun, B.R.; Liu, Y.; Zhang, N.; Zhang, J.H.; Yu, H.; Huang, J.Y.; Peng, Q.M.; Shen, T.D. Selection of grain-boundary segregation elements for achieving stable and strong nanocrystalline Mg. Mater. Sci. Eng. A 2018, 717, 144–153. [Google Scholar] [CrossRef]
- Konrad, H.; Haubold, T.; Birringer, R.; Gleiter, H. Nanostructured Cu-Bi alloys prepared by co-evaporation in a continuous gas flow. Nanostruct. Mater. 1996, 7, 605–610. [Google Scholar] [CrossRef]
- Natter, H.; Schmelzer, M.; Hempelmann, R. Nanocrystalline nickel and nickel-copper alloys: Synthesis, characterization, and thermal stability. J. Mater. Res. 1998, 13, 1186–1197. [Google Scholar] [CrossRef]
- Atwater, M.A.; Roy, D.; Darling, K.A.; Butler, B.G.; Scattergood, R.O.; Koch, C.C. The thermal stability of nanocrystalline copper cryogenically milled with tungsten. Mater. Sci. Eng. A 2012, 558, 226–233. [Google Scholar] [CrossRef]
- Shi, X.H.; Chen, Y.Z.; Ma, X.Y.; Wang, H.T.; Liu, F. Microstructural evolution of nanocrystalline Fe-Zr alloys upon annealing treatment. Mater. Charact. 2016, 103, 58–64. [Google Scholar] [CrossRef]
- Muthaiah, V.M.S.; Mula, S. Effect of zirconium on thermal stability of nanocrystalline aluminium alloy prepared by mechanical alloying. J. Alloy. Compd. 2016, 688, 571–580. [Google Scholar] [CrossRef]
- Sooraj, S.; Muthaiah, V.M.S.; Kang, P.C.; Koch, C.C.; Mula, S. Microstructural evolution and thermal stability of Fe–Zr metastable alloys developed by mechanical alloying followed by annealing. Philos. Mag. 2016, 96, 2649–2670. [Google Scholar] [CrossRef]
- Chakravarty, S.; Sikdar, K.; Singh, S.S.; Roy, D.; Koch, C.C. Grain size stabilization and strengthening of cryomilled nanostructured Cu 12 at% Al alloy. J. Alloy. Compd. 2017, 716, 197–203. [Google Scholar] [CrossRef]
- Kapoor, M.; Kaub, T.; Darling, K.A.; Boyce, B.L.; Thompson, G.B. An atom probe study on Nb solute partitioning and nanocrystalline grain stabilization in mechanically alloyed Cu-Nb. Acta Mater. 2017, 126, 564–575. [Google Scholar] [CrossRef] [Green Version]
- Amram, D.; Schuh, C.A. Interplay between thermodynamic and kinetic stabilization mechanisms in nanocrystalline Fe-Mg alloys. Acta Mater. 2018, 144, 447–458. [Google Scholar] [CrossRef]
- Abaza, M.A.; Al-Sulaiti, L.; Scattergood, R.O.; Youssef, K.M. Influence of 1%Nb Solute Addition on the Thermal Stability of In Situ Consolidated Nanocrystalline Cu. Adv. Eng. Mater. 2019, 21, 1800859. [Google Scholar] [CrossRef]
- Zhang, N.; Gunderov, D.; Yang, T.T.; Cai, X.C.; Jia, P.; Shen, T.D. Influence of alloying elements on the thermal stability of ultra-fine-grained Ni alloys. J. Mater. Sci. 2019, 54, 10506–10515. [Google Scholar] [CrossRef]
- Saber, M.; Kotan, H.; Koch, C.C.; Scattergood, R.O. Thermal stability of nanocrystalline Fe-Cr alloys with Zr additions. Mater. Sci. Eng. A 2012, 556, 664–670. [Google Scholar] [CrossRef]
- Li, L.; Saber, M.; Xu, W.; Zhu, Y.; Koch, C.C.; Scattergood, R.O. High-temperature grain size stabilization of nanocrystalline Fe-Cr alloys with Hf additions. Mater. Sci. Eng. A 2014, 613, 289–295. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.; Mahesh, B.V.; Atwater, M.A.; Chan, T.E.; Scattergood, R.O.; Koch, C.C. Grain size stability and hardness in nanocrystalline Cu-Al-Zr and Cu-Al-Y alloys. Mater. Sci. Eng. A 2014, 598, 217–223. [Google Scholar] [CrossRef]
- Muthaiah, V.M.S.; Babu, L.H.; Koch, C.C.; Mula, S. Feasibility of formation of nanocrystalline Fe-Cr-Y alloys: Mechanical properties and thermal stability. Mater. Charact. 2016, 114, 43–53. [Google Scholar] [CrossRef]
- Grigorian, C.M.; Rupert, T.J. Thick amorphous complexion formation and extreme thermal stability in ternary nanocrystalline Cu-Zr-Hf alloys. Acta Mater. 2019, 179, 172–182. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.; Chakraborty, S.; Gupta, A.K.; Basu Mallick, A.; Koch, C.C. Synergistic effect of Nb and Zr addition in thermal stabilization of nano-crystalline Cu synthesized by ball milling. Mater. Lett. 2020, 271, 127780. [Google Scholar] [CrossRef]
- Kotan, H.; Darling, K.A. Phase transformation and grain growth behavior of a nanocrystalline 18/8 stainless steel. Mater. Sci. Eng. A 2017, 686, 168–175. [Google Scholar] [CrossRef]
- Kotan, H. Thermal stability, phase transformation and hardness of mechanically alloyed nanocrystalline Fe-18Cr-8Ni stainless steel with Zr and Y2O3 additions. J. Alloy. Compd. 2018, 749, 948–954. [Google Scholar] [CrossRef]
- Suntharavel Muthaiah, V.M.; Koch, C.C.; Mula, S. Effect of Nb addition on Fe-7Cr-Nb and Fe-15Cr-Nb metastable alloy formation and their thermal stability. Mater. Res. Express 2018, 5, 56534. [Google Scholar] [CrossRef]
- Muthaiah, V.M.S.; Koch, C.C.; Mula, S. Thermal stability and mechanical properties of Fe-Cr-Zr alloys developed by mechanical alloying followed by spark plasma sintering. J. Alloy. Compd. 2021, 856, 158266. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Fan, Y.; Shi, J.; Liu, Y.; Shi, X.; Xu, J. Thermal stability of the multicomponent nanocrystalline Ni–ZrNbMoTa alloy. J. Alloy. Compd. 2021, 862, 158326. [Google Scholar] [CrossRef]
- Liu, F.; Kirchheim, R. Grain boundary saturation and grain growth. Scr. Materialia. 2004, 51, 521–525. [Google Scholar] [CrossRef]
- Zhou, N.; Hu, T.; Huang, J.; Luo, J. Stabilization of nanocrystalline alloys at high temperatures via utilizing high-entropy grain boundary complexions. Scr. Mater. 2016, 124, 160–163. [Google Scholar] [CrossRef] [Green Version]
- Divinski, S.V.; Reglitz, G.; Wegner, M.; Peterlechner, M.; Wilde, G. Effect of pinning by an orientation gradient on the thermal stability of ultrafine grained Ni produced by equal channel angular pressing. J. Appl. Phys. 2014, 115, 113503. [Google Scholar] [CrossRef]
- Michels, A.; Krill, C.E.; Ehrhardt, H.; Birringer, R.; Wu, D.T. Modelling the influence of grain-size-dependent solute drag on the kinetics of grain growth in nanocrystalline materials. Acta Mater. 1999, 47, 2143–2152. [Google Scholar] [CrossRef]
- Bansal, C.; Gao, Z.Q.; Fultz, B. Grain growth and chemical ordering in (Fe,Mn)3Si. Nanostruct. Mater. 1995, 5, 327–336. [Google Scholar] [CrossRef]
- Weissmüller, J. Alloy effect in nanostructures. Nanostruct. Mater. 1993, 3, 261–272. [Google Scholar] [CrossRef]
- Kirchheim, R. Grain coarsening inhibited by solute segregation. Acta Mater. 2002, 50, 413–419. [Google Scholar] [CrossRef]
- Perrin, A.E.; Schuh, C.A. Stabilized Nanocrystalline Alloys: The Intersection of Grain Boundary Segregation with Processing Science. Annu. Rev. Mater. Res. 2021, 51, 241–268. [Google Scholar] [CrossRef]
- Schuh, C.A.; Lu, K. Stability of nanocrystalline metals: The role of grain-boundary chemistry and structure. MRS Bull. 2021, 46, 225–235. [Google Scholar] [CrossRef]
- Kalidindi, A.R.; Chookajorn, T.; Schuh, C.A. Nanocrystalline materials at equilibrium: A thermodynamic review. J. Miner. Met. Mater. Soc. 2015, 67, 2834–2843. [Google Scholar] [CrossRef]
- Saber, M.; Koch, C.C.; Scattergood, R.O. Thermodynamic grain size stabilization models: An overview. Mater. Res. Lett. 2015, 3, 65–75. [Google Scholar] [CrossRef]
- Locci, A.M. Theoretical assessment of thermodynamic stability in nanocrystalline metallic alloys. Materials 2019, 12, 3408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Locci, A.M.; Torre, F.; Delogu, F. Thermodynamic modelling of polycrystalline multicomponent multiphase metal alloys. Model. Simul. Mater. Sci. Eng. 2020, 28, 045001. [Google Scholar] [CrossRef]
- Tanaka, T.; Hack, K.; Ida, T.; Hara, S. Application of a thermodynamic database to the evaluation of surface tensions of molten alloys, salt mixtures and oxide mixture. Z. Met. 1996, 87, 380–389. [Google Scholar] [CrossRef]
- Kang, Y.-B. Relationship between surface tension and Gibbs energy, and application of constrained Gibbs energy minimization. Comput. Coupling Phase Diagr. Thermochem. 2015, 50, 23–31. [Google Scholar] [CrossRef]
- Kaptay, G. Modeling equilibrium grain boundary segregation, grain boundary energy and grain boundary segregation transition by the extended Butler equation. J. Mater. Sci. 2016, 51, 1738–1755. [Google Scholar] [CrossRef]
- Bakker, H. Enthalpies in Alloys, Miedema’s Semi Empirical Model; Trans Tech Publications Ltd.: Uetikon-Zuerich, Switzerland, 1998. [Google Scholar]
- Weissmüller, J. Some basic notions on nanostructured solids. Mater. Sci. Eng. A 1994, 179–180, 102–107. [Google Scholar] [CrossRef]
- Trelewicz, J.R.; Schuh, C.A. Grain boundary segregation and thermodynamically stable binary nanocrystalline alloys. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 79, 094112. [Google Scholar] [CrossRef]
- Lejček, P.; Šob, M.; Paidar, V. Interfacial segregation and grain boundary embrittlement: An overview and critical assessment of experimental data and calculated results. Prog. Mater. Sci. 2017, 87, 83–139. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S. Prediction of binary interaction coefficients in grain boundary segregation. Surf. Interface Anal. 2018, 50, 640–647. [Google Scholar] [CrossRef]
- Lejček, P.; Všianská, M.; Šob, M. Recent trends and open questions in grain boundary segregation. J. Mater. Res. 2018, 33, 2647–2660. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S. Modeling grain boundary segregation by prediction of all the necessary parameters. Acta Mater. 2019, 170, 253–267. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S.; Paidar, V. The significance of entropy in grain boundary segregation. Materials 2019, 12, 492. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lejček, P.; Hofmann, S. Entropy-driven grain boundary segregation: Prediction of the phenomenon. Metals 2021, 11, 1331. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S. Entropy-dominated grain boundary segregation. J. Mater. Sci. 2021, 56, 7464–7473. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S.; Všianská, M.; Šob, M. Entropy matters in grain boundary segregation. Acta Mater. 2021, 206, 116597. [Google Scholar] [CrossRef]
- Amram, D.; Schuh, C.A. Higher temperature yield smaller grains in a thermally stable phase-transforming nanocrystalline alloy. Phys. Rev. Lett. 2018, 121, 145503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Locci, A.M. On the experimental assessment of thermodynamic stability of nanostructured solid solutions. Mod. Concepts Mater. Sci. 2019, 2, 000537. [Google Scholar] [CrossRef]
- Suryanarayana, C. Mechanical alloying and milling. Prog. Mater. Sci. 2001, 46, 1–184. [Google Scholar] [CrossRef]
- Baláž, P.; Achimovicová, M.; Baláž, M.; Billik, P.; Zara, C.Z.; Criado, J.M.; Delogu, F.; Dutková, E.; Gaffet, E.; Gotor, F.J.; et al. Hallmarks of mechanochemistry: From nanoparticles to technology. Chem. Soc. Rev. 2013, 42, 7571–7637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suryanarayana, C. Recent developments in mechanical alloying. Rev. Adv. Mater. Sci. 2008, 18, 203–211. [Google Scholar]
- Torre, F.; Huminiuc, T.; Musu, E.; Polcar, T.; Delogu, F.; Locci, A.M. Fabrication of nanocrystalline supersaturated W-Al alloys with enhanced thermal stability and high sinterability. J. Phys. Chem. Solids 2021, 148, 109686. [Google Scholar] [CrossRef]
- Ansara, I.; Dinsdale, A.T.; Rand, M.H. COST 507: Thermochemical Database for Light Metal Alloys. Office for Official Publications of the European Communities, Luxembourg 1998. Available online: http://www.opencalphad.com/databases/CGNA18499ENC_001.pdf (accessed on 28 October 2021).
- Lutterotti, L.; Pillière, H.; Fontugne, C.; Boullay, P.; Chateigner, D. Full-profile search–match by the Rietveld method. J. Appl. Crystallogr. 2019, 52, 587–598. [Google Scholar] [CrossRef]
- da Costa, F.A.; da Silva, A.G.P.; Filho, F.A.; Gomes, U.U.; Vieira, F.A. Synthesis of a nanocrystalline composite W-25 wt.% Ag powder by high energy milling. Powder Technol. 2008, 188, 30–33. [Google Scholar] [CrossRef]
- Kaptay, G. Thermodynamic Stability of nano-grained alloys against grain coarsening and precipitation of macroscopic phases. Metall. Mater. Trans. A 2019, 50, 4931–4947. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Herr, U.; Klassen, T.; Averback, R.S. Formation of supersaturated solid solutions in the immiscible Ni-Ag system by mechanical alloying. J. Appl. Phys. 1996, 79, 3935. [Google Scholar] [CrossRef] [Green Version]
- Botcharova, E.; Freudenberger, J.; Schultz, L. Mechanical alloying of copper with niobium and molybdenum. J. Mater. Sci. 2004, 39, 5287–5290. [Google Scholar] [CrossRef]
- Wang, M.; Vo, N.Q.; Campion, M.; Nguyen, T.D.; Setman, D.; Dillon, S.; Bellon, P.; Averback, R.S. Forced atomic mixing during severe plastic deformation: Chemical interactions and kinetically driven segregation. Acta Mater. 2014, 66, 1–11. [Google Scholar] [CrossRef]
- Da Pozzo, A.; Palmas, S.; Vacca, A.; Delogu, F. On the role of mechanical properties in the early stages of the mechanical alloying of Ag50Cu50 powder mixtures. Scr. Mater. 2012, 67, 104–107. [Google Scholar] [CrossRef]
- Garroni, S.; Enzo, S.; Delogu, F. Mesostructural refinement in the early stages of mechanical alloying. Scr. Mater. 2014, 83, 49–52. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, P.; Akhtar, F. Aluminium matrix tungsten aluminide and tungsten reinforced composites by solid-state diffusion mechanism. Sci. Rep. 2017, 7, 12391. [Google Scholar] [CrossRef] [PubMed]
- Cantwell, P.R.; Tang, M.; Dillon, S.J.; Luo, J.; Rohrer, G.S.; Harmer, M.P. Grain boundary complexions. Acta Mater. 2014, 62, 1–48. [Google Scholar] [CrossRef]
- Chookajorn, T.; Schuh, C.A. Nanoscale segregation behavior and high-temperature stability of nanocrystalline W-20 at.% Ti. Acta Mater. 2014, 73, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Chookajorn, T.; Park, M.; Schuh, C.A. Duplex nanocrystalline alloys: Entropic nanostructure stabilization and a case study on W-Cr. J. Mater. Res. 2015, 30, 151–163. [Google Scholar] [CrossRef] [Green Version]
- O’Brien, C.J.; Barr, C.M.; Price, P.M.; Hattar, K.; Foiles, S.M. Grain boundary phase transformations in PtAu and relevance to thermal stabilization of bulk nanocrystalline metals. J. Mater. Sci. 2018, 53, 2911–2927. [Google Scholar] [CrossRef]
- Schuler, J.D.; Rupert, T.J. Materials selection rules for amorphous complexion formation in binary metallic alloys. Acta Mater. 2017, 140, 196–205. [Google Scholar] [CrossRef] [Green Version]
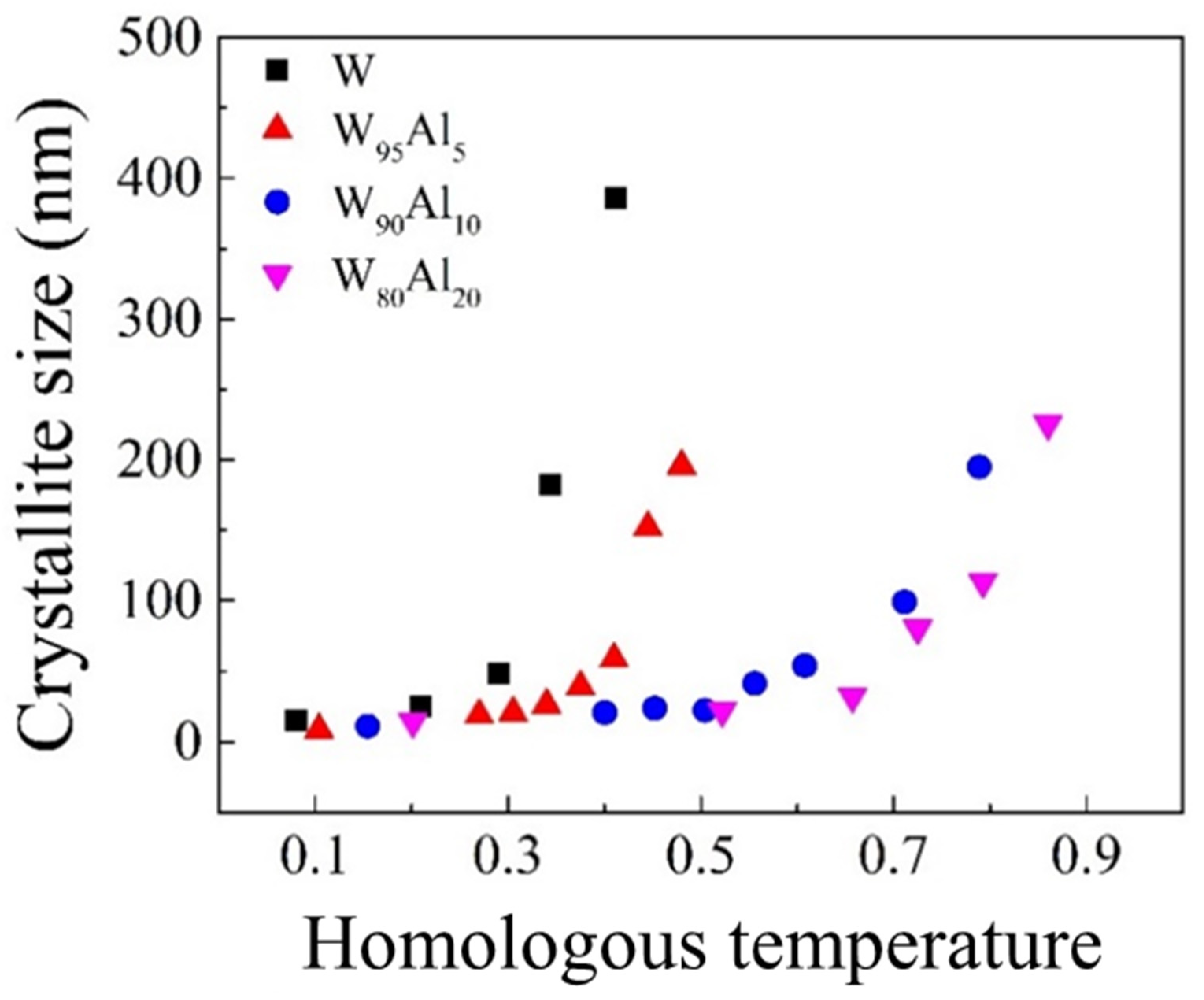



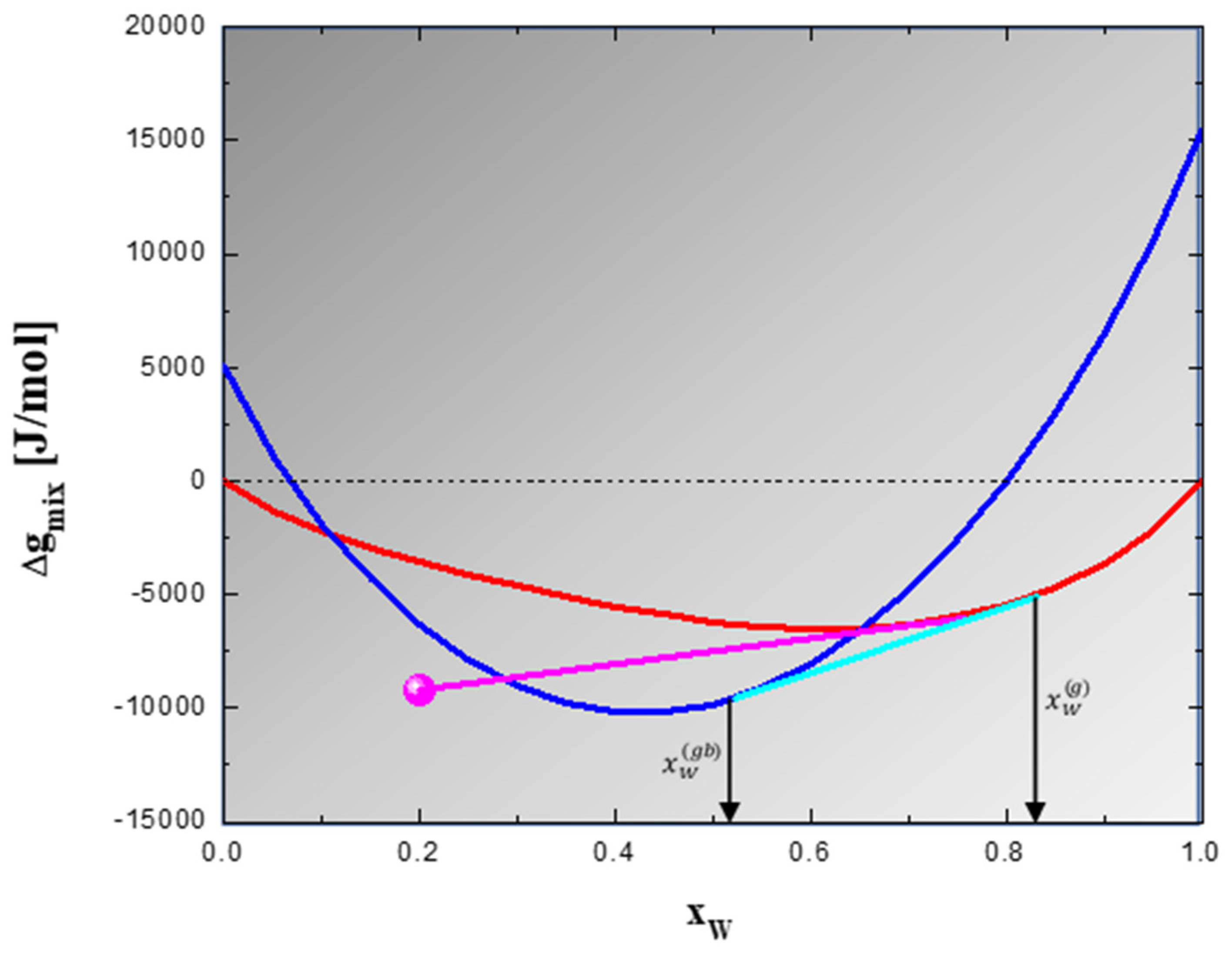
| Tm [°C] | Θ700 °C | Θ900 °C | |
|---|---|---|---|
| W | 3422 | 0.26 | 0.32 |
| W–5 at.% Al | 2587 | 0.34 | 0.41 |
| W–10 at.% Al | 1657 | 0.50 | 0.61 |
| W–20 at.% Al | 1207 | 0.66 | 0.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torre, F.; Mingazzini, C.; Mirabile Gattia, D.; Huminiuc, T.; Rinaldi, A.; Polcar, T.; Delogu, F.; Locci, A.M. Investigation on the Thermodynamic Stability of Nanocrystalline W-Based Alloys: A Combined Theoretical and Experimental Approach. Materials 2021, 14, 7179. https://doi.org/10.3390/ma14237179
Torre F, Mingazzini C, Mirabile Gattia D, Huminiuc T, Rinaldi A, Polcar T, Delogu F, Locci AM. Investigation on the Thermodynamic Stability of Nanocrystalline W-Based Alloys: A Combined Theoretical and Experimental Approach. Materials. 2021; 14(23):7179. https://doi.org/10.3390/ma14237179
Chicago/Turabian StyleTorre, Francesco, Claudio Mingazzini, Daniele Mirabile Gattia, Teodor Huminiuc, Antonio Rinaldi, Tomas Polcar, Francesco Delogu, and Antonio Mario Locci. 2021. "Investigation on the Thermodynamic Stability of Nanocrystalline W-Based Alloys: A Combined Theoretical and Experimental Approach" Materials 14, no. 23: 7179. https://doi.org/10.3390/ma14237179
APA StyleTorre, F., Mingazzini, C., Mirabile Gattia, D., Huminiuc, T., Rinaldi, A., Polcar, T., Delogu, F., & Locci, A. M. (2021). Investigation on the Thermodynamic Stability of Nanocrystalline W-Based Alloys: A Combined Theoretical and Experimental Approach. Materials, 14(23), 7179. https://doi.org/10.3390/ma14237179








