Discrimination of Surface Topographies Created by Two-Stage Process by Means of Multiscale Analysis
Abstract
:1. Introduction
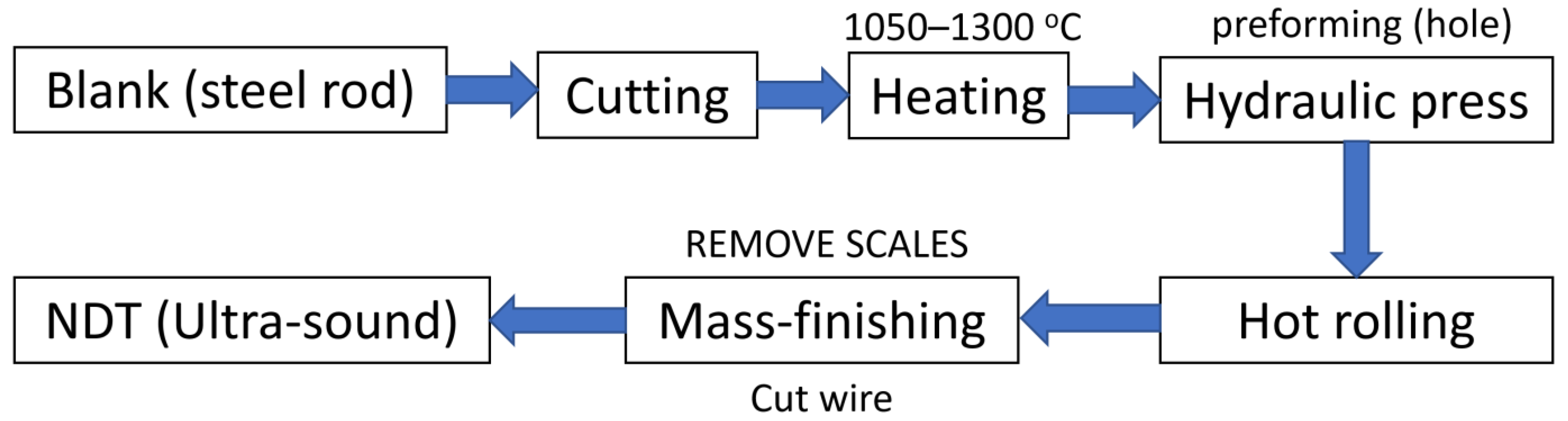
2. Materials and Methods
2.1. Sample Preparations
2.2. Measurements
2.3. Multiscale and Statistical Analysis
3. Results and Analysis
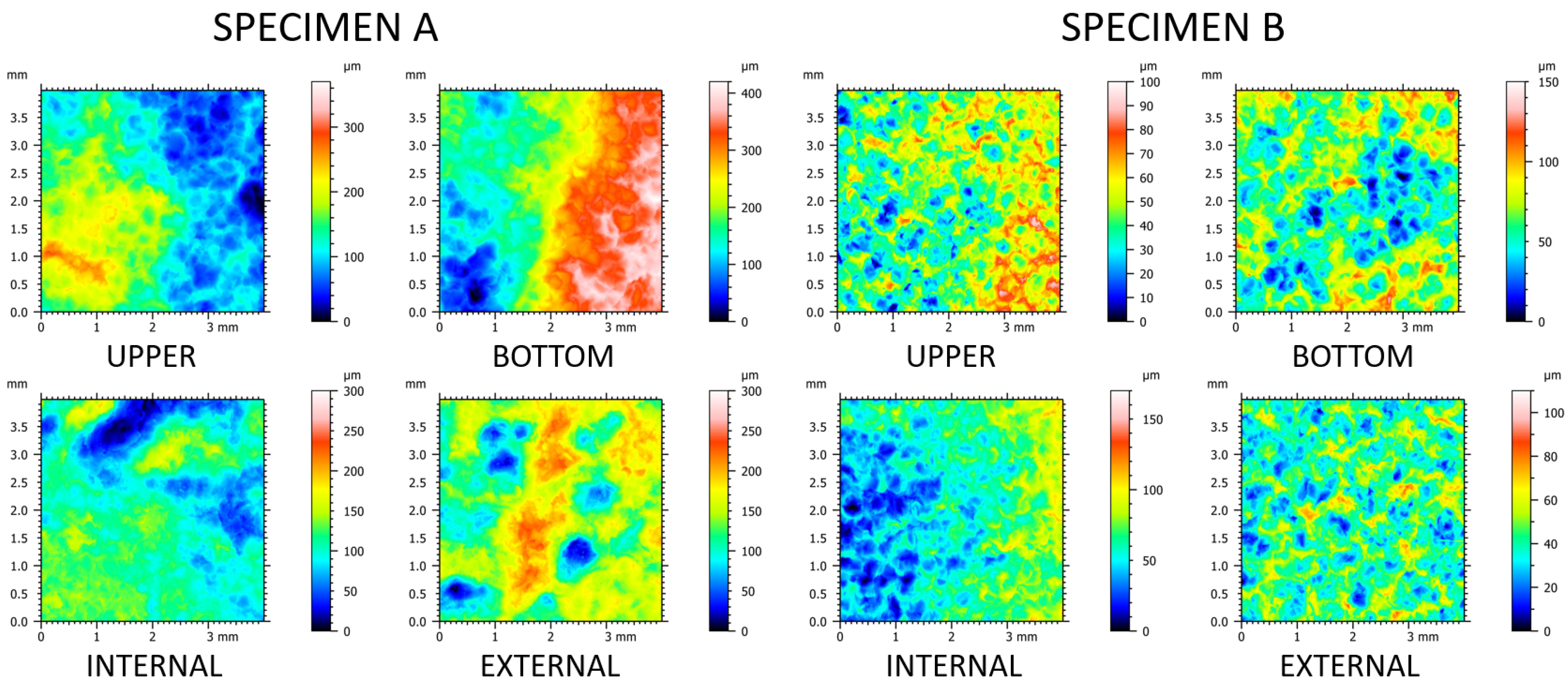
3.1. Surface Topographies
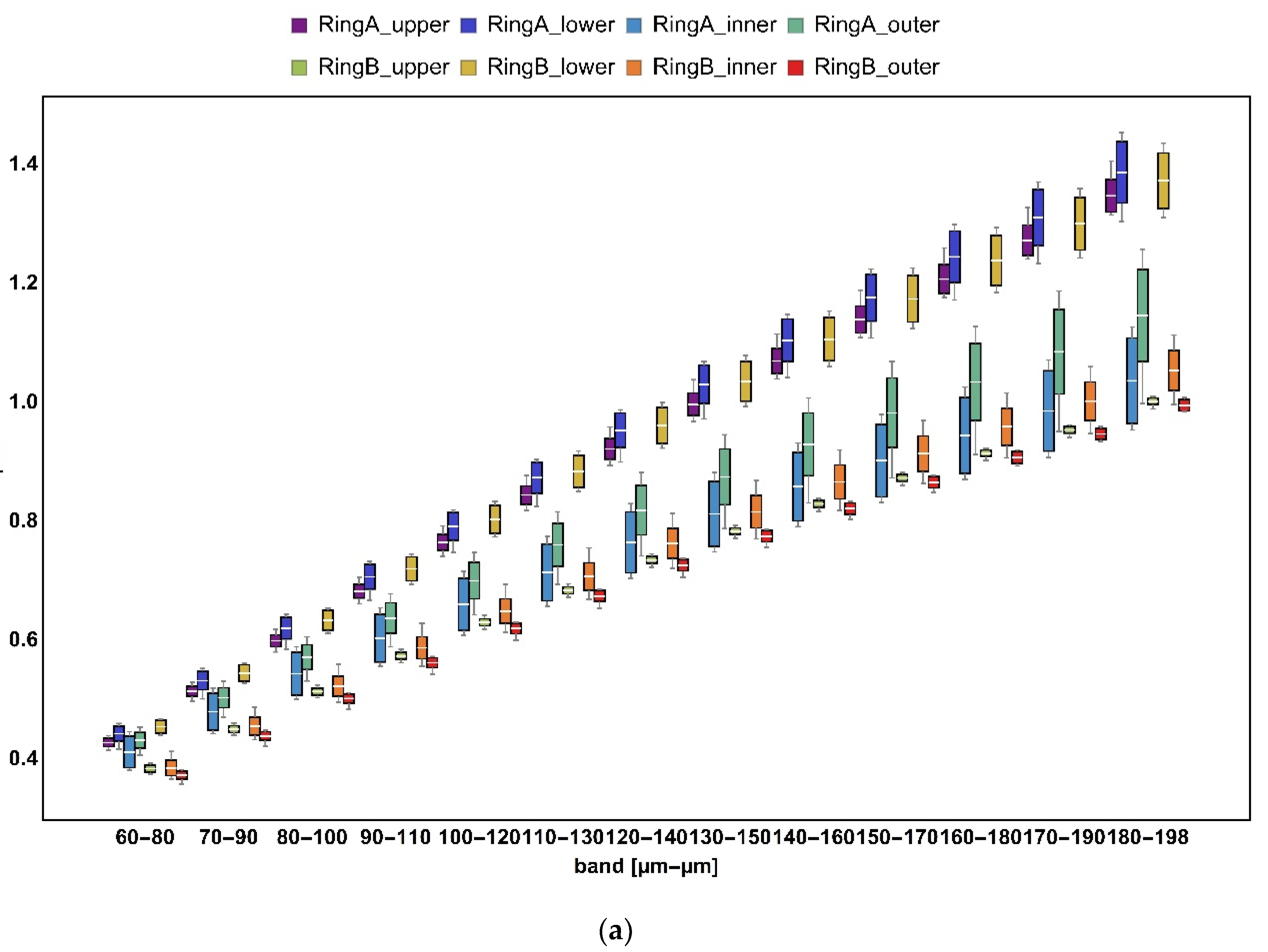
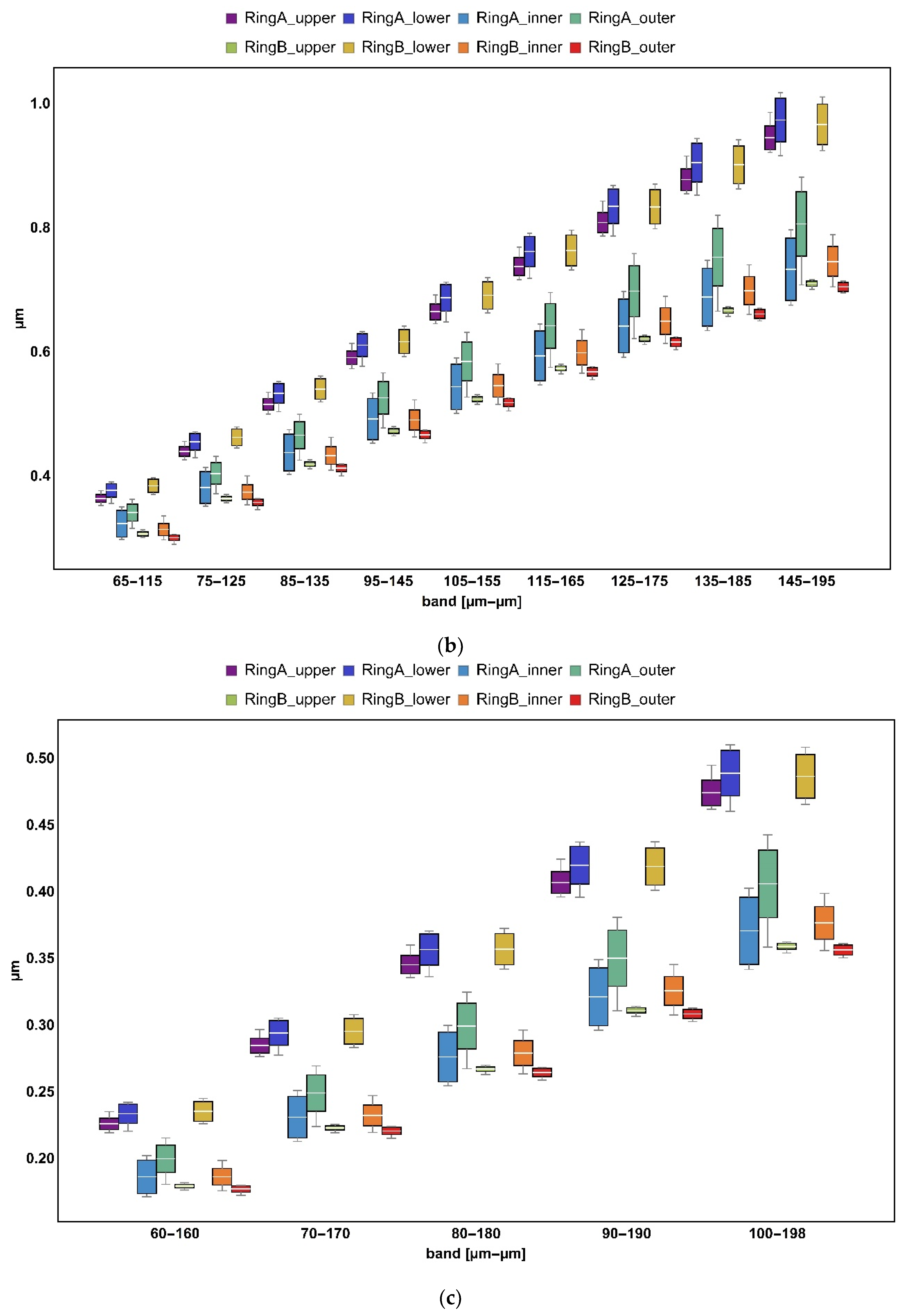
3.2. Bandpass Filter
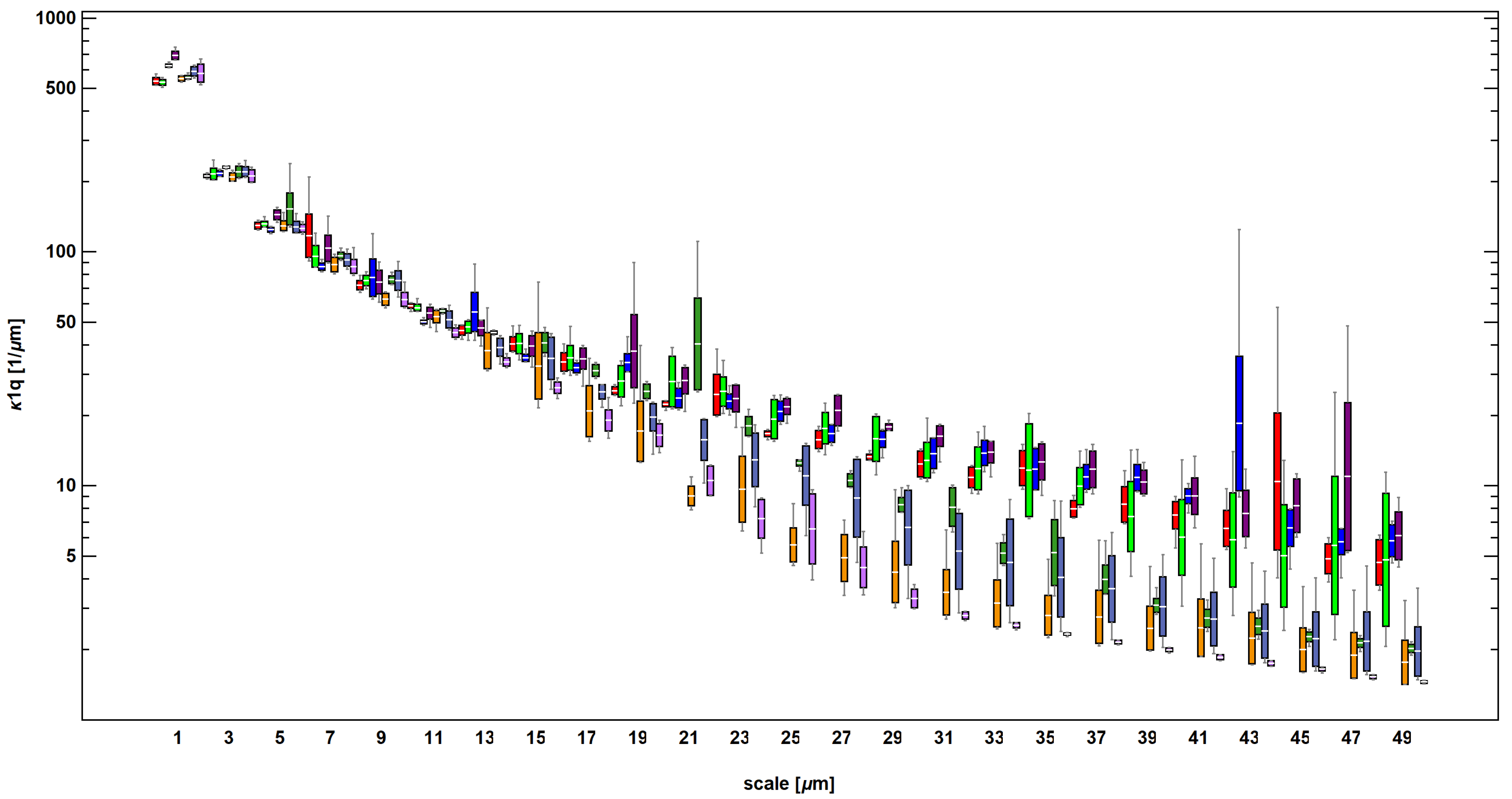
3.3. Length- and Area-Scale Analysis
3.4. Curvature
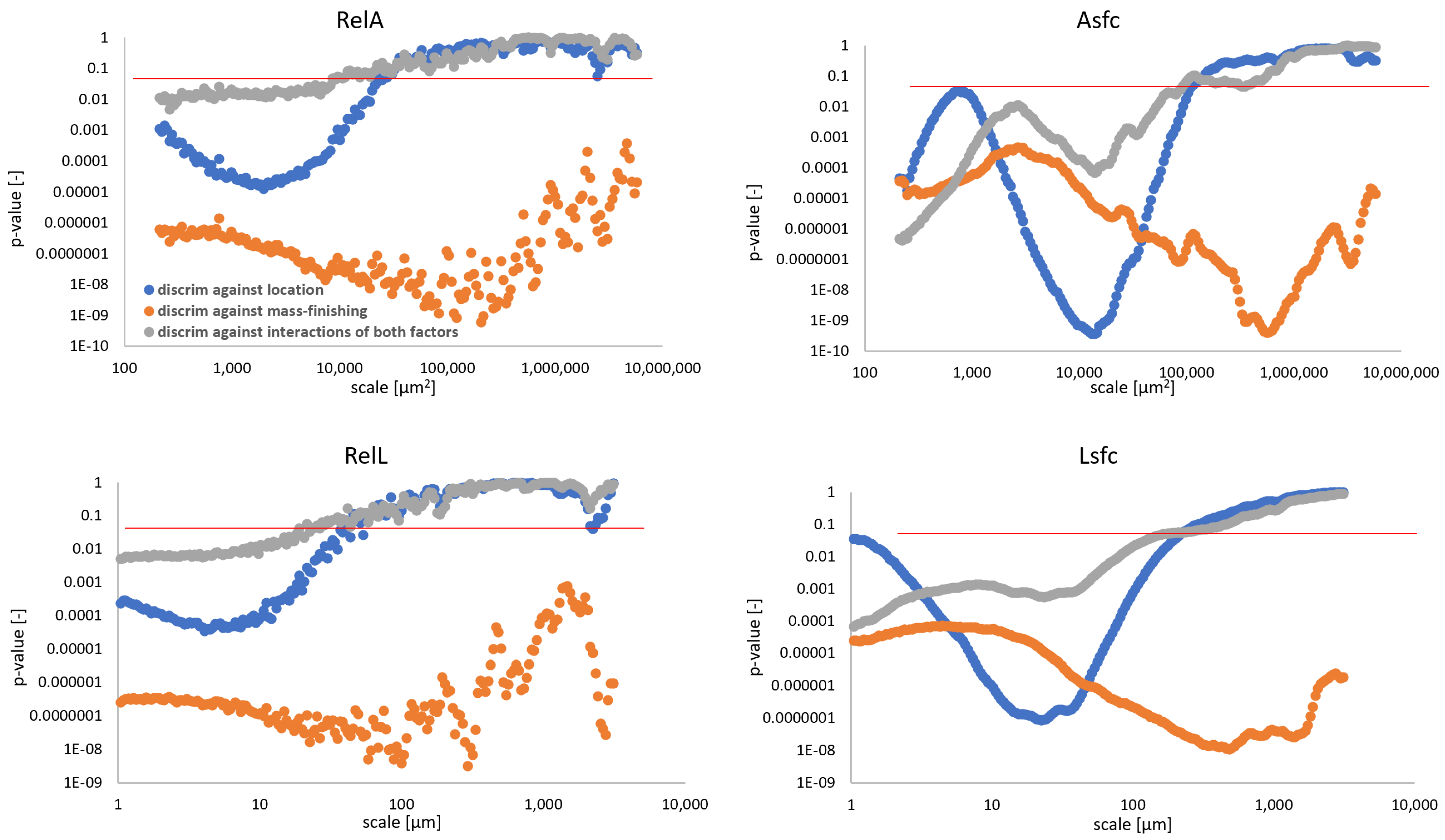
3.5. Discrimination Analysis
4. Discussion
5. Conclusions
- All four studied multiscale methods performed generally well in discriminating against each factor and their combinations;
- Bandpass filtration using Sa and Sq exhibited the best performance as p-value < 0.05 for all three bands. Skewness and kurtosis failed to be used as a statistical discriminator against mass finishing for a bandwidth equal to 50 µm. Other height parameters did not generally provide sufficient confidence levels in the studied case. Hybrid and volume group parameters performed well at differentiation between surface topographies considering all factors with the exceptions of Vm and Vmp for the narrowest and shortest bandwidth (60–80 µm) when considering both factors as superpositions. Most feature parameters can be used to discriminate surfaces taking into account only the location on each ring. Spatial parameters were found to perform poorly. Similar conclusions can be drawn for profile characterization counterparts;
- Asfc and Lsfc both exhibited superior performance in discrimination against all factors and their combinations when compared to RelL and RelA. The latter parameters could be used only when finer scales were considered. Discrimination against mass-finishing was confident no matter the parameter derived from those methods;
- Curvature can be used as a discriminant only when considering measures of variability. Unsigned curvature provides significantly confident discrimination for finer scales.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Full Name |
|---|---|
| Rp | Maximum peak height of the roughness profile |
| Rv | Maximum valley depth of the roughness profile |
| Rz | Maximum height of roughness profile |
| Rc | Mean height of the roughness profile elements |
| Rt | Total height of roughness profile |
| Ra | Arithmetic mean deviation of the roughness profile |
| Rq | Root-mean-square (RMS) deviation of the roughness profile |
| Rsk | Skewness of the roughness profile |
| Rku | Kurtosis of the roughness profile |
| Sq | Root-mean-square height |
| Ssk | Skewness |
| Sku | Kurtosis |
| Sp | Maximum peak height |
| Sv | Maximum pit height |
| Sz | Maximum height |
| Sa | Arithmetic mean height |
| Smr | Areal material ratio |
| Smc | Inverse areal material ratio |
| Sxp | Extreme peak height |
| Sal | Autocorrelation length |
| Str | Texture-aspect ratio |
| Std | Texture direction |
| Sdq | Root-mean-square gradient |
| Sdr | Developed interfacial area ratio |
| Vm | Material volume |
| Vv | Void volume |
| Vmp | Peak material volume |
| Vmc | Core material volume |
| Vvc | Core void volume |
| Vvv | Pit void volume |
| Spd | Density of peak |
| Spc | Arithmetic mean peak curvature |
| S10z | Ten point height |
| S5p | Five point peak height |
| S5v | Five point pit height |
| Sda | Mean dale area |
| Sha | Mean hill area |
| Sdv | Mean dale volume |
| Shv | Mean hill volume |
| Sku | Core roughness depth |
| Spk | Reduced summit height |
| Svk | Reduced valley depth |
| Smr1 | Upper bearing area |
| Smr2 | Lower bearing area |
| RelL | Relative length |
| RelA | Relative area |
| Lsfc | Length-scale fractal complexity |
| Asfc | Area-scale fractal complexity |
| κ1a | Average maximum curvature |
| κ1q | Standard deviation of maximum curvature |
| κ2a | Average minimum curvature |
| κ2q | Standard deviation of minimum curvature |
| Ha | Average mean curvature |
| Hq | Standard deviation of mean curvature |
| Ka | Average Gaussian curvature |
| Kq | Standard deviation of Gaussian curvature |
| κ1aabs | Average absolute maximum curvature |
| κ1qabs | Standard deviation of absolute maximum curvature |
| κ2aabs | Average absolute minimum curvature |
| κ2qabs | Standard deviation of absolute minimum curvature |
| Haabs | Average absolute mean curvature |
| Hqabs | Standard deviation of absolute mean curvature |
| Kaabs | Average absolute Gaussian curvature |
| Kqabs | Standard deviation of absolute Gaussian curvature |
References
- Brown, C.A.; Hansen, H.N.; Jiang, X.J.; Blateyron, F.; Berglund, J.; Senin, N.; Bartkowiak, T.; Dixon, B.; Le Goïc, G.; Quinsat, Y.; et al. Multiscale analyses and characterizations of surface topographies. CIRP Ann. 2018, 67, 839–862. [Google Scholar] [CrossRef]
- Pawlus, P.; Wieczorowski, M.; Mathia, T. The Errors of Stylus Methods in Surface Topography Measurements; ZAPOL: Szczecin, Poland, 2014. [Google Scholar]
- ISO 25178-1. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part1. Available online: https://www.iso.org/standard/46065.html (accessed on 19 November 2021).
- Peta, K.; Bartkowiak, T.; Gałek, P.; Mendak, M. Contact angle analysis of surface topographies created by electric discharge machining. Tribol. Int. 2021, 163, 107139. [Google Scholar] [CrossRef]
- Bigerelle, M.; Mazeran, P.E.; Gong, W.; Giljean, S.; Anselme, K. A Method to determine the Spatial Scale Implicated in Adhesion. Application on Human Cell Adhesion on Fractal Isotropic Rough Surfaces. J. Adhes. 2011, 87, 644–670. [Google Scholar] [CrossRef]
- Jordan, S.E.; Brown, C.A. Comparing Texture Characterization Parameters on Their Ability to Differentiate Ground Polyethylene Ski Bases. Wear 2006, 261, 398–409. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. ASME Standard, B46.1; Surface Texture, Surface Roughness, Waviness and Lay; American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar]
- ISO 25178-2. Geometrical Product Specifications (GPS))—Surface Texture: Areal—Part 2. Available online: https://www.iso.org/standard/42785.html (accessed on 19 November 2021).
- Brown, C.A.; Etievant, D.; Shao, Y.; Nevers, S.; Bartkowiak, T. Multiscale Outlier Filtering with Curvature and Higher Spatial Finite Differences. In Proceedings of the 16th International Conference on Metrology and Properties of Engineering Surfaces, Gothenburg, Sweden, 26–29 June 2017. [Google Scholar]
- Brown, C.A.; Etievan, T.D.; Shao, Y.; Nevers, S.; Bartkowiak, T. Measurement Equipment with Outlier Filter. U.S. Patent App. No. 15/670, 533, 7 August 2017. [Google Scholar]
- Ulcickas, V. Using Area-scale Relations to Investigate Measured Fracture Toughness in Y-TZP Materials. Ceramic Trans. 2000, 122, 211–224. [Google Scholar]
- Mezghani, S.; El Mansori, M.; Massaq, A.; Ghidossi, P. Correlation Between Surface Topography and Tribological Mechanisms of the Belt-finishing Process Using Multiscale Finishing Process Signature. Comptes Rendus Méc. 2008, 336, 794–799. [Google Scholar] [CrossRef]
- Stemp, W.J. A Review of Quantification of Lithic Use-wear Using Laser Profilometry: A Method Based on Metrology and Fractal Analysis. J. Archaeol. Sci. 2014, 48, 15–25. [Google Scholar] [CrossRef]
- Stemp, W.J.; Stemp, M. UBM Laser Profilometry and Lithic Use-wear Analysis: A Variable Length Scale Investigation of Surface Topography. J. Archaeol. Sci. 2001, 28, 81–88. [Google Scholar] [CrossRef]
- Stemp, W.J.; Stemp, M. Documenting Stages of Polish Development on Experimental Stone Tools: Surface Characterization by Fractal Geometry Using UBM Laser Profilometry. J. Archaeol. Sci. 2003, 30, 287–296. [Google Scholar] [CrossRef]
- Stemp, W.J.; Childs, B.E.; Vionnet, S.; Brown, C.A. Quantification and Discrimination of Lithic Use-wear: Surface Profile Measurements and Length-scale Fractal analysis. Archaeon 2009, 51, 366–382. [Google Scholar] [CrossRef]
- Stemp, W.J.; Chung, S. Discrimination of Surface Wear on Obsidian Tools Using LSCM and RelA: Pilot Study Results. Scanning 2011, 33, 279–293. [Google Scholar] [CrossRef]
- Stemp, W.J.; Andruskiewicz, M.D.; Gleason, M.A.; Rashid, Y.H. Experiments in Ancient Maya Blood-Letting: Quantification of Surface Wear on Obsidian Blades. Archaeol. Anthropol. Sci. 2015, 7, 423–439. [Google Scholar] [CrossRef]
- Stemp, W.J.; Lerner, H.J.; Kristant, E.H. Quantifying Microwear on Experimental Mistassini Quartzite Scrapers: Preliminary Results of Exploratory Research Using LSCM and Scale-sensitive Fractal Analysis. Scanning 2013, 35, 28–39. [Google Scholar] [CrossRef]
- Key, A.; Stemp, W.J.; Morozov, M.; Proffitt, T.; Torre, I. Is Loading a Significantly Influential Factor in the Development of Lithic Microwear. An Experimental Test Using LSCM on Basalt from Olduvai Gorge. J. Archaeol. Method Theory 2015, 22, 1193–1214. [Google Scholar] [CrossRef]
- Álvarez, M.; Fuentes, N.O.; Favret, E.A.; Dolce, M.; Forlano, A. Quanti-fying Use-wear Traces through RIMAPS and Variogram Analyses. Archaeol. Anthropol. Sci. 2012, 4, 91–101. [Google Scholar] [CrossRef]
- Favret, E.A.; Fuentes, N.O.; Álvarez, M.R. RIMAPS and Variogram Analyses of Microwear Traces in Experiments with Stone Tools. Microsc. Micro Anal. 2004, 10, 968–969. [Google Scholar] [CrossRef]
- Watson, A.S.; Gleason, M.A. A Comparative Assessment of Texture Analysis Techniques Applied to Bone Tool Use-Wear; Surface Topography. Metrol. Prop. 2016, 4, 1–18. [Google Scholar]
- Berglund, J.; Agunwamba, C.; Powers, B.; Brown, C.A.; Rosén, B.G. On discovering relevant scales in surface roughness measurement an evaluation of a band-pass method. Scanning 2010, 32, 244–249. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Raja, J. Computational Surface and Roundness Metrology; Springer: London, UK, 2009. [Google Scholar]
- Berglund, J.; Wiklund, D.; Rosén, B.G. A method for visualization of surface texture anisotropy in different scales of observation. Scanning 2011, 33, 325–331. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.A.; Charles, P.D.; Johnsen, W.A.; Chesters, S. Fractal Analysis of Topographic Data by the Patchwork Method. Wear 1993, 161, 61–67. [Google Scholar] [CrossRef]
- Brown, C.A.; Johnsen, W.A.; Charles, P.D. Method of Quantifying the Topographic Structure of a Surface. U.S. Patent 5, 307, 292, 24 June 1994. [Google Scholar]
- Theisel, H.; Rössl, C.; Zayer, R.; Seidel, H.P. Normal based estimation of the curvature tensor for triangular meshes. In Proceedings of the 12th Pacific Conference on Computer Graphics and Applications, Seoul, Korea, 6–8 October 2004. [Google Scholar]
- Bartkowiak, T.; Brown, C.A. A characterization of process-surface texture interactions in micro-electrical discharge machining using multiscale curvature tensor analysis; Journal of Manufacturing Science and Engineering. Trans. ASME 2018, 140, 021013. [Google Scholar]
- Bartkowiak, T.; Brown, C.A. Multiscale 3D curvature analysis of processed surface textures of aluminum alloy 6061 T6. Materials 2019, 12, 257. [Google Scholar] [CrossRef] [Green Version]
- Bigerelle, M.M.; Mathia, T.; Bouvier, S. The multi-scale roughness analyses and modeling of abrasion with the grit size effect on ground surfaces. Wear 2012, 286–287, 124–135. [Google Scholar] [CrossRef]
- Bartkowiak, T.; Mendak, M.; Mrozek, K.; Wieczorowski, M. Analysis of Surface Microgeometry Created by Electric Discharge Machining. Materials 2020, 13, 3830. [Google Scholar] [CrossRef] [PubMed]
- Bartkowiak, T.; Berglund, J.; Brown, C.A. Multiscale Characterizations of Surface Anisotropies. Materials 2020, 13, 3028. [Google Scholar] [CrossRef]
- Braatz, R.D.; Alkire, R.C.; Seebauer, E.; Rusli, E.; Gunawan, R.; Drews, T.O.; Li, X.; He, Y. Perspectives on the Design and Control of Multiscale Systems. J. Process Control 2006, 16, 193–204. [Google Scholar] [CrossRef]
- Guibert, R.; Hanafi, S.; Deltombe, R.; Bigerelle, M.; Brown, C.A. Comparison of three multiscale methods for topographic analyses. Surf. Topogr. Metrol. Prop. 2020, 8, 024002. [Google Scholar] [CrossRef]
- Serafin, D.; Bartkowiak, T.; Nowak, W.J.; Wierzba, B. Influence of microgeometry of iron surface on the oxidation process)—A comparison of multiscale geometric methods and their applicability. Appl. Surf. Sci. 2020, 527, 146838. [Google Scholar] [CrossRef]
- Maleki, I.; Wolski, M.; Woloszynski, T.; Podsiadlo, P.; Stachowiak, G. A Comparison of Multiscale Surface Curvature Characterization Methods for Tribological Surfaces. Tribol. Online 2019, 14, 8–17. [Google Scholar] [CrossRef] [Green Version]



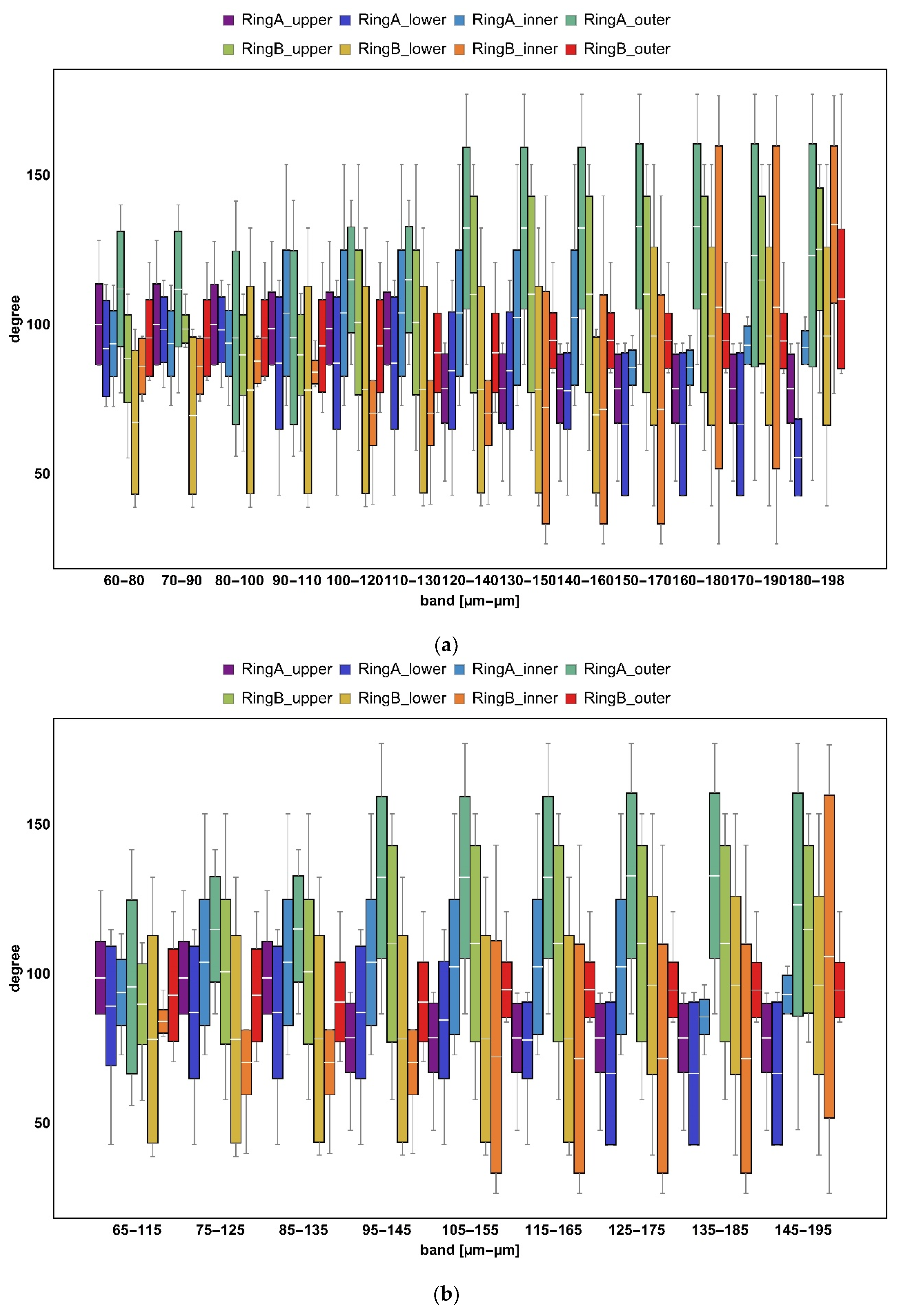
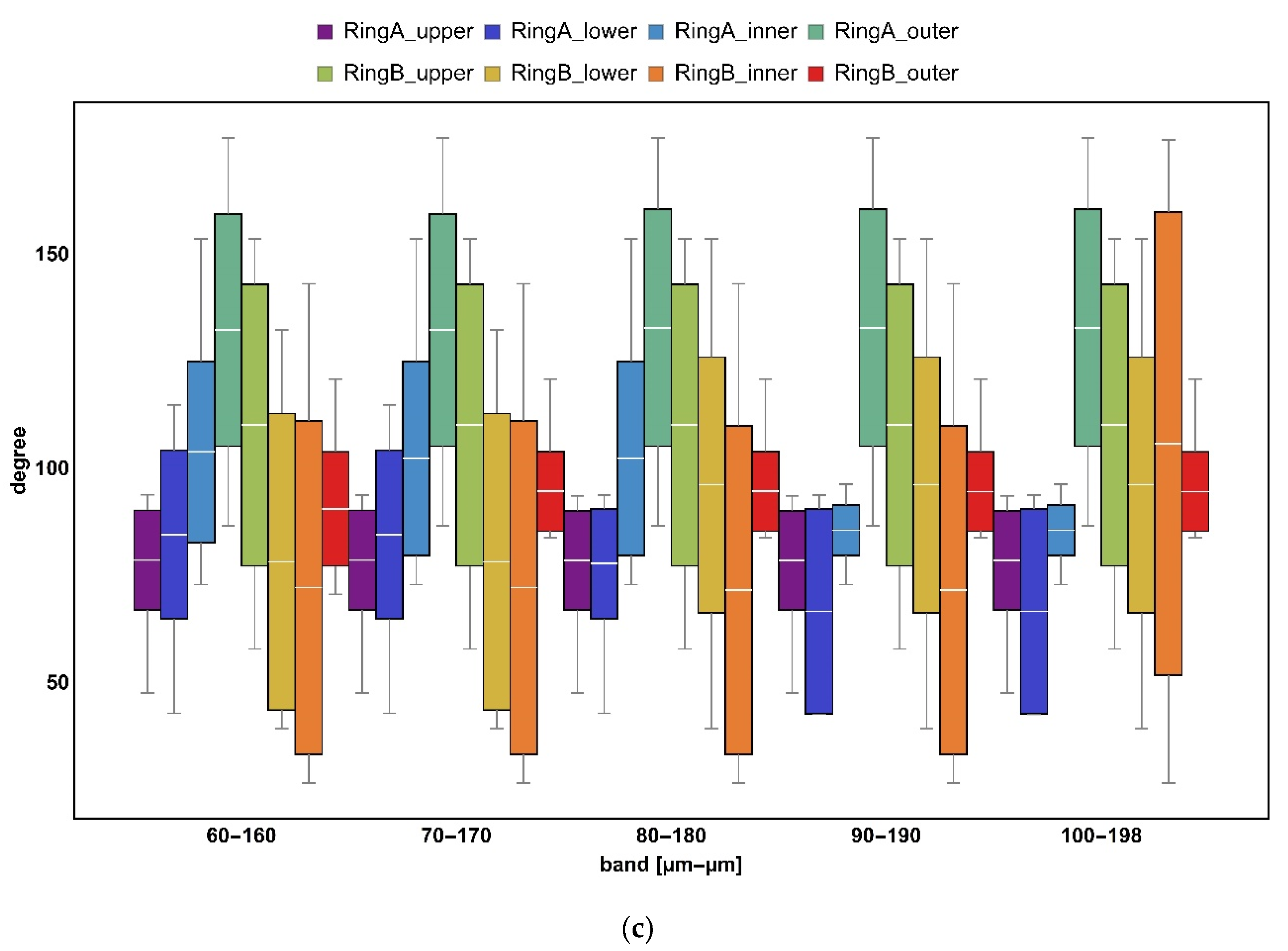

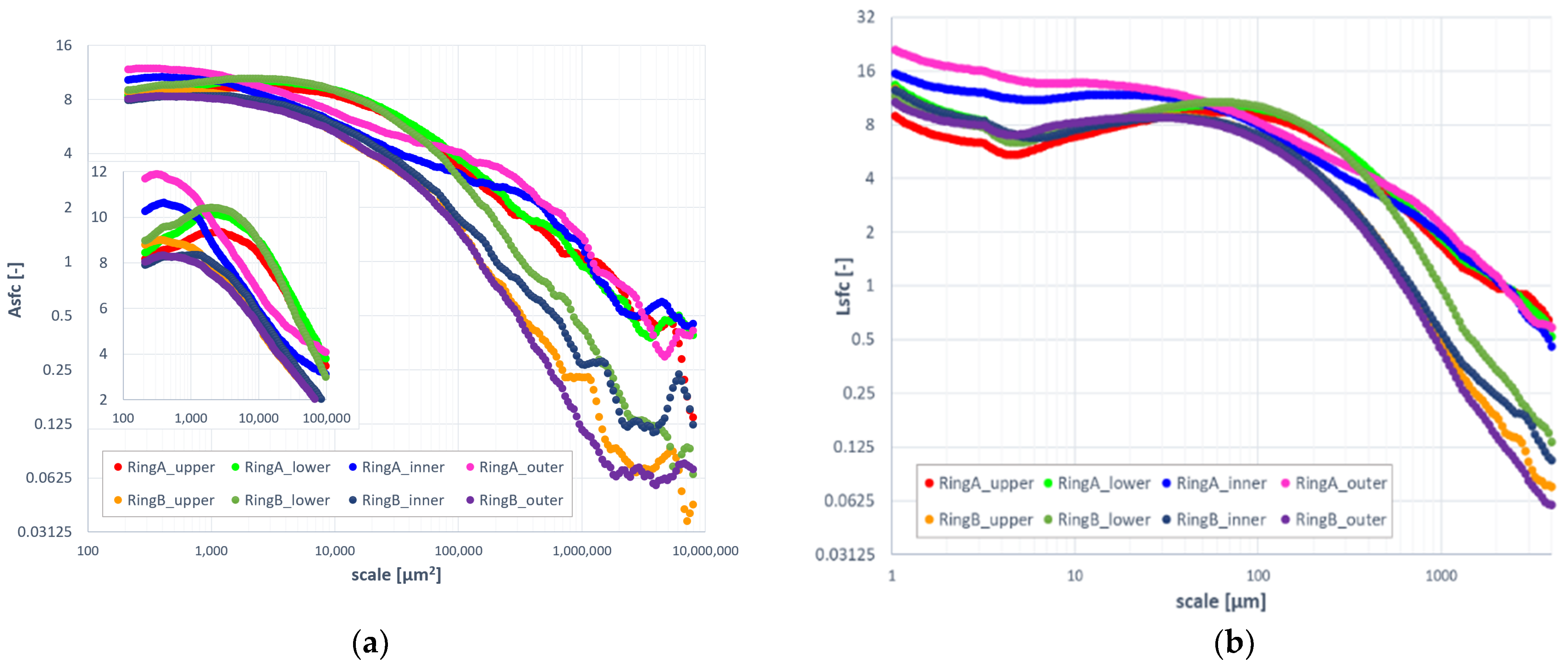

| Bandwidth = 20 μm | Bandwidth = 50 μm | Bandwidth = 100 μm | ||||||
|---|---|---|---|---|---|---|---|---|
| λlc (μm) | λcenter (μm) | λuc (μm) | λlc (μm) | λcenter (μm) | λuc (μm) | λlc (μm) | λcenter (μm) | λuc (μm) |
| 60 | 70 | 80 | 65 | 90 | 115 | 60 | 110 | 160 |
| 70 | 80 | 90 | 75 | 100 | 125 | 70 | 120 | 170 |
| 80 | 90 | 100 | 66 | 110 | 135 | 80 | 130 | 180 |
| 90 | 100 | 110 | 95 | 120 | 145 | 90 | 140 | 190 |
| 100 | 110 | 120 | 105 | 130 | 155 | 100 | 150 | 198 |
| 110 | 120 | 130 | 115 | 140 | 165 | – | – | – |
| 120 | 130 | 140 | 125 | 150 | 175 | – | – | – |
| 130 | 140 | 150 | 135 | 160 | 185 | – | – | – |
| 140 | 150 | 160 | 145 | 170 | 195 | – | – | – |
| 150 | 160 | 170 | – | – | – | – | – | – |
| 160 | 170 | 180 | – | – | – | – | – | – |
| 170 | 180 | 190 | – | – | – | – | – | – |
| 180 | 190 | 198 | – | – | – | – | – | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartkowiak, T.; Grochalski, K.; Gapiński, B.; Wieczorowski, M. Discrimination of Surface Topographies Created by Two-Stage Process by Means of Multiscale Analysis. Materials 2021, 14, 7044. https://doi.org/10.3390/ma14227044
Bartkowiak T, Grochalski K, Gapiński B, Wieczorowski M. Discrimination of Surface Topographies Created by Two-Stage Process by Means of Multiscale Analysis. Materials. 2021; 14(22):7044. https://doi.org/10.3390/ma14227044
Chicago/Turabian StyleBartkowiak, Tomasz, Karol Grochalski, Bartosz Gapiński, and Michał Wieczorowski. 2021. "Discrimination of Surface Topographies Created by Two-Stage Process by Means of Multiscale Analysis" Materials 14, no. 22: 7044. https://doi.org/10.3390/ma14227044
APA StyleBartkowiak, T., Grochalski, K., Gapiński, B., & Wieczorowski, M. (2021). Discrimination of Surface Topographies Created by Two-Stage Process by Means of Multiscale Analysis. Materials, 14(22), 7044. https://doi.org/10.3390/ma14227044









