Mapping Relation between Rail and Bridge Deformation Considering Nonlinear Contact of Interlayer
Abstract
:1. Introduction
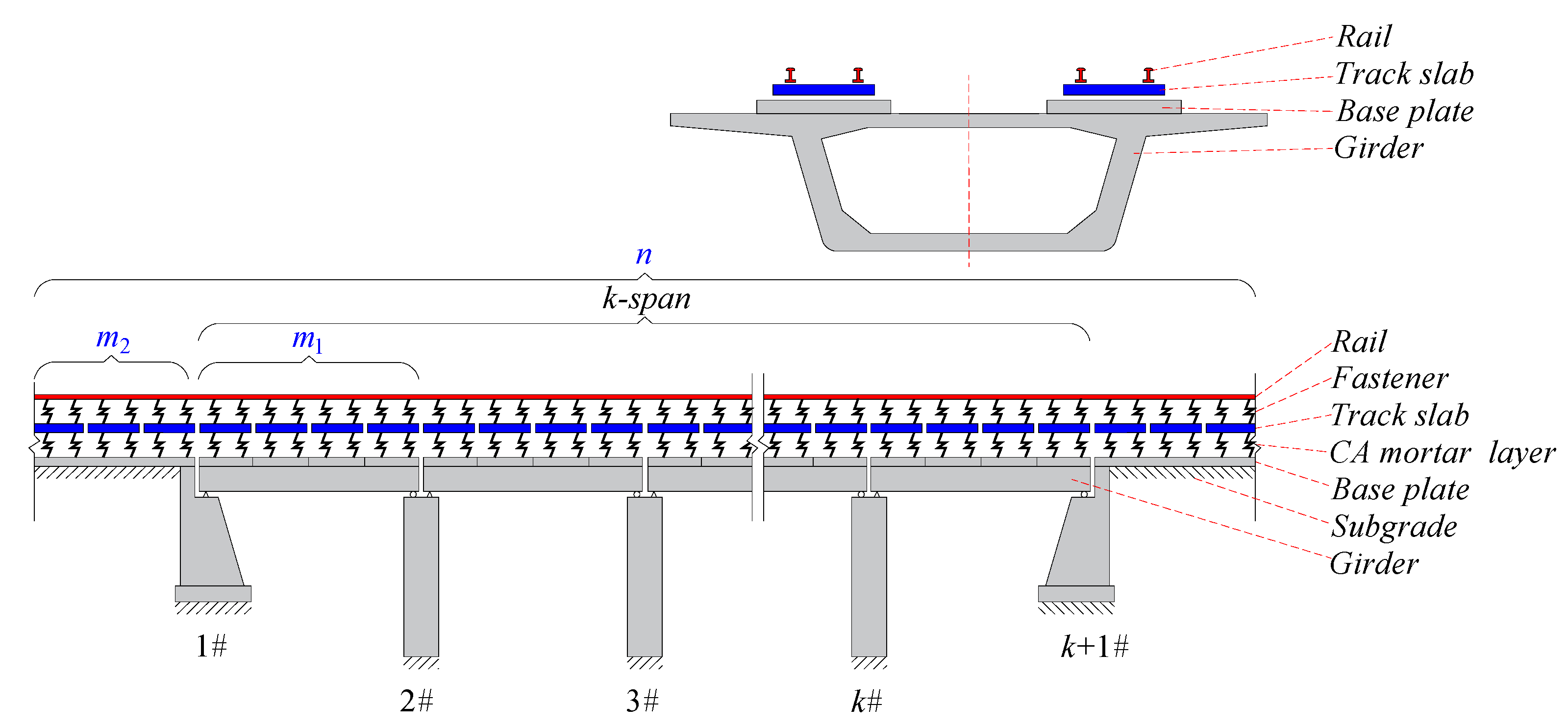
2. Theoretical Model
2.1. Fundamental Assumptions
- (1)
- Theoretical model-1 (AM-1) with linear connect of interlayer
- (a)
- The track and girder structures are simplified as a single composite beam, in which the track slabs were vertically supported by springs (i.e., connected with the mortar layer to the base plates), regarded as free beams with two free ends, without mutual connection along the longitudinal bridge direction; the base plates and girder are firmly connected via embedded rebars. Therefore, they are assumed that deformation of the girder and base plates are synergistic;
- (b)
- Rail in the subgrade section can be simplified as a simply supported beam; the rail boundary effect of the subgrade section is eliminated by considering a sufficiently long section of subgrade;
- (c)
- The fasteners and the CA mortar layer are modeled as linear springs and uniformly distributed along the centerline of the track;
- (d)
- Given that the vertical bending stiffness of bridge is far greater than that of track structure, the influence of track structure on bridge deformation was ignored;
- (e)
- Under the action of the support displacement, the simply supported beam structure suffers vertical rigid-body deformation;
- (f)
- The origin of coordinates is set at the static equilibrium position of the structure under the action of gravity. Under the action of vertical deformation of the structure, the calculation is conducted on the deformation of track structure relative to the static equilibrium position of gravity. Therefore, the action of gravity was ignored in the calculations.
- (2)
- Theoretical model-2 (AM-2) with nonlinear connect of interlayer
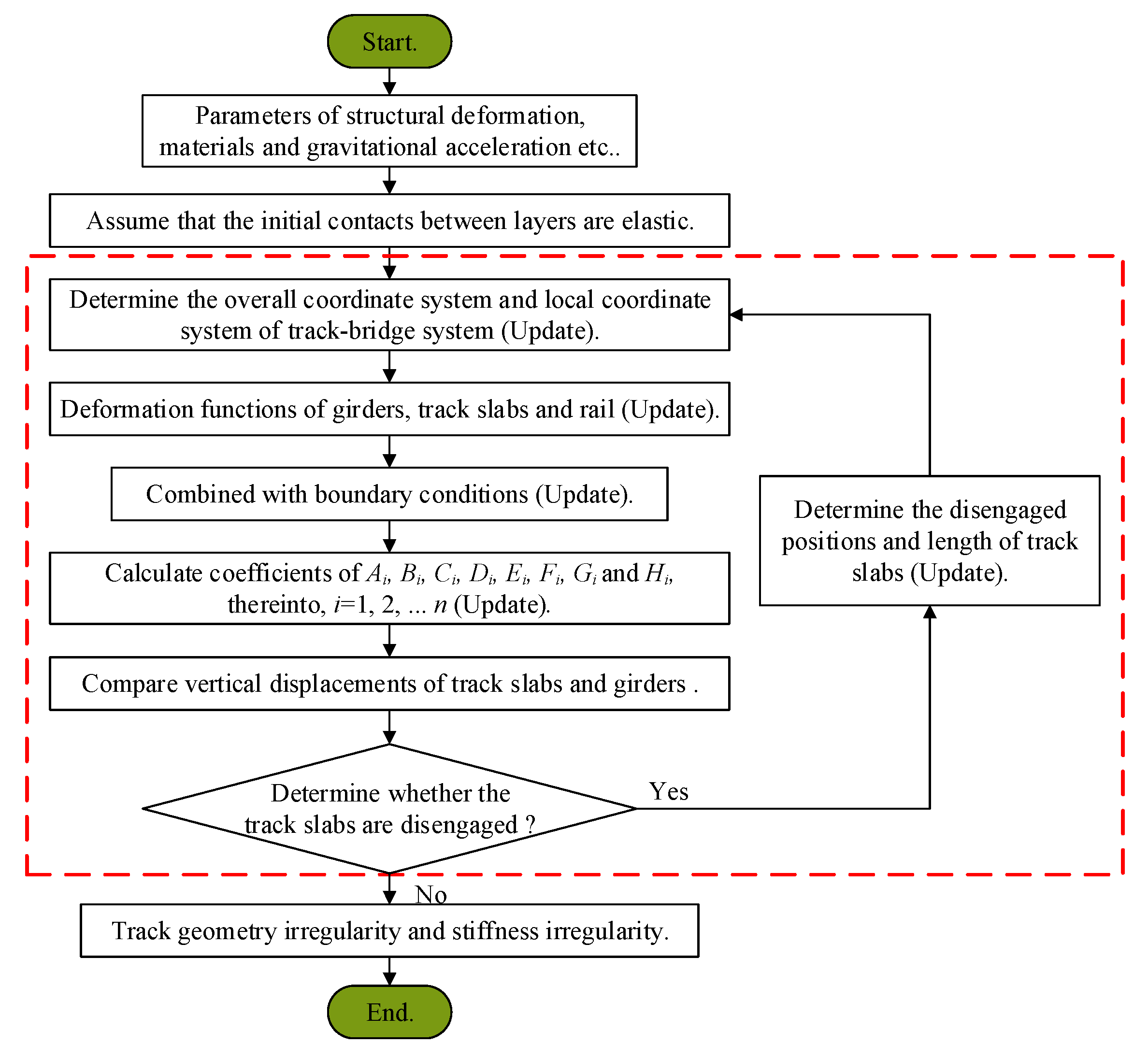
2.2. Establishment of Theoretical Model for Deformation Mapping Relationship
2.2.1. Theoretical Model of Nonlinear Connect of Interlayer without Track Slab Disengagement
2.2.2. Theoretical Model of Nonlinear Connect of Interlayer with Track Slab Disengagement
2.2.3. Theoretical Model of Linear Connect of Interlayer
2.3. Theoretical Solution to Mapping Relationship
3. Verification of Theoretical Model
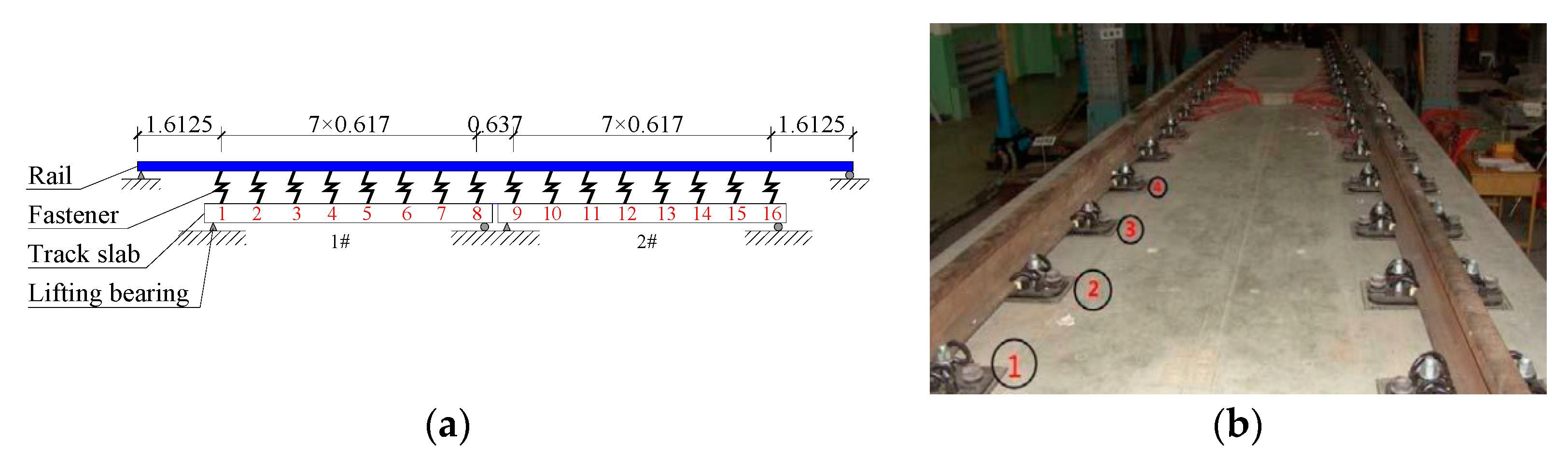
3.1. Finite Element Model
3.2. Experimental Verification
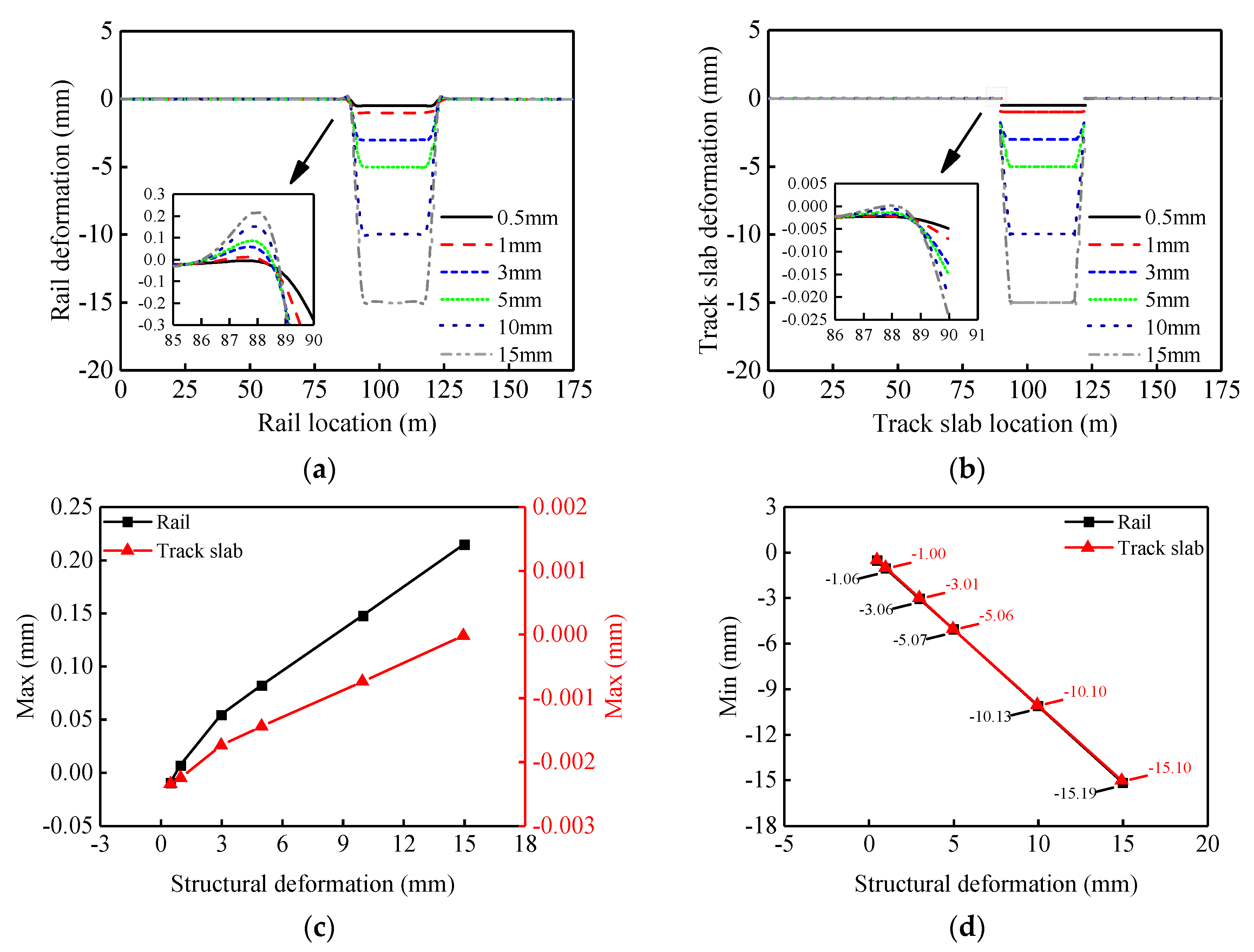
4. The Effect of Deformation Amplitude of Bridge Structure on Track Deformation
4.1. The Effect of Bridge Structure Deformation Amplitude on Track Deformation
4.2. The Effect of Bridge Structure Deformation Amplitude on the Interlayer Contact of Track Structure
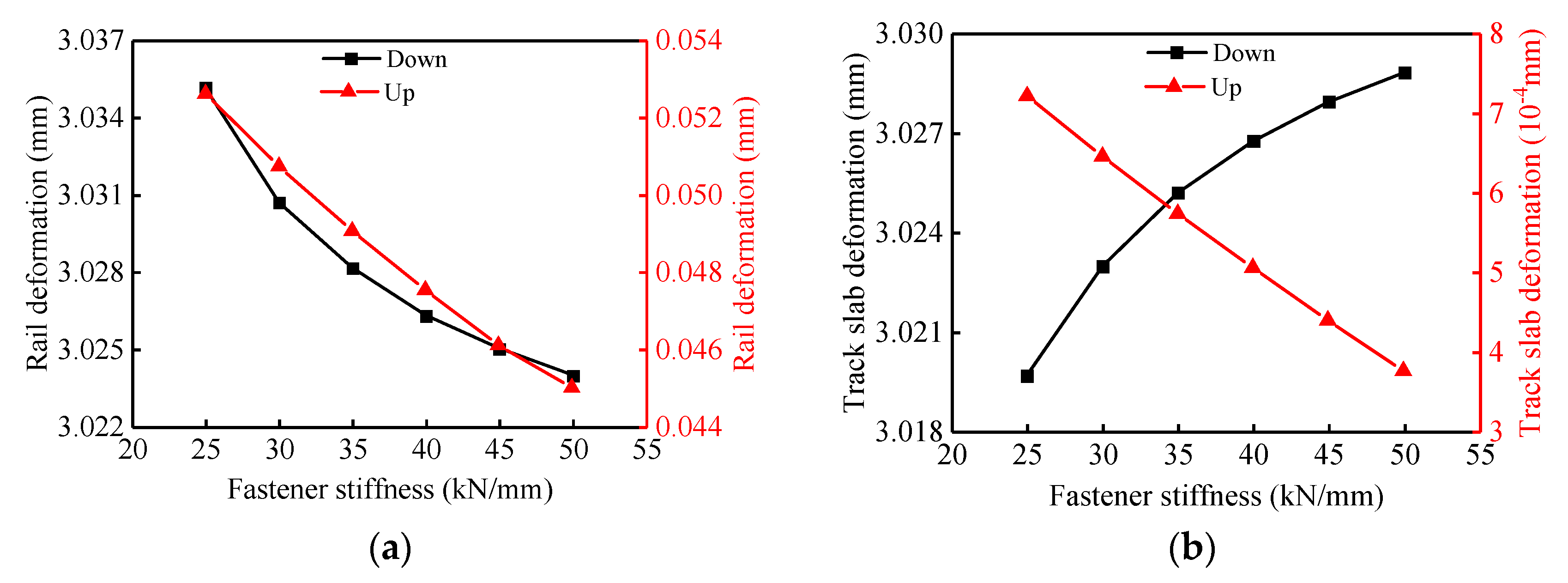
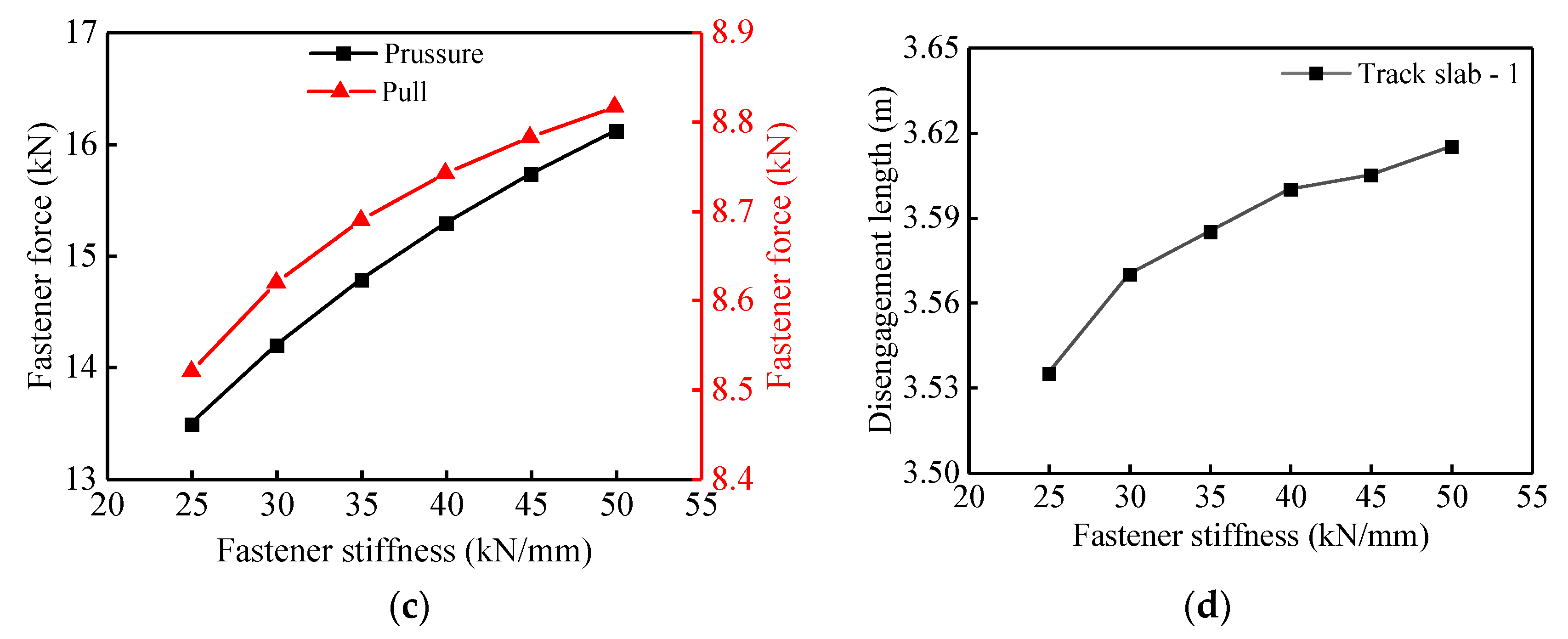
5. The Effects of Interlayer Characteristics of the Track Structure on Track Deformation
5.1. The Effect of the Vertical Stiffness of Fasteners on Track Deformation
5.2. The Effects of the Elastic Modulus of CA Mortar Layer on Track Deformation
6. Conclusions
- (1)
- Theoretical results of rail mapping deformation caused by various typical vertical deformations of the bridge structure agree well with the results of the FEM and the experiment model, which verifies the proposed theoretical model. When the mortar layer is considered as elastic and nonlinear, the rail mapping deformation is obviously different. The nonlinearity of the vertical stiffness of the mortar layer cannot be ignored.
- (2)
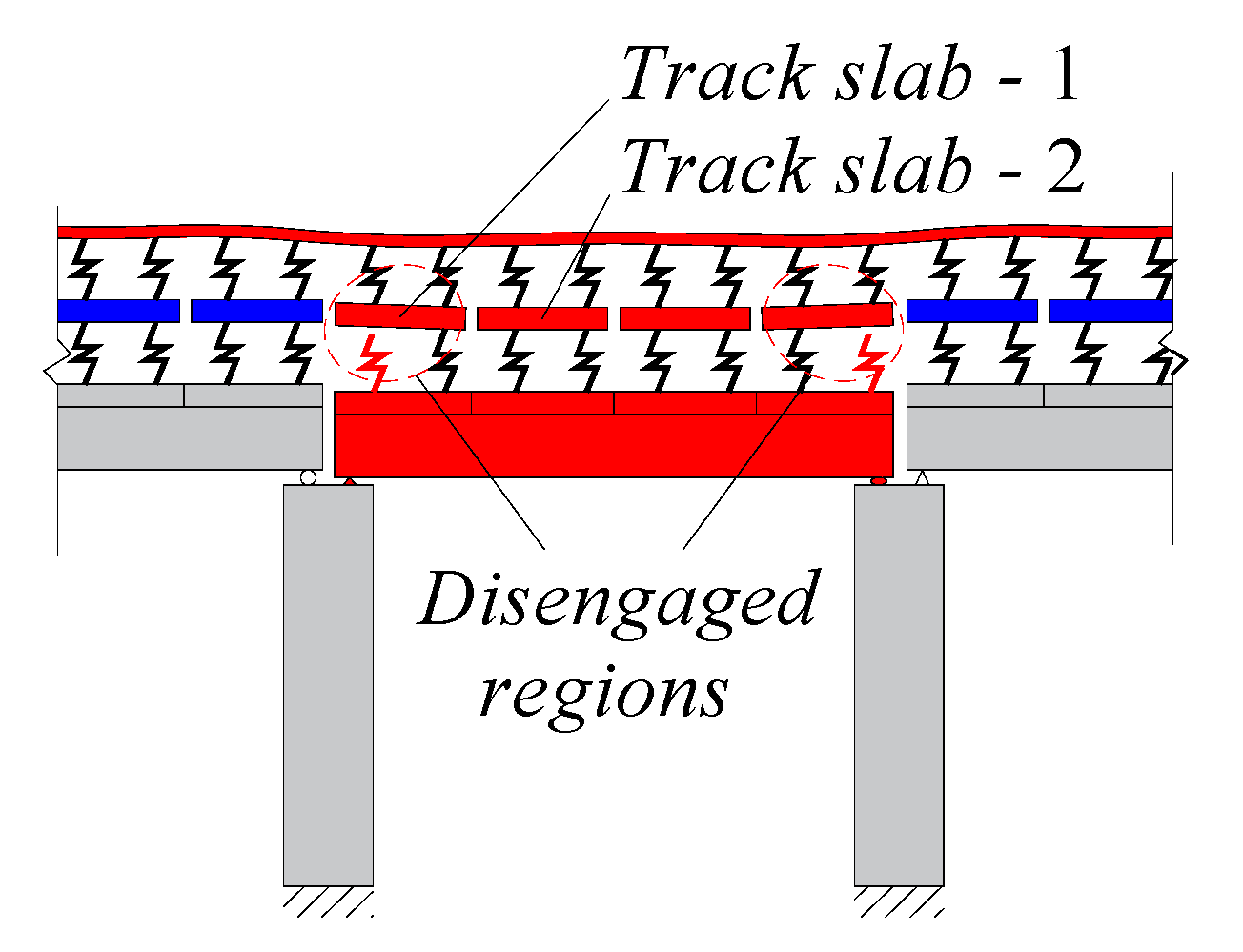
- With the deformation of the bridge structure, the track structure has obvious following property. With the increase of the girder deflection, the upwarping deformation of the track structure shows an obvious nonlinear increasing trend due to the occurrence of the track slabs disengagement. The track slabs’ disengagement mainly occurs near the beam joints (the side of the deformed beam).
- (3)
- When nonlinear contact between mortar layer and track slabs was considered, as the deflection amplitude of the girder increases, the forces of the fasteners and the disengagement length of the track slabs are obviously nonlinear.
- (4)
- As the fastener vertical stiffness and/or the mortar layer elastic modulus increases the track deflection, the fastener force and the track slabs disengagement length are all nonlinear monotonically. The larger vertical stiffness of the fasteners and the elastic modulus of the mortar layer will have adverse effects on the life and safety of the track structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, S.K.; Lee, J. Design and development of smart semi active suspension for nonlinear rail vehicle vibration reductio. Int. J. Struct. Stab. Dyn. 2020, 20, 2050120. [Google Scholar] [CrossRef]
- Guo, W.; Gao, X.; Hu, P.; Hu, Y.; Zhai, Z.; Bu, D.; Jiang, L. Seismic damage features of high-speed railway simply supported bridge-track system under near-fault earthquake. Adv. Struct. Eng. 2020, 23, 1573–1586. [Google Scholar] [CrossRef]
- Rocha, J.M.; Henriques, A.A.; Calçada, R. Probabilistic safety assessment of a short span high-speed railway bridge. Eng. Struct. 2014, 71, 99–111. [Google Scholar] [CrossRef]
- Jin, Z.; Yuan, L.; Pei, S. Efficient evaluation of bridge deformation for running safety of railway vehicles using simplified models. Adv. Struct. Eng. 2020, 23, 454–467. [Google Scholar] [CrossRef]
- Zeng, X.H.; Xie, Y.J.; Deng, D.H.; Wang, P.; Qu, F.L. A study of the dynamic mechanical properties of CRTS I type CA mortar. Constr. Build. Mater. 2016, 112, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Shan, Y.; Zheng, S.; Zhang, X.; Luo, W.; Mao, J.; Kong, D. Fatigue performance of the CA mortar used in CRTS i ballastless slab track under simulated servicing condition. Materials 2018, 11, 2259. [Google Scholar] [CrossRef] [Green Version]
- Gou, H.; Yang, L.; Mo, Z.; Guo, W.; Shi, X.; Bao, Y. Effect of Long-Term bridge deformations on safe operation of High-Speed railway and vibration of vehicle-bridge coupled system. Int. J. Struct. Stab. Dyn. 2019, 19, 1950111. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Z.; Zhang, H.; Fan, J. Dynamic analysis of Train-Rail-Bridge interaction considering concrete creep of a Multi-Span simply supported bridge. Adv. Struct. Eng. 2014, 17, 709–720. [Google Scholar] [CrossRef]
- Kang, X.; Jiang, L.; Bai, Y.; Caprani, C.C. Seismic damage evaluation of high-speed railway bridge components under different intensities of earthquake excitations. Eng. Struct. 2017, 152, 116–128. [Google Scholar] [CrossRef]
- Fahmy, M.F.; Wu, Z.; Wu, G.; Sun, Z. Post-yield stiffnesses and residual deformations of RC bridge columns reinforced with ordinary rebars and steel fiber composite bars. Eng. Struct. 2010, 32, 2969–2983. [Google Scholar] [CrossRef]
- Montalbán, L.; Real, J.; Real, T. Mechanical characterization of railway structures based on vertical stiffness analysis and railway substructure stress state. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 227, 74–85. [Google Scholar] [CrossRef]
- Gou, H.; Long, H.; Bao, Y.; Chen, G.; Pu, Q. Dynamic behavior of hybrid framed arch railway bridge under moving trains. Struct. Infrastruct. Eng. 2019, 15, 1015–1024. [Google Scholar] [CrossRef]
- Ju, S.H.; Leong, C.C.; Ho, Y.S. Safety of maglev trains moving on bridges subject to foundation settlements and earthquakes. J. Bridge Eng. 2014, 19, 91–100. [Google Scholar] [CrossRef]
- Doménech, A.; Museros, P.; Martínez-Rodrigo, M.D. Influence of the vehicle model on the prediction of the maximum bending response of simply-supported bridges under high-speed railway traffic. Eng. Struct. 2014, 72, 123–139. [Google Scholar] [CrossRef]
- Ju, S.H. 3D analysis of high-speed trains moving on bridges with foundation settlements. Arch. Appl. Mech. 2013, 83, 281–291. [Google Scholar] [CrossRef]
- Yau, J.D. Response of a train moving on multi-span railway bridges undergoing ground settlement. Eng. Struct. 2009, 31, 2115–2122. [Google Scholar] [CrossRef]
- Yang, L.A.; Powrie, W.; Priest, J.A.A. Dynamic stress analysis of a ballasted railway track bed during train passage. J. Geotech. Geoenviron. Eng. 2009, 135, 680–689. [Google Scholar] [CrossRef]
- Jiang, H.; Li, X.; Xin, G.; Yao, Z.; Zhang, J.; Liang, M. Geometry mapping and additional stresses of ballastless track structure caused by subgrade differential settlement under self-weight loads in high-speed railways. Transp. Geotechnol. 2019, 18, 103–110. [Google Scholar] [CrossRef]
- Gou, H.; Zhou, W.; Bao, Y.; Li, X.; Pu, Q. Experimental study on dynamic effects of a long-span railway continuous beam bridge. Appl. Sci. 2018, 8, 669. [Google Scholar] [CrossRef] [Green Version]
- Gou, H.; Shi, X.; Zhou, W.; Cui, K.; Pu, Q. Dynamic performance of continuous railway bridges: Numerical analyses and field tests. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2018, 232, 936–955. [Google Scholar] [CrossRef]
- Gou, H.; He, Y.; Zhou, W.; Bao, Y.; Chen, G. Experimental and numerical investigations of the dynamic responses of an asymmetrical arch railway bridge. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2018, 232, 2309–2323. [Google Scholar] [CrossRef]
- Chen, Z.; Zhai, W.; Yin, Q. Analysis of structural stresses of tracks and vehicle dynamic responses in train-track-bridge system with pier settlement. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2018, 232, 421–434. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Thompson, D.J. A theoretical model for ground vibration from trains generated by vertical track irregularities. J. Sound Vib. 2004, 272, 937–965. [Google Scholar] [CrossRef]
- Chen, Z.; Zhai, W.; Cai, C.; Sun, Y. Safety threshold of high-speed railway pier settlement based on train-track-bridge dynamic interaction. Sci. China-Technol. Sci. 2015, 58, 202–210. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, Y.; Zhai, W. Mapping relationship between pier settlement and rail deformation of high-speed railways—Part (I): The unit slab track system. Sci. Sin. Technol. 2014, 44, 770–777. [Google Scholar] [CrossRef]
- Chen, Z.; Zhai, W.; Tian, G. Study on the safe value of multi-pier settlement for simply supported girder bridges in high-speed railways. Struct. Infrastruct. Eng. 2018, 14, 400–410. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, Y.; Zhai, W. Mapping relationship between pier settlement and rail deformation of high-speed railways—Part (II): The longitudinal connected ballastless track system. Sci. Sin. Technol. 2014, 44, 778–785. (In Chinese) [Google Scholar] [CrossRef]
- Gou, H.Y.; Yang, L.C.; Leng, D.; Bao, Y.; Pu, Q.H. Effect of bridge lateral deformation on track geometry of high-speed railway. Steel Compos. Struct. 2018, 29, 219–229. [Google Scholar] [CrossRef]
- Gou, H.; Ran, Z.; Yang, L.; Bao, Y.; Pu, Q. Mapping vertical bridge deformations to track geometry for high-speed railway. Steel Compos. Struct. 2019, 32, 467–478. [Google Scholar] [CrossRef]
- Feng, Y.; Jiang, L.; Zhou, W.; Lai, Z.; Chai, X. An analytical solution to the mapping relationship between bridge structures vertical deformation and rail deformation of high-speed railway. Steel Compos. Struct. 2019, 32, 209–224. [Google Scholar] [CrossRef]
- Zhou, W.; Nie, L.; Jiang, L.; Feng, Y.; Tan, Z.; Chai, X. Mapping relation between pier settlement and rail deformation of unit slab track system. Structures 2020, 27, 1066–1074. [Google Scholar] [CrossRef]
- Jiang, L.; Zheng, L.; Feng, Y.; Lai, Z.; Zhou, W. Mapping the relationship between the structural deformation of a simply supported beam bridge and rail deformation in high-speed railways. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 1081–1092. [Google Scholar] [CrossRef]
- Guo, Y.; Zhai, W.; Sun, Y. A mechanical model of vehicle-slab track coupled system with differential subgrade settlement. Struct. Eng. Mech. 2018, 66, 15–25. [Google Scholar] [CrossRef]
- Sadeghi, J.; Zakeri, J.A.; Tolou Kian, A.R. Effect of unsupported sleepers on rail track dynamic behaviour. Proc. Inst. Civ. Eng.-Transp. 2018, 171, 286–298. [Google Scholar] [CrossRef]
- Sysyn, M.; Przybylowicz, M.; Nabochenko, O.; Liu, J. Mechanism of Sleeper-Ballast dynamic impact and residual settlements accumulation in zones with unsupported sleepers. Sustainability 2021, 13, 7740. [Google Scholar] [CrossRef]
- Wei, Y. Research on Beam End Displacement Relevant Problems for High-Speed Railway Ballastless Track Bridge; China Academy of Railway Sciences: Beijing, China, 2012. (In Chinese) [Google Scholar]






| Structure | Parameters | Value | FEM | AM-1(AM-2) | Notes |
|---|---|---|---|---|---|
| Rail | Elastic modulus | 2.060 × 105 MPa | 1 | 1 | CHN60 |
| Density | 8.005 × 103 kg/m3 | 1 | 1 | ||
| Cross-sectional area | 7.705 × 10−3 m2 | 1 | 4 | ||
| Moment of inertia | 3.217 × 10−5 m4 | 1 | 4 | ||
| Fastener | Vertical stiffness | 40 kN/mm | 1 | 4/0.625 | WJ-7 |
| Horizontal stiffness | 7 kN/mm | 1 | -- | ||
| Interval | 0.625 m | 1 | Continuous | ||
| Track slab | Elastic modulus | 3.600 × 104 MPa | 1 | 1 | C60 concrete; Girder end: 3.75 m |
| Density | 2.549 × 103 kg/m3 | 1 | 1 | ||
| Sectional dimension | 2.4 × 0.19 m | 1 | 2 | ||
| Moment of inertia | 1.372 × 10−3 m4 | 1 | 2 | ||
| Length | 5.000 m | 1 | 1 | ||
| CA mortar layer | Elastic modulus (E) | 200 MPa | 1 | 1 | Compression only; kv = EA/h, A = 1 × b. |
| Sectional dimension (b × h) | 2.4 × 0.05 m | 1 | 2 | ||
| Vertical stiffness (kv) | 9.600 × 109 N/m | 1 | 2 | ||
| Horizontal stiffness | 9.600 × 108 N/m | 1 | -- | ||
| Base plate | Elastic modulus | 3.250 × 104 MPa | 1 | -- | C40 concrete; Assumption (d). |
| Density | 2.549 × 103 kg/m3 | 1 | -- | ||
| Sectional dimension | 2.8 × 0.26 m | 1 | -- | ||
| Length | 5.000 m | 1 | -- | ||
| Girder | Elastic modulus | 3.450 × 104 MPa | 1 | 1 | C50 concrete |
| Density | 2.549 × 103 kg/m3 | 1 | 1 | ||
| Moment of inertia | 1.093 × 101 m4 | 1 | 1 |
| Case | Components | AM-1 | AM-2 | FEM | The Error between AM-2 and FEM | ||||
|---|---|---|---|---|---|---|---|---|---|
| +(mm) | −(mm) | +(mm) | −(mm) | +(mm) | −(mm) | +(%) | −(%) | ||
| 1 | Rail | 0.335 | −10.34 | 0.147 | −10.13 | 0.154 | −10.13 | −4.55 | 0 |
| Track slab | 0 | −10.00 | 0 | −10.10 | 0 | −10.20 | 0 | −0.98 | |
| 2 | Rail | 0.325 | −9.67 | 0.133 | −8.68 | 0.139 | −8.68 | −4.32 | 0 |
| Track slab | 0 | −9.95 | 0 | −8.94 | 0 | −9.04 | 0 | −1.11 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, L.; Jiang, L.; Zhou, W.; Feng, Y. Mapping Relation between Rail and Bridge Deformation Considering Nonlinear Contact of Interlayer. Materials 2021, 14, 6653. https://doi.org/10.3390/ma14216653
Nie L, Jiang L, Zhou W, Feng Y. Mapping Relation between Rail and Bridge Deformation Considering Nonlinear Contact of Interlayer. Materials. 2021; 14(21):6653. https://doi.org/10.3390/ma14216653
Chicago/Turabian StyleNie, Leixin, Lizhong Jiang, Wangbao Zhou, and Yulin Feng. 2021. "Mapping Relation between Rail and Bridge Deformation Considering Nonlinear Contact of Interlayer" Materials 14, no. 21: 6653. https://doi.org/10.3390/ma14216653
APA StyleNie, L., Jiang, L., Zhou, W., & Feng, Y. (2021). Mapping Relation between Rail and Bridge Deformation Considering Nonlinear Contact of Interlayer. Materials, 14(21), 6653. https://doi.org/10.3390/ma14216653









