Analytical Model and Numerical Analysis of Composite Wrap System Applied to Steel Pipeline
Abstract
:1. Introduction
2. Applied Methodologies
2.1. Standards ASME PCC-2 and ISO/TS 24817
2.2. Analytical Approach
Procedure to Find the Thickness tc Based on the Developed Approach
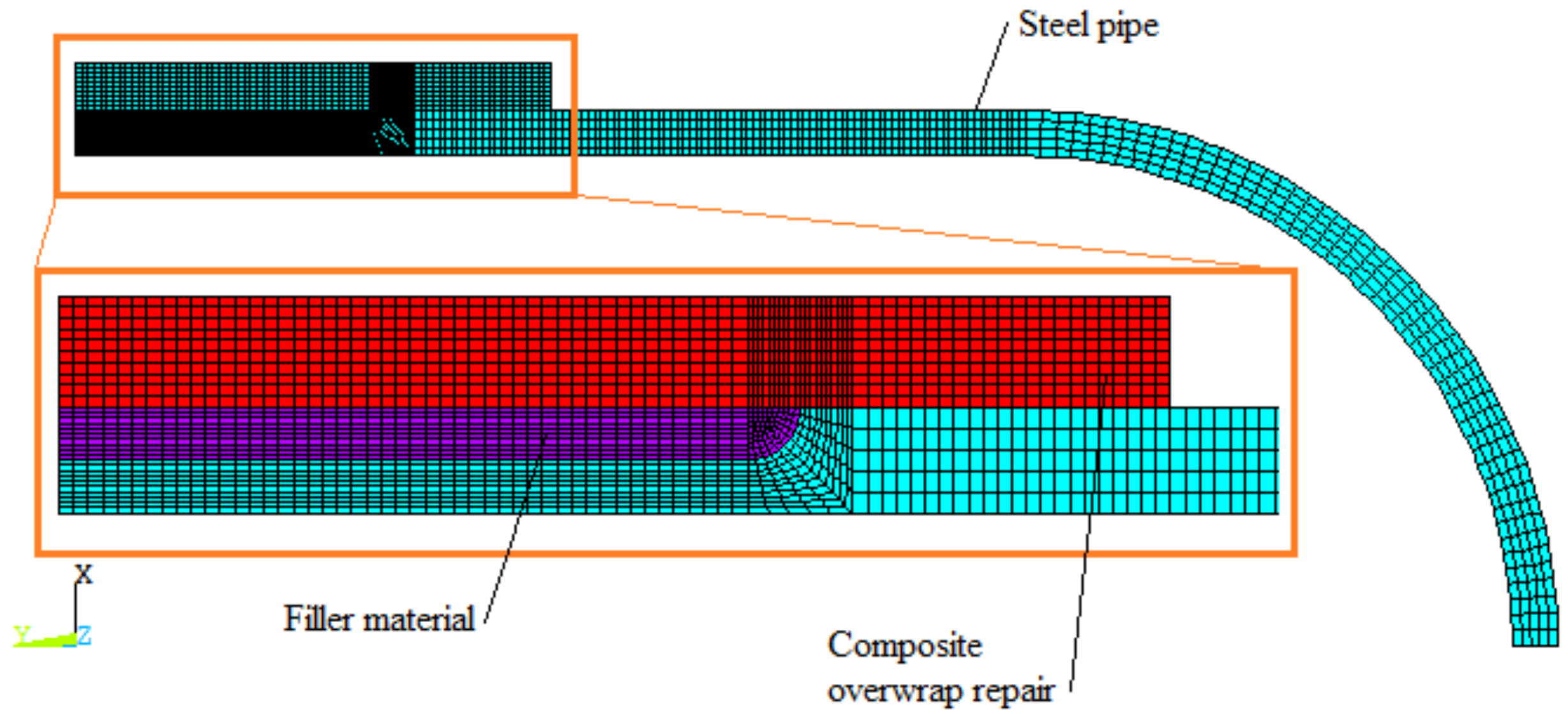
2.3. Finite Element Analysis
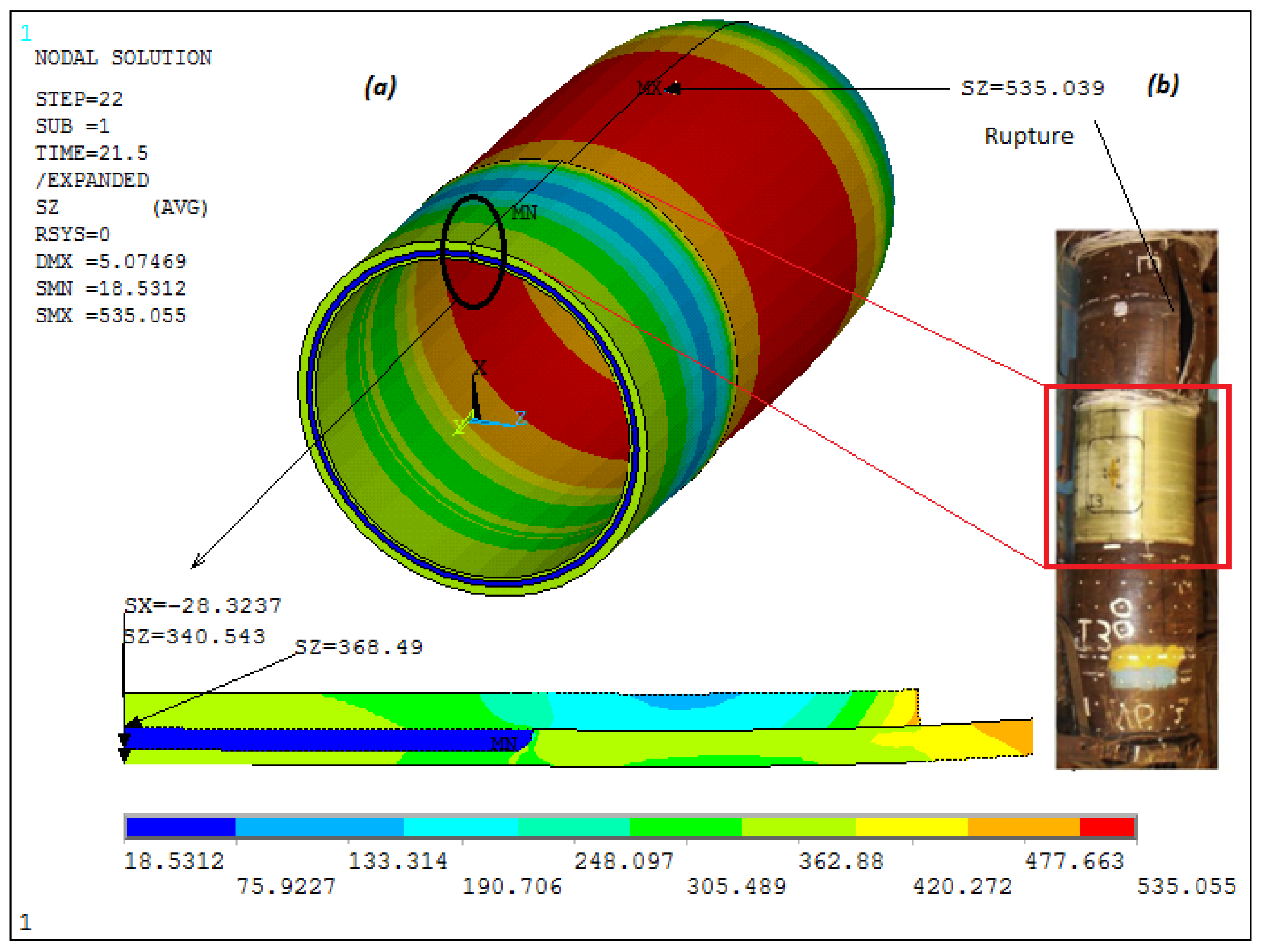
3. Limit Load and Experimental Validation
4. Composite Repair Sleeve Sizing at Design Pressure
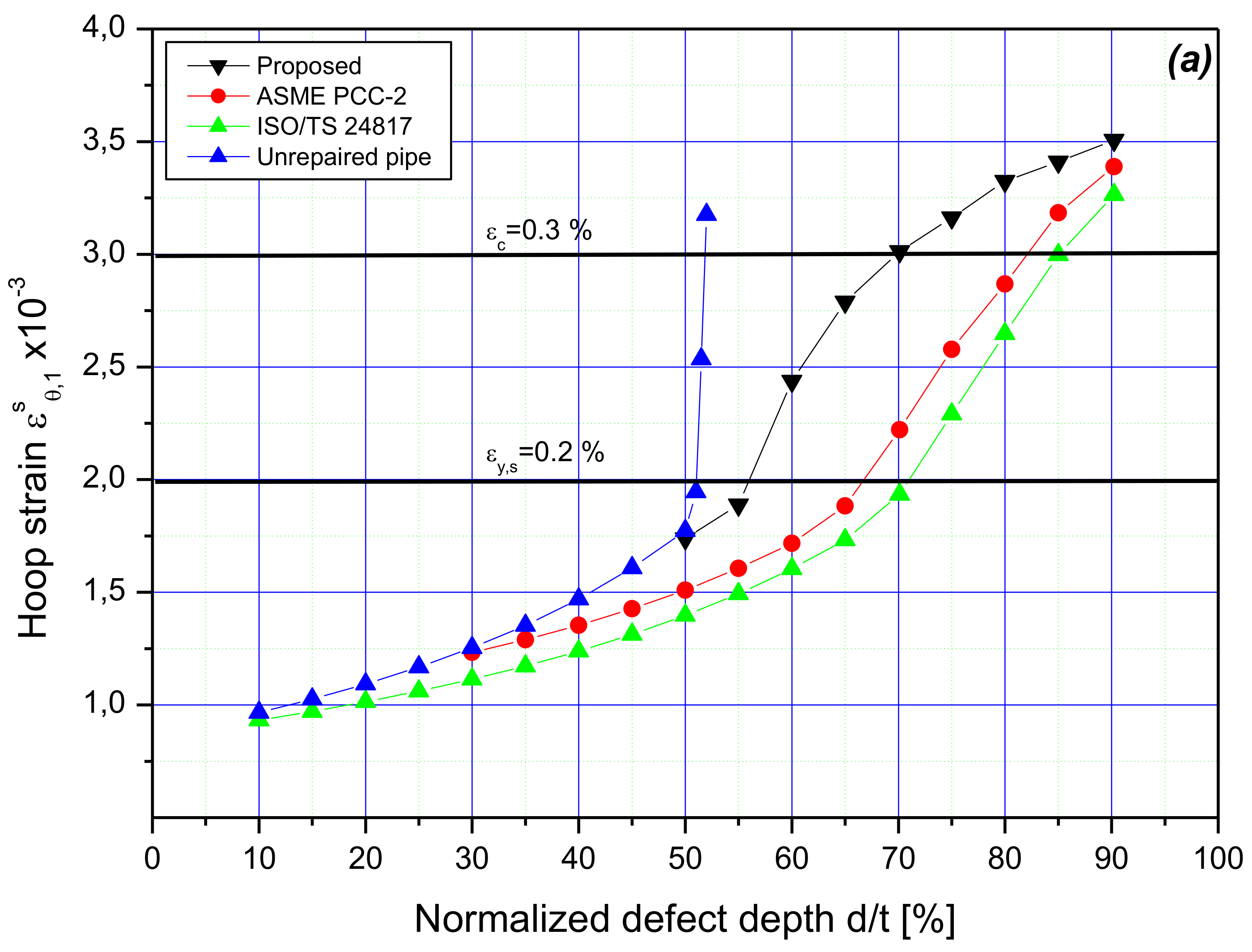
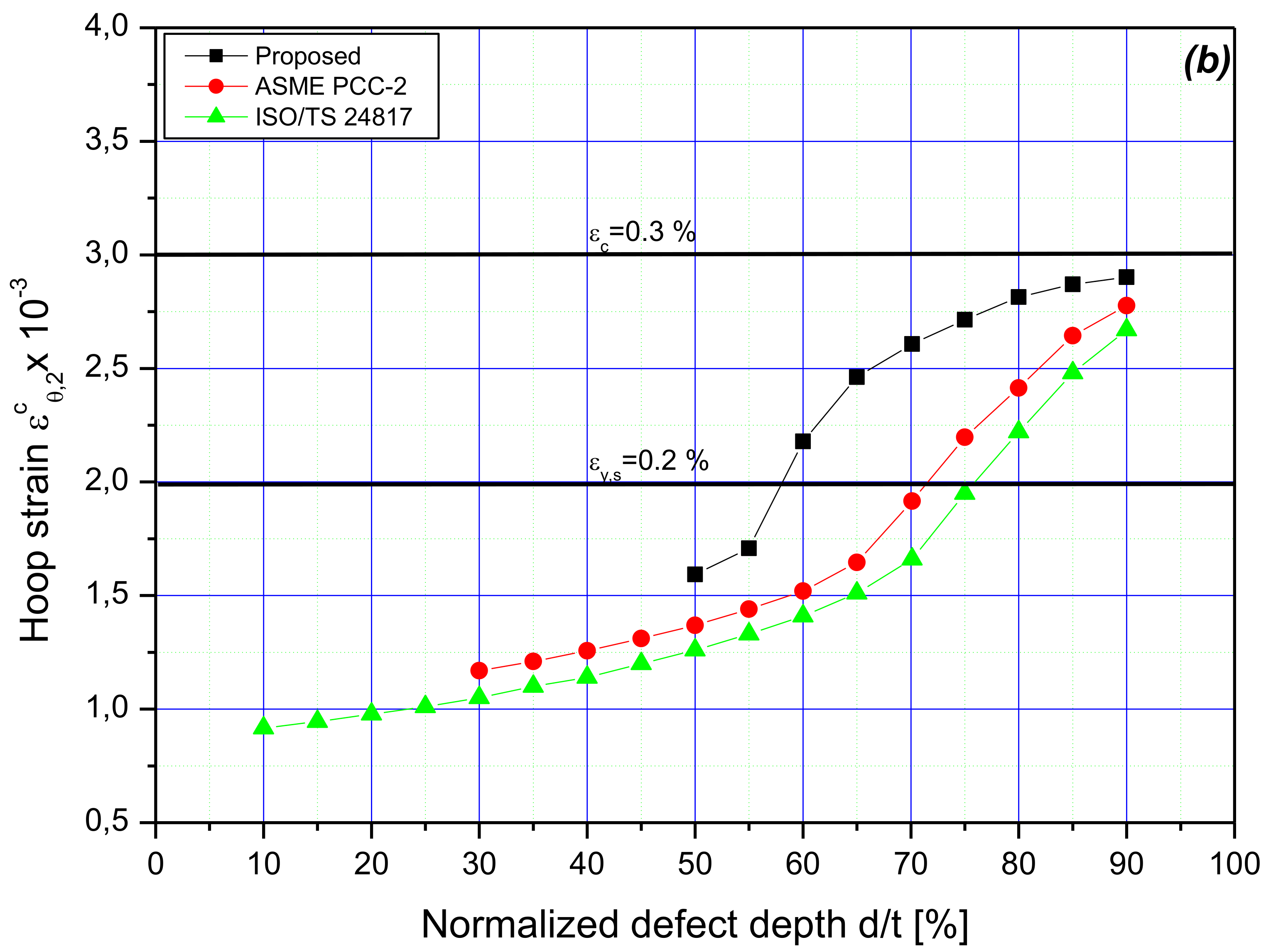
5. Results and Discussion
6. Conclusions
- The composite overwrap sizing calculated according to ASME PCC-2 and ISO/TS 2481 standards is conservative with respect to the obtained sleeve thickness and results in unnecessary repairs of the steel pipe wall thinning, particularly for small depths of material losses. For a medium depth of metal losses, ranging from 50% to 65% of the tube wall, in the case of the new developed solution, the sleeve thickness was reduced as follows:
- -
- by 96% to 42% compared to the results of ASME PCC-2,
- -
- by 97.5% to 54% compared to the results of ISO/TS 2481.
- For the deepest pipe wall metal losses, starting from 70% of wall thickness, the applied sizing algorithm reduces the wrap thickness as follows:
- -
- by 32% to 4% compared to the results of ASME PCC-2,
- -
- by 43% to 8.4% compared to the results of ISO/TS 2481.
- The presented methodology takes into consideration an effect of the external pressure surrounding the tube, as in the case of offshore pipelines, in which the thickness of the fiber-glass sleeve is even less.
- The proposed approach predicts the burst pressure of the defected pipes repaired with a composite overwrap system for practical applications. Due to this fact, the authors are going to conduct experiments to validate the burst pressure of steel tubes repaired with the use of the developed sleeve sizing procedure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Outside diameter of the steel tube | |
| Pressure to be recovered | |
| Internal design pressure of the pipeline | |
| Live pressure | |
| Actual internal pressure | |
| External pressure | |
| Contact pressure at the location j | |
| Burst pressure of the steel pipe | |
| Minimum required thickness of the composite sleeve | |
| Remaining thickness of the pipe wall in the corroded zone | |
| Thickness of the steel pipe | |
| Composite allowable strain | |
| Specified minimum yield stress of steel | |
| Strain hardening exponent | |
| Material strength coefficient | |
| , | Internal radius of the steel tube, internal radius of corrosion defect, external radius of steel tube, and internal radius of composite repair |
| Dimensionless geometric ratio | |
| Actual yield stress | |
| Stress components, respectively, in hoop, axial, and radial directions. The indices i and j denote, respectively, the contact pressure location and the material type | |
| Strain components, respectively, in hoop, axial, and radial directions. The indices i and j denote, respectively, the contact pressure location and the material type | |
| Elastic moduli of the composite, respectively, in the circumferential, axial, and radial directions | |
| Composite material Poisson’s ratio | |
| Shear moduli of the composite, respectively, in the circumferential, axial, and radial directions. | |
| Putty Poisson’s ratio | |
| Corrosion defect half length | |
| Corrosion defect width | |
| Corrosion defect depth | |
| Normalized defect length | |
| Folias factor | |
| Safety factors | |
| MAWP | The maximum allowable working pressure |
| MOP | The maximum operating pressure |
References
- Witek, M. Structural Integrity of Steel Pipeline with Clusters of Corrosion Defects. Materials 2021, 14, 852. [Google Scholar] [CrossRef] [PubMed]
- Adumene, S.; Khan, F.; Adedigba, S.; Zendehboudi, S. Offshore system safety and reliability considering microbial influenced multiple failure modes and their interdependencies. Reliab. Eng. Syst. Saf. 2021, 215, 107862. [Google Scholar] [CrossRef]
- Yu, W.; Huang, W.; Wen, K.; Zhang, J.; Liu, H.; Wang, K.; Gong, J.; Qu, C. Subset simulation-based reliability analysis of the corroding natural gas pipeline. Reliab. Eng. Syst. Saf. 2021, 213, 107661. [Google Scholar] [CrossRef]
- Witek, M.; Uilhoorn, F. A data assimilation approach for estimating strength of steel pipes reinforced with composite sleeves under unsteady pressure-flow conditions. Arch. Thermodyn. 2020, 3–22. [Google Scholar] [CrossRef]
- Bruce, W. Comparison of fiber-reinforced polymer wrapping versus steel sleeves for repair of pipelines. In Rehabilitation of Pipelines Using Fiber-Reinforced Polymer (FRP) Composites; Woodhead Publishing: Sawston, UK, 2015; pp. 61–78. [Google Scholar] [CrossRef]
- ASME. Post construction standard, PCC-2, repair of pressure equipment and piping, article 4.1. In Non-Metallic Composite Repair Systems for Pipelines and Pipework: High Risk Applications; American Society of Mechanical Engineers: New York, NY, USA, 2006. [Google Scholar]
- International Organization for Standardization. ISO/TS 2481: Petroleum, Petrochemical and Natural Gas Industries–Com-posit Repairs of Pipework–Qualification and Design, Installation, Testing and Inspection; ISO: Geneva, Switzerland, 2006. [Google Scholar]
- Malcolm, J. To replace or to wrap the standardization of composite repair. Reinf. Plast. 2009, 53, 42–44. [Google Scholar] [CrossRef]
- Seica, M.V.; Packer, J.A. FRP materials for the rehabilitation of tubular steel structures, for underwater applications. Compos. Struct. 2007, 80, 440–450. [Google Scholar] [CrossRef]
- Alexander, C.; Ochoa, O.O. Extending onshore pipeline repair to offshore steel risers with carbon–fiber reinforced composites. Compos. Struct. 2010, 92, 499–507. [Google Scholar] [CrossRef]
- Keller, M.W.; Jellison, B.D.; Ellison, T. Moisture effects on the thermal and creep performance of carbon fiber/epoxy composites for structural pipeline repair. Compos. Part B Eng. 2013, 45, 1173–1180. [Google Scholar] [CrossRef]
- Mally, T.S.; Johnston, A.L.; Chann, M.; Walker, R.H.; Keller, M.W. Performance of a carbon-fiber/epoxy composite for the underwater repair of pressure equipment. Compos. Struct. 2013, 100, 542–547. [Google Scholar] [CrossRef]
- Shamsuddoha, M.; Islam, M.; Aravinthan, T.; Manalo, A.; Lau, K.T. Effectiveness of using fibre-reinforced polymer composites for underwater steel pipeline repairs. Compos. Struct. 2013, 100, 40–54. [Google Scholar] [CrossRef]
- Da Costa Mattos, H.S.; Reis, J.M.; Paim, L.M.; Da Silva, M.L.; Amorim, F.C.; Perrut, V.A. Analysis of a glass fibre reinforced polyurethane composite repair system for corroded pipelines at elevated temperatures. Compos. Struct. 2014, 114, 117–123. [Google Scholar] [CrossRef]
- Rohem, N.; Pacheco, L.; Budhe, S.; Banea, M.D.; Sampaio, E.; de Barros, S. Development and qualification of a new polymeric matrix laminated composite for pipe repair. Compos. Struct. 2016, 152, 737–745. [Google Scholar] [CrossRef]
- Shamsuddoha; Islam, M.; Aravinthan, T.; Manalo, A.; Djukic, L.P. Effect of hygrothermal conditioning on the mechanical and thermal properties of epoxy grouts for offshore pipeline rehabilitation. AIMS Mater. Sci. 2016, 3, 832–850. [Google Scholar] [CrossRef]
- Freire, J.L.F.; Vieira, R.D.; Diniz, J.L.C.; Meniconi, L.C. Part 7: Effectiveness of composite repairs applied to damaged pipeline. Exp. Tech. 2007, 31, 59–66. [Google Scholar] [CrossRef]
- Duell, J.; Wilson, J.; Kessler, M. Analysis of a carbon composite overwrap pipeline repair system. Int. J. Press. Vessel. Pip. 2008, 85, 782–788. [Google Scholar] [CrossRef]
- Saeed, N.; Ronagh, H.; Virk, A. Composite repair of pipelines, considering the effect of live pressure-analytical and numerical models with respect to ISO/TS 24817 and ASME PCC-2. Compos. Part B Eng. 2014, 58, 605–610. [Google Scholar] [CrossRef]
- Budhe, S.; Banea, M.; Rohem, N.; Sampaio, E.; de Barros, S.; Budhe, S.; Banea, M.; Rohem, N.; Sampaio, E.; de Barros, S. Failure pressure analysis of composite repair system for wall loss defect of metallic pipelines. Compos. Struct. 2017, 176, 1013–1019. [Google Scholar] [CrossRef]
- Da Costa Mattos, H.S.; Reis, J.M.; Paim, L.M.; Da Silva, M.L.; Junior, R.L.; Perrut, V.A. Failure analysis of corroded pipelines reinforced with composite repair systems. Eng. Fail. Anal. 2016, 59, 223–236. [Google Scholar] [CrossRef]
- Shamsuddoha; Manalo, A.; Aravinthan, T.; Islam, M.; Djukic, L. Failure analysis and design of grouted fibre-composite repair system for corroded steel pipes. Eng. Fail. Anal. 2021, 119, 104979. [Google Scholar] [CrossRef]
- Mazurkiewicz, Ł.; Tomaszewski, M.; Małachowski, J.; Sybilski, K.; Chebakov, M.; Witek, M.; Yukhymets, P.; Dmitrienko, R. Experi-mental and numericalstudy of steel pipe with part-walldefectreinforcedwith fibre glass sleeve. Int. J. Press. Vessel. Pip. 2017, 149, 108–119. [Google Scholar] [CrossRef]
- Mazurkiewicz, Ł.; Małachowski, J.; Tomaszewski, M.; Baranowski, P.; Yukhymets, P. Performance of steel pipe reinforced with composite sleave. Compos. Struct. 2018, 183, 199–211. [Google Scholar] [CrossRef]
- ASME B31.8. Gas Transmission and Distribution Piping Systems; ASME International: New York, NY, USA, 2018. [Google Scholar]
- ASME B31G. Manual for Determining the Remaining Strength of Corroded Pipelines; ASME International: New York, NY, USA, 2012. [Google Scholar]
- Abdelghani, M.; Tewfik, G.; Djahida, D.; Ahmed, S.S.; Djouadi, D. Prediction of the Rupture Pressure of Transmission Pipelines with Corrosion Defects. J. Press. Vessel. Technol. 2018, 140, 041701. [Google Scholar] [CrossRef]
- Abdelghani, M.; Tewfik, G.; Djahida, D. Determination of Limit Load Solution for the Remaining Load-Carrying Capacity of Corroded Pipelines. J. Press. Vessel. Technol. 2016, 138, 051701. [Google Scholar] [CrossRef]
- Daniel, I.M.; Ishai, O.; Daniel, I.M.; Daniel, I. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]






| Reference | [18] | [23] |
| Steel grade | A106 Gr B | GOST 8731-74 |
| External diameter (mm) | 152.3 | 220 |
| Pipe wall thickness (mm) | 7.11 | 6.0 |
| Yield stress (MPa) | 300 (0.2% offset) | 305 (0.2% offset) |
| SMYS (MPa) | 241.3 | 241.3 |
| Poisson’s ratio | 0.30 | 0.30 |
| Hollomon true model |
| Reference | [18] | [23] |
| Polymer-based laminate | Carbon fiber/epoxy | Glass fiber/epoxy |
| Modulus in the hoop direction (MPa) | 49,000 | 48,470 |
| Modulus in the axial direction (MPa) | 23,400 | 6770 |
| Modulus in the radial direction (MPa) | 5500 | 6770 |
| Poisson’s ratio | 0.45 | 0.4 |
| Poisson’s ratio | 0.07 | 0.099 |
| Poisson’s ratio | 0.45 | 0.099 |
| Shear modulus (MPa) | 690 | 1670 |
| Shear modulus (MPa) | 2960 | 3200 |
| Shear modulus (MPa) | 690 | 3200 |
| Failure stress in hoop direction (MPa) | 576 | 678 |
| Composite thickness (mm) | 3.1 | 6 |
| Filler Material | ||
| Young’s Modulus (MPa) | 1740 | 3300 |
| Poisson’s ratio | 0.45 | 0.37 |
| Defect Type Length (mm) × Width (mm) | Flaw Depth d/t (%) | Burst Pressure, MPa (Unrepaired) | EXP Burst Pressure, MPa (Repaired) | FEA Burst Pressure, MPa (Repaired) | ANA Burst Pressure, MPa (Repaired) | Reference |
|---|---|---|---|---|---|---|
| Intact steel pipe (Unflawed) | 0% | 45.85 | N/A | N/A | N/A | [18] |
| Axisymmetric | 50% | 29.99 | 43.80 | 43.29 | 44.15 | |
| 152.4 × 152.4 | 50% | 30.34 | 43.10 | N/A | 44.15 | |
| Intact steel pipe (Unflawed) | 0% | 27.59 | N/A | N/A | N/A | [23] |
| 133 × 102 | 60% | 13.8 | 29.06 | 28.32 | 46.4 |
| Polymer-Based Laminate | |
|---|---|
| Modulus in the hoop direction (MPa) | 23,800 |
| Modulus in the axial direction (MPa) | 24,500 |
| Modulus in the radial direction (MPa) | 11,600 |
| Poisson’s ratio | 0.071 |
| Poisson’s ratio | 0.107 |
| Poisson’s ratio | 0.1 |
| Shear modulus (MPa) | 2600 |
| Shear modulus (MPa) | 4700 |
| Shear modulus (MPa) | 3600 |
| Laminate allowable strain (mm/mm) | 0.003 |
| Filler Material | |
| Young’s Modulus (MPa) | 1.740 |
| Poisson’s ratio | 0.45 |
| Pd [MPa] (Equation (49)) | |||||||
|---|---|---|---|---|---|---|---|
| ASME PCC-2 (S = SMYS) | ISO/TS24817 (S = 0.72 SMYS) | ||||||
| 14.68 (Pressure to be recovered) | 10 | 1.86 | 0 | 1.73 | 0 | 0 | 0 |
| 15 | 1.79 | 0 | 2.60 | 0 | 0 | 0 | |
| 20 | 1.73 | 0 | 3.46 | 0 | 0 | 0 | |
| 25 | 1.66 | 0 | 4.33 | 0 | 0 | 0 | |
| 30 | 1.59 | 0.48 | 5.19 | 0 | 0 | 0 | |
| 35 | 1.52 | 1.68 | 6.06 | 0 | 0 | 0 | |
| 40 | 1.45 | 2.88 | 6.92 | 0 | 0 | 0 | |
| 45 | 1.37 | 4.08 | 7.79 | 0 | 0 | 0 | |
| 50 | 1.30 | 5.29 | 8.65 | 0.22 | 0 | 0 | |
| 55 | 1.22 | 6.49 | 9.52 | 1.83 | 0 | 0 | |
| 60 | 1.14 | 7.69 | 10.38 | 3.47 | 0.44 | 0 | |
| 65 | 1.05 | 8.89 | 11.25 | 5.16 | 2.01 | 0 | |
| 70 | 0.97 | 10.09 | 12.11 | 6.89 | 3.61 | 0.67 | |
| 75 | 0.88 | 11.29 | 12.98 | 8.66 | 5.25 | 2.2 | |
| 80 | 0.79 | 12.49 | 13.84 | 10.47 | 6.93 | 3.76 | |
| 85 | 0.69 | 13.70 | 14.71 | 12.34 | 8.65 | 5.36 | |
| 90 | 0.59 | 14.90 | 15.57 | 14.26 | 10.42 | 7.00 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djahida, D.; Tewfik, G.; Witek, M.; Abdelghani, M. Analytical Model and Numerical Analysis of Composite Wrap System Applied to Steel Pipeline. Materials 2021, 14, 6393. https://doi.org/10.3390/ma14216393
Djahida D, Tewfik G, Witek M, Abdelghani M. Analytical Model and Numerical Analysis of Composite Wrap System Applied to Steel Pipeline. Materials. 2021; 14(21):6393. https://doi.org/10.3390/ma14216393
Chicago/Turabian StyleDjahida, Djouadi, Ghomari Tewfik, Maciej Witek, and Mechri Abdelghani. 2021. "Analytical Model and Numerical Analysis of Composite Wrap System Applied to Steel Pipeline" Materials 14, no. 21: 6393. https://doi.org/10.3390/ma14216393
APA StyleDjahida, D., Tewfik, G., Witek, M., & Abdelghani, M. (2021). Analytical Model and Numerical Analysis of Composite Wrap System Applied to Steel Pipeline. Materials, 14(21), 6393. https://doi.org/10.3390/ma14216393






