Abstract
With the aim of decreasing the number of experiments to obtain a perovskite solar cell (PSC) with maximum theoretical efficiency, in this paper, PSC performance was studied using the program solar cell capacitance simulator (SCAPS-1D). The PSC with the architecture ITO/TiO2/perovskite/spiro-MeOTAD/Au was investigated, while the selected perovskite was mixed cation Rb0.05Cs0.1FA0.85PbI3. The analysis was based on an experimentally prepared solar cell with a power conversion efficiency of ~7%. The PSC performance, verified by short-circuit current density (Jsc), open-circuit voltage (Voc), fill factor (FF) and power conversion efficiency (PCE), was studied by optimization of the simulation parameters responsible for improvement of the cell operation. The optimized parameters were absorber layer thickness, doping, defect concentration and the influence of the resistivity (the net effect of ohmic loss, Rs and the leakage current loss represented by the resistivity, Rshunt). The results of SCAPS-1D simulations estimated the theoretical power conversion efficiency of 15% for our material. We have showed that the main contribution to improvement of solar cell efficiency comes with lowering ohmic resistivity of the cell as well as doping and defect concentration, because their concentration is proportional to recombination rate.
1. Introduction
Since their discovery in 2009 [1,2,3], perovskite solar cells (PSCs) have drawn great attention. Besides their low-cost solution processing, PSCs also possess favourable optoelectronic properties including a high absorption coefficient in the visible part of solar spectrum [4], low recombination rate [5], high mobility of charge carriers [6] and a tuneable bandgap [7]. In the past decade, their power conversion efficiency (PCE) has been significantly enhanced from 3.8% in 2009 [1] to more than 25% in single-junction architectures and more than 29% in silicon-based tandem cells [8,9,10]. The enhancement of the PCE, one of the key factors of solar cells, defines PSCs as the promising candidates for commercialization in the solar cell industry. Furthermore, many efforts have been made to develop advanced structures of perovskites [11] for applications in photolysis, photodetectors [12] and various type of solar cells such as flexible cells [13], carbon-electrode-based cells [14], semi-transparent cells [15], tandem cells [16], integrated cells [17], switchable cells [18], and single crystal cells [19]. Perovskite solar cells are photovoltaics with solution processed active layer, one of several recently studied technology. The other broadly investigated photovoltaics with solution processed active layer, include photovoltaics based on the organic semiconductors as active layers [20,21,22]. All of these PSC devices are supposed to have high power efficiency, high stability, and large-scale applicability. However, there are still several issues in practical operations of PSCs, such as the long-term instability due to the perovskite degradation (moisture, UV light, overheating) [11,23,24], the toxicity of the most commonly used compounds [25], and the current-voltage hysteresis in devices [26]. In order to solve these obstacles, many methods have been used, such as doping ions in perovskite materials, charge transporting layer modification, modification of microstructure, and utilizing advanced fabrication techniques [11].
The mostly used perovskite materials are methylammonium lead triiodide (MAPbI3) and formamidinium lead triiodide (FAPbI3), and their use as the absorber layer in PSCs has been extensively studied [27,28]. The results have shown that FAPbI3 is thermally more stable, which makes it the most promising perovskite material for single-junction PSCs. Recently, rubidium and cesium cation (Rb+ and Cs+) incorporation emerged as a strategy to enhance PSCs efficiency [29].
In conjunction with the perovskite materials as the photoactive absorber layer, other thin film materials are used to extract photogenerated electrons and holes, reducing charge recombination inside the absorber layer and improving the overall efficiency of the solar cell. Indeed, such layers have their energy band levels aligned in a way which creates a potential difference that drives the charge separation. For the charge separation of electrons, the material has to have lower conduction band (CB) maximum and valence band (VB) minimum energy levels than those of the absorber layer in order to promote electron extraction and block hole extraction from the active layer. These materials are called electron transport layer (ETLs) and most commonly used are TiO2, ZnO and SnO2 [30]. Analogous to ETLs, materials which have higher CB maximum and VB minimum energy levels in comparison to those levels of the absorber layer, promote hole extraction and block electron extraction. These layers are called hole transport layers (HTLs) and the most popular are spiro-OMeTAD, P3HT, PTTA and PEDOT:PPS organic semiconductors [31].
Since the main aim of numerous experimental studies is increase of the device PCE, it is worth theoretically studying the influence of the specific parameters on the performance of the PSC by applying an appropriate model. In this work, we have employed one dimensional theoretical model of solar cell integrated in the solar cell capacitance simulator (SCAPS-1D) [32] in order to elucidate which experimental procedure could improve the PSC parameters. The parameters that we varied by SCAPS-1D simulation and that can be influenced experimentally are: (1) acceptor doping concentration (NA) of the perovskite absorber layer, (2) defect density in the perovskite absorber layer, (3) the thickness of the perovskite absorption layer, (4) resistivity Rs (the net effect of ohmic loss) and Rshunt (the leakage current loss).
The first mentioned parameter, which can be influenced experimentally, is doping concentration NA. There are several studies which attempted to investigate how to influence the charge carrier concentration during the synthesis of the perovskite thin films. Shi and co-workers [33] investigated the influence of precursor concertation and solvent choice in a two-step deposition method of the absorber layer. They reported that the carrier density and the depletion field decrease with the increase of the concentration of CH3NH3PbI3 immersion solution (CH3NH3I dissolved in isopropanol), and also showed that the inclusion of a polar solvent improved the charge collection by influencing the reaction kinetics for the formation of the perovskite films. Bi et al. [34] investigated the role of the length of thermal annealing and show that the extended annealing time improved the crystallinity and grain size of the perovskite crystals, but also led to the reduction of hole concentration. While improved crystallinity led to better FF and Jsc values, ultraviolet photoelectron spectroscopy studies confirmed the reduction of the work function with increased the annealing time. Several authors also reported the effects of adding the cations or the anions in the perovskite active layer and its impact on carrier concentrations. Liu and co-workers [35] introduced rubidium cations into the perovskite film. While the crystal structure remained the same, the quality of the film worsened, reducing the efficiency of the device. However, rubidium cations made the majority carrier type of the perovskite layer into p-type, and previously formed pn junction between the active layer and the spiro-MeOTAD layer was replaced with a new pn junction between the active layer and TiO2. The influence of the anion composition was investigated by Kiermasch et al. [36], who doped the MAPbI3 perovskite with bromine anions and concluded that bromine’s addition did not influence the carrier concentration, but instead increased carrier lifetime. They hypothesize that the origin of the enhancement lies in the increase in shallow traps close to the conduction or valence band. These states partially trap charge carriers which can then be released back into the band before they recombine, leading to the increase of the Voc while Jsc and FF both decreased.
Second parameter, density of defects, are mainly influenced by the nature of the crystallization of the perovskite thin film. The origin of the defects resides on the grain boundaries of the polycrystalline films as well as dangling bonds, uncoordinated atoms and surface dislocation on the film surface. Influencing the crystallization process, the amount of defect densities that occur in perovskite thin films can be altered. Tan et al. [37] employed an additional post annealing treatment of the methylammonium chloride perovskite films. Those films changed their microstructural orientation from the randomly oriented to the preferred (110) crystal plane growth, made possible by exploiting the chlorine intermediate phase analogous to the mineral bridge phenomenon in the oriented attachment mechanism. FF, Jsc and Voc were improved as a result of lowered trap state densities with regards to oriented crystal growth [38]; indeed, another way to impact the crystallization mechanism is through additive engineering. Yang and associates [39] used the ammonium benzenesulfonate as an active layer additive; its zwitterionic structure passivated both cationic and anionic defects at the grain boundaries, which influenced both the carrier lifetime and the power efficiency of the formed solar cells. Alongside zwitterion molecules, polymers can be also used for the defect passivation. Kojić et al. [40] investigated the influence of polyvinylpyrrolidone as an additive and reported an increase in radiative recombination with smaller Urbach energy values as a consequence of carbonyl interactions with the Pb2+ dangling bonds. Inorganic cations can also improve the amount of the trap states, and Ng et al. [41] confirmed this with the inclusion of germanium cations in a quasi 2D/3D perovskite. The thermally stimulated currents with the addition of Ge2+ impacted the trap states close to the valence or conduction bands, so perovskite had fewer available states for the electrons to occupy.
A third simulated parameter, the influence of the absorber layer thickness on the cell performance, is studied experimentally by several authors. Rai et al. [42] developed an array of perovskite solar cell devices by varying the active layer thickness with the precursor concentration. In their results, the solar cell efficiency increased with the increase of the perovskite thickness primarily as a result of higher Jsc values. This is attributed to the reduction of non-radiative decay channels with the increased thickness, and they conclude that thinner absorber layers lead to insufficient photo-generation and increased SRH recombination. Xiao et al. [43] also varied the perovskite thickness with the precursor concentration, reporting maximum Jsc values for the perovskite thickness of 630 nm. Moreover, they explained that increasing the thickness results in higher current densities as a result of the higher absorption, supported by the external quantum efficiency measurements in the 550–800 nm region. However, increasing the thickness increases the amount of the grain boundaries inside the film, creating charge recombination traps. The authors showed that, by employing a solvent annealing step after the perovskite crystal annealing, it was possible to control the grain size of the film, synthesizing micron thick films with high device efficiency by reducing the amount of grain boundaries.
Furthermore, we investigated the influence of two types of resistance that limit solar cell performance: the net effect of ohmic loss, Rs, and the leakage current loss, Rshunt. Low Rs and high Rshunt are preferred in order to have highly efficient solar cells. The most common contributors to series resistance, Rs, are metal-semiconductor contacts of the solar cells. As the perovskite/hole transport layer/metal contacts are most prone to synthesis variability, influencing their chemical nature and interface can vastly reduce series resistance. The mostly used hole transport layer is the organic material spiro-MeOTAD. Ways to improve the performance of its conductive nature via additives such as tris(2-(1Hpyrazol-1-yl)-4-tert-butylpyridine)cobalt(III) tri[bis-(trifluoromethane)sulfonimide], bis-(trifluoromethane)sulfonimide lithium salt and/or 4-tertbutylpyridine are well established [44]. Rong et al. [45] report the addition of ditetrabutylammonium dichromate in the spiro-MeOTAD hole transport layer by using the four-probe measurements, and found an optimal amount of dichromate addition, which can influence pinhole formation, demonstrates better hole extraction properties and a smaller series resistance compared to the control devices. Guarnera et al. [46] investigated the role of an inorganic Al2O3 buffer layer between the active layer and the spiro- MeOTAD hole transport layer. In their investigation, they have found that the Voc and the Jsc are similar between the control cells and the buffer layer cells. The most pronounced impact is shown in the FF values, with an increase of 25% for cells with the buffer layer. The Al2O3 buffer layer not only inhibited the formation of a direct contact between the perovskite and the metal contact but showed no degradation during the first 350 h under the full solar illumination. In their investigation of carbon contacts for perovskite solar cells, Babu and co-workers [47] have reported that the use of a thin chromium interlayer between the hole transport layer and the metal (carbon) contact with the thickness of 5 nm provided high shunt resistance and no significant series resistance due to its high ductility. Mundhass et al. [48] have studied the series resistance of the perovskite solar cells using Jsc-Voc measurements; in their report, they found that for multi-cation perovskites, the direction of the current sweep (e.g., positive–negative) can impact the value of the series resistance, whereas the series resistance for mono-cation perovskites are independent on the direction of the current sweep. This gives information on how the composition of the perovskite layer can influence the values of the series resistance. In the same paper, they investigated the impact of PTAA hole transport layer thickness on the series resistance and found that the increase of the PTAA thickness reduces the values of FF, requiring optimal synthetic approach for a film thin enough to have an optimal FF but thick enough not to have pinholes, which can contribute towards shunt resistance. Conversely, there are approaches to film surface interactions by forming interlayers; Veeramutuhu and co-workers [49] used polyvinylpyrrolidone as an interlayer between the perovskite and the hole transport layer, which led to the increase in carrier lifetime with significant reduction of the surface roughness of the perovskite. Hemasiri et al. [50] reported similar results with the utilization of a MoS2 interlayer between the perovskite and the hole transport layer; the MoS2 interlayer was shown to facilitate the extraction of the photogenerated carriers, mitigating interfacial charge recombination.
A major contribution to low Rshunt are the formation of pinholes and film porosity, and thus several experimental approaches to increase its value are reported in the literature. Brecker and Wark [51] studied the impact of the solvent on the sequential deposition of the perovskite layer. By taking into account solvent permittivity, they have introduced pentan-1-ol into the MAI/isopropanol mixture, which eliminated the pinhole formations in the film and increased the power conversion efficiency by 60%. The usage of a compact TiO2 blocking layer below the mesoporous TiO2 film has found wide usage in the preparation of the perovskite solar cells, as it provides a way of eliminating shunt resistance issues in combination with the mesoporous TiO2. Singh et al. [52] investigated how the thickness of the compact layer impacts the performance of the solar cells; they report an optimal thickness of ~57 nm in order to reduce shunt losses as well as trap-assisted recombination and bimolecular recombination, which become more pronounced with increased compact layer thickness. Hörantner et al. [53] have shown that long alkyl chained silane molecules can be used to block shunt pathways without obstructing the charge transfer of the solar cell devices, leading to the significant increase in the Voc values, while other inorganic materials can also be used as passivation materials. Saranin et al. [54] report the use of copper (I) iodide, which has been usually applied as a hole transport layer, as an interlayer between the perovskite and the electron transport layer in their experiments; the inclusion of CuI increased the efficiency of the solar cell as well as their shelf-life stability.
In this work, our intention was to simulate an average perovskite solar cell and use simulation to point out which parameters could be influenced to increase the power conversion efficiency of the device. As a starting point we have synthesized the mixed cation lead triiodide perovskite containing formamidinium, Rb+ and Cs+ ions (Rb0.05Cs0.1FA0.85PbI3) and applied it as an absorber layer in PSC devices with the architecture ITO/TiO2/perovskite/spiro-MeOTAD/Au. The obtained PCE was around 7%. In order to find routes to increase the PCE of the device, we have attempted to simulate the perovskite solar cell by using solar cell capacitance simulator (SCAPS) under standard AM1.5G illumination as a way to understand which parameters can affect its performance and what is the highest PCE is that we can theoretically achieve. We used a simulation model to optimize the following parameters influencing the PSC performance: acceptor doping concentrations, defect density, perovskite layer thickness, and resistances: series Rs (net effect of ohmic loss) and parallel Rshunt (the leakage current loss). Moreover, the influence of the interface between layers on PSC performance was discussed in detail.
The main insight of the simulation, showing new input for further optimization of the solar cell efficiency, was finding that the strongest impact on the device performance comes through resistivity of the layers. The negative impact of the resistivity on PSC performances could be improved by influencing layers’ structure quality. Therefore, lowering the density of the defects in layers and interlayers would lower the recombination rate in solar cells.
2. Materials and Methods
2.1. Materials Used for Preparation of Perovskite Solar Cells
For the synthesis of the Rb0.05Cs0.1FA0.85PbI3 perovskite, the following materials were used: lead (II) iodide (Sigma-Aldrich, 99%, St. Louis, MO, USA), formamidinium iodide (FAI) (Sigma-Aldrich, ≥99%, St. Louis, MO, USA), cesium iodide (Sigma-Aldrich, ≥99%, St. Louis, MO, USA), rubidium iodide (Sigma-Aldrich, ≥99%, St. Louis, MO, USA), N,N-dimethylformamide (DMF) (Merck, p.a., Darmstadt, Germany), dimethyl sulfoxide (DMSO) (Merck, p.a., Darmstadt, Germany), chlorobenzene (Merck, p.a., Darmstadt, Germany).
15 × 15 mm indium tin oxide (ITO) coated glass plates (Lumtech, ρ ~15 Ω/sq, CA, USA) were used as substrate and transparent front electrode. For the synthesis of the TiO2 ETL titanium diisopropoxide (Sigma-Aldrich, 99%, St. Louis, MO, USA), acetylacetonate (Sigma-Aldrich, 99%, St. Louis, MO, USA) and ethanol (Merck, p.a., Darmstadt, Germany) were used. For the preparation of the spiro-OMeTAD HTL, spiro-OMeTAD (Merck, ≥99%, Darmstadt, Germany), 4-tert-butylpyridine (tBP) (Sigma-Aldrich, 99%, St. Louis, MO, USA), FK209 (Sigma-Aldrich, 99%, St. Louis, MO, USA), bis-(trifluoromethane)sulfonimide lithium salt (LiTFSI) (Sigma-Aldrich, 99%, St. Louis, MO, USA) and acetonitrile (Merck, p.a., Darmstadt, Germany) were used.
2.2. Preparation and Characterization of Perovskite Solar Cells
In order to prepare the TiO2 ETL, 400 μL of acetylacetonate and 600 μL of titanium diisopropoxide were dissolved in 9 mL of ethanol. 50 μL of the prepared solution was spin coated on ITO glass substrates (4000 rpm, 2000 rpm/s) for 30 s and annealed at 450 °C for 2 h.
To prepare the perovskite thin films 461 mg of PbI2, 172 mg of FAI, 26 mg of CsI and 106 mg of RbI were dissolved in 1 mL of DMF/DMSO mixture (V(DMF):V(DMSO) = 4:1). Perovskite films were prepared inside a nitrogen-filled glovebox by spin coating 50 µL of the perovskite precursor on TiO2 substrates. The spin coating parameters were: 1000 rpm, 200 rpm/s for 10 s and 6000 rpm, 2000 rpm/s for 20 s. During the last 10 s, 50 µL of chlorobenzene was dripped onto the rotating substrate to improve the nucleation and crystal growth of the film. As prepared substrates were annealed on a hotplate at 150 °C for 10 min.
The spiro-OMeTAD was prepared by dissolving 50 mg of spiro-OMeTAD in 498 μL of chlorobenzene and adding 18 μL of tBP, 10 μL of LiTFSI stock solution and 4 μL of FK209 stock solution. The stock solutions of LiTFSI and FK209 were 1.8 mmol/mL and 0.25 mmol/mL in acetonitrile, respectively. Then 50 µL of the spiro-OMeTAD solution was spin coated on the perovskite/TiO2 substrate (4000 rpm, 1000 rpm/s) for 10 s. Before the gold depositions, the substrates were left resting overnight in dark and dry air. The final step included the deposition of 100 nm of gold contacts on the substrates.
Scanning electron microscopy image of prepared PSC was recorded using field emission scanning electron microscope (FE-SEM) model JSM-7000F manufactured by JEOL Ltd., Tokyo, Japan, using an accelerating voltage of 10 kV, equipped with an energy-dispersive X-ray spectrometer (EDS), EDS/INCA 350 (energy-dispersive X-ray analyser) manufactured by Oxford Instruments Ltd., Abingdon, UK.
The current density–voltage (J–V) curves of the solar cells were performed using a Keithley 2400 source meter and a LabView-based software inside a glove box (nitrogen atmosphere). For the J–V curves, the scan rates were adjusted to 100 mVs−1. The illumination area was defined using a shadow mask (0.07 cm2) and the light was provided by a Dedolight DLH500 lamp calibrated to an intensity of 100 mWcm−2 using a reference silicon solar cell (Fraunhofer ISE). The external quantum efficiency (EQE) spectrum was measured using a MuLTImode 4 monochromator (Amko) equipped with a 75 W xenon lamp and a Keithley 2400 source meter. The monochromatic light was chopped at a frequency of 30 Hz and the measurement setup was spectrally calibrated with a silicon photodiode (Newport Corporation, Irvine, CA, USA, 818-UV/DB). UV–Vis measurements of the perovskite absorber layer were performed using the UV/VIS Spectrometer—Lambda 35 by Perkin Elmer.
2.3. Numerical Simulation
Simulation of the solar cell was obtained by using SCAPS-1D software (solar cell capacitance simulator one dimension) which numerically solves one dimensional Poisson and continuity equations that govern the semiconductor material under the steady-state conditions [32]. Poisson equation presents the relationship between the electric field of a p-n junction (E) and the space charge density (ρ) and is given by:
where ψ is the electrostatic potential, q is the elementary charge, εs is the static relative permittivity of the medium, n, p are the electron and hole densities, are the densities of ionized donors and acceptors and Nt is possible defect (acceptor or donor) density [55]. The electron and hole continuity equations in steady-state are given by:
where jn, jp are the electron and hole current densities, G is the electron-hole pair generation rate, and Rn, Rp are the net recombination rates of electrons and holes. The electron and hole current densities are given by:
where q is the elementary charge, µn, µp are the electron and hole mobility and Dn, Dp are the diffusion coefficients of the electrons and holes. SCAPS-1D software can simulate solar cell structures up to seven layers and extract their basic characteristics, such as the band diagram, the generation and recombination rates, the external quantum efficiency, the cell current densities, the J–V characteristic with short-circuit current, open-circuit voltage, fill factor and power conversion efficiency. For SCAPS simulation, the input parameters are listed in Table 1.

Table 1.
Perovskite solar cell input parameters.
3. Results and Discussion
In the first step of our study, we have simulated the current density–voltage (J–V) characteristic and cell performance parameters to obtain a good fit with the J–V characteristic measured for our experimentally prepared PSC (Figure 1).
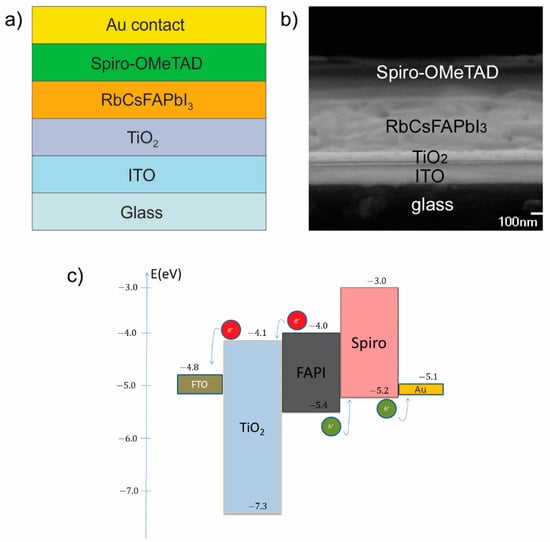
Figure 1.
(a) The Rb0.05Cs0.1FA0.85PbI3 perovskite solar cell layer structure, (b) SEM image of layers in our PSC (without gold contact) and (c) PSC band diagram.
The layer structure of the prepared perovskite solar cell (Rb0.05Cs0.1FA0.85PbI3) is illustrated in Figure 1a, its cross-sectional SEM image is shown in Figure 1b, while the energy band diagram is shown in Figure 1c. The energy band diagram (Figure 1c) shows good matching of ETL and HTL with the absorption layer and allows a smooth flow of charge through the cell.
With the aim of increasing the PCE of our device, we have studied the influence of the specific parameters on performance of the PSC in order to elucidate which experimental procedure could improve the PSC parameters.
Experimental J–V curve was obtained in a two-wire configuration with a Keithley 2400, under 100 mW/cm2 illumination. Following, the simulation has been run with the input parameters of the structure summarized in Table 1. They are based on previously published literature [56,57,58,59,60,61] and our experimental results.
Using above-mentioned initial parameters concerning the J–V characteristic, simulation results gave the following solar cell performance parameters, which are listed and compared to experimentally obtained data in Table 2.

Table 2.
Experimental and simulated parameters of the PSC: short-circuit current density (Jsc), open-circuit voltage (Voc), fill factor (FF) and power conversion efficiency (PCE).
Figure 2 shows a comparison between the simulation results and the experiment. A good match between measurements and simulation was observed for the current density/voltage characteristics validating our simulation.
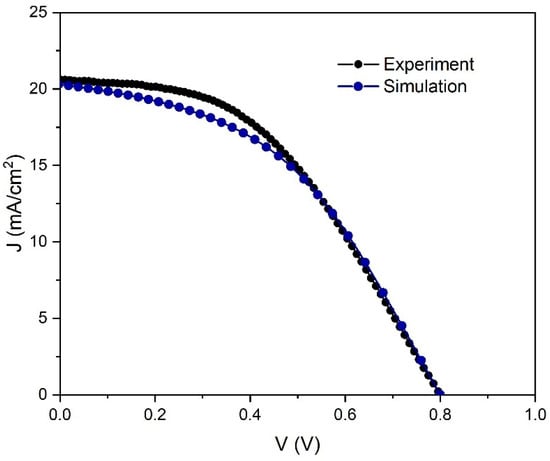
Figure 2.
Current density–voltage characteristics under illumination of the experimental and simulated PSC.
The external quantum efficiency (EQE) spectrum (experiment and simulation), along with the absorbance spectra of the perovskite film, are illustrated in Figure 3. For the simulation of the EQE spectra, the absorption coefficient was calculated from the absorbance spectra. Both EQE curves show the optical absorption edge of the PSC that starts at 800 nm, with the disparity in the lower wavelength region (Figure 3a). Higher experimental values of quantum efficiency on lower wavelength regions are in agreement with the rise in absorbance in the same region (Figure 3b). However, as the mechanism of this experimentally observed behavior is unclear, except for a gradual increase in the EQE values, the simulated spectra could not completely fit the experimental data.
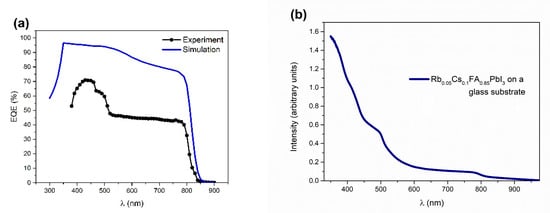
Figure 3.
(a) EQE (%) spectrum as a result of the simulation with input parameters from Table 1. and (b) Absorbance spectra for the Rb0.05Cs0.1FA0.85PbI3 perovskite on a glass substrate.
3.1. Doping Concentration Impact of Perovskite Active Layers on PSC Performance
In order to study how the concentration of NA of the perovskite thin film impacts the performances of the solar cell, we have investigated NA values in the range from 1013 cm−3 to 5·1017 cm−3 in the simulation. The rest of the parameters were fixed to values indicated in Table 1. Figure 4 shows the behavior of the PSC parameters with the change of NA.
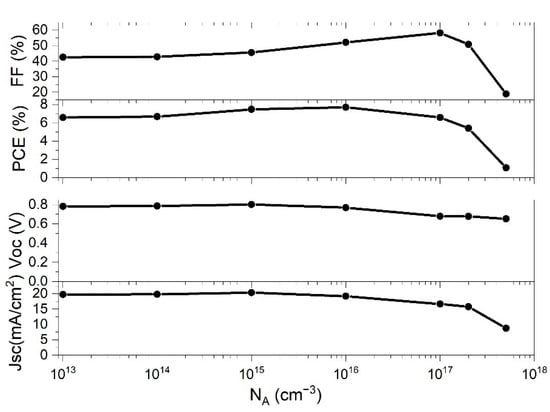
Figure 4.
Effect of changing doping concentration (NA) of absorber layer on PSC parameters.
The FF slowly raised with the enhancement of NA, and then rapidly decreased after NA went beyond 1017 cm−3. PCE exhibited similar behavior, having a maximum value at NA = 1016 cm−3, and then rapidly decreased. The other two parameters, Jsc and Voc are also influenced by the change of NA, both of which have their local maximum at ~1015 cm−3. At higher NA concentrations, Voc decreased slowly, while Jsc decreased very rapidly after NA exceeded 1017 cm−3. The difference of the cell performance in respect to the NA can be explained by the rise of the built-in electric field with the increased concentration of the NA [16,24]. Charge carriers separation is more pronounced with an increased electric field and consequently improves the performance of the cell. However, even larger values of NA will lead to higher Auger recombination rates and subsequently PSC parameters will decrease [62]. As it can be seen in Figure 5, the recombination rate, R, is increased notably, starting with NA values of 1016 cm−3, which is in good correlation with PSC parameters presented in Figure 4.
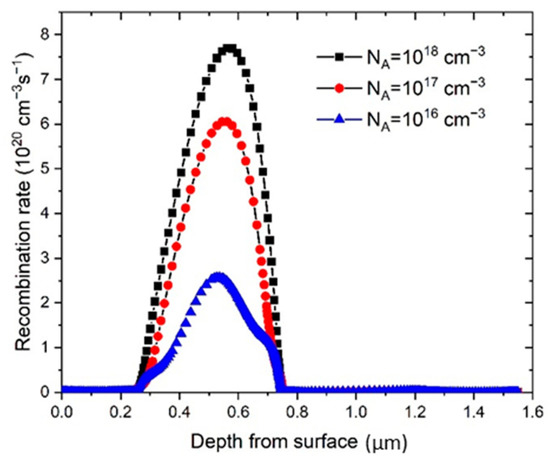
Figure 5.
Change of recombination rate with NA of the perovskite. Zero depth value corresponds to the substrate (ITO surface).
Therefore, only a range of NA values can contribute to the improvement of Jsc and Voc and the increase the PCE value. The deposited perovskite films optimally have low charge carrier concentration in order to maximize the carrier mobility inside the perovskite thin film. At the NA values of 1016 cm−3, the maximum PCE of 7.71% was obtained, while the other parameters of PSC for that NA concentration were Voc = 0.77 V, Jsc = 19.23 mA and FF = 52.07% (see Figure 4). The result of the simulation shows that our starting value for NA, from the parameter set which optimally represents the experimental data (Table 1), is very close to the optimal value obtained by theoretical modelling (NA = 1016 cm−3).
Generally, doping concentration of the active layer in PSC could be optimized experimentally by changing synthesis precursor concentrations, solvent choice [33], changing the length of thermal annealing [34], or by adding the cations or the anions in the perovskite active layer [35,36], as was stated in detail in the introduction.
3.2. Defect Density Impact on PSC Performance
Regarding the improvement of the PSC performance, the defect density is an additional parameter that should be taken into account. The morphology and film quality of the perovskite have been shown to have an important influence on the performance of the perovskite solar cell [63]. Poor quality and film coverage on mesoporous TiO2 has shown to increase the charge recombination inside the active layer [64], and the recombination is explained by the increase in the defect density (Nt), which can impact the Voc of the solar cell.
The Shockley–Read–Hall recombination model (SRH) was used to study the influence of the perovskite active layer defect density on the cell performance. The neutral defects were set at the center of the band gap following the Gaussian distribution with the characteristic energy value of 0.1 eV, and the characteristic energy of 0.1 eV were set to be at the center of the band gap. In the SRH recombination model, the recombination rate, R, is defined as [65,66]:
where n is the concentrations of the mobile electrons and p is the concentrations of the holes. The concentrations of the charge carriers can be found by solving Poison and continuity equations; at positive voltage values, where qV > 3 kT, the term ni2, which explains the thermal generation, can be neglected. Et is energy level, while Nt is the concentration of the trap defects; τn is the lifetime for the electrons, while τp is the lifetime of the holes. They are given by equations:
where σn is the capture cross-sections of the electrons, σp is the captured cross-sections of the holes, while vth is the thermal velocity.
The carrier diffusion length, l, is is defined by the equation:
where D is the diffusion coefficient with the equation:
where μ is the charge carrier mobility. As Equation (7) indicates, when defect density decreases, the charge carrier lifetimes increase, leading to longer diffusion lengths (Equation (8)) and lower recombinations. These were the main factors influencing the improvement of the cell performance.
Defect density, Nt, was investigated as a parameter in the PSC performance, and the defect density values were changed from 1014 cm−3 to 1018 cm−3. The change in the recombination rate (R) (Equation (6)) is shown in Figure 6. It is clear that the reduction of Nt lowers the recombination rate, and at the same time increases the diffusion length, l.
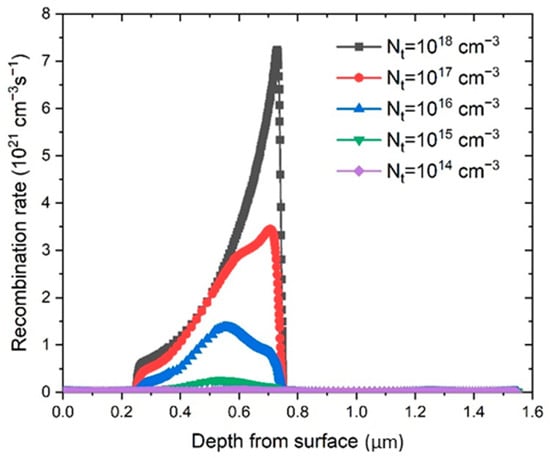
Figure 6.
Recombination rate variance as a function of depth starting from ITO layer surface for different Nt values.
Therefore, the defect density reduction in the perovskite significantly improved the performance of the PSC, which is consistent with the simulation results showed in Figure 7. The obtained simulated J–V characteristics show an improvement of the PSC parameters with the reduction of Nt.
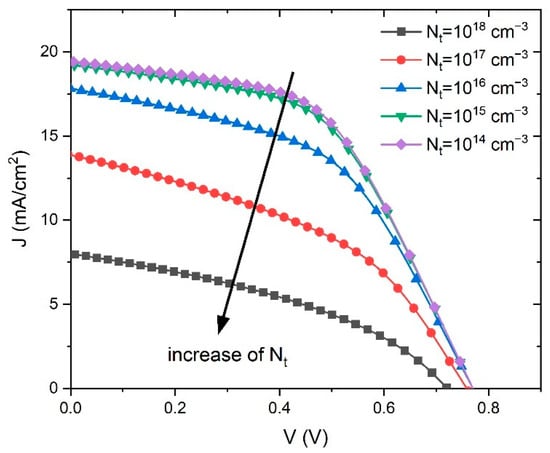
Figure 7.
Current density–voltage curves curves of simulated PSCs as a function of defect density Nt.
The lowest defect density of 1·1014 cm−3 gives the best performance, but obtaining such a low Nt in experiments is very difficult due to the polycrystalline nature of the perovskite films, and thus we set the optimized value of defect density at 1·1015 cm−3. As can be seen from Table 1, that value was also the initial value of Nt, which gave the best fit to the experimental voltage-V curve.
The defects can be interpreted as the faults inside experimentally obtained solar cells due to the grain boundaries or as dangling bonds, uncoordinated atoms, and surface dislocation on the film surface. As was presented in introduction, the defect density can be decreased experimentally by post annealing with the aim to obtain oriented crystal growth [37,38], with additive engineering [39,40], or by the inclusion of cations which impacted the trap states [41].
3.3. Impact of the of the Perovskite Active Layer Thickness on the PCS Performance
Absorbing layer thickness is another parameter that plays a very important role in the performance of thin film solar cells. The influence of the absorber layer thickness on the cell performance with is shown in Figure 8.
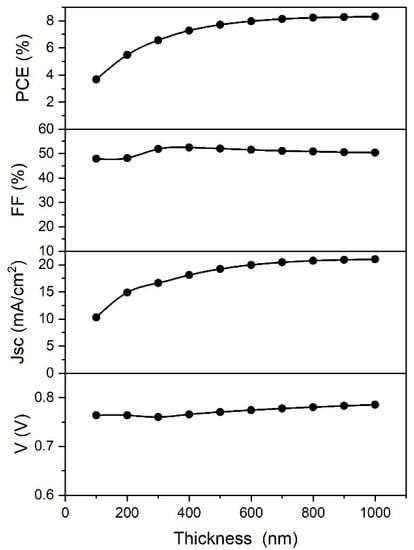
Figure 8.
Variation of PSC parameters with the perovskite layer thickness.
When the thickness is too low, the absorption of the light is also very low, giving lower PCE values. As the thickness of the absorber is increased, the absorption of the light is increased as well, improving the PCE. With the thickness values larger than 800 nm, the PCE of the cell remains invariable. However, an increase in thickness leads to larger recombination rates in the bulk (depending on the diffusion length), saturating the PCE and Jsc values. This is the reason why the PCE shows a similar behavior to the Jsc. The other two parameters, FF and Voc, are not affected significantly by change of the absorber thickness.
Experimentally, the active layer thickness could be varied with the variation of precursor concentration [42,43], as is reported in the introduction.
3.4. Influence of Resistivity Rs and Rshunt on PSC Performance
Under illumination, an ideal solar cell can be represented by a parallel circuit which consists of an ideal diode (D1) and a constant current source of photogenerated current (Jph). The improved equivalent circuit model, so called 2-diode model, is shown in Figure 9 [67,68]. Equivalent circuit for solar cell under dark condition differs only in vanishing photogenerated current source Jph.
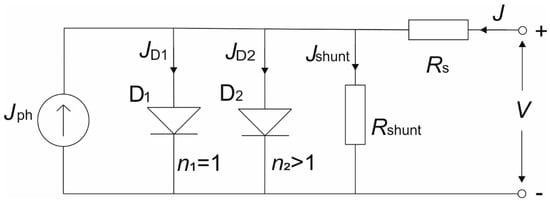
Figure 9.
The equivalent circuit model of solar cell: Jph is photogenerated current, D1 and D2 are ideal and non-ideal diode with ideality factors n1 = 1 and n2 >1 and currents JD1 and JD2, respectively. Rs and Rshunt represent series and parallel resistances with currents J and Jshunt, respectively.
The ideal diode D1 represents the radiative recombination in the solar cell (perovskite layer), while the non-radiative recombination processes are represented by the diode D2. In the equivalent circuit, two resistances are present: series Rs and parallel Rshunt, which have a high impact on solar cell performance, since they govern the shape and slopes of the J–V characteristics. They can be calculated from the slope of the J–V curve at the Voc point (Rs) and at Jsc point (Rshunt). Rs represents the net effect of the ohmic loss and has its origin in the electrical resistance of contacts (ITO and gold in our PSC) and in the electrical dissipation, which is occurring in the layers of PSC (ETL, perovskite and HTL). In contrast, Rshunt represents the leakage current loss induced by defects in the solar cell, such as traps and pinholes. Rs mainly affects the FF and Jsc, while a low Rshunt value results in a photovoltage loss and can affect the collected photocurrent. It is commonly known that a low Rs and high Rshunt are preferred in order to have highly efficient solar cells. The J–V characteristic of the equivalent circuit can be described by the following equation [36]
where J1 and J2 are the saturation current densities of the two diodes, respectively, A is the area of the solar cell, n1 and n2 are the ideality factors of the two diodes.
In order to understand the effect of Rs and Rshunt on the performance of PSCs, the SCAPS model was used with the range of their values 0–50 Ω cm2 and 100–5000 Ω cm2, respectively. The obtained simulation results are given in Figure 10 and Figure 11, and it is clear from the graph in Figure 10 that the Voc is not affected by the change of Rs, while other parameters decreased with the increase in Rs value; indeed, the Jsc decreases slowly from 22 mA cm−2 to less than 15 mA cm−2. The FF value was reduced by half, from 60% to less than 30%, while the PCE decreased from 10% to approximately 3%. It can be observed from the results that PSC parameters are strongly affected by the change of Rs, except the Voc, meaning the best device performance will be for the lowest Rs.
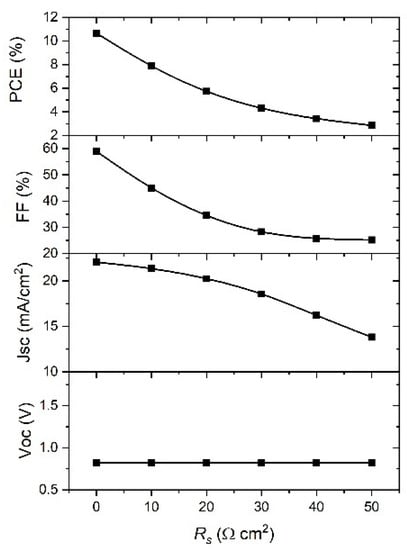
Figure 10.
Effect of Rs on the PSC parameters.
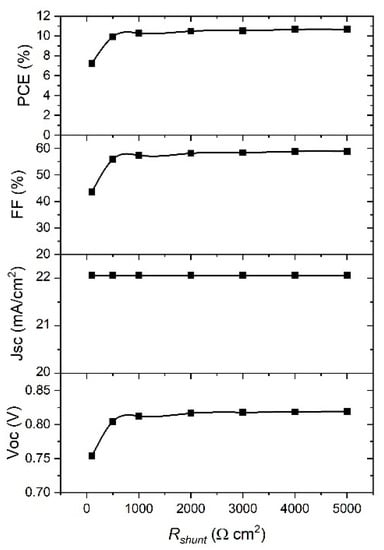
Figure 11.
Effect of Rshunt on the PSC parameters. Rshunt is assumed as infinite in this case.
Considering the dependence of the PSC parameters on Rshunt, Figure 11 clearly shows that Jsc is the parameter that is not affected by Rshunt change. The rest of parameters show a significant increase when Rshunt increased from 100 to 1000 Ω cm−2, and they are saturated for higher values of Rshunt. Therefore, the higher values of Rshunt, the better performance of the device. From the best fit of the experimental J–V curve (Figure 2) we obtained the values for Rs = 9 Ω cm−2 and Rshunt = 1000 Ω cm−2. When we used the ideal values of Rs and Rshunt, and ran a simulation of our device, we achieved a significant improvement in PCE from 7.25% to 10.8%.
There is one more issue in SCAPS model which can significantly affect the performance of the device through Rs and Rshunt, and this is the interface layer between ETL-perovskite and perovskite-HTL. The interface layer is a source of high concentration of defects, which can drastically decrease the device performance. In many studies [56,61], the initial parameter of defect concentration in interface layers is usually set around Nt = 1016–1017 cm−3. We can simulate the reduction in defect concentration and study its influence on performance of the device, and this simulation can be seen in Figure 12.
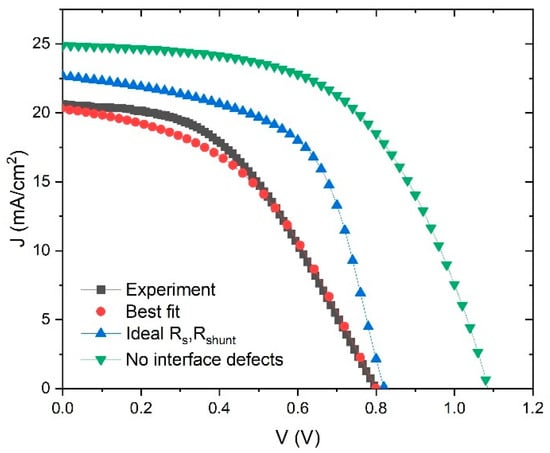
Figure 12.
J–V characteristics: experimental and best fit (Rs = 9 Ω cm−2, Rshunt = Ω cm−2, ideal Rs, Rshunt (Rs = 0 Ω, Rshunt = infinite) and no intefrace defects (removing influence of interface defects with Rs = 0 Ω, Rshunt = infinite).
First, Figure 12 shows the experimental and best fit J–V curves, as in Figure 2. In addition, there is a curve that describes an improvement in device parameters by taking the ideal values of Rs and Rshunt (Voc = 0.82 V, Jsc = 22.7 mA/cm2, FF = 58.2%, PCE = 10.8%). We can improve these parameters even further by taking an ideal structure (no interface defects), but only for academic reasons, to see the theoretical limit of the device performance. In that case, the PSC parameters are: Voc = 1.09 V, Jsc = 24.9 mA/cm2, FF = 56.1% and PCE = 15.17%. This means that, theoretically, our device has enough space to double its PCE from 7.25% to 15%. One way to ensure better performance is to lower resistivity and decrease interface defects by improving structures of the device layers.
Therefore, it is possible to improve the PSC performances experimentally, mainly by influencing Rs and Rshunt. Experimentally, series resistance, Rs, can be decreased by additives in HTL [44,45], by inserting the interlayers in PSCs [46,47,49,50], or by the composition of the perovskite layer [48].
Since low Rshunt is a consequence of pinholes formation and film porosity, it can be increased experimentally by solvents’ additives which eliminate formation of pinholes [51], by the usage of a compact TiO2 blocking layer below the mesoporous TiO2 film [52], or by passivation materials that block shunt pathways [53,54].
4. Conclusions
SCAPS-1D software was used to successfully simulate the J–V characteristics of the experimentally measured perovskite solar cell with an ITO/TiO2/Perovskite/Spiro-MeOTAD/Au structure. The values obtained by modelling (Jsc = 20.29 mA/cm2, Voc = 0.80 V, FF = 44.68% and PCE = 7.25%) were similar to measured values (Jsc = 20.60 mA/cm2, Voc = 0.8 V, FF = 45.51% and PCE = 7.35%).
Acceptor doping concentrations of the perovskite layer were optimized by simulations of the value NA = 1016 cm−3. As a result of the simulation, when the thickness increased above 800 nm, the PCE remained invariable.
It was shown that the Voc is not affected by a change in Rs, while the other parameters decreased with the increase of Rs, so the best device performance will be for the lowest Rs. Regarding the Rshunt, Jsc is not affected by Rshunt change, while the rest of the parameters show a significant increase when Rshunt rose from 100 to 1000 Ω cm2, and they are saturated for higher values of Rshunt.
The reduction of the defect concentration in the interface between layers was also simulated to see its influence on the performance of the device, by taking the ideal values of Rs and Rshunt (no interface defects), so the theoretical limit of the device performance was obtained: Voc = 1.09 V, Jsc = 24.9 mA/cm2, FF = 56.1% and PCE = 15.17%. Therefore, theoretically, our device could double its PCE from 7.25% to 15%.
The results have shown that SCAPS-1D software can be used to adequately simulate non-ideal perovskite solar cells. In this regard, SCAPS can be used as a tool to study potential failure points of obtained perovskite solar cell and as a guide where and how to improve the device performance. Furthermore, the results have shown that, for the PSC experimentally prepared in this work, we can improve PCE mainly by influencing Rs and Rshunt. Taking into account the thermal stability of the material, the Rb0.05Cs0.1FA0.85PbI3 perovskite is a very promising material for further studies.
Author Contributions
Conceptualization, D.S. and V.K.; formal analysis, D.S. and L.B.; funding acquisition, K.J., T.R. and A.G.; investigation, V.K., L.B. and J.M.; supervision, A.G.; validation, T.Č.; visualization, D.S.; writing—original draft, D.S., V.K., K.J. and A.G.; writing—review and editing, D.S., V.K., T.Č., K.J., T.R. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Croatian Science Foundation, grant number HrZZ-IP-2018-01-5246, Center of Excellence for Advanced Materials and Sensing Devices, Ruđer Bošković Institute, Zagreb, Croatia, grant number KK.01.1.1.01.0001, partially supported by European Regional Development Fund (ERDF) under the (IRI) project “Improvement of solar cells and modules through research and development” (KK.01.2.1.01.0115) and Scientific & technological cooperation (WTZ) Austria/Croatia project: “Titanium dioxide nanotube array based perovskite solar cells”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
We acknowledged the support of Gregor Trimmel.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Grätzel, M. The light and shade of perovskite solar cells. Nat. Mater. 2014, 13, 838–842. [Google Scholar] [CrossRef]
- Park, N.-G.; Grätzel, M.; Miyasaka, T.; Zhu, K.; Emery, K. Towards stable and commercially available perovskite solar cells. Nat. Energy 2016, 1, 16152. [Google Scholar] [CrossRef]
- De Wolf, S.; Holovsky, J.; Moon, S.-J.; Loper, P.; Niesen, B.; Ledinsky, M.; Haug, F.-J.; Yum, J.-H.; Ballif, C. Organometallic halide perovskites: Sharp optical absorption edge and its relation to photovoltaic performance. J. Phys. Chem. Lett. 2014, 5, 1035–1039. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, J.; Menelaou, C.; Alcocer, M.J.P.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef] [Green Version]
- Herz, L.M. Charge-carrier mobilities in metal halide perovskites: Fundamental mechanisms and limits. ACS Energy Lett. 2017, 2, 1539–1548. [Google Scholar] [CrossRef]
- Eperon, G.E.; Stranks, S.D.; Menelaou, C.; Johnston, M.B.; Herz, L.M.; Snaith, H.J. Formamidinium lead trihalide: A broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 2014, 7, 982–988. [Google Scholar] [CrossRef]
- NREL. Best Research-Cell Efficiency Chart. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 20 July 2021).
- Kim, G.; Min, H.; Lee, K.S.; Lee, D.Y.; Yoon, S.M.; Seok, S.I. Impact of strain relaxation on performance of α-formamidinium lead iodide perovskite solar cells. Science 2020, 370, 108–112. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, M.; Seo, J.; Lu, H.; Ahlawat, P.; Mishra, A.; Yang, Y.; Hope, M.A.; Eickemeyer, F.T.; Kim, M.; et al. Pseudo-halide anion engineering for α-FAPbI3 perovskite solar cells. Nature 2021, 592, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhao, Y.; Dai, Q. Recent Progress in Perovskite Solar Cell: Fabrication, Efficiency, and Stability. In Development of Solar Cells, Theory and Experiment; Roy, J.K., Kar, S., Leszczynski, J., Eds.; Springer Nature: Basel, Switzerland, 2021; pp. 1–32. [Google Scholar]
- Zuo, C.; Bolink, H.J.; Han, H.; Huang, J.; Cahen, D.; Ding, L. Advances in perovskite solar cells. Adv. Sci. 2016, 3, 1500324. [Google Scholar] [CrossRef]
- Ren, X.; Jung, H.S. Recent progress in flexible perovskite solar cell development. J. Korean Ceram. Soc. 2018, 55, 325–336. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Lin, S. Carbon-electrode based perovskite solar cells: Effect of bulk engineering and interface engineering on the power conversion properties. Sol. RRL 2020, 4, 1900190. [Google Scholar] [CrossRef]
- Shi, B.; Duan, L.; Zhao, Y.; Luo, J.; Zhang, X. Semitransparent perovskite solar cells: From materials and devices to applications. Adv. Mater. 2020, 32, 1806474. [Google Scholar] [CrossRef]
- Eperon, G.E.; Leijtens, T.; Bush, K.A.; Prasanna, R.; Green, T.; Wang, J.T.W.; McMeekin, D.P.; Volonakis, G.; Milot, R.L.; May, R.; et al. Perovskite tandem photovoltaics with optimized bandgaps. Science 2016, 354, 861–865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, J.; Zhu, G.; Lu, Z.; Zhao, P.; Wang, C.; Ma, Y.; Xu, Z.; Wang, Y.; Hu, Y.; Ma, L.; et al. Integrated perovskite solar capacitors with high energy conversion efficiency and fast photo-charging rate. J. Mater. Chem. A 2018, 6, 2047–2052. [Google Scholar] [CrossRef]
- Wheeler, L.M.; Moore, D.T.; Ihly, R.; Stanton, N.J.; Miller, E.M.; Tenent, R.C.; Blackburn, J.L.; Neale, N.R. Switchable photovoltaic windows enabled by reversible photothermal complex dissociation from methylammonium lead iodide. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Dang, Y.; Ju, D.; Wang, L.; Tao, X. Recent progress in the synthesis of hybrid halide perovskite single crystals. CrystEngComm 2016, 18, 4476–4484. [Google Scholar] [CrossRef]
- Kim, S.H.; Saeed, M.A.; Lee, S.Y.; Shim, J.W. Investigating the Indoor Performance of Planar Heterojunction Based Organic Photovoltaics. IEEE J. Photovolt. 2021, 11, 997–1003. [Google Scholar] [CrossRef]
- You, Y.J.; Saeed, M.A.; Shafian, S.; Kim, J.; Kim, S.H.; Kim, S.H.; Kim, K.; Shim, J.W. Energy recycling under ambient illumination for internet-of-things using metal/oxide/metal-based colorful organic photovoltaics. Nanotechnology 2021, 32, 465401. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; You, Y.J.; Saeed, M.A.; Kim, S.H.; Choi, S.H.; Kim, S.; Lee, S.Y.; Park, J.S.; Shim, J.W. Undoped tin dioxide transparent electrodes for efficient and cost-effective indoor organic photovoltaics (SnO2 electrode for indoor organic photovoltaics). NPG Asia Mater. 2021, 13, 43. [Google Scholar] [CrossRef]
- Berhe, T.-A.; Su, W.-N.; Chen, C.-H.; Pan, C.-J.; Cheng, J.-H.; Chen, H.-M.; Tsai, M.-C.; Chen, L.-Y.; Dubale, A.A.; Hwang, B.-J. Organometal halide perovskite solar cells: Degradation and stability. Energy Environ. Sci. 2016, 9, 323–356. [Google Scholar] [CrossRef]
- Snaith, H.J. Present status and future prospects of perovskite photovoltaics. Nat. Mater. 2018, 17, 372–376. [Google Scholar] [CrossRef]
- Babayigit, A.; Ethirajan, A.; Muller, M.; Conings, B. Toxicity of organometal halide perovskite solar cells. Nat. Mater. 2016, 15, 247–251. [Google Scholar] [CrossRef]
- Habisreutinger, S.N.; Noel, N.K.; Snaith, H.J. Hysteresis index: A figure without merit for quantifying hysteresis in perovskite solar cells. ACS Energy Lett. 2018, 3, 2472–2476. [Google Scholar] [CrossRef] [Green Version]
- Pellet, N.; Gao, P.; Gregori, G.; Yang, T.-Y.; Nazeeruddin, M.K.; Maier, J.; Grätzel, M. Mixed-Organic-Cation Perovskite Photovoltaics for Enhanced Solar-Light Harvesting. Angew. Chem. Int. Ed. 2014, 53, 3151–3157. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Krishna, A.; Zakeeruddin, S.M.; Grätzel, M.; Hagfeldt, A. Compositional and Interface Engineering of Organic-Inorganic Lead Halide Perovskite Solar Cells. iScience 2020, 23, 101359. [Google Scholar] [CrossRef]
- Solanki, A.; Yadav, P.; Turren-Cruz, S.-H.; Lim, S.S.; Saliba, M.; Sum, T.C. Cation influence on carrier dynamics in perovskite solar cells. Nano Energy 2019, 58, 604–611. [Google Scholar] [CrossRef]
- Kim, T.; Lim, J.; Song, S. Recent Progress and Challenges of Electron Transport Layers in Organic–Inorganic Perovskite Solar Cells. Energies 2020, 13, 5572. [Google Scholar] [CrossRef]
- Li, S.; Cao, Y.-L.; Li, W.-H.; Bo, Z.-S. A brief review of hole transporting materials commonly used in perovskite solar cells. Rare Met. 2021, 40, 2712–2729. [Google Scholar] [CrossRef]
- Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin Solid Films 2000, 361–362, 527–532. [Google Scholar] [CrossRef]
- Shi, J.; Wei, H.; Lv, S.; Xu, X.; Wu, H.; Luo, Y.; Li, D.; Meng, Q. Control of Charge Transport in the Perovskite CH3NH3PbI3 Thin Film. ChemPhysChem 2015, 16, 842–847. [Google Scholar] [CrossRef]
- Bi, C.; Shao, Y.; Yuan, Y.; Xiao, Z.; Wang, C.; Gao, Y.; Huang, J. Understanding the formation and evolution of interdiffusion grown organolead halide perovskite thin films by thermal annealing. J. Mater. Chem. A 2014, 2, 18508–18514. [Google Scholar] [CrossRef]
- Liu, B.; Zou, X.; Cheng, J.; Ling, T.; Yao, Y.; Chen, D.; Chang, C.; Yu, X.; Wang, J.; Zhou, Z.; et al. Effect of Low-Concentration Rb+ Mixing on Semiconductor Majority Charge Carriers Type of Perovskite Light-Absorption Layer by Using Two-Step Spin-Coating Method. Coatings 2020, 10, 627. [Google Scholar] [CrossRef]
- Kiermasch, D.; Rieder, P.; Tvingstedt, K.; Baumann, A.; Dyakonov, V. Improved charge carrier lifetime in planar perovskite solar cells by bromine doping. Sci. Rep. 2016, 6, 39333. [Google Scholar] [CrossRef] [PubMed]
- Tan, W.L.; Choo, Y.Y.; Huang, W.; Jiao, X.; Lu, J.; Cheng, Y.-B.; McNeill, C.R. Oriented Attachment as the Mechanism for Microstructure Evolution in Chloride-Derived Hybrid Perovskite Thin Films. ACS Appl. Mater. Interfaces 2019, 11, 39930–39939. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Cortecchia, D.; Krishna, A.; Chen, S.; Mathews, N.; Grimsdale, A.C.; Soci, C. Interfacial Charge Transfer Anisotropy in Polycrystalline Lead Iodide Perovskite Films. J. Phys. Chem. Lett. 2015, 6, 1396–1402. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, H.; Liu, C.; Arain, Z.; Ding, Y.; Ma, S.; Liu, X.; Hayat, T.; Alsaedi, A.; Dai, S. Bi-functional additive engineering for high-performance perovskite solar cells with reduced trap density. J. Mater. Chem. A 2019, 7, 6450–6458. [Google Scholar] [CrossRef]
- Kojić, V.; Bohač, M.; Bafti, A.; Pavić, L.; Salamon, K.; Čižmar, T.; Gracin, D.; Juraić, K.; Leskovac, M.; Capan, I.; et al. Formamidinium Lead Iodide Perovskite Films with Polyvinylpyrrolidone Additive for Active Layer in Perovskite Solar Cells, Enhanced Stability and Electrical Conductivity. Materials 2021, 14, 4594. [Google Scholar] [CrossRef] [PubMed]
- Ng, C.H.; Hamada, K.; Kapil, G.; Kamarudin, M.A.; Wang, Z.; Likubo, S.; Shen, Q.; Yoshino, K.; Minemoto, T.; Hayase, S. Reducing trap density and carrier concentration by a Ge additive for an efficient quasi 2D/3D perovskite solar cell. J. Mater. Chem. A 2020, 8, 2962–2968. [Google Scholar] [CrossRef]
- Rai, M.; Wong, L.H.; Etgar, L. The Effect of the Perovskite Thickness on the Electroluminescence and Solar Cell Conversion Efficiency. J. Phys. Chem. Lett. 2020, 11, 8189–8194. [Google Scholar] [CrossRef]
- Xiao, Z.; Dong, Q.; Bi, C.; Shao, Y.; Yuan, Y.; Huang, J. Solvent Annealing of Perovskite-Induced Crystal Growth for Photovoltaic-Device Efficiency Enhancement. Adv. Mater. 2014, 26, 6503–6509. [Google Scholar] [CrossRef]
- Saliba, M.; Correa-Baena, J.P.; Wolff, C.M.; Stolterfoht, M.; Phung, N.; Albrecht, S.; Neher, D.; Abate, A. How to Make over 20% Efficient Perovskite Solar Cells in Regular (n-i-p) and Inverted (p-i-n) Architectures. Chem. Mater. 2018, 30, 4193–4201. [Google Scholar] [CrossRef]
- Rong, B.; Jin, S.; Chen, X.; Wei, Y.; Fang, Y.; Zhao, Y.; Guo, Q.; Huang, Y.; Fan, L.; Wu, J. Improving the efficiency of perovskite solar cells by additive engineering with ditetrabutylammonium dichromate. Org. Electron. 2020, 85, 105845. [Google Scholar] [CrossRef]
- Guarnera, S.; Abate, A.; Zhang, W.; Foster, J.M.; Richardson, G.; Petrozza, A.; Snaith, H.J. Improving the Long-Term Stability of Perovskite Solar Cells with a Porous Al2O3 Buffer Layer. J. Phys. Chem. Lett. 2015, 6, 432–437. [Google Scholar] [CrossRef] [Green Version]
- Babu, V.; Pineda, R.F.; Ahmad, T.; Alvarez, A.O.; Castriotta, L.A.; Di Carlo, A.; Fabregat-Santiago, F.; Wojciechowski, K. Improved Stability of Inverted and Flexible Perovskite Solar Cells with Carbon Electrode. ACS Appl. Energy Mater. 2020, 3, 5126–5134. [Google Scholar] [CrossRef]
- Mundhaas, N.; Yu, Z.J.; Bush, K.A.; Wang, H.; Häusele, J.; Kavadiya, S.; McGehee, M.D.; Holmam, Z.C. Series Resistance Measurements of Perovskite Solar Cells Using Jsc–Voc Measurements. Sol. RRL 2019, 3, 1800378. [Google Scholar] [CrossRef]
- Veeramutuhu, L.; Liang, F.-C.; Zhang, Z.-X.; Cho, C.-J.; Ercan, E.; Chueh, C.-C.; Chen, W.-C.; Borsali, R.; Kuo, C.-C. Improving the Performance and Stability of Perovskite Light-Emitting Diodes by a Polymeric Nanothick Interlayer-Assisted Grain Control Process. ACS Omega 2020, 5, 8972–8981. [Google Scholar] [CrossRef] [PubMed]
- Hemasiri, N.H.; Kazim, S.; Ahmad, S. Reduced trap density and mitigating the interfacial losses by placing 2D dichalcogenide material at perovskite/HTM interface in a dopant free perovskite solar cells. Nano Energy 2020, 77, 105292. [Google Scholar] [CrossRef]
- Brecker, M.; Wark, M. Sequentially Deposited Compact and Pinhole-Free Perovskite Layers via Adjusting the Permittivity of the Conversion Solution. Z. Nat. A 2019, 74, 655–663. [Google Scholar]
- Singh, R.; Sandhu, S.; Lee, J.-J. Elucidating the effect of shunt losses on the performance of mesoporous perovskite solar cells. Sol. Energy 2019, 193, 956–961. [Google Scholar] [CrossRef]
- Hörantner, M.T.; Nayak, P.K.; Mukhopadhyay, S.; Wojciechowski, K.; Beck, C.; McMeekin, D.; Kamino, B.; Eperon, G.E.; Snaith, H.J. Shunt-Blocking Layers for Semitransparent Perovskite Solar Cells. Adv. Mater. Interfaces 2016, 3, 1500837. [Google Scholar] [CrossRef]
- Saranin, D.; Gostischev, P.; Tatarinov, D.; Ermanova, I.; Mazov, V.; Muratov, D.; Tameev, A.; Kuznetsov, D.; Didenko, S.; Di Carlo, A. Copper Iodide Interlayer for Improved Charge Extraction and Stability of Inverted Perovskite Solar Cells. Materials 2019, 12, 1406. [Google Scholar] [CrossRef] [Green Version]
- Minemoto, T.; Murata, M. Impact of work function of back contact of perovskite solar cells without hole transport material analysed by device simulation. Curr. Appl. Phys. 2014, 14, 1428–1433. [Google Scholar] [CrossRef]
- Du, H.-J.; Wang, W.-C.; Zhu, J.-Z. Device simulation of lead-free CH3NH3SnI3 perovskite solar cells with high efficiency. Chin. Phys. B 2016, 25, 108802. [Google Scholar] [CrossRef]
- Stamate, M.D. On the dielectric properties of dc magnetron TiO2 thin films. Appl. Surf. Sci. 2003, 218, 318–323. [Google Scholar] [CrossRef]
- Bansal, S.; Aryal, P. Evaluation of new materials for electron and hole transport layers in perovskite-based solar cells through SCAPS-1D simulations. In Proceedings of the IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 747–750. [Google Scholar] [CrossRef]
- Liu, D.; Kelly, T. Perovskite solar cells with a planar heterojunction structure prepared using room-temperature solution processing techniques. Nat. Photonics 2013, 8, 133–138. [Google Scholar] [CrossRef]
- Karthick, S.; Velumani, S.; Bouclé, J. Experimental and SCAPS simulated formamidinium perovskite solar cells: A comparison of device performance. Sol. Energy 2020, 205, 349–357. [Google Scholar] [CrossRef]
- Abdelaziz, S.; Zekry, A.; Shaker, A.; Abouletta, M. Investigating the performance of formamidinium tin-based perovskite solar cell by SCAPS device simulation. Opt. Mater. 2020, 101, 109738. [Google Scholar] [CrossRef]
- Shi, J.; Li, Y.; Li, Y.; Li, D.; Luo, Y.; Wu, H.; Meng, Q. From Ultrafast to Ultraslow: Charge-Carrier Dynamics of Perovskite Solar Cells. Joule 2018, 2, 879–901. [Google Scholar] [CrossRef] [Green Version]
- Xing, G.C.; Mathews, N.; Sun, S.Y.; Lim, S.S.; Lam, Y.M.; Grätzel, M.; Mhaisalkar, S.; Sum, T.C. Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3. Science 2013, 342, 344–347. [Google Scholar] [CrossRef]
- Hao, F.; Stoumpos, C.C.; Guo, P.; Zhou, N.; Marks, T.J.; Chang, R.P.H.; Kanatzidis, M.G. Solvent-Mediated Crystallization of CH3NH3SnI3 Films for Heterojunction Depleted Perovskite Solar Cells. J. Am. Chem. Soc. 2015, 137, 11445–11452. [Google Scholar] [CrossRef] [PubMed]
- Shockley, W.; Read, W.T.; Sze, S.M. Statistics of the Recombinations of Holes and Electrons. In Semiconductor Devices: Pioneering Papers; World Scientific: London, UK, 1991; pp. 62–69. [Google Scholar] [CrossRef]
- Grove, A.S. Physics and Technology of Semiconductor Devices, 1st ed.; John Wiley and Sons: New York, NY, USA, 1967; pp. 129–133. [Google Scholar]
- Smets, A.; Jager, K.; Isabella, O.; Van Swaaij, R.; Zeman, M. Solar Energy: The Physics and Engineering of Photovoltaic Conversion, Technologies and Systems, 1st ed.; UIT Cambridge Ltd.: Cambridge, UK, 2016; pp. 145–147. [Google Scholar]
- Xu, T.; Wang, Z.; Li, X.; Sha, W.E.I. Loss Mechanism Analyses of Perovskite Solar Cells with an Equivalent Circuit Model. Available online: https://arxiv.org/abs/2103.11141 (accessed on 19 July 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).