Modeling of Polymer Friction on Boundaries of Solids and Inside Materials
Abstract
1. Introduction
2. Models of Polymer Friction on Boundaries of Solids
2.1. Dry Friction Models with Additional Variables
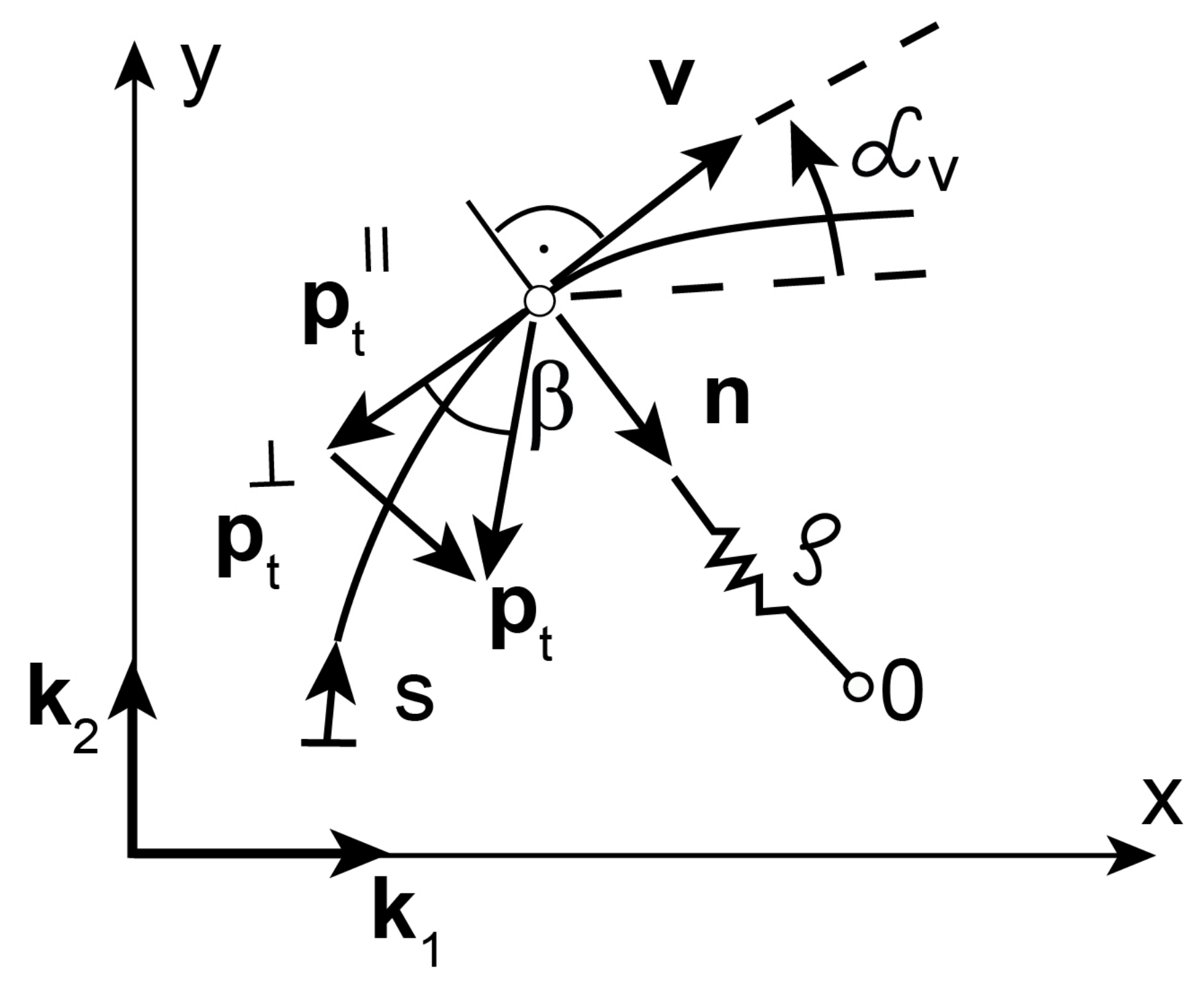
2.1.1. Dependence of the Friction Force on the Sliding Direction
2.1.2. Dependence of the Friction Force on the Oriented Angle
2.1.3. Dependence of the Friction Force on the Sliding Trajectory Curvature
2.2. Thermodynamic Restrictions of the Friction Models
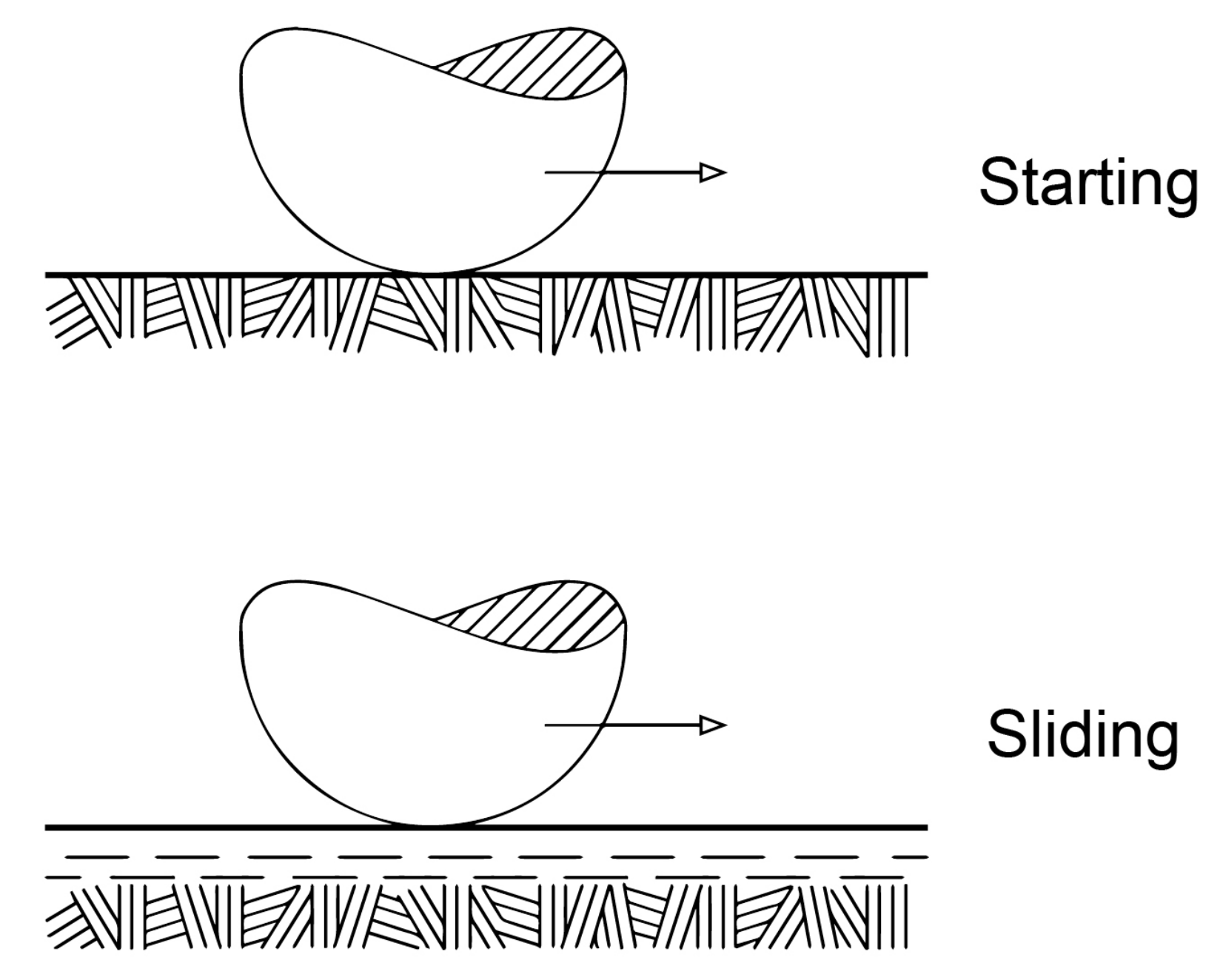
2.3. Movements and Friction of the Polymer Pin in Pin-on-Disc Tests
2.4. Archimedean Spiral as the Sliding Trajectory of the Polymer Pin
2.5. Models of Elastomer Friction on Boundaries of Solids
3. Models of Polymer Friction Inside Materials
3.1. Micromechanical Models of Polymer Macromolecules
3.2. Macromolecule Dynamics including Friction Anisotropy
3.3. Continuum-Based Models of Friction Inside Materials
3.4. The Macromolecule Disc-like Model under Combination of Spinning and Sliding
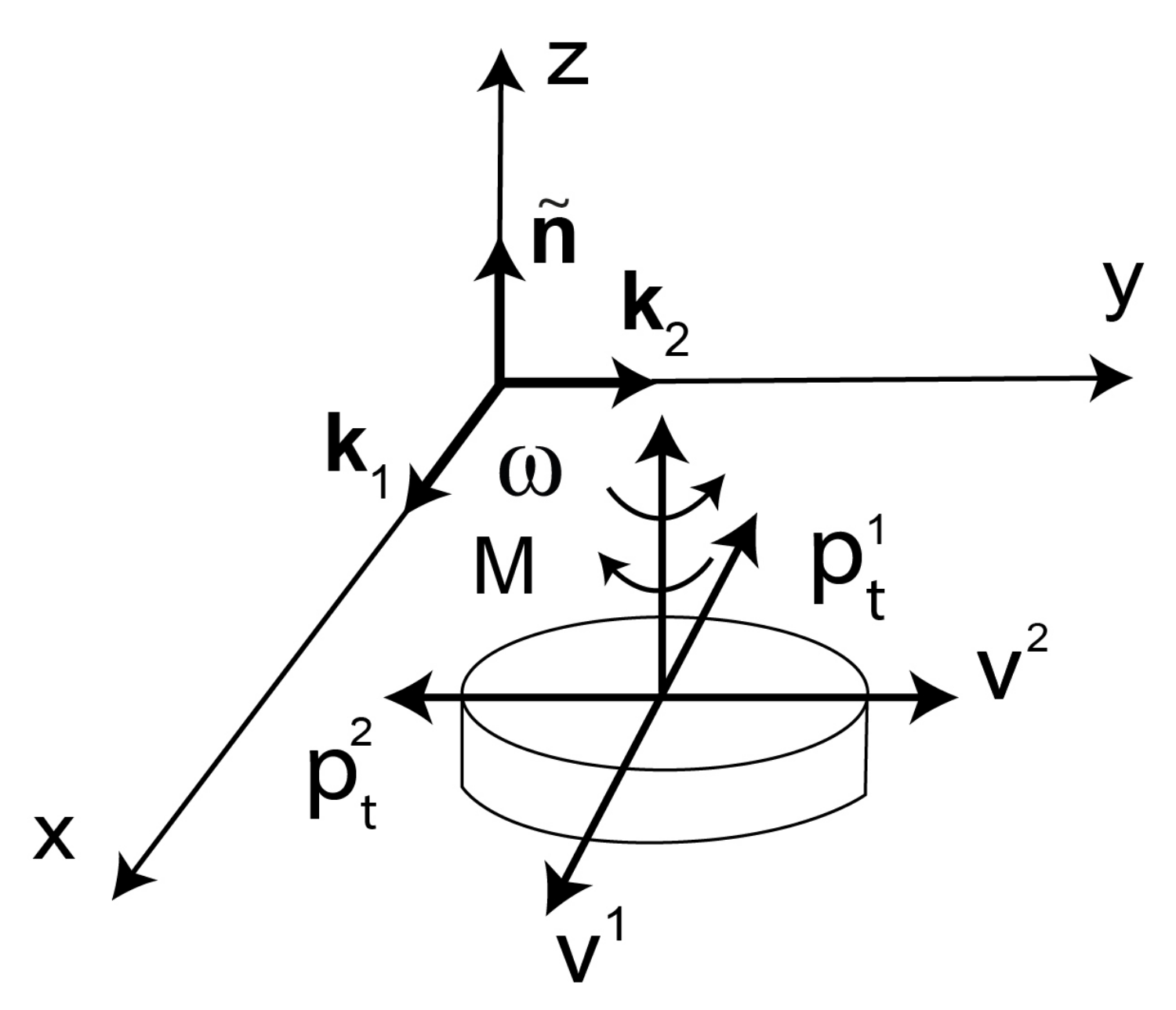
3.5. The Long Macromolecule Model under Snake-like Sliding
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zmitrowicz, A. A multiscale approach to friction on surfaces of polymeric solids and in bulk polymeric materials. In Proceedings of the 14th WCCM-ECCOMAS Congress 2020, Virtual Congress, Scipedia, Barcelona, Spain, 11–15 January 2021; Available online: https://www.scipedia.com/public/Zmitrowicz_2021a (accessed on 10 March 2021).
- Liu, X.-X.; Li, T.-S.; Liu, X.-J.; Lv, R.-G.; Cong, P.-H. An investigation on the friction of oriented polytetrafluoroethylene (PTFE). Wear 2007, 262, 1414–1418. [Google Scholar] [CrossRef]
- Dunn, A.C.; Steffens, J.G.; Burris, D.L.; Banks, S.A.; Sawyer, W.G. Spatial geometric effects on the friction coefficients of UHMWPe. Wear 2008, 264, 648–653. [Google Scholar] [CrossRef]
- Sung, N.-H.; Suh, N.P. Effect of fibre orientation on friction and wear of fibre reinforced polymeric composites. Wear 1979, 53, 129–141. [Google Scholar]
- Zhang, S.W. State-of-the-art of polymer tribology. Tribol. Int. 1998, 31, 49–60. [Google Scholar] [CrossRef]
- Sawyer, W.G.; Argibay, N.; Burris, D.L.; Kirck, B.A. Mechanistic studies in friction and wear of bulk materials. Annu. Rev. Mater. Res. 2014, 44, 395–427. [Google Scholar] [CrossRef]
- Kajiyama, T.; Ohaki, I.; Takahara, A. Surface morphology and frictional property of polyethylene single crystals studied by scanning force microscopy. Macromolecules 1995, 28, 4768–4770. [Google Scholar] [CrossRef]
- Kimura, K.; Kobayashi, K.; Yamada, H.; Matsushige, K. Investigation of molecular chain orientation change of polymer crystals in phase transitions by friction anisotropy measurement. Langmuir 2007, 23, 4740–4745. [Google Scholar] [CrossRef]
- Pearce, R.; Vancso, G.J. Frictional anisotropy and sectorization in poly(4-methyl-1-pentene) lamellar crystals studied by lateral force microscopy. Polymer 1998, 39, 6743–6746. [Google Scholar] [CrossRef]
- Sakamoto, K.; Arafune, R.; Ito, N.; Ushioda, S.; Suzuki, Y.; Morokawa, S. Determination of molecular orientation of very thin rubbed and unrubbed polyimide films. J. Appl. Phys. 1996, 80, 431–439. [Google Scholar] [CrossRef]
- Jabbarzadeh, A. Friction anisotropy and asymmetry in self assembled monolayer. Tribol. Int. 2016, 102, 600–607. [Google Scholar] [CrossRef]
- Greiner, C.; Liu, Z.; Schneider, R.; Pastewka, L.; Gumbsch, P. The origin of surface microstructure evolution in sliding friction. Scr. Mater. 2018, 153, 63–67. [Google Scholar] [CrossRef]
- Sinha, S.K.; Briscoe, B.J. Polymer Tribology; Imperial College Press: Singapore, 2009. [Google Scholar]
- Yu, C.; Yu, B.; Lin, G.; Chen, W.; He, B.; Wang, Q.J. Understanding topographic dependence of friction with micro- and nano-grooved surfaces. Tribol. Lett. 2014, 53, 145–156. [Google Scholar] [CrossRef]
- Noguchi, H.; Takasu, M. Dynamics of DNA in entangled polymer solutions: An anisotropic friction model. J. Chem. Phys. 2001, 114, 7260–7266. [Google Scholar] [CrossRef]
- Szamel, G. Tagged chain diffusion equation and effective friction tensor in dense polymer solutions. J. Chem. Phys. 1998, 108, 368–375. [Google Scholar] [CrossRef][Green Version]
- Xu, Z.; Kim, S.; de Pablo, J.J. Anisotropic friction and excluded-volume effects in freely jointed bead-rod polymer-chain models. J. Chem. Phys. 1994, 101, 5293–5304. [Google Scholar] [CrossRef]
- De Gennes, P.-G. Brownian motion with dry friction. J. Stat. Phys. 2005, 119, 953–962. [Google Scholar] [CrossRef]
- Persson, B.N.J. Sliding Friction. Physical Principles and Applications, 2nd ed.; Springer: Berlin, Germany, 2000. [Google Scholar]
- Zmitrowicz, A. Mathematical descriptions of anisotropic friction. Int. J. Solids Struct. 1989, 25, 837–862. [Google Scholar] [CrossRef]
- Zmitrowicz, A. A constitutive modelling of centrosymmetric and non-centrosymmetric anisotropic friction. Int. J. Solids Struct. 1992, 29, 3025–3043. [Google Scholar] [CrossRef]
- Zmitrowicz, A. Illustrative examples of centrosymmetric and non-centrosymmetric anisotropic friction. Int. J. Solids Struct. 1992, 29, 3045–3059. [Google Scholar] [CrossRef]
- Zmitrowicz, A. An equation of anisotropic friction with sliding path curvature effects. Int. J. Solids Struct. 1999, 36, 2825–2848. [Google Scholar] [CrossRef]
- Zmitrowicz, A. Illustrative examples of anisotropic friction with sliding path curvature effects. Int. J. Solids Struct. 1999, 36, 2849–2863. [Google Scholar] [CrossRef]
- Zmitrowicz, A. Models of kinematics dependent anisotropic and heterogeneous friction. Int. J. Solids Struct. 2006, 43, 4407–4451. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover: New York, NY, USA, 1997. [Google Scholar]
- Tapia, F.; Le Tourneau, D.; Géminard, J.-C. Anisotropic friction: Assessment of force components and resulting trajectories. EPJ Tech. Instrum. 2016, 3, 1–10. [Google Scholar] [CrossRef]
- Briscoe, B.J.; Stolarski, T.A. The influence of contact zone kinematics on wear process of polymers. Wear 1991, 149, 233–240. [Google Scholar] [CrossRef]
- Jang, I.; Burris, D.L.; Dickrell, P.L.; Barry, P.R.; Santos, C.; Perry, S.S.; Phillpot, S.R.; Sawyer, W.G. Sliding orientation effects on the tribological properties of polytetrafluoroethylene. J. Appl. Phys. 2007, 102, 123509. [Google Scholar] [CrossRef]
- Schonherr, H.; Vansco, G.J. Molecular resolution imaging and friction anisotropy of highly oriented polyethylene and poly(tetrafluoroethylene) by scanning force microscopy with chemically modified probes. Macromolecules 1997, 30, 6391–6394. [Google Scholar] [CrossRef]
- Tabor, D.; Williams, D.E. The effect of orientation on the friction of polytetrafluoroethylene. Wear 1961, 4, 391–400. [Google Scholar] [CrossRef]
- Moore, D.F. The Friction and Lubrication of Elastomers; Pergamon Press: Oxford, UK, 1972. [Google Scholar]
- Persson, B.N.J. On the theory of rubber friction. Surf. Sci. 1998, 401, 445–454. [Google Scholar] [CrossRef]
- Besdo, D.; Heimann, B.; Klüppel, M.; Kröger, M.; Wriggers, P.; Nackenhorst, U. (Eds.) Elastomere Friction: Theory, Experiment and Simulation, Series: Lecture Notes in Applied and Computational Mechanics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 51. [Google Scholar]
- Rabinowicz, E. Friction and Wear of Materials, 2nd ed.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Rouse, P.E., Jr. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- De Gennes, P.-G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Montesi, A.; Morse, D.C.; Pasquali, M. Brownian dynamics algorithm for bead-rod semiflexible chain with anisotropic friction. J. Chem. Phys. 2005, 122, 084903. [Google Scholar] [CrossRef]
- Biller, P.; Petruccione, F. Rheological properties of polymer dumbbell models with configuration-dependent anisotropic friction. J. Chem. Phys. 1988, 89, 2412–2418. [Google Scholar] [CrossRef]
- Cyron, C.J.; Wall, W.A. Numerical method for the simulation of the Brownian dynamics of rod like microstructures with three-dimensional nonlinear beam elements. Int. J. Num. Meth. Eng. 2012, 90, 955–987. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Lebedev, L.P.; Altenbach, H. Foundations of Micropolar Mechanics; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Silantyeva, O.; Dmitriev, N. Motion of a thin elliptic plate under symmetric and asymmetric orthotropic friction forces. Surf. Topogr. Metrol. Prop. 2018, 6, 1–13. [Google Scholar] [CrossRef]
- Hu, D.L.; Shelley, M. Slithering locomotion. In Natural Locomotion in Fluids and on Surfaces: Swimming, Flying, and Sliding; Childress, S., Hosei, A., Schultz, W.W., Wang, Z.J., Eds.; Springer Science + Business Media: New York, NY, USA, 2012; pp. 117–135. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zmitrowicz, A. Modeling of Polymer Friction on Boundaries of Solids and Inside Materials. Materials 2021, 14, 6187. https://doi.org/10.3390/ma14206187
Zmitrowicz A. Modeling of Polymer Friction on Boundaries of Solids and Inside Materials. Materials. 2021; 14(20):6187. https://doi.org/10.3390/ma14206187
Chicago/Turabian StyleZmitrowicz, Alfred. 2021. "Modeling of Polymer Friction on Boundaries of Solids and Inside Materials" Materials 14, no. 20: 6187. https://doi.org/10.3390/ma14206187
APA StyleZmitrowicz, A. (2021). Modeling of Polymer Friction on Boundaries of Solids and Inside Materials. Materials, 14(20), 6187. https://doi.org/10.3390/ma14206187





