Effect of Material Heterogeneity on Environmentally Assisted Cracking Growth Rate of Alloy 600 for Safe-End Welded Joints
Abstract
:1. Introduction
2. Theoretical Model for Environmentally Assisted Cracking (EAC) Growth Rate Prediction
3. Calculation Model for EAC Growth Rate Prediction
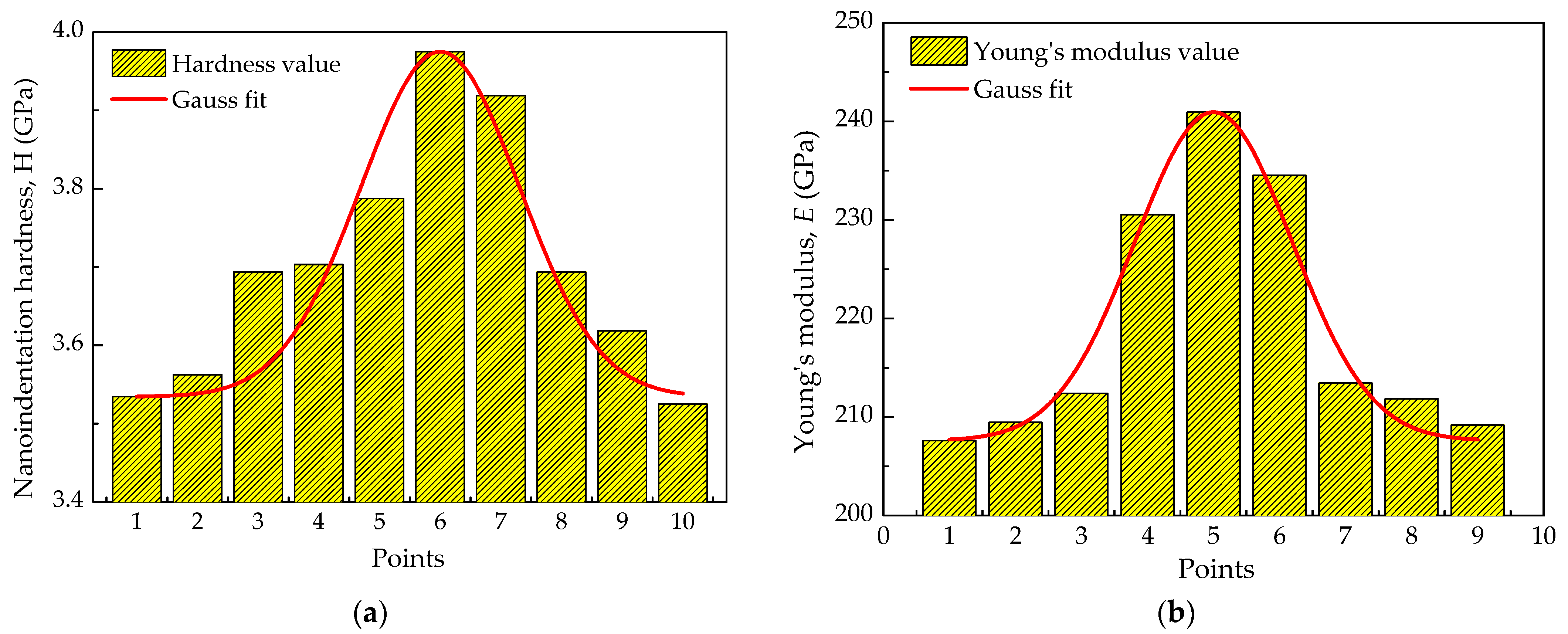
3.1. Material and Simulation Test Conditions
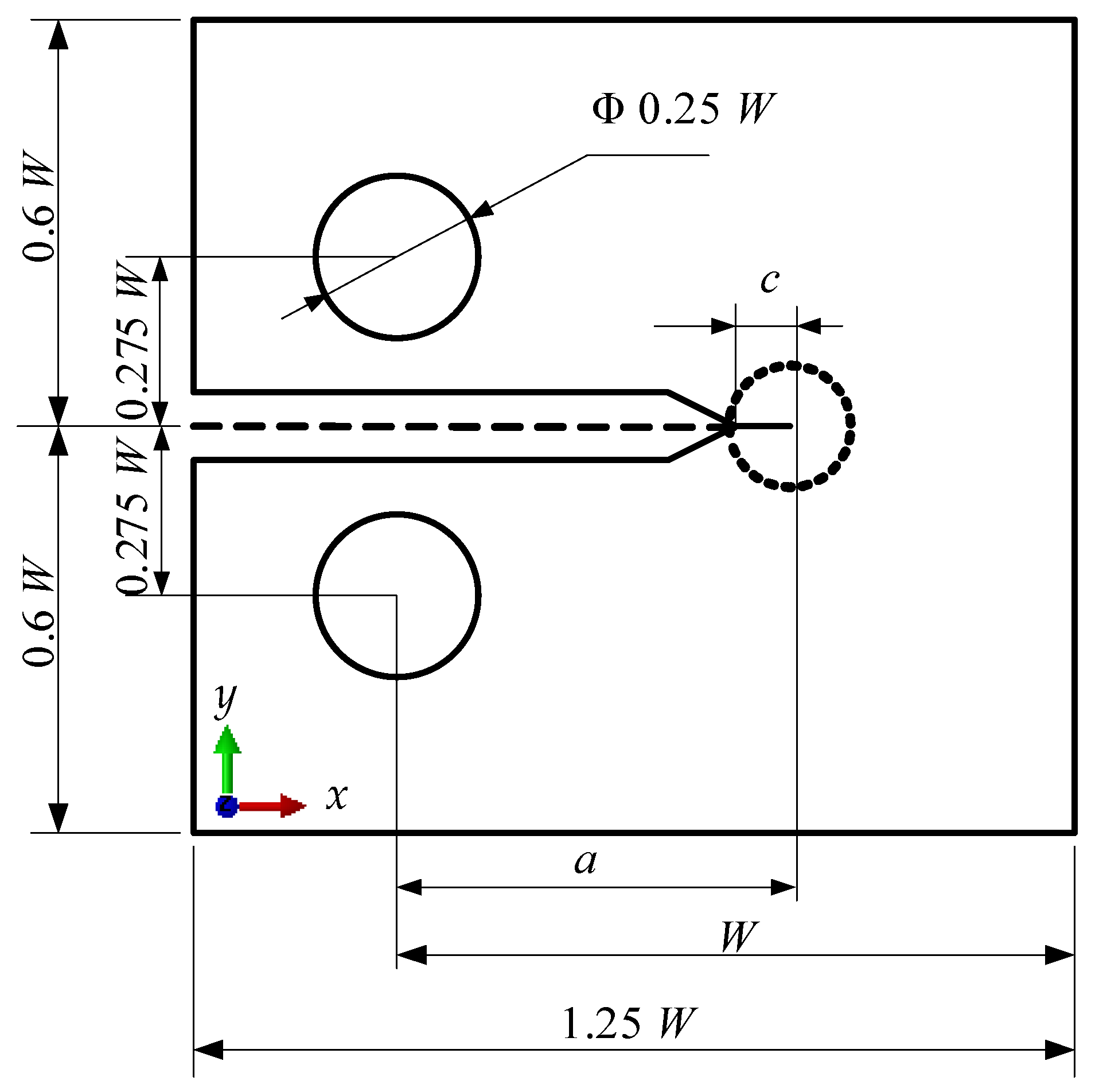
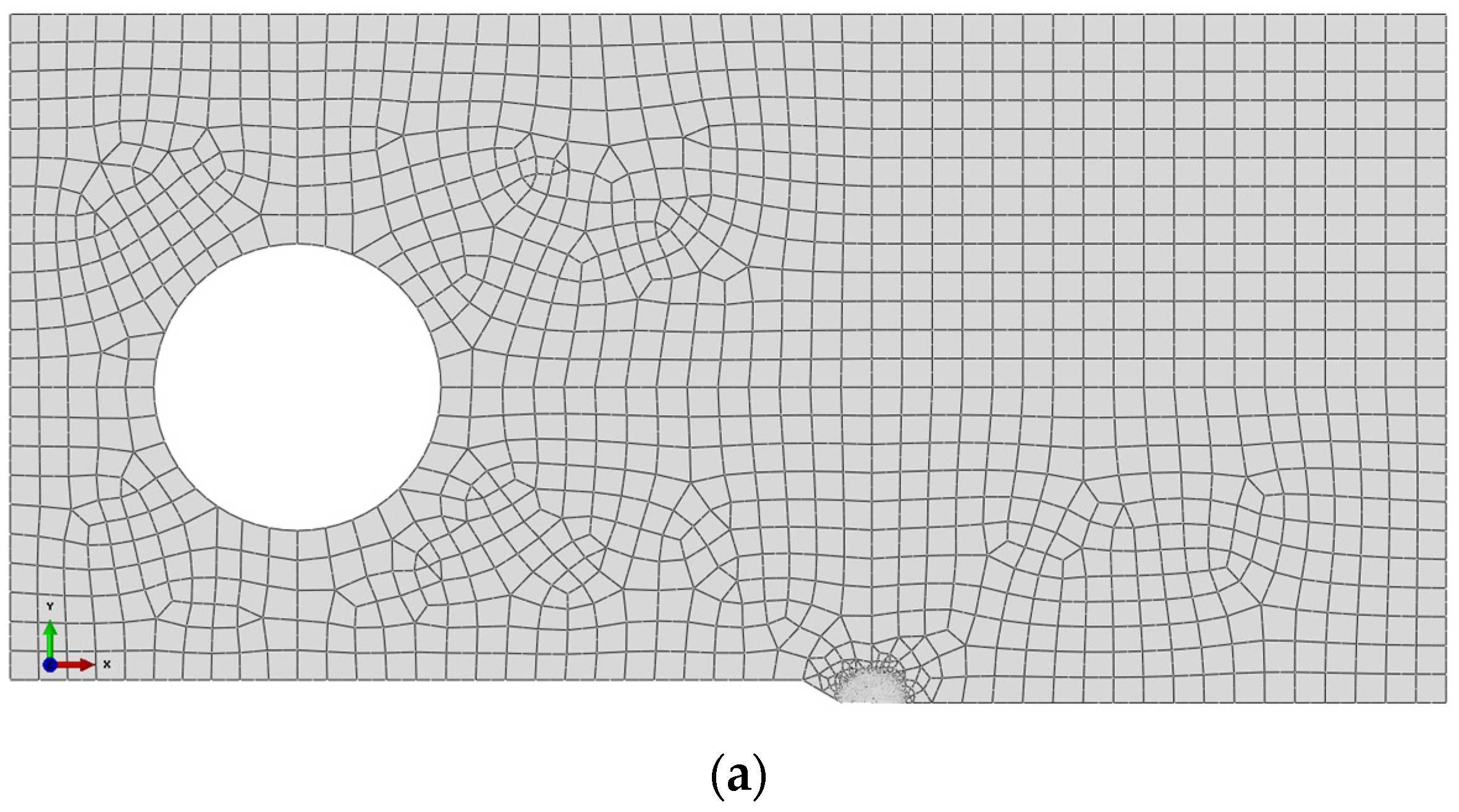
3.2. Specimen and Finite Element Model
3.3. Load Condition
4. Results and Discussion
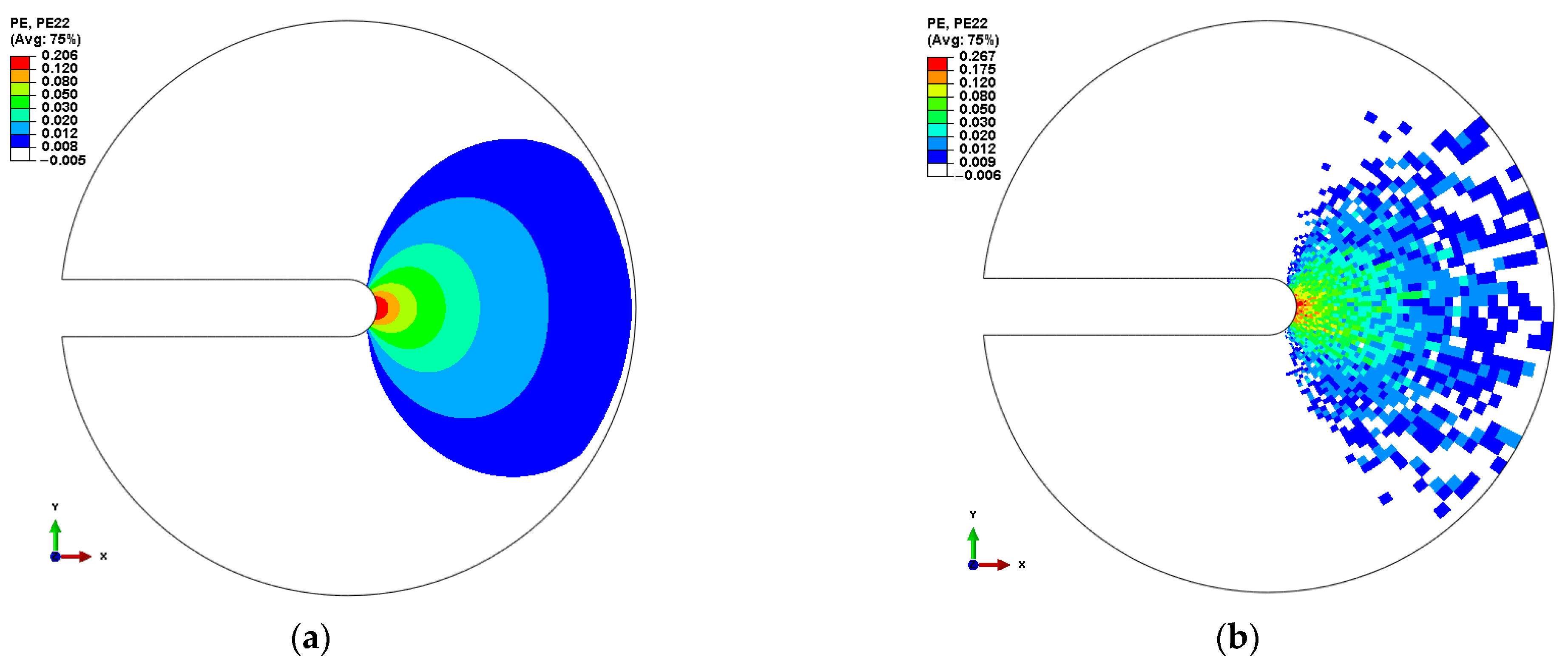
4.1. Effect of Material Properties on the Normal Plastic Strain
4.2. Effect of a Single Random Material Parameter on the Crack Growth Rate
4.3. Effect of Yield Strength Distribution on the Crack Growth Rate
4.4. Comparison of EAC Growth Rate
5. Conclusions
- An approach that will enable the prediction of the EAC growth rate of Alloy 600 for safe-end welded joints is proposed and discussed, considering the material heterogeneity. The approach can be adopted to develop an understanding of the EAC growth rate of Alloy 600 for safe-end welded joints.
- The heterogeneity of the materials is not ignored because it may affect the prediction accuracy of the crack growth rate. The randomness of the yield strength has the most considerable influence on the EAC growth rate, but that of Poisson’s ratio has the smallest.
- A characteristic distance from the crack tip r0 is a critical parameter in the approach proposed here. It is suggested that r0 can be determined by combining experimental EAC data under the same load and test environmental conditions with a finite element analysis considering material heterogeneity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| EAC | Environmentally assisted cracking |
| C.V. | coefficient of variation |
| KΙ | stress intensity factor |
| a | Actual crack size |
| c | Physical crack size including plastic zone |
| M | atomic weight of the metal |
| Z | change in charge due to the oxidation process |
| ρ | density of the metal |
| F | Faraday’s constant |
| i0 | oxidation current density of the bare surface |
| m | exponent of the current decay curve |
| t0 | time before the onset of the current decay |
| εf | degradation strain of the protective film |
| strain rate at the crack tip | |
| εp | tensile plastic strain |
| r0 | characteristic distance |
| The oxidation rate constant | |
| E | Young’s Modulus |
| ν | Poisson’s ratio |
| σ0 | Yield strength |
| α | Yield offset |
| n | Hardening exponent |
| W | Specimen width |
| σθ | hoop stress of the pressure pipeline |
| P | internal pressure of pressure pipeline |
| D | diameter of pressure pipeline |
| b | wall thickness of the AP1000 reactor pressure pipeline |
| Normal plastic strain | |
| tensile plastic strain rate |
References
- Pervaiz, S.; Rashid, A.; Deiab, I.; Nicolescu, M. Influence of tool materials on machinability of titanium-and nickel-based alloys: A review. Mater. Manuf. Process. 2014, 29, 219–252. [Google Scholar] [CrossRef]
- Ming, H.; Wang, J.; Han, E.H. Comparative study of microstructure and properties of low-alloy-steel/nickel-based-alloy interfaces in dissimilar metal weld joints prepared by different GTAW methods. Mater. Charact. 2018, 139, 186–196. [Google Scholar] [CrossRef]
- Yang, J. Micromechanical analysis of in-plane constraint effect on local fracture behavior of cracks in the weakest locations of dissimilar metal welded joint. Acta Metall. Sin. 2017, 30, 840–850. [Google Scholar] [CrossRef]
- Sato, A.; Lyamzina, Y. Diversity of concerns in recovery after a nuclear accident: A perspective from Fukushima. Int. J. Environ. Res. Public Health 2018, 15, 350. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Wang, J.; Du, D.; Andresen, P.L.; Zhang, L. dK/da effects on the SCC growth rates of nickel base alloys in high-temperature water. J. Nucl. Mater. 2018, 503, 13–21. [Google Scholar] [CrossRef]
- Li, Z.; Lu, Y.; Wang, X. Modeling of stress corrosion cracking growth rates for key structural materials of nuclear power plant. J. Mater. Sci. 2020, 55, 439–463. [Google Scholar] [CrossRef]
- Lim, Y.S.; Kim, D.J.; Kim, S.W.; Kim, H.P. Crack growth and cracking behavior of Alloy 600/182 and Alloy 690/152 welds in simulated PWR primary water. Nucl. Eng. Technol. 2019, 51, 228–237. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, T.; Chen, K.; Du, D.; Andresen, P.L.; Zhang, L. Effect of dissolved oxygen and hydrogen on the stress corrosion cracking behavior of alloy 600 in high temperature water. J. Nucl. Mater. 2021, 543, 152603. [Google Scholar] [CrossRef]
- Xue, H.; Sato, Y.; Shoji, T. Quantitative estimation of the growth of environmentally assisted cracks at flaws in light water reactor components. J. Press. Vessel. Technol. 2009, 131, 61–70. [Google Scholar] [CrossRef]
- Xue, H.; Shoji, T. Quantitative prediction of EAC crack growth rate of sensitized type 304 stainless steel in boiling water reactor environments based on EPFEM. J. Press. Vessel. Technol. 2007, 129, 254–258. [Google Scholar] [CrossRef]
- Yang, F.Q.; Xue, H.; Zhao, L.Y.; Fang, X.R. A quantitative prediction model of SCC rate for nuclear structure materials in high temperature water based on crack tip creep strain rate. Nucl. Eng. Des. 2014, 278, 686–692. [Google Scholar] [CrossRef]
- Bashir, R.; Xue, H.; Zhang, J.; Guo, R.; Hayat, N.; Li, G.; Bi, Y. Effect of Material Macrostructural Parameters on Quantitative Stress Corrosion Cracking Plastic Zone Using Extended Finite Element Method in Welded Joints for Light Water Reactor Environment. Corrosion 2020, 76, 826–834. [Google Scholar] [CrossRef]
- Wei, P.; Li, H.; Liu, J.; Li, S.; Zhang, Y.; Zhu, Q.; Lei, Y. The effect of water environment on microstructural characteristics, compositional heterogeneity and microhardness distribution of 16Mn/304L dissimilar welded joints. J. Manuf. Process. 2020, 56, 417–427. [Google Scholar] [CrossRef]
- Dong, L.; Peng, Q.; Xue, H.; Han, E.H.; Ke, W.; Wang, L. Correlation of microstructure and stress corrosion cracking initiation behaviour of the fusion boundary region in a SA508 Cl. 3-Alloy 52M dissimilar weld joint in primary pressurized water reactor environment. Corros. Sci. 2018, 132, 9–20. [Google Scholar] [CrossRef]
- Xue, H.; Ogawa, K.; Shoji, T. Effect of welded mechanical heterogeneity on local stress and strain ahead of stationary and growing crack tips. Nucl. Eng. Des. 2009, 239, 628–640. [Google Scholar] [CrossRef]
- Sarikka, T.; Ahonen, M.; Mouginot, R.; Nevasmaa, P.; Karjalainen-Roikonen, P.; Ehrnstén, U.; Hänninen, H. Microstructural, mechanical, and fracture mechanical characterization of SA 508-Alloy 182 dissimilar metal weld in view of mismatch state. Int. J. Press. Vessel. Pip. 2016, 145, 13–22. [Google Scholar] [CrossRef]
- Chang, J.H.; Liu, T.H.; Chou, J.M.; Hsieh, R.I.; Lee, J.L. Microstructural and microhardness characteristics of induction melted nickel-based alloys. Mater. Chem. Phys. 2010, 120, 702–708. [Google Scholar] [CrossRef]
- Peng, Q.; He, X.; Hou, J.; Sakaguchi, K.; Takeda, Y.; Kuniya, J.; Shoji, T. Role of water chemistry and microstructure in stress corrosion cracking in the fusion boundary region of an Alloy 182-A533B low alloy steel dissimilar weld joint in high temperature water. Corros. Sci. 2011, 53, 4309–4317. [Google Scholar] [CrossRef]
- Ford, F.P. Quantitative prediction of environmentally assisted cracking. Corrosion 1996, 52, 375–395. [Google Scholar] [CrossRef] [Green Version]
- Shoji, T. Quantification of yield strength effects on IGSCC of austenitic stainless steels in high temperature water. In Proceedings of the 11th International Symposium on Environmental Degradation of Materials in Nuclear Power System-Water Reactors, Stevenson, WA, USA, 11–14 August 2003. [Google Scholar]
- Shoji, T.; Lu, Z.; Murakami, H. Formulating stress corrosion cracking growth rates by combination of crack tip mechanics and crack tip oxidation kinetics. Corros. Sci. 2010, 52, 769–779. [Google Scholar] [CrossRef]
- Chung, W.C.; Huang, J.Y.; Tsay, L.W.; Chen, C. Microstructure and stress corrosion cracking behavior of the weld metal in alloy 52-A508 dissimilar welds. Mater. Trans. 2011, 52, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.X.; Li, X.Q.; Hao, B.X.; Yun, Y.L.; Du, Y.Q. Analysis of microstructure and properties and nanoindentation of nickel-based alloy heterogenerous fusion welded 9Ni steel joint. Trans. China Weld. Inst. 2021, 42, 90–96. [Google Scholar]
- Şerban, V.A.; Codrean, C.; Vodă, M.; Chicot, D.; Decoopman, X. Correlation between yield stress and hardness of nickel–silicon–boron-based alloys by nanoindentation. Mater. Sci. Eng. A 2014, 605, 294–300. [Google Scholar] [CrossRef]
- Hu, D.; Mao, J.; Wang, X.; Meng, F.; Song, J.; Wang, R. Probabilistic evaluation on fatigue crack growth behavior in nickel based GH4169 superalloy through experimental data. Eng. Fract. Mech. 2018, 196, 71–82. [Google Scholar] [CrossRef]
- Xiurong, F.; Jinhui, Y.; Yanru, S.; Xue, O. Quantitative Prediction of Stress Corrosion Crack Propagation Rate of Small Crack in Alloy 600 for Nuclear Pressure Vessels. Rare Met. Mater. Eng. 2019, 48, 2424–2431. [Google Scholar]
- Peng, Q.J.; Kwon, J.; Shoji, T. Development of a fundamental crack tip strain rate equation and its application to quantitative prediction of stress corrosion cracking of stainless steels in high temperature oxygenated water. J. Nucl. Mater. 2004, 324, 52–61. [Google Scholar] [CrossRef]
- ASTM E399-90. Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 1997. [Google Scholar]
- Zhang, C.; Yang, X.; Gao, H. Effect of randomness of interfacial properties on fracture behavior of concrete under uniaxial tension. Acta Mech. Solida Sin. 2018, 31, 174–186. [Google Scholar] [CrossRef]
- Rebak, R.B.; Xia, Z.; Szklarska-Smialowska, Z. Effect of temperature and cold work on the crack growth rate of Alloy 600 in primary water. Corrosion 1995, 51, 689–697. [Google Scholar] [CrossRef]



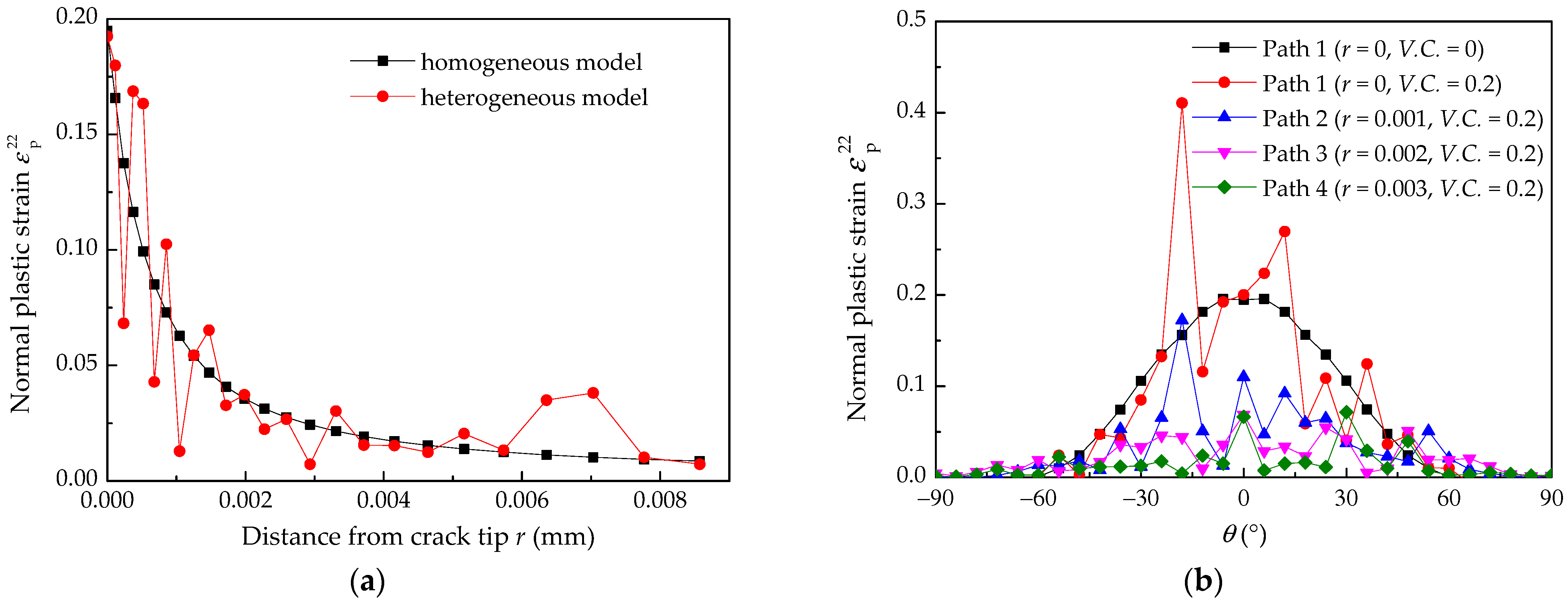

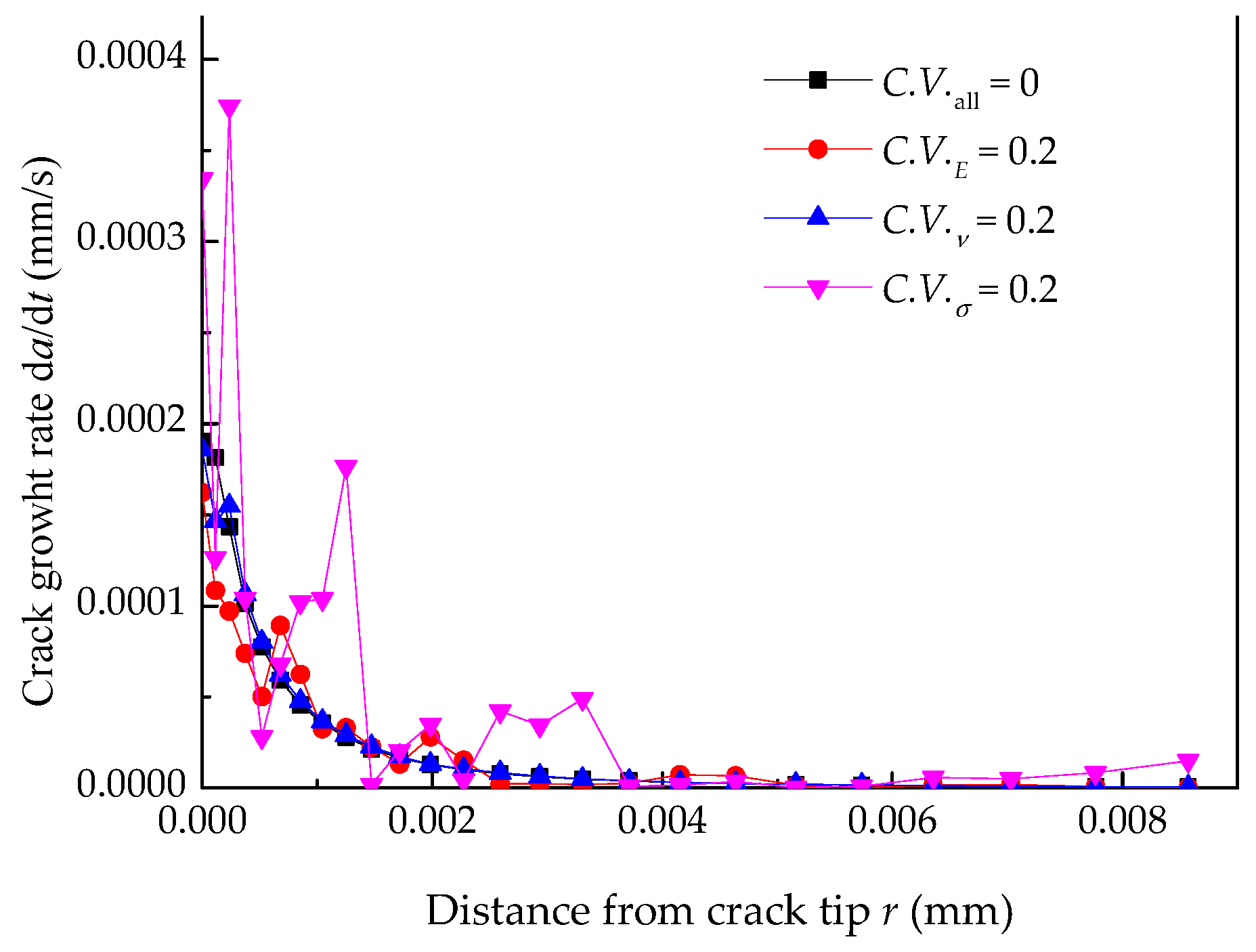
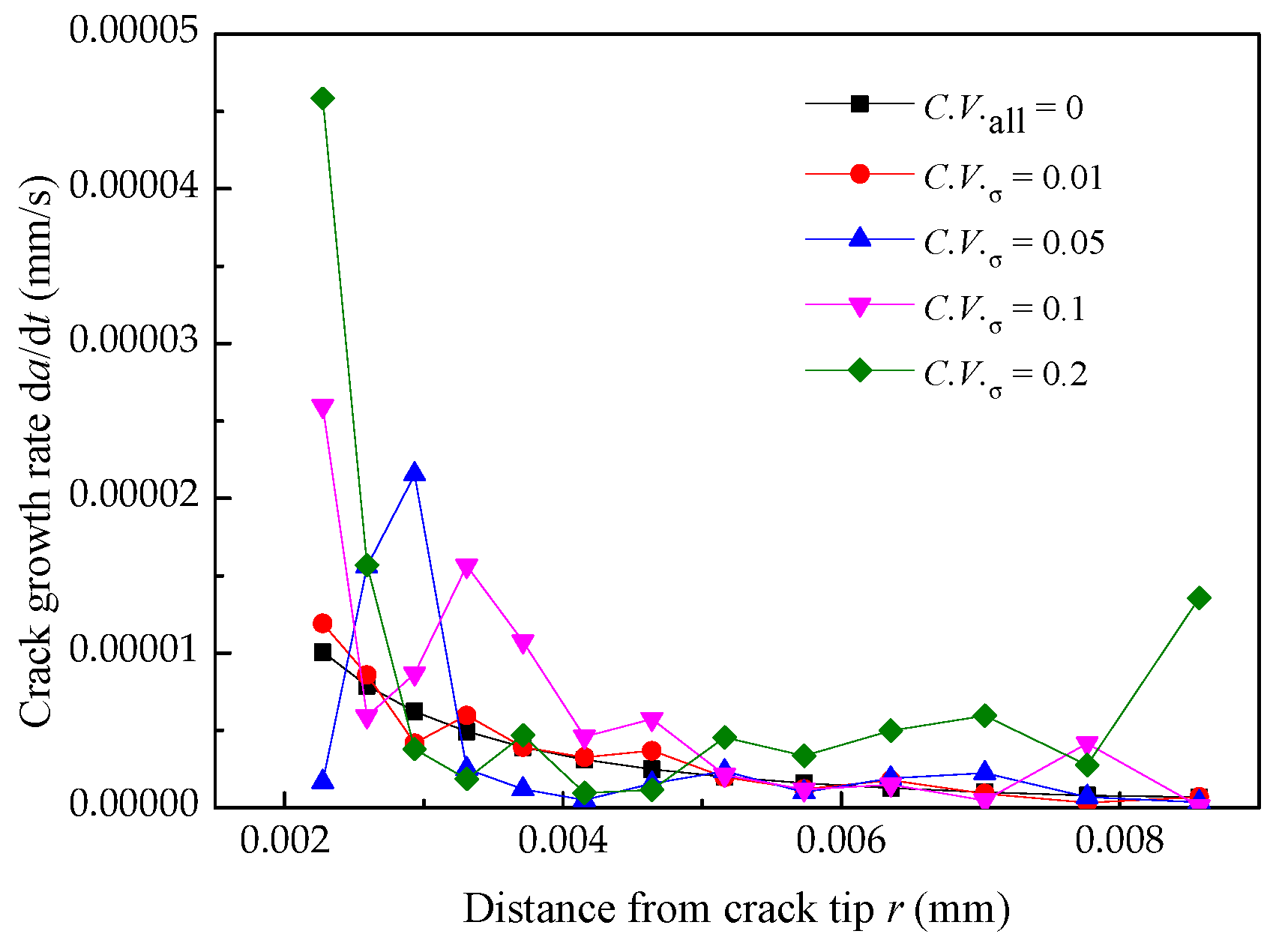
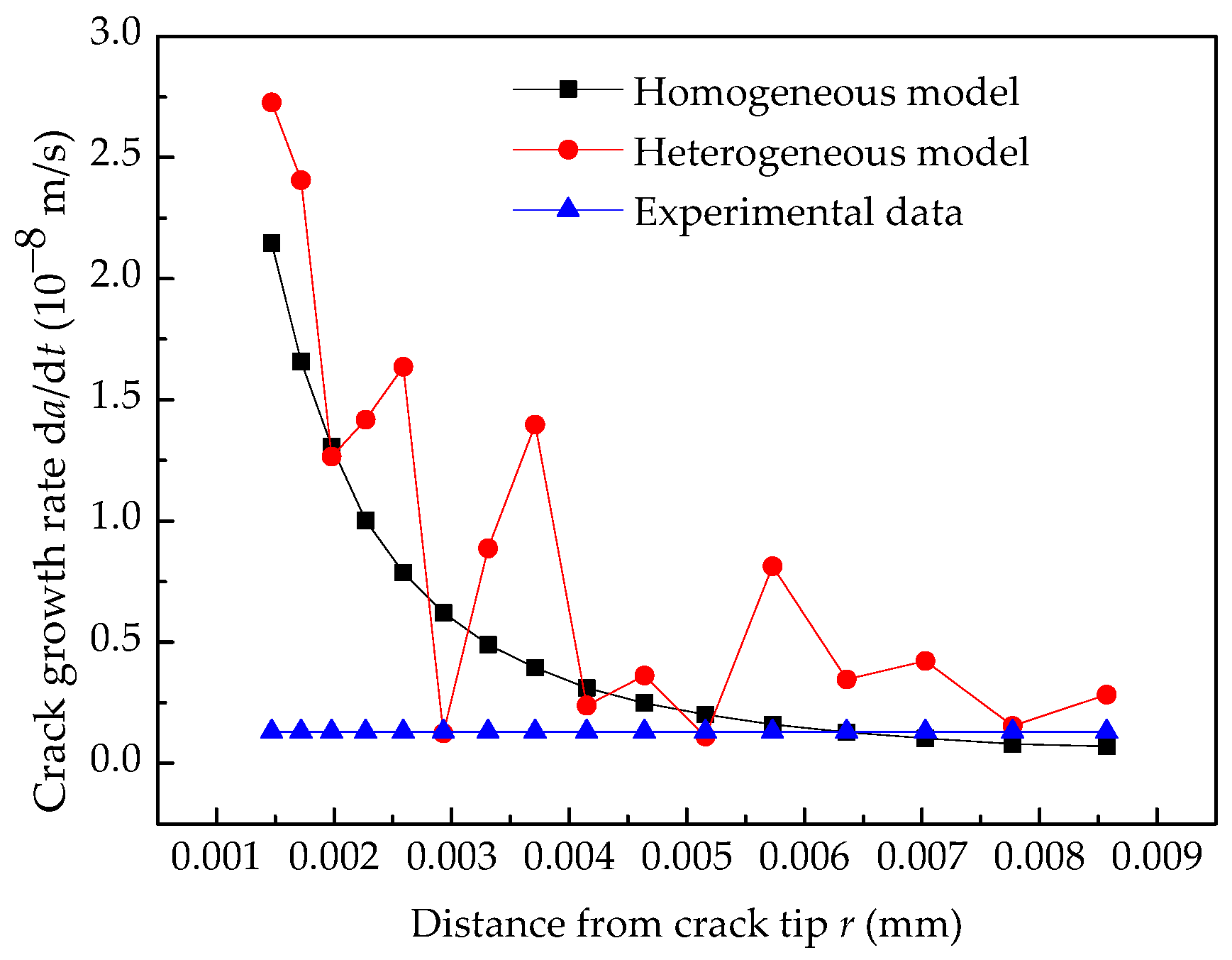
| Material Parameter | Value |
|---|---|
| Young’s Modulus, E (MPa) | 189,500 |
| Poisson’s ratio, ν | 0.286 |
| Yield strength, σ0 (MPa) | 436 |
| Yield offset, α | 3.075 |
| Hardening exponent, n | 6.495 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Wang, S.; Xue, H.; Wang, Z. Effect of Material Heterogeneity on Environmentally Assisted Cracking Growth Rate of Alloy 600 for Safe-End Welded Joints. Materials 2021, 14, 6186. https://doi.org/10.3390/ma14206186
Zhao K, Wang S, Xue H, Wang Z. Effect of Material Heterogeneity on Environmentally Assisted Cracking Growth Rate of Alloy 600 for Safe-End Welded Joints. Materials. 2021; 14(20):6186. https://doi.org/10.3390/ma14206186
Chicago/Turabian StyleZhao, Kuan, Shuai Wang, He Xue, and Zheng Wang. 2021. "Effect of Material Heterogeneity on Environmentally Assisted Cracking Growth Rate of Alloy 600 for Safe-End Welded Joints" Materials 14, no. 20: 6186. https://doi.org/10.3390/ma14206186
APA StyleZhao, K., Wang, S., Xue, H., & Wang, Z. (2021). Effect of Material Heterogeneity on Environmentally Assisted Cracking Growth Rate of Alloy 600 for Safe-End Welded Joints. Materials, 14(20), 6186. https://doi.org/10.3390/ma14206186







