Magneto-Mechanical Coupling in Magneto-Active Elastomers
Abstract
1. Introduction
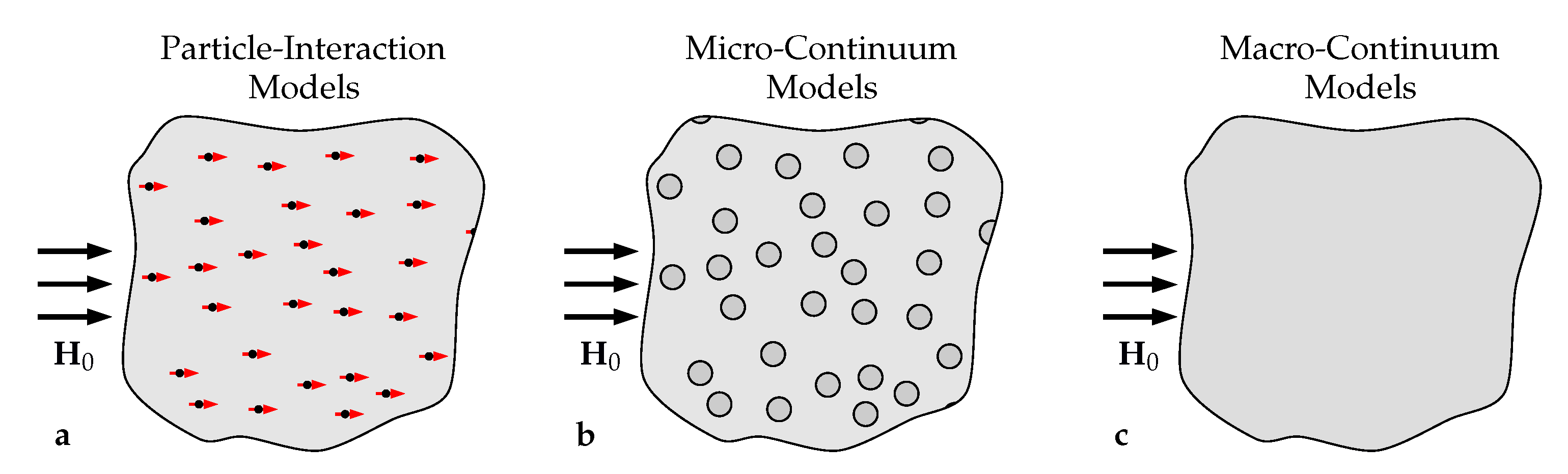
2. Micro-Modeling Strategies
2.1. Micro-Continuum Model
2.1.1. Governing Equations
2.1.2. Constitutive Models
2.1.3. Computational Homogenization Framework
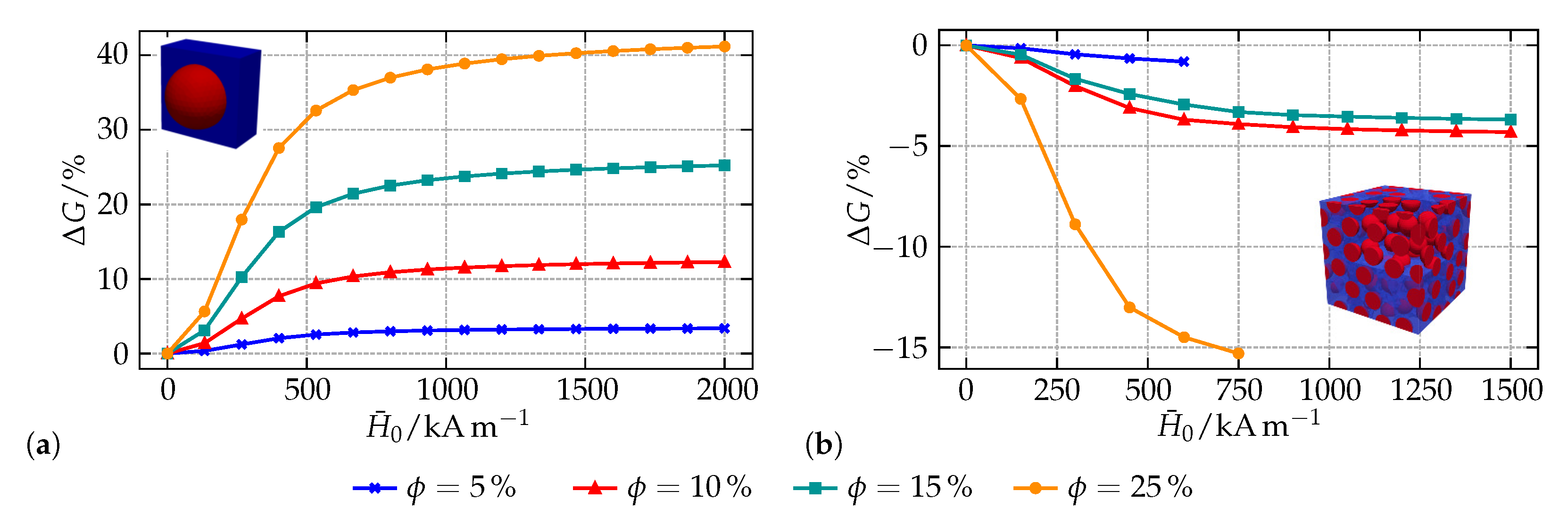
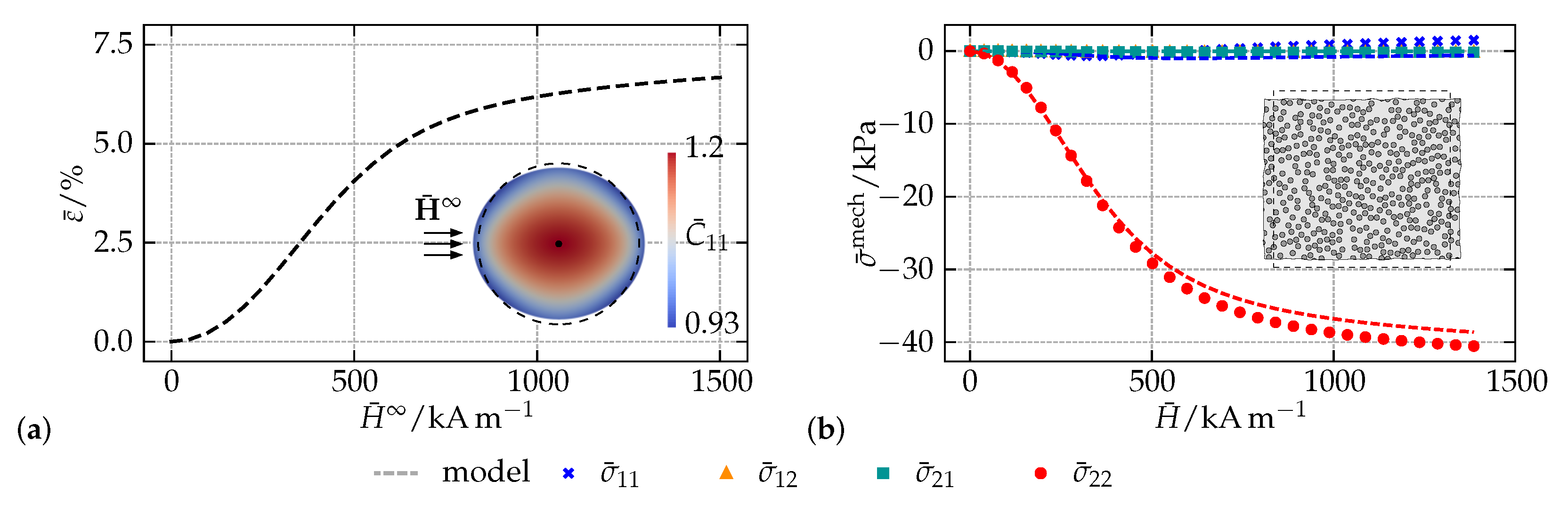
2.1.4. Model Applications
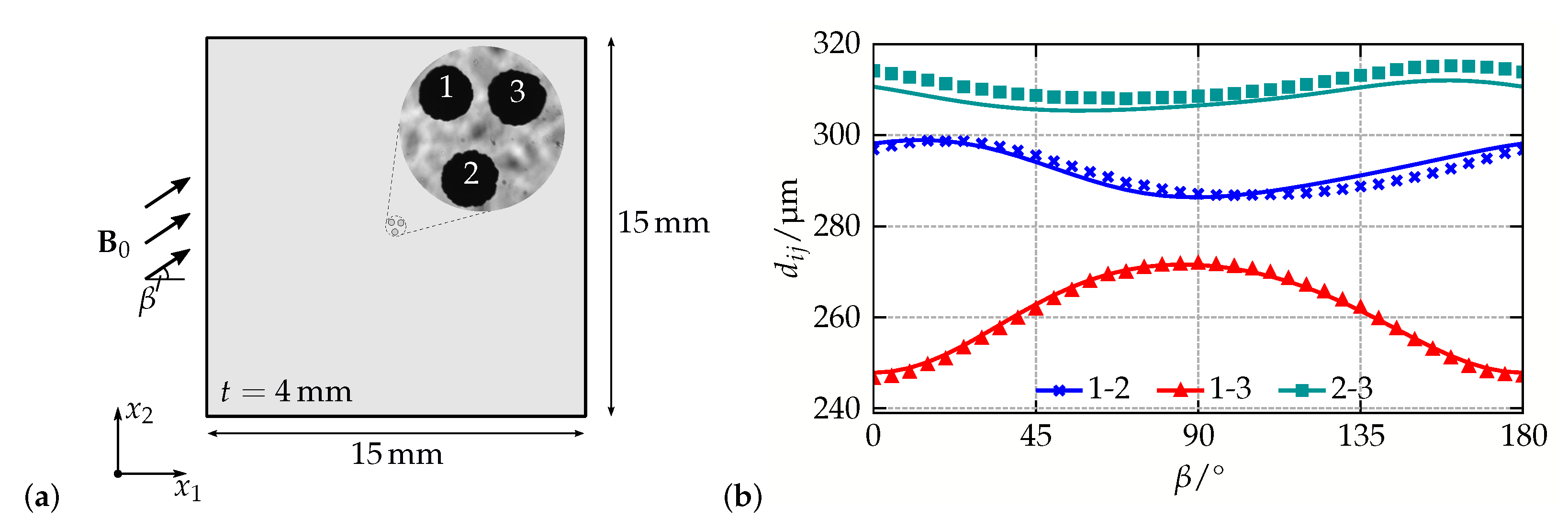
Model Validation by Means of a Simplified MAE Specimen
Field-Dependent Behavior of MAE Microstructures
Macroscopic Model Calibration Using a Decoupled Multiscale Framework
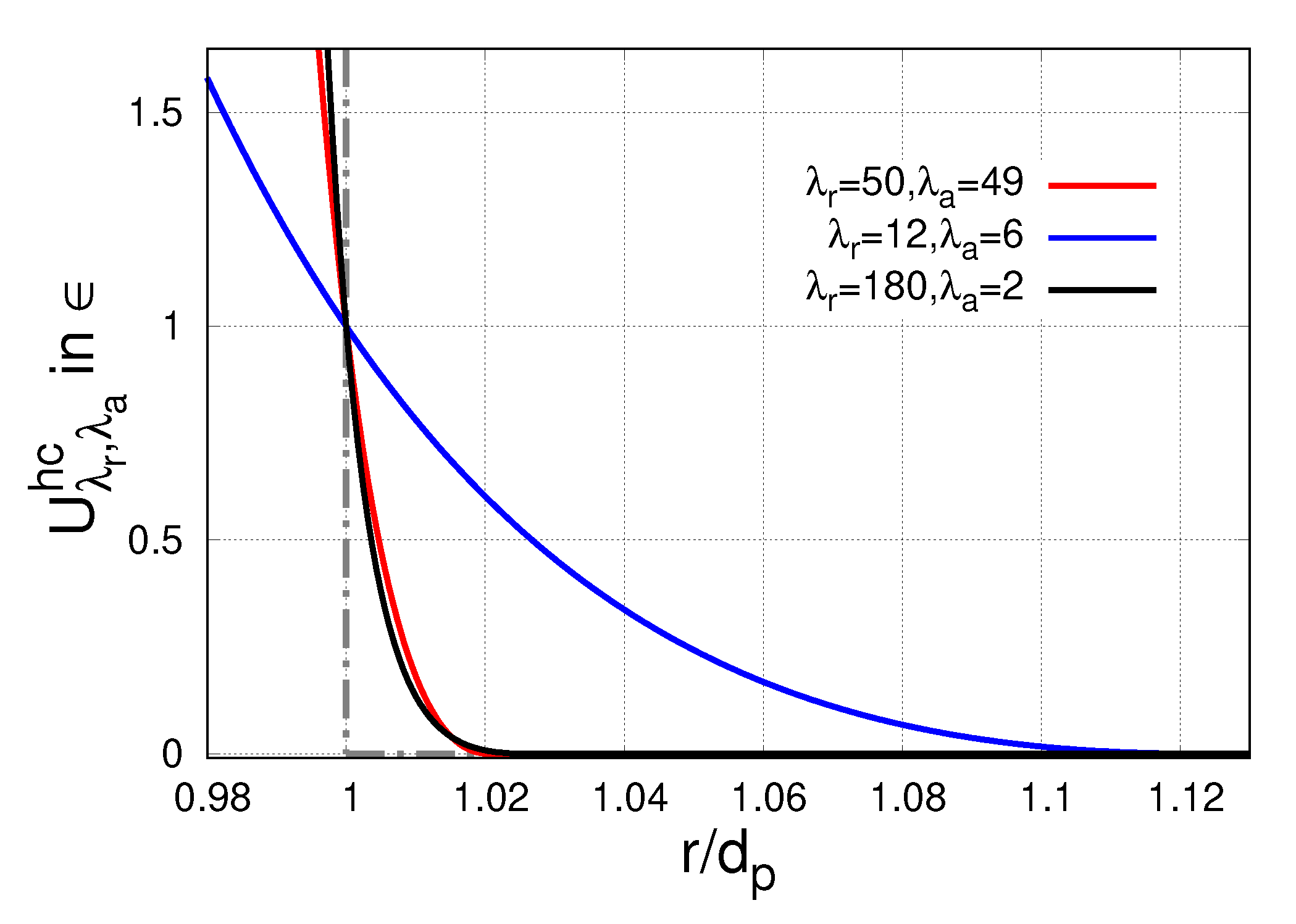
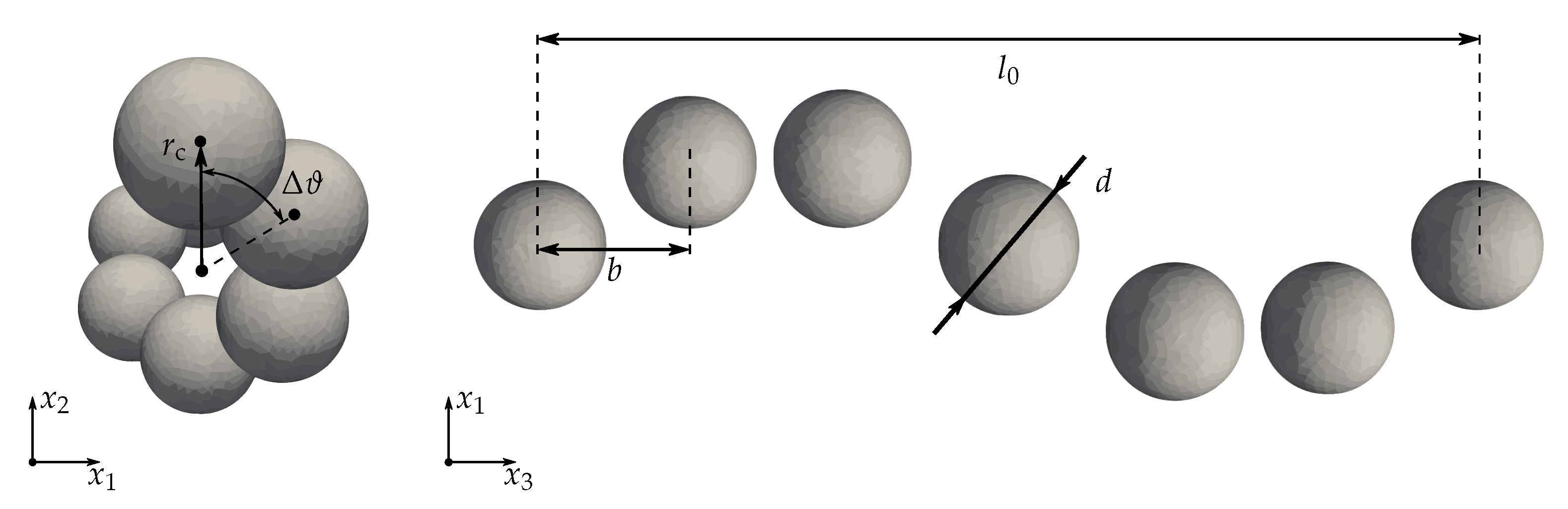
2.2. Dipole Approach to Particle Interactions
2.2.1. Effective Macroscopic Behavior—Minimum of Global Energy
2.2.2. Explicit Particle Structures—Balance of Local Forces
3. Comparison of the Approaches
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Varga, Z.; Filipcsei, G.; Zrínyi, M. Magnetic Field Sensitive Functional Elastomers with Tuneable Elastic Modulus. Polymer 2006, 47, 227–233. [Google Scholar] [CrossRef]
- Abramchuk, S.; Kramarenko, E.; Stepanov, G.; Nikitin, L.V.; Filipcsei, G.; Khokhlov, A.R.; Zrínyi, M. Novel Highly Elastic Magnetic Materials for Dampers and Seals: Part I. Preparation and Characterization of the Elastic Materials. Polym. Adv. Technol. 2007, 18, 883–890. [Google Scholar] [CrossRef]
- Stepanov, G.; Chertovich, A.; Kramarenko, E. Magnetorheological and Deformation Properties of Magnetically Controlled Elastomers with Hard Magnetic Filler. J. Magn. Magn. Mater. 2012, 324, 3448–3451. [Google Scholar] [CrossRef]
- Hintze, C.; Borin, D.Y.; Ivaneyko, D.; Toshchevikov, V.; Saphiannikova-Grenzer, M.; Heirich, G. Soft Magnetic Elastomers with Controllable Stiffness: Experiments and Modelling. Kautsch. Gummi Kunststoffe 2014, 67, 53–59. [Google Scholar]
- Stepanov, G.; Abramchuk, S.; Grishin, D.; Nikitin, L.; Kramarenko, E.; Khokhlov, A. Effect of a Homogeneous Magnetic Field on the Viscoelastic Behavior of Magnetic Elastomers. Polymer 2007, 48, 488–495. [Google Scholar] [CrossRef]
- Chertovich, A.V.; Stepanov, G.V.; Kramarenko, E.Y.; Khokhlov, A.R. New Composite Elastomers with Giant Magnetic Response. Macromol. Mater. Eng. 2010, 295, 336–341. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Ecker, E.; Stepanov, G.V.; Shamonin, M.; Monkman, G.J.; Kramarenko, E.Y.; Khokhlov, A.R. Experimental Study of the Magnetic Field Enhanced Payne Effect in Magnetorheological Elastomers. Soft Matter 2014, 10, 8765–8776. [Google Scholar] [CrossRef] [PubMed]
- Stoll, A.; Mayer, M.; Monkman, G.J.; Shamonin, M. Evaluation of Highly Compliant Magneto-Active Elastomers with Colossal Magnetorheological Response. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Stepanov, G.V.; Shamonin, M.; Monkman, G.J.; Khokhlov, A.R.; Kramarenko, E.Y. Hysteresis of the Viscoelastic Properties and the Normal Force in Magnetically and Mechanically Soft Magnetoactive Elastomers: Effects of Filler Composition, Strain Amplitude and Magnetic Field. Polymer 2015, 76, 191–202. [Google Scholar] [CrossRef]
- Samal, S.; Škodová, M.; Abate, L.; Blanco, I. Magneto-Rheological Elastomer Composites. A Review. Appl. Sci. 2020, 10, 4899. [Google Scholar] [CrossRef]
- Coquelle, E.; Bossis, G. Magnetostriction and Piezoresistivity in Elastomers Filled with Magnetic Particles. J. Adv. Sci. 2005, 17, 132–138. [Google Scholar] [CrossRef]
- Becker, T.I.; Zimmermann, K.; Borin, D.Y.; Stepanov, G.V.; Storozhenko, P.A. Dynamic Response of a Sensor Element Made of Magnetic Hybrid Elastomer with Controllable Properties. J. Magn. Magn. Mater. 2018, 449, 77–82. [Google Scholar] [CrossRef]
- Becker, T.I.; Böhm, V.; Chavez Vega, J.; Odenbach, S.; Raikher, Y.L.; Zimmermann, K. Magnetic-Field-Controlled Mechanical Behavior of Magneto-Sensitive Elastomers in Applications for Actuator and Sensor Systems. Arch. Appl. Mech. 2019, 89, 133–152. [Google Scholar] [CrossRef]
- Liu, F.; Alici, G.; Zhang, B.; Beirne, S.; Li, W. Fabrication and Characterization of a Magnetic Micro-Actuator Based on Deformable Fe-Doped PDMS Artificial Cilium Using 3D Printing. Smart Mater. Struct. 2015, 24, 035015. [Google Scholar] [CrossRef]
- Diguet, G.; Sebald, G.; Nakano, M.; Lallart, M.; Cavaillé, J.Y. Magnetic Particle Chains Embedded in Elastic Polymer Matrix under Pure Transverse Shear and Energy Conversion. J. Magn. Magn. Mater. 2019, 481, 39–49. [Google Scholar] [CrossRef]
- Diguet, G.; Sebald, G.; Nakano, M.; Lallart, M.; Cavaillé, J.Y. Optimization of Magneto-Rheological Elastomers for Energy Harvesting Applications. Smart Mater. Struct. 2020, 29, 075017. [Google Scholar] [CrossRef]
- Lallart, M.; Sebald, G.; Diguet, G.; Cavaille, J.Y.; Nakano, M. Anisotropic Magnetorheological Elastomers for Mechanical to Electrical Energy Conversion. J. Appl. Phys. 2017, 122, 103902. [Google Scholar] [CrossRef]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic Soft Continuum Robots. Sci. Robot. 2019, 4, 1–15. [Google Scholar] [CrossRef]
- Said, M.M.; Yunas, J.; Bais, B.; Hamzah, A.A.; Majlis, B.Y. The Design, Fabrication, and Testing of an Electromagnetic Micropump with a Matrix-Patterned Magnetic Polymer Composite Actuator Membrane. Micromachines 2017, 9, 13. [Google Scholar] [CrossRef]
- Guðmundsson, Í. A Feasibility Study of Magnetorheological Elastomers for a Potential Application in Prosthetic Devices. Ph.D. Thesis, University of Iceland, Reykjavyk, Iceland, 2011. [Google Scholar]
- Ubaidillah; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent Progress on Magnetorheological Solids: Materials, Fabrication, Testing, and Applications. Adv. Eng. Mater. 2014, 17, 563–597. [Google Scholar] [CrossRef]
- Lopez-Lopez, M.T.; Duran, J.D.G.; Iskakova, L.Y.; Zubarev, A.Y. Mechanics of Magnetopolymer Composites: A Review. J. Nanofluids 2016, 5, 479–495. [Google Scholar] [CrossRef]
- Cantera, M.A.; Behrooz, M.; Gibson, R.F.; Gordaninejad, F. Modeling of Magneto-Mechanical Response of Magnetorheological Elastomers (MRE) and MRE-Based Systems: A Review. Smart Mater. Struct. 2017, 26, 023001. [Google Scholar] [CrossRef]
- Shamonin, M.; Kramarenko, E.Y. Chapter 7–Highly Responsive Magnetoactive Elastomers. In Novel Magnetic Nanostructures; Advanced Nanomaterials; Domracheva, N., Caporali, M., Rentschler, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 221–245. [Google Scholar]
- Samal, S.; Kolinova, M.; Blanco, I. The Magneto-Mechanical Behavior of Active Components in Iron-Elastomer Composite. J. Compos. Sci. 2018, 2, 54. [Google Scholar] [CrossRef]
- Samal, S.; Škodová, M.; Blanco, I. Effects of Filler Distribution on Magnetorheological Silicon-Based Composites. Materials 2019, 12, 3017. [Google Scholar] [CrossRef] [PubMed]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Modeling of Particle Interactions in Magnetorheological Elastomers. J. Appl. Phys. 2014, 116, 114904. [Google Scholar] [CrossRef]
- Yaremchuk, D.; Toshchevikov, V.; Ilnytskyi, J.; Saphiannikova, M. Magnetic Energy and a Shape Factor of Magneto-Sensitive Elastomer beyond the Point Dipole Approximation. J. Magn. Magn. Mater. 2020, 513, 167069. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Mechanical Properties of Magneto-Sensitive Elastomers: Unification of the Continuum-Mechanics and Microscopic Theoretical Approaches. Soft Matter 2014, 10, 2213–2225. [Google Scholar] [CrossRef]
- Puljiz, M.; Huang, S.; Auernhammer, G.K.; Menzel, A.M. Forces on Rigid Inclusions in Elastic Media and Resulting Matrix-Mediated Interactions. Phys. Rev. Lett. 2016, 117, 238003. [Google Scholar] [CrossRef]
- Yao, J.; Yang, W.; Gao, Y.; Scarpa, F.; Li, Y. Magnetorheological Elastomers with Particle Chain Orientation: Modelling and Experiments. Smart Mater. Struct. 2019, 28, 095008. [Google Scholar] [CrossRef]
- Romeis, D.; Toshchevikov, V.; Saphiannikova, M. Elongated Micro-Structures in Magneto-Sensitive Elastomers: A Dipolar Mean Field Model. Soft Matter 2016, 12, 9364–9376. [Google Scholar] [CrossRef]
- Danas, K. Effective Response of Classical, Auxetic and Chiral Magnetoelastic Materials by Use of a New Variational Principle. J. Mech. Phys. Solids 2017, 105, 25–53. [Google Scholar] [CrossRef]
- Metsch, P.; Kalina, K.A.; Spieler, C.; Kästner, M. A Numerical Study on Magnetostrictive Phenomena in Magnetorheological Elastomers. Comput. Mater. Sci. 2016, 124, 364–374. [Google Scholar] [CrossRef]
- Galipeau, E.; Ponte Castañeda, P. A Finite-Strain Constitutive Model for Magnetorheological Elastomers: Magnetic Torques and Fiber Rotations. J. Mech. Phys. Solids 2013, 61, 1065–1090. [Google Scholar] [CrossRef]
- Chatzigeorgiou, G.; Javili, A.; Steinmann, P. Unified Magnetomechanical Homogenization Framework with Application to Magnetorheological Elastomers. Math. Mech. Solids 2012, 19, 193–211. [Google Scholar] [CrossRef]
- Keip, M.A.; Rambausek, M. Computational and Analytical Investigations of Shape Effects in the Experimental Characterization of Magnetorheological Elastomers. Int. J. Solids Struct. 2017, 121, 1–20. [Google Scholar] [CrossRef]
- Zabihyan, R.; Mergheim, J.; Pelteret, J.P.; Brands, B.; Steinmann, P. FE2 Simulations of Magnetorheological Elastomers: Influence of Microscopic Boundary Conditions, Microstructures and Free Space on the Macroscopic Responses of MREs. Int. J. Solids Struct. 2020, 193–194, 338–356. [Google Scholar] [CrossRef]
- Rambausek, M.; Göküzüm, F.S.; Nguyen, L.T.K.; Keip, M.A. A Two-Scale FE-FFT Approach to Nonlinear Magneto-Elasticity. Int. J. Numer. Methods Eng. 2019, 117, 1117–1142. [Google Scholar] [CrossRef]
- Danas, K.; Kankanala, S.V.; Triantafyllidis, N. Experiments and Modeling of Iron-Particle-Filled Magnetorheological Elastomers. J. Mech. Phys. Solids 2012, 60, 120–138. [Google Scholar] [CrossRef]
- Haldar, K.; Kiefer, B.; Menzel, A. Finite Element Simulation of Rate-Dependent Magneto-Active Polymer Response. Smart Mater. Struct. 2016, 25, 104003. [Google Scholar] [CrossRef]
- Kalina, K.A.; Metsch, P.; Brummund, J.; Kästner, M. A Macroscopic Model for Magnetorheological Elastomers Based on Microscopic Simulations. Int. J. Solids Struct. 2020, 193–194, 200–212. [Google Scholar] [CrossRef]
- Mukherjee, D.; Bodelot, L.; Danas, K. Microstructurally-Guided Explicit Continuum Models for Isotropic Magnetorheological Elastomers with Iron Particles. Int. J. Non-Linear Mech. 2020, 120, 103380. [Google Scholar] [CrossRef]
- Lefèvre, V.; Danas, K.; Lopez-Pamies, O. Two Families of Explicit Models Constructed from a Homogenization Solution for the Magnetoelastic Response of MREs Containing Iron and Ferrofluid Particles. Int. J. Non-Linear Mech. 2020, 119, 103362. [Google Scholar] [CrossRef]
- Rambausek, M.; Keip, M.A. Analytical Estimation of Non-Local Deformation-Mediated Magneto-Electric Coupling in Soft Composites. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170803. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.Y.; Jiang, Z.Y. Deformation in Magnetorheological Elastomer and Elastomer—Ferromagnet Composite Driven by a Magnetic Field. Smart Mater. Struct. 2004, 13, 309. [Google Scholar] [CrossRef]
- Ginder, J.M.; Clark, S.M.; Schlotter, W.F.; Nichols, M.E. Magnetostrictive Phenomena in Magnetorheological Elastomers. Int. J. Mod. Phys. B 2002, 16, 2412–2418. [Google Scholar] [CrossRef]
- Guan, X.; Dong, X.; Ou, J. Magnetostrictive Effect of Magnetorheological Elastomer. J. Magn. Magn. Mater. 2008, 320, 158–163. [Google Scholar] [CrossRef]
- Romeis, D.; Metsch, P.; Kästner, M.; Saphiannikova, M. Theoretical Models for Magneto-Sensitive Elastomers: A Comparison between Continuum and Dipole Approaches. Phys. Rev. E 2017, 95, 042501. [Google Scholar] [CrossRef]
- Saveliev, D.V.; Belyaeva, I.A.; Chashin, D.V.; Fetisov, L.Y.; Romeis, D.; Kettl, W.; Kramarenko, E.Y.; Saphiannikova, M.; Stepanov, G.V.; Shamonin, M. Giant Extensional Strain of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields. Materials 2020, 13, 3297. [Google Scholar] [CrossRef]
- Borin, D.; Stepanov, G.; Dohmen, E. Hybrid Magnetoactive Elastomer with a Soft Matrix and Mixed Powder. Arch. Appl. Mech. 2019, 89, 105–117. [Google Scholar] [CrossRef]
- Winger, J.; Schümann, M.; Kupka, A.; Odenbach, S. Influence of the Particle Size on the Magnetorheological Effect of Magnetorheological Elastomers. J. Magn. Magn. Mater. 2019, 481, 176–182. [Google Scholar] [CrossRef]
- Martin, J.E.; Anderson, R.A.; Williamson, R.L. Generating Strange Magnetic and Dielectric Interactions: Classical Molecules and Particle Foams. J. Chem. Phys. 2003, 118, 1557–1570. [Google Scholar] [CrossRef]
- De Groot, S.R.; Suttorp, L.G. Foundations of Electrodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Metsch, P.; Kalina, K.A.; Brummund, J.; Kästner, M. Two- and Three-Dimensional Modeling Approaches in Magneto-Mechanics: A Quantitative Comparison. Arch. Appl. Mech. 2019, 89, 47–62. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. Nonlinear Magnetoelastic Deformations. Q. J. Mech. Appl. Math. 2004, 57, 599–622. [Google Scholar] [CrossRef]
- Eringen, A.C.; Maugin, G.A. Electrodynamics of Continua I: Foundations and Solid Media; Springer: New York, NY, USA, 1990. [Google Scholar]
- Coleman, B.D.; Noll, W. The Thermodynamics of Elastic Materials with Heat Conduction and Viscosity. Arch. Ration. Mech. Anal. 1963, 13, 167–178. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Nachdruck, K., Ed.; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Spieler, C.; Kästner, M.; Goldmann, J.; Brummund, J.; Ulbricht, V. XFEM Modeling and Homogenization of Magnetoactive Composites. Acta Mech. 2013, 224, 2453–2469. [Google Scholar] [CrossRef]
- Metsch, P.; Schmidt, H.; Sindersberger, D.; Kalina, K.A.; Brummund, J.; Auernhammer, G.K.; Monkman, G.J.; Kästner, M. Field-Induced Interactions in Magneto-Active Elastomers—A Comparison of Experiments and Simulations. Smart Mater. Struct. 2020, 29, 085026. [Google Scholar] [CrossRef]
- Hill, R. Elastic Properties of Reinforced Solids: Some Theoretical Principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Pössinger, T. Experimental Characterization, Modeling and Simulation of Magneto-Rheological Elastomers. Ph.D. Thesis, École Polytechnique, Paris, France, 2015. [Google Scholar]
- Schümann, M.; Odenbach, S. In-Situ Observation of the Particle Microstructure of Magnetorheological Elastomers in Presence of Mechanical Strain and Magnetic Fields. J. Magn. Magn. Mater. 2017, 441, 88–92. [Google Scholar] [CrossRef]
- Dargahi, A.; Sedaghati, R.; Rakheja, S. On the Properties of Magnetorheological Elastomers in Shear Mode: Design, Fabrication and Characterization. Compos. Part B Eng. 2019, 159, 269–283. [Google Scholar] [CrossRef]
- Borin, D.Y.; Stepanov, G.V.; Odenbach, S. Tuning the Tensile Modulus of Magnetorheological Elastomers with Magnetically Hard Powder. J. Phys. Conf. Ser. 2013, 412, 012040. [Google Scholar] [CrossRef]
- Kalina, K.; Raßloff, A.; Wollner, M.; Metsch, P.; Brummund, J.; Kästner, M. Multiscale Modeling and Simulation of Magneto-Active Elastomers Based on Experimental Data. Phys. Sci. Rev. 2020. accepted for publication. [Google Scholar]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C.; Bullions, T.A. The Magnetoviscoelastic Response of Elastomer Composites Consisting of Ferrous Particles Embedded in a Polymer Matrix. J. Intell. Mater. Syst. Struct. 1996, 7, 613–622. [Google Scholar] [CrossRef]
- Galipeau, E.; Rudykh, S.; de Botton, G.; Ponte Castañeda, P. Magnetoactive Elastomers with Periodic and Random Microstructures. Int. J. Solids Struct. 2014, 51, 3012–3024. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.P.; Saphiannikova, M.; Heinrich, G. Magneto-Sensitive Elastomers in a Homogeneous Magnetic Field: A Regular Rectangular Lattice Model. Macromol. Theory Simul. 2011, 20, 411–424. [Google Scholar] [CrossRef]
- Gebhart, P.; Attaran, A.; Wallmersperger, T. Multiphysics Modeling of Fluid-Saturated Porous Ferrogels at Finite Strains. Phys. Sci. Rev. 2020. accepted for publication. [Google Scholar] [CrossRef]
- Puljiz, M.; Huang, S.; Kalina, K.A.; Nowak, J.; Odenbach, S.; Kästner, M.; Auernhammer, G.K.; Menzel, A.M. Reversible Magnetomechanical Collapse: Virtual Touching and Detachment of Rigid Inclusions in a Soft Elastic Matrix. Soft Matter 2018, 14, 6809–6821. [Google Scholar] [CrossRef]
- Kalina, K.A.; Metsch, P.; Brummund, J.; Kästner, M. A Macroscopic Model for Magneto-Active Elastomers Based on Microscopic Simulations. Proc. Appl. Math. Mech. 2020. accepted for publication. [Google Scholar]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Effects of Particle Distribution on Mechanical Properties of Magneto-Sensitive Elastomers in a Homogeneous Magnetic Field. Condens. Matter Phys. 2012, 15, 33601. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M. Dynamic Moduli of Magneto-Sensitive Elastomers: A Coarse-Grained Network Model. Soft Matter 2015, 11, 7627–7638. [Google Scholar] [CrossRef] [PubMed]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M. Dynamic-Mechanical Behaviour of Anisotropic Magneto-Sensitive Elastomers. Polymer 2018, 147, 95–107. [Google Scholar] [CrossRef]
- Romeis, D.; Kostrov, S.A.; Kramarenko, E.Y.; Stepanov, G.V.; Shamonin, M.; Saphiannikova, M. Magnetic-Field-Induced Stress in Confined Magnetoactive Elastomers. Soft Matter 2020, 16, 9047–9058. [Google Scholar] [CrossRef]
- Romeis, D.; Toshchevikov, V.; Saphiannikova, M. Effects of Local Rearrangement of Magnetic Particles on Deformation in Magneto-Sensitive Elastomers. Soft Matter 2019, 15, 3552–3564. [Google Scholar] [CrossRef] [PubMed]
- Chougale, S.; Romeis, D.; Saphiannikova, M. Transverse Isotropy in Magnetoactive Elastomers. J. Magn. Magn. Mater. 2021, 523, 167597. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Gundermann, T.; Dobroserdova, A.; Kantorovich, S.S.; Odenbach, S. Importance of Matrix Inelastic Deformations in the Initial Response of Magnetic Elastomers. Soft Matter 2018, 14, 2170–2183. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, P.A.; Minina, E.S.; Kantorovich, S.S.; Kramarenko, E.Y. Surface Relief of Magnetoactive Elastomeric Films in a Homogeneous Magnetic Field: Molecular Dynamics Simulations. Soft Matter 2019, 15, 175–189. [Google Scholar] [CrossRef] [PubMed]
- Stolbov, O.V.; Raikher, Y.L. Mesostructural Origin of the Field-Induced Pseudo-Plasticity Effect in a Soft Magnetic Elastomer. IOP Conf. Ser. Mater. Sci. Eng. 2019, 581, 012003. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Raikher, Y.L. Magnetostriction Effect in Soft Magnetic Elastomers. Arch. Appl. Mech. 2019, 89, 63–76. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Sánchez, P.A.; Kantorovich, S.S.; Raikher, Y.L. Magnetostriction in Elastomers with Mixtures of Magnetically Hard and Soft Microparticles: Effects of Non-Linear Magnetization and Matrix Rigidity. arXiv 2020, arXiv:2010.03684. [Google Scholar]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Mesoscopic Magnetomechanical Hysteresis in a Magnetorheological Elastomer. Phys. Rev. E 2015, 92, 023202. [Google Scholar] [CrossRef]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Dipolar Models of Ferromagnet Particles Interaction in Magnetorheological Composites. J. Optoelectron. Adv. Mater. 2015, 17, 1106–1113. [Google Scholar]
- Puljiz, M.; Menzel, A.M. Forces and Torques on Rigid Inclusions in an Elastic Environment: Resulting Matrix-Mediated Interactions, Displacements, and Rotations. Phys. Rev. E 2017, 95, 053002. [Google Scholar] [CrossRef] [PubMed]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Zhang, J.; Pang, H.; Wang, Y.; Gong, X. The Magneto-Mechanical Properties of off-Axis Anisotropic Magnetorheological Elastomers. Compos. Sci. Technol. 2020, 191, 108079. [Google Scholar] [CrossRef]
- Martin, J.E.; Anderson, R.A.; Read, D.; Gulley, G. Magnetostriction of Field-Structured Magnetoelastomers. Phys. Rev. E 2006, 74, 051507. [Google Scholar] [CrossRef] [PubMed]
- Fischer, L.; Menzel, A.M. Towards a Soft Magnetoelastic Twist Actuator. Phys. Rev. Res. 2020, 2, 023383. [Google Scholar] [CrossRef]
- Fischer, L.; Menzel, A.M. Magnetically Induced Elastic Deformations in Model Systems of Magnetic Gels and Elastomers Containing Particles of Mixed Size. Smart Mater. Struct. 2020, 30, 014003. [Google Scholar] [CrossRef]
- Han, Y.; Mohla, A.; Huang, X.; Hong, W.; Faidley, L.E. Magnetostriction and Field Stiffening of Magneto-Active Elastomers. Int. J. Appl. Mech. 2015, 07, 1550001. [Google Scholar] [CrossRef]
- Mie, G. Zur Kinetischen Theorie Der Einatomigen Körper. Annalen der Physik 1903, 316, 657–697. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Jover, J.; Haslam, A.J.; Galindo, A.; Jackson, G.; Müller, E.A. Pseudo Hard-Sphere Potential for Use in Continuous Molecular-Dynamics Simulation of Spherical and Chain Molecules. J. Chem. Phys. 2012, 137, 144505. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metsch, P.; Romeis, D.; Kalina, K.A.; Raßloff, A.; Saphiannikova, M.; Kästner, M. Magneto-Mechanical Coupling in Magneto-Active Elastomers. Materials 2021, 14, 434. https://doi.org/10.3390/ma14020434
Metsch P, Romeis D, Kalina KA, Raßloff A, Saphiannikova M, Kästner M. Magneto-Mechanical Coupling in Magneto-Active Elastomers. Materials. 2021; 14(2):434. https://doi.org/10.3390/ma14020434
Chicago/Turabian StyleMetsch, Philipp, Dirk Romeis, Karl A. Kalina, Alexander Raßloff, Marina Saphiannikova, and Markus Kästner. 2021. "Magneto-Mechanical Coupling in Magneto-Active Elastomers" Materials 14, no. 2: 434. https://doi.org/10.3390/ma14020434
APA StyleMetsch, P., Romeis, D., Kalina, K. A., Raßloff, A., Saphiannikova, M., & Kästner, M. (2021). Magneto-Mechanical Coupling in Magneto-Active Elastomers. Materials, 14(2), 434. https://doi.org/10.3390/ma14020434





