Silicon Nanowires: A Breakthrough for Thermoelectric Applications
Abstract
:1. Introduction
2. Thermoelectric Properties of Nanostructured Silicon
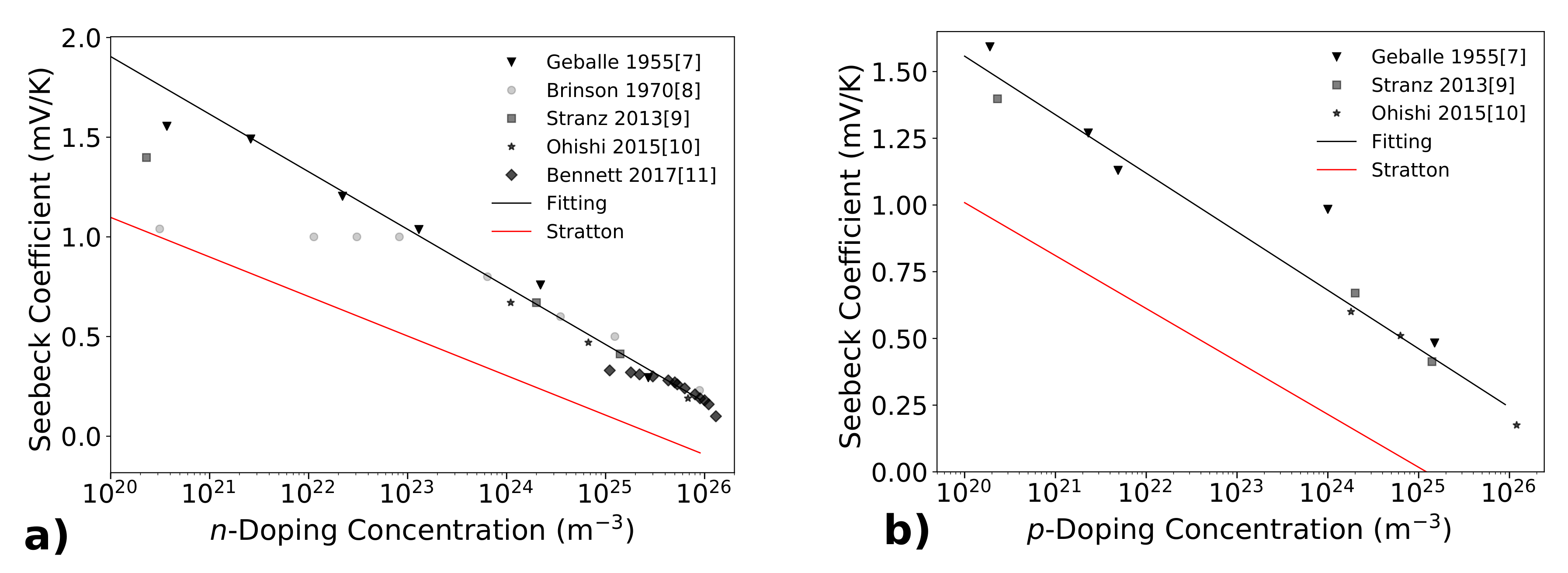
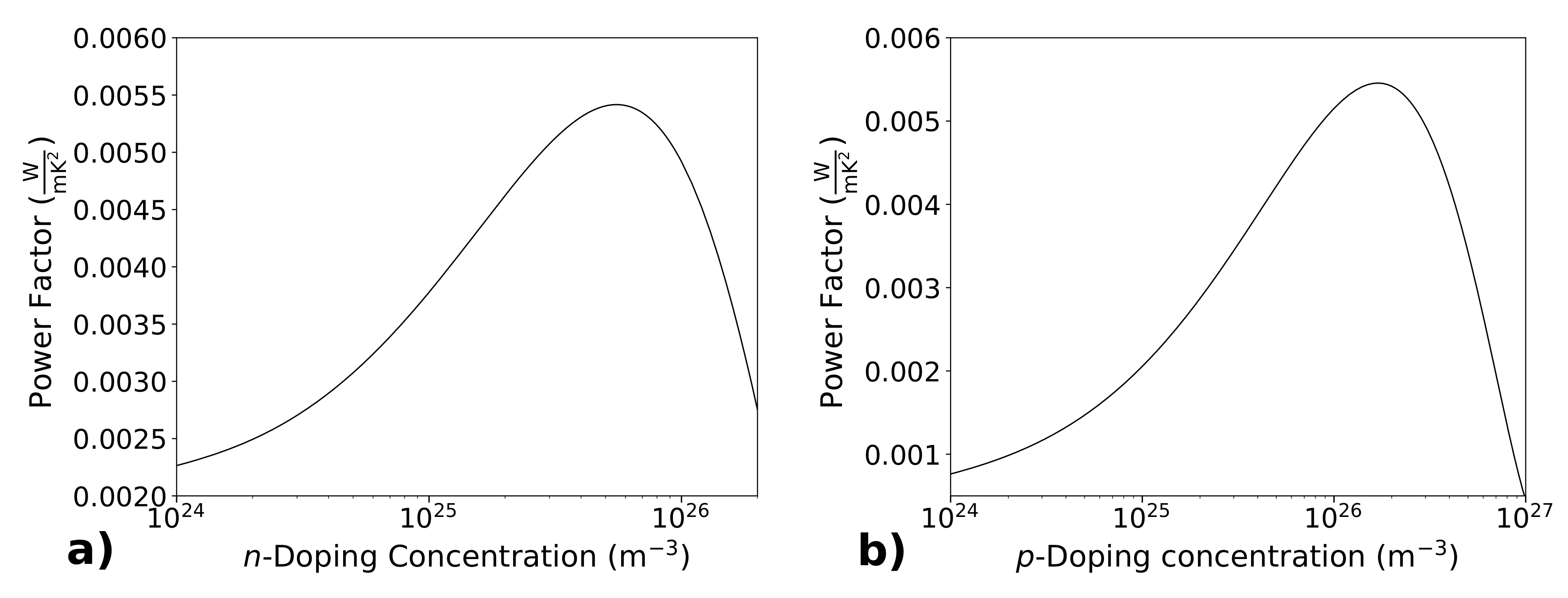
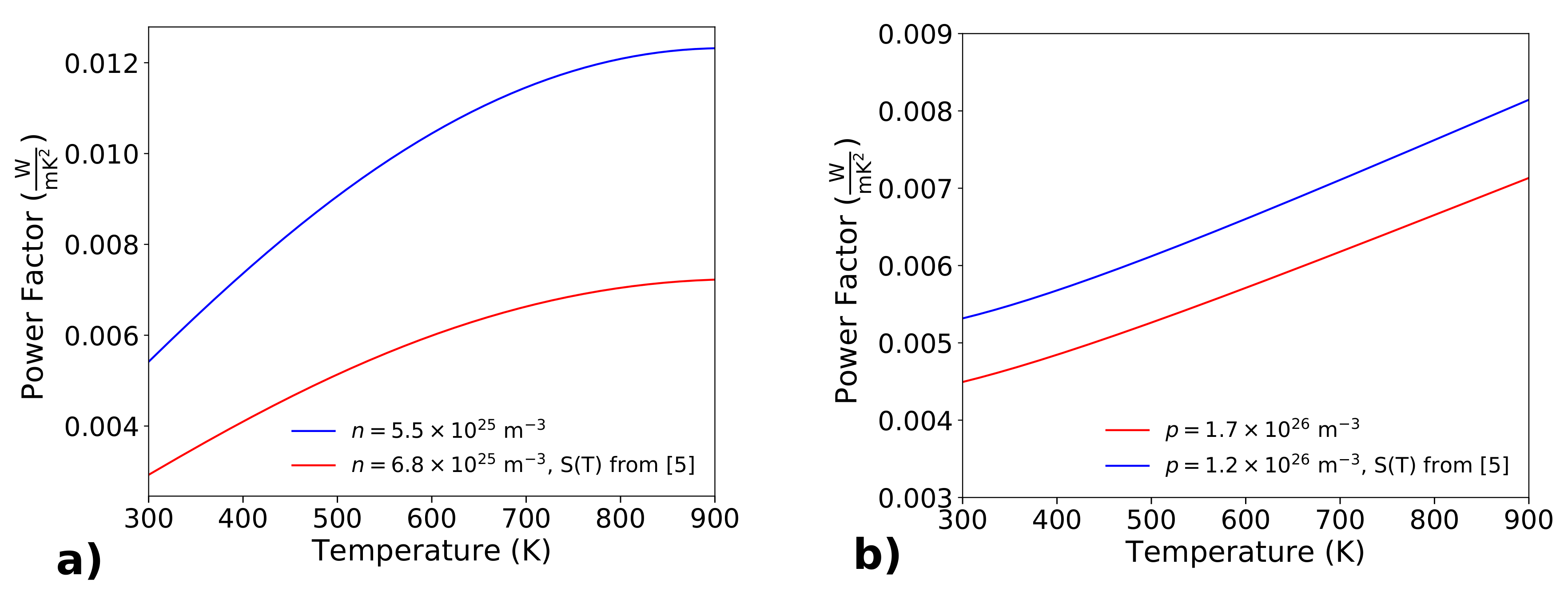
2.1. Electrical Conductivity, Seebeck Coefficient and Power Factor
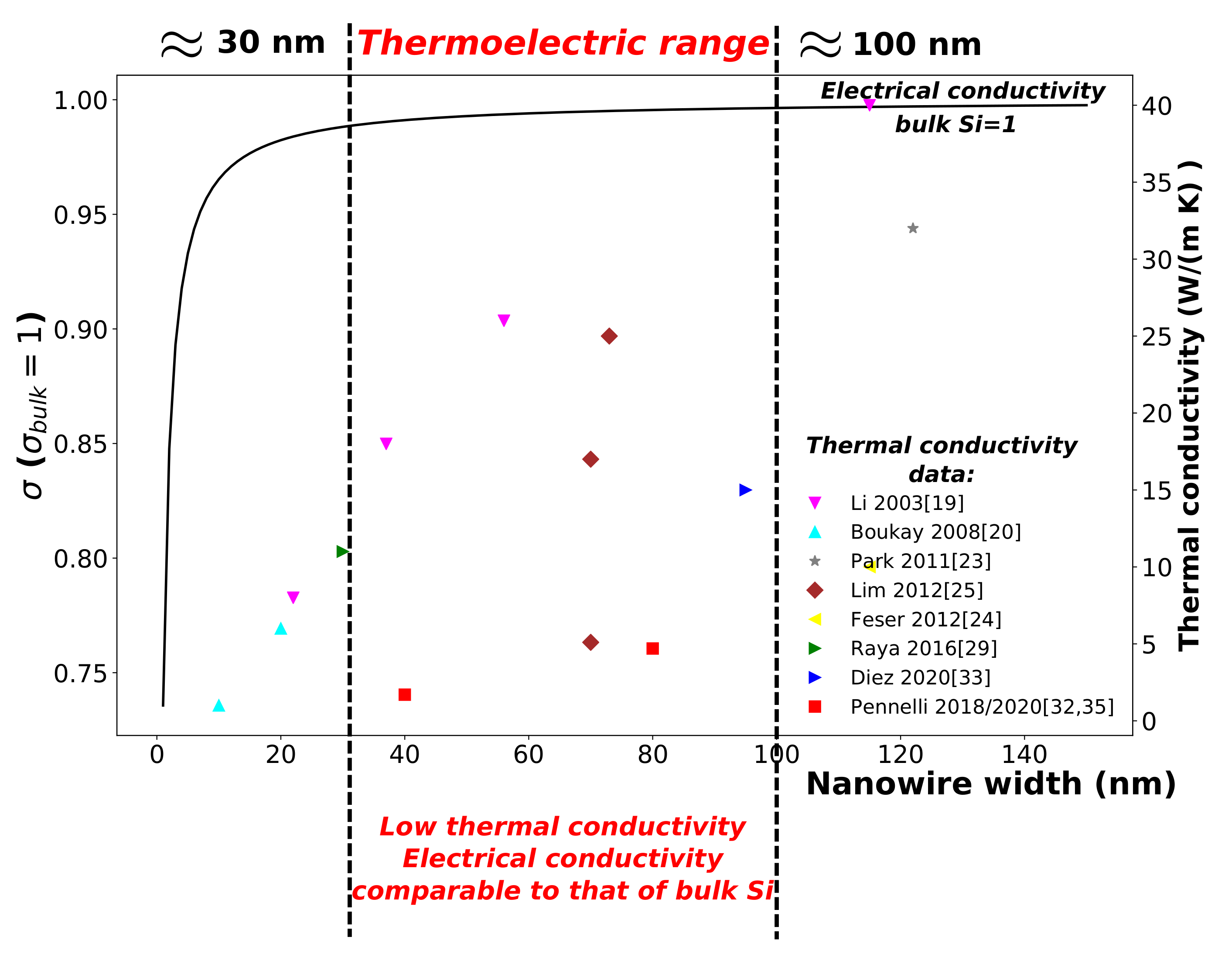
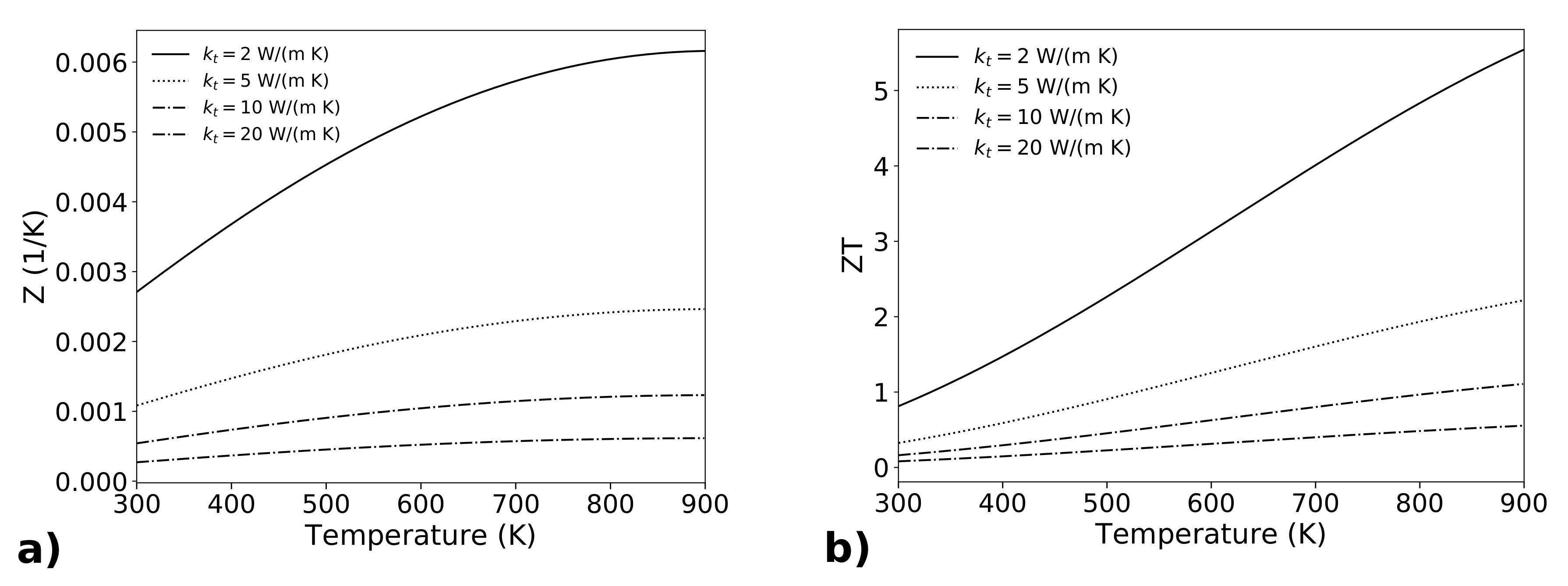
2.2. Thermal Conductivity and Figure of Merit
3. Techniques for All-Silicon Thermoelectric Devices
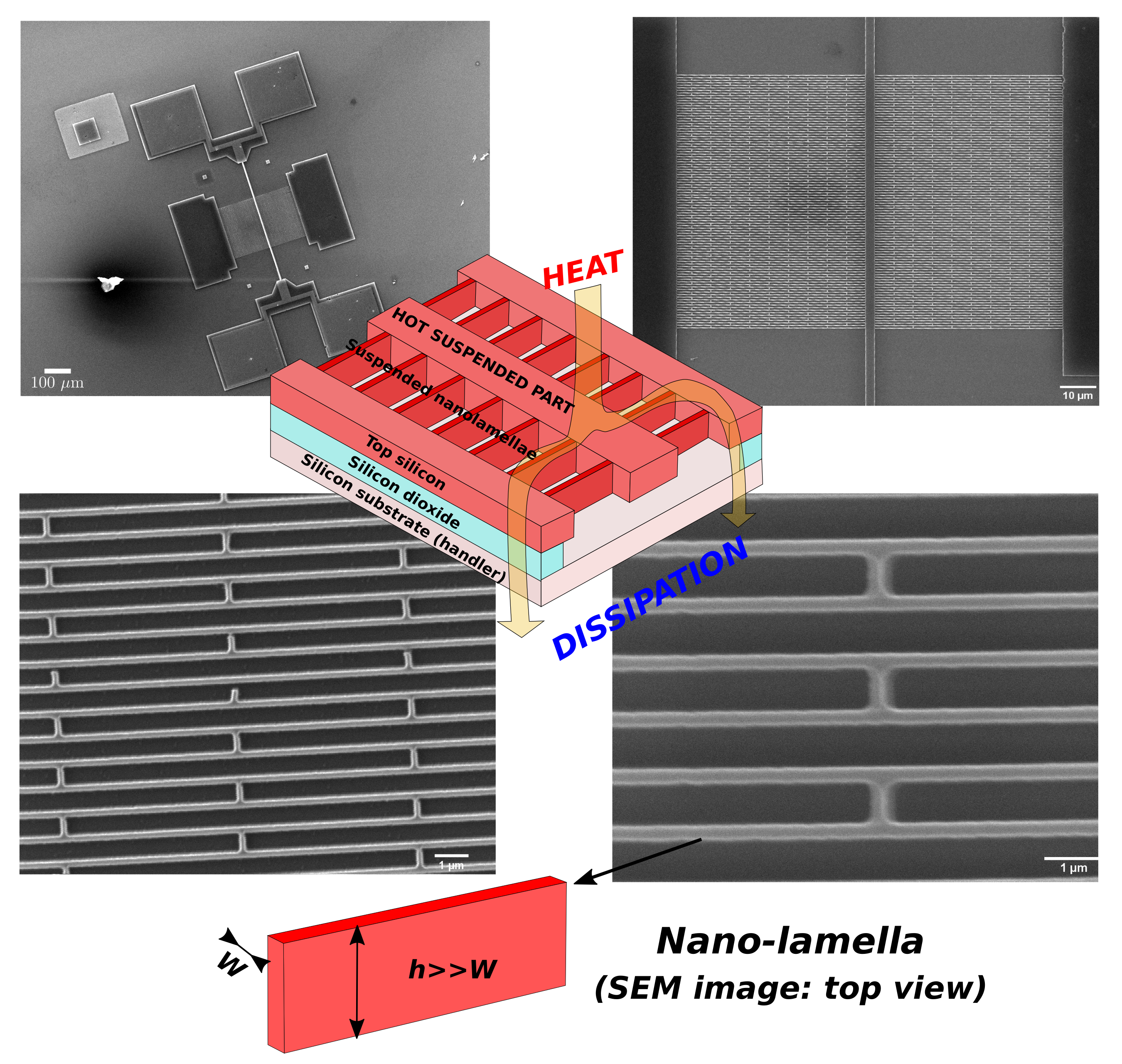
3.1. On-Chip Si Nanowires/Nanostructures for Energy Scavenging
3.2. Si Nanowires/Nanostructures for Energy Macroharvesting
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pourkiaei, S.M.; Ahmadi, M.H.; Sadeghzadeh, M.; Moosavi, S.; Pourfayaz, F.; Chen, L.; Pour Yazdi, M.A.; Kumar, R. Thermoelectric cooler and thermoelectric generator devices: A review of present and potential applications, modeling and materials. Energy 2019, 186, 115849. [Google Scholar] [CrossRef]
- Caballero-Calero, O.; Ares, R.; Martin-Gonzalez, M. Environmentally Friendly Thermoelectric Materials: High Performance from Inorganic Components with Low Toxicity and Abundance in the Earth. Adv. Sustain. Syst. 2021, 2100095. [Google Scholar] [CrossRef]
- Chen, L.; Meng, F.; Ge, Y.; Feng, H.; Xia, S. Performance optimization of a class of combined thermoelectric heating devices. Sci. China Technol. Sci. 2020, 63, 2640–2648. [Google Scholar] [CrossRef]
- Pennelli, G. Review of nanostructured devices for thermoelectric applications. Beilstein J. Nanotechnol. 2014, 5, 1268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pennelli, G. Top-down fabrication of silicon nanowire devices for thermoelectric applications: Properties and perspectives. Eur. Phys. J. B 2015, 88, 121. [Google Scholar] [CrossRef]
- Arora, N.D.; Hauser, R.J.; Roulston, J.D. Electron and Hole Mobilities in Silicon as a Function of Concentration and Temperature. IEEE Trans. Electron Devices 1982, ED-29, 292. [Google Scholar] [CrossRef]
- Masetti, G.; Severi, M.; Solmi, S. Modeling of Carrier Mobility Against Carrier Concentration in Arsenic-, Phosphorus-, and Boron-doped Silicon. IEEE Trans. Electron Devices 1983, 30, 764. [Google Scholar] [CrossRef]
- Reggiani, S.; Valdinoci, M.; Colalongo, L.; Rudan, M.; Baccarani, G.; Stricker, A.D.; Illien, F.; Felber, N.; Fichtner, W.; Zullino, L. Electron and Hole Mobility in Silicon at Large Operating Temperatures—Part I: Bulk Mobility. IEEE Trans. Electron Devices 2002, 49, 490. [Google Scholar] [CrossRef]
- Geballe, T.H.; Hull, G.W. Seebeck Effect in Silicon. Phys. Rev. 1955, 98, 940. [Google Scholar] [CrossRef]
- Brinson, M.E.; Dunstant, W. Thermal conductivity and thermoelectric power of heavily doped n-type silicon. J. Phys. C Solid State Phys. 1970, 3, 483. [Google Scholar] [CrossRef]
- Stranz, A.; Kahler, J.; Waag, A.; Peiner, E. Thermoelectric Properties of High-Doped Silicon from Room Temperature to 900 K. J. Electron. Mater. 2013, 42, 2381. [Google Scholar] [CrossRef]
- Ohishi, Y.; Xie, J.; Miyazaki, Y.; Aikebaier, Y.; Muta, H.; Kurosaki, K.; Yamanaka, S.; Uchida, N.; Tada, T. Thermoelectric properties of heavily boron- and phosphorus-doped silicon. Jpn. J. Appl. Phys. 2015, 54, 071301. [Google Scholar] [CrossRef]
- Bennett, N.S. Thermoelectric performance in n-type bulk silicon: The influence of dopant concentration and dopant species. Phys. Status Solidi 2017, 214, 1700307. [Google Scholar] [CrossRef]
- Dimaggio, E.; Pennelli, G. Potentialities of silicon nanowire forests for thermoelectric generation. Nanotechnology 2018, 29, 135401. [Google Scholar] [CrossRef]
- Stranz, A.; Kahler, J.; Merzsch, A.; Peiner, E. Nanowire silicon as a material for thermoelectric energy conversion. Microsyst. Technol. 2012, 18, 857. [Google Scholar] [CrossRef]
- Neophytou, N.; Foster, S.; Vargiamidis, V.; Pennelli, G.; Narducci, D. Nanostructured potential well/barrier engineering for realizing unprecedentedly large thermoelectric power factors. Mater. Today Phys. 2019, 11, 100159. [Google Scholar] [CrossRef]
- Graziosi, P.; Kumarasinghe, C.; Neophytou, N. Impact of the scattering physics on the power factor of complex thermoelectric materials. J. Appl. Phys. 2019, 126, 155701. [Google Scholar] [CrossRef]
- Neophytou, N.; Zianni, X.; Kosina, H.; Frabboni, S.; Lorenzi, B.; Narducci, D. Simultaneous increase in electrical conductivity and Seebeck coefficient in highly boron-doped nanocrystalline Si. Nanotechnology 2013, 24, 205402. [Google Scholar] [CrossRef]
- Zulian, L.; Segrado, F.; Narducci, D. Annealing of heavily boron-doped silicon: Effect on electrical and thermoelectric properties. J. Nanosci. Nanotechnol. 2017, 17, 1657–1662. [Google Scholar] [CrossRef]
- Bux, S.; Blair, R.; Gogna, P.; Lee, H.; Chen, G.; Dresselhaus, M.; Kaner, R.; Fleurial, J. Nanostructured Bulk Silicon as an Effective Thermoelectric Material. Adv. Funct. Mater. 2009, 19, 2445–2452. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Kim, P.; Shi, L.; Yang, P.; Majumdar, A. Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 2003, 83, 2934–2936. [Google Scholar] [CrossRef]
- Boukay, A.; Bunimovich, Y.; Tahir-Kheli, J.; Yu, J.K.; Goddard, W.A., III; Heat, J.R. Silicon nanowires as efficient thermoelectric materials. Nat. Lett. 2008, 451, 168–171. [Google Scholar] [CrossRef]
- Hochbaum, A.I.; Chen, R.; Delgrado, R.D.; Liang, W.; Garnett, C.E.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nat. Lett. 2008, 451, 163–167. [Google Scholar] [CrossRef]
- Pennelli, G.; Nannini, A.; Macucci, M. Indirect measurement of thermal conductivity in silicon nanowires. J. Appl. Phys. 2014, 115, 084507. [Google Scholar] [CrossRef]
- Park, Y.H.; Kim, J.; Kim, H.; Kim, I.; Lee, K.Y.; Seo, D.; Choi, H.J.; Kim, W. Thermal conductivity of VLS-grown rough Si nanowires with various surface roughnesses and diameters. Appl. Phys. A 2011, 104, 7–14. [Google Scholar] [CrossRef]
- Feser, J.; Sadhu, J.; Azeredo, B.; Hsu, H.; Ma, J.; Kim, J.; Seong, M.; Fang, N.; Li, X.; Ferreira, P.; et al. Thermal conductivity of silicon nanowire arrays with controlled roughness. J. Appl. Phys. 2012, 112, 114306. [Google Scholar] [CrossRef]
- Lim, J.; Hippalgaonkar, K.; Andrews, C.S.; Majumdar, A.; Yang, P. Quantifying surface roughness effects on phonon transport in silicon nanowires. Nano Lett. 2012, 12, 2475–2482. [Google Scholar] [CrossRef] [PubMed]
- Karg, S.; Mensch, P.; Gotsmann, B.; Schmid, H.; DasKanungo, P.; Ghoneim, H.; Schmidt, V.; Bjork, M.; Troncale, V.; Riel, H. Measurement of thermoelectric properties of single semiconductor nanowires. J. Electron. Mater. 2013, 42, 2409. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, S.; Zheng, R.; Cheng, G. Significant reduction of thermal conductivity in silicon nanowire arrays. Nanotechnology 2013, 24, 505718. [Google Scholar] [CrossRef] [PubMed]
- Sadhu, J.; Tian, H.; Ma, J.; Azeredo, B.; Kim, J.; Balasundaram, K.; Zhang, C.; Li, X.; Ferreia, P.; Sinha, S. Quenched Phonon Drag in Silicon Nanowires Reveals Significant Effect in the Bulk at Room Temperature. Nano Lett. 2015, 15, 3159. [Google Scholar] [CrossRef]
- Raja, S.N.; Rhyner, R.; Vuttivorakulchai, K.; Luisier, M.; Poulikakos, D. Length Scale of Diffusive Phonon Transport in Suspended Thin Silicon Nanowires. Nano Lett. 2017, 17, 276–283. [Google Scholar] [CrossRef] [PubMed]
- Glynn, C.; Jones, K.; Mogili, V.; McSweeney, W.; O’Dwyer, C. The Nature of Silicon Nanowire Roughness and Thermal Conductivity Suppression by Phonon Scattering Mechanisms. ECS J. Solid State Sci. Technol. 2017, 6, N3029. [Google Scholar] [CrossRef] [Green Version]
- Fan, D.; Sigg, H.; Spolenak, R.; Ekinci, Y. Strain and thermal conductivity in ultrathin suspended silicon nanowires. Phys. Rev. B 2017, 96, 115307. [Google Scholar] [CrossRef] [Green Version]
- Elyamny, S.; Dimaggio, E.; Magagna, S.; Narducci, D.; Pennelli, G. High Power Thermoelectric Generator Based on Vertical Silicon Nanowires. Nano Lett. 2020, 20, 4748–4753. [Google Scholar] [CrossRef]
- Diez, G.; Gordillo, J.; Pujadó, M.; Salleras, M.; Fonseca, L.; Morata, A.; Rubio, A. Enhanced thermoelecric figure of merit of individual Si nanowires with ultralow contact resistance. Nano Energy 2020, 67, 104191. [Google Scholar] [CrossRef]
- Melosh, N.; Boukay, A.; Diana, F.; Gerardot, B.; Badolato, A.; Petroff, P.; Heath, J. Ultrahigh-Density Nanowires Lattices and Circuits. Science 2003, 300, 112–115. [Google Scholar] [PubMed] [Green Version]
- Pennelli, G.; Elyamny, S.; Dimaggio, E. Thermal conductivity of silicon nanowire forests. Nanotechnology 2018, 2018, 505402. [Google Scholar] [CrossRef] [PubMed]
- Donadio, D.; Galli, G. Temperature dependence of the thermal conductivity of thin silicon nanowires. Nano Lett. 2004, 10, 847. [Google Scholar] [CrossRef]
- Martin, P.; Aksamija, Z.; Pop, E.; Ravaioli, U. Impact of phonon-surface roughness scattering on thermal conductivity of thin Si nanowires. Phys. Rev. Lett. 2009, 102, 125503. [Google Scholar] [CrossRef]
- Sojo Gordillo, J.; Gadea Diez, G.; Pacios Pujadó, M.; Salleras, M.; Estrada-Wiese, D.; Dolcet, M.; Fonseca, L.; Morata, A.; Tarancón, A. Thermal conductivity of individual Si and SiGe epitaxially integrated NWs by scanning thermal microscopy. Nanoscale 2021, 13, 7252–7265. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Asheghi, M. Thermal conduction in ultrathin pure and doped single-crystal silicon layers at high temperatures. J. Appl. Phys. 2005, 98, 123523. [Google Scholar] [CrossRef]
- Dimaggio, E.; Pennelli, G.; Macucci, M. Thermal conductivity reduction in rough silicon nanomembranes. IEEE Trans. Nanotechnol. 2018, 17, 500. [Google Scholar]
- Pennelli, G.; Dimaggio, E.; Macucci, M. Improvement of the 3ω thermal conductivity measurement technique for its application at the nanoscale. Rev. Scient. Instrum. 2018, 89, 016104. [Google Scholar] [CrossRef] [Green Version]
- Hics, L.; Dresselhaus, M. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 1993, 47, 12727–12731. [Google Scholar] [CrossRef] [PubMed]
- Hics, L.; Dresselhaus, M. Thermoelectric figure of merit of a one-dimensional conductor. Phys. Rev. B 1993, 47, 16631–16634. [Google Scholar] [CrossRef]
- Pennelli, G.; Macucci, M. Optimization of the thermoelectric properties of nanostructured silicon. J. Appl. Phys. 2013, 114, 214507. [Google Scholar] [CrossRef]
- Lee, J.; Lee, W.; Lim, J.; Yu, Y.; Konq, Q.; Urban, J.; Yang, P. Thermal transport in silicon nanowires at high temperature up to 700 K. Nano Lett. 2016, 16, 4133. [Google Scholar] [CrossRef]
- Pennelli, G.; Dimaggio, E.; Macucci, M. Fabrication Techniques for Thermoelecric Devices based on Nanostructured Silicon. J. Nanosci. Nanotechnol. 2017, 17, 1627. [Google Scholar] [CrossRef]
- Gaeda, G.; Pacios, M.; Morata, A.; Tarancon, A. Silicon-based Nanostructures for Integrated Thermoelectric Generators. J. Phys. D Appl. Phys. 2018, 51, 423001. [Google Scholar] [CrossRef]
- Li, Y.; Buddharaju, K.; Singh, N.; Lo, G.; Lee, S. Chip-level thermoelectric power generators based on high-density silicon nanowire array prepared with top-down CMOS technology. IEEE Electron Device Lett. 2011, 32, 674–676. [Google Scholar] [CrossRef]
- Donmez Noyan, I.; Dolcet, M.; Salleras, M.; Stranz, A.; Calaza, C.; Gadea, G.; Pacios, M.; Morata, A.; Tarancon, A.; Fonseca, L. All-silicon thermoelectric micro/nanogenerator including a heat exchanger for harvesting applications. J. Power Sources 2019, 413, 125–133. [Google Scholar] [CrossRef]
- Fonseca, L.; Donmez-Noyan, I.; Dolcet, M.; Estrada-Wiese, D.; Santander, J.; Salleras, M.; Gadea, G.; Pacios, M.; Sojo, J.M.; Morata, A.; et al. Transitioning from Si to sige nanowires as thermoelectric material in silicon-based microgenerators. Nanomaterials 2021, 11, 517. [Google Scholar] [CrossRef]
- Domnez Noyan, I.; Gadea, G.; Salleras, M.; Pacios, M.; Calaza, C.; Stranz, A.; Dolcet, M.; Morata, A.; Tarancon, A.; Fonseca, L. SiGe nanowire arrays based thermoelectric microgenerator. Nano Energy 2019, 57, 492–499. [Google Scholar] [CrossRef]
- Tomita, M.; Oba, S.; Himeda, Y.; Yamato, R.; Shima, K.; Kumada, T.; Xu, M.; Takezawa, H.; Mesaki, K.; Tsuda, K.; et al. Modeling, simulation, fabrication, and characterization of a 10-μW/cm2 class si-nanowire thermoelectric generator for IoT applications. IEEE Trans. Electron Devices 2018, 65, 5180–5188. [Google Scholar] [CrossRef]
- Davila, D.; Tarancon, A.; Calaza, C.; Salleras, M.; Fernandez-Regulez, M.; SanPaulo, A.; Fonseca, L. Monolithically integrated thermoelectric energy harvester based on silicon nanowire arrays for powering micro/nanodevices. Nano Energy 2012, 1, 812. [Google Scholar] [CrossRef]
- Davila, D.; Tarancon, A.; Fernandez-regulez, M.; Calaza, C.; Salleras, M.; SanPaulo, A.; Fonseca, L. Silicon nanowire arrays as thermoelectric material for a power microgenerator. J. Micromechan. Microeng. 2011, 21, 104007. [Google Scholar] [CrossRef]
- Gadea, G.; Morata, A.; Tarancon, A. Semiconductor Nanowires for Thermoelectric Generation. Semicond. Semimetals 2018, 98, 321–407. [Google Scholar] [CrossRef]
- Fonseca, L.; Santos, J.D.; Roncaglia, A.; Narducci, D.; Calaza, C.; Salleras, M.; Donmez, I.; Tarancon, A.; Morata, A.; Gadea, G.; et al. Smart integration of silicon nanowire arrays in all-silicon thermoelectric micro-nanogenerators. Semicond. Sci. Technol. 2016, 31, 084001. [Google Scholar] [CrossRef] [Green Version]
- Calaza, C.; Fonseca, L.; Salleras, M.; Donmez, I.; Tarancón, A.; Morata, A.; Santos, J.; Gadea, G. Thermal Test of an Improved Platform for Silicon Nanowire-Based Thermoelectric Micro-generators. J. Electron. Mater. 2016, 45, 1689–1694. [Google Scholar] [CrossRef] [Green Version]
- Gadea Díez, G.; Sojo Gordillo, J.; Pacios Pujadó, M.; Salleras, M.; Fonseca, L.; Morata, A.; Tarancón Rubio, A. Enhanced thermoelectric figure of merit of individual Si nanowires with ultralow contact resistances. Nano Energy 2020, 67, 104191. [Google Scholar] [CrossRef]
- Yuan, Z.; Ziouche, K.; Bougrioua, Z.; Lejeune, P.; Lasri, T.; Leclercq, D. A planar micro thermoelectric generator with high thermal resistance. Sens. Actuators A Phys. 2015, 221, 67–76. [Google Scholar] [CrossRef]
- Ziouche, K.; Yuan, Z.; Lejeune, P.; Lasri, T.; Leclercq, D.; Bougrioua, Z. Silicon-Based Monolithic Planar Micro Thermoelectric Generator Using Bonding Technology. J. Microelectromechan. Syst. 2017, 26, 45–47. [Google Scholar] [CrossRef]
- Ziouche, K.; Bel-Hadj, I.; Bougrioua, Z. Thermoelectric properties of nanostructured porous-polysilicon thin films. Nano Energy 2021, 80, 105553. [Google Scholar] [CrossRef]
- Pennelli, G.; Totaro, M.; Piotto, M.; Bruschi, P. Seebeck coefficient of nanowires interconnected into large area networks. Nano Lett. 2013, 13, 2592. [Google Scholar] [CrossRef]
- Totaro, M.; Bruschi, P.; Pennelli, G. Top down fabricated silicon nanowire networks for thermoelectric applications. Microelectron. Eng. 2012, 97, 157. [Google Scholar] [CrossRef]
- Pennelli, G.; Macucci, M. High-power thermoelectric generators based on nanostructured silicon. Semicond. Sci. Technol. 2016, 31, 054001. [Google Scholar] [CrossRef]
- Pournia, M.; Firoozabadi, S.; Fathipour, M.; Kolahdouz, M. Fabrication of ultra-high-aspect-ratio nano-walls and nano-structures on silicon substrates. J. Micromechan. Microeng. 2020, 30, 125008. [Google Scholar] [CrossRef]
- Nguyen, V.; Shkondin, E.; Jensen, F.; Hübner, J.; Leussink, P.; Jansen, H. Ultrahigh aspect ratio etching of silicon in SF6-O2plasma: The clear-oxidize-remove-etch (CORE) sequence and chromium mask. J. Vac. Sci. Technol. A Vac. Surfaces Film. 2020, 38, 053002. [Google Scholar] [CrossRef]
- Bagolini, A.; Scauso, P.; Sanguinetti, S.; Bellutti, P. Silicon Deep Reactive Ion Etching with aluminum hard mask. Mater. Res. Express 2019, 6, 085913. [Google Scholar] [CrossRef]
- Parasuraman, J.; Summanwar, A.; Marty, F.; Basset, F.; Angelescu, D.; Bourouina, T. Deep reactive ion etching of sub-micrometer trenches with ultra high aspect ratio. Microelectron. Eng. 2014, 113, 35. [Google Scholar] [CrossRef]
- Stranz, A.; Waag, A.; Peiner, E. High-temperature performance of stacked silicon nanowires for thermoelectric power generation. J. Electron. Mat. 2013, 42, 2233. [Google Scholar] [CrossRef]
- Huang, Z.; Geyer, N.; Werner, P.; de Boor, J.; Gosele, U. Metal-assisted chemical etching of silicon: A review. Adv. Mater. 2011, 23, 285–308. [Google Scholar] [CrossRef]
- Kim, J.; Han, H.; Kim, Y.; Choi, S.H.; Kim, J.C.; Lee, W. Au/Ag bilayered metal mesh as a Si etching catalyst for controlled fabrication of Si nanowires. ACS Nano 2011, 5, 3222. [Google Scholar] [CrossRef]
- Magagna, S.; Narducci, D.; Alfonso, C.; Dimaggio, E.; Pennelli, G.; Charaï, A. On the mechanism ruling the morphology of silicon nanowires obtained by one-pot metal-assisted chemical etching. Nanotechnology 2020, 31, 404002. [Google Scholar] [CrossRef]
- To, W.; Tsang, C.; Li, H.; Huang, Z. Fabrication of n-Type Mesoporous Silicon Nanowires by One-Step Etching. Nano Lett. 2011, 11, 5252–5258. [Google Scholar] [CrossRef]
- Bollani, M.; Osmond, J.; Nicotra, G.; Spinella, C.; Narducci, D. Strain-induced generation of silicon nanopillars. Nanotechnology 2013, 24, 335302. [Google Scholar] [CrossRef]
- Mallavarapu, A.; Ajay, P.; Barrera, C.; Sreenivasan, S. Ruthenium-Assisted Chemical Etching of Silicon: Enabling CMOS-Compatible 3D Semiconductor Device Nanofabrication. ACS Appl. Mater. Interfaces 2021, 13, 1169–1177. [Google Scholar] [CrossRef]
- Peng, K.; Yan, Y.; Gao, S.; Zhu, J. Dendride-assisted growth of silicon nanowires in electroless metal deposition. Adv. Funct. Mater. 2003, 13, 127. [Google Scholar] [CrossRef]
- Peng, K.; Hu, J.; Yan, Y.; Wu, Y.; Fang, H.; Xu, Y.; Lee, S.; Zhu, J. Fabrication of single-crystalline silicon nanowires by scratching a silicon surface with catalytic metal particles. Adv. Funct. Mater. 2006, 16, 387–394. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, Z.; Zhang, M.; Yang, F.; Wang, Z. A Processing Window for Fabricating Heavily Doped Silicon Nanowires by Metal-Assisted Chemical Etching. J. Phys. Chem. C 2013, 117, 25090. [Google Scholar] [CrossRef]
- Dimaggio, E.; Narducci, D.; Pennelli, G. Fabrication of Silicon Nanowire Forests for Thermoelectric Applications by Metal-Assisted Chemical Etching. J. Mater. Eng. Perform. 2018, 27, 6279–6285. [Google Scholar] [CrossRef]
- Elyamny, S.; Dimaggio, E.; Pennelli, G. Seebeck coefficient of silicon nanowire forests doped by thermal diffusion. Beilstein J. Nanotechnol. 2020, 11, 1707–1713. [Google Scholar] [CrossRef] [PubMed]
- Sadhu, J.S.; Tian, H.; Spila, T.; Kim, J.; Azeredo, B.; Ferreira, P.; Sinha, S. Controllable doping and wrap-around contacts to electrolessly etched silicon nanowire arrays. Nanotechnology 2014, 25, 375701. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Fobelets, K. Spin-on-doping for output power improvement of silicon nanowire array based thermoelectric power generators. J. Appl. Phys. 2014, 115, 214306. [Google Scholar] [CrossRef]
- Dimaggio, E.; Pennelli, G. Reliable Fabrication of Metal Contacts on Silicon Nanowire Forests. Nano Lett. 2016, 7, 4348. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pennelli, G.; Dimaggio, E.; Masci, A. Silicon Nanowires: A Breakthrough for Thermoelectric Applications. Materials 2021, 14, 5305. https://doi.org/10.3390/ma14185305
Pennelli G, Dimaggio E, Masci A. Silicon Nanowires: A Breakthrough for Thermoelectric Applications. Materials. 2021; 14(18):5305. https://doi.org/10.3390/ma14185305
Chicago/Turabian StylePennelli, Giovanni, Elisabetta Dimaggio, and Antonella Masci. 2021. "Silicon Nanowires: A Breakthrough for Thermoelectric Applications" Materials 14, no. 18: 5305. https://doi.org/10.3390/ma14185305
APA StylePennelli, G., Dimaggio, E., & Masci, A. (2021). Silicon Nanowires: A Breakthrough for Thermoelectric Applications. Materials, 14(18), 5305. https://doi.org/10.3390/ma14185305







