The Influence of Welding Heat Source Inclination on the Melted Zone Shape, Deformations and Stress State of Laser Welded T-Joints
Abstract
1. Introduction
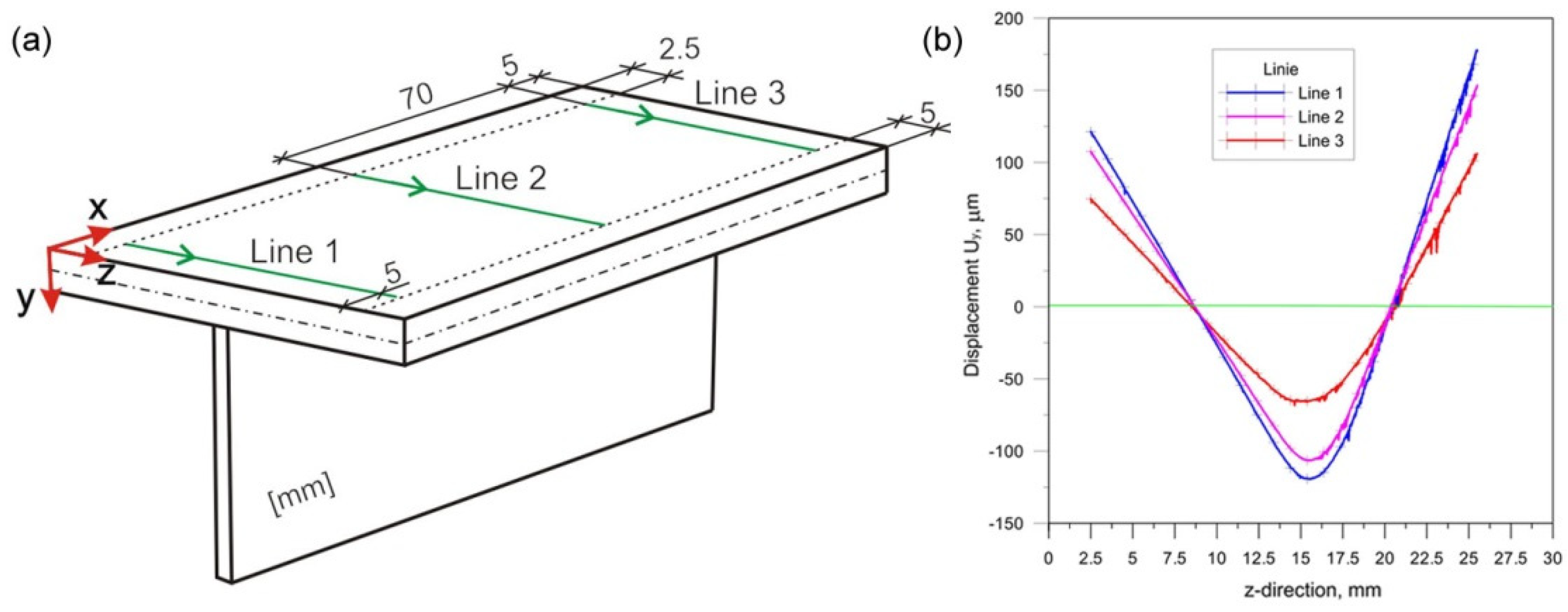
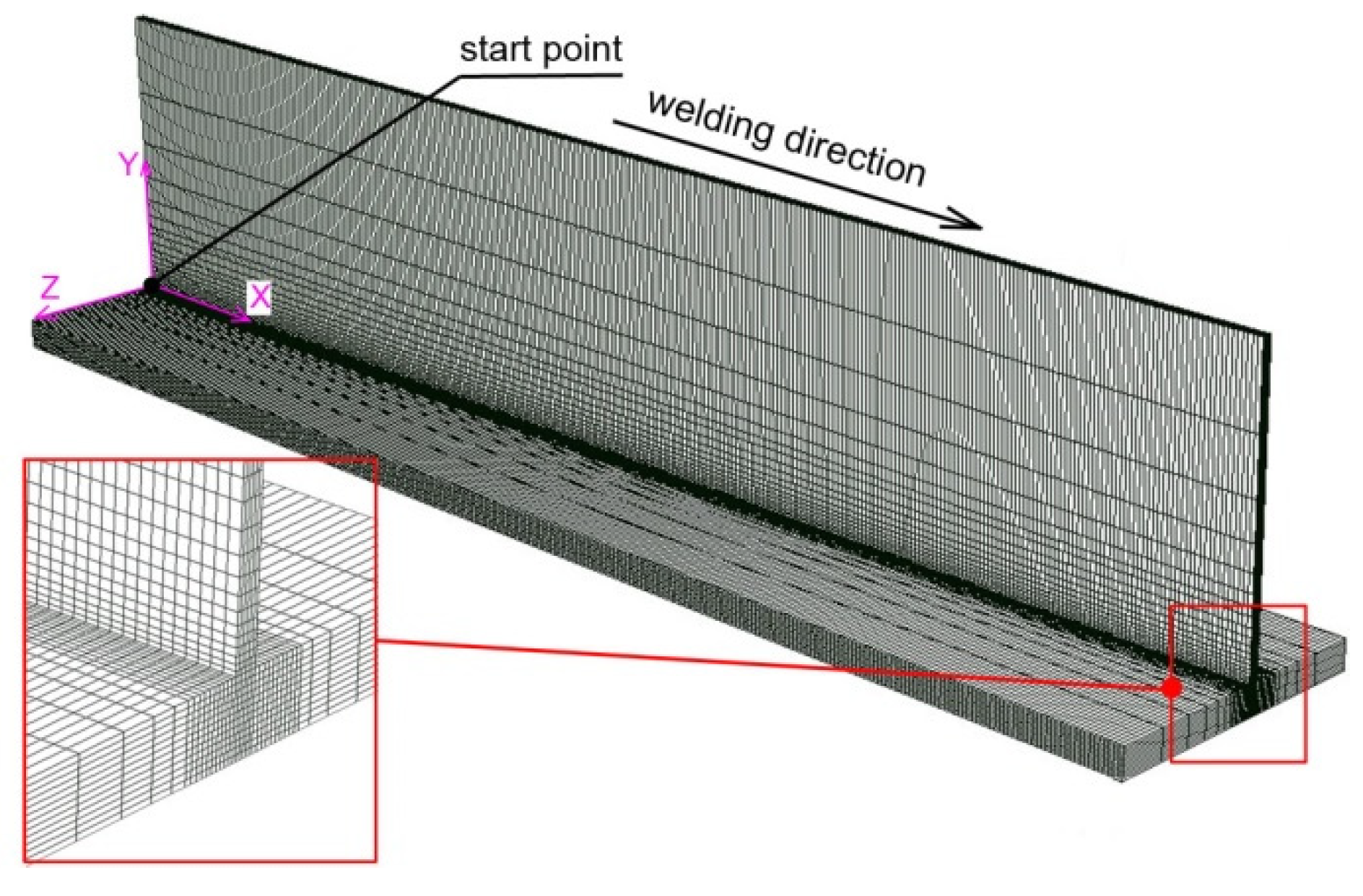
2. The Experiment
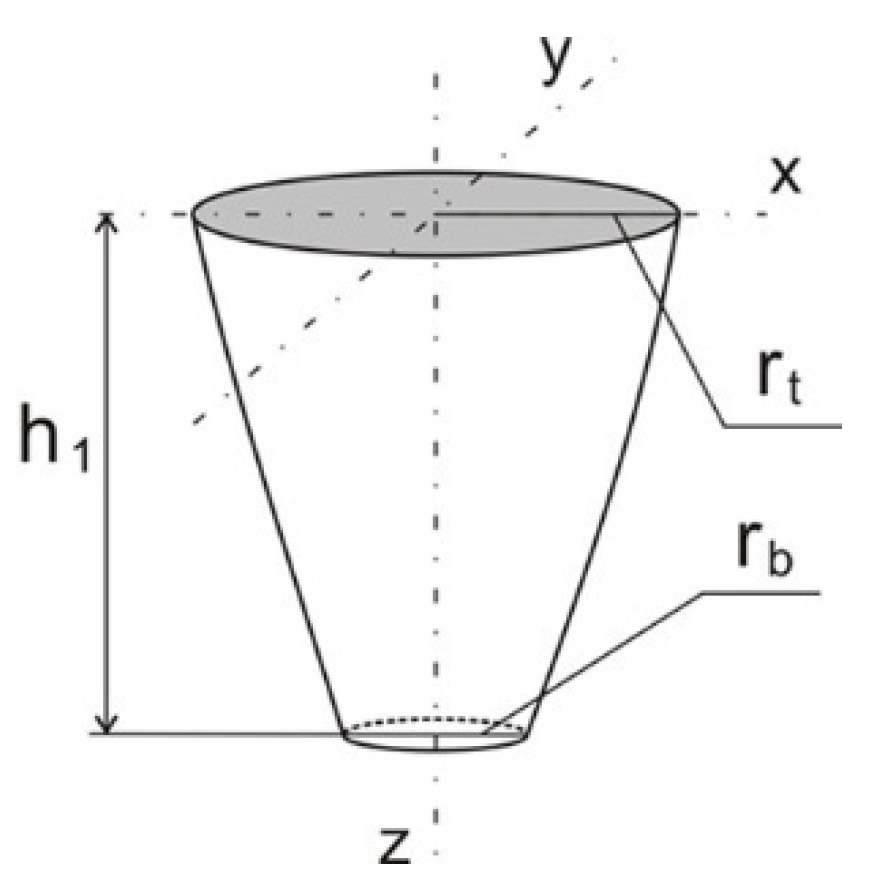
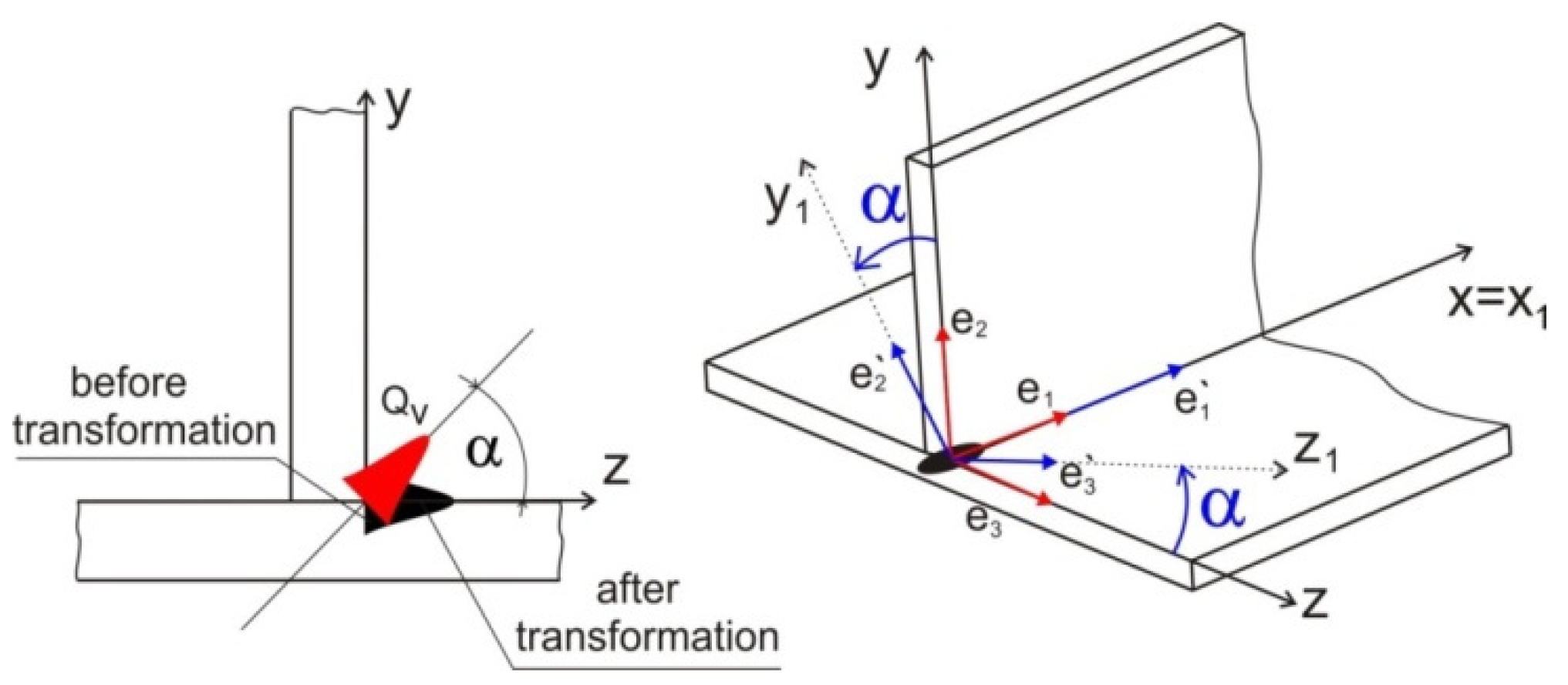
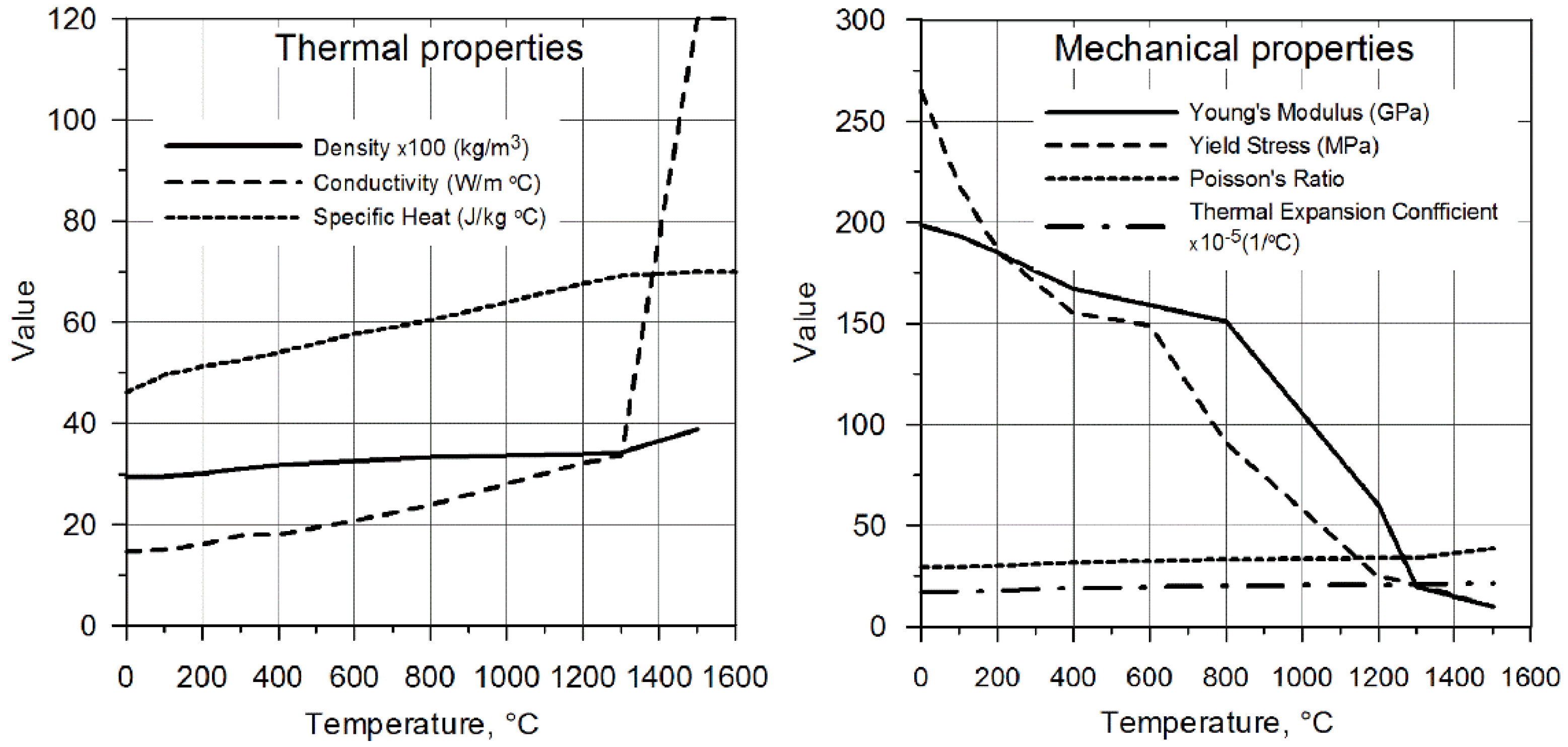
3. Mathematical Model
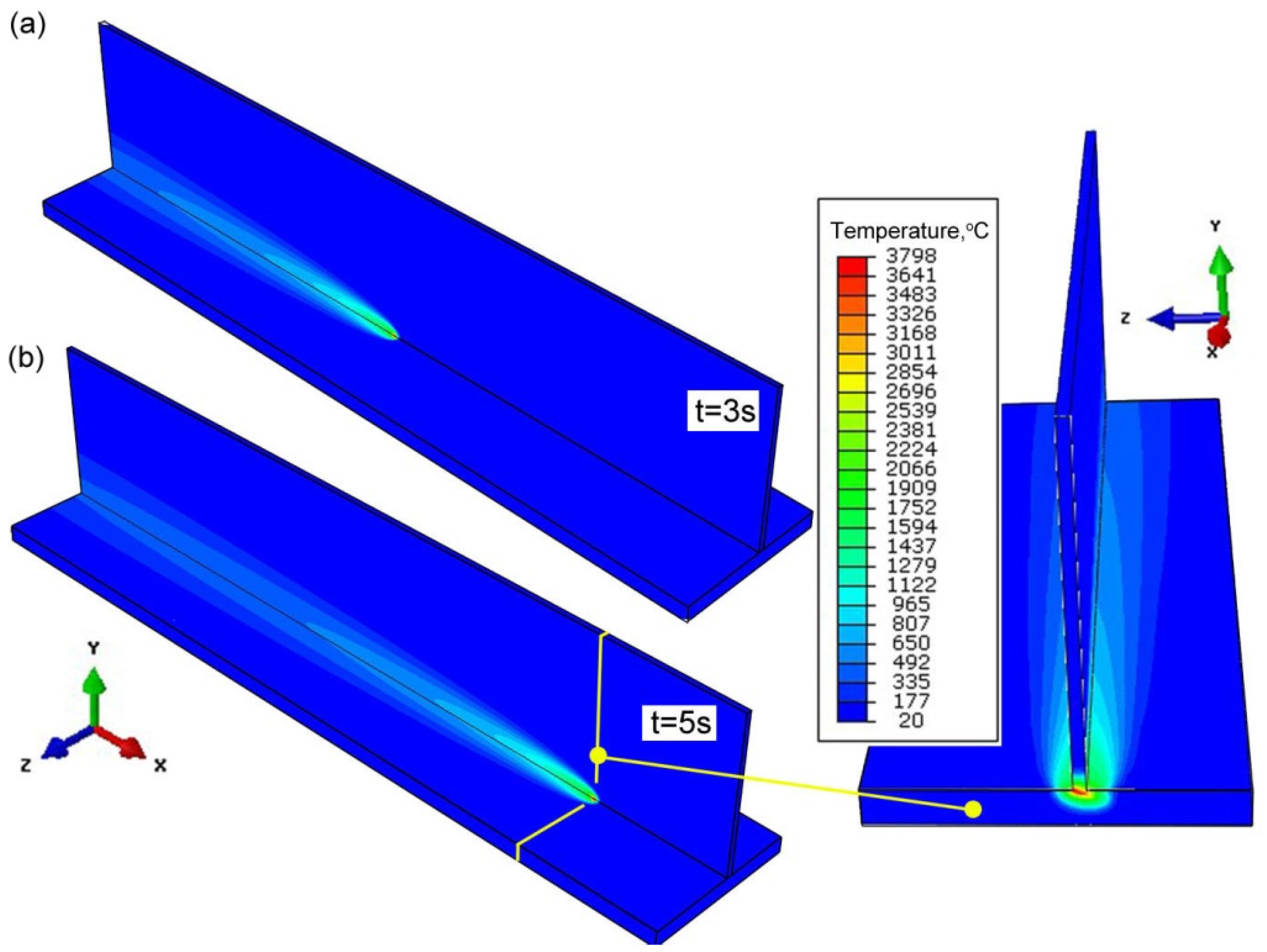
4. Numerical Simulation
5. Conclusions
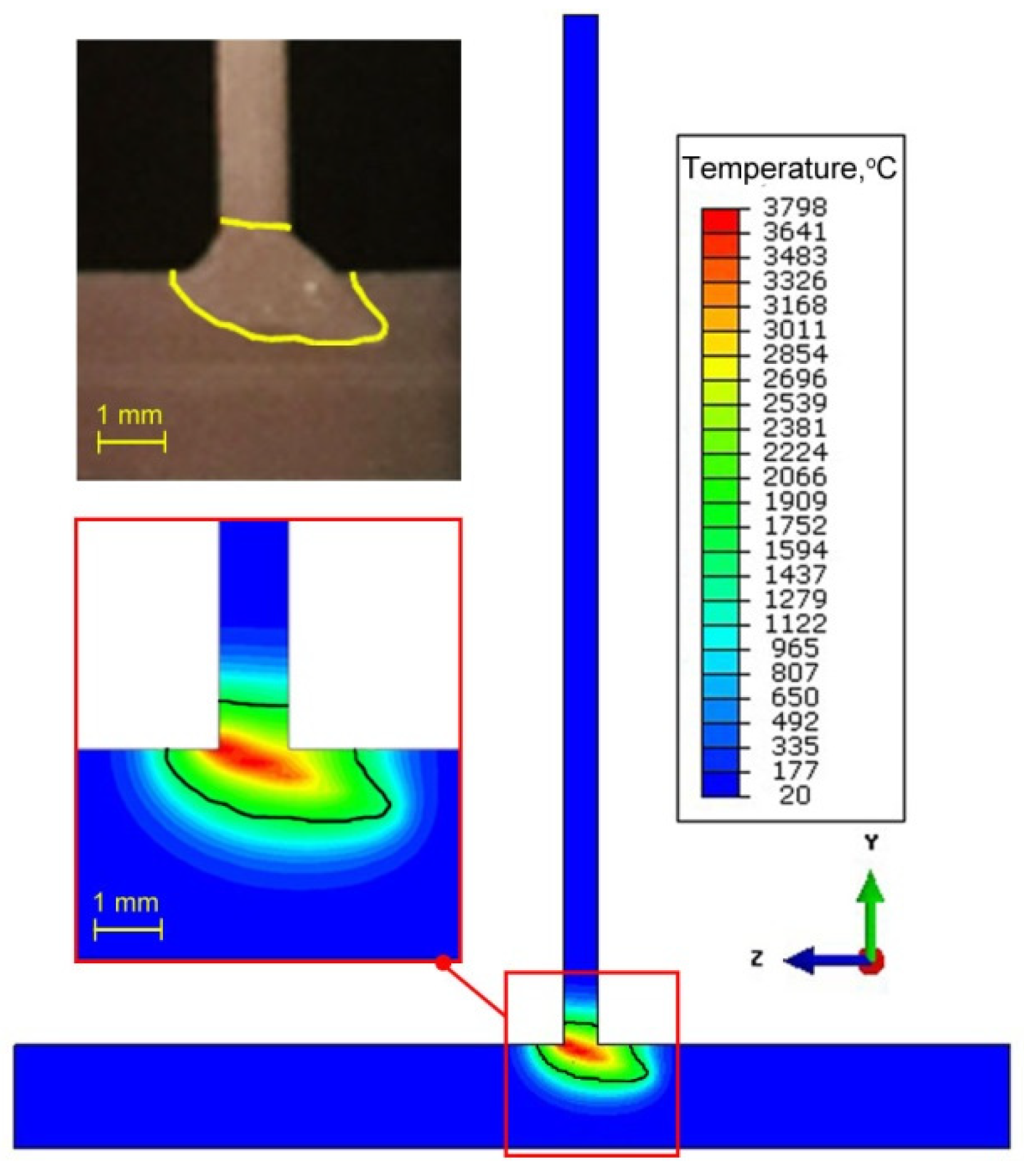
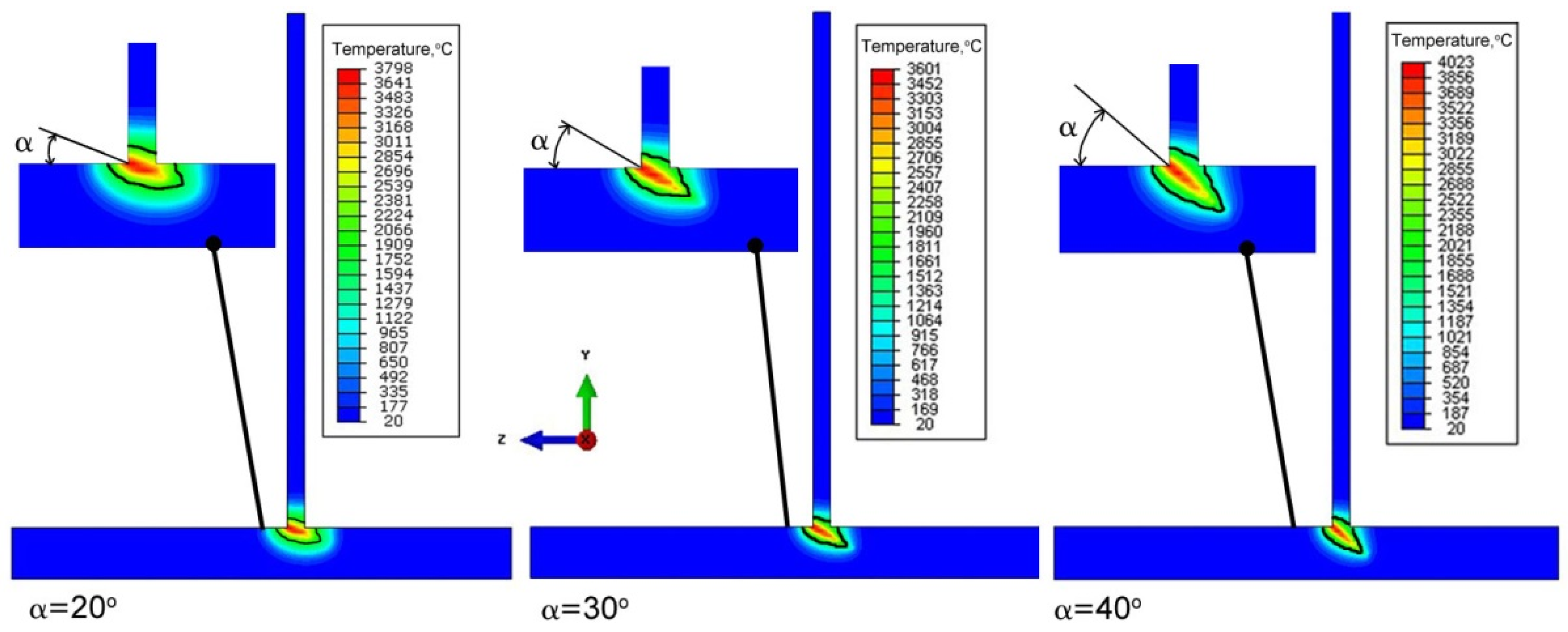
- Changing the inclination of the heat source changes the shape and size of the melted zone. As the angle of inclination increases, the depth of fusion into the base of T-joint increases, and the width of the fusion zone decreases at the same time. A further increase in the angle of inclination of the source may lead to a reduction of the quality of the joint (see Figure 16).
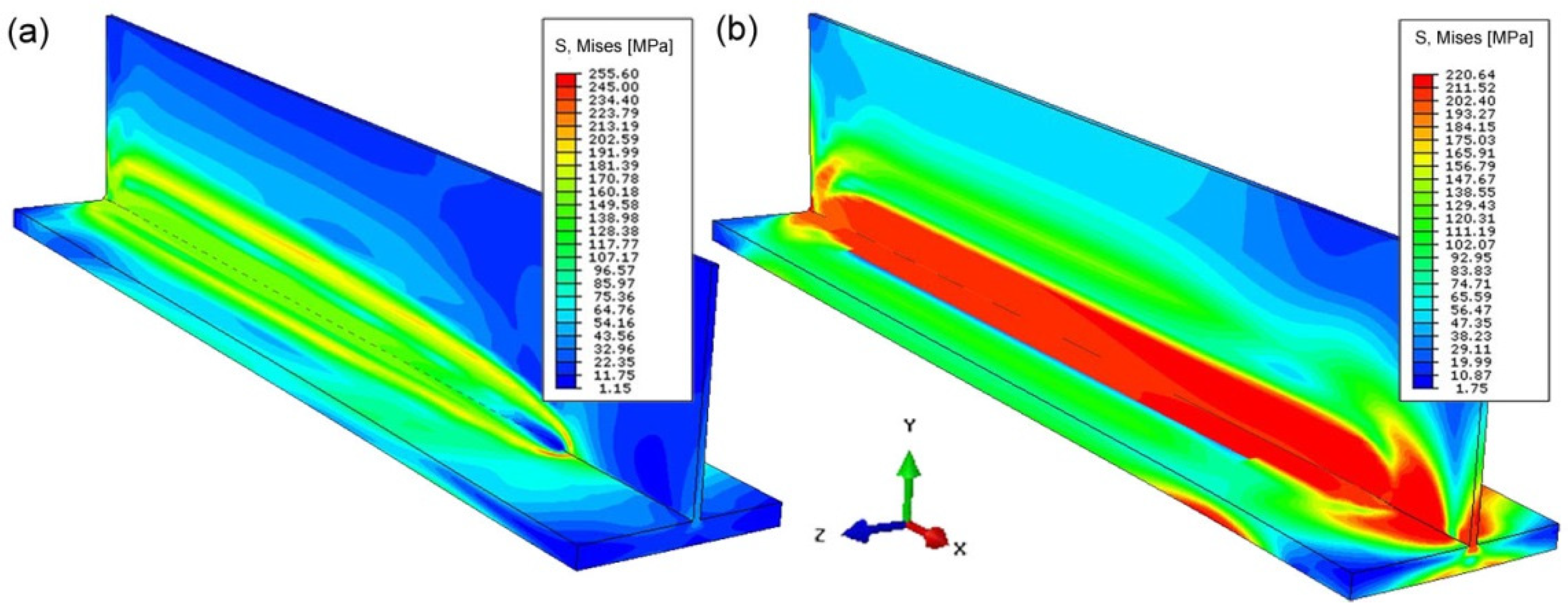
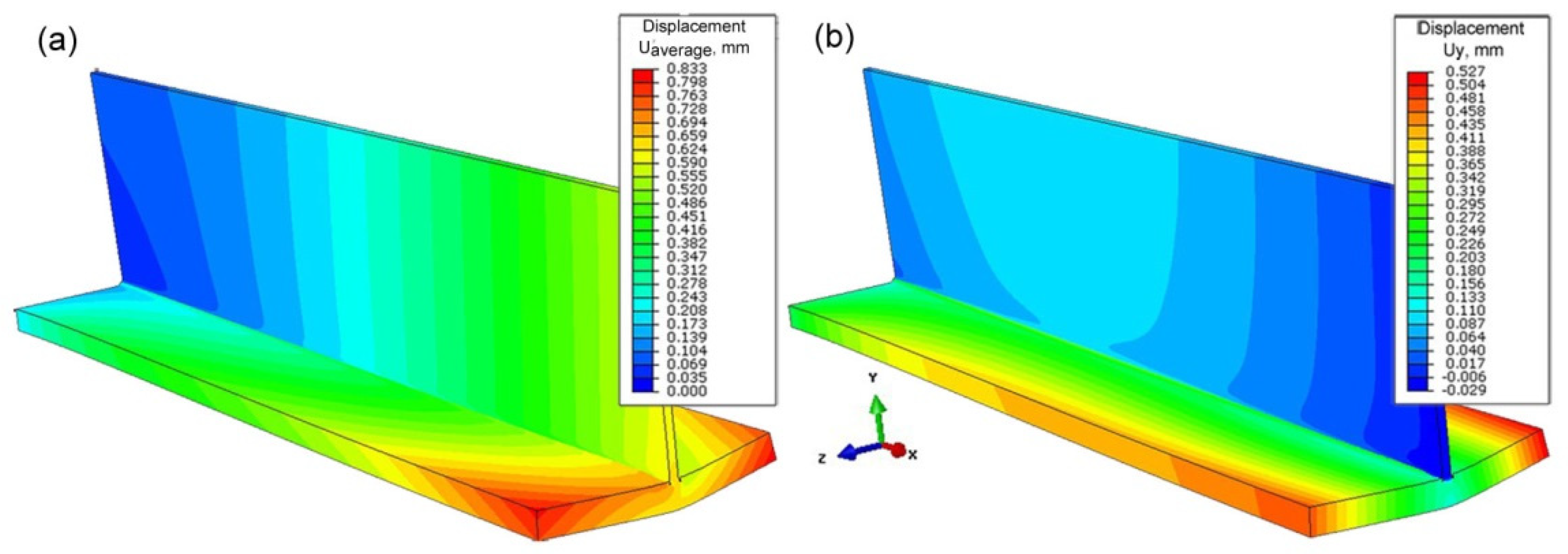
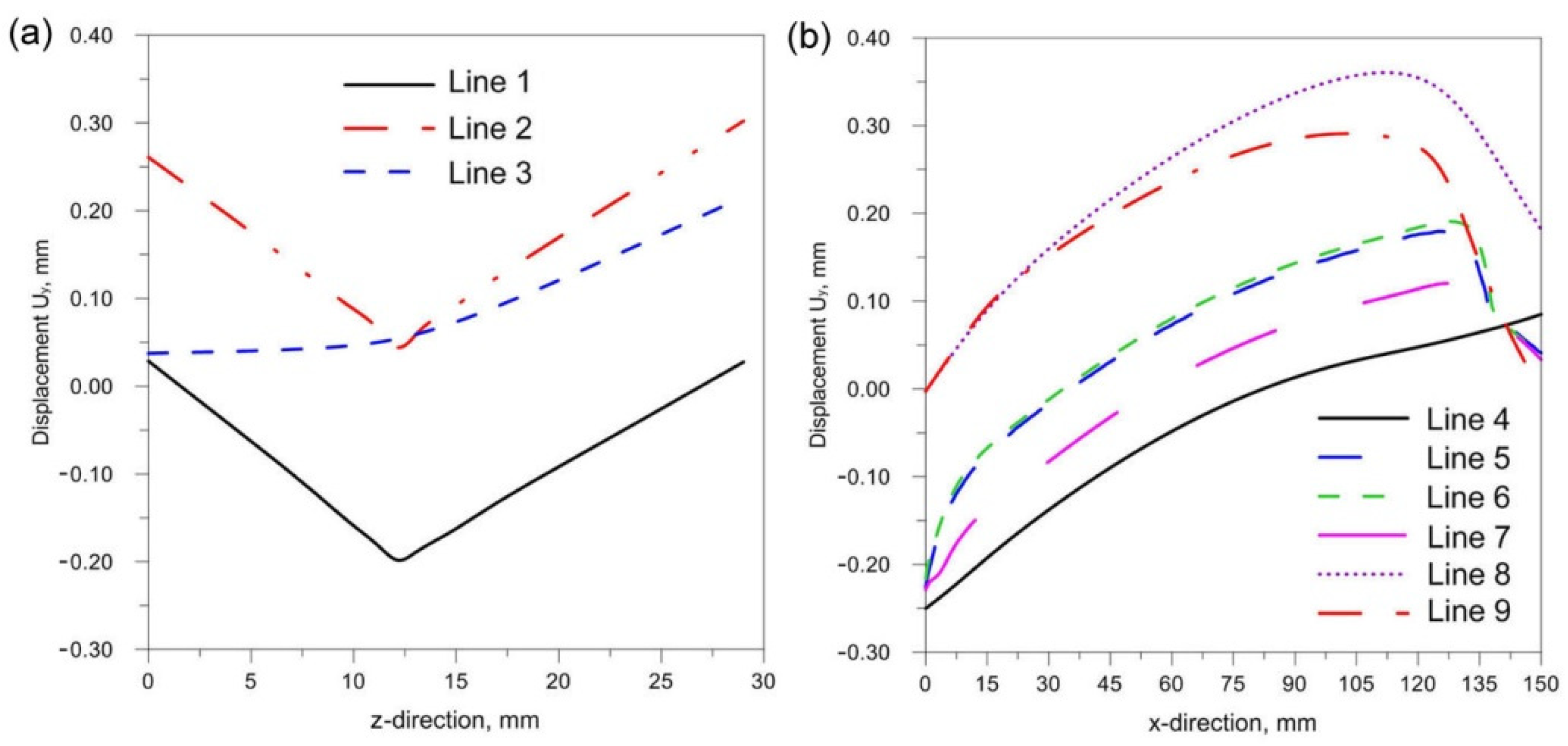
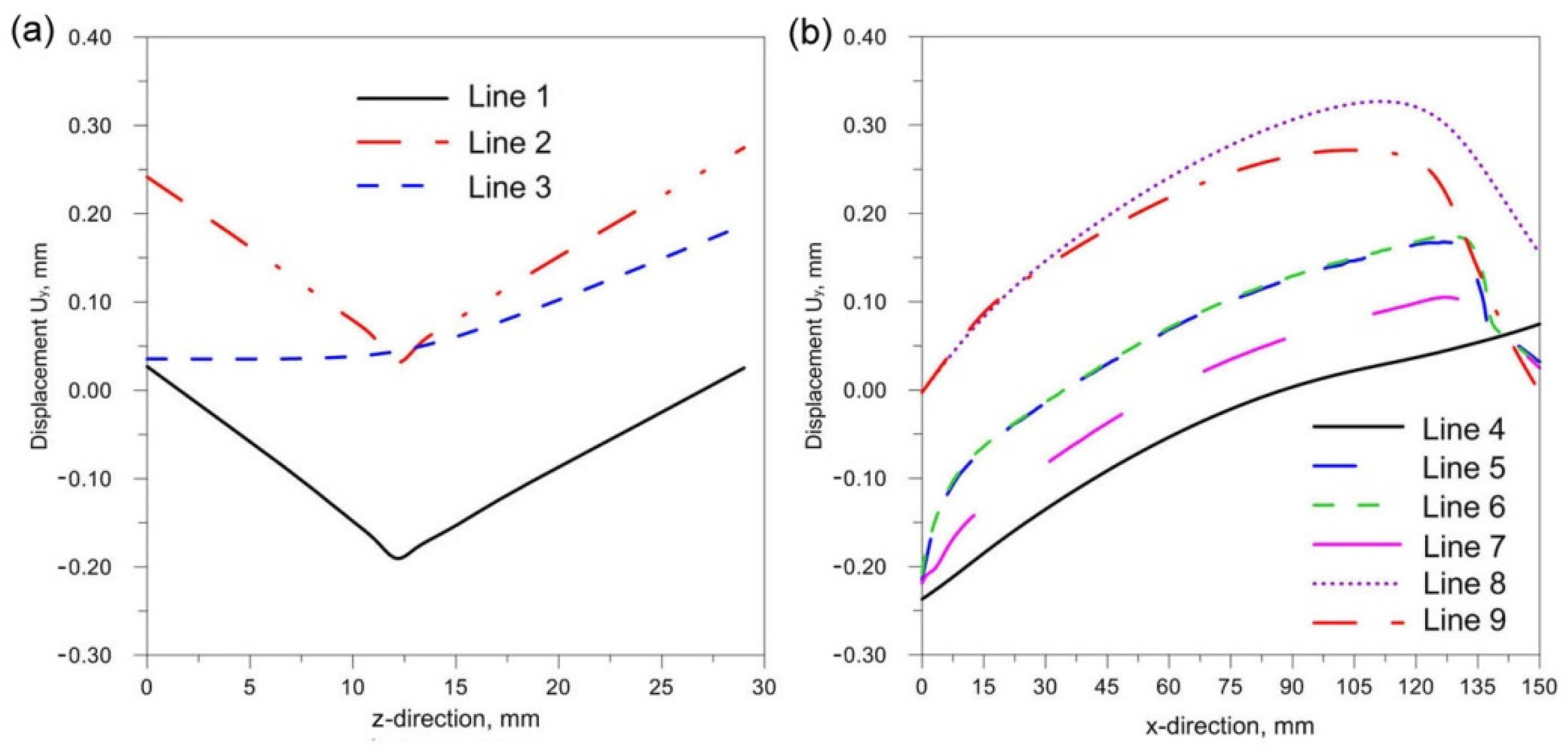
- Changing the inclination of the heat source changes the deformation of the joint. Increasing the angle of inclination reduces the amount of deformation (Figure 24). For the analyzed joint, the differences are at the level of 0.03 mm.
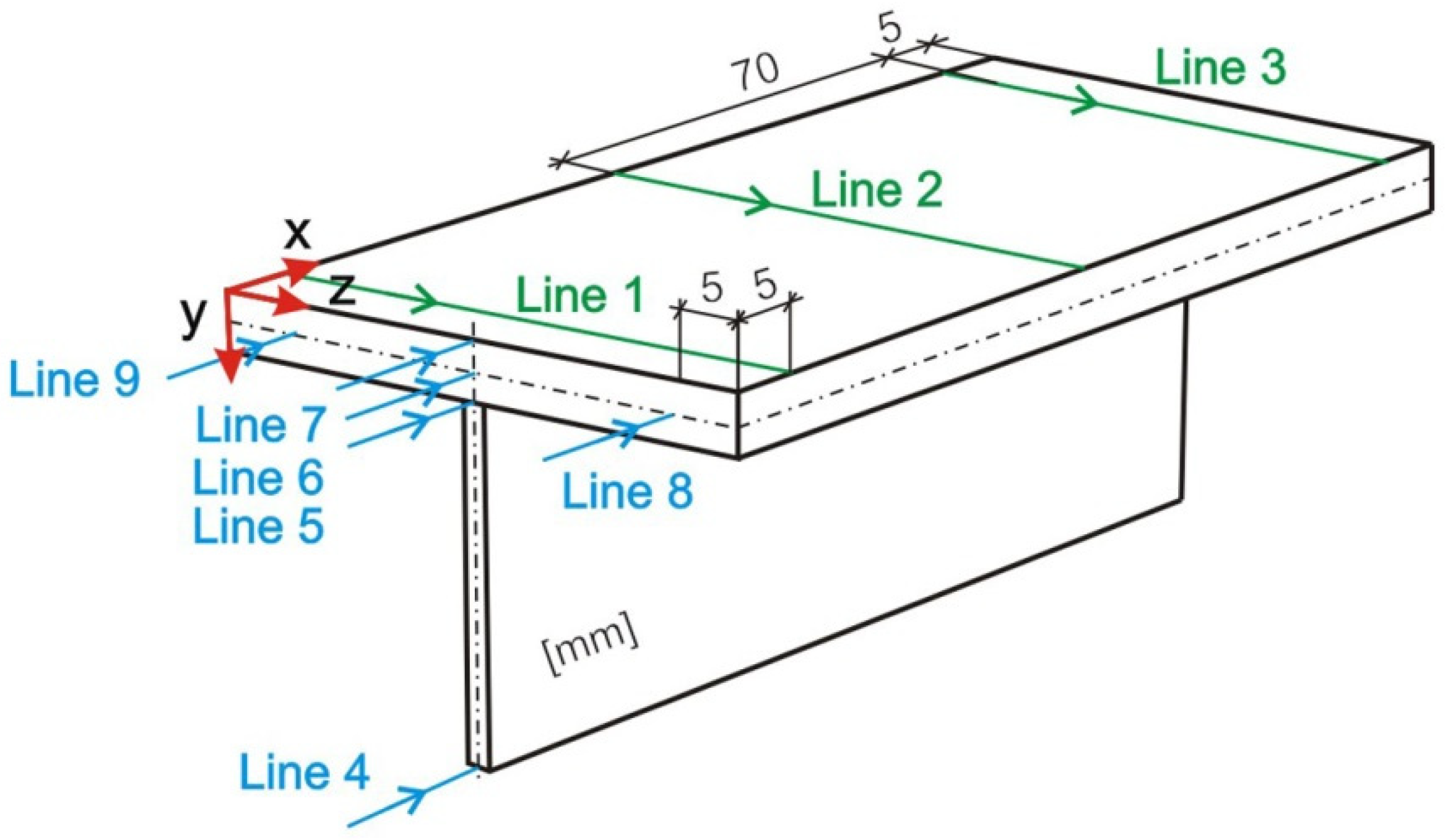
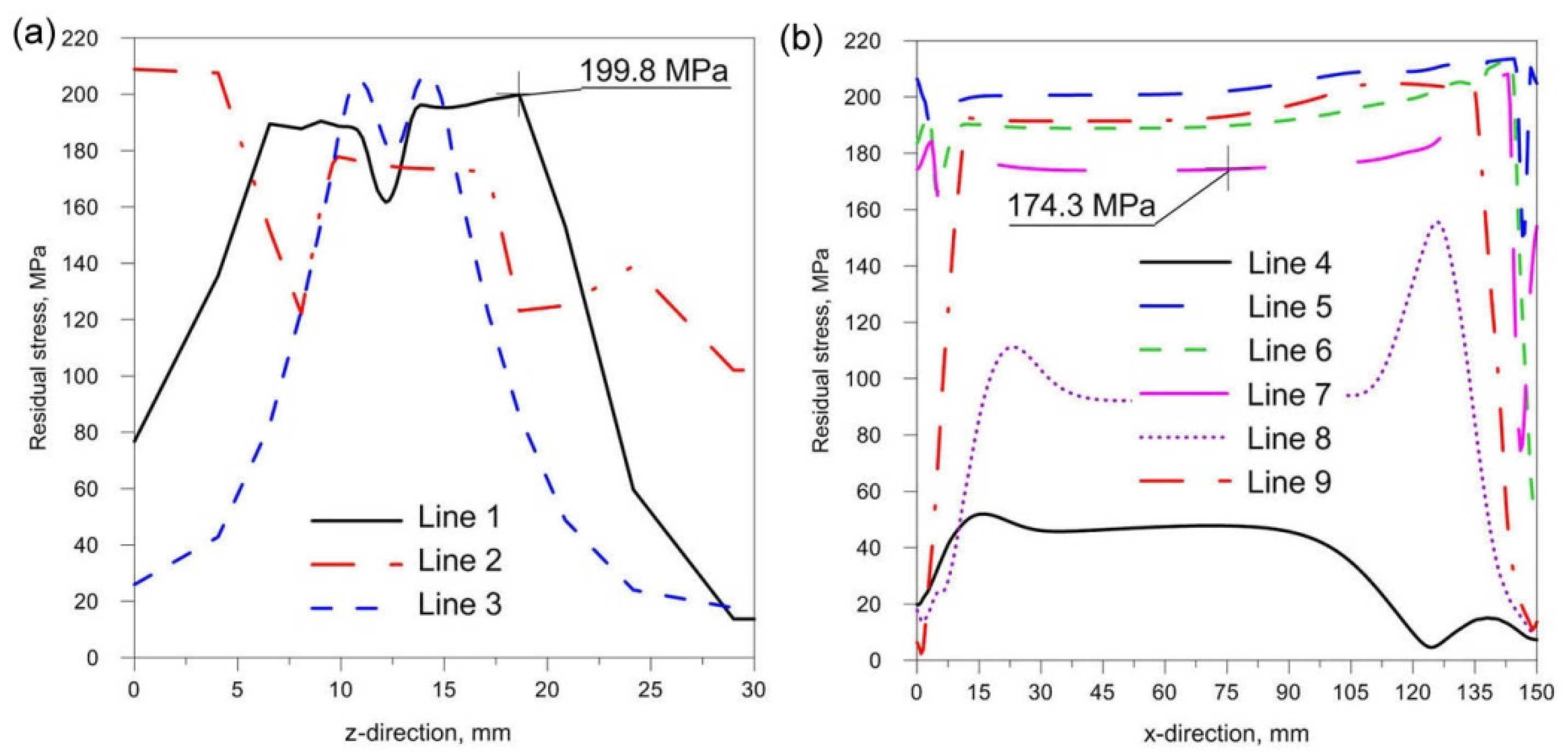
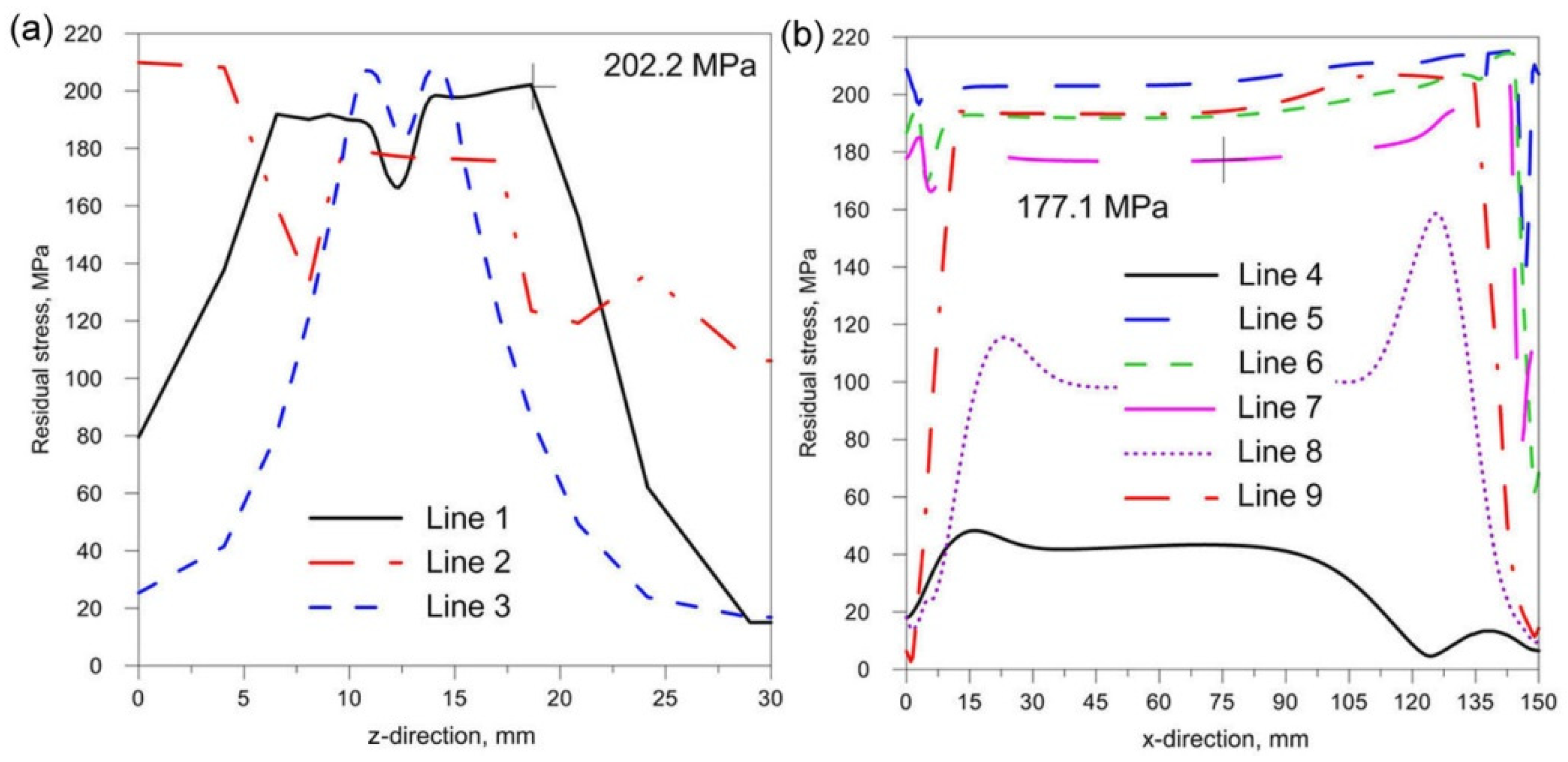
- Changing the inclination of the heat source has no significant effect on the stress state (see Figure 18, Figure 19 and Figure 20). In general, increasing the angle of inclination of the heat source slightly increases residual stress. The predicted magnitudes and distributions of are determined only by numerical simulations, according to the model adopted in the Abaqus FEA software. Detailed analysis of the stress state in single-side welded T-joint requires experimental verification. Stress measurement in T-joints is complex, requires special equipment and will be the subject of further research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, H.; Wang, J.; Li, L.; Ma, N. Prediction of laser welding induced deformation in thin sheets by effcient numerical modeling. J. Mater. Process. Technol. 2016, 227, 117–128. [Google Scholar] [CrossRef]
- Li, Y.; Wang, K.; Jin, Y.; Xu, M.; Lu, H. Prediction of welding deformation in stiffened structure by intro ducing thermo-mechanical interface element. J. Mater. Process. Technol. 2015, 216, 440–446. [Google Scholar]
- Torkamany, M.J.; Sabbaghzadeh, J.; Hamedi, M.J. Effect of laser welding mode on the microstructure and mechanical performance of dissimilar laser spot welds between low carbon and austenitic stainless steels. Mater. Des. 2012, 34, 666–672. [Google Scholar] [CrossRef]
- Danielewski, H.; Skrzypczyk, A. Steel Sheets Laser Lap Joint Welding—Process Analysis. Materials 2020, 13, 2258. [Google Scholar] [CrossRef]
- Khan, M.M.A.; Romoli, L.; Dini, G. Laser beam welding of dissimilar ferritic/martensitic stainless steels in a butt joint configuration. Opt. Laser Technol. 2013, 49, 125–136. [Google Scholar] [CrossRef]
- Francis, J.A.; Holtum, N.; Olschok, S.; Roy, M.J.; Vasileiou, A.N.; Jakobs, S.; Reisgen, U.; Smith, M.C. Vacuum laser welding of SA508 steel. J. Mater. Process. Technol. 2019, 274, 116269. [Google Scholar] [CrossRef]
- Danielewski, H.; Skrzypczyk, A.; Hebda, M.; Tofil, S.; Witkowski, G.; Długosz, P.; Nigrovic, R. Numerical and metallurgical analysis of laser welded, sealed lap joints of S355J2 and 316L steels under different configurations. Materials 2020, 13, 5819. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Li, S.; Hu, L.; Deng, D. Effects of pass arrangement on angular distortion, residual stresses and lamellar tearing tendency in thick-plate T-joints of low alloy steel. J. Mater. Process. Technol. 2019, 274, 116293. [Google Scholar] [CrossRef]
- Zhang, Y.; Tao, W.; Chen, Y.; Nan, T. Effects of heat treatment on microstructure and mechanical properties of double-sided laser-welded AA2060/AA2099 T-Joint. J. Mater. Process. Technol. 2020, 285, 116777. [Google Scholar] [CrossRef]
- Hammada, A.; Churiaqueb, C.; Sanchez-Amayab, J.; Abdel-Nasser, Y. Experimental and numerical investigation of hybrid laser arc welding process and the influence of welding sequence on the manufacture of stiffened flat panels. J. Manu Process. 2021, 61, 527–538. [Google Scholar] [CrossRef]
- Shanmugam, N.S.; Buvanashekaran, G.; Sankaranarayanasamy, K.; Kumar, S.R. A transient finite element simulation of the temperature and bead profiles of T-joint laser welds. Mater. Design. 2010, 31, 4528–4542. [Google Scholar] [CrossRef]
- Unt, A.; Poutiainen, I.; Salminen, A. Effects of sealing run welding with defocused laser beam on the quality of T-joint fillet weld. Phys. Procedia 2014, 56, 497–506. [Google Scholar] [CrossRef][Green Version]
- Kujala, P.; Klanac, A. Steel Sandwich Panels in Marine Applications. BrodoGradnja 2005, 56, 305–314. [Google Scholar]
- Kozak, J. All steel sandwich panels—New possibilities introduced by laser welding techniques. Weld. Technol. Rev. 2007, 10, 53–59. [Google Scholar]
- Piekarska, W.; Kubiak, M.; Saternus, Z. Numerical Simulation of Deformations in T-Joint Welded by the Laser Beam. Arch. Metall. Mater. 2013, 58, 1391–1396. [Google Scholar] [CrossRef]
- Macckwood, A.P.; Cafer, R.C. Thermal modeling of laser of laser welding and related processes: A literature review. Opt. Laser Technol. 2009, 37, 99–115. [Google Scholar] [CrossRef]
- Banik, S.; Kumar, S.; Kumar Singh, P.; Bhattacharya, S.; Mahapatra, M.M. Distortion and residual stresses in thick plate weld joint of austenitic stainless steel: Experiments and analysis. J. Mater. Process. Technol. 2021, 289, 116944. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y. The infuence of welding mechanical boundary condition on the residual stress and distortion of a stiffened-panel. Mar. Struct. 2019, 65, 259–270. [Google Scholar] [CrossRef]
- Geng, S.; Jiang, P.; Shao, X.; Guo, L.; Gao, X. Heat transfer and fluid flow and their effects on the solidification microstructure in full-penetration laser welding of aluminum sheet. J. Mater. Sci. Technol. 2020, 46, 50–63. [Google Scholar] [CrossRef]
- Svenungssona, J.; Choqueta, I.; Kaplan, A.F.H. Laser welding process—a review of keyhole welding modeling. Phys. Procedia 2015, 78, 182–191. [Google Scholar] [CrossRef]
- De, A.; Maiti, S.K.; Walsh, C.A.; Bhadesia, K.D.H. Finite element simulation of laser spot welding. Sci. Technol. Weld. Join. 2003, 8, 377–384. [Google Scholar] [CrossRef]
- Oliveira, A.C.; Siqueira, R.H.M.; Riva, R.; Lima, M.S.F. One-sided laser beam welding of autogenous T-joints for 6013-T4 aluminium alloy. Mater. Des. 2015, 65, 726–736. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Prediction of welding distortion and residual stress in a thin plate butt-welded joint. Comput. Mater. Sci. 2008, 43, 353–365. [Google Scholar] [CrossRef]
- Deng, D.; Liang, W.; Murakawa, H. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements, J. Mater. Process. Technol. 2007, 183, 219–225. [Google Scholar] [CrossRef]
- Dowden, J.M. The Mathematics of Thermal Modeling; Taylor & Francis Group: New York, NY, USA, 2001. [Google Scholar]
- Moumni, Z.; Roger, F.; Thuy Trinh, N. Theoretical and numerical modeling of the thermomechanical and metallurgical behavior of steel. Int. J. Plast. 2011, 27, 414–439. [Google Scholar] [CrossRef]
- Rong, Y.; Huang, Y.; Wang, L. Evolution mechanism of transient strain and residual stress distribution in al 6061 laser welding. Crystals 2021, 11, 205. [Google Scholar] [CrossRef]
- Rong, Y.; Xu, J.; Lei, T.; Huang, Y.; Shao, X.; Wang, C. Magnetism aided mitigation of deformation and residual stress in dissimilar joint 316L with EH36. J. Mater. Process. Technol. 2018, 259, 23–32. [Google Scholar] [CrossRef]
- Rong, Y.; Lei, T.; Xu, J.; Huang, Y.; Wang, C. Residual stress modelling in laser welding marine steel EH36 considering a thermodynamics-based solid phase transformation. Int. J. Mech. Sci. 2018, 146–147, 180–190. [Google Scholar] [CrossRef]
- Dassault System. Abaqus Theory Manual; Version 6.7; SIMULIA: Johnston, RI, USA, 2007. [Google Scholar]
- Tsirkas, S.A.; Papanikos, P.; Kermanidis, T. Numerical simulation of the laser welding process in butt-joint specimens. J. Mater. Process. Technol. 2003, 134, 59–69. [Google Scholar] [CrossRef]
- Piekarska, W.; Kubiak, M.; Saternus, Z.; Stano, D.T. Numerical prediction of deformations in laser welded sheets made of X5CrNi18-10 steel. Arch. Metall. Mater. 2015, 60, 1965–1972. [Google Scholar] [CrossRef]
- Ahn, J.; Davies, C.M.; He, E.; Wimpory, R.C.; Chen, L.; Dear, J.P. Prediction and measurement of residual stresses and distortions in fibre laser welded Ti-6Al-4V considering phase transformation. Mater. Des. 2017, 117, 441–457. [Google Scholar] [CrossRef]
- Guoxiang, X.; Chuansong, W.; Xuezhou, M.; Xuyou, W. Numerical analysis of welding residual stress and distortion in laser+GMAW hybrid welding of aluminum alloy T-joint. Acta Metall. Sin. 2013, 26, 352–360. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Rohde, J.; Jeppsson, A. Literature review of heat treatment simulations with respect to phase transformation, residual stresses and distortion. Scand. J. Metall. 2000, 29, 47–62. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saternus, Z.; Piekarska, W.; Kubiak, M.; Domański, T. The Influence of Welding Heat Source Inclination on the Melted Zone Shape, Deformations and Stress State of Laser Welded T-Joints. Materials 2021, 14, 5303. https://doi.org/10.3390/ma14185303
Saternus Z, Piekarska W, Kubiak M, Domański T. The Influence of Welding Heat Source Inclination on the Melted Zone Shape, Deformations and Stress State of Laser Welded T-Joints. Materials. 2021; 14(18):5303. https://doi.org/10.3390/ma14185303
Chicago/Turabian StyleSaternus, Zbigniew, Wiesława Piekarska, Marcin Kubiak, and Tomasz Domański. 2021. "The Influence of Welding Heat Source Inclination on the Melted Zone Shape, Deformations and Stress State of Laser Welded T-Joints" Materials 14, no. 18: 5303. https://doi.org/10.3390/ma14185303
APA StyleSaternus, Z., Piekarska, W., Kubiak, M., & Domański, T. (2021). The Influence of Welding Heat Source Inclination on the Melted Zone Shape, Deformations and Stress State of Laser Welded T-Joints. Materials, 14(18), 5303. https://doi.org/10.3390/ma14185303





